Multiscale design of graphyne-based materials for high-performance separation membranes

Abstract

By varying the number of acetylenic linkages connecting aromatic rings, a new family of atomically thin graph-n-yne materials can be designed and synthesized. Generating immense scientific interest due to its structural diversity and excellent physical properties, graph-n-yne opened new avenues towards numerous promising engineering applications, especially for separation membranes with precise pore sizes. Having these tunable pore sizes in combination with their excellent mechanical strength to withstand high pressures, free-standing graph-n-yne is theoretically posited to be an outstanding membrane material for separating or purifying mixtures of either gas or liquid, rivaling or even dramatically exceeding the capabilities of current, state-of-art separation membranes. Computational modeling and simulations play an integral role in the bottom-up design and characterization of these graph-n-yne materials. Thus, the present review discusses the state of the art in modeling α-, β-, γ-, δ-, and 6,6,12-graphyne nanosheets for synthesizing graph-2-yne materials and 3D architectures thereof. We describe different synthesis methods and provide a broad overview of computational characterizations of graph-n-yne’s electrical, chemical, and thermal properties. We further review a series of in-depth computational studies that delved into the specifics of graph-n-yne’s mechanical strength and porosity that confer superior performance for separation and desalination membranes.

In the literary sense, describing an object as two-dimensional (2D) may evoke less than appealing qualities of lacking sufficient depth or complexity. Yet, in materials science and engineering, the properties of 2D materials are so exceptional and richly diverse that there was an explosion in both basic and applied research of these materials over the past two decades. This explosive growth was initiated when Andre Geim and Konstantin Novoselov published their seminal research on a remarkably simple but significant method for isolating one-atom thick monolayers of graphite, very well known by now as graphene. By repeatedly peeling and thinning graphite with adhesive tape, these research initiated a revolution in nanomaterials.^[1] Being extremely strong,^[2] stiff, atomically thin, and having exceedingly high thermal^[3] and electrical conductivity^[4] with unusual electronic properties,^[5] graphene was deemed so promising as an engineering material that Geim and Kim dubbed it the “Carbon Wonderland”.^[6] In fact, this notion can now be updated to be a “2D Wonderland” with the continuous discovery of elements and compounds that can be made atomically thin, spanning the III-V groups, as well as the transition metals along the periodic table.^[7] A high-throughput algorithm has even predicted that a thousand more compounds are potentially layered and can be easily exfoliable.^[8] Not to mention all the possible combinations of these 2D layered materials as if we would be combining them like playing cards. This is just the beginning.

While the 2D material library is constantly expanding with new elements and compounds, carbon remains truly the mainstay of this library as an old dog that learns new tricks, counting graphane, graphone, and graphyne amongst the ever-growing ranks of carbon-based 2D materials.^[9] Among them, graphyne, in particular, is generating immense interest in material engineering due to its structural diversity and excellent physical properties, which opens new avenues towards promising applications (Figure 1). The appellation “graphyne” was first coined by Baughman et al. in their semi-empirical quantum chemical study of planar sheets that are one-atom thick and uniformly populated by sp and sp² carbon atoms.^[10] More vividly, graphyne can be described as a lattice of benzene rings that are linked together with acetylenic (-C≡C-) bonds (Figure 1). By varying the number of these acetylenic linkages, as denoted by n, graph-n-yne sheets can be synthesized to achieve precise pore sizes, where the effective van der Waals pore diameter ranges from 2.2 Å in γ-graph-2-yne to more than 8.6 Å in γ-graph-6-yne and beyond. Having these tunable pore sizes in combination with their excellent mechanical strength to withstand high pressures, free-standing graph-n-yne has been theoretically posited to be an outstanding membrane material for separating or purifying mixtures of either gas or liquid, rivaling or even dramatically exceeding the capabilities of the current state-of-art separation membranes. If these theoretical predictions are translated into actual experimental devices, the dent in the cost of recovering scarce resources, such as pure water and helium, would be significant. This is especially pertinent for water desalination, where hefty costs are incurred due to the massive energy expenditure of squeezing water through semi-permeable membranes at high pressure.

Figure 1.

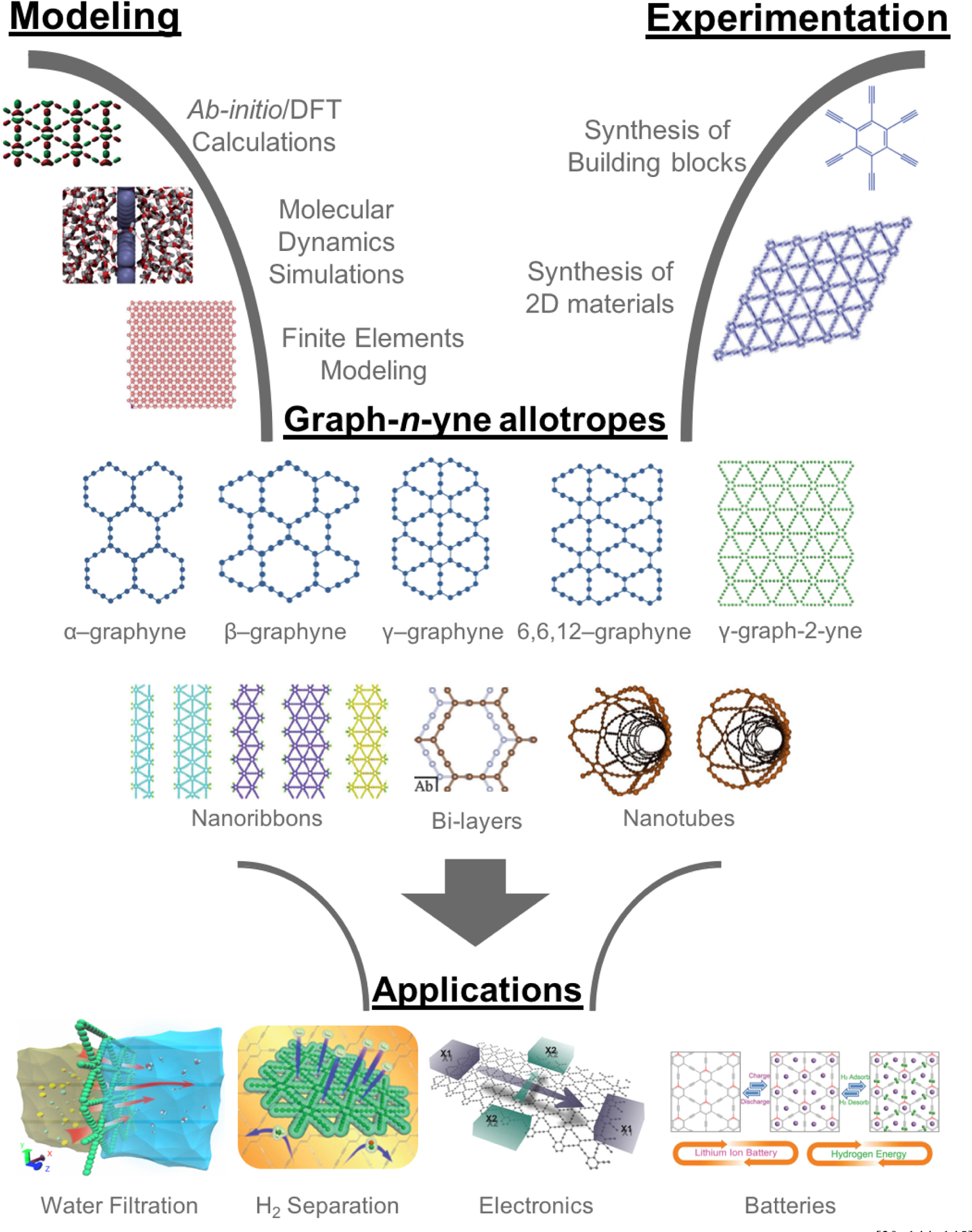
Graphyne – The multifunctional material of the future. Adapted from ^{[30, 144, 145]} with permission from American Chemical Society, from^{[11, 42, 43, 129]} with permission from Royal Society of Chemistry, from^[128] with permission from IOP Publishing, from^[143] with permission from Hindawi Publishing Corporation, from^[146] with permission from SAGE Publishing, and from^[147] with permission from American Institute of Physics.

Within this framework, the integral role of computational modeling and simulations in the bottom-up design and characterization of graph-n-yne materials cannot be understated, where simulations already determined the stability of α-, β-, γ-, δ-, and 6,6,12-graphyne nanosheets, nanoribbons, and nanotubes. The predictive capabilities of computational multiscale modeling have provided a strong basis for the pursuit and eventual development of techniques for synthesizing a wide array of γ-graph-2-yne materials and 3D architectures thereof (Figure 1). Herein, we describe different synthesis methods and provide a broad overview of the computational characterizations of graph-n-yne’s electrical, chemical, and thermal properties. In view of graph-n-yne’s potential as the main component of new revolutionary filtration membranes, we review in special depth the computational studies that delved into the specifics of graph-n-yne’s mechanical strength and porosity that confer superior performance for separation and desalination membranes. By traversing this exceptional region of the “Carbon Wonderland”, we hope to showcase the possibility that the future narrative of mitigating the scarcity of water and gas resources may indeed turn out to be two-dimensional.

2. Experimental Synthesis of γ-graph-2-yne

Synthesis of graphyne gradually matured over several decades, culminating in the successful fabrication of small, multi-layered sheets, nanotubes, and nanowires of γ-graph-2-yne.^[11–14] Prior to these milestones, several chemical pathways were proposed, and experimental evidence provided further proof of concept for producing small subunits of graphyne, despite the skepticisms arising from the expected reactivity of the acetylenic bonds.^[10,15–20] In particular, monolayers that resembled graph-2-yne were fabricated into a diverse array of 2D and 3D structures.^[21] These structures were synthesized by crosslinking monomers that contain aromatic and alkyne functional groups on SiO₂ and Si₃N₄ substrates, catalyzed by Mo and Cu. γ-graph-2-yne thin films with large areas up to 3.61 cm² were eventually synthesized by cross-coupling hexaethynylbenzene (HEB) monomers on Cu foil in the presence of pyridine (Figure 2A).^[11] The reaction was performed over 72 hours at 60 °C in an inert nitrogen atmosphere and the Cu foil served the dual purpose of catalyst and substrate for growth. The average thickness of the film was characterized by atomic force microscopy (AFM) to be 970 nm and the electrical conductivity was measured to be 2.516 × 10⁻⁴ S/m. These synthesis methods were developed further to create γ-graph-2-yne nanotubes with a wall thickness of 15 nm after annealing (Figure 2B).^[12] These nanotubes had a turn-on field and threshold field of 4.20 and 8.83 V/μm, which indicated their suitability for vacuum device applications. γ-graph-2-yne nanowires were also synthesized by a vapor-liquid-solid (VLS) growth process with a silicon slice as a substrate and ZnO nanorod arrays as catalysts (Figure 2C).^[13] The nanowires were approximately 0.6 to 1.8 μm in length, 20 to 50 nm in diameter, an electrical conductivity of 1.9 × 10³ S/m, and a mobility of 7.1 m²/Vs at room temperature. ZnO nanorod arrays were also used as catalysts with the VLS process to grow highly-ordered, large-area γ-graph-2-yne films, with a controllable number of layers.^[14] By reducing the quantity of graph-2-yne powder during the process, the thickness of the samples could be decreased down to 22 nm. The largest film obtained by these means had an area greater than 4.8 mm² with an estimated thickness of 540 nm. The conductivity was on the order of 28 S/m with field effect mobility that reached 1 m²/Vs. Current state-of-art techniques reduced the thickness even further to an unprecedented dimension of 3.0 nm, corresponding to few-layer γ-graph-2-yne.^[22,23] The first method synthesized nanosheets of single-crystalline γ-graph-2-yne by placing a mixture of HEB, dichloromethane, and toluene on the surface of an aqueous solution with a copper catalyst at room temperature and an argon atmosphere.^[22] This method generated crystalline, hexagonal domains with ABC-stacked layers. The second method utilized pristine graphene as the surface template on an SiO₂/Si substrate with Hiyama coupling.^[23,24] This strategy was also extendable to surface templates of hexagonal boron nitride (hBN) as it resembled graphene structurally. These recent developments will pave the way towards roll-to-roll synthesis of γ-graph-2-yne membranes required in large-scale industrial applications, especially for desalination and gas separation.

Figure 2.

Different γ-graph-2-yne structures were chemically synthesized and characterized, such as (A) films (reprinted from ^[11] with permission from Royal Society of Chemistry),^[11] (B) tubes (reprinted from^[12] with permission from American Chemical Society),^[12] and (C) wires (reprinted from^[13] with permission from Royal Society of Chemistry).^[13]

3. Electronic Properties

The electronic properties of graph-n-yne depend on the actual topology of the layer. Slight differences in the band structure and electronic band gap of the material depend on how the acetylenic bonds adopt a distribution that leads to α-, β-, γ-, δ-, and 6,6,12-graphyne nanosheets. Density Functional Theory (DFT) calculations with non-equilibrium Green functions (NEGF) showed that 6,6,12-graphyne presents two Dirac cones located at different points in the Brillouin zone, leading to a strong directional transport property that could be manipulated by the application of an external strain.^[25] Similar to graphene, α-graphyne had a Dirac cone in its electronic structure at the K and K’ points of the Brillouin zone, while β-graphyne also had a single Dirac cone located in a line between the Γ and M points. Thus, both α-graphyne and β-graphyne behaved as zero-band-gap semiconductors or semimetals,^[26] in contrast to 6,6,12-graphyne which was suggested to have a carrier mobility that was even larger than that of graphene, according to DFT calculations.^[27] The existence of macrocyclic conjugation of graphyne cores was expected to provide superior electronic transport conductance.^[28] Several efforts were devoted to opening the band gap of graphyne allotropes with zero-band-gap electronic structures, a property that is similar to pristine graphene. In this regard, ab initio calculations on the electronic structure and the lattice stability of pristine and functionalized α-graphyne systems described two mechanisms leading to gap opening in the Dirac-Fermion electronic spectrum of these systems: symmetry-breaking connected with the lattice instabilities and partial incorporation of an sp³ character in the bonding network.^[29] Large carrier mobility was also observed for graph-2-yne sheets and nanoribbons,^[30] for which different types of functionalization^[31] and transverse electric fields^[32] was implemented to tune the band gap. Further details on the chemical properties and modifications of graph-n-ynes are reviewed in Section 4 herein.

4. Chemical Properties

The intrinsic bonding scheme of graph-n-yne implies its suitability to undergo different chemical reactions, especially for hydrogenating graph-n-yne’s characteristic electron-rich triple bonds that are uniformly distributed throughout graph-n-yne’s chemical structure. This bonding feature encompasses a chemical richness that was an inherent challenge for the synthesis and stability of large graph-n-yne sheets, but this feature also provides an interesting route for further crosslinking and functionalization. Thus, characterizing the chemical reactivity of graph-n-yne materials provides guidance for developing new nanoarchitectures derived from graph-n-yne.

4.1. Theoretical Chemical Reactivity: Fukui Analysis

Due to the dearth of chemical characterizations for graphyne in current literature, the likelihood of graphyne to undergo nucleophilic or electrophilic attack upon chemical reaction was determined here by analyzing the reactivity of a small γ-graphyne flake according to the principles of conceptual DFT.^[33] To this end, the dual descriptor of the Fukui function was calculated to identify local reactivity areas in graphyne model molecules (Figure 3). The B3LYP hybrid functional, together with 6–31G (d) basis set (Figure 3) was used, as implemented in the Orca computational package.^[33–35] Isovalues of +0.0005 and −0.0005 were used to visualize the reactive sites with VMD software.^[36] Due to the presence of two-degenerated orbitals in the electronic structure of the graphyne molecule, the highest occupied molecular orbital (HOMO) and the HOMO-1 were combined for the Fukui function calculations, since their close proximity in energy makes it impossible to discern the orbitals from which an electron would be removed upon electrophilic attack. The same reasoning applies to the two-degenerated lowest unoccupied molecular orbital (LUMO) and the LUMO+1 orbital, which were also combined in the calculation of the Fukui function. Thus, the dual descriptor of the Fukui function, was calculated from the electron densities of the merged HOMOs and LUMOs, as just described. This approximation has been proved accurate for estimating the dual descriptor of the Fukui function.^[37]

Figure 3.

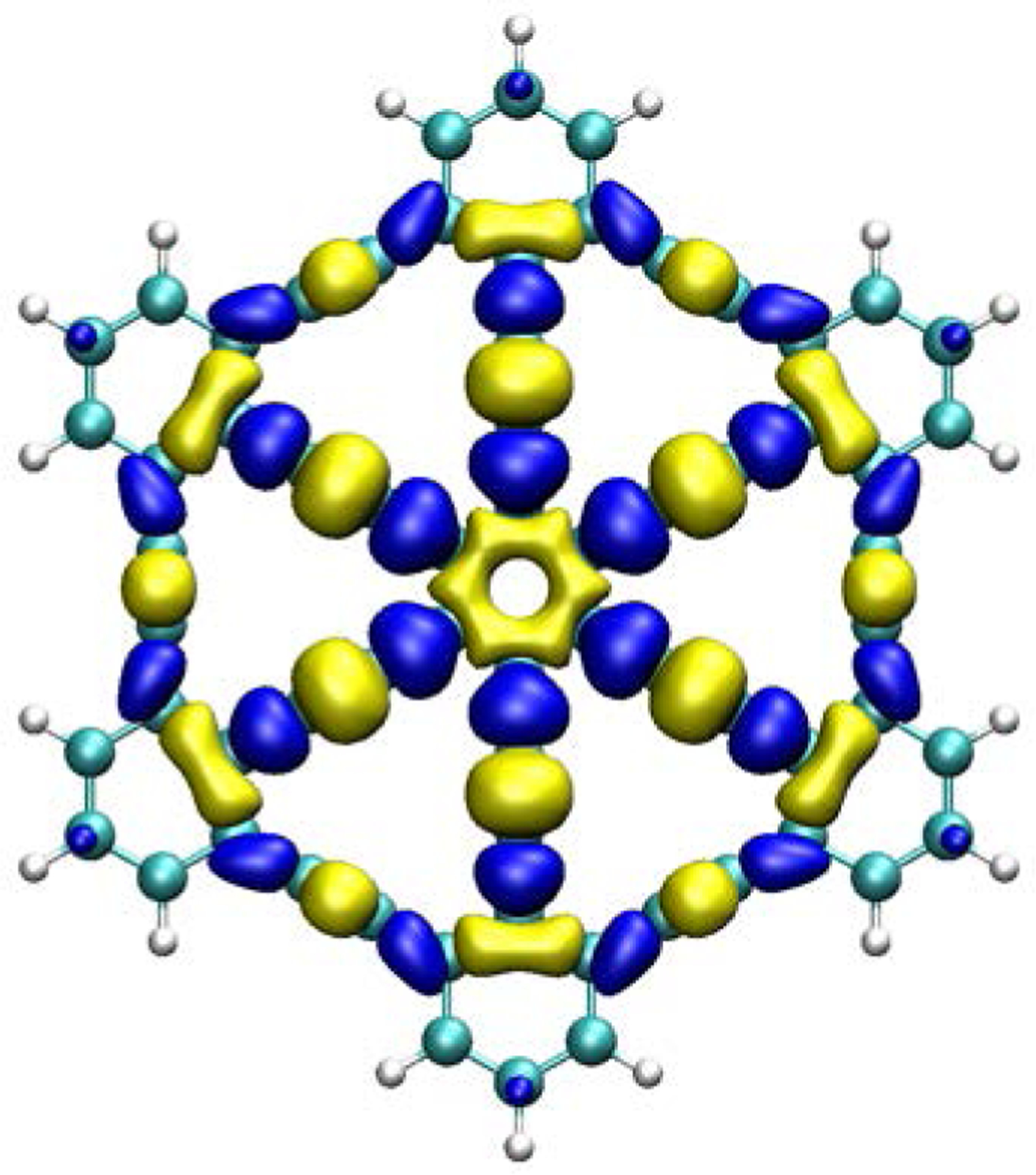
Dual descriptor Fukui analysis of graphyne with the B3LYP functional, plotted with isovalues of 0.0005 and −0.0005.

4.2. Chemical Modification of Graphyne and Graph-2-yne

Several chemical modification methods, particularly through chemical functionalization and doping, have been studied.^[31,38–45] These studies have helped build insights into how 2D carbon materials like modified graphyne and graph-2-yne may serve as promising candidates for a large number of applications, including semiconductor devices,^[31,38–41] energy storage systems,^[42] and separation/purification membranes for gas purification processes.^[43–45] Various studies have demonstrated the ability to tune the band structure in graphyne and graphdiyne through numerous chemical modification methods, showing the potential for tunable band gaps for semiconductor material applications.^[31,38–41] Specifically, recent DFT-based studies have focused on the effects of halogenation (F, Cl, Br) and hydrogenation of graph-2-yne,^[38] such as fluorine functionalization of both graphyne and graph-2-yne,^[39] CCl₂ additions (both α-graphyne and β-graphyne)^[40], and with N, O, and hydroxyl groups on graph-2-yne.^[31]

DFT calculations found that with hydrogenation and halogenation, graph-2-yne may be more suitable than graphene for electronic applications because of favorable band gap tunability and molecular grouping characteristics, as it has been discussed before. Specifically, their study found these chemically-modified versions of graph-2-yne to both have superior band gap modification abilities (functionalized graph-2-yne was shown to be tunable by a range of 5 eV, while hydrogenated graphene was shown to be tunable by a range of around 3 eV) and have a lower likelihood than graphene to experience halogen grouping.^[38] The effects of fluorination were also studied for both graphyne and graph-2-yne at various sites of the structure. It was shown that an increase in fluorination reduced the stability of the material and that the location of the added fluorine changed the band gap value. Graphyne with no modifications showed a band gap value of 0.454 eV, while an increase in band gap value was observed with the addition of fluorine (chain-location fluorine showed 1.647 eV, ring-location fluorine showed 3.750 eV, and fluorine at both the ring and chain showed 3.318 eV). The study also used projected density of states and Crystal Orbital Hamilton Population techniques to understand the orbital and bonding characteristics of the system better, showing a distinction between the C-C and C-F atom interfaces, i.e. carbon-carbon (bonding) and carbon-fluorine (anti-bonding).^[39]

Further DFT calculations demonstrated that the concentration of CCl₂ on both α- and β-graphyne affected the band gap value of the material. Specifically, the amount of CCl₂ determined the band gap value: when the number of CCl₂ molecules increased from 1 to 8, the band gap value decreased from approximately −5.1 eV to −2.4 eV for α-graphyne and −7.5 eV to −3.5 eV for β-graphyne. The calculations were made with local density approximation (LDA) and generalized gradient approximation (GGA), and no significant differences were noted between the two.^[40] Graph-2-yne synthesized through cross-coupling reactions were analyzed using both DFT and x-ray emissions spectroscopy (XES) and x-ray absorption spectroscopy (XAS).^[31] The band gaps of three samples with varying chemical content and varying thickness were measured: a band gap of 0.6 eV was measured for a 1 μm thick graph-2-yne sample with 34% pyridinic nitrogen, 16% oxygen, and 50% hydroxyl group. A 2 μm sample of 12% pyridinic nitrogen, 54% oxygen, and 34% hydroxyl sample of graphdiyne showed a band gap of 0.8 eV. The third sample with 5 μm thickness, 36% pyridinic nitrogen, 8% substituted, 22% oxygen, and 34% hydroxyl showed a band gap of 0.9 eV. There was good agreement between DFT-calculated results and experimental results of the three samples, showing the effects of synthesis techniques and sample thickness with band gap values. Results from this study suggested that the band gap values of graph-2-yne might be tunable according to the sample’s thickness.^[31]

DFT simulations were performed to examine the effects of adding 5.5 – 33.3% carbonyl and carboxylic groups to the edges of graphyne and graph-2-yne nanoflakes, as well as with 5.5 – 33.3% nitrogen and sulfur doping concentration. The band gap could be controlled at a value of around 1.20 eV with carbonyl edge functionalization, as well as from 0.11 to 0.68 eV by changing the amounts of N and S doping. However, the band gap was not affected by the number of carboxylic functional groups. Moreover, this study revealed that the nitrogen-modified molecules exhibit certain energy shifts within the material that would make them good candidates for UV protection materials.^[41] In addition to promising applications as semiconductors, chemically-modified graphyne was demonstrated to have great potential for energy storage applications.^[42] Using a multi-scale computational approach of DFT, MD, and grand canonical ensemble Monte Carlo simulations, boron-modified graphyne material exhibited the potential for lithium and hydrogen storage capabilities in applications as batteries.^[42] Specifically, by adding boron to graphyne, the material had approximately 1,130 mAhg⁻¹ of lithium storage capacity, making it a great candidate for lithium battery applications. The boron-modified graphyne also showed great promise for hydrogen storage as well.^[42]

While a more detailed review of graphyne-based separation membranes will be provided in Section 7, we briefly mention the excellent capabilities of chemically functionalized graphyne for gas separation. Chemically modified graphyne and graph-2-yne were demonstrated to be useful for separating hydrogen as well.^[43–45] Through DFT simulations, the addition of nitrogen to graph-2-yne^[43] as well as with the addition of a positive charge^[45] were studied for hydrogen purification applications. The addition of nitrogen to form N-graph-2-yne nano-meshes improved the separation of hydrogen from both methane and CO by increasing the permeation of CO by 15%.^[43] The separation of CO₂, N₂, CH₄ via graph-2-yne modified with H, F, and O atoms was examined with combined DFT and MD methods. Hydrogen-modified graphdiyne was a poor candidate for these types of separation applications due to high-energy barriers. However, both fluorine- and oxygen-modified graph-2-yne demonstrated the ability to successfully separate CO₂ and N₂ from CH₄, achieving a separation factor of 8.9–57 for CO₂ at high temperatures of 600 K versus a typical value of around 6 in industrial applications, as well as a 10⁵-10⁷ factor increase in permeability of CO₂ and N₂. Additionally, at low temperatures that were less than 300 K, oxygen-modified graph-2-yne also showed good separation properties.^[44] Adding a positive charge to graph-2-yne could reduce the need for complicated synthesis techniques for hydrogen separation. The added charge to graph-2-yne not only increased the permeation of CO by 32% and CH₄ by 7%, but also decreased the permeation of hydrogen, thus increasing the ability for hydrogen refinement.^[45]

5. Thermal Properties

5.1. Computational Modeling of Thermal Properties

Three distinct MD simulation techniques are frequently employed to determine the thermal properties of materials. Firstly, in the equilibrium method, also known as equilibrium molecular dynamics (EMD) or the Green-Kubo (GK) method,^[46] the integral of the heat current autocorrelation function (HCACF) is used to determine the material’s thermal transport coefficients, such that the thermal conductivity (TC) is given by

$$\lambda =\frac{1}{V{k}_B{T}^2}\underset{0}{\overset{\infty }{\int }}\langle J_s\left(t\right)J_s\left(0\right)\rangle dt$$ (Equation 5.1)

where the heat flux is

$$J_s=\frac{d}{dt}\sum _{i=1}^{N_a}{s}_i\frac{1}{2}\left(m_i{v}_i^2+\sum _{j\ne i}U\left(r_{ij}\right)\right)$$ (Equation 5.2)

Here, N_a denotes the number of particles or atoms in the system; m_i the mass of a particle i; s_i the x, y, or z-component of the position vector of particle i; v_i(t) the velocity of particle i at time t; U(r_ij) the system’s governing potential function; and k_B the Boltzmann’s constant. Therefore, through long equilibrium simulations of the system of interest, the thermal conductivity (TC) of the system can be obtained once the integral of the HCACF has plateaued (Figure 4A).^[46]

Figure 4.

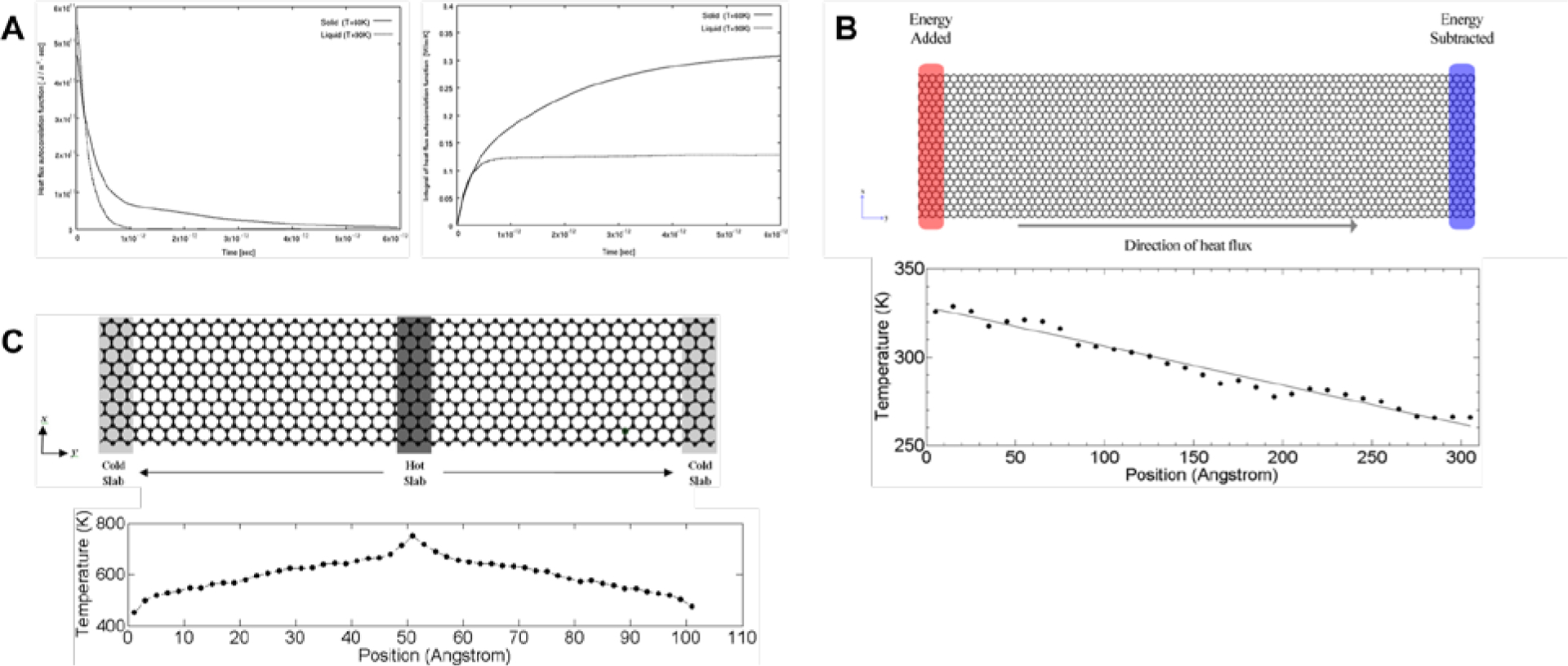
(A) Equilibrium molecular dynamics simulations to determine the thermal conductivity by equilibrating the heat current autocorrelation function (left) and its integral (right).^[46] Reprinted from^[46] with permission from Springer Nature. (B) Direct nonequilibrium molecular dynamics method which adds and subtracts energy from reservoirs at two ends of the system (top), thereby obtaining a linear temperature gradient across the system at steady state (bottom).^[47,48] Reprinted from^[48] with permission from Springer Nature. (C) Reverse nonequilibrium molecular dynamics method which swaps energy from the “hot” slab to the “cold” one (top), thereby generating an almost bilinear temperature gradient across the system at steady state (bottom).^[66] Reprinted from^[66] with permission from IOP Publishing.

Secondly, two nonequilibrium methods are used predominantly: the direct and the reverse nonequilibrium molecular dynamics (NEMD). In direct NEMD, a temperature gradient is directly imposed on the system of interest by maintaining “hot” and “cold” reservoirs at each end of the simulation box by adding (subtracting) non-translational kinetic energy to the “hot” (“cold”) reservoir, while conserving the aggregate momentum (Figure 4B).^[47,48] Upon equilibration till a linear temperature gradient is achieved in the direction of heat flux (Figure 4B), the TC can then simply be determined from Fourier’s Law:

$$\lambda =\frac{J_s}{dT/ds}$$ (Equation 5.3)

where J_s can be determined in a similar manner as (Equation 5.2). On close examination of Fourier’s law, one can envision imposing a heat flux instead, while measuring the corresponding temperature gradient once the system attains equilibrium. This method is known as the reverse NEMD (RNEMD).^[49] Here, the system of interest is divided into slabs in the direction of heat flux. The first slab is designated as the “cold” slab, while the slab in the middle of the system is designated as the “hot” slab (Figure 4C). Heat flux is imposed by identifying the atom that has the highest kinetic energy (the “hottest” atom) within the “cold” slab, then swapping its energy with that of the atom with the lowest kinetic energy (the “coldest” atom) within the “hot” slab. By repeating this swap periodically, a temperature gradient will be induced across the system over time due to the flux from the “hot” slab to the “cold” one (Figure 4C). The flux is determined by

$$J_s=\frac{1}{2tA}\sum _{N_{\mathit{\text{swap}}}}\frac{m_i}{2}\left(v_{\mathit{\text{hot}}}^2-v_{\mathit{\text{cold}}}^2\right)$$ (Equation 5.4)

Here, t is the total simulation time; A the cross-sectional area of the system that is orthogonal to the direction of heat flux; N_swap the total number of swaps; m_i the atomic mass; and v_hot and v_cold the velocities of the “hot” and “cold” atoms respectively. The temperature profile of the system at steady state can be sampled by time-averaging the temperature of each slab:

$$\frac{3}{2}{N}_{slab}{k}_{B}T=\frac{1}{2}\langle \sum _i^{N_{\mathit{\text{slab}}}}{m}_i{v}_i^2\rangle$$ (Equation 5.5)

where N_slab is the number of atoms in the slab and T_slab is the temperature of the slab. Finally, the average temperature gradient is determined from linear regression of the temperatures of the slabs that display linear variation of temperature with distance and the thermal conductivity will again be determined by Fourier’s Law in (Equation 5.3).

However, there is a crucial caveat when using NEMD techniques for determining the TC of any material system. As the simulation box sizes are generally finite and much smaller than the typical phonon mean free path (MFP) of crystalline systems, the TC calculated with NEMD methods will be limited by the size of the simulation box.^[50] Therefore, to derive the bulk thermal conductivity for graphene or graphyne allotropes, a systematic study must be performed by determining the TC at several length scales first, then linearly extrapolating the plot of 1/λ vs. 1/L to theoretically infinite length scales.^[51]

5.2. Thermal Properties of Graph-n-yne Allotropes

Due to widely varying operating temperatures and pressures of high-performance separation membranes that depend on their applications, the thermal properties of graphyne as an engineering material must be clearly understood to minimize energy losses while maintaining their structural stability. Numerous studies of the thermal conductivity (TC) along both the zigzag and armchair directions of α-, β-, γ-, δ-, and 6,6,12-graphyne nanosheets, nanoribbons, and nanotubes were determined with combinations of RNEMD or EMD simulations with the AIREBO or REBO interatomic potentials.^[52–59] These graphyne variants had significantly reduced TC compared to pristine graphene and carbon nanotubes (CNTs), even when extrapolated to infinite lengths (Table 1, Figure 5A). A number of fundamental reasons were proposed to explain this dramatic reduction in TC. One crucial reason was the lower stiffness of the sp bonds present in graph-n-ynes’ acetylenic linkages, compared to sp² bonds of pristine graphene and CNTs.^[52–54] This was affirmed through measurements of the binding energy of graph-2-yne at 300 K.^[53] The aromatic ring’s sp² hybridized atoms had an estimated binding energy of 7.8 eV/atom, while the acetylenic linkages’ sp hybridized atoms had a binding energy of 5.66 eV/atom.

Table 1.

Thermal conductivity for nanosheets of graphyne allotropes. Quantum corrected values are shown wherever available. Chirality refers to the chirality in the direction of heat flux in NEMD simulations.

Interatomic Potential	Simulation Method	Length (nm)	Width (nm)	Graphyne Structure Type	Chirality	Thermal Conductivity (W/m·K)
[52]AIREBO	RNEMD	20	20	α-graphyne	Zigzag	12
				α-graphyne	Armchair	12
				β-graphyne	Zigzag	10
				β-graphyne	Armchair	9
				γ-graphyne	Zigzag	18
				γ-graphyne	Armchair	18
				6,6,12-graphyne	Zigzag	16
				6,6,12-graphyne	Armchair	12
[53]AIREBO	EMD	7.1	6.8	γ-graphyne	-	31
				γ-graph-2-yne	-	15
				γ-graph-3-yne	-	10
[54]REBO	RNEMD	20	20	γ-graphyne	Zigzag	19.7
				γ-graphyne	Armchair	19.4
				δ-graphyne	Zigzag	12.2
				δ-graphyne	Armchair	12.1
[57]AIREBO	RNEMD	570	21	γ-graphyne to γ-graph-10-yne	Zigzag	55 to 8
				γ-graphyne to γ-graph-10-yne	Armchair	54 to 8
		50 to 570	21	γ-graphyne	Zigzag	35 to 55
				γ-graphyne	Armchair	35 to 54
				γ-graph-5-yne	Zigzag	10 to 12.5
				γ-graph-5-yne	Armchair	10 to 12.5
				γ-graph-10-yne	Zigzag	7.5 to 7.6
				γ-graph-10-yne	Armchair	7.5 to 7.6
		l∞	21	γ-graphyne	Zigzag	64.3
				γ-graphyne	Armchair	63.4
				γ-graph-5-yne	Zigzag	12.9
				γ-graph-5-yne	Armchair	13.5
				γ-graph-10-yne	Zigzag	8.4
				γ-graph-10-yne	Armchair	8.8
		500	l∞	γ-graphyne	Zigzag	54.8
				γ-graphyne	Armchair	54.1
				γ-graph-5-yne	Zigzag	12.3
				γ-graph-5-yne	Armchair	12.4
				γ-graph-10-yne	Zigzag	8.1
				γ-graph-10-yne	Armchair	8.4

Figure 5.

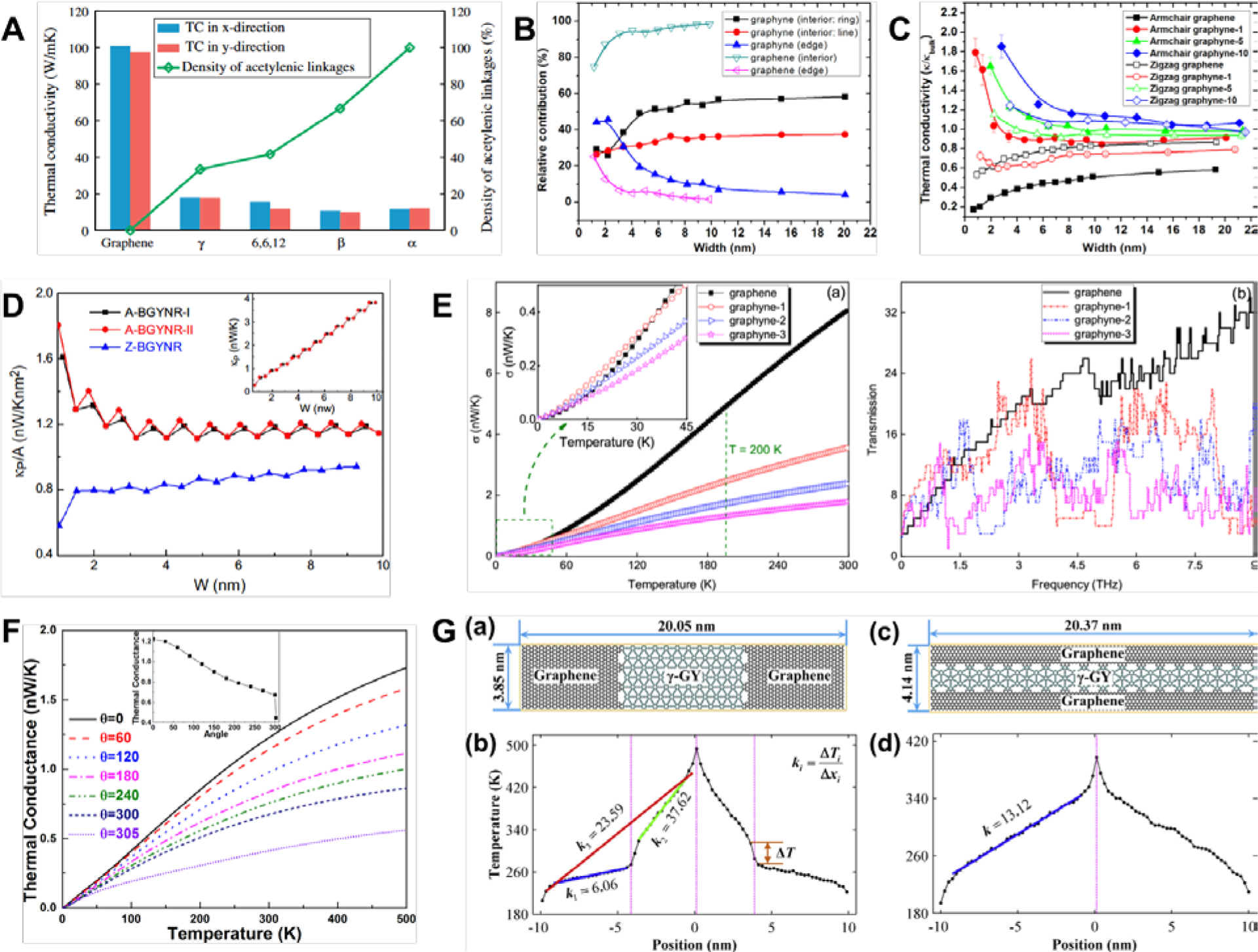
(A) TC of α-, β-, γ-, and 6,6,12-graphyne-based nanosheets were all several times lower than that of graphene. Only 6,6,12-graphyne showed significant anisotropy with lower conductivity in the armchair direction.^[52] Reprinted from^[52] with permission from Elsevier. (B) Relative contributions of armchair γ-GYNRs’ interior regions and edges to the total heat flux as a function of NRs’ width.^[57] Reprinted from^[57] with permission from Elsevier. (C) TC of armchair-edged γ-GYNRs had higher TC than zigzag-edged, which runs counter to the trend in GNRs. Armchair-edged γ-GYNRs’ TC also increased rapidly as the NR width decreased below the threshold of 2 nm.^[57] Reprinted from^[57] with permission from Elsevier. (D) Oscillatory behavior in armchair edges of β-GYNR due to the stepwise dependence of the thermal conductance with width.^[53] Reprinted from^[53] with permission from IOP Publishing. (E) γ-graph-n-yne’s thermal conductance had a quadratic dependence with the temperature at temperatures below 60 K (left) and variation of the transmission coefficient with frequency (right).^[69] Reprinted from^[69] with permission from IOP Publishing. (F) Thermal conductance of γ-GYNRs decreases with both decreases in temperature as well as increases in the applied rotational strain.^[70] Reprinted from^[69] with permission from AIP Publishing. (G) Temperature distribution across graphye-graphene heterojunctions can be either bilinear (left) or linear (right).^[58] Reprinted from^[58] with permission from Elsevier.

Furthermore, this difference in the bond structure and stiffness strongly affected the vibrational properties. In a comprehensive analysis, Jing et al.^[57] found that increasing acetylenic linkages led to a concomitant increase in the number of peaks in the low-frequency region of graph-n-yne’s vibrational density of states (VDOS), as the acetylenic linkages were responsible for the low frequency response. In contrast, there were no significant changes in the high-frequency regions as these were only affected by variations in the aromatic rings. This mismatch in the lattice vibrations led to the dramatic reduction in graph-n-yne’s TC. Moreover, the contribution of thermal energy transport in acetylenic linkages increased in tandem with their increasing numbers, thereby decreasing the contribution of aromatic rings as the numbers of these rings remained constant (Figure 5B). Graphene’s total heat flux was largely contributed by out-of-plane vibrations, i.e. the soft flexural modes dominated in phonon transport. In contrast, longitudinal modes were dominant for thermal transport in graph-n-yne, where the contributions from flexural modes decreased and longitudinal modes increased as n increased until a plateau was attained at n > 5.^[57] This vibrational analysis explained numerous findings of monotonically decreasing TC with increasing numbers of acetylenic linkages,^[53,54,57] while vibrational analysis of graph-n-yne nanotubes (GYNTs) arrived at the same conclusions as well.^[55] Additionally, the averaged group velocity of low-frequency phonons in graph-2-yne was found to be only 3.8 km/s which was a drastic reduction from the velocity of 13.8 km/s in pristine graphene.^[53] This further emphasized the outsized influence that low-frequency phonon modes had on the thermal properties of graph-n-ynes.

In particular, in a detailed comparison of the thermal properties of α-, β-, and γ-GYNTs with CNTs,^[56] analysis of the phonon DOS showed that increased percentages of acetylenic bonds correspondingly increased the number of high-energy phonon modes as the higher stretching frequency of these bonds became more dominant. There were increases in scattering events in tandem with the widening of the characteristic peaks in the phonon DOS as temperatures increased. Both zigzag and armchair γ-GYNTs also had the high phonon group velocities for all polarizations. However, GYNTs generally had lower longitudinal acoustic (LA) phonon relaxation times compared to CNTs, where a power law, τ∝ν^-n, suitably described the dependence of relaxation time on the frequency and the order of dependence was α-GYNTs > β-GYNTs > γ-GYNTs > CNTs. The mean free paths (MFPs) were also much lower than CNTs at all polarizations. Similarly, increased acetylenic bonds decreased the MFPs such that α-GYNTs had the smallest value. The Debye temperature and volumetric heat capacities were also lower in GYNTs than CNTs.

With the exception of 6,6,12-graphyne nanosheets which had lower TC in the armchair direction,^[52] minimal differences were found in the TC along the armchair or zigzag direction for infinitely-wide nanosheets (Table 1, Figure 5A). Likely a result of its structure having lower rotational symmetry, 6,6,12-graphyne nanosheets had stronger anisotropy in its mechanical, electronic, and thermal properties.^[60,61] The independence of the TC from chirality was similarly found in graphene nanosheets.^[47,62] In contrast, there was strong directional dependence of thermal conductivity for pristine graphene nanoribbons (GNRs), where the TC tended to be significantly higher in the zigzag direction by between 15% to more than 50%.^[63–67] Interestingly, the opposite was found for γ-graph-n-yne nanoribbons (γ-GYNRs) where the TC in the armchair direction was approximately 25% higher than in the zigzag direction until there were six acetylenic linkages (Table 2).^[58] Subsequent studies verified this phenomenon (Figure 5C),^[57,59] and non-equilibrium Green’s function was applied to understand the detailed mechanisms underlying the edge effects.^[68,69]

Table 2.

Thermal conductivity for nanoribbons of graphyne allotropes. Quantum corrected values are shown wherever available.

Interatomic Potential	Simulation Method	Length (nm)	Width (nm)	Graphyne Structure Type	Nanoribbon Edge Chirality	Thermal Conductivity (W/m·K)
[58]REBO	RNEMD	20.06	3.84	γ-graphyne to γ-graph-6-yne	Armchair	23.1 to 12.8
		20.06	3.84	γ-graphyne to γ-graph-6-yne	Zigzag	17.5 to 11.5
		l∞	3.84	γ-graphyne	Armchair	31.43

The thermal conductance in narrow γ-GYNRs with zigzag edges exhibited a stepwise dependence on its width and it localized more lattice vibrations compared to armchair edges, leading to a less dispersive phonon spectrum with fewer phonon bands at any particular frequency.^[68] As a result, zigzag-edged GYNRs had a lower phonon transmission than armchair-edged GYNRs as the phonon transmission coefficient is equivalent to the number of phonon bands at that particular frequency in the ballistic transport regime.^[68] In contrast, although the thermal conductance of β-GYNRs was anisotropic, zigzag edges had lower thermal conductance compared to two separate configurations of armchair edges.^[69] In computations with the non-equilibrium Green’s function method, armchair β-GYNRs’ thermal conductance normalized by their cross-sectional area had an oscillatory behavior as a function of their width, whereas this behavior was muted with zigzag edges. The oscillatory behavior in armchair edges was due to the stepwise dependence of the thermal conductance with width (Figure 5D), while zigzag edges had a diminished contribution to the thermal transport.^[69] By analyzing the phonon DOS at the edges and the central region of armchair β-GYNRs, increasing width added more phonon modes but the transmission of these new modes were profoundly inhibited by the width at the narrowest region of the NRs, thus effectively preventing their contribution to the thermal transport and leading to the stepwise dependence on width.^[69]

More intriguingly, the TC of γ-GYNRs increased substantially as the width decreased, especially below a critical value of 2 nm (Table 2, Figure 5B and C).^[57] This strongly contrasted with the opposite trend found in GNRs, where the TC dropped instead. Below the critical width, γ-GYNRs’ edge atoms contributed significantly to the overall thermal transport due to the localization of the flux at the edge atoms, hence this effect diminished as the width increased beyond the critical value. This heat flux localization arose from ineffective scattering of these phonon modes at the boundaries.^[57] The dependence of γ-GYNTs’ TC with its diameter had also been examined.^[55] The TC of γ-graphyne NTs was invariant with diameter above the critical threshold of 2nm. Below this threshold, its TC rose steeply in tandem with decreasing diameter. Similarly, γ-graph-10-yne NTs’ TC was mostly independent of both chirality and changes in diameter ranging from 2 to 18 nm (Table 3).^[55]

Table 3.

Thermal conductivity for nanotubes of graphyne allotropes. Quantum corrected values are shown wherever available.

Interatomic Potential	Simulation Method	Length (nm)	Diameter (nm)	Graphyne Structure Type	Chirality	Thermal Conductivity (W/m·K)
[55]AIREBO	RNEMD	500	3.4	γ-graphyne to γ-graph-10-yne	zigzag	38 – 8.24
				γ-graphyne to γ-graph-10-yne	armchair	29 – 7.04
[56]REBO	EMD	50	15.4	α-graphyne	Zigzag	7.6
		50	15.56	α-graphyne	Armchair	7.6
		50	15.72	β-graphyne	Zigzag	7.5
		50	15.13	β-graphyne	Armchair	7.5
		50	15.19	γ-graphyne	Zigzag	10.7
		50	15.34	γ-graphyne	Armchair	10.7

Numerous studies had also examined the influence of temperature on the TC of graphyne allotropes, where the general consensus was that the TC was significantly reduced as the temperature rose.^[52–56] At extremely low temperatures below 60K, γ-graph-n-yne’s thermal conductance had a quadratic dependence with temperature, thus behaving similarly to graphene (Figure 5E). Below 30K, the γ-graph-n-yne’s thermal conductance was even predicted to be approximately equivalent to graphene.^[53] This anomalous thermal conductance was attributed to graphyne have a frequency-dependent transmission coefficient that was higher than graphene in the low-frequency regions of 0.15–1.5 THz and 2.45–2.65 THz, while the reverse was true for the higher frequency region beyond 4 THz (Figure 5E). Therefore, low-temperature thermal conductance was higher as low-frequency phonons contributed the most. In δ-graphyne, the TC increased approximately linearly as the temperature decreased from 900 to 150 K.^[54] Likewise at these higher temperatures, both armchair and zigzag γ-graphyne nanosheets displayed the same trend of declining TC with increasing temperature in the range of 200 K and 800 K, dropping by 37.5% and 41.7% respectively.^[52] Strangely, γ-GYNRs showed the opposite trend of decreasing thermal conductance with decreasing temperature, which was fundamentally attributed to the reduced excitation of phonon modes as the temperature decreased.^[68] Further comparisons ought to be performed with a consistent set of parameters, force fields, and simulation methods to resolve these conflicting results. The TC of both armchair and zigzag α-, β-, and γ-GYNTs slightly decreased below 150K if quantum-corrections were applied, but the general trend was still an increasing TC as the temperature decreased from 400 to 150 K.^[56]

A number of other methods to tune the thermal properties of graphyne allotropes had also been proposed, particularly by applying lateral and rotational strain.^[52,54,70] Application of both uniaxial and biaxial strain on γ-graphyne nanosheets decreased the TC, although the change is marginal if the strain small. Furthermore, the impact of strain was more evident if the TC was measured in the armchair direction. The TC of δ-graphyne nanosheets also showed the same decreasing trend with applied strain, which also affected the TC measured in the armchair direction more than the zigzag direction.^[54] Analysis of the VDOS showed softening of the high-frequency peaks as the amount of strain increased. Application of rotational strain also greatly influenced the TC of γ-GYNRs in a similar manner as applying plane strain (Figure 5F).^[70] With the NEGF method while neglecting phonon (electron)-phonon interactions, thermal conductance decreased monotonically with increasing twist angles from 0° to 300°, although the effect diminished as the temperature decreased to 0 K.^[70] However, the precise mechanism of such strain engineering has not been fully elucidated in the literature, although it is speculated that the application of strain decreases the material stiffness while increasing the lattice anharmonicity, thereby reducing the phonon group velocity, mean free path, and the specific heat of each propagating phonon mode.^[71,72] Construction of graphyne-based heterostructures was also proposed for modulating the thermal properties.^[58] As the bond lengths and the shapes of the unit cells of graphene and γ-graph-n-yne are largely similar, heterojunctions can be constructed with these two allotropes to obtain an interface that was perfectly matched (Figure 5G). Depending on the construction, the temperature gradient could either be bilinear or fully linear but with increased TC.

Considering the large body of research into the thermal properties of 1D and 2D graphyne-based materials, comparatively little to no studies have examined the effects of topological defects in detail, similar to what has been done in numerous studies for graphene^{[47,51,66,73–75]}. Furthermore, it will be of considerable interest to the community if further computational simulations of larger 3D structures of graph-n-yne can be performed to guide the design of nanoscale 3D thermoelectric devices, especially since experimental synthesis had been achieved. Interestingly, the natural thermal fluctuation of graphyne allotropes and their stability in various solvents are also not extensively characterized so far in the literature, in contrast to the significant body of data available for graphene. These are critical areas of future research to advance our understanding of the fundamental properties of graphyne.

5.3. Thermal Devices

As a result of the unique thermal and electronic properties detailed herein, several studies considered the application of graphyne in phonovoltaic and thermoelectric devices for energy conversion.^{[56,69,76–80]} Similar in function to photovoltaic devices, phonovoltaic devices convert energy from phonons into electrical currents, where electron-hole pairs generated by harnessing nonequilibrium optical phonons that are more energetic than the material’s band gap. In particular, zigzag α-GYNTs that had diameters of 2.22 nm and 2.89 nm fulfilled the requirements for such phonovoltaic devices as the direct band gap could be excited by the optical phonons while the energy was an order of magnitude higher than the thermal energy at 300 K.^[56] However, there is greater interest in implementing graph-n-ynes in thermoelectric devices due to their electronic semiconductivity (see Section 3herein) and considerably lower thermal conductivity compared to graphene.

The thermoelectric properties were examined in a series of first-principles calculations.^[69,76–80] The Seebeck coefficient of γ-graphyne was on the order of 1 mV/K especially at temperatures below 300K, and this was an order of magnitude larger then graphene (Figure 5G).^[80] As a consequence of the low thermal conductance and high Seebeck coefficient, γ-graphyne’s thermoelectric figure of merit (ZT) could be more than an order of magnitude higher than that of graphene, especially at room temperature where γ-graphyne had a ZT of 0.157 compared to graphene’s ZT of 0.0094.^[80] γ-GYNRs and γ-graphyne nanojunctions (γ-GYNJs) also had such remarkable thermoelectric performance.^[78] Zigzag-edged γ-GYNRs generally had a higher peak ZT compared armchair-edged γ-GYNRs across a wide temperature range of 100 to 700 K, but the general trend was decreasing ZT as the temperature decreased. Moreover, the ZT of armchair-edged γ-GYNRs was three times that of pristine armchair-edged GNRs while that of zigzag-edged γ-GYNRs was approximately 13 times the ZT of pristine zigzag-edged GNRs.

The thermoelectric performance was greatly enhanced by creating nanojunctions, such that a larger difference between the width of the left and right leads corresponded to a larger enhancement in the ZT. This was attributed to the more rapid degradation of the thermal conductance compared to the reduction in electronic conductance as a function of increasing width disparity.^[78] However, only γ-graphyne had a dramatically larger ZT than graphene as the Seebeck coefficients of α-, β-, and 6,6,12-graphyne were similar to that of graphene, although their ZT values were still much higher.^[69,81] Furthermore, γ-graph-2-yne could have even superior thermoelectric properties as it had ZT values that were more than 3.0 in a wide temperature range of 300 to 900K, attaining a maximum ZT of 5.3 at 580 K.^[79] The thermoelectric performance of γ-GYNRs could be boosted further by reducing the thermal conductance through the introduction of ¹⁴C isotopes or defects.^[76] These modifications served as phonon scattering centers, thus improving the ZT. Finally, γ-GYNTs were potential candidates as thermoelectric devices as well, although their ZT values diminished in an oscillatory manner as the diameter decreased.^[77] Hydrogenation of γ-GYNTs also failed to bring about improvements in the ZT similar to the effects of introducing isotopes or defects,^[76] and this was attributed to surface reconstructions due to strain relaxation which enhanced the thermal conductance.^[77]

6. Mechanical Properties of Graphyne

6.1. Computational modeling: reactive molecular dynamics

The mechanical properties of a material are fundamental characteristics that must be considered in engineering applications to ensure the materials are stable and perform properly. Multiscale computational models based on bottom-up approaches are useful tools to understand the mechanisms governing nano-scale behaviors with broad applications ranging from biological systems to 2D materials.^[73,82–84] DFT and quantum chemical calculations based on first principles provide a greater understanding of fundamental electronic and elastic properties of nano-materials at the molecular scale. However, the effects of strain fields from defects or cracks are relatively long-ranged. Computational quantum mechanics cannot handle these long-ranged effects for modeling material deformation and failure. Classical MD with CHARMM-like force fields^[85] can successfully reveal the failure mechanisms of biomolecules, including silk, collagen, intermediate filaments, and amyloids,^{[82,83,86,87]} as well as characterize the effects of nano-confinement on the biomaterials’ mechanical properties.^[88,89] However, modeling the deformation and crack propagation of graphene, graphyne, or any other graphene-based carbon allotropes require MD force fields that can capture the breaking of covalent bonds. As the breaking of chemical bonds relies on the changing states of electrons, classical MD methods are inadequate for modeling these phenomena as the chemical bonds in classical MD are typically pre-defined and not dynamically changeable.

To address this deficiency, the Tersoff-type potential was devised for covalent bond formation and dissociation during MD simulations.^[90,91] The potential energy term is expressed as

$$E_b=f_c\left(r_{ij}\right)\left[V_R\left(r_{ij}\right)+b_{ij}{V}_A\left(r_{ij}\right)\right]$$ (Equation 6.1)

where r_ij is the atomic distance between atom i and j; V_R the repulsive term; V_A the attractive term; b_ij the bond order parameter; and f_C the switching function. The original form of the Tersoff potential utilized complicated analytical form of the bond order parameter, b_ij, to model the properties of materials derived from carbon, silicon, and germanium. The value of b_ij only depended on the local coordination number and angles to represent many-body effects. Brenner proposed a more flexible form of b_ij by adding a correction term for the bond order. This correction term resolved the over-binding of Tersoff types in the intermediate bonding states.^[92] Stuart et al. extended Brenner’s Reactive Empirical Bond Order (REBO) potential to include dihedral, torsional and LJ terms, called Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO).^[93] Both the repulsive and attractive terms, V_R and V_A, are Morse-type potentials of the mathematical form, Ae^-λx. The Morse-type potential has some disadvantages when dealing with collisions relating to the compressive force and thus, the second generation REBO was proposed with a modified (1+Q/r) Ae^-λx term to resolve these issues.^[94] Currently, this modified AIREBO potential is one of the most popular reactive force fields for studying the mechanical behaviors of graphene and various carbon allotropes. The salient feature of this potential is that the bond order term only depends on the local coordination without the need to consider explicit charges and long-range Coulombic interactions, allowing for excellent computational performance as fast Fourier transforms (FFT) calculations are not needed. However, the cutoffs of the switching functions in the REBO terms must be carefully selected and this is discussed later.

Van Duin et al. proposed a different type of reactive force field for hydrocarbon systems called ReaxFF that included Lennard-Jones (LJ) and Coulombic interactions.^[95] ReaxFF is fundamentally different from the REBO and other Tersoff-type potentials. First, the bond order parameter in ReaxFF is a function of the distance between interacting atoms. Second, the ReaxFF calculates the atomic charges with the Electron Equilibrium Method (EEM),^[96,97] a method that is similar to the Charge Equilibration (QEq) method^[98] that inspired another type of reactive force field known as the Charge-Optimized Many-Body (COMB) potential.^[99] The atomic charges in ReaxFF are dynamically optimized during the simulations, thus ReaxFF is more transferable and suitable for complex chemical reactions. Therefore, the force field theoretically can handle the interactions between graphene or graphyne with other molecules in various environments. While several studies reported the elastic properties of graphene based on the ReaxFF, the measured properties strongly depended on the version of ReaxFF parameters that was used because the parameters were fitted from specific training data sets. Jensen et al.^[100] investigated the difference in elastic properties from ReaxFF_C-2013 and ReaxFF_CHO. The ReaxFF_C-2013 parameters were based on a data set that included graphite and diamond, thereby showing significant improvements in reproducing the fundamental physical properties of graphene compared to ReaxFF_CHO. Many early studies of graphynes were based on the ReaxFF_CHO, which might have some discrepancies from the later versions of ReaxFF_C-2013 and DFT calculations. There are other many-body potentials for modeling graphene, such as the Gaussian Approximation Potential (GAP)^[101] and Tersoff potentials,^[102] which were also utilized for modeling the failure and determining the strength of graphene. However, these potentials are limited for studying graphyne, and few studies are reported.

6.2. Switching function in REBO for failures

Properly formulating the switching function in REBO-based potentials is critical for describing the failure of carbon systems. The switching function utilized has the same form as the function from the Tersoff potential in (Equation 6.1),

$$f_c\left(r_{ij}\right)=\{\frac{1}{2}\begin{array}{c}1,\\ \left\{1+\cos \left[\frac{\pi \left(r_{ij}-R_{min}\right)}{R_{max}-R_{min}}\right]\right\},\\ 0,\end{array}\begin{array}{c}{r}_{ij}<R_{min}\\ R_{min}<r_{ij}<R_{max}\\ r_{ij}>R_{max}\end{array}$$ (Equation 6.2)

where the switching function varies from 1 to zero over the range of R_min to R_max. Since the cutoff radius is very short (R_max = 2Å for carbon in the AIREBO potential), the attractive and repulsive potential terms (V_A and V_R in (Equation 6.1)) have substantial values at the point where the bonds are breaking, i.e., the potential is highly discontinuous when bonds break. This problem with the discontinuity in the switching function can simply be solved by smoothly varying the value of the potential at R_min to zero at R_max. However, an unexpected effect of this switching function was reported in a study on the fracture of polycrystalline diamond.^[103] They observed unphysical and high stresses due to the switching function and proposed adjusting R_min to alleviate the problem.

Two methods of adjusting the switching functions were proposed, although there were no clear explanations of how these methods could reproduce the failure of graphene. Firstly, two representative studies utilized the switching functions but with a cutoff of 1.92 Å for R_min instead.^[104,105] Wei et al. obtained stress-strain curves of pristine graphene with the AIREBO potential and compared these curves with results obtained from DFT calculations.^[105] This study showed that there were no stiffening effects from the switching function if R_min was larger than 1.92 Å. Many subsequent studies utilized this adjustment in R_min. However, without considering the exact role of the switching function, adjusting R_min in this arbitrary manner is problematic, especially when examining the effects of grain boundaries or defects on the mechanical properties of graphene. These issues become clearer when the changes in the potential energy and force between interacting pairs of C-C atoms is examined closely (Figure 6A and B). The basic role of switching function is to smoothly vary the potential from a non-zero value to zero smoothly, implying that a stronger force than the original potential is applied to remove the discontinuity between the two points of R_min and R_max. We note that the stiffening effects do not disappear with smaller ranges of the switching function, which can artificially increase the strength of graphene with grain boundaries or 5–7 defects. Since the C-C bonds in 5–7 defects can have longer bond lengths than in pristine hexagonal graphene, the stiffening effects appear when one of these longer bonds is within the range of the switching function. The observed stress-strain behaviors depend on the loading rate because the stiffening effect can be “missed” if the loading rate is too fast and the stress is not sampled adequately. While not observed in the stress-strain curve of pristine graphene, the stiffening effects still exist and can lead to wrong conclusions, especially for systems with 5–7 ring defects. The stiffening effects can still appear even with a low R_min value of 1.95Å and at low temperature (10 K) and loading rate (0.02 Å/ps) (Figure 6C and D). The stiffening artifacts worsen as R_min decreased, as demonstrated by the spike in forces between C-C atoms (Figure 6B). Thus, the previous AIREBO or REBO studies showing strengthening with defects and grain boundaries using R_min = 1.92 Å should be re-examined to confirm whether the strengthening is an artifact of the switching functions because this effect is completely unphysical and undesirable.

Figure 6.

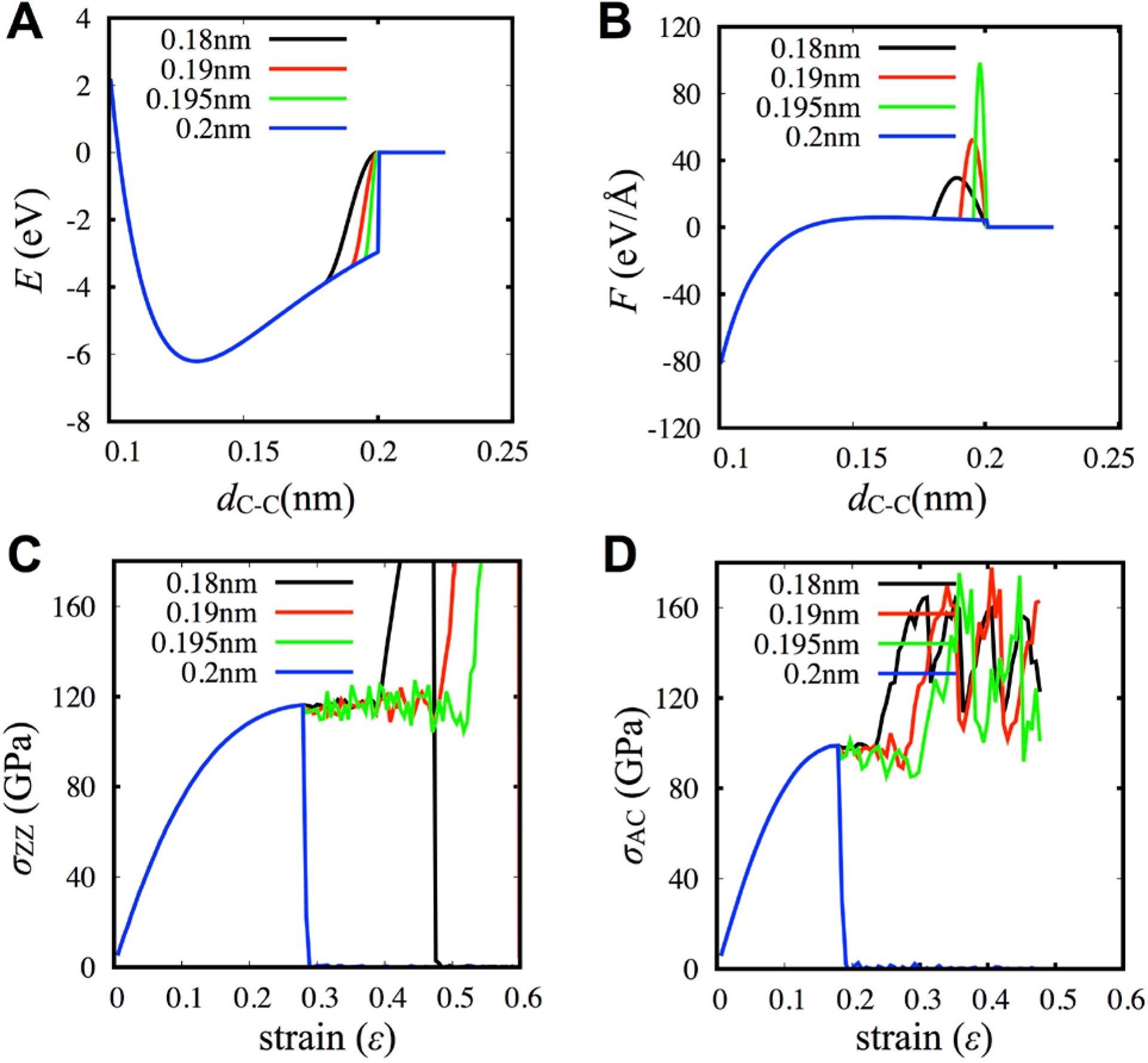
(a, b) The effects come from the modified potential energy (a) and force (b). (c, d) The effects of radius cutoff of AIREBO on the stress-strain behaviors under loadings in the zigzag direction (c) and armchair direction (d). They clearly show that only turning off switching function provides reliable stress-strain curves.

The second method to adjust the switching function is to set both R_min and R_max to be 2 Å to completely disable the switching function. This method was originally proposed for modeling the fracture of diamond by Brenner et al.^[103] As shown in Figure 6 (blue lines), equal values of R_min and R_max completely remove the stiffening effects and show reliable stress-strain curves of graphene with brittle failure. Although this setting solves the unphysical stiffening, there is still a discontinuity in the potential, and the graphene simulation becomes unstable easily as the temperature increases. The temperature dependence is due to kinetic vibrations that may cause a C-C bond length to exceed 2 Å temporarily, resulting in a broken bond. Thus, carefully setting the loading and performing the analysis are required to understand the failure behaviors with AIREBO or REBO. This choice of cutoffs was utilized by various studies to examine flaw insensitive fracture in nano-crystalline graphene^[106] and toughness enhancement in graphene ruga.^[107] Also, removing the stiffening effect made it possible to construct models of well-stitched polycrystalline graphene with mainly 5–7 defects. It was also found that fracture toughness could be enhanced with grain boundaries and the mechanisms strongly depended on the out-of-plane deformation.^[108] Utilizing topological defects, more complex 3D geometries of gyroidal minimal surfaces were generated to study their mechanical and thermal properties as a function of porosity.^[51,109]

The REBO potential has a relatively simple analytical form compared to other reactive FFs. This simplicity allows easy removal of unphysical stiffening and obtaining reliable stress-strain curves that are comparable with DFT calculations. However, charge-based reactive FFs are comparatively too complicated to easily circumvent undesirable stiffening and optimize parameters for failure behaviors with proper stress-strain curves. To improve these potentials, not only the data of equilibrium states must be included in the training data set, but also data near the failure of the material.

6.3. Bond Lengths

Unlike graphene, graphyne mainly consists of three different types of C-C bonds: single, aromatic, and triple bonds. Thus, the equilibrium distances of each bond type in graphyne are important features. Figure 7 and Table 4 show the bond lengths calculated from different MD potentials of AIREBO and ReaxFF_CHO for various kinds of graphyne.^[110] The bond lengths of aromatic rings in graphene are 1.40 and 1.44 Å for AIREBO and ReaxFF, respectively. The lengths of single and triple bonds are accurately captured with ReaxFF, being around 1.45 Å and 1.2 Å, respectively. However, the AIREBO potential overestimates the length of a triple bond at about 1.3 Å while a single bond is approximately 1.4 Å. Cranford et al.^[111] found a lattice constant a as a function of the number n of γ-graph-n-yne from MD simulations based on ReaxFF_CHO, where a_n =4.45 + 2.66n. The acetylene linkages increased the lattice constants homogeneously, which could be generalized for other graphynes.

Figure 7.

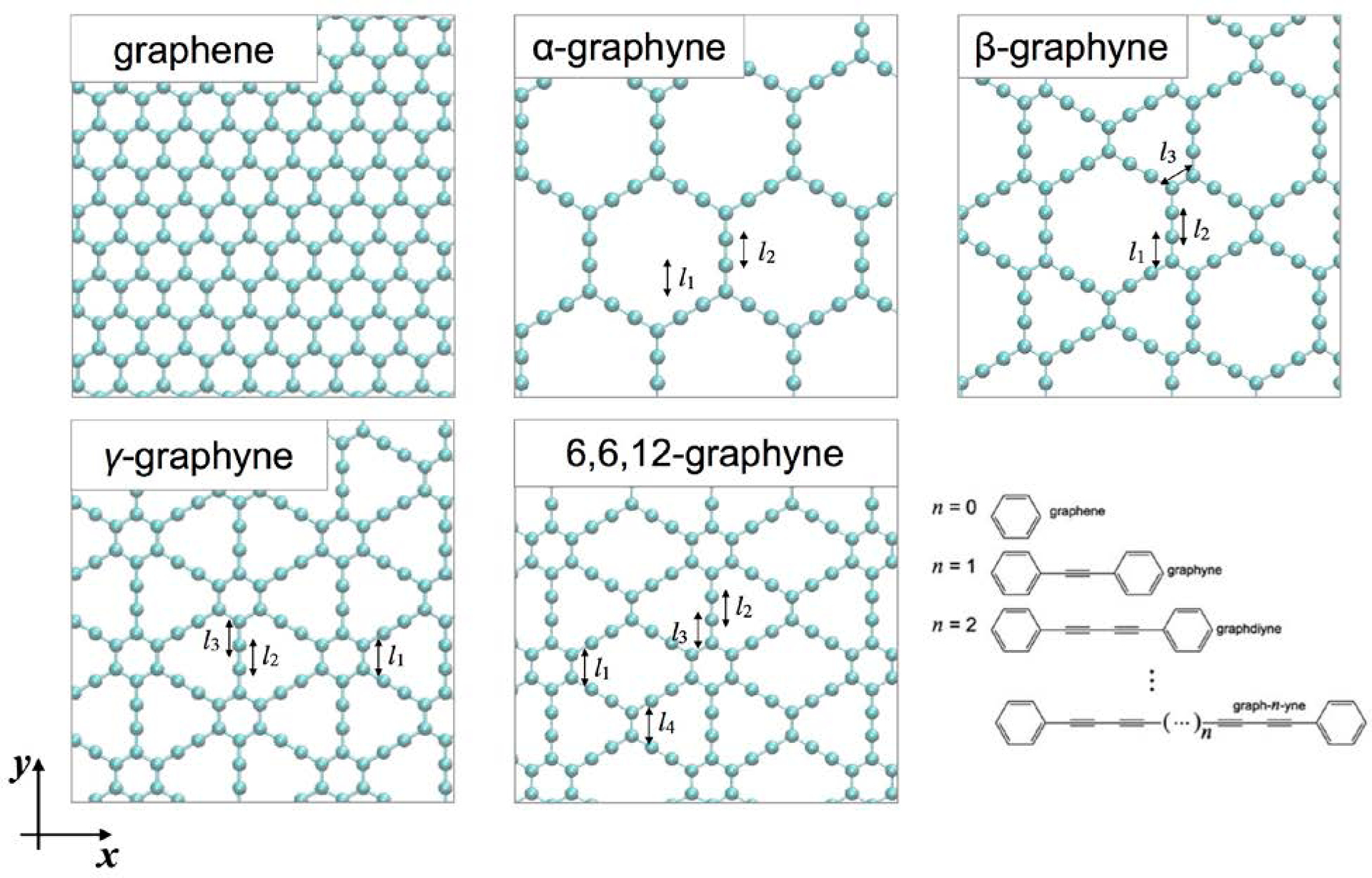
The geometries of graphene and four different graphynes. There are different types of bonds (l ₁ ~ l₄), and the values from AIREBO, ReaxFF and DFT from the previous studies are listed in Table 4. Based on the lengths of carbyne chains, graphynes are extended to graph-n-ynes.

Table 4.

Bond lengths of graphene and graphynes, the data are adopted from reference^[110]. (Ref a^[141], Ref b,^[142])

Structure Type	Bond Type	AIREBO (Å)	ReaxFF (Å)	DFT (Å)
Graphene	Aromatic	1.400	3.84	1.42a
α-Graphyne	l1 (Single)	1.386	1.447	1.397b
	l2 (Triple)	1.331	1.217	1.24b
β-Graphyne	l1 (Single)	1.398	1.481	1.46b
	l3 (Single)	1.386	1.420	1.39b
	l2 (Triple)	1.331	1.227	1.23b
γ-Graphyne	l1 (Aromatic)	1.397	1.442	1.426b
	l3 (Single)	1.385	1.435	1.408b
	l2 (Triple)	1.331	1.221	1.223b
6,6,12-Graphyne	l1 (Aromatic)	1.398	1.442	-
	l3 (Single)	1.384	1.442	-
	l4 (Double)	1.397	1.442	-
	l2 (Triple)	1.332	1.218	-

6.4. Elastic Moduli and Strength

The mechanical properties of graph-n-yne changes according to how the basic building blocks are assembled, including the relative geometries and the length of acetylene linkages. These changes in the properties are crucial when applying graph-n-yne in engineering materials. Table 5 summarized the elastic moduli of graphene. The Young’s modulus and strength were reported as 1 TPa and 130 GPa from nanoindentation experiments. These values were predicted with DFT calculations.^[112] As described in the previous section, the ReaxFF and AIREBO potentials are the leading force fields for modeling graphene and carbon-related materials. In particular, the modified cutoff is mandatory for accurately modeling the failure of graphene with the AIREBO potential, and proper training sets are required to parameterize ReaxFF. The elastic properties of graphene modeled with AIREBO and the modified cutoff showed good agreement with both DFT and experimental data (Table 5).

Table 5.

Elastic moduli of graphene (DFT, AIREBO, Reax_CHO, and Reax_C-2013)^[100]

Elastic Constants	Exp.	DFT	ReaxFFC-2013	ReaxFFCHO	AIREBO
C11 (GPa)	1028	1067	1005	5320	972
C12 (GPa)	170	148	505	4662	332
C66 (GPa)	280	459	186	311	320
E (GPa)	1000	1047	751	1235	858
ν	0.165	0.139	0.502	0.876	0.34

The ReaxFF_CHO has some shortcomings in determining the mechanical properties of carbon materials as this potential was originally developed for modeling the oxidation of hydrocarbons. For example, the elastic constants of graphene were too high, and the Poisson’s ratio was not consistent with both experiments and DFT calculations.^[100] These inaccuracies mainly originated from the omission of data on the mechanical properties of condensed carbon materials. Srinivasan et al. improved the parameters in ReaxFF_C-2130 by including the data for the condensed phases of carbon.^[113] The overall elastic properties from these new parameters improved significantly (Table 5). However, the Poisson’s ratio of graphene was still rather high (>0.5) and the nonlinearity of stress-strain curves compared poorly with DFT calculations.^[100] Graphyne-based materials have periodic structures of aromatic rings and carbyne chains. Therefore, the description of mechanical properties of graphene is a crucial factor to validate its reliability for modeling graphyne-based materials.

Furthermore, the AIREBO potential is not extensively validated for systems containing carbyne chains. As described in the previous section, the lengths of triple bonds were not in good agreement with DFT calculations. Thus, the AIREBO potential must be validated for examining the mechanical properties of graph-n-yne. Wang et al. compared the stress-strain curves of γ-graphyne in both the zigzag (ZZ) and armchair (AC) directions (Figure 8A) based on results from previous DFT^[114] and first-principles (FP) MD simulations.^[115] The failure strains, the nonlinearity of the stress-strain curves, and the ultimate strengths calculated from the AIREBO potential showed better agreement with DFT calculations while the length of the triple bond was overestimated. Thus herein, we focused on the results from AIREBO for fracture and strengths. Where necessary, we produced our data for atomic stress distributions based on the AIREBO potential.

Figure 8.

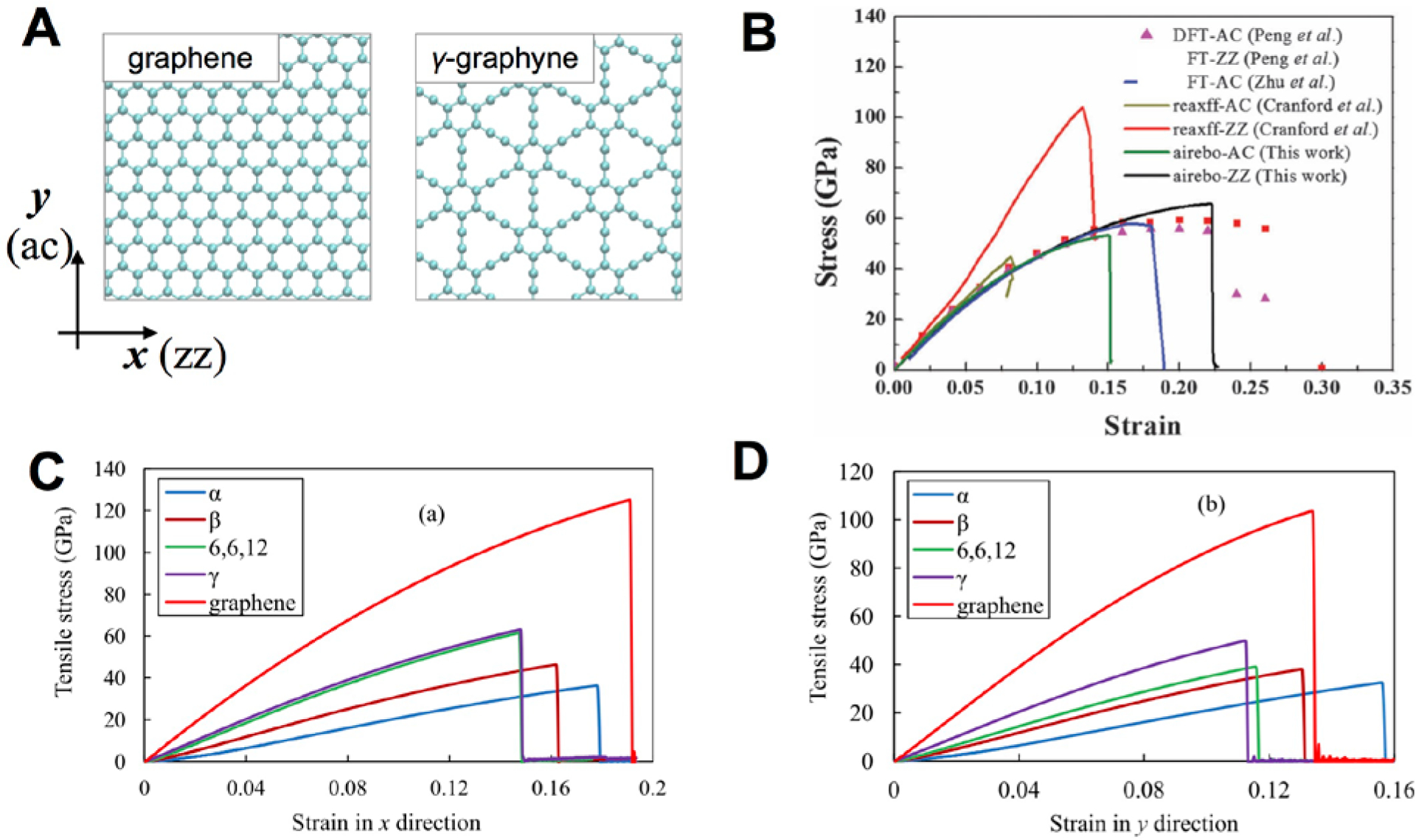
(a) Schematic for the loading directions: armchair (ac) and zigzag (zz). (b) The stress-strain curves of γ-graphynes from DFT, ReaxFF, and AIREBO for comparison^[110] (c-d) Stress-strain curves of graphene and various graphynes from AIREBO.^[61]

Figure 8B illustrates the stress-strain behaviors of various types of graphyne allotropes while the strengths are summarized in Table 6. To provide mechanistic insights into the difference of the deformation and failure, we calculated the virial atomic stress for various graphyne allotropes (Figure 9). The volume of each carbon atom was considered as the averaged atomic volume of graphene. Under the tensile loading in the AC (y) direction, the stress was concentrated in the carbine chains while the aromatic rings were more involved in the mechanical response if the loading was in the ZZ (x) direction. The chain perpendicular to the loading direction had relatively lower atomic stress before failure while the atomic stress of pristine graphene was distributed more homogeneously. This distribution explained why the specific strengths of graphynes were lower compared to graphene.

Table 6.

Strengths and elastic properties of various graphynes. (Ref a,^[61] Ref b,^[100] Ref c,^[111] Ref d,^[110] Ref e,^[115])

Structure Types	DFT (zig, arm)	ReaxFFCHO (zig, arm)	ReaxFFC-2013 (zig, arm)	AIREBO (zig, arm)
Graphene	139b, 114b	96b, 134b	138b, 125b	125.2a, 103.6a
				116d, 99d
α-Graphyne	-	-	-	36.36a, 32.48a
β-Graphyne	-	-	-	46.26a, 38.06a
γ-Graphyne	65e, 60e	107.5c, 48.2c	-	63.17a, 49.78a
6,6,12-Graphyne	-	-	-	61.62a, 39.06a

Figure 9.

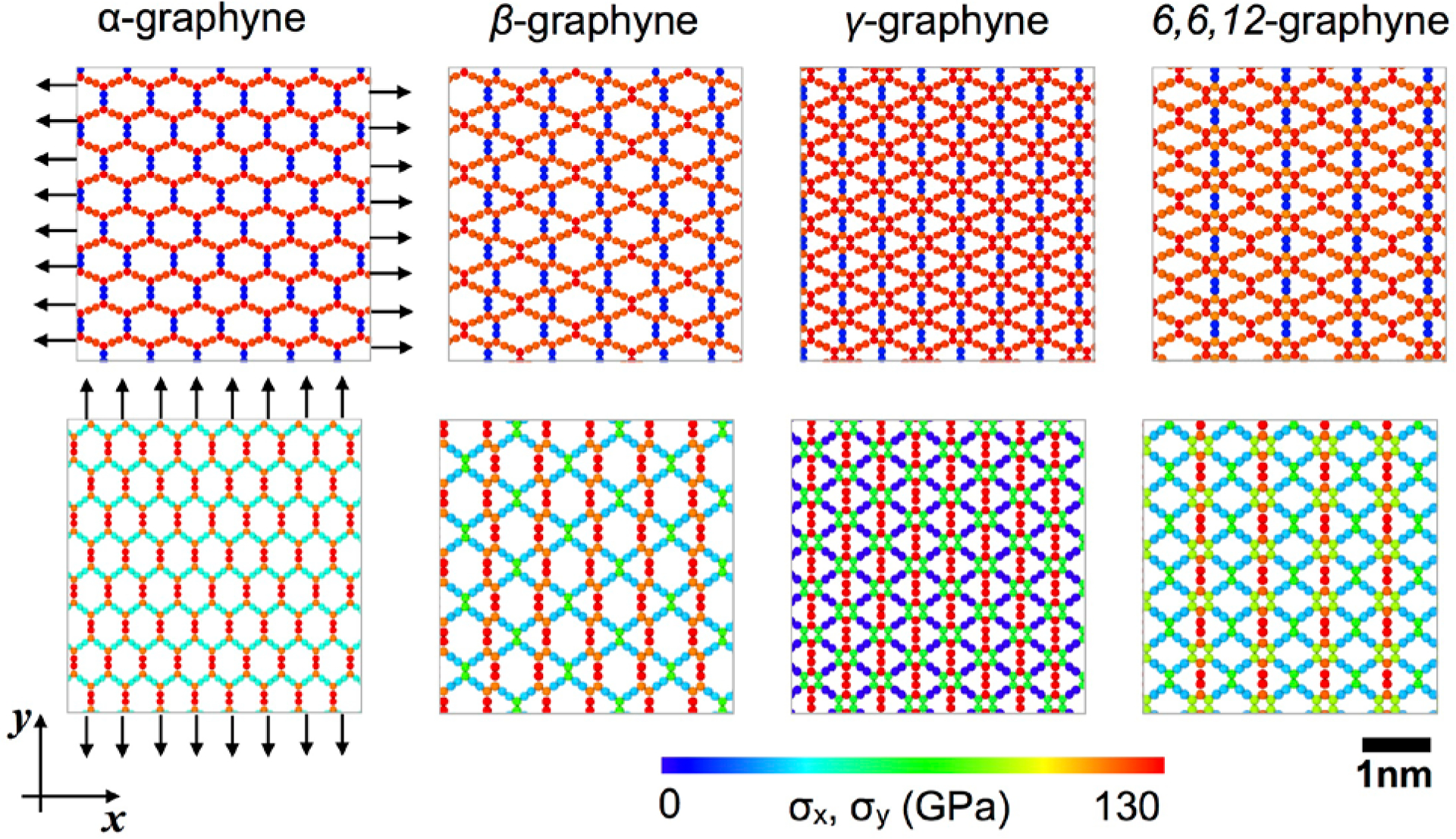
Atomic stress distributions of four different graphynes before failures under tensile loads in the x (zz) and y (ac) directions.

6.5. Fracture and Crack propagation

The elastic properties and strengths of materials are not sufficient to fully characterize the materials for various engineering applications. Cracking behaviors govern the mechanical failure from stress concentrations near the crack tip. Due to its atomically thinness, the cracking behaviors of graphene and other 2D materials are strongly affected by atomic configurations near the crack tip, e.g., defects, grain boundaries, or other layers.^{[108,116,117]} Therefore, crack behaviors and stress distributions near the crack tip are also critical of understanding the failure mechanisms of graphynes. Figure 10 shows the stress distributions near the crack tips of four different graphyne allotropes before crack propagation. The fracture patterns followed that of pristine graphene. The crack inserted in the ZZ direction propagated along the lattice direction when subjected to loading in the AC direction, while the crack inserted in the AC direction propagated in a more jagged fashion. The stress distribution near the crack showed similar patterns as compared to the stress distribution from graphynes without a crack (Figure 9). The region with high stress concentration was strongly affected by the crack direction and the graphyne’s geometry. The difference regarding specific fracture toughness is an interesting topic to be investigated in the future for geometric designs of tough graphyne sheets.

Figure 10.

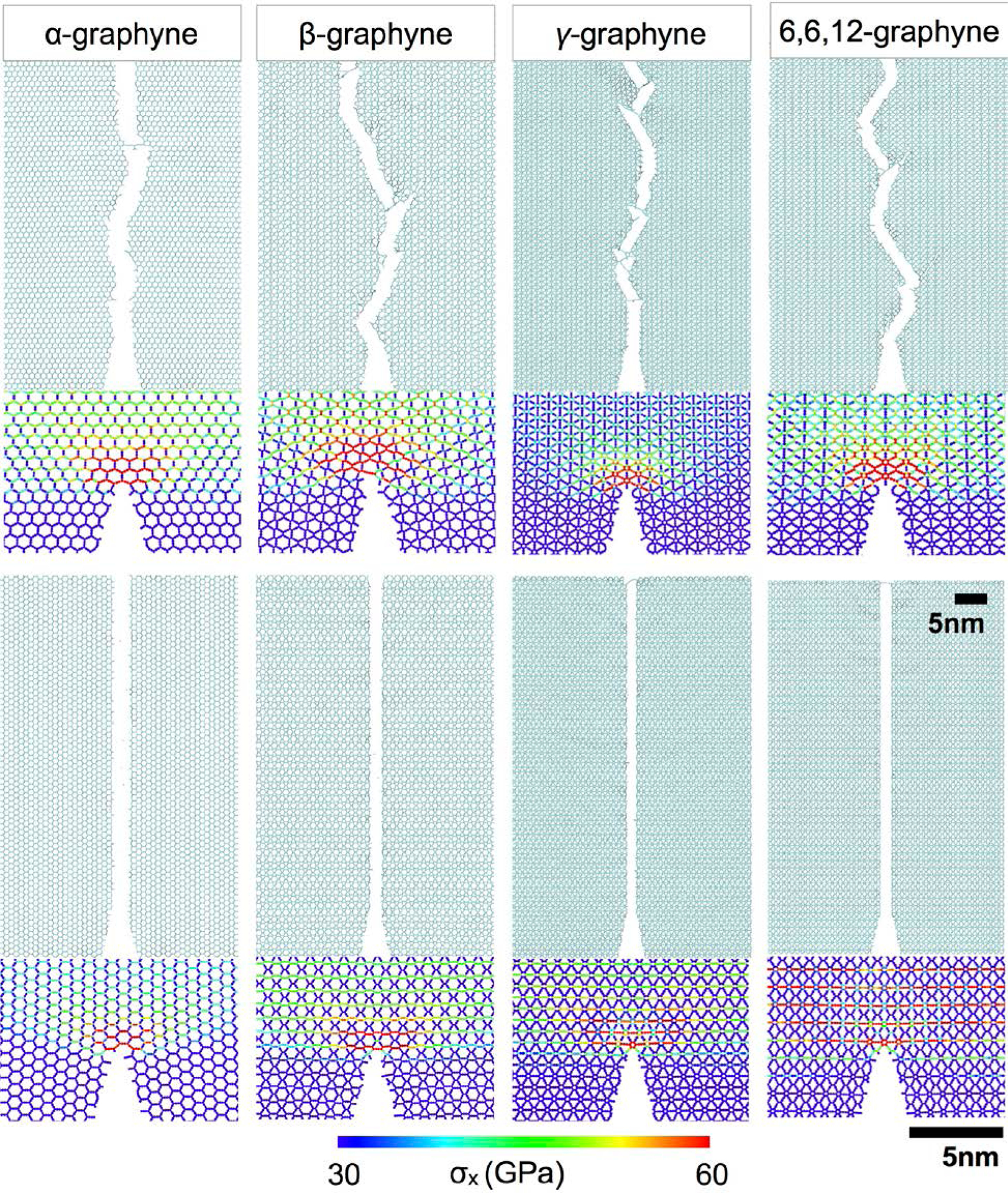
The patterns of crack propagation, and the stress concentrations of various graphynes near a sharp crack tip before crack propagation. The stress distributions vary significantly due to the loading direction and lattice geometries.

Given graphyne’s superior but orientation-dependent mechanical and fracture characteristics in conjunction with their unique nanoporosity and thermoelectric properties, we anticipate that macroscopic fibers, films, or composites containing dispersed graphyne flakes will exhibit similarly exceptional features. For instance, upscaling the production of graphyne may potentially advance the development of flexible and stretchable organic polymer composites for thermoelectric films and devices that can operate well in complex environments and wrinkled surfaces.

7. Graphyne-based Separation Membranes

7.1. Separating Gas Mixtures

Numerous studies proposed that graphyne allotropes might be extremely efficient membranes for molecular separation^{[43–45,118–127]} and water filtration^{[115,128–135]} due to the natural and highly configurable porosity of these allotropes. In contrast, the dense electron cloud of pristine graphene monolayers is generally impermeable even to hydrogen atoms, although graphene was recently discovered to be sufficiently porous for proton transport^[136] and was able to separate protons from deuterons.^[137] The natural, uniform, and tunable porosity of graph-n-yne enables enhanced permeability for a wider range of sizes of atoms and molecules. Hydrogen purification is one such application (Figure 1). Jiao et al. showed that the most stable configuration of adsorbed H₂ was parallel to the surface of the γ-graph-2-yne plane at the height of 1.75 Å and an adsorption energy of only 0.07 eV, thus indicating weak vdW interactions.^[121] H₂ only had to overcome a low energy barrier of 0.10 eV to pass through the pores of γ-graph-2-yne. In comparison, CH₄ and CO faced much larger energetic barriers of 0.72 and 0.33 eV, respectively. The diffusion rate and selectivity were calculated with transition state theory where the selectivity of H₂ from CH₄ (H₂/CH₄) and H₂/CO was 10¹⁰ and 10³ respectively at room temperature (Figure 11A).

Figure 11.

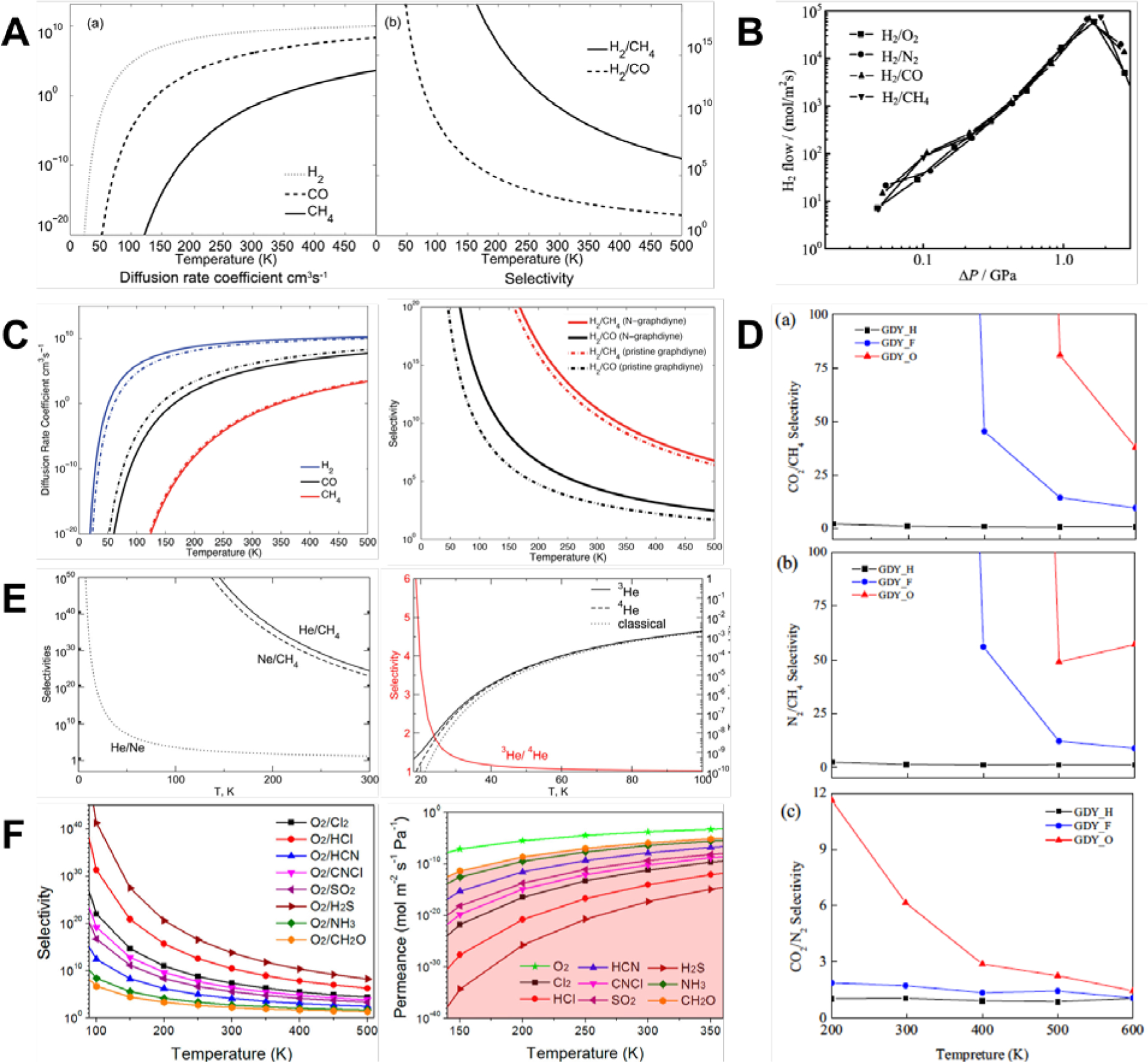
(A) Monotonic variation of the diffusion coefficient (left) and selectivity (right) of H₂ with decreasing temperature for γ-graph-2-yne membranes.^[121] Reprinted from^[121] with permission from Royal Society of Chemistry. (B) Variation of H₂ flow rate with applied pressure across γ-graph-2-yne membranes for different gas mixtures.^[122] Reprinted from^[122] with permission from AIP Publishing. (C) Diffusion coefficients (left) and selectivity (right) of H₂ were improved by doping γ-graph-2-yne membranes with nitrogen.^[43] Reprinted from^[43] with permission from Royal Society of Chemistry. (D) Selectivity of different gas mixtures for γ-graph-2-yne membranes modified by H, F, and O atoms.^[44] Reprinted from^[44] with permission from Elsevier. (E) Selectivity of noble gas mixtures (left) and isotopes of He (right) decreased monotonically with increasing temperatures.^[126] Reprinted from^[126] with permission from ACS Publications. (F) As temperature increased, oxygen selectivity (left) decreased monotonically and permeance (right) increased monotonically when mixed with harmful gases.^[119] Reprinted from^[119] with permission from ACS Publications.

Zhao et al. compared the selectivity of several gas mixtures of H₂/O₂, H₂/N₂, H₂/CH₄, and H₂/CO with MD simulations while varying the applied pressure across a γ-graph-2-yne membrane (Figure 11B).^[122] H₂ molecules crossed the membrane rapidly at a pressure range of 47 MPa to 4 GPa, while all the O2, N2, CO, and CH4 molecules were blocked. This allowed a H₂ flow rate that ranged from 7 mol/m²s to 6 × 10⁵ mol/m²s. A single molecule of H₂ faced a low energy barrier of 0.15 eV while passing a γ-graph-2-yne pore, in good agreement with DFT calculations.^[121] This low barrier was in contrast to the much larger energy barriers for O₂, N₂, CO, and CH₄ that were as high as 1.09, 1.78, 1.97, and 2.63 eV, respectively. Furthermore, low pressures of 0.047 to 0.091 GPa resulted in minimal amounts of H₂ being filtered, while pressures higher than 4.4 GPa led to almost solid-like behavior. Therefore, an intermediate pressure was preferable to rapid permeation and separation of H₂ molecules.^[122] γ-graph-2-yne was also an excellent filter for a mixture of H₂/CO/CH₄, also known as syngas.^[123] Simulations with full atomistic reactive MD showed the mass flux of H₂ from this mixture across the membrane was on the order of 7 to 10 g/cm²s in the temperature range of 300 to 500 K. CO and CH₄ molecules were isolated effectively. Adding small amounts of pressure on the order of 100 to 500 kPa could improve the separation of H₂, while much larger driving forces were needed to separate CO and CH₄, suggesting that pure H₂ gas could be obtained with γ-graph-2-yne membranes at atmospheric conditions with minimal energetic costs.^[123]

As the pore size and shape strongly influenced the filtration and separation capabilities of the membrane, a further comparison was made between other graphyne allotropes of γ-graphyne, γ-graph-2-yne, and rhombic-graphyne.^[124] γ-graphyne was unsuitable as a separation membrane for H₂ as the energy barrier for H₂ was 1.98 eV. The barrier was a much lower value of 0.54 eV in rhombic-graphyne, while the barriers for CO, N2, and CH4 were 1.55, 1.73, and 3.00 eV, respectively. At room temperature, the selectivities of rhombic-graphyne were approximately 10¹⁶, 10¹⁹, and 10⁴¹ for H₂/CO, H₂/N₂, and H₂/CH₄ respectively, using the calculated diffusion barriers and the Arrhenius equation. Furthermore, assuming an incoming pressure of 3 bar and a pressure drop of 1 bar across the pore of rhombic-graphyne, the H₂ permeance was on the order of 10⁻⁹ mol/m²sPa at room temperature. This permeance was on par with industrially acceptable permeance for gas separation.^[138]

As noted in Section 4, chemical modifications and functionalizations of neat graphyne membranes could also alter the manner and efficiency of filtering or separating H₂. In a DFT study of nitrogen-doped γ-graph-2-yne (N-γ-graph-2-yne),^[43] the H₂ molecule diffused across the pore by a transition state (TS) that was perpendicular to N-γ-graph-2-yne. There was no lattice distortion and electron transfer was negligible, thus indicating minimal interactions between the H₂ molecule and the pore. The energy barrier for crossing the N-doped pore was 0.08 eV, lower than that of pristine γ-graph-2-yne and rhombic-graphyne membranes.^[121–124] In contrast, CH₄ and CO molecules distorted the lattice and the energy barrier was higher at 0.73 and 0.38 eV respectively. N-doping had the further effects of increasing the diffusion rate coefficients of H₂ molecules while decreasing that of CO molecules. These effects became more noticeable as the temperature dropped below room temperature. Through combinations of all these factors, N-doped γ-graph-2-yne membranes could achieve greatly enhanced selectivity of hydrogen in H2/CO mixtures across a wide range of temperatures, potentially 100 times higher at room temperature (Figure 11C).^[43] Inducing a 1e positive charge could also alter the selectivity of γ-graph-2-yne membranes by enhancing the interactions between H₂ and the membrane.^[45] The permeability was enhanced as the penetration barrier for H₂ to diffuse through the membrane was 0.01eV lower than the barrier for diffusing through neutral membranes. Moreover, the penetration barrier for CO was increased considerably from 0.34 to 0.45 eV in the positively charged membrane. Similarly, the penetration barrier for CH₄ is also higher, increasing from 0.69 to 0.74 eV. These changes in the penetration barriers boosted the selectivity across a wide range of temperatures. At room temperature, the selectivity of H₂/CO and H₂/CH₄ was 10⁶ and 10¹¹, respectively, and were substantially larger than the corresponding selectivity in neutral membranes of 10⁴ and 10¹⁰ for H₂/CO and H₂/CH₄, respectively.

Other than hydrogen separation, Zhao et al. examined the possibility of filtering gas mixtures of CO₂, N₂, and CH₄ after widening the pore sizes in γ-graph-2-yne membranes by removing a diacetylenic linkage and capping the resulting dangling bonds with either hydrogen, fluorine, or oxygen.^[44] From DFT calculations, the effective pore areas were 57.22 Ų, 48.00 Ų, and 44.36 Ų for H, F, and O functionalization respectively. Gas molecules of CO₂, N₂, and CH₄ easily passed through H-modified pores as the energy barriers were rather low, ranging from 0.06 to 0.16 eV. F- and O-modified pores had low energy barriers for CO₂ and N₂ molecules (0.03 to 0.18 eV), while the barriers were considerably higher for CH₄ molecules (0.40 and 0.39 eV for F- and O-modified pores respectively). This gap in energy barriers enabled effective separation of CO₂/CH₄ and N₂/CH₄ gas mixtures. At 298K, H-modified pores had low selectivities of 36, 47, and 0.78 for the CO₂/CH₄, N₂/CH₄, and CO₂/N₂ gas mixtures respectively (Figure 11D). In contrast, the selectivities were significantly enhanced, attaining up to orders of 10⁵ and 10³ in F- and O-modified membranes for CO₂/CH₄ and N₂/CH₄ gas mixtures respectively. The permeances of CO₂ and N₂ were also 10³ to 10⁵ times higher than the permeance of 10⁻⁸ mol/m²sPa for CH₄. Furthermore, O-modified pores also improved the selectivity of CO₂/N₂ gas mixtures to 1.7 × 10², while the permeance of CO₂ was 10⁻² mol/m²sPa, a hundred times larger than the permeance of N₂. The high selectivity and permeance of CO₂ strongly suggest that O-modified γ-graph-2-yne membranes could effectively separate CO₂/N₂ gas mixtures.

γ-graph-2-yne might be a potential material for separating noble gases as well.^[126,127] Using the “coupled” supermolecular second-order Møller−Plesset perturbation theory (MP2C) level of theory,^[139] the penetration barrier of a He atom was a mere 0.033 eV. Aided by this low barrier, the diffusion rate at 300K was estimated to be on the order of 10¹⁰ s⁻¹. The penetration barrier was much higher for a neon atom (0.106 eV) and methane (1.460 eV). Due to the large disparity in the penetration barriers between noble gases and methane, the membrane had exceptionally high selectivities of 10²⁴ and 10²³ for He/CH₄ and Ne/CH₄ gas mixtures respectively at room temperature (Figure 11E). However, the selectivity for He/Ne mixtures was only 27 at 300 K as a result of the smaller difference in penetration barriers between these two elements. Isotopes of ³He and ⁴He could potentially be separated as well due to minor differences in their tunneling probabilities. If the kinetic energies were higher than the classical barrier, the transmission probability of ⁴He was higher than ³He and vice-versa. To exploit this difference, the gas temperature should be kept as low as possible and the isotopic selectivity at 77 K was estimated at 1.04. The selectivity increased rapidly as the temperature decreased, attaining a selectivity of 6 at 20 K. If the membrane was assumed to be fully porous, the permeance was estimated to be 1.5 × 10⁻⁸ mol/cm²sbar at ideal gas conditions, a pressure of 3 bar and a temperature of 20K.^[126]

Graphyne-based membranes might also be capable of segregating harmful gases (Figure 11F). For instance, hydrogen sulfide (H₂S) preferentially adsorbed onto γ-graphyne membranes compared to CH₄.^[118] Oxygen can also be separated from a whole range of harmful gases with γ-graph-2-yne membranes, including Cl₂, HCl, HCN, CNCl, SO₂, H₂S, NH₃, and CH₂O.^[119] A high oxidation energy of 1.97 eV was required to oxidize the acetylenic bonds, ensuring that the structure of γ-graph-2-yne remained stable while separating O₂ from the other gases. Furthermore, O₂ had the lowest diffusion energy barrier of only 0.21 eV compared to the other gases. The permeance of O₂ was also the highest at 1 × 10⁻⁴ mol/m²sPa at 300 K. The low diffusion barrier and high permeance of O₂ allowed for high selectivities when O₂ was mixed with the harmful gases. The selectivity was highest for O₂/H₂S at approximately 10¹⁴, while even the lowest selectivity of 2 × 10² for O₂/CH₂O mixtures was sufficiently high for potential industrial usage.

7.2. Desalinating and Filtering Water

Another critical application of graphyne membranes might be in water purification and desalination (Figure 1). Several computational studies highlighted this remarkable potential for low-cost membranes. Through MD simulations, Kou et al. found that water molecules are unable to diffuse through γ-graph-2-yne membranes, whereas the pore sizes of γ-graph-3-yne membranes were sufficiently large for water penetration.^[130] Net water flux through γ-graph-3-yne membranes was also faster (27.5 ns⁻¹) compared to (5,5) CNTs (13.5 ns⁻¹) that had similar diameters to the pore sizes of γ-graph-3-yne (Figure 12A). Hydrogen bonds that bridged both sides of the membrane were critical for facilitating the passage of water molecules. Water molecules also had a lower penetration barrier of 2.3k_BT compared to 3.5k_BT for (5,5) CNTs. Generally, the permeability of water molecules increased as the number of acetylenic linkages increased where γ-graph-3-yne membranes had the smallest pore sizes possible for water permeation.^[115,129] From MD simulations, applying hydrostatic pressure led to strong molecular layering close to the membranes on the side of the feed reservoir due to the formation of ordered hydrogen bond networks.^[115] These ordered networks reduced the ease of passage for the water molecules. Furthermore, water molecules were transported in a quantized manner across the membranes, leading to the strong dependence of water permeability on the pore sizes of the membranes. Discrete water flow transitioned into continuous flow for pore sizes that were larger than those of γ-graph-7-yne membranes.^[115] Also, similar velocities of water flux as γ-graph-3-yne membranes could be obtained using β-graphyne membranes while α-graphyne membranes were permeable but at a reduced rate (Figure 12B).^[128] However, further verification of this phenomenon might be necessary due to a dearth of data in this respect.

Figure 12.

(A) Comparing the net flux of water molecules across γ-graphyne membranes and CNTs of various diameters.^[130] Reprinted from^[130] with permission from AIP Publishing. (B) Linear increase in water flux across α-, β-, and γ-graphyne membranes as the pressure applied increased.^[128] Reprinted from^[128] with permission from IOP Publishing. (C) Water permeability (top) and contamination rejection rate (bottom) for a variety of pore sizes and contaminants.^[129] Reprinted from^[129] with permission from Royal Society of Chemistry. (D) Water flux (unfilled triangles) and salt rejection rates (filled squares) for γ-graph-3-yne nanotubes.^[133] Reprinted from^[133] with permission from Royal Society of Chemistry. (E) Graphyne-based membranes improved in energy consumption dramatically when compared to conventional TFC membranes.^[135] Reprinted from^[135] with permission from Royal Society of Chemistry.

The molecular filtration capabilities of γ-graph-3-yne to γ-graph-6-yne membranes were also analyzed.^[129] MD simulations were performed on water mixtures with contaminants of CuSO₄, CCl₄, C₆H₆, and NaCl. Independent of the type of contaminant, water permeability increased with increasing numbers of acetylenic linkages, ranging between 2.9 to 4.5 × 10⁻⁹ m/sPa and plateauing when the number of acetylenic linkages was more than 5 (Figure 12C). By applying a pressure of 50 MPa and measuring the contamination rejection rates, CuSO₄ was 100% rejected by all the membranes and the general trend of rejection rates was CuSO₄ > NaCl > CCl₄ > C₆H₆. Hydrophilic molecules of CuSO₄ and NaCl were rejected more efficiently as they tended to cluster with water molecules as well as with themselves. Not surprisingly, rejection rates fell as the pore sizes increased with increasing numbers of acetylenic linkages. More critically, γ-graph-3-yne were the only membranes that had a 100% rejection rate for all the contaminants while having acceptable levels of water permeability. Increasing the hydrostatic pressure also increased the water permeability slightly by around 3% due to elongation of the acetylenic linkages. Interestingly, one study found that both γ-graph-3-yne and γ-graph-4-yne had a 100% rejection rate of NaCl if a pressure of more than 100 MPa was applied.^[115] However, this observation was not borne out in subsequent studies where pore sizes larger than those of γ-graph-3-yne were unable to fully reject NaCl ions at pressures above 100 MPa.^[128,131] γ-graph-3-yne, α-graphyne, and β-graphyne membranes were also capable of achieving complete salt rejection for a wide variety of ions of Na⁺, K⁺, Mg²⁺, Ca²⁺, and Cl⁻.^[128] Water molecules had to overcome an energy barrier of less than 2 kcal/mol to pass through the membranes, while monovalent and divalent ions had to overcome barriers of approximately 10 kcal/mol and 60 kcal/mol respectively.^[128] Moreover, the percentage of NaCl rejection decreased monotonically with increasing pressure for γ-graph-3-yne to γ-graph-5-yne membranes.^[131,134]

γ-graph-3-yne nanotubes were also able to retain NaCl ions within itself while allowing water to diffuse outwards while having a nanotube diameter of 1.93 nm resulted in the highest water flux of 203.69 L/cm²h.^[133] For nanotubes with smaller diameters, capillary effects caused water molecules to diffuse rapidly back into the tube, resulting in lower fluxes of approximately 120.00 L/cm²h (Figure 12D). Additionally, the diffusion coefficients of water molecules along the axis of the nanotube were estimated to be 2 orders of magnitude higher than water molecules that were not confined. This increase in diffusivity was attributed to the formation of strong hydrogen bond networks due to capillarity and the pressure difference between the interior and exterior of the nanotubes.^[133] The diffusion coefficients of water across graphyne-based membranes could also be enhanced through the addition of charges,^[131,134] similar to the enhanced penetration and selectivity of hydrogen atoms.^[45] Both positively and negatively charged γ-graph-4-yne membranes improved water’s diffusion coefficient by more than three-fold.^[134] This improvement was due to salt ions being adsorbed or repelled more strongly on charged membranes while the passage of water molecules was not obstructed. However, the presence of protons and hydroxyl radicals in water would likely lead to functionalized acetylenic linkages in graphyne-based membranes as the linkages are more reactive. Hydrogen functionalization would considerably reduce the flux of water. At high pressures of 2.5 GPa, the reduction ranged from approximately 50% for hydrogenated γ-graph-4-yne membranes to 92% for hydrogenated γ-graph-2-yne membranes.^[135] Water in ethanol mixtures could also be purified with γ-graph-n-yne membranes as ethanol molecules would encounter steep energy barriers of penetration.^[120] For γ-graph-3-yne membranes, these barriers were approximately 50 to 65 kJ/mol, depending on the orientation of the ethanol molecule relative to the pore. Furthermore, ethanol molecules adsorbed more preferentially to graphyne than water molecules as the dispersion attraction was stronger. γ-graph-4-yne membranes were also the most efficient membranes for separation of water from ethanol as they had the highest molar flux ratio.

From the body of research reviewed here, graphyne-based membranes have tremendous potential to drive down the cost of desalination membranes dramatically. The potential cost savings were analyzed with a 1D numerical model of a reverse osmosis system that accounted for fluid dynamics and mass transport.^[135] Almost all the graphyne-based membranes had better recovery of the permeate than reverse osmosis membranes of both thin-film composites (TFC) and nanoporous graphenes. The flow rate that produced the peak permeate recovery for TFC membranes was 710 m³/day. At this flow rate, graphyne-based membranes recovered 60 to 80% more permeate than TFC membranes and 20% more permeate than nanoporous graphene. Also, if the targeted production rate for permeates was 150 m³/day, up to 6% less energy or 6 times fewer pressure vessels would be needed compared to TFC membranes (Figure 12E). Graphyne-based membranes’ salient features of controllable porosity, atomic thinness, and high strength might truly disrupt the current market for water desalination^[140] and hydrogen purification^[138] membranes.

8. Conclusions

Over the past decade, novel chemical routes were devised to synthesize a new class of atomically thin, carbon-based materials known as graphyne. Herein, we reviewed computational predictions and validations of the remarkably diverse and exceptional physical, electrical, and chemical properties of graphyne-based nanomaterials, including nanosheets, nanotubes, and nanoribbons. Structurally, pristine graphyne allotropes consist of a lattice of benzene rings that are linked together with variable numbers of acetylenic (-C≡C-) bonds. The tunable structures of graphyne allotropes lead to fundamentally varying electronic properties: both α-graphyne and β-graphyne were zero-band-gap semiconductors or semimetals, while 6,6,12-graphyne might have carrier mobility exceeding that of pristine graphene. Fukui analysis illustrated the reactivity of graphyne, where the acetylenic bonds are likely targets for a multitude of chemical functionalizations to achieve an even wider variety of properties. Through nonequilibrium molecular dynamics simulations, graphyne-based nanomaterials were found to have significantly poorer thermal properties compared to pristine graphene that was directly related to the number of acetylenic linkages present in the material and their structural arrangements. Due to the aforementioned combinations of electronic and thermal properties, graphyne-based nanomaterials might be ideal for thermoelectric applications. More crucially, graphyne allotropes were theoretically predicted to be exceedingly efficient separation and desalination membranes, owing to the excellent mechanical performance of graphyne-based materials, coupled with their tunable pore sizes. A broad variety of gas mixtures can potentially be purified with these membranes, especially for hydrogen and other small molecules such as oxygen and noble gases. Sheets of graph-n-yne may also revolutionize the engineering of desalination membranes, being capable of withstanding large hydrostatic pressures while highly discriminating of salts and other impurities. The combination of remarkable separation efficiency and low cost of production can lead to truly disruptive technologies for desalination membranes, drastically lowering the massive cost of operating and replacing membranes that are currently in use. Nonetheless, significant technological challenges stand in the way of this vision, such as roll-to-roll synthesis of large-area graph-n-yne monolayers with precise molecular control over the pore sizes, preventing stacking or agglomeration between sheets of graph-n-yne, or understanding the impact of graph-n-yne waste on the environment and human health. This quantum leap in multiscale design for the next generation of atomically thin, graphyne-based materials for high-performance separation membranes and other nanotechnologies can be fully realized by careful and tight integration of computational simulations and experimental data, allowing scientists and engineers alike to traverse heretofore unknown regions of the “Carbon Wonderland”.

Table 7.

γ-graph-n-ynes (Ref^[115])

Structure n	DFT E (GPa)
n=1	527a
n=2	453a
n=3	368a
n=4	307a
n=5	271a
n=6	235a