Electrochemically Induced Changes in TiO₂ and Carbon Films Studied with QCM-D

Abstract

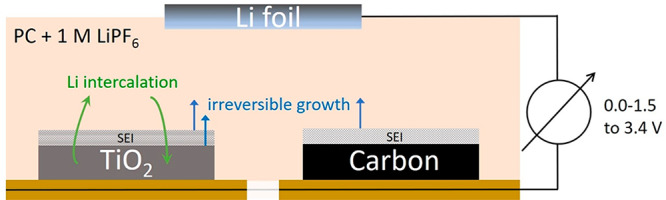
Semi-solid fluid electrode-based battery (SSFB) and supercapacitor technologies are seen as very promising candidates for grid energy storage. However, unlike for traditional batteries, their performance can quickly get compromised by the formation of a poorly conducting solid–electrolyte interphase (SEI) on the particle surfaces. In this work we examine SEI film formation in relation to typical electrochemical conditions by combining cyclic voltammetry (CV) with quartz crystal microbalance dissipation monitoring (QCM-D). Sputtered layers of typical SSFB materials like titanium dioxide (TiO₂) and carbon, immersed in alkyl carbonate solvents, are cycled to potentials of relevance to both traditional and flow systems. Mass changes due to lithium intercalation and SEI formation are distinguished by measuring the electrochemical current simultaneously with the damped mechanical oscillation. Both the TiO₂ and amorphous carbon layers show a significant irreversible mass increase on continued exposure to (even mildly) reducing electrochemical conditions. Studying the small changes within individual charge–discharge cycles, TiO₂ shows mass oscillations, indicating a partial reversibility due to lithium intercalation (not found for carbon). Viscoelastic signatures in the megahertz frequency regime confirm the formation and growth of a soft layer, again with oscillations for TiO₂ but not for carbon. All these observations are consistent with irreversible SEI formation for both materials and reversible Li intercalation for TiO₂. Our results highlight the need for careful choices of the materials chemistry and a sensitive electrochemical screening for fluid electrode systems.

1. Introduction

Novel solutions to grid energy storage such as semi-solid flow batteries (SSFBs) and flow supercapacitors (FSCs) have gained strong interest in the recent past.¹⁻⁶ Most of these systems store energy in electrode slurries of active and conductive particles suspended in an electrolyte. Here the active particles store charge through capacitance or redox reactions, while the conductive particles form extended networks that electronically wire the active particles to current collectors. The liquid-suspended state of the particles not only offers great flexibility in operating the battery but also poses new challenges. The reason lies in the dynamic structure of the fluid: imposed or thermal motions lead to rejuvenation of the particle assembly and hence also of the individual particle contacts. This repeated making and breaking of particle contacts causes the entire surface of each particle to be exposed to electrochemically induced changes. Because these surface modifications are incorporated in the (re)assembled particle aggregates or networks, vital processes in SSFBs or FSCs can get compromised.⁷⁻¹⁰

It is well-known that during electrochemical cycling surface layers termed solid–electrolyte interphase (SEI) can form on solid electrode components (see e.g. ref (11) for a recent review). These layers are formed by the decomposition of the electrolyte solution and impurities on the anode.¹¹⁻¹⁴ The SEI is typically ionically conductive and electronically insulating. SEI is a critical component of rechargeable lithium ion batteries as it passivates the anode and thus allows operation at potentials that exceed the thermodynamic stability window of the electrolyte. While essential for solid lithium ion batteries, such layer formation has been identified as potentially very detrimental to semi-solid flow systems.^9,15 It increases the interparticle resistance (and overall cell resistance) and decreases the mechanical strength of the conductive particle network. A mitigation strategy suggested by some researchers is to avoid SEI formation by using materials that operate within the electrochemical stability window of the electrolytes.^1,2,15 An example of this is the operation of lithium titanate (LTO) or TiO₂-based SSFB anodes (lithium intercalation potential: ∼1.5 V vs Li/Li⁺) at voltages above 1.0 V in alkyl carbonate solvents with LiPF₆.¹⁶ However, recent works have shown that significant detrimental effects due to layer formation can occur even within these conservative operating potential windows.^9,10 (In fact, even in the absence of an applied voltage, a very thin SEI layer can get formed through equilibration of the Fermi levels;^11,17 because of their nanometric thickness, these layers should not affect electron transport drastically.)

While there have been many studies on the formation and optimization of SEI, the scope of almost all has been traditional solid lithium batteries (e.g., refs (18−24)). A few studies have found indications of SEI layer formation within commonly used operating windows; however, these (relatively weak) effects were mostly not investigated further, probably because their relevance for traditional batteries was low. However, for SSFBs and FSCs, even thin SEI layers are potentially detrimental, as explained above. Examination for the presence and effect of thin SEI layers through the use of very (surface-) sensitive techniques is hence warranted for SSFB and FSC systems.

Electrochemical quartz crystal microbalance with dissipation monitoring (eQCM-D) is an emerging technique^25,26 which combines the recent extensions of QCM with electrochemical functionality (i.e., eQCM)^18,27,28 and dissipation mode (i.e., QCM-D).^29,30 The acoustic shear wave of a quartz resonator is used to probe the mass changes and viscoelastic characteristics of electrochemically deposited layers. The central part of the setup consists of a quartz disc (sensor area 79 mm²) enclosed between two metallic layers, of which one is additionally coated with the material of electrochemical interest. This electrode is immersed in an electrolyte within an electrochemical cell. While the cell potential is controlled, the mass and mechanical properties of the material deposited on the electrode are monitored by piezoelectrically exciting the crystal and measuring the “ring down” of the damped mechanical oscillation. This method is very suitable for in situ probing of the formation and characteristics of SEI layers.^23,31−33

In the present work we use eQCM-D to investigate two materials that have been studied in the context of SEI formation and growth in solid Li batteries: TiO₂^34,35 and carbon.^{18,19,21,36,37} Both these materials are also broadly available in the form of colloidal particles and are considered for use in fluid electrodes.^2,3,16 We examine these materials in the form of sputtered layers, immersed in alkyl carbonate solvents with 1 M LiPF₆ as in traditional lithium-ion batteries. While exploring typical voltages for these systems, we focus in particular on the mildly reductive regime where SEI formation is often ignored. Four increasingly reductive voltage windows are addressed, and many charge–discharge cycles are performed in each of them.

Another specific focus of the present work lies in the mechanical compliance of the growing SEI layer. Extracting these from the eQCM-D data is not trivial, since they have to be obtained by fitting to a viscoelastic model. Standard models such as Voigt–Kelvin are likely to be oversimplistic³¹ while for more sophisticated models the number of fit parameters should be kept appropriately small. We take these issues into account and also examine the effect of slightly different model choices on the fitted masses and compliances. Building on the outcome of our analysis, we find semiquantitative trends in the compliances, and quantitative information about the mass evolution. Besides the gradual evolutions over many cycles, we also examine the changes within single charge–discharge cycles. As we will show, the latter allows us to obtain additional insights from correlations between the elastic compliance, the mass, and the amount of injected charge.

2. Materials and Methods

2.1. Materials

Propylene carbonate (PC), ethylene carbonate (EC), and dimethyl carbonate (DMC) were obtained from Sigma-Aldrich (anhydrous, 99%+ purity). LiPF₆ (98% purity) and lithium foil (99.9% purity) were purchased from Alfa Aesar. All chemicals were stored in an argon-filled MBraun LABstar glovebox with H₂O and O₂ concentrations below 0.5 ppm. The electrolytes used in the experiments were 1 M LiPF₆ salt solutions in PC (viscosity: 8 mPa·s), unless mentioned otherwise.

2.2. Sensor Preparation

Gold-coated 5 MHz quartz QCM sensors (Renelux Crystal) were used. After cleaning, they were first coated with 200 nm of sputtered copper. Amorphous carbon films were then deposited by dc magnetron sputtering using a graphite (99.999%) target disk in an argon plasma at a pressure of 6.6 μbar. The film thickness was controlled via the deposition time and verified to be ∼77 ± 2 nm by using ellipsometry. Additional characterization with X-ray diffraction and confocal Raman microscopy revealed a disordered structure (see Figures S7 and S8 in the Supporting Information); also the carbon blacks used in SSFBs and LIBs³⁸ are relatively disordered (compared to graphitic carbon³⁹). TiO₂ films were prepared by reactive sputtering (dc power 500 W) of a titanium (99.999%) target. After the deposition of a few nanometers of pure Ti to aid adhesion, also oxygen gas (6 sccm) was admitted to the chamber to deposit an amorphous TiO₂ layer. Via control over the deposition time a thickness of ∼100 nm was obtained, with a peak-to-peak roughness <10 nm, as measured with AFM. A postannealing step was performed at 500 °C in an atmospheric environment for 8 h to crystallize the amorphous film to anatase; this preparation was done in accordance with ref (40), in which also the characterization results are described.

2.3. eQCM Cell

A custom eQCM cell (Figure 1) was designed to enable studying lithium-based electrochemistry in alkyl carbonate solvents. The cell uses a modified bottom holder of the commercial QSense EQCM cell (Biolin Scientific). The top part was fabricated out of PEEK and has channels to allow introduction of the electrolyte into the chamber via PEEK microfluidic connections. Directly above the fluid chamber is a replaceable lithium foil which acts as a counter electrode. The lithium foil and quartz sensor are sealed against the chamber with identical O-rings to keep their working area the same. The eQCM cell was assembled in the glovebox, completely sealed, and then connected to the QCM-D (Biolin Scientific) and electrochemical potentiostat outside. The electrode with the sputtered layer was at the common ground of both instruments.

Figure 1.

Cartoon of the eQCM cell. See text for further details.

2.4. Electrochemistry

The QCM-D cell was connected to a Biologic VSP300 potentiostat for electrochemical control. After a 1 h equilibration period resulting in a stable baseline (i.e., resonance frequency), the QCM-D measurement was initiated, and cyclic voltammetry sweeps were started from the open circuit potential. The CV’s were performed at a constant rate of 10 mV/s over four increasingly reducing voltage windows—all having 3.4 V vs Li/Li⁺ as the highest potential and with 1.5, 1.0, 0.5, and 0.0 V as the lowest potential.

2.5. QCM-D Analysis

Theory

The QCM-D measures, through a ring-down procedure, a complex resonance frequency f̑ that contains a real frequency f and a half-bandwidth Γ. We note here that the Q-sense QCM-D instrument outputs a dissipation factor which is a frequency-normalized bandwidth (D = 2Γ/f).

1

The instrument measures these values for multiple odd overtones n. In our experiments, we only consider the overtones from 5 to 13 as these are least affected by the mounting which can vary due to effects like O-ring swelling.⁴¹

As the QCM sensor is loaded (with a film, e.g., SEI), its complex resonance frequency shifts. If the shift is small compared to the reference resonance frequency, we can use the small load approximation (eq 2) which states that the shift is proportional to the load impedance (Z̃_load) on the crystal surface:⁴¹

2

where f₀ is the fundamental frequency of the unloaded crystal and Z_q the acoustic shear wave impedance of the AT cut quartz. For a thin film in liquid, using the small load approximation and referencing the shifts to the unloadeda immersed crystal, the complex shift is given by⁴¹

3

where n is the overtone number, m a mass, ρ a mass density, J̃(ω) the complex compliance at the frequency ω = 2πnf, and η a viscosity. The subscript f represents the deposited film while l refers to the liquid.

The complex compliance of the film J̃_f is defined as

4

where J′ and J″ are the frequency-dependent elastic and viscous compliances. The prefactor in eq 3 has the same form as the Sauerbrey equation (referenced to the bare crystal in liquid). Indeed, if the film has a zero viscoelastic compliance (a perfectly rigid film), the equation reduces to the Sauerbrey result. It can also be seen from eqs 3 and 4 that J′ affects the half-bandwidth Γ, while J″ affects the resonance frequency f.

Model Fitting

In principle, the above equations can be solved (using all overtones) to obtain the mass and viscoelastic properties; however, as the mass is not known a priori, this is not trivial. To reduce the number of fit parameters, we impose relations between the viscoelastic compliances at different frequencies. Because viscoelastic relaxation spectra inherently show a very gradual frequency dependence and the QCM-D probes only 1 decade in frequency, we can assume power law forms for both compliances. This approach is hardly restrictive and certainly preferable to overly simplistic models such as Kelvin–Voigt, which ignores the possibility that a material can have multiple relaxations. The power law compliances are given by

5a

5b

where the reference frequency is chosen close to the middle of the operating range (35 MHz). The viscoelastic exponents are determined by the spectral distance between the measurement frequency range and the layer material’s intrinsic relaxation frequencies. Assuming that no drastic changes in the material composition occur during the growth of the SEI layer, the exponents β′ and β″ can be considered as constant throughout the entire experiment. Because the elastic and viscous compliances are interrelated by the Kramers–Kronig relations, β′ must lie between −2 and 0 and β″ between −1 and 1.^41,42

Making reasonable estimates for ρ_f, we are left with 5 unknown parameters (m_f, J′_ref, β′, J″_ref, and β″) and 10 relations for 5 overtones. A method is now required to obtain reasonable initial guesses for these parameters to avoid trapping in local minima during fitting. A first estimate for m_f is obtained by fitting the Sauerbrey equation (J̃_f = 0) for all overtones. Using this value in the complex part of eq 3, we can directly calculate estimates for J′(ω) from the various half-bandwidth shifts and thus J′_ref and β′. While it is tempting to use the same method to approximate J″(ω), this would give erroneous results since m_f was already approximated from the frequency shifts. Instead, we first assume a constant (i.e., frequency independent) J″, estimated from the real part of eq 3 for the reference frequency. Using the above initial guesses, we systematically explore all combinations of viscoelastic exponents β′ and β″ while allowing m_f, J′_ref, and J″_ref to vary as fit parameters.

In this scheme, the time-dependent properties of the layer are found by fitting m_f, J′_ref, and J″_ref over the course of the entire experiment (i.e., voltage–time profile) while keeping β′ and β″ fixed. This fitting operation is performed for 100 different (β′, β″) combinations, as obtained by varying each exponent over the entire possible range, in steps of 0.2. The total mean-squared error (TMSE) of the fit is then mapped versus β′ and β″, after which the (β′, β″) combination that produces the minimum TMSE is chosen to obtain the time-dependent m_f, J′_ref, and J″_ref signals. A detailed description of the model fitting along with a discussion of the uncertainty in the fitted parameters can be found in the Supporting Information.

We mention here that we use in fact a slightly modified version of eq 3—a third-order perturbation analysis⁴¹ equation that contains (small) corrections to deal with violations of the small load approximation. Frequency and half-bandwidth shifts that were large enough to necessitate this correction were mainly found in the last (i.e., fourth) stage of the experiment. The Supporting Information (section 1.1) contains a brief description of this equation. Also, the effects of SEI multilayers and roughness are briefly discussed in sections 1.5 and 1.6.

3. Results and Discussion

3.1. Measured QCM-D Signals and Model Fits

In Figure 2 the direct output signals from the QCM-D instrument, i.e., the frequency and half-bandwidth shifts, of the various overtones for the four different voltage regimes are shown (solid lines and circles). The current responses of the cyclic voltammograms are shown in Figure S9. The experiments on the different materials are grouped for comparison, as TiO₂ is a good intercalation material while amorphous carbon is not.

Figure 2.

Applied cell potential (top), frequency shift (middle), and half-bandwidth shift (bottom) for TiO₂ (left) and carbon (right) electrodes when cycled over four voltage windows of 25 cycles each. The various odd overtones (5–13) are shown in different colors. Both experimental data and model fits are shown as solid lines, where the half-bandwidth shifts have been Savitzky–Golay (SG) smoothed to reduce noise. To highlight the slow changes, markers have been added: (○) for experiments and (×) for fits. Note that the frequency shifts are in kHz, while it is Hz for the half-bandwidth shifts.

It is clear that for both materials, over time scales much longer than one CV cycle, the (kilohertz range) negative frequency shift gets progressively larger, with sudden changes in the slope at the points where a more reductive voltage regime is entered. The (hertz range) half-bandwidth shift also increases with time for most regimes—the only exception being the amorphous carbon in the most reductive regime. A noticeable difference between the TiO₂ and the carbon is that the former material shows very clear oscillations in Δf and ΔΓ, in phase with the charge–discharge cycles (as we will see below).

Also shown in Figure 2 are model fits to the data. All frequency shift differences are below 50 Hz, and half-bandwidth shift differences are below 8 Hz (see Figures S2 and S3). The root-mean-squared fitting error was below 25 Hz for all overtones, which corresponds to a Sauerbrey mass “fitting error” of around 5 × 10^–7 kg/m². This error is of the same magnitude as the measurement noise. The goodness of fits and trends were not affected by small variations of the grid fit parameters (β′, β″). See Supporting Information section 1 for a discussion about the accuracy and robustness of the fitting.

3.2. Global Changes in Mass and Viscoelastic Compliance

Assuming that the shifts are due to a uniform viscoelastic layer and using the model described in section 2.5, we obtain the QCM areal mass density (m_f) shown in Figure 3. Here m_f is plotted along with a theoretical areal lithium mass density (m_e). The latter signal should be helpful in the detection of processes other than Li intercalation. To find m_e, we integrate the current and convert the obtained faradaic charge to an areal mass of lithium atoms. We henceforth refer to the areal mass as just the mass.

Figure 3.

m_e (red), m_f (blue), J′(35 MHz) (orange), and J″(35 MHz) (purple) derived from the model in section 2.5 for the experiment in Figure 2. Dashed vertical lines highlight the cycles examined in Figure 4. Viscoelastic compliances have been SG smoothed and share the same scale for both experiments.

For both materials, m_f and m_e are observed to grow irreversibly with time. In the first few cycles of the initial (i.e., least reductive) regime, the two signals are similar but well before the end of that regime, m_f gets significantly larger than m_e, and the difference keeps growing. We emphasize here that a difference between the m_e and m_f signals implies the (co)occurrence of process(es) that differ from Li intercalation. The irreversible mass increases, along with differences between the m_e and m_f, thus indicate the formation of a solid–electrolyte interphase. The parallel occurrence of irreversible lithium intercalation cannot be excluded; the good correspondence between m_e and m_f in the early stage suggests that this process does take place as well.

It is remarkable that for both the TiO₂ and the carbon significant irreversible layer growth is found even in the least reducing voltage window of 1.5 V, well within the (for traditional Li batteries) accepted operating window of the electrolyte. Assuming a layer density of 1500 kg/m³, we find that the layers on both surfaces are already several nanometers thick after a few CV cycles. (The consequences of choosing a different layer density are discussed in Supporting Information section 1.4; there we show that m_f remains essentially unaffected while J′_ref and J″_ref change but their trends do not.) By the end of the 25 cycles a thickness of ∼20 nm is reached. While such thin layers are of minimal consequence in solid lithium ion batteries, flow systems can be strongly affected by thin layers (especially if the latter are insulating). Electron conduction paths between current collectors and active particles generally involve a huge number of interparticle contacts. When the particles are very close (as in a gel network), conduction is governed either by fluctuation-induced tunneling or by the limiting intrinsic electronic conductivity of the separating medium.^43,44 In the respective cases, there is an inverse exponential or inverse dependence of the conductivity on the insulating gap length. In traditional solid electrode systems, the interparticle contacts themselves are static. Therefore, most contacts are exposed to little electrolyte or protected by the binder. The overall electrode resistance is then only slightly affected by thin SEI. In SSFB systems, however, particle contacts are refreshed due to restructuring by flow. The incorporation of many of these thin insulating layers in the conduction path can thus have a dramatic effect on the electrode resistance.⁹

As a general trend, on continuing the cycling inside a given voltage window, the layer properties tend to saturate (i.e., the SEI growth rate tends to decrease). When a new, more reducing window is started, the growth rate generally increases again, presumably due to a greater potential drop over the pre-existing layer and/or the activation of new reactions. One exception can be found for the carbon sample, where the growth rate strongly decreases right at the beginning of the 0 V window. Here, the SEI layer is calculated to be around 100 nm thick, which is still well below the penetration depth (the maximum sensing depth) of the shear wave through it (∼900 nm at 65 MHz). The slowing down of the layer growth is thus real. This might be due to an almost complete passivation of the carbon electrode.

Figure 3 also shows the global variation of the elastic and viscous compliances, which are of comparable magnitude. In general, cycling at more reducing voltages diminishes both compliances, i.e., stiffens the layer. During the initial cycles when the layers are still very thin, the contribution of the compliance term to eq 3 is too small to resolve it with accuracy.

3.3. Changes per Voltage Cycle

The second cycle of each voltage window of the experiment in Figure 2 is plotted as a cyclic voltammogram in Figure 4. In addition to the current, also the changes in m_e and m_f (referenced to the beginning of the cycle) are plotted. The signals corresponding to Δm_f are relatively noisy, as the mass changes within each cycle are small and close to the noise limit (σ ≈ 5 × 10^–7 kg m^–2) of the QCM-D for this system.

Figure 4.

CVs with current (black ○) and change in m_e (red ×) and m_f (blue ×) for the second cycle of each window (highlighted in Figure 3). In each cycle the potential vs Li/Li⁺ starts at 3.4 V and returns there after a clockwise trajectory in the I–V plot. Also, the m–V curves run clockwise. Left: TiO₂. Right: carbon. For each sample the axis scales are kept the same to allow comparison.

In the TiO₂ sample, both mass changes are largely reversible within a single cycle. Below ∼2.5 V the current starts to increase and consequently also m_e. m_f closely follows the trend of m_e, suggesting that most of its growth is due to lithium intercalation. On the reverse half-cycle, the reduction in m_e is also closely followed by m_f, again pointing at lithium (de)intercalation as the dominant process. At the end of the cycle there is a small overall positive growth in both the m_e and m_f, in agreement with the trend over multiple cycles shown in Figure 3. This net effect per cycle is thus significant and is attributed to irreversible SEI growth, along with a possible contribution from irreversible intercalation. Of note is how close the values and trends of the changes of m_f and m_e are, lending confidence to the accuracy of the analysis.

For the carbon sample, the currents and mass changes are significantly smaller than for TiO₂, causing the m_f signals to be even more noisy. The behavior is qualitatively different from TiO₂: while both m_f and m_e grow upon reducing the voltage, in the reverse part of the cycle only a slight decrease in m_e is seen while m_f appears to remain constant (or even grow a little). This clearly suggests that the growth of m_f is not determined by reversible lithium intercalation.

3.4. Changes per Charge–Discharge Cycle

So far, a cycle has referred to the cell starting at 3.4 V, going down to the low voltage boundary (1.5/1.0/0.5/0.0 V) and then back up to the initial voltage. However, in this potential based scheme, the growth or shrinkage of a layer is not complete at the end of a cycle (see Figure 5). The layer changes the least when the current is zero. We henceforth use every third current zero crossing to demarcate cycles.

Figure 5.

Top: typical cell graph of potential and current versus time (here for TiO₂ in the most reductive voltage window; 340 s per cycle). The blue arrows indicate voltage-based cycles while the orange ones designate current-based cycles. Bottom: the change in m_e with the growth (red arrows) and shrinkage (green arrows).

We now look at the changes in the viscoelastic compliance and the mass during the second cycle of each window (Figure 6). Again, the changes are referenced to the beginning of the cycle. For the first voltage window, for both samples, the compliance signals are very noisy and difficult to extract, even though a change in mass is easily detected. This is because the layer is still extremely thin (∼2 nm).

Figure 6.

First column: plots of the change in m_e (red ○) and m_f (blue ×). Second column: the viscoelastic compliances J′(35 MHz) (orange) and J″(35 MHz) (purple) versus time for the second cycle of each voltage window of the experiment in Figure 2. For the compliances both the raw (light thin lines) and SG smoothed (dark thick lines) data are shown. Left: TiO₂. Right: carbon.

For the subsequent voltage widows, the TiO₂ sample shows a noticeable change in the elastic compliance J′ when the mass changes. When lithium is intercalated into a host, it can change the structure and consequently the mechanical properties of the latter. Lithium intercalation is known to decrease the compliance of metal oxides and layered materials, while it increases the compliance of materials it alloys with.⁴⁵ The changes in the elastic compliance may thus be related to lithium intercalation. At the end of the cycles for TiO₂, the elastic compliance almost returns to its original value after deintercalation. However, the recovery is not full. This can be seen from the general reduction of the elastic compliance as cycling is continued (see Figure 3).

We add here that for the TiO₂ sample the raw data show a strong change in the half-bandwidth shift (which is directly proportional to the layer’s elastic compliance and mass; see eq 3) in the two distinct stages of the charge–discharge cycle. Here the bandwidth shift decreases despite the layer mass increasing, and vice versa. Thus, the trend in the compliance is not a spurious fitting effect induced by the changing layer mass.

A second observation for the TiO₂ sample is that Δm_f is not precisely equal to Δm_e, as would be expected for a perfectly reversible lithium intercalation. In particular, the amplitude of Δm_e per half-cycle is somewhat larger than Δm_f, and the same for the “reversible mass change” (Δm^max – Δm^final) per cycle. The meaning hereof it is not precisely clear. Assuming that the fitted m_f accurately represents the real mass, some reversible side reaction would be implied—electron transfer without mass deposition on the QCM electrode.

For the carbon sample, despite significant mass changes, the changes in compliance are only minor (while still leading to a small overall decrease per cycle; see Figure 3). Lithium insertion in layered carbons is expected to have a much stronger effect on the compliance than that in metal oxides. Our findings thus imply that the mass change of the carbon layer is mainly due to SEI growth and not irreversible lithium insertion.

3.5. Correlation between Changes in Mass and Compliance

We extend our analysis of the charge–discharge cycles by correlating the net changes in m_f, m_e, and J′(35 MHz) per half-cycle. Defining the cycles as in Figure 5, Δm_e will inherently be positive in the first half-cycle and negative in the second one. Accordingly, we define the first half-cycle as “growth” and the second one as “shrinkage” (which thus refers strictly to m_e). To facilitate comparison of the magnitudes, we take the negative of Δm_e in the shrinkage regime and denote it as Δ_sm_e. For notational consistency, Δm_e in the growth regime is just replaced with Δ_gm_e. Similar definitions are applied to Δm_f and ΔJ′. It is noted here that m_f does not have to change in the same direction as m_e; one case was encountered where m_f increased during “shrinkage”. This was however an exception. For the far majority of our data, the diagnosis becomes more straightforward with these definitions. For example, comparisons between Δ_gm_f and Δ_sm_f (of the same cycle) allow examination of the reversibility of mass deposition, while differences between Δ_gm_e and Δ_sm_e indicate irreversible electron transfer.

Figure 7 shows the (half-cycle) changes in m_f, m_e, and J′ for the entire experiment, for TiO₂ (left panel) and carbon (right panel). Important differences between the two materials become immediately evident. For the TiO₂ sample, Δm_e is similar to the total mass change, for nearly all half-cycles and irrespective of the (growth or shrinkage) stage. In fact, the magnitude of Δm_e is even somewhat larger than that of Δm_f (as already noted above). The near equality of Δ_gm_e and Δ_sm_e indicates a high degree of reversibility, which would also be expected for lithium intercalation. The changes in m_f are largely reversible as well, albeit less so than for m_e (this causes the overall m_f to grow over m_e as seen in Figure 3). Looking at the elastic compliance J′, a strong anticorrelation with both m_e and m_f is observed. This corroborates lithium intercalation.

Figure 7.

Cycle by cycle growth (red) and shrinkage (green) of (top) m_f (×) and m_e (○) and (bottom) J′(35 MHz) for TiO₂ (left) and carbon (right). J′ data are omitted for the first four cycles for both experiments. Note that the vertical scales for the carbon sample are much smaller than for TiO₂.

For the carbon sample the mass changes are significantly smaller than for the TiO₂. Here the Δm_e signals are generally smaller than Δm_f (except for the most reductive voltage window where Δm_f has become very small), indicating the occurrence of other processes than Li intercalation. The changes in m_f are less reversible (compared to m_e) also for this material. Meanwhile, the changes in elastic compliance fluctuate randomly. The m_f and m_fe growths are weakly correlated while the shrinkages are not. These correlations (further illustrated in Figure S10) indicate (more clearly now) that the majority of the mass changes in the carbon sample are due to irreversible SEI formation in the growth stage (Δm_e > 0).

3.6. Cycling of Carbon Directly to 0 V

We continue our study of the carbon system in PC with 1 M LiPF₆ by cycling directly over the entire voltage range as done in traditional lithium battery systems: between 3.4 and 0 V. This corresponds to the fourth voltage window in the previous experiment, but with a different electrochemical history since we now start with pristine carbon (not yet covered by SEI).

Figure 8 shows the masses and viscoelastic compliances extracted from the QCM-D and current measurements, similar to Figure 3. During the initial cycles, there is significantly larger (approximately an order of magnitude) SEI growth per cycle as compared to cycling the pristine carbon in a 1.5 V voltage window (Figure 3). Again, the gradual mass changes are much stronger for m_f than for m_e, while this time there is almost no reversibility in m_f within the cycle. As the cycling is continued, the layer growth slows down while approaching a slightly larger thickness as compared to Figure 3. The elastic compliance is very similar to that in Figure 3, while the viscous compliance is higher now; this could indicate slight differences in the structure of the SEI formed in different voltage regimes. Importantly, cycling to strongly reducing voltages thus leads to quicker formation of an irreversible thick SEI, which is potentially catastrophic to flow systems.

Figure 8.

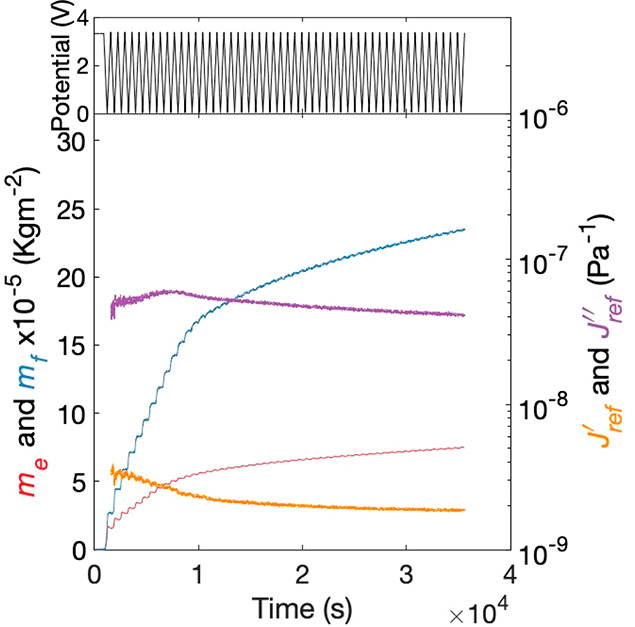
Carbon layer cycled to 0 V for 50 cycles. Top: applied cell potential. Bottom: m_e (pink), m_f (blue), J′(35 MHz) (orange), and J″(35 MHz) (purple) versus time.

3.7. Cycling of Carbon in EC:DMC Electrolyte

In Figure 9 we examine the behavior of the carbon layer in a different electrolyte: EC-DMC with 1 M LiPF₆, subsequently exploring two voltage windows: 3.4–1.5 and 3.4–0 V. Though the growth in m_e is similar to that in Figure 3, the growth in m_f is much larger. Thus, more SEI mass per unit charge is deposited in EC-DMC as compared to PC. In addition, the viscoelastic compliances are much higher (along with the half-bandwidth shift). Because of the latter, the QCM-D was unable to track the experiment beyond the 49th cycle. Assuming a similar mass density, the layer is around 15 nm thick after just the first cycle and grows to over 200 nm at the end of the experiment. The partial reversibility in m_f per cycle, evidenced by temporary mass decreases, largely disappears already after the first few cycles. Thus, in EC:DMC a permanent, “fluffier” and heavier SEI than that in PC is formed at the same voltages. Such a layer, if insulating, would almost completely block electron transfer in a flow system. We note here that due to the much higher layer compliance; the model fits and outputs are very sensitive to the viscoelastic parameter choices unlike the previous experiments.

Figure 9.

Carbon layer in EC DMC 1 M LiPF₆ cycled over two voltage windows. Top: applied cell potential. Bottom: m_e (pink), m_e (blue), J′(35 MHz) (orange), and J″(35 MHz) (purple) versus time.

4. Conclusions

Using the sensitive eQCM-D, we have shown the formation of surface layers on carbon and TiO₂ surfaces (that emulate fluid electrode particles) in an alkyl carbonate solvent with dissolved LiPF₆ during electrochemical cycling. Applying increasingly reductive potentials, the same gradual evolutions are observed for TiO₂ and carbon: an irreversible growth in deposited mass and the formation of a viscoelastic layer. Focusing on the changes within individual charge–discharge cycles reveals additional information. For TiO₂ the mass changes per cycle are dominated by reversible Li intercalation, but the net effect of the cycle is a systematic mass growth, attributed to SEI. Also for carbon a systematic mass growth is observed, but without clear indications for reversible intercalation. Correlating the changes in the mass and elastic compliance per cycle, we find a strong anticorrelation for TiO₂ and a lack of correlation for carbon. This underlines that while both intercalation and SEI growth lead to mass deposition, the former reduces the elastic compliance while the latter does not.

Our finding that even when cycling to 1.5 V vs lithium (a voltage considered to be within the operating window of most alkyl carbonate electrolytes) surface layers tens of nanometers thick form is of significance for slurry-based electrodes, whose performance can be destroyed by thin insulating layers. Operating at less conservative voltages results in an even more SEI layer formation and layer thicknesses up to O(100 nm). Our observations thus highlight the need for careful screening of systems for fluid electrode technologies, as they can be affected by SEI in operating regimes traditionally considered free of it.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsaem.9b02233.

• Accuracy and robustness of the viscoelastic modeling: (a) third-order perturbation analysis, (b) quality of overall fit as a function of viscoelastic exponents, (c) fitted mass and compliances as a function of viscoelastic exponents, (d) fitted mass and compliances as a function of estimated layer density, (e) effect of multilayers, and (f) effect of roughness; other graphs: (i) confocal Raman microscopy of carbon layer, (ii) X-ray diffraction of carbon layer, (iii) cyclic voltammograms, and (iv) correlation plots for the shrinkage and growth of mass and elastic compliance (PDF)

The authors declare no competing financial interest.