Abstract
Background
Induced hypertension has been used to promote cerebral blood flow under vasospastic conditions although there is no randomised clinical trial to support its use. We sought to mathematically model the effects of vasospasm on the cerebral blood flow and the effects of induced hypertension.
Methods
The Anatomically Detailed Arterial Network (ADAN) model is employed as the anatomical substrate in which the cerebral blood flow is simulated as part of the simulation of the whole body arterial circulation. The pressure drop across the spastic vessel is modelled by inserting a specific constriction model within the corresponding vessel in the ADAN model. We altered the degree of vasospasm, the length of the vasospastic segment, the location of the vasospasm, the pressure (baseline mean arterial pressure [MAP] 90 mm Hg, hypertension MAP 120 mm Hg, hypotension), and the presence of collateral supply.
Results
Larger decreases in cerebral flow were seen for diffuse spasm and more severe vasospasm. The presence of collateral supply could maintain cerebral blood flow, but only if the vasospasm did not occur distal to the collateral. Induced hypertension caused an increase in blood flow in all scenarios, but did not normalise blood flow even in the presence of moderate vasospasm (30%). Hypertension in the presence of a complete circle of Willis had a marginally greater effect on the blood flow, but did not normalise flow.
Conclusion
Under vasospastic condition, cerebral blood flow varies considerably. Hypertension can raise the blood flow, but it is unable to restore cerebral blood flow to baseline.
Keywords: Cerebral vasospasm, Modelling, Induced hypertension, Subarachnoid haemorrhage
Introduction
Cerebral vasospasm and delayed cerebral ischaemia are the principal causes of the poor outcome in patients admitted to tertiary care centres with acute subarachnoid haemorrhage. Although numerous treatment paradigms have been tried, a major breakthrough is yet to be discovered. For approximately 30 years, triple-H therapy − hypertension, hypervolaemia, and haemodilution − has been used with the hope of improving cerebral perfusion [1]. These changes seek to alter various components of Poiseuille's law to improve flow through the arterial system and increase cerebral perfusion. However, this treatment is not supported by randomised controlled trials, and there is a risk of complications and side effects. Of the three different components of the treatment, induced hypertension appears to be the only component that is successful in increasing cerebral perfusion [2].
We sought to model the effects of varying degrees of vasospasm on the distal cerebral arteriolar pressure and the effect of induced hypertension. In addition, we also analysed the differing effect of focal and diffuse spasm as well as the effect of the circle of Willis (CoW).
Materials and Methods
Circulation Model
The Anatomically Detailed Arterial Network (ADAN) model is employed as the anatomical substrate in which the cerebral blood flow is simulated as part of the simulation of the whole body arterial circulation [3, 4]. The ADAN model represents an average arterial vasculature of a male subject and includes over 2,200 arterial vessels, supplying blood to 28 specific organs (brain, liver, etc.) and 116 distributed vascular territories (skin, muscles, etc.).
Importantly, since our goal is to analyse the impact of vasospasms on the cerebral circulation, the anatomy of the CoW is a major determinant of blood distribution to the brain. This is why we consider two different scenarios in this work: (1) A complete CoW with both anterior and posterior communicating arteries. (2) An incomplete CoW with neither anterior nor ipsilateral posterior communicating arteries.
The ADAN model employed represents a patient-generic scenario in which conditions can be computationally simulated with the aim of gaining insight into the outcomes of the location and severity of vasospasms in the cerebral circulation.
Mathematical Model
Blood flow is modelled using a one-dimensional version of the Navier-Stokes equations to describe the flow of an incompressible Newtonian fluid in compliant vessels. In a single-vessel model, this amounts to solve the following set of non-linear partial differential equations, which stand for the conservation of mass and momentum:
where Q is the flow rate, A is the lumen area, P is the blood pressure described in the space-time domain (t, x) ∈ (0, T) × (0, L) defined by the vessel length L and by the cardiac period T. In the system (1) to (2), parameters ρ and μ are blood density and viscosity, respectively. In addition, the hypothesis of a Poiseuille velocity profile has been assumed to account for the viscous dissipation.
In order to relate the blood pressure to the lumen area, we consider the following constitutive equation:
where
with R, A = πR2 (Ro, Ao being reference values of the vessel radius and area, respectively, at the reference pressure Po = 1 × 105 dyn/cm2). In equation 3, h is the arterial wall thickness, and EE and EC are effective stiffness moduli for the elastin and collagen components, respectively. Finally, εo and εr account for the fibre recruitment through the localisation and width of the distribution of the fibre strain activation. When connecting vessels to form a network, junctions are created at which the following coupling conditions are considered:
with NT the number of arterial segments converging at the junction. Since the model is truncated at a certain arterial generation, the remaining downstream vasculature is incorporated through the following lumped parameter models:
where PT is a reference terminal pressure, C is the peripheral compliance, and RA and RB are resistive elements which represent the viscous resistance in the peripheral beds.
The system of equations formed by (1) to (6) is numerically solved using the methodology described by Müller et al. [5]. To guarantee a periodic state, ten cardiac cycles are simulated in each case. The parameters in the ADAN model are calibrated according to the criteria proposed by Blanco et al. [3]. Blood flow is documented as mL/min and pressure as mm Hg.
Spastic Scenarios
The vasospasm of a given vessel is modelled by introducing a constriction in the vessel. The pressure drop across the spastic vessel is modelled by inserting a specific constriction model within the corresponding vessel in the ADAN model. This model, which has exhaustively been employed in modelling the blood flow through constricted vessels [6, 7, 8, 9], relates the pressure drop across the constriction with the flow rate through the vessel as follows [10]:
where U = Q ∣ A is the blood velocity, Ls represents the spastic extension length, As is the minimum area in the spastic vessel, and Kv, Kt, and Ku are parameters to characterise the pressure drop due to viscous dissipation, turbulence, and inertial effects [10].
In this work we considered spastic scenarios of two kinds, focal and distributed, more specifically: (1) focal spasm assumed to have a length of 10 mm − chosen so as to limit the stenosis to a single arterial segment, e.g., only M1; (2) distributed spasm assumed to have a length of 30 mm − chosen to affect a length of artery greater than an individual segment, e.g., M1 and M2.
We selected varying degrees of vasospasm to determine the effects that this would have on flow in the distal vessels. For each spastic segment we chose a reduction in the diameter of the vessel of 30, 50, and 70% in keeping with moderate, severe, and critical vasospastic conditions.
We chose to model vasospasm unilaterally in the left internal carotid artery (ICA), the left middle cerebral artery (MCA), and both. We chose not to model vasospasm in the anterior cerebral artery (ACA) in order to limit the number the potential variables and to observe the effects of vasospasm in the ICA and MCA on the flow in the ACA.
The baseline modelling assumptions described above were performed at a mean arterial pressure (MAP) of 90 mm Hg. In order to determine the effect of induced hypertension on the flow, we repeated the simulations with an MAP of 120 mm Hg. This was achieved by increasing peripheral arterial resistance in the entire model. We also modelled the effects of hypotension with an MAP of 73 mm Hg.
Thus, the combination of the anatomical variations of the CoW (complete or incomplete), with the possibility of developing focal and distributed vasospasm as well as the chance of vasospasm occurring in different vessels and the arterial pressure levels, resulted in a battery of 180 simulation scenarios.
The model predictions were analysed using a baseline model reference solution. This reference solution was obtained simulating the blood flow in the ADAN model in its original state, i.e., with a complete CoW, with no vasospasm, and with an MAP of 90 mm Hg.
Results
Using the various parameters described above, we analysed the changes in blood flow along the whole cerebral vasculature. The results of the changes in the anterior circulation are summarised in Table 1.
Table 1.
Overall results of flow reduction as a percentage of baseline in the different vessels according to the different variables tested
| Incomplete CoW |
Complete CoW |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACA L | ACA L Hype | ACA L Hypo | MCA L | MCA L Hype | MCA L Hypo | ACA L | ACA L Hype | ACA L Hypo | MCA L | MCA L Hype | MCA L Hypo | |
| ICA_30d | 87.2 | 92.2 | 81.4 | 86.7 | 94.6 | 78.3 | 94.7 | 96.0 | 88.8 | 94.0 | 95.4 | 85.2 |
| ICA_50d | 64.0 | 70.7 | 57.8 | 62.8 | 71.8 | 54.9 | 91.3 | 93.5 | 84.5 | 90.2 | 92.7 | 80.6 |
| ICA_70d | 28.5 | 34.4 | 23.9 | 26.8 | 33.9 | 21.8 | 89.0 | 92.0 | 81.5 | 87.5 | 91.0 | 77.4 |
| MCA_30d | 100.6 | 103.5 | 95.9 | 83.0 | 91.0 | 74.9 | 100.6 | 100.4 | 95.7 | 83.0 | 85.8 | 74.8 |
| MCA_50d | 101.7 | 104.3 | 97.0 | 56.1 | 64.2 | 49.3 | 101.4 | 101.2 | 96.6 | 56.1 | 60.5 | 49.2 |
| MCA_70d | 103.2 | 105.8 | 98.5 | 16.6 | 20.2 | 13.8 | 102.7 | 102.4 | 97.8 | 16.5 | 19.0 | 13.8 |
| ICA_30f | 92.4 | 96.6 | 87.0 | 92.1 | 99.3 | 83.9 | 96.3 | 97.2 | 90.8 | 95.8 | 96.8 | 87.3 |
| ICA_50f | 73.3 | 79.1 | 67.3 | 72.3 | 80.7 | 64.4 | 92.7 | 94.5 | 86.3 | 91.7 | 93.8 | 82.5 |
| ICA_70f | 37.6 | 43.5 | 32.6 | 35.9 | 43.4 | 30.3 | 89.6 | 92.4 | 82.3 | 88.2 | 91.4 | 78.2 |
| MCA_30f | 100.3 | 103.2 | 95.5 | 91.0 | 98.2 | 83.0 | 100.3 | 100.2 | 95.4 | 91.0 | 92.5 | 82.9 |
| MCA_50f | 101.1 | 103.9 | 96.4 | 70.5 | 78.4 | 63.2 | 101.0 | 100.8 | 96.1 | 70.5 | 73.9 | 63.1 |
| MCA_70f | 102.9 | 105.5 | 98.2 | 24.7 | 28.5 | 20.4 | 102.5 | 102.2 | 97.6 | 24.7 | 26.8 | 20.3 |
| ICA_30d_MCA_30d | 88.7 | 93.4 | 83.1 | 73.4 | 82.2 | 65.2 | 95.5 | 96.6 | 89.7 | 78.5 | 82.2 | 69.9 |
| ICA_30d_MCA_50d | 91.2 | 95.5 | 85.7 | 51.0 | 59.3 | 44.2 | 96.9 | 97.7 | 91.2 | 53.6 | 58.4 | 46.5 |
| ICA_30d_MCA_70d | 95.0 | 99.1 | 89.5 | 15.5 | 19.0 | 12.8 | 98.8 | 99.5 | 93.2 | 16.0 | 18.4 | 13.2 |
| ICA_50d_MCA_30d | 66.2 | 72.6 | 60.1 | 54.9 | 63.8 | 47.4 | 92.4 | 94.3 | 85.7 | 75.8 | 80.1 | 66.6 |
| ICA_50d_MCA_50d | 70.2 | 76.4 | 64.1 | 40.3 | 48.1 | 34.0 | 94.0 | 95.6 | 87.5 | 52.1 | 57.2 | 44.7 |
| ICA_50d_MCA_70d | 77.4 | 83.7 | 70.9 | 13.0 | 16.4 | 10.4 | 96.4 | 97.7 | 90.0 | 15.6 | 18.1 | 12.8 |
| ICA_70d_MCA_30d | 29.9 | 35.9 | 25.2 | 24.3 | 31.1 | 19.5 | 90.2 | 92.8 | 82.9 | 73.8 | 78.7 | 64.3 |
| ICA_70d_MCA_50d | 32.7 | 39.1 | 27.8 | 19.3 | 25.1 | 15.2 | 92.1 | 94.2 | 84.9 | 51.1 | 56.4 | 43.5 |
| ICA_70d_MCA_70d | 39.7 | 47.2 | 33.7 | 7.0 | 9.6 | 5.2 | 94.8 | 96.6 | 87.9 | 15.4 | 17.9 | 12.5 |
| ICA_30f_MCA_30d | 93.7 | 97.6 | 88.5 | 77.4 | 85.9 | 69.3 | 97.1 | 97.7 | 91.7 | 79.9 | 83.3 | 71.5 |
| ICA_30f_MCA_50d | 95.8 | 99.4 | 90.6 | 53.3 | 61.5 | 46.5 | 98.3 | 98.8 | 93.0 | 54.4 | 59.1 | 47.4 |
| ICA_30f_MCA_70d | 98.8 | 102.3 | 93.7 | 16.0 | 19.6 | 13.3 | 100.1 | 100.4 | 94.8 | 16.2 | 18.6 | 13.4 |
| ICA_50f_MCA_30d | 75.6 | 81.1 | 69.8 | 62.6 | 71.4 | 55.0 | 93.7 | 95.2 | 87.4 | 76.9 | 80.9 | 68.0 |
| ICA_50f_MCA_50d | 79.5 | 84.7 | 73.8 | 45.1 | 53.1 | 38.7 | 95.2 | 96.4 | 89.1 | 52.8 | 57.7 | 45.5 |
| ICA_50f_MCA_70d | 86.2 | 91.3 | 80.2 | 14.3 | 17.7 | 11.6 | 97.5 | 98.5 | 91.4 | 15.8 | 18.3 | 12.9 |
| ICA_70f_MCA_30d | 39.4 | 45.4 | 34.4 | 32.4 | 39.6 | 27.0 | 90.8 | 93.2 | 83.6 | 74.4 | 79.1 | 64.9 |
| ICA_70f_MCA_50d | 43.0 | 49.2 | 37.8 | 25.3 | 31.5 | 20.6 | 92.6 | 94.6 | 85.6 | 51.3 | 56.6 | 43.8 |
| ICA_70f_MCA_70d | 51.3 | 58.4 | 45.1 | 9.0 | 11.7 | 6.9 | 95.3 | 96.9 | 88.4 | 15.4 | 18.0 | 12.5 |
ACA, anterior cerebral artery; CoW, circle of Willis; d, distributed spasm; f, focal spasm; Hype, hypertension; Hypo, hypotension; ICA, internal carotid artery; L, left vessel; MCA, middle cerebral artery.
Effect of Vasospasm Severity
The changes in flow distal to the vasospasm were related to the degree of vasospasm, with the largest drops in flow seen in cases of the most severe vasospasm. For example, flow in the MCA dropped by 17% in response to a focal 30% reduction in the diameter of the M1 segment, whereas it dropped by over 83.6% when the degree of vasospasm increased to 70%.
Focal versus Diffuse Spasm
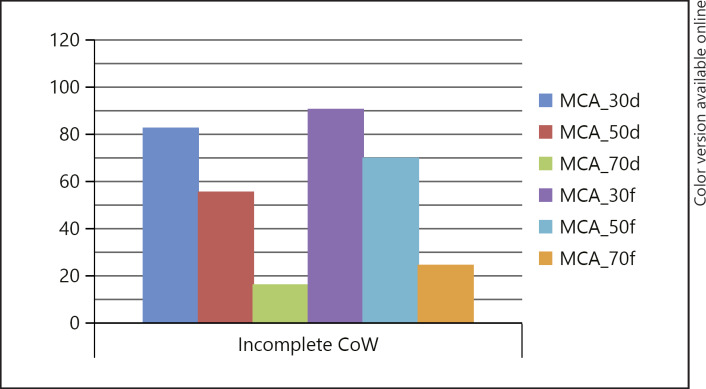
Larger decreases in cerebral flow were seen for diffuse spasm relative to focal spasm (Fig. 1). For example, with 50% narrowing of the MCA, the flow was 70.5% of normal when the spasm was focal; however, the flow was only 56.1% of normal if the spasm was diffuse within the MCA. This greater decrease in flow associated with diffuse spasm compared to focal spasm was also seen for the ICA. Furthermore, if diffuse vasospasm was present in two connected arteries, there was a greater reduction in cerebral blood flow than if there was focal and diffuse vasospasm. For example, focal 70% ICA spasm and diffuse 50% spasm resulted in a 50.8% decrease in blood flow in the MCA territory; however, diffuse 70% ICA stenosis and diffuse 50% MCA stenosis resulted in an 80.7% decrease in blood flow.
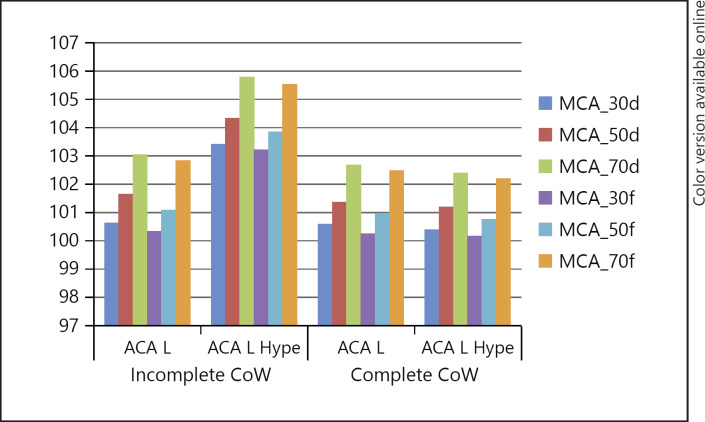
Fig. 1.
Diffuse vasospasm of the MCA results in greater decreases in blood flow even if the degree of vasospasm is the same. The results were the same with a complete CoW. CoW, circle of Willis; d, distributed spasm; f, focal spasm; MCA, middle cerebral artery.
Complete versus Incomplete CoW
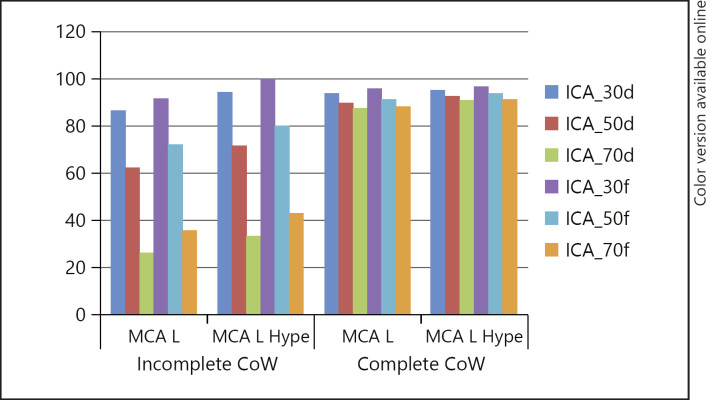
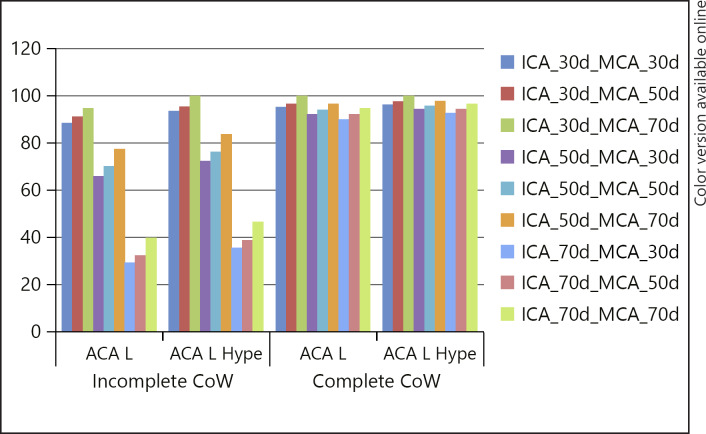
The presence of a complete CoW maintained blood flow in the ACA at near normal levels despite the presence of severe vasospasm affecting the ICA. For example, in the presence of diffuse 70% stenosis of the ICA there was an 11% reduction in blood flow, whereas there was a 71.5% drop in blood flow when the CoW was incomplete. Similarly, flow in the MCA was well maintained in the presence of ICA vasospasm if there was a complete CoW (Fig. 2).
Fig. 2.
Flow in the MCA is reduced as the severity of the ICA vasospasm increases; however, the effects are minimised by the presence of a complete CoW. Hypertension increases blood flow, but does not restore flow to 100% of baseline. CoW, circle of Willis; d, distributed spasm; f, focal spasm; Hype, hypertension; ICA, internal carotid artery; L, left vessel; MCA, middle cerebral artery.
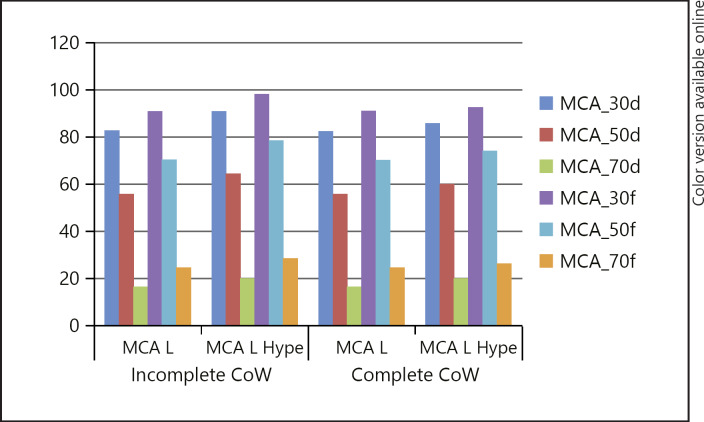
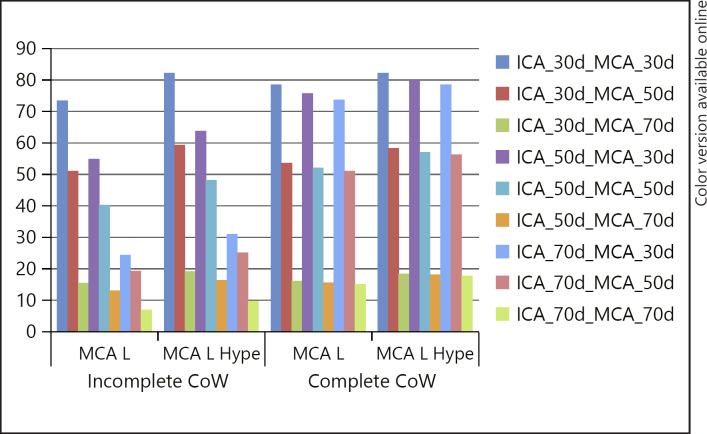
However, the presence of a complete CoW did not affect blood flow when the vasospasm occurred only distal to the anterior and posterior communicating arteries. For example, diffuse 50% vasospasm of the MCA resulted in a 43.9% drop in blood flow in both the presence and absence of a complete CoW (Fig. 3). In the presence of vasospasm affecting vessels proximal and distal to the anterior and posterior communicating arteries, there was a greater drop in blood flow in the absence of a complete CoW (Fig. 4). For example, in the scenario with diffuse 50% vasospasm of the ICA and diffuse 30% vasospasm of the MCA, flow dropped by 45.1% in the incomplete CoW, but fell by only 24.2% if there was a complete CoW.
Fig. 3.
Blood flow in the MCA is only marginally affected by the presence of a complete CoW when the vasospasm affects the MCA itself. In this scenario the blood flow is related to the severity of the vasospasm and the length of the affected segment. CoW, circle of Willis; d, distributed spasm; f, focal spasm; Hype, hypertension; L, left vessel; MCA, middle cerebral artery.
Fig. 4.
In the presence of diffuse vasospasm affecting both the ICA and MCA, there are decreases in the blood flow in the MCA, and hypertension, whilst causing a slight increase in the flow supply, is unable to restore it to normal. The largest flow reduction is observed in cases involving long segment disease of the worst severity and in the case of an incomplete CoW. In the presence of a complete CoW, the flow is related principally to the vasospasm within the MCA, being less sensitive to the vasospasm occurring in the ICA. CoW, circle of Willis; d, distributed spasm; Hype, hypertension; ICA, internal carotid artery; L, left vessel; MCA, middle cerebral artery.
Effect of Hypertension
Induced hypertension (MAP 120 mm Hg) caused an increase in blood flow in all scenarios (Fig. 2, 3, 4, 5, 6). However, it did not result in a normalisation of blood flow distal to the vasospasm even in the presence of moderate vasospasm (30%). Hypertension in the presence of a complete CoW had a marginally greater effect on the blood flow, but this did not allow normalisation of the blood flow. For example, with diffuse 70% ICA vasospasm and an incomplete CoW, there was a decrease in flow in the MCA by 64.1%, which was marginally improved after hypertension (56.6%). However, with a complete CoW, there was a reduction in blood flow of only 11.8%, with only a 8.6% decrease in flow after induced hypertension.
Fig. 5.
Blood flow in the ACA increased in the presence of MCA stenosis as a result of shunting. ACA, anterior cerebral artery; CoW, circle of Willis; d, distributed spasm; f, focal spasm; Hype, hypertension; L, left vessel; MCA, middle cerebral artery.
Fig. 6.
Flow in the ACA is dependent upon the presence of a complete CoW as well as the degree of vasospasm in the proximal ICA and the MCA. Much larger drops in blood flow are seen in the ACA when the CoW is incomplete. ACA, anterior cerebral artery; CoW, circle of Willis; d, distributed spasm; f, focal spasm; Hype, hypertension; ICA, internal carotid artery; L, left vessel; MCA, middle cerebral artery.
Effect of Hypotension
Hypotension can occur in patients undergoing treatment with vasodilators such as nimodipine. Hypotension, even at a relatively mild MAP of 73 mm Hg, caused marked drops in flow rate that were exacerbated by an incomplete CoW and compounded the drops in flow rate seen within more severe and more diffuse vasospasm. For example, the flow rate in normotensive patients with a 50% focal stenosis of the MCA and incomplete CoW was 72.3% of normal compared to 64.4% in hypotensive conditions. With a complete CoW, flow was better preserved at 82.5% of normal under hypotensive conditions. Flow was severely reduced in cases of severe vasospasm and concomitant hypotension (6.9% with an incomplete CoW).
The full results are shown in Table 1.
Flow Changes in Non-Spastic Vessels
Blood flow in non-spastic arteries increased in relation to vasospasm in adjacent connected arteries (Fig. 5). As a result of a steal phenomenon, blood flow in the ACA increased in the presence of MCA vasospasm, and there was a marginally greater increase in the flow in relation to diffuse vasospasm compared to focal vasospasm. For example, blood flow in the ACA increased by 2.9% in the presence of focal 70% MCA vasospasm and by 3.2% in the presence of diffuse 70% MCA vasospasm. Flow in the ACA is dependent upon the anterior communicating artery. Vasospasm in the ipsilateral ICA with an incomplete CoW results in pronounced drops in blood flow (Fig. 6).
Discussion
Our results show that flow changes in the cerebral circulation are altered by a variety of factors, including the degree of vasospasm, the length of the affected segment(s), and the presence of collateral circulation via a complete CoW. Furthermore, vasospasm in certain territories can result in an increased blood flow in unaffected arterial territories and that hypertension can improve cerebral blood flow, but the effect of hypertension is very variable and dependent upon the above-mentioned factors. These factors are not routinely assessed when determining which patients may benefit from induced hypertension.
The results of our study have important clinical consequences. Induced hypertension has been routinely used to treat patients with symptomatic vasospasm in the hope that it will improve cerebral perfusion and prevent cerebral ischaemia and infarction. However, the available clinical evidence is inconclusive as to whether induced hypertension does improve cerebral perfusion. Gathier et al. [11] assessed cerebral perfusion in patients treated with induced hypertension after acute subarachnoid haemorrhage. They showed, using CT perfusion, that despite a rise in the MAP of 12 mm Hg, there was no statistically significant change in the cerebral perfusion between patients with induced hypertension and those in a control group who did not undergo hypertensive treatment. However, Engquist et al. [12] showed, using xenon CT perfusion imaging, that triple-H therapy did improve cerebral perfusion, particularly in those areas with the most severe perfusion deficits. Similarly, there was a reduction in the proportion of the area of cerebral perfusion < 20 mL/100 g/min compared to pretreatment perfusion scans. Although there was a small elevation in the systolic blood pressure after triple-H therapy had been begun, this was not significant. Given this non-significant increase in the systolic blood pressure, the authors suggest that the hypervolaemia and reduced haematocrit may have had a greater contribution to the increased cerebral perfusion. Numerous studies have been published documenting the use of induced hypertension in patients with symptomatic vasospasm [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26], with symptomatic improvement seen in approximately 70–80% of patients. However, until recently there have been no randomised trials to determine the effectiveness of induced hypertension in comparison to a control group. Gathier et al. [27] recently published the results of the only published randomised controlled trial to look at the effect of induced hypertension in patients with delayed cerebral ischaemia. Although the trial aimed to recruit 240 patients, due to slow enrolment and lack of effect on cerebral perfusion only 21 were randomised to the hypertension and 20 to the control group with no induced hypertension. In the treatment cohort, the MAP over the first 24 h was 11.1 mm Hg (95% CI 7.1–15.1 mm Hg), higher than in the control group. This dropped to 5.7 mm Hg (95% CI 4.2–8.5 mm Hg) over 72 h. A poor outcome, defined as a score of 4–6 on the modified Rankin Scale at 3 months, was seen in 12 of 21 (57%) patients in the treatment group and in 8 of 20 (40%) in the control group. With induced hypertension, the adjusted risk ratio was 1.0. Within the first 24 h of symptoms, 18 patients showed a clinical improvement (n = 12 [57%] in the treatment cohort and n = 6 [30%] in the control group) defined as any improvement in the Glasgow Coma Scale score or improvement of focal deficits. Five of the 12 patients with initial improvement after induced hypertension had a poor outcome at 3 months, whereas 0 of the 6 patients with initial improvement without induced hypertension had a poor outcome at 3 months. Perhaps most importantly, serious adverse events occurred in 11 of 21 patients (52%) in the induced hypertension cohort and in 5 of 20 (25%) of patients in the control group (risk ratio 2.1, 95% CI 0.9–5.0). This study, although small, is extremely important as it highlights that immediate clinical improvement may not result in long-term functional improvement and that hypertension carries a significant risk of associated complications. The authors state that induced hypertension may have a benefit in certain subgroups of patients with delayed cerebral ischaemia; however, they are uncertain which patients would benefit from hypertension. These comments are congruent with our own findings, which suggest that a multitude of factors are relevant in determining whether hypertension will sufficiently raise the blood flow to normal or near normal.
Another implication of this work is the effect it may have on the intra-arterial use of vasodilating drugs. The use of intra-arterial vasodilators in cases of medically refractory vasospasm is widespread. However, inappropriate use of these medications or angioplasty may result in a negative outcome [28]. Levitt et al. [29] recently published their experience of real-time assessment of angiographic perfusion after endovascular treatment for cerebral vasospasm. They demonstrated that cerebral blood flow was improved in all treated segments, but deteriorated in untreated segments. For example, in one case after treatment of the spasm in the M1 segment with balloon angioplasty, there was an increase in the cerebral blood flow in the MCA territory; however, there was a concomitant drop in the flow within the ACA territory, suggesting a steal phenomenon deviating blood into the MCA after treatment. Similarly, Shimamura et al. [28] recently published their case series of asymptomatic vasospastic patients treated with intra-arterial vasodilators. In three of the cases the vasodilators were injected in the ICA rather than in a superselective fashion, and the authors noted that patients rapidly went from being asymptomatic to symptomatic. The authors analysed the time density contrast curves of the pre- and posttreatment angiograms for the different intracranial arteries in order to determine the cause of this deterioration. They observed that the non-selective injection of vasodilators resulted in a relatively greater improvement of flow in the non-spastic artery and hence in an iatrogenic steal phenomenon that caused the deterioration of the patient. These results agree with our own modelling results, which show that in the presence of MCA spasm there is a slight increase in flow into the non-spastic ACA and therefore, if vasodilating drugs were injected via the ICA in a non-selective manner, they would flow preferentially into the non-spastic ACA, resulting in vasodilatation of this asymptomatic vascular bed and hence producing a greater blood flow steal from the symptomatic MCA territory. The clinical implication of the results published by both Shimamura et al. [28] and Levitt et al. [29] are the following: (1) The treatment of vasospasm must occur at the site of the vasospasm to prevent a positive reinforcement of the steal phenomenon, i.e., the treatment must be at the site of the vasospasm and not proximal. (2) If more than one territory is affected, then all the affected territories will potentially require treatment so as to prevent steal from occurring after the treatment of only one territory and the consequent deterioration of flow in adjacent vascular territories. Similarly, the use of vasodilating drugs can result in drops in blood pressure, and our results show that this results in drops in flow even in situations where the MAP is only mildly hypotensive (73 mm Hg), as was tested in our model.
Our modelling study appears congruent with these previously published clinical experiences. We believe that the results of this computational modelling analysis bring new elements into the understanding of the problem, as the groundwork on top of which the model has been built relies on solid physical laws that govern the circulation of fluids in deformable pipes. We have been able to demonstrate that although hypertension can improve blood flow in the presence of vasospasm, the results are extremely variable and dependent upon a variety of factors. The treatment of vasospasm should be directed at the site of vasospasm with either locally delivered vasodilators, balloon angioplasty, or stent angioplasty [30, 31, 32], and as many of the affected vasospastic segments as possible should be treated in order to prevent worsening iatrogenic steal phenomenon. Although not shown, we also modelled the flow changes that occurred after restoration of calibre in the spastic MCA segment to replicate the effects of balloon or stent angioplasty. This, as expected, showed an improvement of flow; for example, in the case of 50% focal stenosis and of the ICA and MCA, dilatation of the MCA restored flow to the same degree as 50% ICA stenosis alone.
Limitations
The present study is based on computational simulations. The natural limitation is that the model does not correspond to a specific individual. However, the ADAN model has been largely verified to deliver consistent physiological and pathophysiological predictions in different contexts [3, 4, 33]. The lack of validation is without doubt a limitation, but we should note that validation of this kind of predictions is impossible with current technology because regional pressure and flow rate measurements are not available. In this regard, we strongly rely on the correctness of the mathematical/physical model to describe the flow of an incompressible fluid in compliant vessels. This, in turn, has been validated against experimental measurements as well as in controlled in vivo conditions [34, 35, 36].
Conclusion
The results of our modelling study demonstrate that the cerebral blood flow, in the presence of cerebral vasospasm, varies considerably and is dependent upon the degree of vasospasm, whether the vasospasm is diffuse or focal, and the presence of collateral supply via the CoW. Hypertension can raise the blood flow, but it is unable to restore cerebral blood flow to baseline. The treatment of vasospasm should be targeted to the site of the vasospasm because of the potential to inadvertently cause an iatrogenic steal phenomenon.
Statement of Ethics
Ethics committee approval was not required for this type of study.
Disclosure Statement
P. Bhogal: proctoring and consultancy agreements with phenox. The other authors declare no conflict of interests. This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
References
- 1.Sen J, Belli A, Albon H, Morgan L, Petzold A, Kitchen N. Triple-H therapy in the management of aneurysmal subarachnoid haemorrhage. Lancet Neurol. 2003 Oct;2((10)):614–21. doi: 10.1016/s1474-4422(03)00531-3. [DOI] [PubMed] [Google Scholar]
- 2.Dankbaar JW, Slooter AJ, Rinkel GJ, Schaaf IC. Effect of different components of triple-H therapy on cerebral perfusion in patients with aneurysmal subarachnoid haemorrhage: a systematic review. Crit Care. 2010;14((1)):R23. doi: 10.1186/cc8886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Blanco PJ, Watanabe SM, Passos MA, Lemos PA, Feijóo RA. An anatomically detailed arterial network model for one-dimensional computational hemodynamics. IEEE Trans Biomed Eng. 2015 Feb;62((2)):736–53. doi: 10.1109/TBME.2014.2364522. [DOI] [PubMed] [Google Scholar]
- 4.Blanco PJ, Müller LO, Watanabe SM, Feijóo RA. Computational modeling of blood flow steal phenomena caused by subclavian stenoses. J Biomech. 2016 Jun;49((9)):1593–600. doi: 10.1016/j.jbiomech.2016.03.044. [DOI] [PubMed] [Google Scholar]
- 5.Müller LO, Blanco PJ, Watanabe SM, Feijóo RA. A high-order local time stepping finite volume solver for one-dimensional blood flow simulations: application to the ADAN model. Int J Numer Methods Biomed Eng. 2016 Oct;32((10)):e02761. doi: 10.1002/cnm.2761. [DOI] [PubMed] [Google Scholar]
- 6.Taylor CA, Draney MT. Experimental and Computational Methods in Cardiovascular Fluid Mechanics. Annu Rev Fluid Mech. 2004;36((1)):197–231. [Google Scholar]
- 7.Olufsen MS, Peskin CS, Kim WY, Pedersen EM, Nadim A, Larsen J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann Biomed Eng. 2000 Nov-Dec;28((11)):1281–99. doi: 10.1114/1.1326031. [DOI] [PubMed] [Google Scholar]
- 8.Stergiopulos N, Young DF, Rogge TR. Computer simulation of arterial flow with applications to arterial and aortic stenoses. J Biomech. 1992 Dec;25((12)):1477–88. doi: 10.1016/0021-9290(92)90060-e. [DOI] [PubMed] [Google Scholar]
- 9.van de Vosse FN, Stergiopulos N. Pulse Wave Propagation in the Arterial Tree. Annu Rev Fluid Mech. 2011;43((1)):467–99. [Google Scholar]
- 10.Young DF, Tsai FY. Flow characteristics in models of arterial stenoses. II. Unsteady flow. J Biomech. 1973 Sep;6((5)):547–59. doi: 10.1016/0021-9290(73)90012-2. [DOI] [PubMed] [Google Scholar]
- 11.Gathier CS, Dankbaar JW, van der Jagt M, Verweij BH, Oldenbeuving AW, Rinkel GJ, et al. HIMALAIA Study Group Effects of Induced Hypertension on Cerebral Perfusion in Delayed Cerebral Ischemia After Aneurysmal Subarachnoid Hemorrhage: A Randomized Clinical Trial. Stroke. 2015 Nov;46((11)):3277–81. doi: 10.1161/STROKEAHA.115.010537. [DOI] [PubMed] [Google Scholar]
- 12.Engquist H, Rostami E, Ronne-Engström E, Nilsson P, Lewén A, Enblad P. Effect of HHH-Therapy on Regional CBF after Severe Subarachnoid Hemorrhage Studied by Bedside Xenon-Enhanced CT. Neurocrit Care. 2017;••• doi: 10.1007/s12028-017-0439-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Awad IA, Carter LP, Spetzler RF, Medina M, Williams FC., Jr Clinical vasospasm after subarachnoid hemorrhage: response to hypervolemic hemodilution and arterial hypertension. Stroke. 1987 Mar-Apr;18((2)):365–72. doi: 10.1161/01.str.18.2.365. [DOI] [PubMed] [Google Scholar]
- 14.Frontera JA, Fernandez A, Schmidt JM, Claassen J, Wartenberg KE, Badjatia N, et al. Clinical response to hypertensive hypervolemic therapy and outcome after subarachnoid hemorrhage. Neurosurgery. 2010 Jan;66((1)):35–41. doi: 10.1227/01.NEU.0000359530.04529.07. [DOI] [PubMed] [Google Scholar]
- 15.Kassell NF, Peerless SJ, Durward QJ, Beck DW, Drake CG, Adams HP. Treatment of ischemic deficits from vasospasm with intravascular volume expansion and induced arterial hypertension. Neurosurgery. 1982 Sep;11((3)):337–43. doi: 10.1227/00006123-198209000-00001. [DOI] [PubMed] [Google Scholar]
- 16.Kosnik EJ, Hunt WE. Postoperative hypertension in the management of patients with intracranial arterial aneurysms. J Neurosurg. 1976 Aug;45((2)):148–54. doi: 10.3171/jns.1976.45.2.0148. [DOI] [PubMed] [Google Scholar]
- 17.Miller JA, Dacey RG, Jr, Diringer MN. Safety of hypertensive hypervolemic therapy with phenylephrine in the treatment of delayed ischemic deficits after subarachnoid hemorrhage. Stroke. 1995 Dec;26((12)):2260–6. doi: 10.1161/01.str.26.12.2260. [DOI] [PubMed] [Google Scholar]
- 18.Muizelaar JP, Becker DP. Induced hypertension for the treatment of cerebral ischemia after subarachnoid hemorrhage. Direct effect on cerebral blood flow. Surg Neurol. 1986 Apr;25((4)):317–25. doi: 10.1016/0090-3019(86)90205-3. [DOI] [PubMed] [Google Scholar]
- 19.Murphy A, de Oliveira Manoel AL, Macdonald RL, Baker A, Lee TY, Marotta T, et al. Changes in Cerebral Perfusion with Induced Hypertension in Aneurysmal Subarachnoid Hemorrhage: A Pilot and Feasibility Study. Neurocrit Care. 2017 Aug;27((1)):3–10. doi: 10.1007/s12028-017-0379-6. [DOI] [PubMed] [Google Scholar]
- 20.Otsubo H, Takemae T, Inoue T, Kobayashi S, Sugita K. Normovolaemic induced hypertension therapy for cerebral vasospasm after subarachnoid haemorrhage. Acta Neurochir (Wien) 1990;103((1-2)):18–26. doi: 10.1007/BF01420187. [DOI] [PubMed] [Google Scholar]
- 21.Qureshi AI, Suarez JI, Bhardwaj A, Yahia AM, Tamargo RJ, Ulatowski JA. Early predictors of outcome in patients receiving hypervolemic and hypertensive therapy for symptomatic vasospasm after subarachnoid hemorrhage. Crit Care Med. 2000 Mar;28((3)):824–9. doi: 10.1097/00003246-200003000-00035. [DOI] [PubMed] [Google Scholar]
- 22.Raabe A, Beck J, Keller M, Vatter H, Zimmermann M, Seifert V. Relative importance of hypertension compared with hypervolemia for increasing cerebral oxygenation in patients with cerebral vasospasm after subarachnoid hemorrhage. J Neurosurg. 2005 Dec;103((6)):974–81. doi: 10.3171/jns.2005.103.6.0974. [DOI] [PubMed] [Google Scholar]
- 23.Roy B, McCullough LD, Dhar R, Grady J, Wang YB, Brown RJ. Comparison of Initial Vasopressors Used for Delayed Cerebral Ischemia after Aneurysmal Subarachnoid Hemorrhage. Cerebrovasc Dis. 2017;43((5-6)):266–71. doi: 10.1159/000458536. [DOI] [PubMed] [Google Scholar]
- 24.Swift DM, Solomon RA. Unruptured aneurysms and postoperative volume expansion. J Neurosurg. 1992 Dec;77((6)):908–10. doi: 10.3171/jns.1992.77.6.0908. [DOI] [PubMed] [Google Scholar]
- 25.Touho H, Karasawa J, Ohnishi H, Shishido H, Yamada K, Shibamoto K. Evaluation of therapeutically induced hypertension in patients with delayed cerebral vasospasm by xenon-enhanced computed tomography. Neurol Med Chir (Tokyo) 1992 Aug;32((9)):671–8. doi: 10.2176/nmc.32.671. [DOI] [PubMed] [Google Scholar]
- 26.Macdonald RL. Delayed neurological deterioration after subarachnoid haemorrhage. Nat Rev Neurol. 2014 Jan;10((1)):44–58. doi: 10.1038/nrneurol.2013.246. [DOI] [PubMed] [Google Scholar]
- 27.Gathier CS, van den Bergh WM, van der Jagt M, Verweij BH, Dankbaar JW, Müller MC, et al. HIMALAIA Study Group Induced Hypertension for Delayed Cerebral Ischemia After Aneurysmal Subarachnoid Hemorrhage: A Randomized Clinical Trial. Stroke. 2018 Jan;49((1)):76–83. doi: 10.1161/STROKEAHA.117.017956. [DOI] [PubMed] [Google Scholar]
- 28.Shimamura N, Naraoka M, Matsuda N, Kakuta K, Ohkuma H. Prophylactic intra-arterial injection of vasodilator for asymptomatic vasospasm converts the patient to symptomatic vasospasm due to severe microcirculatory imbalance. BioMed Res Int. 2014;2014:382484. doi: 10.1155/2014/382484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levitt MR, Morton RP, Haynor DR, Cohen W, Ghodke BV, Hallam DK, et al. Angiographic perfusion imaging: real-time assessment of endovascular treatment for cerebral vasospasm. J Neuroimaging. 2014 Jul-Aug;24((4)):387–92. doi: 10.1111/jon.12046. [DOI] [PubMed] [Google Scholar]
- 30.Bhogal P, Loh Y, Brouwer P, Andersson T, Söderman M. J Neurointerventional Surg; 2016. Treatment of cerebral vasospasm with self-expandable retrievable stents: proof of concept. [DOI] [PubMed] [Google Scholar]
- 31.Bhogal P, Paraskevopoulos D, Makalanda HL. The use of a stent-retriever to cause mechanical dilatation of a vasospasm secondary to iatrogenic subarachnoid haemorrhage. Interv Neuroradiol. 2017 Jun;23((3)):330–5. doi: 10.1177/1591019917694838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kwon HJ, Lim JW, Koh HS, Park B, Choi SW, Kim SH, et al. Stent-Retriever Angioplasty for Recurrent Post-Subarachnoid Hemorrhagic Vasospasm - A Single Center Experience with Long-Term Follow-Up. Clin Neuroradiol. 2018 Aug;••• doi: 10.1007/s00062-018-0711-3. [DOI] [PubMed] [Google Scholar]
- 33.Blanco PJ, Watanabe SM, Dari EA, Passos MA, Feijóo RA. Blood flow distribution in an anatomically detailed arterial network model: criteria and algorithms. Biomech Model Mechanobiol. 2014 Nov;13((6)):1303–30. doi: 10.1007/s10237-014-0574-8. [DOI] [PubMed] [Google Scholar]
- 34.Matthys KS, Alastruey J, Peiró J, Khir AW, Segers P, Verdonck PR, et al. Pulse wave propagation in a model human arterial network: assessment of 1-D numerical simulations against in vitro measurements. J Biomech. 2007;40((15)):3476–86. doi: 10.1016/j.jbiomech.2007.05.027. [DOI] [PubMed] [Google Scholar]
- 35.Reymond P, Bohraus Y, Perren F, Lazeyras F, Stergiopulos N. Validation of a patient-specific one-dimensional model of the systemic arterial tree. Am J Physiol Heart Circ Physiol. 2011 Sep;301((3)):H1173–82. doi: 10.1152/ajpheart.00821.2010. [DOI] [PubMed] [Google Scholar]
- 36.Müller LO, Toro EF. A global multiscale mathematical model for the human circulation with emphasis on the venous system. Int J Numer Methods Biomed Eng. 2014 Jul;30((7)):681–725. doi: 10.1002/cnm.2622. [DOI] [PubMed] [Google Scholar]