A Methodological Approach for Predicting COVID-19 Epidemic Using EEMD-ANN Hybrid Model

Abstract

Predicting the Coronavirus epidemic, popularly known as COVID-19, that has been explored more than 200 countries and already declared as a pandemic by the World Health Organization is an invaluable task. This virus was first identified around December 2019, from central China, but later spread in the rest of the world. To ensure better healthcare service management, an accurate prediction of the uncertain gruesomeness is situational demand. In orders with limited information frameworks, demonstrating and predicting COVID-19 turns into a challenging endeavor. The primary objective of this study is to propose a hybrid model that incorporates ensemble empirical mode decomposition (EEMD) and artificial neural network (ANN) for predicting the COVID-19 epidemic. A real-time COVID-19 time series data has been used on the window periods January 22, 2020, to May 18, 2020. The time-series data first decomposed using EEMD to produce sub-signals and make original data denoised, and ANN architecture has built to train the denoised data. Finally, the result of the proposed model has compared with some traditional statistical analysis. The result of this investigation shows our proposed model outperforms compared with traditional statistical analysis. Thus the model might be promising for COVID-19 epidemic prediction. The government and healthcare provider can take preventive action by understanding the upcoming COVID-19 situation for better healthcare management.

1. . Introduction

COVID-19 first case confirmed at Wuhan, China, in late 2019 [8], and within a short time, the picture has dramatically changed to around 5 million on May 18, 2020. Globally, approximately 3.4% of cases have reported died, which is comparatively higher than seasonal flu generally fewer than 1% accountable [2] ("Coronavirus (COVID-19) Mortality Rate," 2020). During this present pandemic, the world's leading countries, i.e., USA, Italy, France, somehow failed to maintain better healthcare management to take preventive action. Though the COVID-19 patients’ growth rate has exponentially and dramatically increased, the early prediction would use to improve healthcare facilities. Currently, this pandemic has spread more than 200 countries, and many newly affected countries are failing to manage better healthcare services due to a lack of accurate prediction.

Regarding this condition, the early prediction might improve the healthcare service facility. Considerably, COVID-19 time series modeling and predicting is an area of enormous interest for both government and healthcare providers. Thus the main objective of this study is to propose an efficient, cost-effective time series modeling for COVID-19 prediction using an ensemble empirical mode decomposition (EEMD) based artificial neural network (ANN).

Recent literature reveals that; it is obscure to discover inquire about exertion on COVID-19 to investigate the method of controlling spared of the virus. For example, Singh, Singh, Shaikh, Singh, and Misra [16] focuses on prospective medicine treatment for boosting future research. Tosepu et al. [18] investigated the weather impact to prevent the spread of COVID-19 and Shim, Tariq, Choi, Lee, and Chowell [15] measuring the outbreak situation by implementing rapid control of social distance. However, very few research giving the effort to predict the COVID-19 epidemic. Fanelli and Piazza [6] offer in their forecasting research employing the simple susceptible-infected-recovered-deaths model for specific countries. Findings reveal that there is particular universality within the time evaluation of the COVID-19 epidemic spreading. Petropoulos and Makridakis [14] found past data of COVID-19 will not change the role of “business-as-usual” (nothing change) employing a simple time series forecasting analysis. Though predicting the future of the epidemic is much more difficult as the cases are exponentially growing and data is non-linear and non-stationary. Still predicting COVID-19 is invaluable for a better understanding of the current situation and for making a short-term plan by the policymakers. Both of the previous studies have been used in the traditional forecasting method with statistical modeling—however, rear literature deals with the machine learning approach for COVID-19 epidemic prediction. Tuli, Tuli, Tuli, and Gill [19] proposed a cloud-based machine learning model for COVID-19 prediction and offers research opportunities for integrating the time-series model such as ARIMA with their proposed mathematical model. Thus, introducing an efficient model with the best accuracy is the situational demand. As discussed earlier, COVID-19 data is non-linear and non-stationary, it's more effective to apply decomposition methods rather than directly implement the ARIMA model [4]. Bridging the emerging literacy gap, this study proposes a hybrid EEMD-ANN hybrid model for the prediction of the COVID-19 epidemic.

Besides, the COVID-19 growth rate is non-linear and non-stationary. Early and accurate prediction of COVID-19 growth could be helpful to healthcare providers for cost-effective healthcare management and might reduce gruesomeness of the pandemic. In general, predicting non-linear and non-stationary time series data is a crucial task in the health analytics domain. Managing operational excellence in healthcare, accurate prediction of COVID-19 plays a vital role. It is a challenging task to predict the growth rate of COVID-19 patients due to inconsistent, non-linear, and non-stationary data. In the recent past, various non-linear data-driven models such as ANN, Support vector machine (SVM) [10] have been proposed for multiple research domains. Despite an enormous literature, these models have no complete execution that has been made significance in healthcare informatics. However, ANN is most widely used in the time series prediction due to its powerful parallel processing and capacity to estimate for virtually any function up to a self-assertive level of precision. But regardless of the excellent execution of ANN, there is still space to improve its estimate accuracy [17].

Furthermore, noise-contaminated time-series signals might affect prediction analysis using ANN. Literature compelling evidence that decomposition technique enhances the predicting accuracy producing clear signals as model input [1]. Based on this theory, numerous studies have been done to improve the prediction accuracy using ANN. For example, El-Hendawi and Wang [5] developed wavelet packet transform with ANN for short term electricity load forecasting, Olanrewaju, Jimoh, and Kholopane [12] investigated energy potentiality using index decomposition analysis with ANN. However, EEMD-ANN based prediction is somehow not a new approach in other research domains [17] rather than health analytics. Empirical mode decomposition (EMD) is a recently adapted method to decompose noise assisted data, which is extensively used in time series data analytics. EMD disintegrated the original data into intrinsic mode functions (IMFs). Due to some drawbacks of EMD, i.e., stopping criteria of shifting process, mode mixing, and border effect problem, EEMD [20] is a white noise assisted decomposition process widely used recently. EEMD repeatedly decomposes the original signal by adding white noise into a series of IMFs by applying the original EMD process.

As stated earlier, the main objective of this study is to propose a hybrid model for prediction of COVID-19 epidemic compared to traditional statistical modeling. In line with that, the EEMD based decomposition technique has combined with ANN modeling. The primary motivation behind the usage of the EEMD technique is to denoising the time series non-stationary and non-linear signals first. Then ANN used to predict the COVID-19 epidemic. This study contributes to current literature in some aspects, which are summarized: first, we proposed a hybrid EEMD-ANN method for predicting the COVID-19 outbreak. While existing researches have focused on traditional forecasting analysis or used a single machine learning approach for predicting the COVID-19 epidemic, limited work has investigated using the hybrid method. Secondly, unlike some other studies, we used the EEMD based decomposition method first for avoiding noise signal then take the data into account as input for training the model. Thirdly, by using a real-time COVID-19 epidemic data, the proposed hybrid model outperforms against some well-established counterparts, which provides a clear indication that the proposed hybrid EEMD-ANN method can be a promising alternative for predicting COVID-19 epidemic.

The remaining of the paper is organized as follows: section 2, undertake the materials and method followed by the result and discussion part presented into section 3. Then, the conclusion and implications are presented. Finally, we consider some limitations and provided some further improvement direction.

2. Materials and Method

2.1. EEMD

Empirical mode of decomposition (EMD) is a method of non-linear and non-stationary signal transformation developed by Huang et al. [9]. To drawback, the mode-mixing function an extended version of EMD has designed called EEDM [20]. EEMD provides excellent performance to decompose non-linear and non-stationary time series. It decomposes the original time series into a few independent finite set function named intrinsic mode function (IMF). Gaussian white noise is applied to the original data during decomposition to create a coherent structure, which is ultimately eliminated by averaging the respective IMFs and residues. EEMD algorithm is based on the following steps:

2.2. ANN

Modeling non-linear and non-stationary data, ANN is widely applied for a more flexible computational strategy for desire level accuracy [1]. Several layers and number of neurons at each layer can vary due to its flexible architecture without having prior assumptions. Among the widely used domain, single hidden layer, and multi-layer perception architecture is vastly used in time series analysis [13]. Besides, ANN in time series analysis usually consists of three layers: input, hidden, and output (figure 1 ). The neurons of the layers are acyclically linked. To model the time series forecasting using this three-layer network as obtaining from the following (eq 1) between the output x_t and past n values of series x_t-1, x_t-2, x_{t-3, …………………} x_t-n, where n is the input number of ANN.

$$Y_t=f(w_0+\sum _{j=1}^k{w}_{j}g({\beta }_{0j}+\sum _{i=1}^n{w}_{ij}{x}_{t-1}))$$ (1)

$$Sigmoid\left(x\right)=\frac{1}{1+e^{-x}}$$ (2)

Figure 1.

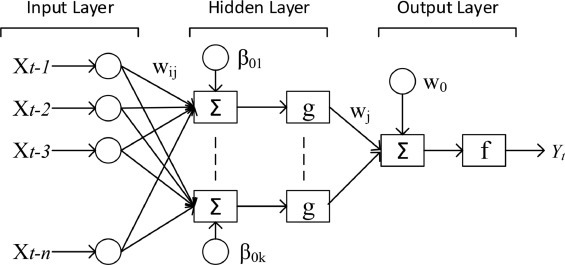
Three-layer ANN architecture

Where, $w_j\left(j=0,1,2,\dots \dots \dots \dots \dots k\right)$ is the weight between the hidden neuron and output neurons, bias unit of output neuron is denoted by W_0, β_0j represents the bias of hidden neurons, w_ij indicates the weight between i^th input and j^th hidden neuron. n is the number of inputs, and k is the number of hidden layers. However, sigmoid function (eq 2) is used at a hidden layer, whereas the linear activation function is used at the output layer. Therefore, before ANN modeling original time series first transform to a set of pattern k-n+1 pattern, consist of n inputs like x_t-1, x_t-2, x_{t-3, …………………} x_t-n and one target Y_t

2.3. Proposed Hybrid EEMD-ANN model

As mentioned earlier, real-time time-series data with non-linear and non-stationary properties used, which has poor generalization ability of numerous models. Therefore, to improve the prediction ability of the ANN model, the EEMD based decomposition technique has been applied. EEMD is used to decompose the time series data and produce sub-signals, avoiding the noise of the data. Then, ANN was created on the denoising data for predicting of COVID-19 global confirm case. The proposed EEMD based ANN model consists of six steps described in Algorithm 2 and Figure 2 .

Algorithm 1.

Ensemble Empirical Mode Decomposition

Step 1	Define a noise signal Yt
Step 2	Obtain Xt = Yt + ng; (with adding white Gaussian noise ng)
Step 3	Identify local extrema for the time series Yt
Step 4	To form the upper emax(t) and lower envelop emin(t), aggregate all local maxima and all local minima with cubic splines interpolation
Step 5	Compute mean envelop mi(t) = [emax(t)+ emin(t)]/2
Step 6	Calculate the difference hi(t) = Xt - mi(t)
Step 7	Check hi(t)satisfy the stopping criteria condition (IMF is symmetric with zero mean and have the same number of zero-crossing), if hi(t) satisfy then h1(t) = IMF1(t), otherwise hi(t) replicate step 1 to step 4 until stopping criteria met.
Step 8	Compute the residual rt = Xt – IMFi(t)
Step 9	Consider rt is a new time series yt until getting a constant residual rn[t].

Algorithm 2.

Steps of Proposed hybrid model

Definition	n is the number of imf and X(t) is the original time series
Step 1	Apply EEMD on X(t) and calculate imfi, where i = 1, 2, 3, ……………..,n
Step 2	Compute average$im{f}_i:{}_{a}imf=\frac{1}{n}\sum _1^{n}im{f}_i$
Step 3	Compute denoise time series: x(t) - aimf
Step 4	Normalize the denoise time series satisfy min-max [0,1] criteria
Step 5	Compute x(t) based on past values xt-1, xt-2, xt-3, ………………… xt-n
Step 6	Train ANN and evaluate the test data

Figure 2.

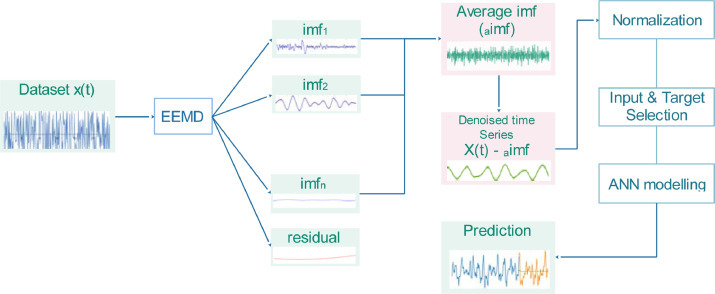
Block Diagram of the proposed hybrid EEMD-ANN model

2.4. Data Description and Decomposition

The cumulative global data of daily level information by country were retrieved from the Center for Systems Science and Engineering (CSSE) at the Johns Hopkins University GitHub repository (https://github.com/CSSEGISandData/COVID-19) accessed on 19/05/2020. This study focuses only on the number of global cumulative confirm cases of COVID-19, the number of cumulative death and recover cases from the period January 22, 2020, to May 18, 2020, presented in figure 3 a. Onwards, this study emphasizes the importance of the number of confirmed cases for the prediction of the COVID-19 epidemic.

Figure 3.

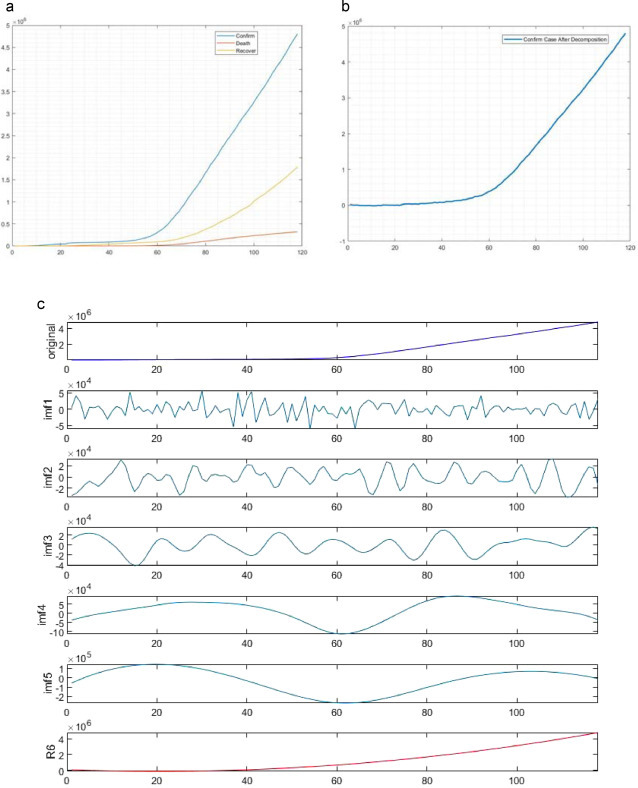
(a) Trend of daily cumulative confirm, death, and recover case. (b) Trend of daily cumulative confirm after decomposition of time-series

However, the primary objective was to decompose the data into several sub-signals using EEMD presented in figure 3c. The original signal X(t) was decomposed into five independent IMFs and one residual where the frequency of the sub-signals become smoother gradually. IMF1 shows a higher noise frequency, which smothers consequently. The ensemble number for the ensemble EMD is set to 100, and the standard deviation of the added white noise is set to 0.2 by the rule of thumb. However, Figure 3b shows the trend of noise-free cumulative global confirms case after decomposing the original data.

2.5. Normalization

Normalization is a typical standard requirement for time series modeling. The objective of normalization is to change the estimations of numeric segments in the dataset to a regular scale, without distorting differences in the ranges of values. Standardization is helpful when information has shifting scales, and the calculation usually used doesn't make assumptions about the distribution of your data. Literature indicates that the normalization using MinMaxScaler has achieved better accuracy [3] for time series modeling. Thus the dataset was preprocessed by the linear transformation using MinMaxScaler with the range 0 to 1, which preserves the shape of the original distribution.

2.6. Input Selection and Data Partitioning

An ordered number of daily observations of the noise-free time series has considered for modeling the ANN. A real-time univariate desecrates time series of the global number of confirming COVID-19 cases was used. During ANN modeling of univariate data, past x_t-1, x_t-2, x_t-3, ………………… x_t-n have been tried to predict the next value x_t. Moreover, after the steps of decomposing, normalization, and input selection, the next step is to divide signals into three parts: training, validation, and testing. In this study, 80% of the data were used for training purposes, 10% of data were for validation, and the remaining 10% of data were used for testing purposes.

2.7. Network Modelling

An important task is to configure the hyperparameter whose values cannot be estimated from data rather than determined by the practitioner. As there is no standard rule of estimating the optimization parameter, this study assessed the hyperparameter using the trial and error method. After some trial and error, our ANN configuration trained using Levenberg-Marquartd algorithm with 20 hidden neurons with 2 delay and one output layer. We considered the epoch from 1 to 1000, and stopping criteria of training was chosen when the minimum validation error has achieved [11]. However, A MATLAB (R2019a) software was used to developing the ANN on the environment of an Intel(R) Core(TM) i5-8250U CPU @ 1.80 GHz processor with 16GB primary memory and 64-bit windows operating systems.

2.8. Performance Evaluation

The performance evaluation of the proposed EEMD-ANN model was assessed by using the hidden layer transfer function varying from the hidden layer neurons number. Mean square error (MSE), and R² values were taken as a measure to assess success. Additionally, to evaluate the performance, we compare the accuracy with several traditional statistical methods, i.e., Regression analysis and moving average strategy. The performance indicator (MSE and R square) is presented mathematically using (eq 3 and eq 4).

$$MSE=\frac{1}{N}\sum _{i=1}^N{(O_i-P_i)}^2$$ (3)

$$R^2=1-\frac{{\sum }_{i=1}^N{(O_i-P_i)}^2}{{\sum }_{i=1}^N{\left(O_i\right)}^2}$$ (4)

Where N = the number of observations, O_i is the observed values, and P_i is the predicted values.

3. Result and Discussion

This study divided the analysis outcome into three phases, i.e., calculating regression analysis and moving average review with three trend categories (linear, exponential and polynomial) and developed the ANN model with EEMD based decomposition technique. Finally, we made a comparison between the models. EEMD-ANN model helps to develop a network architecture with several neurons and hidden layers to the best fit of the time series data. Both regression analysis and moving average review were calculated with three categories: linear, exponential, and polynomial to observed the traditional trend, and lastly, the effectiveness of these models was evaluated by comparison of the results.

The ANN model performance is presented in Fig 4 a for all three types of data: training, validation, and testing at all epoch. From Fig 4a, it is indicating there is no overfitting in the network as all the MSE is showing consistent after around epoch 5, and Fig 4b shows the satisfactory gradient, Mu, and validation check results. However, at epoch 62, the training was stopped showing the best validation performance.

Figure 4.

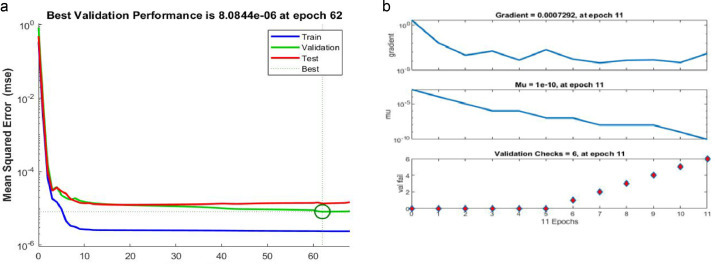
(a) Performance of the network at different epochs for each data set. (b) The ANN Validation Checks, Mu and Gradient.

The efficiency of the model finally calculated using R² performance, which is the relationship between the input signal and the target signal. Figure 5 shows the regression analysis between the input signal and the output signal at each epoch of the ANN model. The training and testing phase performance obtained by height R² values 0.9997 and 0.99982, respectively. The R² of validation is 0.99981. This indicates that training data is well prepared, and training accuracy is perfect. The validation process is executed only once after each epoch or iteration to test a trained network's output on unseen data. From figure 5, it is clear that the validation dataset was predicted (R² = 0.99981) using a trained network. Thus the prediction/test dataset truly does not participate in the training process (R² = 0.99982). The probability of extrapolation may have emerged as the total data is randomized until it is separated into the three phases. The overall data, including the data points for the preparation, validation, and prediction process, is given in Fig 5 and the outputs of their ANN model. However, the overall output of R² found to be satisfactory 0.99991.

Figure 5.

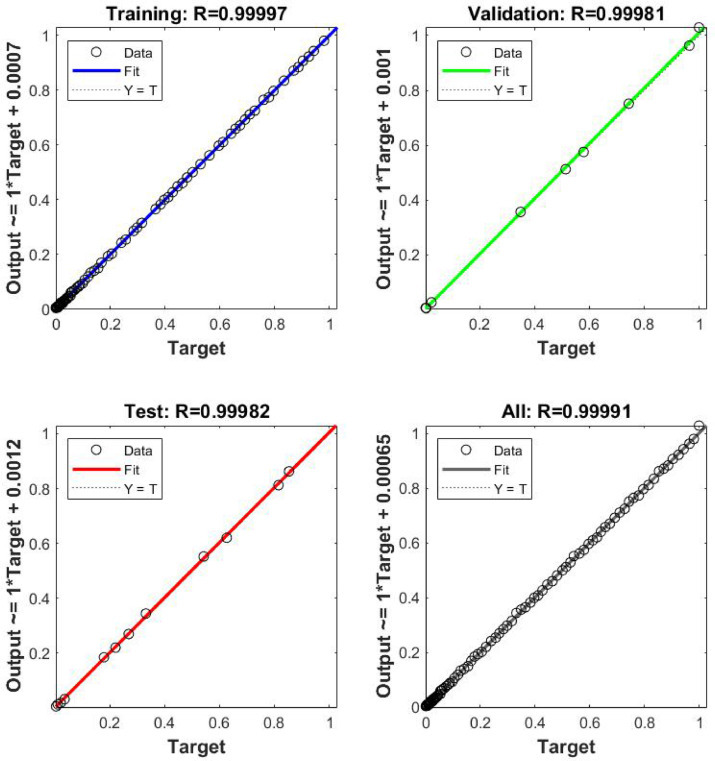
Regression analysis of the predicted and targeted output from the trained ANN network showing R² of each phase

In this stage, we calculated the regression analysis and moving average analysis output with three popular categories of traditional statistical methods to compare the result with the EEMD-ANN based hybrid model. Table 1 shows the MSE and R² values along with the respective significant level. Table 1 shows that EEMD-ANN outperforms the traditional statistical process to predict the COVID-19 epidemic. The error and R² values of all processes are presented in table 1. The training and prediction error is far smaller than the other traditional approach. Though exponential and polynomial in both regression and moving average cases are a little bit satisfactory, the error rate is very high in both cases. Model performance mostly depends on the right network architecture. The traditional statistical process is faster, easy to understand, and easily implemented but unable to predict accurately rather than machine learning techniques. Figs. 6 a and b reveal the output of traditional predicting methods, whereas figuring 7 the prediction accuracy response of all forms of time series data. Specifically, Figure 8 shows the actual and prediction values with lower error rate (training RMSE = 0.02095, testing RMSE = 0.00559).

Figure 7.

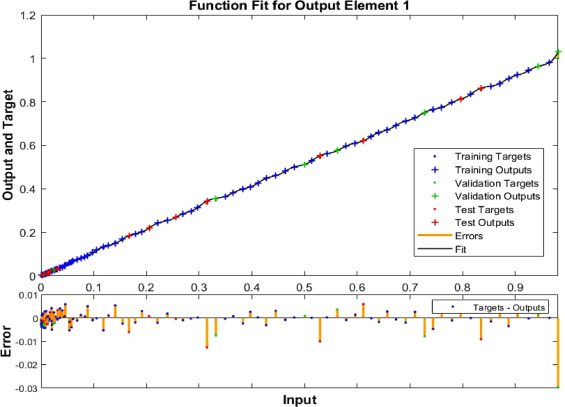
ANN Prediction Accuracy Response

Table 1.

ANN Performance Comparison Analysis with some Traditional Statistical Analysis

		MSE	R-Squared	significance
Regression Analysis	Linear	6.59e+05	0.8146	< 0.0001
	Exponential	2.87e+05	0.9646	< 0.0001
	Polynomial	1.44e+05	0.9912	< 0.0001
Moving Average	Linear	2.36e+09	0.9990	< 0.0001
	Exponential	0.024238	0.9957	< 0.0001
	Polynomial	1.87e+08	0.9999	< 0.0001
EEMD-ANN	Training	6.42E-06	0.99997	< 0.0001
	Validation	8.72E-05	0.99981	< 0.0001
	Testing	3.76E-05	0.99982	< 0.0001

Figure 6.

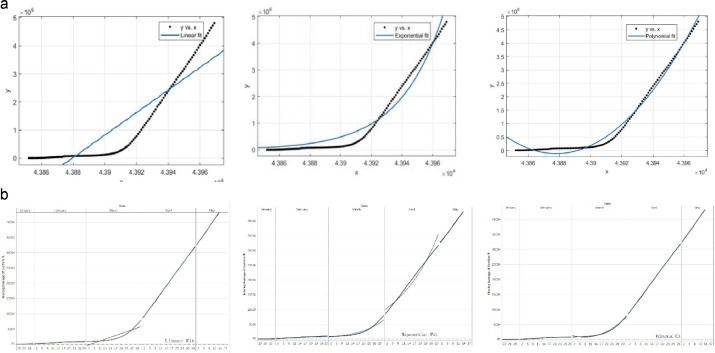
(a) Regression Analysis. (b) Moving Average.

Figure 8.

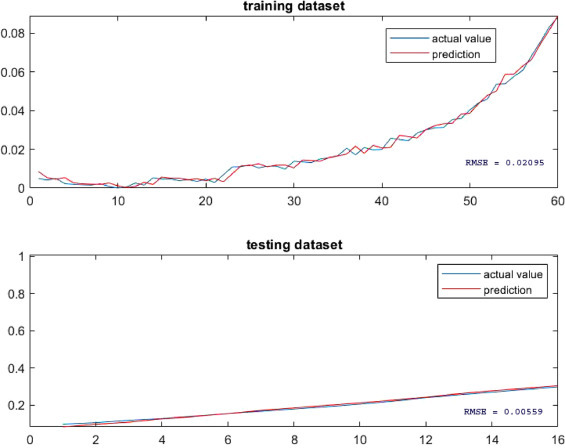
Prediction Accuracy of Training and Testing Set

4. Conclusion and Implication

COVID-19 epidemic prediction is a situational demand globally. Nowadays, the uncertainty of the growth rate and accurate prediction is responsible for healthcare services mismanagement in most of the countries. Being able to reliable prediction trend of the growth rate will react to formulate the new strategy and other significant discussions. Thus it is worth improving the prediction of the COVID-19 epidemic.

This study proposed and investigated a hybrid model EEMD-ANN technique to predict the daily trend of the COVID-19 epidemic based on the real-time global COVID-19 time series dataset. First, we employed the EEMD decomposition technique to denoise the time series and then build an ANN model to train and predict the data. Finally, we compare the proposed EEMD-ANN model with some traditional statistical techniques. Following the output, EEMD-ANN provides a promising indicator to predict the COVID-19 epidemic.

This study has some significant implications. Firstly, our model offers decision-makers the chance to analyze the effects of the new COVID-19 pandemic in their jurisdictions and can get the idea of implementing social-distancing mitigation strategies such as a lockdown. Secondly, the government and national policymaker might apply this EEMD-ANN model for short term prediction for better handling of an imminent uncertain hazard. Thirdly, the health care provider or hospital management may use this model for understanding the short-term future demand for understanding the healthcare equipment demand like medicine, ICU, ventilator, and also can get a clear understanding of managing the number of nurses and doctors.

5. Limitation and Further Study

Practically statistics show that number of the death rate in this year's due to seasonal flue does not match with previous statistics [7]. Thus we may conclude the increased death rate this year might have other reasons, and this might be the COVID-19 epidemic. Contrary, all death might not be responsible for COVID-19. Thus there is a doubt about data reliability because of the pandemic situation. However, we employed the most reliable data hub center of Johns Hopkins University. Similarly, this study has proposed a hybrid model and evaluated the model for COVID-19 prediction. In our next project, we will elaborate on simulation-based prediction for multi-step ahead time series prediction for unseen data.

On the other hand, Tosepu et al. [18] show the correlation between weather and COVID-19 pandemic in the south Asian region. This study only considered univariate time-series data. As future work, weather data could be considered as input variables, and multivariate time series analysis might be conducted. In that case, multivariate EMD (MEMD) can be implemented for the decomposition process. Before training the ANN model, any optimization process, i.e., particle swarm optimization (PSO), can be applied for better prediction accuracy of the COVID-19 pandemic.

Declaration of Competing Interest

There is no potential Conflict of Interest