Insights into the dynamics and control of COVID-19 infection rates

Abstract

This work aims to model, simulate and provide insights into the dynamics and control of COVID-19 infection rates. Using an established epidemiological model augmented with a time-varying disease transmission rate allows daily model calibration using COVID-19 case data from countries around the world. This hybrid model provides predictive forecasts of the cumulative number of infected cases. It also reveals the dynamics associated with disease suppression, demonstrating the time to reduce the effective, time-dependent, reproduction number. Model simulations provide insights into the outcomes of disease suppression measures and the predicted duration of the pandemic. Visualisation of reported data provides up-to-date condition monitoring, while daily model calibration allows for a continued and updated forecast of the current state of the pandemic.

1. Introduction

Since the emergence of SARS-CoV-2, more commonly known as coronavirus, the related disease (COVID-19) has quickly spread around the world. On the 11^th of March 2020, the WHO declared it a pandemic. Numerous features of COVID-19 make control of the pandemic challenging. The virus is new, its dynamics are therefore uncertain, and there are no effective cures or vaccines. Besides, data is incomplete, with the potential of a significant number of unknown (recovered and active) cases and an uncertain incubation period. Current suggestions are that 40 – 50%, with up to 81% of cases only present only mild symptoms, see discussions in [1]. However, a substantial number of known infected individuals eventually develop severe pneumonia, which requires treatment in intensive care units. Without effective measures to control the disease, the number of probable severe cases would disrupt public health systems leaving patients without crucial life support, potentially exacerbating fatality rates [2].

1.1. Non-pharmaceutical interventions

As of 16^th May 2020, 4.65 million cases, with 1.7 million recovered patients and 300,000 deaths due COVID-19 have been reported in 213 countries worldwide [3]. All over the world, governments have issued recommendations such as intensified hand hygiene and have taken measures such as closing borders, enforcing lockdowns, etc. These non-pharmaceutical interventions (NPIs) reduce infection rates, keeping the number of severe cases below hospital capacity limit. A strategy popularly referred to as ‘flattening the curve’. Estimates of the effect various types of NPIs have on the reduction of the effective reproduction number are provided in [2] where it is reported that lockdown leads to an average reduction of the transmission of the disease by 50%, school closure, 20% and other measures around 10% (there are relatively large confidence bounds around these figures).

Because of stringent lockdown measures, the disease appears to have been contained in Wuhan, China. Following a lockdown, within a relatively short period (around ten days), the actual number of cases stopped increasing and began to drop exponentially. While China adopted an aggressive strategy of almost total lockdown, the measures adopted in other counties typically have been less “draconian”. However, the containment strategies do appear to be working, with a number of countries, including Germany, Italy and South Korea, having passed the peak of cumulative infectious cases.

1.2. Effective management of the reproduction number

In the absence of a proven vaccine, effective management of the long-term return to normality is required. This should consider both the minimisation of death rates and economic impact. Key parameters used by epidemiologists to quantify contagion are the basic and effective reproduction numbers. These dimensionless numbers describe the average number of expected secondary infections generated by each infected person for a completely susceptible population in the absence and presence of controlled interventions, respectively. Epidemiologists track the effective reproduction number through verification of the number of secondary infected arising from confirmed infected cases. This is difficult to estimate accurately; it requires a robust regime of contact tracing and the capacity to perform large numbers of tests to confirm whether individuals are infected.

Current opinion suggests that the COVID-19 has a basic reproduction number1 $\sim 2-3$. NPIs slow the spread of the virus, and as a result, there is a reduction in the effective reproduction number over time. If it is possible to maintain this number below one, then the pandemic will eventually die out. Keeping the effective reproduction number either close to, or below one, will require careful adjustment of NPIs2 .

1.3. Hybrid modelling and predictive simulation

In this work, hybrid models of the dynamics of COVID-19 infection rates are developed3 . The hybrid model must capture essential system dynamics for calibration, predictive modelling and simulation studies to be meaningful. These are an initial exponential growth in active cases, slowing as the NPIs influence disease transmission. After a peak in the number of cumulative cases, there will typically be a slow decline in active cases, provided the NPIs are not excessively relaxed.

Several efforts around the world are attempting to forecast the behaviour of COVID-19 transmission rates. The methods used include mechanistic transmission models [4], statistical models [5, 6], deterministic epidemiological models [7], [8], [9] and a statistical dynamical growth model [10]. In this work, a novel hybrid model is developed that may be used for forecasting and monitoring the effective reproductive number which several countries are using as an indicator to measure the effectiveness of NPIs. As an established backbone of fundamental knowledge, we use a susceptible – infected – removed (SIR)compartmental ordinary differential equations model [11], [12], [13]. The equations are augmented with a differential equation that models an exponential decline in the disease transmission rate, and hence the effective reproduction number. Daily monitoring and model calibration (through a customized model parameter estimation) allows classification of the potential and severity of the outbreak and an assessment of the effectiveness of current NPIs. Model simulation allows predictions to be made of the expected time course of the epidemic, which is conditional upon known current and past reported data.

2. Methods

Up-to-date daily information regarding the number of active, recovered and fatal cases for most countries around the world is available from [3]. Retrieving this information allows daily calibration of the hybrid model, on a country-by-country basis, as well as the monitoring of the status of the pandemic.

2.1. Mathematical modelling

Defining S(t) as the number of susceptible, I(t) the number of infected and R(t) the number of removed (recovered and deceased) individuals, from a constant population N at time t the differential equations of the Susceptible – Infectious - Removed (SIR) model are,

$$\frac{dS\left(t\right)}{dt}=-\frac{\beta \left(t\right)}{N}·S\left(t\right)I\left(t\right)$$ (1)

$$\frac{dI\left(t\right)}{dt}=\frac{\beta \left(t\right)}{N}·S\left(t\right)I\left(t\right)-\gamma ·I\left(t\right)$$ (2)

$$\frac{dR\left(t\right)}{dt}=x·\gamma ·I\left(t\right)$$ (3)

In these equations, β(t) represents the transmission rate of the virus $\left(\text{da}{\mathrm{y}}^{-1}\right)$ while γ $\left(\text{da}{\mathrm{y}}^{-1}\right)$ is the removal rate of reported infectious individuals, both of which can be time-dependent parameters. The transmission rate varies because of NPIs and the data-driven component of the hybrid model captures the dynamics of disease suppression. Here, a constant removal rate is used. However, it can also change with respect to time: as normally, the chance of recovery in a particular time interval is initially small. That chance of recovery then increases over time [see discussions in, e.g. [14]].

The additional parameter x is included within the equations to account for under-reporting of removed individuals from the infectious class. Emphasis around the world has focused on the reporting of infectious cases (typically hospital admissions) and the subsequent death rates of these patients. A relatively recent report [15] assessed the extent of under-reporting of symptomatic COVID-19 cases globally, and their results indicated significant under-reporting by a large number of countries. Furthermore, this number can be highly variable as case data can be missing, incomplete, incorrect, based on different definitions, or dated (or a combination of all of these)4 . The reported fraction x and an under-reported fraction $\left(1-x\right)$ maintain the conservation relationship inherent within the SIR model.

Using the model, provided the number of infected cases is relatively small compared to the total population size, so that, S(t) ≈ N, the effective reproduction number at time t is given by,

$$R_E\left(t\right)=\frac{\beta \left(t\right)}{\gamma }$$ (4)

2.2. Capturing the variation in disease transmission rate

Social distancing and lockdown measures reduce the transmission of the virus and the number of active infected cases. In terms of the SIR model, this translates into a reduction in the value of β(t). Using a first-order linear ordinary differential equation (ODE) to capture the variation in disease transmission rates, models any reduction as an exponential decay,

$$\tau ·\frac{d{\beta }^{\prime }\left(t\right)}{dt}+\beta {}^{\prime }\left(t\right)=-k\overline{u}\left(t\right),\beta {}^{\prime }\left(0\right)=0,\overline{u}\left(0\right)=0$$

$$\beta {}^{\prime }\left(t\right)\ge 0,\forall t$$

$$\beta \left(t\right)={\beta }_I+{\beta }^{\prime }\left(t\right)$$ (5)

The time-dependent variable $\overline{u}\left(t\right)$ models the effect of NPIs. This has a range between zero and one. A value of $\overline{u}\left(0\right)=0$ implies no NPIs and a constant disease transmission rate, i.e. $\beta \left(t\right)={\beta }_I$. A value of $\overline{u}\left(t\ge t_c\right)=1$ represents the maximum control effort/policies applied in any particular country because of the cumulative effect of NPIs initially introduced to reduce disease transmission. The time t_c is the time when the maximum control measures are introduced. In the differential equation, the time constant τ defines the rate of exponential decrease after the introduction of NPIs, and the gain parameter k is the magnitude of the final reduction in disease transmission rate, β(t). As a country relaxes (or strengthens again) the applied NPIs, the value of $\overline{u}\left(t\right)$ may be altered to account of any change. Defining a time t_ri an estimate can be made of the reduced control effort, $\overline{u}\left(t\ge t_{ri}\right)={\widehat{u}}_{ri}$. This provides a quantitative measure of the relative relaxation of the NPIs in any particular country and updated predictions of the dynamics of the number of cumulative infected individuals.

2.3. Model calibration

To quantify the discrepancy between model response and reported case data, the sum of the squared error between the normalized reported cumulative infected individuals I_R(t) and the model prediction I(t) as well as the reported removed individuals, $R_R\left(t-t_d\right)$ and the model prediction R(t) is calculated as,

$$J=\sum _{t=t_1}^{t_2}{\left(\frac{I_R\left(t\right)-I\left(t\right)}{I_{Rmax}}\right)}^2+\sum _{t=t_1}^{t_2}{\left(\frac{R_R\left(t-t_d\right)-R\left(t\right)}{R_{Rmax}}\right)}^2$$ (6)

The sum is over the time-period t ₁ (the initial outbreak reaching exponential growth) and t ₂ (current time), I_Rmax is the maximum of the reported infected individuals and R_Rmax the maximum reported removed individuals. The parameter t_d represents a time delay associated with the reporting of recovered / deceased individuals. This delay accounts for the time it takes for confirmation of deaths, recoveries, or the validation of data from tests.

To calibrate the hybrid model, a gradient-based optimisation algorithm, lsqnonlin 5 , minimises (6) by adjusting unknown model parameters. This involves repeated numerical solution of the ODEs, coded in Simulink to accommodate the time delay term and integrated using MATLAB's built-in routine ode15s for efficient integration of stiff ODEs. The use of lsqnonlin allows the additional MATLAB function nlparci 6 to calculate the 95% confidence intervals on the model parameters.

Using a constant value for the removal rate7 , $\gamma =\frac{1}{8}\text{da}{\mathrm{y}}^{-1}$ [16] successful minimisation of (6) using reported case data, provides an estimate of the numerical values of the hybrid model parameters, β_I, τ, k, x, the time delay, t_d and their associated confidence bounds. For countries where NPI relaxations are being introduced, given the timing of these relaxations, t_ri, an estimate can also be made of the reduced control effort, $\overline{u}\left(t\ge t_{ri}\right)={\widehat{u}}_{ri}$ during model calibration.

2.4. Data screening for model calibration

As discussed in [17] initially, prior to an outbreak becoming fully established, daily new case numbers are relatively low and the cumulative number of infectious cases typically grows at a sub-exponential rate [18]. However, an established outbreak driven mainly by community transmission is more likely after around one hundred reported cumulative cases [19]. Following [17], it is assumed that the initial time of the outbreak as the day when there are (as close as possible) one hundred reported cumulative cases in a particular country. This provides the start-time for data visualisation as well as the initial conditions for the ODEs.

For each country, the timing of the introduction of the most severe NPI's defines the control time t_c and hence, $\overline{u}\left(t\ge t_c\right)=1$. While most countries introduced NPIs in a staged manner, e.g. suggesting improved hygiene regimes, closing entertainment venues, closing schools, to full lockdown measures, we assume that the speed of introduction of these measures was generally rapid such that the subtleties of any fast ramp in interventions would not be discernible from the inaccuracies in the data. However, we note that recent work [20] quantify the effect of staged interventions in Germany, where large events were cancelled, followed by the closing of schools and many shops prior to a final intervention on March 23^rd 2020.

3. Results

To demonstrate and discuss our predictive modelling, we use reported case data from Spain, Germany, Sweden and South Korea. Predictions for a selection of other countries are in the supplementary material. These selected countries have a reasonable COVID-19 testing capacity (test coverage per thousand residents is over 15), which would imply reasonably robust data. As with any data-driven approach, it will only be possible to have representative and reliable results if the data is also reliable.

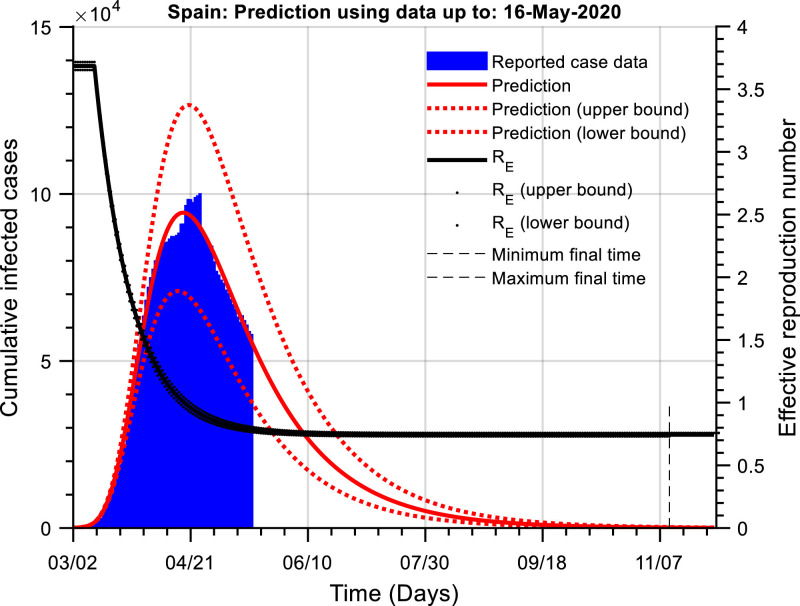
Fig. 1 presents the actual cumulative numbers of active cases as well as the hybrid model prediction for Spain using data up to 16^th May 2020. Around three weeks ago, Spain ‘flattened the curve’, and since then the number of cumulative cases has been decreasing.

Fig. 1.

The cumulative number of active infected cases as a function of time (Spain). The red line is the prediction of the actual number of cumulative active cases (blue) using our dynamic model. The black line is an estimate of the effective reproduction number. The dotted lines show the predictor confidence intervals. Simulation of our dynamic model allows for a prediction of the time when the cumulative infected cases is lower than a threshold; this threshold was set at 100 cases. The current estimate is that the number of cases will be lower than this threshold around 10^th November 2020 – 19^th December 2020.

At the peak, Spain had around 100,000 cumulative infected cases, and the hybrid model predicts it will take a significant time to reduce the number of active cases. The red line shows the model prediction of cumulative active cases ($R_{\text{squared}}=99.2\%$). Currently, this indicates that this will not reach a lower threshold of 100 cases (our chosen threshold) until between 10^th November 2020 and the 19^th December 2020. Note that this assumes that there is no relaxation in current NPIs8 . At this stage, and as may be expected, the prediction of the time to reach the chosen threshold of cases is not particularly accurate with a wide range in the final forecast because of the model confidence bounds. However, through continuous monitoring of case data and continual model re-calibration, we will obtain improved predictions.

The current calibrated model constants obtained using the Spanish data are,

${\beta }_I$	$k$	$\tau$	$x(\%)$	$t_d$
$0.460\pm 0.004$	$0.368\pm 0.002$	$15.74\pm 1.12$	$41.62\pm 1.12$	$1.215\pm 0.822$

These provide an estimate of the basic reproduction number, $R_0=3.68\pm 0.03$ and a current effective reproduction number9 of, $R_E=0.74\pm 0.01$. The model calibrations would also indicate a significant under-reporting of removed individuals. While this number is not required to predict the number of active cumulative cases, it is necessary for model calibration to the reported number of recovered patients. Note also that the estimated time constant of the disease suppression dynamics is relatively large at around 2 weeks.

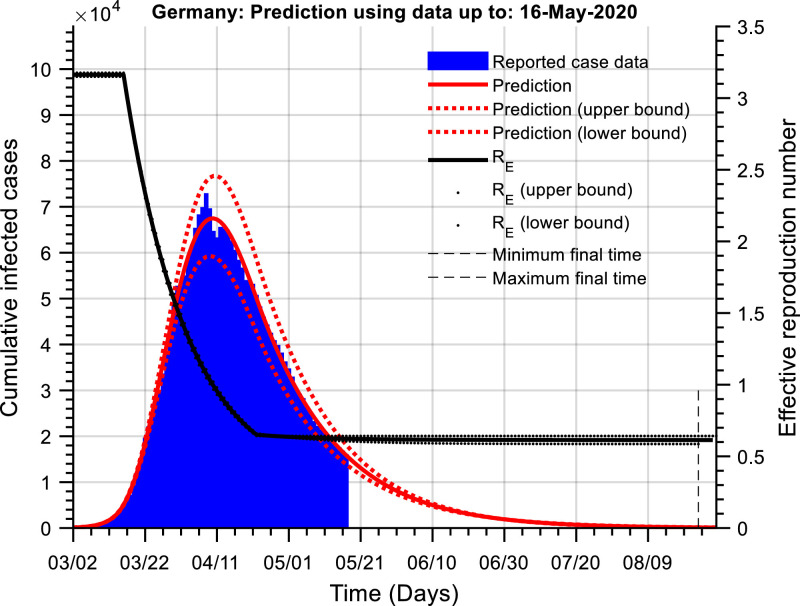
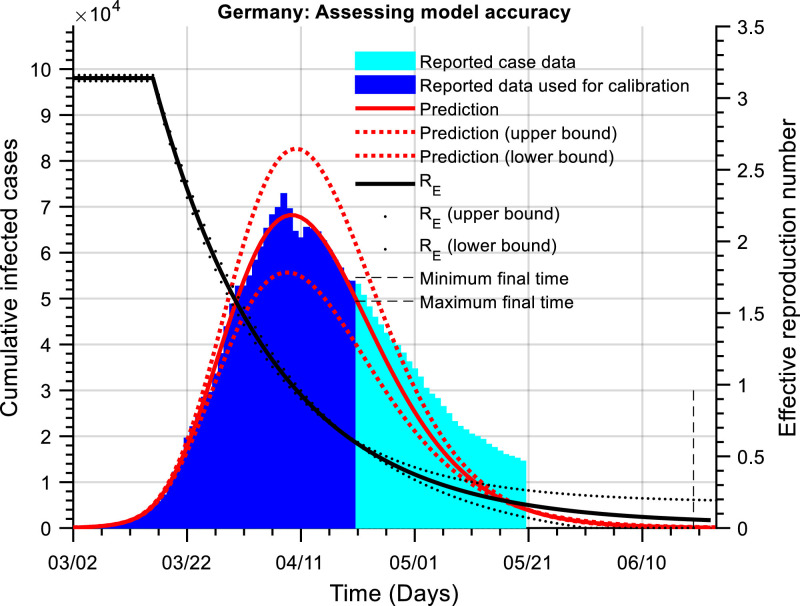
Fig. 2 shows the cumulative active cases and a predictive simulation for Germany. As may be observed, the curve of cumulative active cases has passed their initial peak and has been declining for a significant number of days. Indeed, Germany first began to relax NPIs around April 20^th 2020. Therefore, to calibrate the hybrid model, as well as estimating the unknown model parameters an estimate is also made of the relative reduction in NPIs using, $\overline{u}\left(t\ge t_{ri}\right)={\widehat{u}}_{ri}$. Assuming t_ri is April 20^th 2020 gives the following calibrated model constants,

${\beta }_I$	$k$	$\tau$	$x(\%)$	$t_d$	$\Delta {\widehat{u}}_{ri}$
$0.395\pm 0.002$	$0.358\pm 0.006$	$17.62\pm 0.90$	$53.14\pm 0.69$	$5.05\pm 0.837$	$-0.11\pm 0.03$

Fig. 2.

The cumulative number of active infected cases as a function of time (Germany). The red line is the prediction of the actual number of cumulative active cases (blue) using our dynamic model. The black line is an estimate of the effective reproduction number. Simulation of our dynamic model allows for a prediction of the time when the cumulative infected cases is lower than a threshold; this threshold was set at 100 cases. The current estimate is that the number of cases will be lower than this threshold around the 22^nd – 30^th August 2020.

These provide an estimate of the basic reproduction number, $R_0=3.16\pm 0.1$ and a current effective reproduction number10 of, $R_E=0.61\pm 0.03$. Note, again that the model calibrations would also indicate a significant under-reporting of removed individuals.

Fig. 2 also shows the model predictions ($R_{\text{squared}}=99.4\%$), with associated confidence bounds; indicating that the cumulative number of active cases would reach a lower threshold of 100 around the 22^nd – 30^th August 2020. The estimate of the relative NPI relaxation since April 20^th 2020 is around 11 %. To obtain this figure, we calibrate the model initially assuming that $\overline{u}\left(t\ge t_c\right)=1$ and estimate the reduction from this number as, $\Delta {\widehat{u}}_{ri}$ giving, $\overline{u}\left(t\ge t_{ri}\right)=1+\Delta {\widehat{u}}_{ri}$. Model calibration is relatively insensitive to a change in the assumed day that the NPIs were relaxed. Model calibration was still possible when t_ri was varied by five days on either side of April 20^th 2020. However, this does affect the predicted time to get to the lower threshold of 100 active cumulative cases.

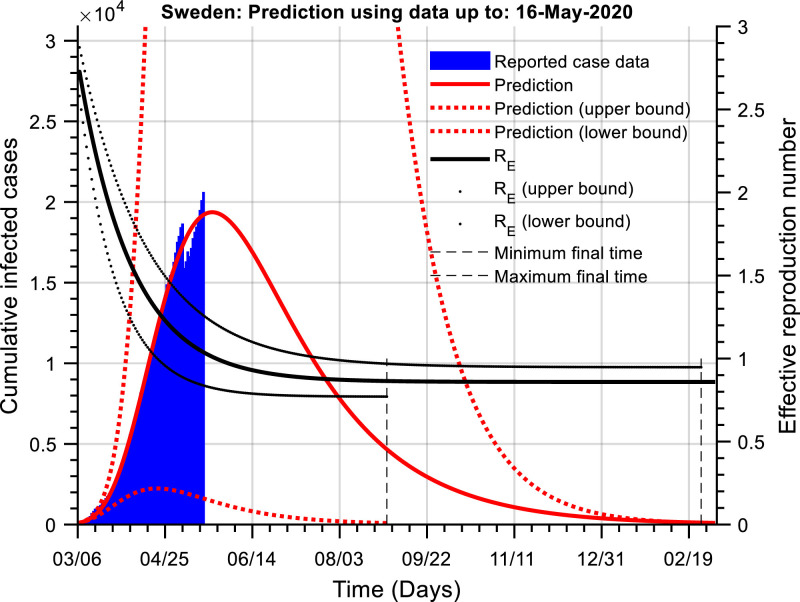
Fig. 3 presents the cumulative active cases as well as their prediction for Sweden ($R_{\text{squared}}=99.4\%$). Sweden is the only European country not to implement full lockdown measures. They did implement NPIs, where the measures in Sweden include closing of universities and high schools and asking older and at-risk residents to avoid social contact while keeping restaurants and primary schools open. As may be observed from the figure, the curve of cumulative active cases may peak in the coming days.

Fig. 3.

The cumulative number of active infected cases as a function of time (Sweden). The red line is the prediction of the actual number of cumulative active cases (blue) using our dynamic model. The black line is an estimate of the effective reproduction number. The confidence bounds are large, as is the estimation of the effective reproduction number and the time to achieve a lower threshold of 100 cases. The current estimate is that the number of cases will be lower than this threshold around December 2020 – mid February 2021.

In terms of model calibration, there are relatively large confidence bounds associated with the parameter estimates,

${\beta }_I$	$k$	$\tau$	$x(\%)$	$t_d$
$0.341\pm 0.018$	$0.234\pm 0.007$	$30.28\pm 8.70$	$17.20\pm 2.05$	$9.92\pm 2.43$

In turn, this leads to large bounds in the estimate of the cumulative number of effective cases, the effective reproduction number and the time to reach a lower threshold of 100 cumulative active cases. In the fullness of time, these issues will be resolved. Once the reported number of cases have passed the peak and they continue to decline, it will be possible to obtain a significantly more robust estimation of the model parameters and improved model predictions. Currently, the hybrid model parameters indicate the basic reproduction number, $R_0=2.73\pm 0.15$ and a current effective reproduction number close to one.

3.1. Long-range forecasts are always uncertain

If there were a first law of forecasting, it would be that long-range forecasts are always uncertain. In the present context, this may arise because of future changes in NPIs, which, when known to occur have to be accommodated in future predictions. To demonstrate the forecasting accuracy of the hybrid model, we use reported case data from South Korea and Germany. South Korea have successfully ‘flattened the curve’; they acted rapidly and decisively to suppress the disease through contact tracing using mobile phones and a rigorous testing regime, and have far fewer cases and deaths than the majority of countries around the world [21].

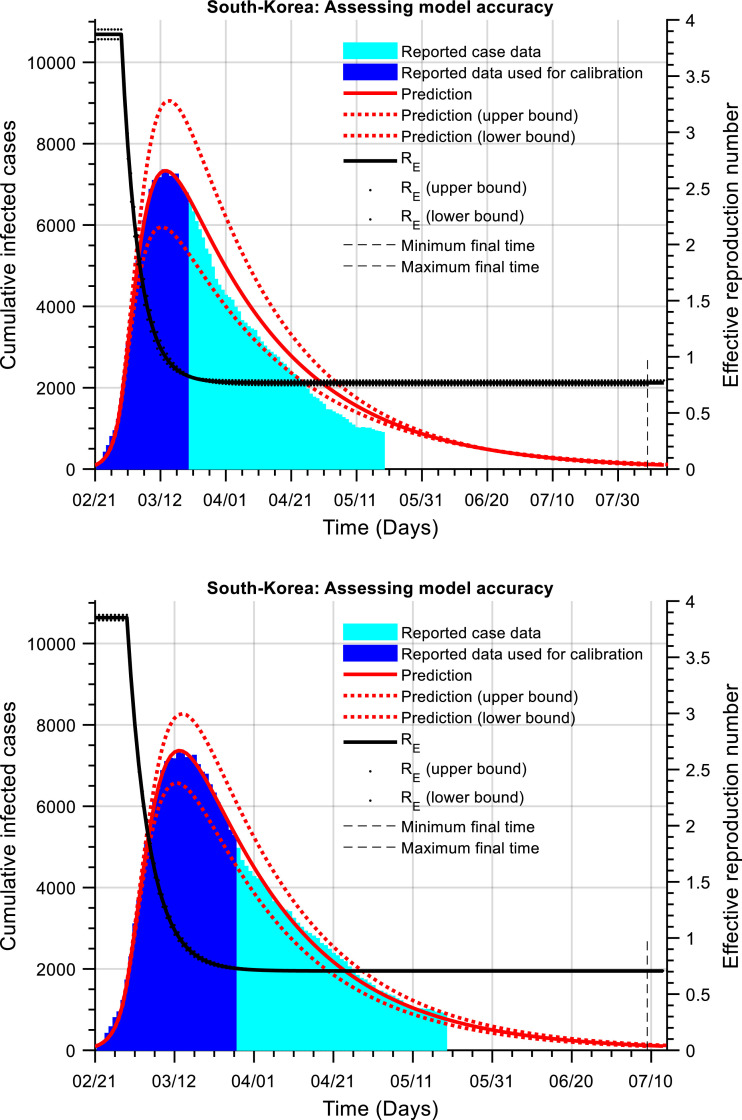
Fig. 4 shows a prediction of the number of cumulative active cases (red curve) and the effective reproduction number (black curve) of the disease.

Fig. 4.

The cumulative number of active infected cases as a function of time (South Korea). The red line is the prediction of the actual number of cumulative active cases (blue and cyan) using our dynamic model. Model calibration using the blue data (data up to the 19^th April 2020). Comparison of model simulations to the assumed ‘unknown’ reported case data (cyan). The black line is an estimate of the effective reproduction number.

The hybrid model was calibrated using reported case data up to one week (top figure) then two weeks (bottom figure) after the flattening of the peak. Observe the accuracy of the model predictions. Model calibration using data up to one week after the turning point produces an inaccurate forecast of the number of active cases although the dynamics show a similar trend. However, with the additional data, the calibrated model provides a much-improved forecast of the actual number of infected cases.

The hybrid model provides predictions of the disease suppression dynamics and time to reach a low threshold of cases within the bounds of ~30 and ~50 days, using data for model calibration up to one and two weeks after the turning point in the cumulative number of active cases. The estimated times being 7^th – 27th August 2020 (using data up to one week after the peak) and with the use of additional data (two weeks after the peak), this estimate changes to 28^th June – 7^th July 2020. After, recalibration of the hybrid model using data up to the 19^th May 2020 the current estimate is the 13 – 19^th July 2020.

Fig. 5 shows the results of a model calibration for Germany using reported case data up-to the 19^th April 2020 (before relaxation of NPIs). While the future forecast captures the qualitative behaviour of the response, the predicted number of cases are inaccurate (compare the prediction to the subsequently reported actual data). The model predicts that the number of cases will reduce at a faster rate, but because of NPI relaxation, this rate has actually slowed. However, as demonstrated in Fig. 2 daily re-calibration of the hybrid model can account for any observable changes, caused, for example, through relaxation of current NPIs. This allows an up to date forecast to be made of the future decline in cumulative active cases.

Fig. 5.

The cumulative number of active infected cases as a function of time (Germany). The red line is the prediction of the actual number of cumulative active cases (blue and cyan) using our dynamic model. Model calibration using the blue data (data up to the 19^th April 2020). Comparison of model simulations to the assumed ‘unknown’ reported case data (cyan). The black line is an estimate of the effective reproduction number. Observe that inaccurate model predictions as the forecast does not account for the relaxation of NPIs, which have a clear and observable effect on the dynamics of the number of active cases.

4. Discussion and conclusions

We describe a hybrid model of the dynamics of cumulative active cases because of COVID-19 and a methodology for the model calibration. Model simulation allows predictions to be made of the expected time course of the epidemic, which is conditional upon available current and past reported data. We have highlighted the trend in the cumulative number of active cases in Spain, Germany, Sweden and South Korea. In the supplementary material, we provide additional figures demonstrating the status of the pandemic in a selection of other countries (Italy, France, Switzerland, Turkey, USA and Colombia). Our results would indicate that the data-driven component of our hybrid model accurately captures an exponential decline in disease transmission.

We elected to keep our hybrid model comparatively simple using the established SIR model as a fundamental backbone to a data driven component that modelled an exponential decline in disease transmission rate. We find that this exponential decline adequately represented by a first order linear ordinary differential equation. Model calibration using reported case data requires the determination of four model parameters (β_I, k, τ, x) as well as a time delay associated with the reporting of removed cases, t_d. As NPIs are relaxed we can introduce additional model terms that may be used to quantify the relative relaxation of NPIs. Defining a time t_ri that an NPI relaxation occurs then an estimate can be made of the reduced control effort, $\overline{u}\left(t\ge t_{ri}\right)={\widehat{u}}_{ri}$. We demonstrated how this affects future predictions of the number of active cases using reported case data from Germany. As more case data becomes available, we will rigorously test the viability of including phased NPI changes as part of the hybrid model calibration.

Regarding alternative work that considers forecasting the dynamics of the reduction in the number of active cases of COVID-19, we note that [9] has adopted a similar approach to the estimation of the time it would take to achieve a lower threshold of active cases. However, calibration of their SIR model only considers daily cases with respect to time, recovered data is not considered and the method does not explicitly account for a varying transmission rate in the model equations or the tracking of, R_E(t).

In conclusion, our hybrid modelling approach allows the prediction of future infected case number scenarios as well as providing a measure of the effect of the relaxation of government interventions. Using a linear ODE, we capture the dynamics associated with disease suppression. For the countries we consider, the estimated time constant, τ, associated with the disease suppression dynamics is large (over 2 weeks for both Spain and Germany). In making a change to a dynamic system, the time constant provides an indication of the speed of the response and it takes approximately 3 – 4 time constants to move from the original to the final state. This would suggest that the easing of lockdown measures would be a difficult task requiring patience and careful planning.

Declaration of Competing Interest

The authors declare that they have no competing interests.