The impact of COVID-19 pandemic upon stability and sequential irregularity of equity and cryptocurrency markets

Highlights

• •45 cryptocurrency and 16 international stock markets are analyzed
• •A Big Data set is investigated before and during the COVID-19 pandemic period
• •We estimate stability and regularity metrics to infer on the predictability of price fluctuations
• •We find that cryptocurrencies embed higher instability and irregularity
• •Investing in digital assets during big crises could be considered riskier compared to equities

Abstract

We explore the evolution of the informational efficiency in 45 cryptocurrency markets and 16 international stock markets before and during COVID-19 pandemic. The measures of Largest Lyapunov Exponent (LLE) based on the Rosenstein's method and Approximate Entropy (ApEn), which are robust to small samples, are applied to price time series in order to estimate degrees of stability and irregularity in cryptocurrency and international stock markets. The amount of regularity infers on the unpredictability of fluctuations. The t-test and F-test are performed on estimated LLE and ApEn. In total, 36 statistical tests are performed to check for differences between time periods (pre- versus during COVID-19 pandemic samples) on the one hand, as well as check for differences between markets (cryptocurrencies versus stocks), on the other hand. During the COVID-19 pandemic period it was found that (a) the level of stability in cryptocurrency markets has significantly diminished while the irregularity level significantly augmented, (b) the level of stability in international equity markets has not changed but gained more irregularity, (c) cryptocurrencies became more volatile, (d) the variability in stability and irregularity in equities has not been affected, (e) cryptocurrency and stock markets exhibit a similar degree of stability in price dynamics, whilst finally (f) cryptocurrency exhibit a low level of regularity compared to international equity markets. We find that cryptos showed more instability and more irregularity during the COVID-19 pandemic compared to international stock markets. Thus, from an informational efficiency perspective, investing in digital assets during big crises as the COVID-19 pandemic, could be considered riskier as opposed to equities.

1. Introduction

Since the financial crisis of 2008, a large number of studies has focused on the response of equity markets to such long and significant economic crises. For instance, scholars have examined the effect of the subprime mortgage crisis of 2008 upon the hierarchical structure of stock markets [1], markets contagion [2], [3], [4], [5], crude oil markets [6,7], fertilizer markets [8,9], serial correlations in stocks [10], [11], [12], [13], [14] and currency markets [15], or upon the changes in market risk [16], volatility transmission [17], [18], [19], [20], [21], [22], and markets’ connectedness [23,24].

Since the world health organization has declared the Covid-19 pandemic as global health emergency, the world economy has been drastically affected. Sales declined, consumers changed their behaviour, the production was reduced, companies were in serious financial burden, and unemployment rates increased worldwide. Such severe shifts in business and economy across the world are expected to affect equities as well as alternative investments such as cryptocurrency markets. To date, from an investment perspective, there is a need to assess how Covid-19 pandemic affected efficiency in cryptocurrency and stock markets. The purpose of the current work is to examine any complexity traits in cryptocurrency and stock markets before and during Covid-19 Pandemic.

Indeed, this the first study to conduct a formal and robust empirical investigation on the effect of Covid-19 Pandemic upon the efficiency of cryptocurrency and equity markets, to the best of our knowledge. The Covid-19 pandemic is not over yet. However, investors and traders still have time to adjust their decisions based on the current shifts and intrinsic dynamics of these markets. Indeed, market agents and policy makers need a first assessment of current impacts of the COVID-19 outbreak on equity markets to provide better decision making in the short run.

The main purpose of this study is to assess complexity patterns in cryptocurrency and stock markets before and during the Covid-19 pandemic based on the estimation of chaos and randomness in their respective prices. To this end, the Largest Lyapunov Exponent (LLE) [25] and approximate entropy (ApEn) [26] will be applied to price time series in order to estimate the degrees of chaos and randomness respectively. The LLE describes the rate of divergence/convergence of initially close trajectories with time in a given non-stationary signal. It reveals the chaotic characteristic of a nonlinear signal and describes its stable/unstable state. The approximate entropy is suitable to measure the sequential and temporal regularity/irregularity of a nonlinear signal. Hence, measuring both LLE and approximate entropy in price time series allows to assess divergence/convergence and regularity/irregularity of cryptocurrency and stock time series before and during Covid-19 pandemic. The main advantage of using the LLE methodology in [25] and approximate entropy is that they provide efficient estimates even in case the length of original signals is small [26]. For each category of equity markets, the difference in estimated LLE between pre- and during pandemic periods will be tested via a Student t-test and an F-test. Similar tests will be applied to estimated approximate entropy measures.

Our contributions include a fist attempt to investigate the effect of COVID-19 pandemic on the stability of a Big Data set composed of 45 cryptocurrencies and 16 international stock markets. Next, we compare the effects of COVID-19 pandemic across cryptocurrency and stock markets to shed light on which markets have been more affected by such outbreak. Moreover, we enrich the relevant literature on the efficiency of cryptocurrency markets [27], [28], [29], [30], [31], [32] and spillovers of stock markets due to financial crises [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24]. Section 2 presents the Largest Lyapunov Exponent (LLE) and approximate entropy (ApEn) approaches. Section 3 describes the Big Data sets and provides with the empirical results. Finally, Section 4 concludes.

2. Regularity and stability methodologies

2.1. The largest Lyapunov exponent

The largest Lyapunov Exponent describes the divergence/convergence of two trajectories with similar initial conditions. Following the approach by Rosenstein et al [25], let's define a time series {x ₁,x ₂,…,x _N} and X_i=(x_i,x_{i + J},…,x_{i +( m - t ) J}) a system state at discrete time i, where J is the lag or reconstruction delay and m is the embedding dimension. Thus, the reconstructed trajectory is X = (X₁ X₂ … X_M)^T. Afterwards, the method requires localizing the nearest neighbor of each point of the reconstructed trajectory X. The nearest neighbor X _j to X _i is determined by calculating the smallest distance d_j(0) expressed as follows [25]:

$$d_j\left(0\right)=min{\mathit{X}}_j-{\mathit{X}}_i$$ (1)

The divergence is the average exponential rate characterized by the largest Lyapunov exponent λ₁ as follows:

$$d\left(t\right)\approx C{e}^{{\lambda }_{1}t}$$ (2)

where d(t) is the average divergence at time t and C is a constant that normalizes the initial separation. If we assume that the j-th pair of nearest neighbors diverges approximately at a rate given by the LLE, then we obtain:

$$d_j\left(i\right)\approx C_j{e}^{{\lambda }_1\left(i\Delta t\right)}$$ (3)

where Δt is the sampling rate and d_j(i) the distance between the jth pair of nearest neighbors after i discrete-time steps. By taking the logarithm of both sides of Eq.3, we obtain:

$$log\left(d_j\left(i\right)\right)\approx log\left(C_j\right)+{\lambda }_1\left(i\Delta t\right)$$ (4)

Then, Eq.4 describes a set of almost parallel lines (for j = 0, 1,…, M-1), with slope roughly analogous to λ₁ [25]. Finally, the LLE is estimated by using a least-squares fit to the average line expressed as:

$$y\left(i\right)=\frac{1}{\Delta t}log\left(d_j\left(i\right)\right)$$ (5)

where 〈⋅〉 denotes the average over all pairs of j. Following the approach in [25], it is assumed that the delay J corresponds to the lag before the first decline of the autocorrelation function, and the embedding dimension m is determined based on the smallest value that allows convergence. This way fast computation is enhanced. Recall that a positive value of λ₁ indicates divergent trajectories (unstable system) whilst a negative value indicates convergent trajectories (stable system). Accuracy, robustness to small and noisy data sets, and fast computation are the main advantages of using the approach by Rosenstein et al [25].

2.2. Approximate entropy

The Approximate entropy [26] was introduced to measure regularity/irregularity of a time-series. Consider a time series 〈x(n) = x(1), x(2), x(3), . . ., x(N)〉 where N is the time series length. Let m be a positive integer used to represent an embedding dimension and let r be a filter factor. Then, let's form the m-vectors X(1), X(2),…, X(N−m+1) where X(i)=[x(i), x(i+1),…, x(i+m−1)] and i=1, N−m+1. The distance between X(i) and X(j) is expressed as follows:

$$d\left[X\left(i\right),X\left(j\right)\right]=\underset{k=0,m-1}{max}\left[\left|x\left(i+k\right)-x\left(j+k\right)\right|\right]$$ (6)

Next, for each i=1, (N−m+1), the $C_r^m\left(i\right)$ are computed where:

$$C_r^m\left(i\right)=\frac{numberofd\left[X\left(i\right),X\left(j\right)\right]\le r}{N-m+1}$$ (7)

The quantity Φ^m(r) is computed as follows:

$${\Phi }^m\left(i\right)=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}log\left(C_r^m\left(i\right)\right)$$ (8)

In a similar way, the quantity Φ^{m +1}(r) is computed after increasing the dimension to m+1. Finally, the ApEn value of the time series can be calculated by:

$$ApEn\left(m,r,N\right)={\Phi }^m\left(r\right)-{\Phi }^{m+1}\left(r\right)$$ (9)

Hence, a large value of ApEn represents strong irregularity and unpredictability of the current time series as opposed to a low ApEn value which implies regularity.

3. Data and empirical results

The COVID-19 outbreak started in December 2019 in Wuhan city in China and has been declared by the world health organization as pandemic on 30th January 2020. To investigate the impact of COVID-19 pandemic upon the stability of daily prices of cryptocurrency and stock markets, we consider two different time periods. The pre-pandemic period spans September 2019 to December 2019 and the pandemic period from January 2020 to April 2020. The data was gathered from Yahoo finance. There comprise respectively 123 and 120 samples in the pre-pandemic and pandemic periods. Thus, we explore the chaotic and irregularity properties of 45 cryptocurrency markets and 16 international stock markets under a Big Data framework. The list of cryptocurrencies includes Bitcoin, Ethereum, XRP, Tether, Bitcoin Cash, Litecoin, Binance, EOS, Stellar, Cardano, Chainlink, Monero, Tron, Ethereum, Dash, Neo, IOTA, Zcash, NEM, Dogecoin, BigiByte, Basic Attention Token, VeChain, 0X, Decred, Bitcoin Gold, Qtum, ICON, Lisk, Augur, Kyber Network, Waves, OmiseGO, Status, Siacoin, MCO, MonaCoin, Nano, DigixDAO, Komodo, Steem, Verge, BitShares, Bytecoin, Horizen, MaidSafeCoin. The list of international stock markets comprises TSX (Canada), S&P500 (USA), DAX (Germany), CAC40 (France), BEL20 (Belgium), MOEX (Russia), Nikkei225 (Japan), HANG SENG (China), SSE Composite (Shanghai), All Ordinaries (Australia), BSE SENSEX (Bombay, India), KOSPI (South Korea), TSEC (Taiwan), IBOVESPA (Brazil), IPC (Mexico), and MERVAL (Argentina).

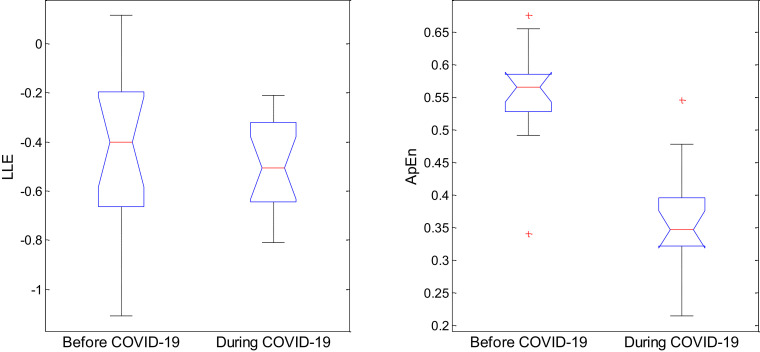
For illustration purposes, Fig. 1 plots Bitcoin price evolution before and during COVID-19 pandemic and Fig. 2 depicts the S&P500 price evolution. As shown, the dynamics of each price data are different across pre- and during the COVID-19 pandemic. In addition, Fig. 3 displays the boxplots of LLE and ApEn for cryptocurrency markets, and Fig. 4 the boxplots of LLE and ApEn for international equity markets.

Fig. 1.

Plots of Bitcoin price data before and during the COVID-19 pandemic.

Fig. 2.

Plots of S&P500 price index before and during the COVID-19 pandemic.

Fig. 3.

Boxplots of the LLE and ApEn metrics for cryptocurrency markets before and during COVID-19 pandemic. The dataset includes 45 cryptocurrency markets.

Fig.4.

Boxplots of the LLE and ApEn metrics for international equity markets before and during COVID-19 pandemic. The dataset includes 16 international equity markets.

To check if the distributions of the LLE and ApEn of each category of markets are significantly altered by the impact of the COVID-19 pandemic, a Student's t-test (test for equality of means) and an F-test (test for equality of variances) are both applied to the estimated sample populations of the LLE and ApEn metrics. The results are provided in Tables 1 and 2 respectively. Table 3 provides the results from the t-test and F-test when performed to check if LLE and ApEn metrics are different between cryptocurrency and international stock markets. In other words, the two statistical tests are applied at two different levels: firstly, checking differences between time periods and secondly checking for differences between markets. Consequently, the total number of performed statistical tests is 36, all at 5% statistical significance level. A given null hypothesis is rejected when the test p-value is less than 5%.

Table 1.

Reported probability values from t-test

Null hypothesis	Cryptocurrency markets	Stock markets
Two-side tests
LLE mean before pandemic = LLE mean during pandemic	0.0474	0.7562
ApEn mean before pandemic = ApEn mean during pandemic	0.0200	8.8244×10−08
One-side tests
LLE mean before pandemic > LLE mean during pandemic	0.9763	0.3781
LLE mean before pandemic < LLE mean during pandemic	0.0237	0.6219
ApEn mean before pandemic > ApEn mean during pandemic	0.0100	4.4122×10−08
ApEn mean before pandemic < ApEn mean during pandemic	0.9900	1.0000

Table 2.

Reported probability values from F-test

Null hypothesis	Cryptocurrency markets	Stock markets
Two-side tests
LLE variance before pandemic = LLE variance during pandemic	2.9275×10−04	0.2629
ApEn variance before pandemic = ApEn variance during pandemic	0.0916	0.8502
One-side tests
LLE variance before pandemic > LLE variance during pandemic	1.4637×10−04	0.1315
LLE variance before pandemic < LLE variance during pandemic	0.9999	0.8685
ApEn variance before pandemic > ApEn variance during pandemic	0.0458	0.5749
ApEn variance before pandemic < ApEn variance during pandemic	0.9542	0.4251

Table 3.

Reported probability values of comparative testing of cryptocurrency vs. stock markets

Null hypothesis	p-value
t-tests applied to LLE samples
LLE mean in cryptocurrency markets before pandemic = LLE mean in stock markets before pandemic	0.0305
LLE mean in cryptocurrency markets before pandemic > LLE mean in stock markets before pandemic	0.9847
LLE mean in cryptocurrency markets before pandemic < LLE mean in stock markets before pandemic	0.0153
LLE mean in cryptocurrency markets during pandemic = LLE mean in stock markets during pandemic	0.3289
LLE mean in cryptocurrency markets during pandemic > LLE mean in stock markets during pandemic	0.8355
LLE mean in cryptocurrency markets during pandemic < LLE mean in stock markets during pandemic	0.1645
F-tests applied to LLE samples
LLE variance in cryptocurrency markets before pandemic = LLE variance in stock markets before pandemic	0.1103
LLE variance in cryptocurrency markets before pandemic > LLE variance in stock markets before pandemic	0.0551
LLE variance in cryptocurrency markets before pandemic < LLE variance in stock markets before pandemic	0.9449
LLE variance in cryptocurrency markets during pandemic = LLE variance in stock markets during pandemic	0.8294
LLE variance in cryptocurrency markets during pandemic > LLE variance in stock markets during pandemic	0.4147
LLE variance in cryptocurrency markets during pandemic < LLE variance in stock markets during pandemic	0.5853
t-tests applied to ApEn samples
ApEn mean in cryptocurrency markets before pandemic = ApEn mean in stock markets before pandemic	0.3529
ApEn mean in cryptocurrency markets before pandemic > ApEn mean in stock markets before pandemic	0.1764
ApEn mean in cryptocurrency markets before pandemic < ApEn mean in stock markets before pandemic	0.8236
ApEn mean in cryptocurrency markets during pandemic = ApEn mean in stock markets during pandemic	1.1670×10−08
ApEn mean in cryptocurrency markets during pandemic > ApEn mean in stock markets during pandemic	5.8348×10-09
ApEn mean in cryptocurrency markets during pandemic < ApEn mean in stock markets during pandemic	1.0000
F-tests applied to ApEn samples
ApEn variance in cryptocurrency markets before pandemic = ApEn variance in stock markets before pandemic	0.0689
ApEn variance in cryptocurrency markets before pandemic > ApEn variance in stock markets before pandemic	0.0344
ApEn variance in cryptocurrency markets before pandemic < ApEn variance in stock markets before pandemic	0.9656
ApEn variance in cryptocurrency markets during pandemic = ApEn variance in stock markets during pandemic	0.6012
ApEn variance in cryptocurrency markets during pandemic > ApEn variance in stock markets during pandemic	0.3006
ApEn variance in cryptocurrency markets during pandemic < ApEn variance in stock markets during pandemic	0.6994

According to Table 1, in case of cryptocurrency markets, the null hypothesis of equality of means for the LLE across the two time periods is rejected. The one-side t-test results show that the null that the mean of LLEs before COVID-19 pandemic is larger than the one during the pandemic period is not rejected. On the contrary, the reverse null hypothesis is rejected. Therefore, for cryptocurrency markets the average level of LLEs has decreased during the COVID-19 period, hence stability has significantly diminished. Similarly, according to Table 1, the null hypothesis of equality of the means of ApEn across the two time periods is rejected. Interestingly, the null hypothesis that the mean of ApEn before the period in question is smaller than the mean of ApEn during COVID-19 pandemic, is strongly not rejected. We see that the average level of ApEn has increased during the COVID-19 pandemic and consequently irregularity in cryptocurrency markets significantly augmented.

Turning to international stock markets, we can see that the null hypothesis of equality of means of the LLE across the two time periods is not rejected. The one-side t-test findings reveal that the null that the mean of the LLEs before the pandemic is larger than during this period is not rejected. Likewise, the null that the mean before the COVID-19 is smaller than the mean of LLEs during the pandemic is not rejected too. Thus, for equity markets, the average level of the LLE has not statistically altered during the pandemic and the level of stability remained unchanged during the pandemic period. Similarly, the null of equality of means for the ApEn across the two time periods is rejected. Also, the null hypothesis that the mean of the ApEn before the pandemic period is smaller than the mean of ApEn during the outbreak, is strongly not rejected. For international stock markets, the average level of ApEn has increased hence they demonstrated higher irregularity during the pandemic time period.

Next we analyze Table 2. In case of cryptocurrency markets, the two-side F-test shows that the variance of the LLEs for the pre-COVID-19 period is not equal to the one during the pandemic. In this regard, an one-side F-test indicates that the variance of LLEs in cryptocurrency markets has significantly increased during the outbreak and we deduce that stability was severely perturbed across cryptocurrency markets during the pandemic period. Furthermore, the variance of ApEn has significantly increased during the pandemic, thus the level of sequential irregularity increased across cryptocurrency markets. Now, for international stock markets based on the F-tests the variance of the LLE as well as the variance of ApEn has not been altered during COVID-19. In other words, the variability in stability and irregularity in stock markets has not been affected by the pandemic.

According to the comparative Table 3, we show that the mean of the LLEs in cryptocurrency markets before the pandemic is higher than that of equity markets whilst during the outbreak it is statistically equal to that of stock markets during the pandemic. While the variance of LLE for the cryptos before COVID-19 is statistically lower than if stock markets before the pandemic, yet they are similar during the pandemic period. It also concluded from our testing that the mean of ApEn in cryptocurrency markets before the pandemic is equal to that of stock markets when the mean of ApEn in cryptocurrencies is lower compared to stock markets. Finally, while we observe that the fluctuations of the ApEn variance in cryptocurrency markets before the pandemic are lower than in stock markets, during the pandemic the variance of ApEn in cryptocurrency markets is equal to that of equity indices. Therefore, cryptocurrency and stock markets exhibit a similar degree of stability in price dynamics during the pandemic. In addition, during the pandemic time period, the cryptocurrency markets exhibit a low level of regularity compared to equity indices but with equal variability.

Our empirical findings can be summarized as follows:

• •The level of stability in cryptocurrency markets has significantly decreased during the pandemic whilst irregularity augmented.
• •While the level of stability in international stock markets has not been altered during the pandemic outbreak, yet equity markets embedded more irregularity.
• •Stability became severely perturbed and volatile across cryptocurrency markets during the pandemic period and sequential irregularity presented higher volatility across cryptocurrencies rendering them more unpredictable and chaotic.
• •The variability in stability and irregularity in stock markets has not been affected by the pandemic.
• •Both cryptocurrency and stock markets exhibit similar degree of stability in price dynamics during the pandemic, albeit cryptos exhibit lower level of regularity compared to international stock markets.

4. Conclusions

The COVID-19 pandemic has seriously affected global economy causing major declines in sales, production, and employment rates. In this study we attempted to analyze the stability and sequential regularity detected within the prices of 45 cryptocurrencies and 16 stock markets prior and during the COVID-19 pandemic by estimating the Largest Lyapunov Exponents and the Approximate Entropy. A large number of robust statistical tests was employed to check any differences between prior and during COVID-19 outbreak and across cryptocurrencies and stock markets.

We concluded that both stability and regularity in these markets have been significantly altered during the pandemic time period. Cryptocurrency fluctuations are found to be more affected by the pandemic than international stock markets. Specifically, cryptocurrency markets revealed more instability and higher irregularity during the pandemic period compared to the equities. Therefore, cryptocurrency markets are riskier and more unpredictable.

Although our empirical findings are preliminary in nature, our study constitutes a first attempt to assess the stability and regularity of fluctuations in both cryptocurrency and stock markets. Our results could be essential to investors, traders and policy makers in order to take appropriate decisions. Hopefully, our future work will consider a longer time period incorporating the aftermath of the pandemic for optimal comparative purposes.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests.