Machine learning predictive system based upon radiodensitometric distributions from mid-thigh CT images

Abstract

The nonlinear trimodal regression analysis (NTRA) method based on radiodensitometric CT images distributions was developed for the quantitative characterization of soft tissue changes according to the lower extremity function of elderly subjects. In this regard, the NTRA method defines 11 subject-specific soft tissue parameters and has illustrated high sensitivity to changes in skeletal muscle form and function. The present work further explores the use of these 11 NTRA parameters in the construction of a machine learning (ML) system to predict body mass index and isometric leg strength using tree-based regression algorithms. Results obtained from these models demonstrate that when using an ML approach, these soft tissue features have a significant predictive value for these physiological parameters. These results further support the use of NTRA-based ML predictive assessment and support the future investigation of other physiological parameters and comorbidities.

Data Availability Statement

The AGES I-II dataset cannot be made publicly available, since the informed consent signed by the participants prohibits data sharing on an individual level, as outlined by the study approval by the Icelandic National Bioethics Committee. Requests for these data may be sent to the AGES-Reykjavik Study Executive Committee, contact: Ms. Gudny Eiriksdottir, gudny@hjarta.is.

Ethical Participation Statement

We confirm that we have read the journal’s position on ethical issues involved in publication and affirm that this report is consistent with those guidelines.

Muscle deterioration in elderly individuals is commonly characterized by the loss of muscle strength and lean tissue mass, along with the concomitant replacement of lean tissue with intermuscular and intramyocellular adipose tissue. These phenomena have been consistently implicated as independent mortality risks in aging individuals. The incidence of muscle degeneration in aging, commonly referred to as sarcopenia, significantly affects the quality of life and physical activity of aging individuals.^1-4 Artificial intelligence (AI)technologies, particularly those utilizing machine learning (ML) algorithms, are becoming increasing used in healthcare data applications.^5-6 The increased availability of healthcare data and the continued development of big data analytics methods has driven the success of ML modelling in many quantitative fields, such as medical image processing or predictive system development, as well as other specialties such as neurology, cardiology, and oncology.^7-10 Mid-thigh computed tomography (CT) images from the AGES dataset have been used to quantitatively characterize subject-specific changes in soft tissue using a novel method known as Nonlinear Trimodal Regression Analysis (NTRA). The NTRA method works by generating soft tissue regression profiles described by 11 unique NTRA model parameters. The utility of these parameters in quantifying differences in fat, lean muscle, and loose connective tissue was first explored in comparing young, aging, and pathological subjects.^11-13 Results from this work illustrated the sensitivity of NTRA parameters to changes in soft tissue and suggested the employment of this method in the context of a larger CT image database. The Age Gene/Environment Susceptibility Study (AGES-Reykjavík) is an Icelandic dataset designed to examine risk factors and gene/environment interactions in relation to disease and disability in aging people. This dataset was assembled using 3,152 volunteers from 66-92 years of age and contains more than 10 thousand features obtained from two separate time points separated by 5 years. The AGES-Reykjavík dataset thereby presents a unique opportunity for the employment of big data analytics methods such as ML modelling.¹⁴ As ML algorithms have illustrated strong predictive value in the regression of body mass index (BMI)¹⁵ and isometric leg strength (ISO), the present study sought to demonstrate their prediction using NTRA parameters obtained from CT mid-femur cross-sections in the AGES-Reykjavík dataset. Results from this work further solidify the predictive power of NTRA parameters using BMI and ISO as test parameters. The methods reported here may be useful in prediction studies of cardiocirculatory,¹⁶ and mobility diseases.

Materials and Methods

Database & NTRA Parameters

AGES-Reykjavík database is composed of two measurement time points separated by approximately five years (AGES-I and AGES-II, respectively). These two datasets contain the same features using the same subjects; as such, assessing each subject independently yields a total subject population of 6,314. From these data, subject BMI [kg/m²] and ISO [N] were extracted, and the aforementioned 11 NTRA parameters were obtained from mid-femur CT scans, as described by Edmunds et al.¹² The NTRA method begins by defining radiodensitometric absorption distributions from CT number values of summed pixels in each CT slice. This process involves the standardized linear transformation of CT number to Hounsfield units (HU), according to the following expression:

HU = CT × 2,26625 – 190

Next, soft tissue HU values (across the range of -200 to 200 HU) were segmented into 128 bins, in accordance with typical quantitative CT assessment protocols.¹⁷HU histograms from this binning procedure were then smoothed to define probability density functions (PDF) for each histogram. Each PDF was then exported for NTRA regression analysis. As a form of modified nonlinear regression analysis, the NTRA method computationally describes each HU distribution as a quasi-probability density function containing three Gaussian distributions: one standard (non-skewed) and two skewed:

where N is the distribution amplitude, μ is the peak location, σ is the distribution width, and α is its skewness. These parameters are evaluated iteratively at each CT bin, x, using a modified reduced generalized gradient algorithm. Here, it is important to note the assumption that soft tissue can be optimally defined as a trimodal PDF consisting of three unique superimposed tissue types: fat (i=1) [-200 to -10 HU], loose connective tissue (i=2) [-9 to 40 HU], and lean muscle (i=3) [41 to 200 HU]. The central connective tissue is assumed to be non-skewed, while fat and muscle are described by, respectively, a positive and negative skewness. This method ultimately yields 11 patient-specific parameters: four that describe intermuscular and intramyocellular fat, four that describe lean muscle, and three that describe water-equivalent loose connective tissue (Figure 1).

Fig 1.

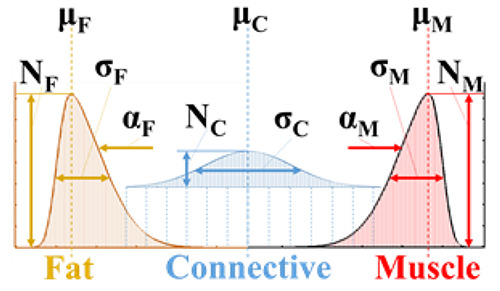
The 11 NTRA parameters represented on their three respective PDF’s. N defines the distribution amplitude, μ is the peak location, σ is the distribution width, and α is the distribution’s skewness.

Machine Learning Methodology

Tree-Based algorithms are considered for ML regression analysis; in particular, only ensemble learning forms of the decision tree are employed. This study compares four of these algorithms: random forest (RF),¹⁸ EXTRA Tree (EX-T),¹⁹ AdaBoosting (ADA-B,)²⁰ and gradient-boosting (GRAD-B).²¹ Python (PY) was used as a coding language along with the relative ML library Scikit-Learn (SL).²² To assess the performances of each prediction, the coefficient of determination (R²) was considered. K-fold cross-validation was used to visualize all possible R² results using 8, 12, 16, or 18 folds. To obtain the best results, many different combinations of k-fold divisions and the four tree-based ML algorithms were tested, using the 11 NTRA parameters as features from combining the two AGES-Reykjavík databases (AGES I+II). As an example, using the NTRA features with a k-fold division of 12 sets with the GRAD-B algorithm resulted in12 total R² values obtained for comparison.

Results and Discussion

Table 1 contains the mean and max R² values for BMI classification comparing the four ML algorithms, with all combinations of feature selections and k-fold divisions shown. The highest R² of 0.8305 was obtained using the GRAD-B algorithm with 200 estimators combined with NTRA features and a k-fold of 16. From regression, the most important NTRA parameters were connective and fat amplitudes: these always accounted for more than 50% of the total feature importance. Table 2 shows the R² results from ISO regression. The maximum mean R² value was obtained from GRAD-B (0.536), but the greatest maximum R² value (0.614) resulted from the EX-T algorithm. Muscle amplitude accounted for nearly 50% of the total feature importance, while all three connective tissue parameters – particularly the location – also yielded high predictive value. These results strengthen those achieved with BMI classification: connective tissue is significant as a predictor and should be considered as a main feature for further soft tissue investigations.

Table 1.

BMI prediction results

	R2 Max	R2 Mean
GRAD-B	0.8305	0.783 ± 0.020
ADA-B	0.817	0.775 ± 0.019
EX-T	0.813	0.759 ± 0.022
RF	0.811	0.757± 0.023

Mean ± std and max value of R² for the four ML algorithms.54 results are considered, obtained from all the k_fold divisions with k=8,12,16,18

Table 2.

ISO prediction results

	R2 Max	R2 Mean
GRAD-B	0.613	0.560± 0.040
ADA-B	0.587	0.519± 0.052
EX-T	0.614	0.511± 0.051
RF	0.599	0.512± 0.057

Mean ± std and max value of R2 for the four ML algorithms.54 results are considered, obtained from all the k_fold divisions with k=8,12,16,18

The present study illustrates excellent results in using NTRA parameters to classify BMI and ISO in aging subjects. In particular, tree-based ML algorithms gave the best results, but future exploration of other ML algorithms should be done to confirm and/or extend the results achieved here. The feature importance results for BMI and ISO are particularly relevant: those obtained from the three connective tissue parameters deserve additional discussion. Much importance is typically given to the dimetric comparison of muscle and fat tissue in CT scan analyses, but the present results strongly suggest that soft tissue assessment and predictive analysis should additionally consider water-equivalent loose connective tissue, which may actually yield the strongest predictive capacity in some applications, as evidenced by their high relative feature importance here for BMI and ISO.

The use of NTRA parameters as predictive features for aging subjects should be extended to other physiological measurements in future work exploring the AGES-Reykjavík database. Further investigation of the connections between these parameters and their related risk factors could further extend the field of translational myology into the discussion of sarcopenic muscle degeneration and its downstream effects on aging health. The present study provides an original approach to study the correlation between physiological parameters such as BMI and ISO and CT-based imaging, through the use of AI technologies.

List of acronyms

ADA-B

AdaBoosting

AGES

Age Gene/Environment Susceptibility Study

AI

Artificial Intelligence

BMI

Body Mass Index

CT

Computed Tomography

EX-T

EXTRA Tree

GRAD-B

Gradient-Boosting

HU

Hounsfield Unit

ISO

Isometric Leg Strength

ML

Machine Learning

NTRA

Nonlinear Trimodal Regression Analysis

PDF

Probability Density Functions

R2

Coefficient of Determination

RF

Random Forest

Funding Statement

Funding: None.