Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 May 11;5(20):11369–11377. doi: 10.1021/acsomega.0c00345

Comparison of CH4 and CO2 Adsorptions onto Calcite(10.4), Aragonite(011)Ca, and Vaterite(010)CO3 Surfaces: An MD and DFT Investigation

Ming Zhang †,*, Jian Li ‡,*, Junyu Zhao ‡, Youming Cui ‡, Xian Luo §
PMCID: PMC7254519  PMID: 32478225

Abstract

graphic file with name ao0c00345_0005.jpg

The interaction between greenhouse gases (such as CH4 and CO2) and carbonate rocks has a significant impact on carbon transfer among different geochemical reservoirs. Moreover, CH4 and CO2 gases usually associate with oil and natural gas reserves, and their adsorption onto sedimentary rocks may influence the exploitation of fossil fuels. By employing the molecular dynamics (MD) and density functional theory (DFT) methods, the adsorptions of CH4 and CO2 onto three different CaCO3 polymorphs (i.e., calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3) are compared in the present work. The calculated adsorption energies (Ead) are always negative for the three substrates, which indicates that their adsorptions are exothermic processes and spontaneous in thermodynamics. The Ead of CO2 is much more negative, which suggests that the CO2 adsorption will form stronger interfacial binding compared with the CH4 adsorption. The adsorption precedence of CH4 on the three surfaces is aragonite(011)Ca > vaterite(010)CO3 > calcite(10.4), while for CO2, the sequence is vaterite(010)CO3 > aragonite(011)Ca > calcite(10.4). Combining with the interfacial atomic configuration analysis, the Mulliken atomic charge distribution and overlap bond population are discussed. The results demonstrate that the adsorption of CH4 is physisorption and that its interfacial interaction mainly comes from the electrostatic effects between H in CH4 and O in CO32–, while the CO2 adsorption is chemisorption and the interfacial binding effect is mainly contributed by the bonds between O in CO2 and Ca2+ and the electrostatic interaction between C in CO2 and O in CO3.

1. Introduction

Calcium carbonate (CaCO3) extensively exists as sedimentary rocks in the earth’s crust.1,2 The carbonate rocks are expected to influence and regulate the carbon transfer between different geochemical reservoirs.1,3 It is reported that these minerals might be helpful in converting atmospheric greenhouse gases (such as carbon dioxide and methane) into solid carbonate.4−6 For instance, CaCO3 can be regarded as the products of CO2 capture reactions with CaO and can also be decarbonated to CaO;7 vaterite CaCO3 microspheres can be synthesized and used as a novel CO2 storage material;8 and mixed alkali metal salt MgO–CaCO3 sorbents are capable of adsorbing CO2 at an ultrafast rate, high capacity, and good stability.9 Thus, carbonate rocks may have an impact on global climate change.

On the other hand, a considerable proportion of the world’s oil and natural gas reserve is found associated with carbonate sedimentary rocks, such as limestone, chalk, and dolomite, in which CaCO3 is the main constituent.10−13 Meanwhile, the injection of carbon dioxide (CO2) is utilized as an approach to enhance fuels’ recovery. So, the interaction between the gas constituents and sedimentary rocks may have an impact on fossil fuels’ exploiting efficiency. Until now, the studies on CH4 and CO2 adsorptions on carbonate rocks are insufficient. Aiming to make a further clarification of the adsorptions, we have investigated the competitive adsorption of CH4 and CO2 onto different polymorphs of CaCO3, which will be helpful in enhancing oil12 and natural gas14 recovery rates.

Calcium carbonate (CaCO3) can exist as different polymorphs, in which the three phases of calcite, aragonite, and vaterite are commonly reported, and their thermodynamic stability decreases as per the sequence.15 Although vaterite is reported to not commonly found in geological conditions, it is an important precursor in several carbonate-forming systems.15 So, in the present work, all of the three CaCO3 polymorphs are considered.

In recent decades, the methods of DFT calculation and MD simulations have been successfully implemented in the study of molecule adsorption onto carbonate substrates. For instance, for the interaction between water and the calcite(10.4) surface, the dissociated and associated H2O molecules were compared and the dissociated ones were confirmed as a metastable state.16 The adsorptions of several organic molecules (hexane, cyclohexane, and benzene) are studied on the surface (10.4) of dolomite CaMg(CO3)2, and the adsorption energies of these organic molecules are compared with that of the water molecule.12 Chun et al.17 characterized the adsorption of benzoate and stearate on the surface of calcite(10.4), and the binding energies of adsorbed molecules were investigated in the presence of water and oil phases. The adsorption energies of a series of small molecules (i.e., water, several alcohols, and acetic acid) were determined and compared on three synthetic CaCO3 polymorphs (calcite, aragonite, and vaterite).18 Ataman et al.13,19 investigated the adsorptions of some functional groups on calcite(10.4), including oxygen-, nitrogen-, and sulfur-containing molecules and nonpolar organic molecules.

Narrowly, for the adsorptions of CH4 and CO2 onto CaCO3 rocks, several important studies20−23 can be noted and classified into experimental and theoretical sides:

  • (1)

    On the experimental side, the competitive adsorption of CH4 and CO2 onto limestone was investigated in the temperature range of 50–150 °C and the higher affinity of CO2 to the rock was confirmed, which can be ascribed to the strong electrostatic attraction between the CO2 molecule and limestone.23 Mixing of 10% CO2 into CH4 would enhance the adsorption of methane at 150 °C. Due to the high adsorption affinity of CO2, the total uptake increased, depending on the CO2 partial pressure. The adsorption of CO2 on limestone was confirmed to be four times higher than that of CH4. The higher natural selectivity of carbonate toward CO2 was thermodynamically supported by the lower adsorption heat of CO2.

  • (2)

    For theoretical studies of the CH421,22 and CO220−22 adsorptions onto calcite substrates, the methods of MD simulations20−22 and grand canonical Monte Carlo (GCMC)21 have been employed. The adsorptions of H2O, CO2, CH4, and N2 gases on calcite(11̅0) are compared, and the preferential order is confirmed as follows: H2O > CO2 > CH4 > N2; CO2 molecules could form an adsorbed layer on the surface, while no significant feature indicates that CH4 molecules would be adsorbed on calcite(11̅0).22 Furthermore, the adsorption and diffusion of CH4 and CO2 in calcite nanosized pores (width ∼22 Å) were compared, and it was confirmed that CO2 has much higher adsorption capacity and much less diffusion capacity compared with CH4.21 Finally, the adsorption behavior of CO2 molecules on calcite(10.4) was investigated, which demonstrates that CO2 molecules would be adsorbed perpendicularly at the sites of Ca ions and the desorption of CO2 molecules would be positively correlated with temperature.20

Based on our literature availability, the hierarchical comparisons of CH4 and CO2 adsorptions onto different CaCO3 polymorphs are still insufficient and need further clarification. In the present work, by combining MD and DFT methods, the CH4 and CO2 adsorptions onto various CaCO3 polymorphs (i.e., calcite, aragonite, and vaterite) are investigated and compared. The interactions between adsorbents (CaCO3 polymorphs) and adsorbates (gas molecules) are emphasized and compared; therefore, the adsorption systems are specifically studied in vacuum environments. All our DFT calculations are performed on a static molecular system, and the temperature effect is out of discussion in this work (the temperature is fixed at 0 K).

First, bulk unit cells of three CaCO3 polymorphs are established and relaxed with DFT calculations, and the bulk properties, such as lattice parameters and bulk modulus, are calculated. Then, various surfaces are created based on these relaxed unit cells, and the surface energies are examined. After that, the interface systems are established by putting gas molecules on the surfaces, and MD geometry optimizations are conducted for the interface models to achieve rough estimates of atomic configurations. Finally, the rough estimates are continually relaxed with the DFT method to reach their ground states, and based on these final atomic configurations, the remaining properties, such as adsorption energy, electron distribution, and density of states, are determined with the DFT method.

2. Results and Discussion

2.1. Bulk Calculations

The space groups of calcite and aragonite are experimentally identified as R3̅c (167)13 and Pmcn (62),24 respectively. However, the space group of vaterite is still in controversy, and based on previous literature works,25,26 the space group Pbnm (62) is adopted in this work. The unit cells of these three polymorphs are depicted in Figure 1.

Figure 1.

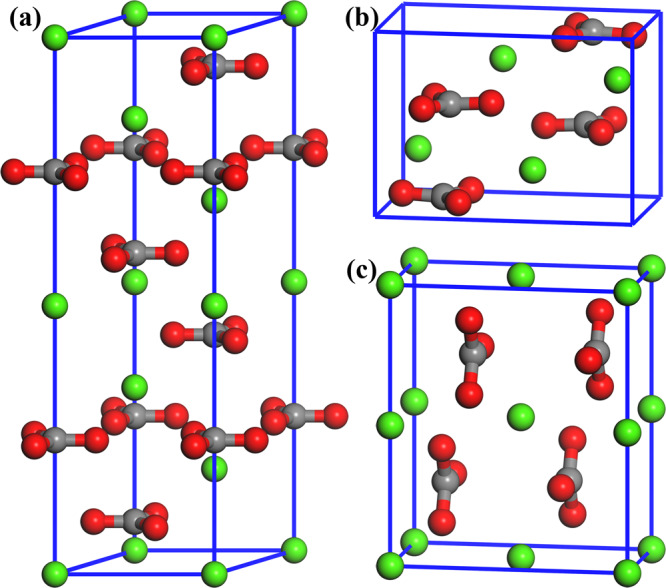
Figure 1

Open in a new tab

Unit cells of CaCO3 polymorphs: (a) calcite, (b) aragonite, and (c) vaterite. Different color spheres denote Ca (green), O (red), C (dark gray), and H (white) atoms.

The calculated lattice constants (a, b, and c) and bulk moduli (B) of bulk calcite, aragonite, and vaterite are listed in Table 1. Our results are in good accordance with the previous experimental and theoretical data. Especially for the lattice constants, they agree well with the experimental data for bulk calcite, aragonite, and vaterite.

Table 1. Lattice Constants (a, b, and c) and Bulk Moduli (B) of Bulk Calcite, Aragonite, and Vaterite.

          lattice constants (Å)
  
phases space group Pearson symbol Strukturbericht designation data sources a b c B (GPa)
calcite R3̅c (167) hR10 G01 present work 5.0527 5.0527 17.2510 71.8
        previous calculation 4.797 4.797 17.48227 69.628
        previous calculation 5.06 5.06 17.2513 75.629
        previous calculation 4.933 4.933 17.24230 85.731
        previous calculation 5.039 5.039 17.45632  
        experimental 4.99 4.99 17.0613 78.033
        experimental 4.988 4.988 17.06130 73.534
        experimental 4.991 4.991 17.06235  
aragonite Pmcn (62) oP20 G02 present work 5.0180 8.0388 5.8155 67.8
        previous calculation 4.8314 7.8359 5.791127 67.731
        previous calculation 5.003 8.047 5.65930 66.836
        previous calculation 5.112 8.230 5.91532  
        previous calculation 4.9609 7.9936 5.702037  
        experimental 4.9633 7.9703 5.744124 66.833
        experimental 4.961 7.967 5.74130 64.838
        experimental 4.962 7.969 5.74339  
        experimental 4.9614 7.9671 5.740440  
vaterite Pbnm (62) oP28 S12 present work 4.5423 6.6792 8.5127 70.8
        previous calculation 4.531 6.640 8.47741 69.131
        previous calculation 4.43 6.62 8.0427  
        previous calculation 4.531 6.640 8.47741  
        experimental 4.13 7.15 8.4825 63.842
Open in a new tab

2.2. Surface and Interface Models

Surface stability can be characterized by surface energy (γs) values; the surface with smaller γs is thermodynamically more stable. The surface energies of CaCO3 polymorphs have been investigated and compared by Leeuw and Parker,27 Sekkal and Zaoui,31 Massaro et al.37 Based on these data (refer to Table 2), the calcite(10.4) and CO32– terminated vaterite(010) can be identified as the most stable surfaces for both polymorphs. For aragonite, although the literature works27,37,43 consent that the (011) plane is the most stable surface, it is still controversial for its termination, namely, CO327 and Ca2+ 27,37,43 terminations (illustrated in Figure 2) are both reported as the most stable configurations. Therefore, we recalculated the surface energies of both terminations. The surface energy (γs) of aragonite(011) is ascertained as

2.2. 1

where As denotes the surface area, nCaCO3 is the number of CaCO3 formula contained in the surface slab, and Earagonite(011)slab and Earagonite are total energies of aragonite(011) surface slab and bulk aragonite per formula, respectively. Our calculated data are also listed in Table 2, and the values are 0.636 and 0.469 J/m2 for CO32– and Ca2+ terminations, respectively. This result indicates that Ca2+ termination will be more stable for aragonite(011), which is in line with the data of Massaro et al.37

Table 2. Surface Energies (J/m2) of Calcite, Aragonite, and Vaterite Reported in Literature Works and Calculated Values in This Work.

surfaces Leeuw et al.27 Sekkal et al.31 Massaro et al.37 Bano et al.43 Rohl et al.44 Massaro et al.45 Aquilano46 Bruno47 present work
calcite(10.4) 0.59 0.71   0.7113 0.534 0.536 0.536 0.503  
aragonite(011)CO3 0.69 0.90 0.801           0.636
aragonite(011)Ca     0.578           0.469
aragonite(011)       0.8406          
vaterite(010)CO3 0.62 0.75              
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Two different terminations of aragonite(011): (a) terminated with Ca2+ and (b) terminated with CO32–. Different color spheres denote Ca (green), O (red), C (dark gray), and H (white) atoms.

As aforementioned, the surfaces calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3 are identified as stable surfaces for the three polymorphs. Consequently, the adsorptions of CH4 and CO2 are compared on these three surfaces in the following parts.

The surface slabs are created on the basis of optimized bulk structures. The supercells of calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3 are modeled as (1 × 2), (2 × 1), and (1 × 2) slabs, respectively. Their surface areas are 8.2 × 10.1, 10.0 × 9.9, and 8.5 × 9.1 Å2, respectively. To avoid the imaginary interaction between top and bottom sides, a 30 Å vacuum space is inserted in all surface models in depth. The calcite(10.4) slab contains four layers of CO32– and Ca2+; the top two layers are free to relax, and the bottom two layers are constrained. For the Ca-terminated aragonite(011), eight layers of Ca2+ and eight layers of CO3 are included, and the bottom part (four layers of Ca2+ and four layers of CO32–) is frozen and the rest are free to move. For the CO3-terminated vaterite(010), four layers of Ca2+ and eight layers of CO3 are used to mimic the surface, and the bottom two layers of Ca2+ and four layers of CO32– are fixed to exhibit a bulklike interior.

The interface models are established by putting one molecule on the surfaces. Assuming that each Ca atom on the surface is an adsorption site for a molecule, all of the above configurations correspond to 0.25 ML coverage. First, the interface models are optimized using the MD method by employing COMPASS forcefield. Then, the DFT geometry optimizations are continually conducted to achieve equilibrium states of the adsorption systems.

2.3. Equilibrium Configurations and Adsorption Energies

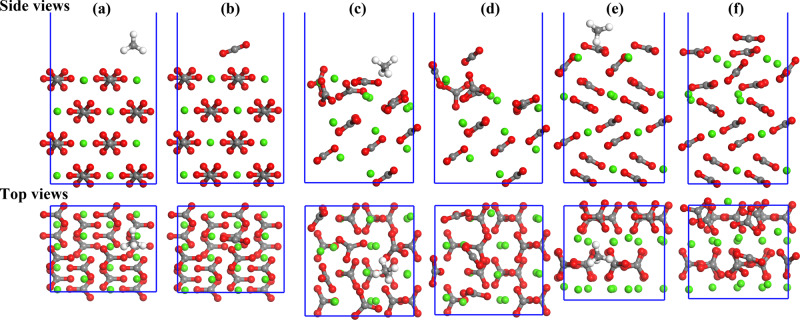
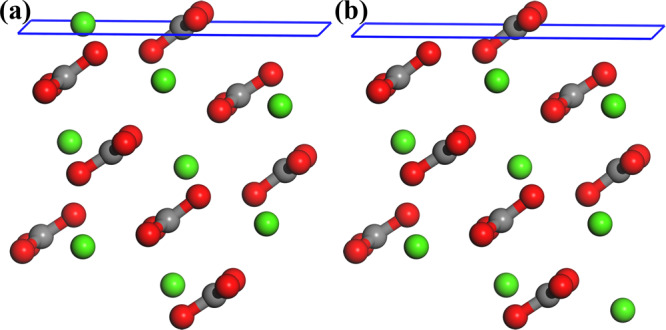
After the calculations of MD and DFT procedures, the equilibrium configurations of adsorption systems can be achieved (as shown in Figure 3).

Figure 3.

Figure 3

Open in a new tab

Fully relaxed configurations of CH4 and CO2 adsorbed on CaCO3 polymorphs: (a) CH4 on calcite(10.4), (b) CO2 on calcite(10.4), (c) CH4 on aragonite(011)Ca, (d) CO2 on aragonite(011)Ca, (e) CH4 on vaterite(010)CO3, and (f) CO2 on vaterite(010)CO3. Different color spheres denote Ca (green), O (red), C (dark gray), and H (white) atoms.

For all three CaCO3 polymorphs, surface reconstruction can be observed in the equilibrium models. Especially for aragonite(011)Ca and vaterite(010)CO3, surface reconstruction is more obvious. This phenomenon is consistent with the previous studies that the absorbed molecules (CO220 and H2O48−50) influence the surface reconstruction of calcite(10.4).

Based on these fully optimized interfacial configurations, the adsorption energies (Ead) can be ascertained as51

2.3. 2

where Einterface, Esurface, and Emolecule denote the energies of the interface slab, surface slab, and adsorbed molecule, respectively. The calculated results are listed in Table 3. Our calculated Ead is −51.04 kJ/mol for the system of CO2 adsorbed on calcite(10.4), which is very close to the previous experimental study (52–67 kJ/mol).52 So, our calculation results are accurate and reasonable.

Table 3. Calculated Adsorption Energies (Ead) of CH4 and CO2 on Calcite(10.4), Aragonite(011)Ca, and Vaterite(010)CO3 Surfaces.

  Ead of molecules (kJ/mol)
surfaces CH4 CO2
calcite(10.4) –22.75 –51.04
aragonite(011)Ca –35.01 –52.94
vaterite(010)CO3 –27.94 –74.79
Open in a new tab

If the adsorption energy is negative, the adsorption process will occur spontaneously, which also means that it is an exothermic process. Moreover, the relation between adsorption energy (Ead) and binding energy (Eb) can be expressed as Eb = – Ead.5353 So, if the adsorption energy is more negative, then the adsorption process will have larger potential (or driving force) and will tend to form stronger binding with the adsorbent. By examining our calculated results within this theorem, the following statements can be concluded:

  • (1)

    The adsorption energies of CH4 and CO2 on calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3 surfaces are always negative, which suggests that the adsorptions are spontaneous and exothermic processes.

  • (2)

    The Ead of CO2 are more negative than those of CH4; therefore, compared with CH4, the interfacial interaction between CO2 and CaCO3 surfaces should be stronger. This statement is also consistent with the previous studies.22,23,54

  • (3)

    By comparing Ead values of the same molecule on different surfaces, the adsorption precedence of the three surfaces can be described as follows: (i) for CH4, the sequence is aragonite(011)Ca > vaterite(010)CO3 > calcite(10.4); (ii) for CO2, the sequence is vaterite(010)CO3 > aragonite(011)Ca > calcite(10.4).

2.4. Mulliken Population and Atomic Configuration Analyses

The Mulliken population analysis is commonly employed in the DFT adsorption investigations.55−57 Although the absolute values of the atomic charges generated by the population analysis are regarded to have a little physical meaning, these values are strongly influenced by the atomic basis set with which the DFT calculations were conducted.58 However, consideration of their relative values can yield useful information.59−61

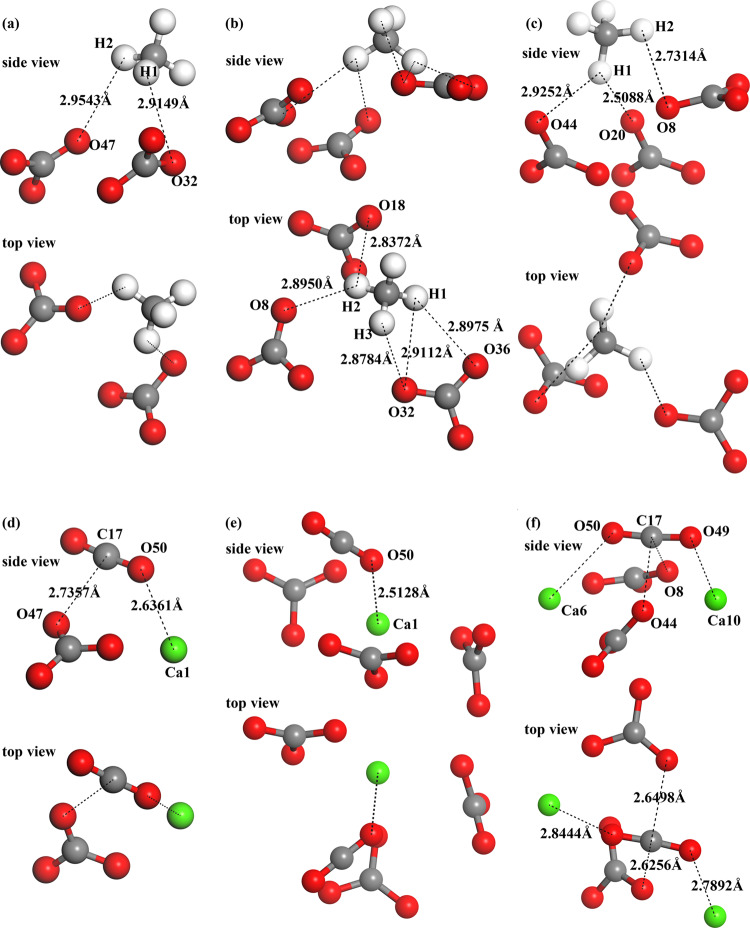
In the present work, Mulliken populations have been calculated for these equilibrium interfacial models. By examining the final atomic configurations together with the Mulliken population analysis, some implications can be obtained, and more importantly, these implications are helpful to shed light on the adsorption mechanism. The interfacial atomic configurations are shown in Figure 4. The results of the Mulliken atomic charge and overlap population are summarized in Tables 4 and 5, respectively. The overlap population may be useful to assess the bond nature; the bond’s covalency level increases with an increase in positive values, while negative values suggest an antibonding state.59,60 To clarify the interfacial interaction nature, the analysis is focused on the adsorbed molecules and some atoms in neighboring surface ions.

Figure 4.

Figure 4

Open in a new tab

Interfacial atomic configurations of six models: (a) CH4 on calcite(10.4), (b) CH4 on aragonite(011)Ca, (c) CH4 on vaterite(010)CO3, (d) CO2 on calcite(10.4), (e) CO2 on aragonite(011)Ca, and (f) CO2 on vaterite(010)CO3. Different color spheres denote Ca (green), O (red), C (dark gray), and H (white) atoms.

Table 4. Mulliken Charge Distribution in Adsorbed Molecules (CH4, CO2) and Some Atoms in Neighboring Surface Ions (Ca2+, CO32–)a.

      atomic population
absorption systems atoms’ origin atom no. s p d total charge (e)
CH4 on calcite(10.4) CH4 C17 1.48 3.61   5.09 –1.09
    H1 0.74 0.00   0.74 0.26
    H2 0.73 0.00   0.73 0.27
    H3 0.71 0.00   0.71 0.29
    H4 0.77 0.00   0.77 0.23
  CO32– O32 1.81 4.93   6.74 –0.74
    O47 1.81 4.88   6.69 –0.69
CH4 on aragonite(011)Ca CH4 C17 1.47 3.61   5.07 –1.07
    H1 0.76 0.00   0.76 0.24
    H2 0.78 0.00   0.78 0.22
    H3 0.71 0.00   0.71 0.29
    H4 0.73 0.00   0.73 0.27
  CO32– O8 1.81 4.89   6.70 –0.70
    O20 1.82 4.85   6.67 –0.67
    O44 1.83 4.88   6.71 –0.71
CH4 on vaterite(010)CO3 CH4 C17 1.46 3.59   5.05 –1.05
    H1 0.80 0.00   0.80 0.20
    H2 0.75 0.00   0.75 0.25
    H3 0.73 0.00   0.73 0.27
    H4 0.73 0.00   0.73 0.27
  CO32– O8 1.81 4.91   6.71 –0.71
    O18 1.81 4.89   6.70 –0.70
    O32 1.81 4.90   6.71 –0.71
    O36 1.81 4.90   6.71 –0.71
CO2 on calcite(10.4) CO2 C17 0.69 2.33   3.02 0.98
    O49 1.83 4.63   6.46 –0.46
    O50 1.82 4.69   6.51 –0.51
  Ca2+ Ca1 2.12 6.00 0.46 8.58 1.42
  CO32– O47 1.81 4.90   6.71 –0.71
CO2 on aragonite(011)Ca CO2 C17 0.68 2.32   3.00 1.00
    O49 1.84 4.59   6.43 –0.43
    O50 1.81 4.71   6.53 –0.53
  Ca2+ Ca2 2.10 6.00 0.48 8.57 1.43
CO2 on vaterite(010)CO3 CO2 C17 0.71 2.33   3.03 0.97
    O49 1.82 4.68   6.50 –0.50
    O50 1.82 4.66   6.48 –0.48
  Ca2+ Ca6 2.10 6.00 0.51 8.61 1.39
    Ca10 2.10 6.00 0.51 8.61 1.39
  CO32– O8 1.81 4.88   6.69 –0.69
    O44 1.81 4.92   6.73 –0.73
Open in a new tab
a

The atom no. is labeled in Figure 4.

Table 5. Mulliken Bond Population for the Atom Pairs between Adsorbed Molecules (CH4, CO2) and Neighboring Surface Ions (Ca2+, CO32–)a.

absorption systems atom pairs overlap population interatomic length (Å)
CH4 on calcite(10.4) H1–O32 –0.01 2.9149
  H2–O47 0.00 2.9543
CH4 on aragonite(011)Ca H1–O32 –0.01 2.9112
  H1–O36 0.00 2.8975
  H2–O8 0.00 2.8950
  H2–O18 –0.01 2.8372
  H3–O32 –0.01 2.8784
CH4 on vaterite(010)CO3 H1–O20 –0.01 2.5088
  H1–O44 –0.01 2.9252
  H2–O8 –0.01 2.7314
CO2 on calcite(10.4) O50–Ca1 0.05 2.6361
  C17–O47 0.01 2.7357
CO2 on aragonite(011)Ca O50–Ca2 0.06 2.5128
CO2 on vaterite(010)CO3 O49–Ca10 0.03 2.7892
  O50–Ca6 0.03 2.8444
  C17–O8 0.01 2.6498
  C17–O44 0.00 2.6256
Open in a new tab
a

The atom no. is shown in Figure 4.

The Mulliken charge distribution (Table 4) indicates that the H atoms in CH4 act as charge donors and O atoms act as charge acceptors. For the atoms in the surface ions, the O atoms in CO32– act as charge acceptors and Ca atoms act as charge donors. So, the interfacial interactions between H in CH4 and O in CO3 (likewise between O in CO2 and surface Ca2+) can be assumed.

The bond population results in Table 5 support the above assumption. Especially for the atom pairs of O in CO2 and surface Ca, their bond populations are positive values (0.03–0.06), which indicates that weak bonds form between the atoms. As for the atom pairs of H in CH4 and O in CO32–, the bond population values are basically negative around zero, so the interactions between them are mainly electrostatic effects. Therefore, the adsorptions of CH4 and CO2 on CaCO3 polymorphs can be featured as physisorption and chemisorptions, respectively. This is also the reason why CO2 adsorptions have larger Ead compared with that of CH4 adsorptions.

Furthermore, for the models of CO2 on calcite(10.4) and vateriate(010)CO3, we noticed that the interactions between C in CO2 and O in CO32– also contribute to their interfacial binding effect. However, their overlap bond populations are around zero, and the interactions between these atoms are mainly electrostatic effects.

Summarily, for the interfacial interaction nature of absorbed molecule and CaCO3 surfaces, the following statements can be deduced:

  • (1)

    CH4 adsorptions on the three CaCO3 polymorphs can be characterized as phsisorptions, and the interfacial interactions are mainly contributed by the electrostatic effects between H in CH4 and O in CO32–.

  • (2)

    CO2 may form chemisorption on the three surfaces, and the interfacial binding effect mainly comes from the bonds between O in CO2 and Ca2+ ions. Besides that, the electrostatic interactions between C in CO2 and O in CO32– also make some contributions.

3. Conclusions

The adsorptions of CH4 and CO2 onto calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3 are investigated and compared by employing MD and DFT calculations.

  • (1)

    In the equilibrium atomic configurations, surface reconstruction is observed.

  • (2)

    The calculated adsorption energies (Ead) of CH4 and CO2 are always negative for the three substrates, which indicates that the adsorptions are exothermic processes and spontaneous in thermodynamics.

  • (3)

    Comparing with that of CH4, the Ead of CO2 is more negative, which suggests that there is a stronger driving force for the adsorption of CO2, leading to stronger interfacial interactions after adsorption.

  • (4)

    The adsorption precedence for the three surfaces can be confirmed as follows: for CH4, aragonite(011)Ca > vaterite(010)CO3 > calcite(10.4); while for CO2, the sequence is vaterite(010)CO3 > aragonite(011)Ca > calcite(10.4).

  • (5)

    Combining with interfacial atomic configuration analysis, the Mulliken charge distribution and population suggest that the adsorption of CH4 is physisorption and the interfacial interaction mainly comes from the electrostatic effect between H in CH4 and O in CO32–, while the adsorption of CO2 is chemisorption and the interfacial binding effect is mainly contributed by the bonds between O in CO2 and Ca2+ and the electrostatic interaction between C in CO2 and O in CO3.

4. Computation Methodology

All DFT calculations were performed with the CASTEP package,62,63 wherein planewave ultrasoft pseudopotentials64,65 were employed to describe the cores. The electronic exchange correlation effects were treated within generalized gradient approximation (GGA) in the formalism of the Perdew–Burke–Ernzerhof (PBE) functional.66 The van der Waals dispersion corrections were included using the semiempirical DFT-D approach with the Tkatchenko and Scheffler (TS) scheme,67 which can generate accurate results for the adsorption of small molecules on solid surfaces.68 The Brillouin zone is sampled by the Monkhorst–Pack k-point grid.69 Convergence tests have been conducted to determine the cutoff energy and k-point grid separation. The details are described in the Supporting Information.

To ensure that the calculation results of different adsorption systems are comparable, the computation parameters employed in the DFT calculations should be the same (or as close to each other as possible). For this reason, the cutoff energy is fixed as 450 eV in all DFT calculations. Similarly, for the different adsorption systems, the k-point grid separation (or actual grid spacing) should be as close to each other as possible, so the grid separation is fixed as 0.03 Å–1 in all DFT calculations, and the k-points are automatically generated as 8 × 8 × 2, 6 × 4 × 6, and 8 × 4 × 4 for bulk unit cells of calcite, aragonite, and vaterite, respectively. Likewise, the k-points are automatically set as 4 × 3 × 1, 3 × 3 × 1, and 4 × 4 × 1 for the adsorption systems on the substrates of calcite(10.4), aragonite(011)Ca, and vaterite(010)CO3 respectively. We also noticed that the cutoff energy of 450 eV and k-point grid separation of around 0.03 Å–1 have been successfully implemented in the adsorption system containing the calcite(10.4) surface70 and calcium carbonate hydrates.71

Acknowledgments

The authors acknowledge the financial support for the research from the Natural Science Foundation of Shaanxi Province (Program no. 2019JM-388), the Scientific Research Program of Shaanxi Provincial Education Department (Program no. 15JK1570), the Science and Technology Innovation Fund of Xi’an Shiyou University (Program no. 2015BS12), the Youth Innovation Team of Xi’an Shiyou University (no. 2019QNKYCXTD04), and the Materials Science and Engineering of Provincial Advantage Disciplines of Xi’an Shiyou University (no. YS37020203). The authors also acknowledge the support from the Center for High Performance Computing of Northwestern Polytechnical University.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00345.

  • Convergence tests of computation parameters (cutoff energy and k-point grid separation) for bulk aragonite, calcite, and vaterite (PDF)

Author Contributions

All authors have discussed the results and commented on the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao0c00345_si_001.pdf (307.3KB, pdf)

References

  1. Merlini M.; Hanfland M.; Crichton W. A. CaCO3-III and CaCO3-VI, high-pressure polymorphs of calcite: Possible host structures for carbon in the Earth’s mantle. Earth Planet. Sci. Lett. 2012, 333–334, 265–271. 10.1016/j.epsl.2012.04.036. [DOI] [Google Scholar]
  2. Oganov A. R.; Ono S.; Ma Y.; Glass C. W.; Garcia A. Novel high-pressure structures of MgCO3, CaCO3 and CO2 and their role in Earth’s lower mantle. Earth Planet. Sci. Lett. 2008, 273, 38–47. 10.1016/j.epsl.2008.06.005. [DOI] [Google Scholar]
  3. Dasgupta R.; Hirschmann M. M. The deep carbon cycle and melting in Earth’s interior. Earth Planet. Sci. Lett. 2010, 298, 1–13. 10.1016/j.epsl.2010.06.039. [DOI] [Google Scholar]
  4. Kim B.; Park E.; Choi K.; Kang K. Synthesis of CaCO3 using CO2 at room temperature and ambient pressure. Mater. Lett. 2017, 190, 45–47. 10.1016/j.matlet.2016.12.030. [DOI] [Google Scholar]
  5. Kong H.; Kim B.; Kang K. Synthesis of CaCO3–SiO2 composite using CO2 for fire retardant. Mater. Lett. 2019, 238, 278–280. 10.1016/j.matlet.2018.12.033. [DOI] [Google Scholar]
  6. Zhao T.; Guo B.; Zhang F.; Sha F.; Li Q.; Zhang J. Morphology Control in the Synthesis of CaCO3 Microspheres with a Novel CO2-Storage Material. ACS Appl. Mater. Interfaces 2015, 7, 15918–15927. 10.1021/acsami.5b03568. [DOI] [PubMed] [Google Scholar]
  7. Yu C.; Huang C.; Tan C. A review of CO2 capture by absorption and adsorption. Aerosol Air Qual. Res. 2012, 12, 745–769. 10.4209/aaqr.2012.05.0132. [DOI] [Google Scholar]
  8. Guo B.; Zhao T.; Sha F.; Zhang F.; Li Q.; Zhao J.; Zhang J. Synthesis of vaterite CaCO3 micro-spheres by carbide slag and a novel CO2-storage material. J. CO2 Util. 2017, 18, 23–29. 10.1016/j.jcou.2017.01.004. [DOI] [Google Scholar]
  9. Cui H.; Zhang Q.; Hu Y.; Peng C.; Fang X.; Cheng Z.; Galvita V. V.; Zhou Z. Ultrafast and Stable CO2 Capture Using Alkali Metal Salt-Promoted MgO–CaCO3 Sorbents. ACS Appl. Mater. Interfaces 2018, 10, 20611–20620. 10.1021/acsami.8b05829. [DOI] [PubMed] [Google Scholar]
  10. Nwidee L. N.; Al-Anssari S.; Barifcani A.; Sarmadivaleh M.; Lebedev M.; Iglauer S. Nanoparticles influence on wetting behaviour of fractured limestone formation. J. Pet. Sci. Eng. 2017, 149, 782–788. 10.1016/j.petrol.2016.11.017. [DOI] [Google Scholar]
  11. Kabir S.; Haftbaradaran R.; Asghari R.; Sastre J. Understanding Variable Well Performance in a Chalk Reservoir. SPE Reservoir Eval. Eng. 2016, 19, 83–94. 10.2118/175436-PA. [DOI] [Google Scholar]
  12. Escamilla-Roa E.; Sainz-Díaz C. I.; Huertas F. J.; Hernández-Laguna A. Adsorption of molecules onto (10-14) dolomite surface: An application of computational studies for microcalorimetry. J. Phys. Chem. C 2013, 117, 17583–17590. 10.1021/jp404529e. [DOI] [Google Scholar]
  13. Ataman E.; Andersson M. P.; Ceccato M.; Bovet N.; Stipp S. L. S. Functional group adsorption on calcite: I. oxygen containing and nonpolar organic molecules. J. Phys. Chem. C 2016, 120, 16586–16596. 10.1021/acs.jpcc.6b01349. [DOI] [Google Scholar]
  14. Liu J.; Xi S.; Chapman W. G. Competitive Sorption of CO2 with Gas Mixtures in Nanoporous Shale for Enhanced Gas Recovery from Density Functional Theory. Langmuir 2019, 35, 8144–8158. 10.1021/acs.langmuir.9b00410. [DOI] [PubMed] [Google Scholar]
  15. Kabalah-Amitai L.; Mayzel B.; Kauffmann Y.; Fitch A. N.; Bloch L.; Gilbert P. U. P. A.; Pokroy B. Vaterite Crystals Contain Two Interspersed Crystal Structures. Science 2013, 340, 454. 10.1126/science.1232139. [DOI] [PubMed] [Google Scholar]
  16. Lardge J. S.; Duffy D. M.; Gillan M. J. Investigation of the interaction of water with the calcite (10.4) surface using ab initio simulation. J. Phys. Chem. C 2009, 113, 7207–7212. 10.1021/jp806109y. [DOI] [Google Scholar]
  17. Chun B. J.; Lee S. G.; Choi J. I.; Jang S. S. Adsorption of carboxylate on calcium carbonate (10-14) surface: Molecular simulation approach. Colloids Surf., A 2015, 474, 9–17. 10.1016/j.colsurfa.2015.03.003. [DOI] [Google Scholar]
  18. Okhrimenko D. V.; Nissenbaum J.; Andersson M. P.; Olsson M. H. M.; Stipp S. L. S. Energies of the adsorption of functional groups to calcium carbonate polymorphs: The importance of −OH and −COOH groups. Langmuir 2013, 29, 11062–11073. 10.1021/la402305x. [DOI] [PubMed] [Google Scholar]
  19. Ataman E.; Andersson M. P.; Ceccato M.; Bovet N.; Stipp S. L. S. Functional group adsorption on calcite: II. nitrogen and sulfur containing organic molecules. J. Phys. Chem. C 2016, 120, 16597–16607. 10.1021/acs.jpcc.6b01359. [DOI] [Google Scholar]
  20. Tao L.; Li Z.; Wang G.; Cui B.; Yin X.; Wang Q. Evolution of calcite surface reconstruction and interface adsorption of calcite-CO2 with temperature. Mater. Res. Express 2019, 6, 025035 10.1088/2053-1591/aaeef8. [DOI] [Google Scholar]
  21. Sun H.; Zhao H.; Qi N.; Qi X.; Zhang K.; Sun W.; Li Y. Mechanistic insight into the displacement of CH4 by CO2 in calcite slit nanopores: the effect of competitive adsorption. RSC Adv. 2016, 6, 104456 10.1039/C6RA23456A. [DOI] [Google Scholar]
  22. Wang S.; Zhou G.; Ma Y.; Gao L.; Song R.; Jiang G.; Lu G. Molecular dynamics investigation on the adsorption behaviors of H2O, CO2, CH4 and N2 gases on calcite (1 -1 0) surface. Appl. Surf. Sci. 2016, 385, 616–621. 10.1016/j.apsusc.2016.05.026. [DOI] [Google Scholar]
  23. Eliebid M.; Mahmoud M.; Shawabkeh R.; Elkatatny S.; Hussein I. A. Effect of CO2 adsorption on enhanced natural gas recovery and sequestration in carbonate reservoirs. J. Nat. Gas Sci. Eng. 2018, 55, 575–584. 10.1016/j.jngse.2017.04.019. [DOI] [Google Scholar]
  24. Carteret C.; De La Pierre M.; Dossot M.; Pascale F.; Erba A.; Dovesi R. The vibrational spectrum of CaCO3 aragonite: A combined experimental and quantum-mechanical investigation. J. Chem. Phys. 2013, 138, 014201 10.1063/1.4772960. [DOI] [PubMed] [Google Scholar]
  25. Meyer H. J. Uber Vaterit und seine Struktur. Angew. Chem. 1959, 71, 678. [Google Scholar]
  26. Christy A. G. A Review of the structures of vaterite: The impossible, the possible, and the likely. Cryst. Growth Des. 2017, 17, 3567–3578. 10.1021/acs.cgd.7b00481. [DOI] [Google Scholar]
  27. de Leeuw N. H.; Parker S. C. Surface Structure and Morphology of Calcium Carbonate Polymorphs Calcite, Aragonite, and Vaterite: An Atomistic Approach. J. Phys. Chem. B 1998, 102, 2914–2922. 10.1021/jp973210f. [DOI] [Google Scholar]
  28. Elstnerová P.; Friák M.; Fabritius H. O.; Lymperakis L.; Hickel T.; Petrov M.; Nikolov S.; Raabe D.; Ziegler A.; Hild S.; Neugebauer J. Ab initio study of thermodynamic, structural, and elastic properties of Mg-substituted crystalline calcite. Acta Biomater. 2010, 6, 4506–4512. 10.1016/j.actbio.2010.07.015. [DOI] [PubMed] [Google Scholar]
  29. Ungureanu C. G.; Cossio R.; Prencipe M. An Ab-initio assessment of thermo-elastic properties of CaCO3 polymorphs: Calcite case. CALPHAD: Comput. Coupling Phase Diagrams Thermochem. 2012, 37, 25–33. 10.1016/j.calphad.2011.12.007. [DOI] [Google Scholar]
  30. Raiteri P.; Gale J. D.; Quigley D.; Rodger P. M. Derivation of an Accurate Force-Field for Simulating the Growth of Calcium Carbonate from Aqueous Solution: A New Model for the Calcite–Water Interface. J. Phys. Chem. C 2010, 114, 5997–6010. 10.1021/jp910977a. [DOI] [Google Scholar]
  31. Sekkal W.; Zaoui A. Nanoscale analysis of the morphology and surface stability of calcium carbonate polymorphs. Sci. Rep. 2013, 3, 1587 10.1038/srep01587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Akiyama T.; Nakamura K.; Ito T. Atomic and electronic structures of CaCO3 surfaces. Phys. Rev. B 2011, 84, 085428 10.1103/PhysRevB.84.085428. [DOI] [Google Scholar]
  33. Salje E.; Viswanathan K. The phase diagram calcite-aragonite as derived from the crystallographic properties. Contrib. Mineral. Petrol. 1976, 55, 55–67. 10.1007/BF00372754. [DOI] [Google Scholar]
  34. Redfern S. A. T.; Angel R. J. High-pressure behaviour and equation of state of calcite, CaCO3. Contrib. Mineral. Petrol. 1999, 134, 102–106. 10.1007/s004100050471. [DOI] [Google Scholar]
  35. Maslen E. N.; Streltsov V. A.; Streltsova N. R. X-ray study of the electron density in calcite, CaCO3. Acta Crystallogr., Sect. B: Struct. Sci. 1993, 49, 636–641. 10.1107/S0108768193002575. [DOI] [Google Scholar]
  36. Ungureanu C. G.; Prencipe M.; Cossio R. Ab initio quantum-mechanical calculation of CaCO3 aragonite at high pressure: thermodynamic properties and comparison with experimental data. Eur. J. Mineral. 2010, 22, 693–701. 10.1127/0935-1221/2010/0022-2054. [DOI] [Google Scholar]
  37. Massaro F. R.; Bruno M.; Rubbo M. Surface structure, morphology and (110) twin of aragonite. CrystEngComm 2014, 16, 627–635. 10.1039/C3CE41654B. [DOI] [Google Scholar]
  38. Martinez I.; Zhang J.; Reeder R. J. In situ X-ray diffraction of aragonite and dolomite at high pressure and high temperature: Evidence for dolomite breakdown to aragonite and magnesite. Am. Mineral. 1996, 81, 611–624. 10.2138/am-1996-5-608. [DOI] [Google Scholar]
  39. Balmain J.; Hannoyer B.; Lopez E. Fourier transform infrared spectroscopy (FTIR) and X-ray diffraction analyses of mineral and organic matrix during heating of mother of pearl (nacre) from the shell of the mollusc Pinctada maxima. J. Biomed. Mater. Res. 1999, 48, 749–754. . [DOI] [PubMed] [Google Scholar]
  40. Devilliers J. P. Crystal structures of aragonite, strontianite, and witherite. Am. Mineral. 1971, 56, 758–767. [Google Scholar]
  41. Medeiros S. K.; Albuquerque E. L.; Maia F. F.; Caetano E. W. S. Jr.; Freire V. N. First-principles calculations of structural, electronic, and optical absorption properties of CaCO3 Vaterite. Chem. Phys. Lett. 2007, 435, 59–64. 10.1016/j.cplett.2006.12.051. [DOI] [Google Scholar]
  42. Maruyama K.; Kagi H.; Komatsu K.; Yoshino T.; Nakano S. Pressure-induced phase transitions of vaterite, a metastable phase of CaCO3. J. Raman Spectrosc. 2017, 48, 1449–1453. 10.1002/jrs.5162. [DOI] [Google Scholar]
  43. Bano A. M.; Rodger P. M.; Quigley D. New Insight into the Stability of CaCO3 Surfaces and Nanoparticles via Molecular Simulation. Langmuir 2014, 30, 7513–7521. 10.1021/la501409j. [DOI] [PubMed] [Google Scholar]
  44. Rohl A. L.; Wright K.; Gale J. D. Evidence from surface phonons for the (2 × 1) reconstruction of the (10-14) surface of calcite from computer simulation. Am. Mineral. 2003, 88, 921–925. 10.2138/am-2003-5-622. [DOI] [Google Scholar]
  45. Roberto M. F.; Marco B.; Dino A. Effect of the Surface Relaxation on the Theoretical Equilibrium Shape of Calcite. 1. The [001] Zone. Cryst. Growth Des. 2010, 10, 4096–4100. 10.1021/cg100774q. [DOI] [Google Scholar]
  46. Aquilano D.; Bruno M.; Massaro F. R.; Rubbo M. Theoretical Equilibrium Shape of Calcite. 2. [-441] Zone and Its Role in Biomineralization. Cryst. Growth Des. 2011, 11, 3985–3993. 10.1021/cg2005584. [DOI] [Google Scholar]
  47. Bruno M.; Massaro F. R.; Prencipe M.; Aquilano D. Surface reconstructions and relaxation effects in a centre-symmetrical crystal: the {00.1} form of calcite (CaCO3). CrystEngComm 2010, 12, 3626–3633. 10.1039/c002969f. [DOI] [Google Scholar]
  48. Baltrusaitis J.; Grassian V. H. Calcite (10-14) surface in humid environments. Surf. Sci. 2009, 603, L99–L104. 10.1016/j.susc.2009.06.021. [DOI] [Google Scholar]
  49. Villegas-Jiménez A.; Mucci A.; Whitehead M. A. Theoretical Insights into the Hydrated (10.4) Calcite Surface: Structure, Energetics, and Bonding Relationships. Langmuir 2009, 25, 6813–6824. 10.1021/la803652x. [DOI] [PubMed] [Google Scholar]
  50. Kendall T. A.; Martin S. T. Water-Induced Reconstruction that Affects Mobile Ions on the Surface of Calcite. J. Phys. Chem. A 2007, 111, 505–514. 10.1021/jp0647129. [DOI] [PubMed] [Google Scholar]
  51. Zhu B.; Zhang L.; Xu D.; Cheng B.; Yu J. Adsorption investigation of CO2 on g-C3N4 surface by DFT calculation. J. CO2 Util. 2017, 21, 327–335. 10.1016/j.jcou.2017.07.021. [DOI] [Google Scholar]
  52. Tabrizy V. A.; Hamouda A. A.; Soubeyrand-Lenoir E.; Denoyel R. CO2 Adsorption Isotherm on Modified Calcite, Quartz, and Kaolinite Surfaces: Surface Energy Analysis. Pet. Sci. Technol. 2013, 31, 1532–1543. 10.1080/10916466.2011.586962. [DOI] [Google Scholar]
  53. Würger T.; Heckel W.; Sellschopp K.; Müller S.; Stierle A.; Wang Y.; Noei H.; Feldbauer G. Adsorption of acetone on rutile TiO2: A DFT and FTIRS study. J. Phys. Chem. C 2018, 122, 19481–19490. 10.1021/acs.jpcc.8b04222. [DOI] [Google Scholar]
  54. Duan S.; Gu M.; Du X.; Xian X. Adsorption Equilibrium of CO2 and CH4 and Their Mixture on Sichuan Basin Shale. Energy Fuels 2016, 30, 2248–2256. 10.1021/acs.energyfuels.5b02088. [DOI] [Google Scholar]
  55. Chandiramouli R.; Nagarajan V. Adsorption studies of NH3 molecules on functionalized germanene nanosheet - A DFT study. Chem. Phys. Lett. 2016, 665, 22–30. 10.1016/j.cplett.2016.10.048. [DOI] [Google Scholar]
  56. Chandiramouli R.; Srivastava A.; Nagarajan V. NO adsorption studies on silicene nanosheet: DFT investigation. Appl. Surf. Sci. 2015, 351, 662–672. 10.1016/j.apsusc.2015.05.166. [DOI] [Google Scholar]
  57. Nagarajan V.; Chandiramouli R. NO2 adsorption behaviour on germanene nanosheet: A first-principles investigation. Superlattices Microstruct. 2017, 101, 160–171. 10.1016/j.spmi.2016.11.032. [DOI] [Google Scholar]
  58. Davidson E. R.; Chakravorty S. A test of the Hirshfeld definition of atomic charges and moments. Theor. Chim. Acta 1992, 83, 319–330. 10.1007/BF01113058. [DOI] [Google Scholar]
  59. Segall M. D.; Pickard C. J.; Shah R.; Payne M. C. Population analysis in plane wave electronic structure calculations. Mol. Phys. 1996, 89, 571–577. 10.1080/002689796173912. [DOI] [PubMed] [Google Scholar]
  60. Segall M. D.; Shah R.; Pickard C. J.; Payne M. C. Population analysis of plane-wave electronic structure calculations of bulk materials. Phys. Rev. B 1996, 54, 16317–16320. 10.1103/PhysRevB.54.16317. [DOI] [PubMed] [Google Scholar]
  61. Winkler B. O.; Pickard C. J.; Segall M. D.; Milman V. Density-functional study of charge disordering in Cs2Au(I) Au(III)Cl6 under pressure. Phys. Rev. B 2001, 63, 214103 10.1103/PhysRevB.63.214103. [DOI] [Google Scholar]
  62. Segall M. D.; Lindan P. J. D.; Probert M. J.; Pickard C. J.; Hasnip P. J.; Clark S. J.; Payne M. C. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys.: Condens. Matter 2002, 14, 2717. 10.1088/0953-8984/14/11/301. [DOI] [Google Scholar]
  63. Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
  64. Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
  65. Laasonen K.; Pasquarello A.; Car R.; Lee C.; Vanderbilt D. Car-Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials. Phys. Rev. B 1993, 47, 10142–10153. 10.1103/PhysRevB.47.10142. [DOI] [PubMed] [Google Scholar]
  66. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  67. Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
  68. Wang W.; Fan L.; Wang G.; Li Y. CO2 and SO2 sorption on the alkali metals doped CaO(100) surface: A DFT-D study. Appl. Surf. Sci. 2017, 425, 972–977. 10.1016/j.apsusc.2017.07.158. [DOI] [Google Scholar]
  69. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  70. Pinto H.; Haapasilta V.; Lokhandwala M.; Öberg S.; Foster A. S. Adsorption and migration of single metal atoms on the calcite (10.4) surface. J. Phys.: Condens. Matter 2017, 29, 135001 10.1088/1361-648X/aa5bd9. [DOI] [PubMed] [Google Scholar]
  71. Zhou Y.; Liu Q.; Hu M.; Xu G.; Xu R.; Chong X.; Feng J. Investigation on the stability, electronic, optical, and mechanical properties of novel calcium carbonate hydrates via first-principles calculations. Int. J. Quantum Chem. 2020, e26219 10.1002/qua.26219. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00345_si_001.pdf (307.3KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES