Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 May 12;5(20):11570–11577. doi: 10.1021/acsomega.0c00820

Impact of the Substituents on the Electronic Structure of the Four Most Stable Tautomers of Purine and Their Adenine Analogues

Anna Jezuita †,*, Halina Szatylowicz ‡,*, Tadeusz M Krygowski §
PMCID: PMC7254788  PMID: 32478247

Abstract

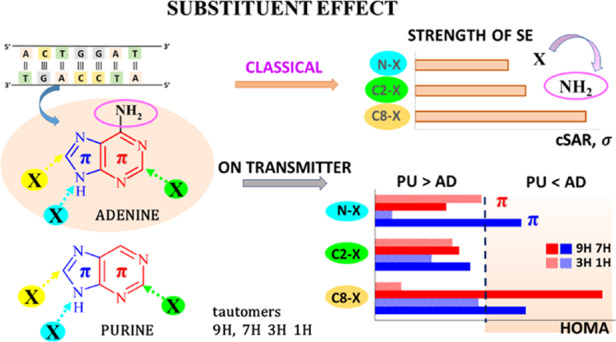
graphic file with name ao0c00820_0010.jpg

Substituent effects at the C2-, C8-, and N-positions of adenine and purine on the structural and π-electronic changes in their four tautomers were studied using the B97D3/aug-cc-pvdz computational level. The effect of various substituents (NO2, CN, CHO, Cl, F, H, Me, OMe, OH, and NH2) was characterized by the charge of the substituent active region (cSAR) approach and Hammett substituent constants σ. It has been found that for both adenine and purine derivatives, substituents from the C8–X position have a stronger influence on their electronic structure than from the C2–X and N–X positions. The presence of the amino group in adenine enhances the substituent effect compared to that which occurs in purine. In addition, its electronic structure is more sensitive to the effect of the substituent in 3H and 1H than in the 9H and 7H adenine tautomers. For a given substituent, a large variation in cSAR(X) values is observed, strongly dependent on the substitution position. For 7H and 9H adenine tautomers for C8–X systems, substituents reduce the aromaticity of the five-membered rings but increase the aromaticity of the six-membered rings.

Introduction

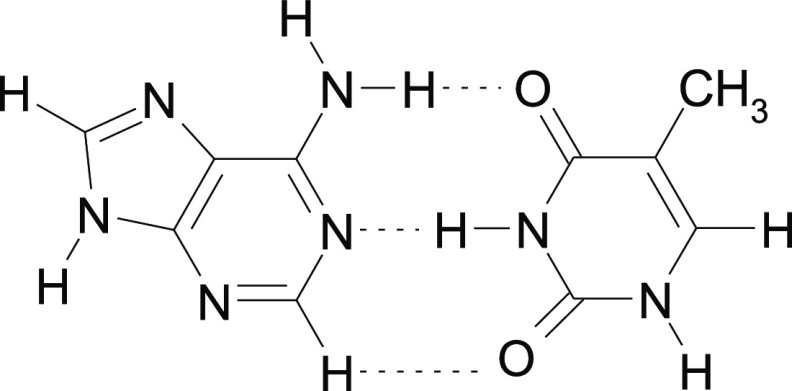
Adenine (AD) is one of the five important DNA and RNA components1 and differs from purine (PU) only by the presence of the amino group in position 6. In the helices of DNA and RNA, adenine interacts by means of H-bonding with thymine,2,3 in which a 2pxy lone pair at N1 and N–H in the amino group is involved (Scheme 1).

Scheme 1. Adenine–Thymine Watson–Crick Base Pair.

Scheme 1

Open in a new tab

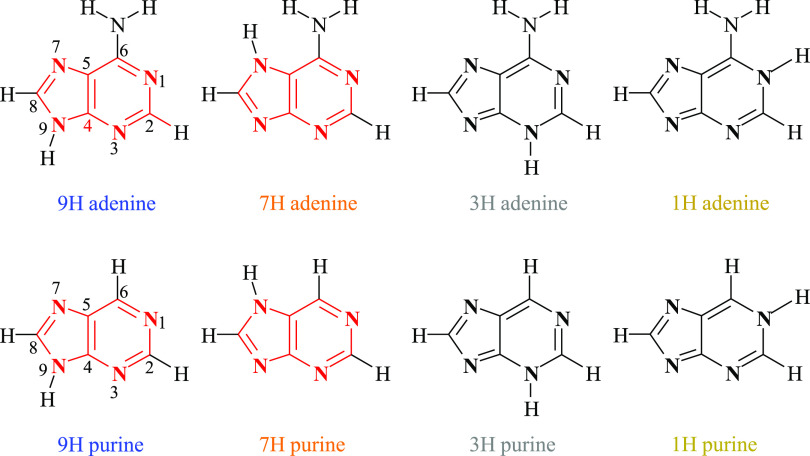
Adenine in helices also interacts in a spatial way by stacking with other nucleic acid bases.4,5 Therefore, the problem of the electronic structure of adenine and the role of the amino group are essential. This is illustrated by comparison with the data of purine. The question arises how the amino group affects the electronic structure of purine molecule, which is just a parent system for adenine. They are both aromatic6,7 and may exist in several prototropic tautomers.8 The complete adenine tautomeric mixture consists of 23 tautomers (9 amine and 14 imino forms), while purine can exist in the form of 9 tautomers (4 NH and 5 CH isomers). Structural parameters and energetic stabilities of all adenine9−11 and purine12−14 tautomers were studied in detail using quantum chemistry methods, taking into account both various oxidation states and environments. In the case of neutral purine in the gas phase, the stability of tautomers decreases in the following order: 9H, 7H, 3H, and 1H. The first three tautomers are also the most stable for adenine. Therefore, this study is focused on the four most stable purine tautomers and their adenine analogues, as presented in Scheme 2.

Scheme 2. Structures and Numbering of Atoms in the Studied Tautomers of Adenine and Purine.

Scheme 2

Open in a new tab

Rings following the Hückel 4N + 2 rule (H+) marked in red and not meeting this rule (H-) marked in black; the colors used to label the tautomers are used in the figures and tables.

It has been accepted for a long time that five- and six-membered rings (R5 and R6, respectively) are just imidazole and pyrimidine moieties fused together into molecules of adenine or purine. Very recently, it was shown15 that this is correct only in the case of tautomers 7H and 9H. In these cases, both rings contain six π-electrons; thus, they follow the Hückel 4N + 2 rule and demonstrate proper π-electron delocalization for aromatic systems.16 For this reason, these rings are abbreviated as H+, i.e., fulfilling the Hückel rule (red in Scheme 2). In contrast, the rings R5 and R6 in tautomers 1H and 3H do not follow this rule. They contain either five or seven π-electrons, exhibit different π-electronic properties, and are abbreviated as H- (black in Scheme 2). Hence, tautomers 7H and 9H in purine are significantly more stable than 1H and 3H.15 In adenine, this rule is somewhat perturbed by the interaction of rings with the amino group. These properties, substituent effects on the interactions between the amino group and various parts of the π-electron structure of adenine, and a comparison with the data of purine are subject of this report.

Recently, numerous studies have been carried out on the classical SE for meta- and para-disubstituted benzene series,17−21 cyclohexa-1,3-diene,22 and bicyclo[2.2.2]octane23,24 derivatives with different reaction sites (Y = NO2, COOH, OH, NH2) and a wide range of substituents X properties. For the above-mentioned systems, it has been documented that quantum-chemical models of the SE (charge of the substituent active region (cSAR), substituent effect stabilization energy (SESE), pi/sigma electron donor–acceptor (pEDA/sEDA); explanation and references are given in the Methodology section) show good compatibility with substituent constants and allow us to compare the electronic structures of X and Y. Therefore, it is very important to establish how such approaches work in heterocyclic systems composed of different π-electron rings, as in the case of adenine and purine structures. The use of substituent effect stabilization energy (SESE)25−27 to describe the effect of a substituent on the stability of adenine and purine tautomers has been shown recently.28 This work is mainly devoted to the effect of substituents on the electronic structure of title systems.

Results and Discussion

The results of the application of the quantum chemistry-based descriptors of the substituent effect (cSAR, charge flow index (CFI), harmonic oscillator model of aromaticity (HOMA), and pEDA/sEDA) to C8–X-, C2–X-, and N–X-substituted adenine (AD) and purine (PU) tautomers are presented in Tables S1–S16 (Supporting Information).

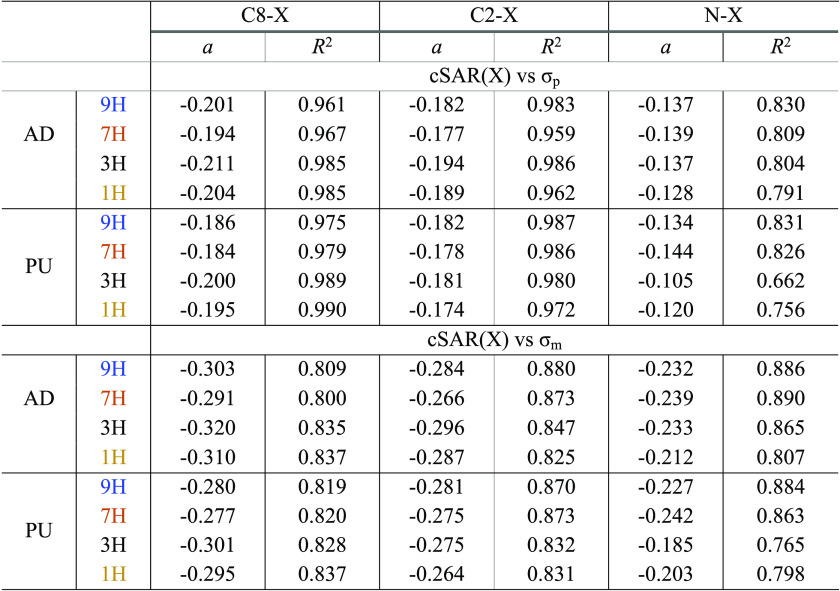
A comparison of the relationships between the cSAR(X) values obtained for adenine and those for purine gives a good insight into understanding the basic relations for electronic characteristics between these two molecular systems. It should be noted that the cSAR(X) values, as SE characteristics, are usually well correlated with the Hammett σ constants,29−31 mainly σpara and σmeta (abbreviated as σp and σm, respectively) constants. However, it should be stressed that the substituent constant values are determined for particular reference systems. In the case of the Hammett σ constants, they describe exactly the electronic properties of substituents only in meta- and para-substituted benzoic acids.32,33 When they are used as SE characteristics for other systems, similarity models are applied by means of linear regressions of a given physicochemical property P(X) plotted against given σ’s. The differences in the electronic properties of substituents attached to various systems in question are expressed by the slopes of the linear regression and the precision of the similarity model by the determination coefficient R2 (where 100 × R2 describes the percentage by which the similarity models describe variability of P(X) in a given sample).34 In the case of our studies, the σp constants are more suitable than σm, as presented in Table 1.

Table 1. Slopes of the Obtained Linear Dependences cSAR(X) vs σp and σm for C8–X, C2–X, and N–X Substitutions of Adenine (AD) and Purine (PU) Derivatives.

graphic file with name ao0c00820_0006.jpg

Open in a new tab

For the C–X (both C8–X and C2–X) substitution, the determination coefficients for cSAR(X) on σp dependences are always higher than 0.96, indicating a high similarity for the interaction discussed. They are significantly worse for N–X systems, always below 0.831, for both adenine and purine systems and particularly worse for PU 1H and 3H tautomers R2 < 0.756. In general, the slopes are (as absolute values) slightly larger for AD tautomers than for PU ones, but the differences seem to be insignificant. This may be understood as a high similarity for the substituent effect in PU and AD for 2- and 8-substituted systems. This conclusion is not as clear for N–X substitution for 1H and particularly for 3H tautomers. Nevertheless, it can be concluded that the cSAR(X) approach could be successfully applied to the investigation of SE in PU- and AD-like systems.

Classical Substituent Effect

The application of the classical interpretation of the SE allows us to consider how the substituent may affect the properties of the reaction site, in our case the distinguished group NH2. For this purpose, a Hammett-type linear equation is used, in which the slope (also known as reaction constant) describes the sensitivity of the reaction site on the impact of substituents X. In adenine, a good example of the classical approach is illustrated by dependences of cSAR(NH2) on substituent constants, σm and σp, as presented in Table S17 and Figure 1. The number of bonds between C6, where the NH2 group is attached, and C2 and C8 positions of attachment of the substituent X is two and three, respectively. This resembles the well-known situation for meta- and para-substituted benzene derivatives,35 in which σm and σp are used in similarity models, respectively.36 This analogy between meta- and para-substituted benzene derivatives and C2- and C8-substituted adenine derivatives is very well shown by the data in Table S17.

Figure 1.

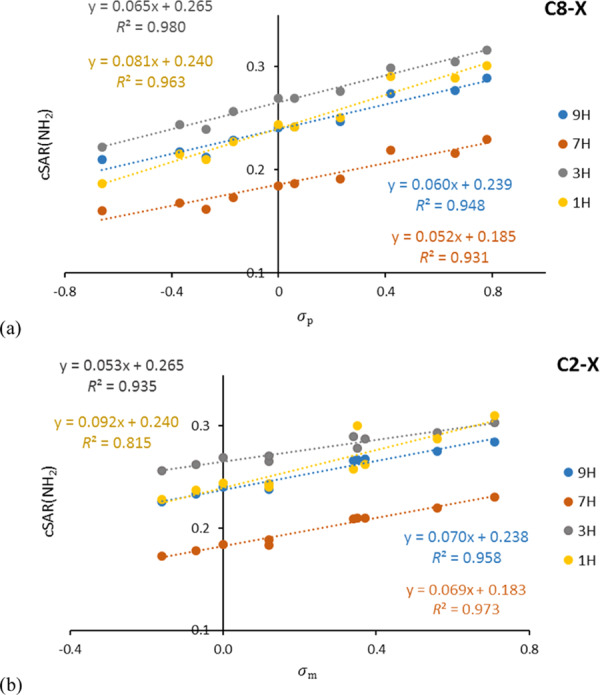
Figure 1

Open in a new tab

Correlations of cSAR(NH2) on σp for (a) C8–X- and cSAR(NH2) on σm for (b) C2–X-substituted derivatives of adenine.

The mean R2 value for regression lines cSAR(NH2) vs σp for C8–X substitution is 0.955, and for C2–X vs σm, it is 0.920. Excluding the deviating point for CHO, the average R2 value is 0.947. Therefore, σp should be used for describing C8–X-substituted systems, while σm should be used for the C2–X ones. For N–X-substituted systems, no clear conclusion can be drawn. This is most probably due to the fact that the lone pair at the substituted nitrogen may interact strongly with the substituents, particularly with the electron-attracting ones. In addition, for C8–X-substituted adenine derivatives, the obtained slope values (Table S17) reveal a greater impact of the electronic structure of the amino group on the substituent effect in 3H and 1H tautomers than in 9H and 7H series.

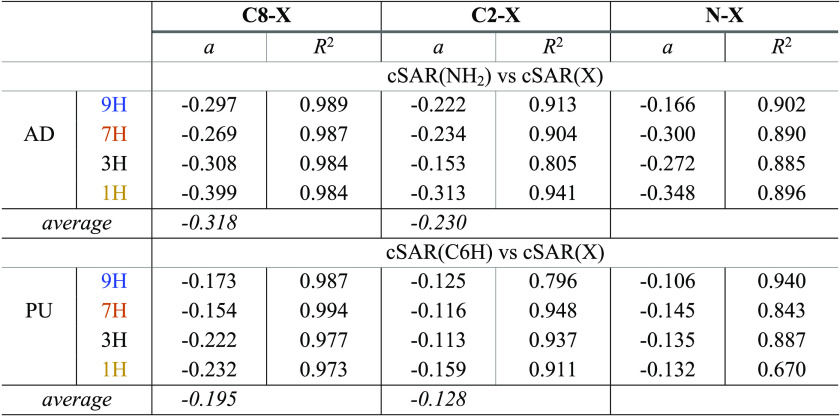
The impact of substituent on the amino group in adenine can be also presented by the linear equation cSAR(NH2) vs cSAR(X), which reveals the interactions between two substituents through the heterocyclic π-system. For comparison, also shown are the appropriate dependences of cSAR(C6-H in purine) on C2–X and C8–X. The obtained results of linear correlations are presented in Table 2 and shown in Figure S1.

Table 2. Slopes of the Obtained Linear Dependences cSAR(NH2) vs cSAR(X) and cSAR(C6H) vs cSAR(X) for C8–X-, C2–X-, and N–X-Substituted Derivatives of Adenine and Purine.

graphic file with name ao0c00820_0007.jpg

Open in a new tab

The advantage of this approach is that there is no need to distinguish between meta- and para-type interactions because the relationships between cSAR(X) and cSAR(NH2) or cSAR(C6H) automatically take into account differences in the nature of these interactions. In almost all cases, regressions have good or at least acceptable determination coefficients, with the only exception being the N–X-substituted 1H PU tautomer (R2 = 0.670). In all cases, the slopes (their absolute values) are greater for regression for the cSAR(NH2) equation than cSAR(C6H), indicating the important role of the participation of the lone pair at NH2 in the interactions under consideration. It is important to note that for adenine the correlation trends in both cases are similar; the slopes are substantially steeper for the C8–X substitution (mean value, −0.318) compared to the C2–X-substituted systems (mean value, −0.230). Similar relations are found for purine. For regression cSAR(CH6) vs cSAR(X), the mean slope values are −0.195 and −0.128, respectively. This indicates a stronger SE when the number of bonds between the substituent and the amino group (or H in purines) is odd (C8 vs C6) rather than even (C2 vs C6). This strongly supports our previously suggested rule, presented in ref (35). In addition, for C8–X adenine and purine derivatives, the 3H and 1H tautomers are more sensitive to the impact of substituent than the 9H and 7H ones.

Reverse Substituent Effect

In addition to the correlations presented above, it should be emphasized that the same substituent X in a different position in adenine may have a quite different cSAR(X) value. Moreover, the same picture is observed for purine. This is due to the fact that various positions in adenine or purine have different abilities for electron attraction or donation. Hence, cSAR(X) may be considered as a numerical measure of these properties in given chemical moieties. In other words, cSAR(X) can be used to measure the reverse substituent effect, describing changes of the electronic properties of the substituent, either due to the position in the transmitting moiety or due to the nature of the fixed group (reaction site).

The analysis of the data in Tables S1–S4 allows us to show the ranges of variability of cSAR(X) values dependent on the position of substitution (C8–X, C2–X), taking into account all types of tautomers (9H, 7H, 3H, and 1H). Table 3 presents the ranges of cSAR(X) values for particular substituents for adenine and purine tautomers. This changeability is usually more strongly expressed in adenine than in purine tautomers. It should be emphasized again that the variability of cSAR(X) is in contradiction with the traditional concept of using the fixed values of substituent constants σ(X) and reveals a new type of substituent properties.

Table 3. Ranges of cSAR(X) Values for Substituents for Adenine and Purine C8–X- and C2–X-Substituted Tautomersa.

cSAR(X)
  C8–X
 C2–X
  AD PU AD PU
NO2 0.061 0.036 0.044 0.045
CN 0.048 0.021 0.034 0.028
CHO 0.054 0.025 0.036 0.032
Cl 0.056 0.031 0.058 0.053
F 0.041 0.022 0.042 0.037
H 0.039 0.019 0.032 0.028
Me 0.050 0.027 0.049 0.045
OMe 0.066 0.026 0.055 0.050
OH 0.047 0.022 0.047 0.043
NH2 0.020 0.013 0.061 0.035
range 0.046 0.023 0.029 0.025
average 0.048 0.024 0.046 0.040
SD 0.013 0.006 0.010 0.009
Open in a new tab
a

Entries in bold underline the obtained values for unsubstituted adenine and purine tautomers.

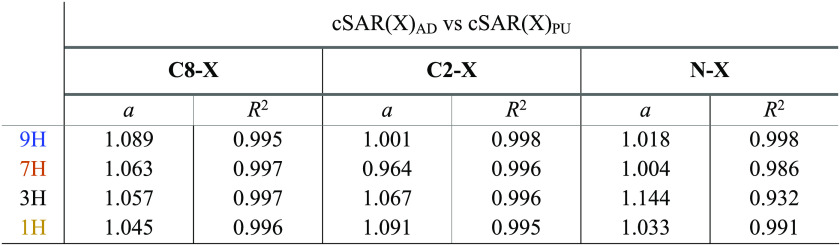
A clear illustration of the reverse substituent effect is shown by comparing the cSAR(X) values for C8–X, C2–X, and N–X substitution in adenine with those in purine (Table 4). The obtained slope values, depending on the type of tautomer and substitution position, illustrate changes in the properties of substituents at different reaction sites NH2 and H.

Table 4. Slopes of the Obtained Linear Dependences of cSAR(X)AD vs cSAR(X)PU for C8–X, C2–X, and N–X Substitution.

graphic file with name ao0c00820_0008.jpg

Open in a new tab

These data indicate a slightly greater impact of the NH2 group on the electronic properties of the substituent in adenine compared to its properties in purine.

Substituent Effect on Transmitting Moiety

Interactions between the amino group with other substituents, from different positions, cause changes in π-electron delocalization in the adenine rings. However, no valuable correlations between HOMA values for five- or six-membered rings and cSAR(X) are obtained, as shown for adenine and purine systems in Table S18. The reason may be both small variability of HOMA values in these systems and proximity effects (interactions with adjacent atoms or lone electron pair). However, if substituents are considered in two subgroups, i.e., electron-donating and electron-attracting, the correlations become clearer, especially for C8-substituted adenine derivatives (Table S18). In this series, for 9H and 7H tautomers, π-electron delocalization of the five-membered ring decreases, while that of the six-membered ring increases, both with decreasing electron-attracting and increasing electron-donating abilities of substituents (i.e., slopes are negative and positive, respectively). In addition, the aromaticity of six-membered rings increases more with electron-attracting substituents than with electron donors.

Much more informative is the consideration of the substituent effect on HOMA for five- and six-membered rings when comparisons are carried out between adenine and purine derivatives. The slopes of the linear regressions and their determination coefficients are summarized in Table S19.

The data in Figure 2a show that for C8–X systems, imidazole-like rings are more sensitive to C8 substituents on 9H and 7H tautomers (the slopes are higher than those for 3H and 1H tautomers). Thus, the enhancement of SE by the amino group (a > 1.0) is observed only for cases where the substituent is attached to the five-membered ring in the neighborhood of the NH group (7H, 9H). The data for C2–X are not conclusive due to too low R2 values.

Figure 2.

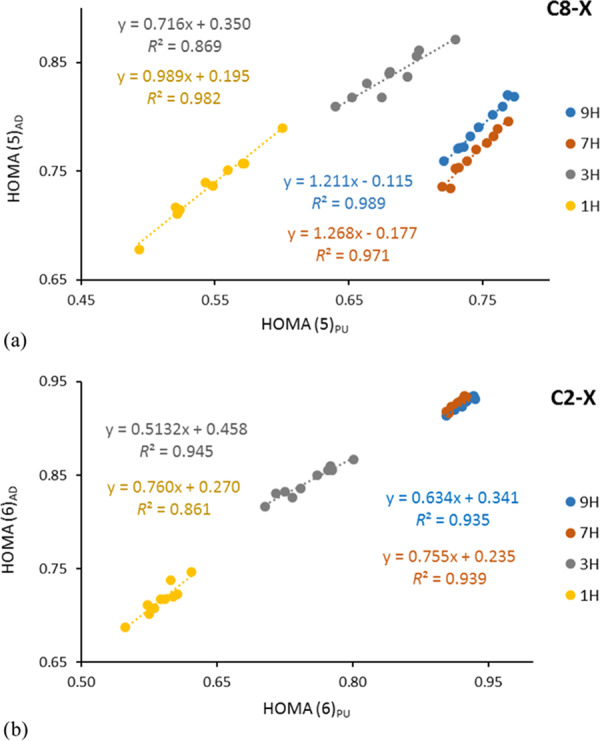
Figure 2

Open in a new tab

Dependence of HOMA(5)AD vs HOMA(5)PU for C8–X (a) and HOMA(6)AD vs HOMA(6)PU for C2–X (b) substitution of adenine and purine.

The data in Table S19 also allow for a comparison of the HOMA values of six-membered rings (HOMA(6)) in AD and PU moieties. The slopes are very differentiated, but unfortunately, the precision of regressions is rather low (R2 < 0.8); hence, deeper interpretation is not allowed. Nevertheless, for C8–X systems, the slopes for 9H and 7H tautomers are much greater than those for the two other tautomers, and their R2 values are between 0.75 and 0.80. Thus, for 9H and 7H tautomers and C8–X substitution, the adenine amino group enhances the substituent effect on the π-electron delocalization of both rings (in these cases, slopes > 1.0).

In contrast to these data, the linear regressions of HOMA(6)AD vs HOMA(6)PU for C2–X series (Figure 2b) have good or at least acceptable R2 (0.861), and the slopes are always less than 1.0 (between 0.513 and 0.755), indicating a smaller sensitivity of the aromatic character of the six-membered rings in all tautomers in adenine than in purine.

Five- and six-membered rings in adenine and purine tautomers may contain five (3H, 1H, five-membered rings), six (9H, 7H, both rings), or seven (3H, 1H, six-membered rings) π-electrons. The pEDA approach allows the determination of these quantities for all particular cases, as documented in ref (15). It should be stressed that substituents do not change this picture in a significant way, as shown in Figures 3, S2, and S3 (Supporting Information). In addition, the presented relationships between pEDA and cSAR(X) indicate that the values of pEDA increase with increasing electron-donating ability of the substituent. The values of sEDA do not clearly correlate with cSAR(X) (low R2 values).

Figure 3.

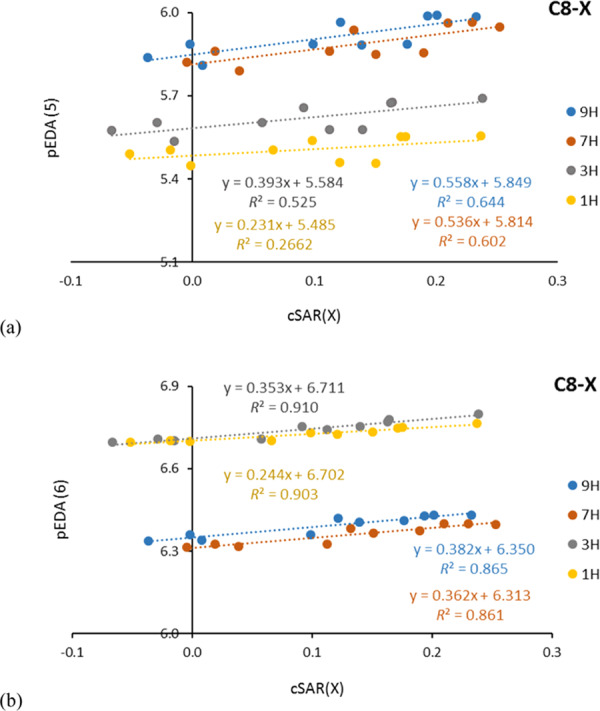
Figure 3

Open in a new tab

Dependence of pEDA vs cSAR(X) for five- (a) and six-membered (b) rings of adenine tautomers for C8–X derivatives.

Another view on changes of the transmitting properties caused by SE is shown by the charge flow index (CFI) values presented in Tables S7 and S8. The slopes of linear regression between CFI for adenine and purine tautomers, shown in Table 5, indicate that the transmission of the substituent effect is more significant in adenine than in purine tautomers. The slopes are greater than ∼1.1, which evidently shows an increase of charge flow in adenine due to the impact of the amino group.

Table 5. Slopes of the Obtained Linear Dependences of CFIAD vs CFIPU for C8–X-, C2–X-, and N–X-Substituted Series.

graphic file with name ao0c00820_0009.jpg

Open in a new tab

Conclusions

The use of cSAR, quantum-chemical-based descriptors of the substituent effect, allows us to show the influence of the substituent on the electronic structure of adenine and purine.

A comparison of the relationships between cSAR(X) and Hammett σ constants reveals that for carbon-substituted systems (C2–X, C8–X), better correlations are found with σpara than with σmeta, while for N–X-substituted series, better correlations are found with σmeta.

The undoubted advantage of the cSAR(X) descriptor is that it describes the electronic structure of the X substituent regardless of the system to which X is attached. It is worth noting that the cSAR characteristic, in contrast to the traditional substituent constants (σ), shows the variability of the electronic properties of a given substituent, depending on the type of tautomers and the position of substitution in adenine and purine.

The results of the classical substituent effect analysis indicate stronger interactions of substituents from C8–X position than from C2–X and N–X positions, both in adenine and purine derivatives.

The changes induced by substituents in the π-electron structure of the rings are almost similar in adenine and purine, as estimated by the HOMA index. However, the presence of the NH2 group in adenine enhances the substituent effect compared to that found in purine.

A more pronounced effect of the substituent on HOMA values is observed for C8–X-substituted systems. In addition, in the case of 7H and 9H tautomers that follow the Hückel rule, substituents reduce the aromaticity of the five-membered rings but increase it for the six-membered rings.

The results of the pEDA analysis for the five- and six-membered rings in adenine and purine tautomers indicate that the substituents do not significantly change the π-electron population for both “Hückel” (9H, 7H) and “anti-Hückel” (3H, 1H) tautomers.

The more effective transmission of the substituent effect in adenine than in purine tautomers is also shown by CFI.

Methodology

To investigate the substituent effects in C2–X-, C8–X-, and N–X-substituted derivatives of the four most stable purine tautomers and their adenine analogues, various substituents X (where X = NO2, CN, CHO, Cl, F, H, Me, OMe, OH, and NH2) were used (Scheme 2).

For all studied systems, optimization without any symmetry constraints was performed using the Gaussian 09 program.37 Based on the experience from our previous research,38 the density functional theory (DFT)-D method was applied, that is, functionals B97D339 with Dunning’s40 aug-cc-pvdz basis set. The harmonic vibrational frequencies were calculated at the same level of theory to confirm that all obtained structures correspond to the minima on the potential energy surface. No imaginary frequencies were found for the obtained series. In the case of asymmetric substituents (CHO, OMe, and OH), a lower-energy rotamer was considered.

The electronic properties of substituents in adenine and purine were characterized by the charge of the substituent active region (cSAR) parameter.29,30 The Hirshfeld method was used to calculate all cSAR values.41 The cSAR descriptor was calculated as a sum of charges at all atoms of the substituent X and the charge at the ipso carbon atom

graphic file with name ao0c00820_m001.jpg 1

In this study, the cSAR(X) in N–X substitution was calculated as the sum of charges at all atoms of the substituent X and the charge at the ipso nitrogen atom for individual tautomers

graphic file with name ao0c00820_m002.jpg 2

The effect of the SE on the electronic structure of the system was described by a charge flow index (CFI), defined as

graphic file with name ao0c00820_m003.jpg 3

where Y = NH2 for adenine and Y = H for purine tautomers.

The effect of substituents on the π-electron delocalization of the adenine and purine rings was investigated by a geometry-based aromaticity index harmonic oscillator model of aromaticity (HOMA).42,43 HOMA is defined as a normalized sum of squared deviations of bond lengths from the values of a system assumed to be fully aromatic. The appropriate expression is presented by eq 4

graphic file with name ao0c00820_m004.jpg 4

where n is the number of bonds taken into account when carrying out the summation, i means the type of bond (CC or CN), αi is an empirical normalization constant (for CC and CN bonds, αCC = 257.7 and αCN = 93.52) chosen to give HOMA = 0 for nonaromatic system, and HOMA = 1 for the system where all bonds are equal to the optimal value dopt,i assumed to be realized for full aromatic systems (for CC and CN bonds, dopt,CC = 1.388 Å and dopt,CN = 1.334 Å), and di,j are the bond lengths taken into calculation.

The pi/sigma electron donor–acceptor (pEDA/sEDA) models44 were used to show the electronic structures of five- and six-membered rings in adenine and obtained according to eqs 5 and 6

graphic file with name ao0c00820_m005.jpg 5
graphic file with name ao0c00820_m006.jpg 6

where for the planar part (in XY plane) of the system in question, σXi denotes the sum of occupancies of 2s, 2px, and 2py sigma orbitals, πXi means the occupancy of the 2pz π orbital of the i-th atom in the structure (for C and N atoms in adenine rings, respectively), and n denotes the sum of atoms, i.e., for adenine six-membered ring (6): n = 6, five-membered ring (5): n = 5. To obtain occupancy of individual orbitals, an analysis of natural bond orbital (NBO)45 was performed using the Gaussian program (with the use of NBO 6.0 module).46 Unlike in the original paper,44 in this report, pEDA and sEDA were not standardized.

Acknowledgments

The authors gratefully acknowledge the Interdisciplinary Center for Mathematical and Computational Modeling (Warsaw, Poland) and Wrocław Centre for Networking and Supercomputing for providing computer time and facilities. They thank the National Science Centre of Poland for supporting this work under grant no. UMO-2016/23/B/ST4/00082.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00820.

  • cSAR(X) and cSAR(NH2) values for C8–X and C2–X substitution of adenine (Tables S1 and S2); cSAR(X) and cSAR(C6H) values for C8–X and C2–X substitution of purine (Tables S3 and S4); cSAR(X) and cSAR(NH2) values for N–X substitution of adenine (Table S5); cSAR(X) and cSAR(C6H) values for N–X substitution of adenine (Table S6); CFI values for C8–X and C2–X substitution for adenine and purine tautomers (Tables S7 and S8); HOMA for imidazole (5) and pyrimidine (6) rings for C8–X, C2–X, and N–X of adenine (Tables S9, S10, and S11); HOMA for imidazole (5) and pyrimidine (6) rings for C8–X, C2–X, and N–X of purine (Tables S12, S13, and S14); pEDA and sEDA values for C8–X substitution for adenine tautomers (Tables S15 and S16); slopes of the linear dependences of cSAR(NH2) on substituent constants σp, σm for C8–X-, C2–X-, and N–X-substituted derivatives of adenine (Table S17); dependence HOMA vs cSAR(X) for all substituents and with separation on EA and ED substituents for all types of substitution for five- and six-membered rings of adenine and purine tautomers (Table S18); slopes of the obtained linear dependences of HOMA(5)AD vs HOMA(5)PU for C8–X, C2–X, and N–X substitution (Table S19); Cartesian coordinates of equilibrium geometries of C8–X- and C2–X-substituted adenine and purine 9H, 7H, 3H, and 1H tautomers (Tables S20 and S22); Cartesian coordinates of equilibrium geometries of NX-substituted adenine and purine 9H, 7H, 3H, and 1H tautomers (Tables S21 and S23); dependences of cSAR(NH2) vs cSAR(X) for C8–X-, C2–X-, and N–X (c)-substituted derivatives of adenine (Figure S1); dependence of pEDA vs cSAR(X) for five- and six-membered rings of adenine tautomers for C2–X derivatives (Figure S2); and dependence of pEDA vs cSAR(X) for five- and six-membered rings of adenine tautomers for NX derivatives (Figure S3) (PDF)

The authors declare no competing financial interest.

Dedication

Dedicated to our friend, professor Jerzy Błażejewski, outstanding Polish chemist, on the occasion of his 75th birthday.

Supplementary Material

ao0c00820_si_001.pdf (3.6MB, pdf)

References

  1. Saenger W.Principles of Nucleic Acids Structures; Springer: New York, 1990. [Google Scholar]
  2. Watson J. D.; Crick F. C. Molecular Structure of Nucleic Acids; a Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. 10.1038/171737a0. [DOI] [PubMed] [Google Scholar]
  3. Rejnek J.; Hobza P. Hydrogen-Bonded Nucleic Acid Base Pairs Containing Unusual Base Tautomers: CompleteBasis Set Calculations at the MP2 and CCSD(T) Levels. J. Phys. Chem. B 2007, 111, 641–645. 10.1021/jp0661692. [DOI] [PubMed] [Google Scholar]
  4. Šponer J.; Leszczyński J.; Hobza P. Nature of Nucleic Acid–Base Stacking: Nonempirical ab Initio and Empirical Potential Characterization of 10 Stacked Base Dimers. Comparison of Stacked and H-Bonded Base Pairs. J. Phys. Chem. A 1996, 100, 5590–5596. 10.1021/jp953306e. [DOI] [Google Scholar]
  5. Hobza P.; Šponer J. Structure, Energetics, and Dynamics of the Nucleic Acid Base Pairs: Nonempirical Ab Initio Calculations. Chem. Rev. 1999, 99, 3247–3276. 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
  6. Stasyuk O. A.; Szatyłowicz H.; Krygowski T. M. Effect of H-Bonding and Complexation with Metal Ions on the π-Electron Structure of Adenine Tautomers. Org. Biomol. Chem. 2014, 12, 456–466. 10.1039/C3OB41653D. [DOI] [PubMed] [Google Scholar]
  7. Stasyuk O. A.; Szatyłowicz H.; Krygowski T. M. Effect of the H-Bonding on Aromaticity of Purine Tautomers. J. Org. Chem. 2012, 77, 4035–4045. 10.1021/jo300406r. [DOI] [PubMed] [Google Scholar]
  8. Raczyńska E. D.; Makowski M.; Hallmann M.; Kaminska B. Geometric and Energetic Consequences of Prototropy for Adenine and its Structural Models – a Review. RSC Adv. 2015, 5, 36587–36604. 10.1039/C4RA17280A. [DOI] [Google Scholar]
  9. Raczyńska E. D.; Makowski M.; Zientara-Rytter K.; Kolczyńska K.; Stępniewski T. M.; Hallmann M. Quantum-Chemical Studies on the Favored and Rare Tautomers of Neutral and Redox Adenine. J. Phys. Chem. A 2013, 117, 1548–1559. 10.1021/jp3081029. [DOI] [PubMed] [Google Scholar]
  10. Raczyńska E. D.; Kolczyńska K.; Stępniewski T. M.; Kamińska B. On Relation between Prototropy and Electron Delocalization for Neutral and Redox Adenine – DFT Studies. Comput. Theor. Chem. 2013, 1022, 35–44. 10.1016/j.comptc.2013.08.009. [DOI] [Google Scholar]
  11. Raczyńska E. D.; Makowski M. Geometric Consequences of Electron Delocalization for Adenine Tautomers in Aqueous Solution. J. Mol. Model. 2014, 24, 2234–2243. 10.1007/s00894-014-2234-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Raczyńska E. D.; Kamińska B.; Szeląg M. Influence of One-Electron Oxidation and One-Electron Reduction on the Tautomeric Preferences for Purine. Anal. Bioanal. Electrochem. 2009, 1, 83–97. [Google Scholar]
  13. Raczyńska E. D.; Kamińska B. Prototropy and pi-Electron Delocalization for Purine and its Radical Ions – DFT Studies. J. Phys. Org. Chem. 2010, 23, 828–835. 10.1002/poc.1668. [DOI] [Google Scholar]
  14. Raczyńska E. D.; Kamińska B. Variations of the Tautomeric Preferences and π-Electron Delocalization for the Neutral and Redox Forms of Purine when Proceeding from the Gas Phase (DFT) to Water (PCM). J. Mol. Model. 2013, 19, 3947–3960. 10.1007/s00894-013-1926-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jezuita A.; Szatyłowicz H.; Marek P. H.; Krygowski T. M. Aromaticity of the Most Stable Adenine and Purine Tautomers in Terms of Hückel’s 4N+2 Principle. Tetrahedron 2019, 75, 130474 10.1016/j.tet.2019.130474. [DOI] [Google Scholar]
  16. Streitwieser A., Jr.Molecular Orbital Theory for Organic Chemists; J. Wiley: New York, 1961; p 256. [Google Scholar]
  17. Szatylowicz H.; Jezuita A.; Ejsmont K.; Krygowski T. M. Classical and Reverse Substituent Effects in Meta- and Para-Substituted Nnitrobenzene Derivatives. Struct. Chem. 2017, 28, 1125–1132. 10.1007/s11224-017-0922-2. [DOI] [Google Scholar]
  18. Szatylowicz H.; Jezuita A.; Ejsmont K.; Krygowski T. M. Substituent Effect on the σ- and π-Electron Structure of the Nitro Group and the Ring in Meta- and Para-Substituted Nitrobenzenes. J. Phys. Chem. A 2017, 121, 5196–5203. 10.1021/acs.jpca.7b03418. [DOI] [PubMed] [Google Scholar]
  19. Shahamirian M.; Szatylowicz H.; Krygowski T. M. How OH and O– Groups Affect Electronic Structure of Meta-Substituted and Para-Substituted Phenols and Phenolates. Struct. Chem. 2017, 28, 1563–1572. 10.1007/s11224-017-0965-4. [DOI] [Google Scholar]
  20. Varaksin K. S.; Szatylowicz H.; Krygowski T. M. Towards a Physical Interpretation of Substituent Effect: Quantum Chemical Interpretation of Hammett Substituent Constants. J. Mol. Struct. 2017, 1137, 581–588. 10.1016/j.molstruc.2017.02.074. [DOI] [Google Scholar]
  21. Szatylowicz H.; Siodla T.; Stasyuk O. A.; Krygowski T. M. Towards Physical Interpretation of Substituent Effects: the case of Meta- and Para-Substituted Anilines. Phys. Chem. Chem. Phys. 2016, 18, 11711–11721. 10.1039/C5CP06702B. [DOI] [PubMed] [Google Scholar]
  22. Szatylowicz H.; Jezuita A.; Siodla T.; Varaksin K. S.; Ejsmont K.; Shahamirian M.; Krygowski T. M. How far the Substituent Effects in Disubstituted Cyclohexa-1,3-diene Derivatives differ from those in Bicyclo[2.2.2]octane and Benzene?. Struct. Chem. 2018, 29, 1201–1212. 10.1007/s11224-018-1113-5. [DOI] [Google Scholar]
  23. Szatylowicz H.; Siodla T.; Krygowski T. M. Olefinic vs Aromatic Way of Substituent Effects: The Case of 3-and 4-Substituted Cyclohexa-1,3-dienamine Derivatives. J. Phys. Org. Chem. 2017, 30, e3694 10.1002/poc.3694. [DOI] [Google Scholar]
  24. Szatylowicz H.; Jezuita A.; Siodla T.; Varaksin K. S.; Domanski M. A.; Ejsmont K.; Krygowski T. M. Toward the Physical Interpretation of Inductive and Resonance Substituent Effects and Reexamination Based on Quantum Chemical Modeling. ACS Omega 2017, 2, 7163–7171. 10.1021/acsomega.7b01043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. George P.; Trachtman M.; Bock C. W.; Brett A. M. Homodesmotic Reactions for Assessment of Stabilization Energies in Benzenoid and other Conjugated Cyclic Hydrocarbons. J. Chem. Soc., Perkin Trans. 2 1976, 11, 1222–1227. 10.1039/p29760001222. [DOI] [Google Scholar]
  26. Pross A.; Radom L.; Taft R. W. Theoretical Approach to Substituent Effects - Phenols and Phenoxide Ions. J. Org. Chem. 1980, 45, 818–826. 10.1021/jo01293a012. [DOI] [Google Scholar]
  27. Cyrański M. K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. 10.1021/cr0300845. [DOI] [PubMed] [Google Scholar]
  28. Szatylowicz H.; Jezuita A.; Marek P. H.; Krygowski T. M. Substituent Effects on the Stability of the Four Most Stable Tautomers of Adenine and Purine. RSC Adv. 2019, 9, 31343–31356. 10.1039/C9RA04615A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sadlej-Sosnowska N. On the Way to Physical Interpretation of Hammett Constants: How Substituent Active Space Impacts on Acidity and Electron Distribution in p-Substituted Benzoic Acid Molecules. Polish J. Chem. 2007, 81, 1123–1134. [Google Scholar]
  30. Sadlej-Sosnowska N. Substituent Active Region - a Gate for Communication of Substituent Charge with the Rest of a Molecule: Monosubstituted Benzenes. Chem. Phys. Lett. 2007, 447, 192–196. 10.1016/j.cplett.2007.09.023. [DOI] [Google Scholar]
  31. Siodla T.; Oziminski W. P.; Hoffmann M.; Koroniak H.; Krygowski T. M. Toward a Physical Interpretation of Substituent Effects: The Case of Fluorine and Trifluoromethyl Groups. J. Org. Chem. 2014, 79, 7321–7331. 10.1021/jo501013p. [DOI] [PubMed] [Google Scholar]
  32. Hammett L. P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. 10.1021/ja01280a022. [DOI] [Google Scholar]
  33. Hammett L. P.Physical Organic Chemistry; McGraw-Hill: New York, 1940; p 196. [Google Scholar]
  34. Krygowski T. M.; Woźniak K.. Similarity Models in Organic Chemistry, Biochemistry and Related Fields; Zalewski R. I.; Krygowski T. M.; Shorter J., Eds.; Elsevier: Amsterdam, 1991; Chapter 1. [Google Scholar]
  35. Szatyłowicz H.; Krygowski T. M.; Palusiak M.; Poater J.; Sola M. Routes of pi-Electron Delocalization in 4-Substituted-1,2-benzoquinones. J. Org. Chem. 2011, 76, 550–556. 10.1021/jo102065e. [DOI] [PubMed] [Google Scholar]
  36. Exner O.Advances in Linear Free Energy Relationships; Chapman N. B.; Shorter J., Eds.; Plenum Press: London, 1972; Chapter 1, p 1. [Google Scholar]
  37. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, revision D.01; Gaussian Inc.: Wallingford, CT, 2013.
  38. Marek P. H.; Szatylowicz H.; Krygowski T. M. Stacking of Nucleic Acid Bases: Optimization of the Computational Approach - the Case of Adenine Dimers. Struct. Chem. 2019, 30, 351–359. 10.1007/s11224-018-1253-7. [DOI] [Google Scholar]
  39. Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  40. Kendall R. A.; Dunning T. H. Jr.; Harrison R. J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
  41. Hirshfeld F. L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Acta 1977, 44, 129–138. 10.1007/BF00549096. [DOI] [Google Scholar]
  42. Kruszewski J.; Krygowski T. M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 13, 3839–3842. 10.1016/S0040-4039(01)94175-9. [DOI] [Google Scholar]
  43. Krygowski T. M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of π-Electron Systems. J. Chem. Inf. Model. 1993, 33, 70–78. 10.1021/ci00011a011. [DOI] [Google Scholar]
  44. Oziminski W. P.; Dobrowolski J. C. σ- and π-Electron Contributions to the Substituent Effect: Natural Population Analysis. J. Phys. Org. Chem. 2009, 22, 769–778. 10.1002/poc.1530. [DOI] [Google Scholar]
  45. Weinhold F.; Landis C. R.. Valency and Bonding. In A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: New York, 2005. [Google Scholar]
  46. Glendening E. D.; Badenhoop J. K.; Reed A. E.; Carpenter J. E.; Bohmann J. A.; Morales C. M.; Landis C. R.; Weinhold F.. NBO 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, 2013.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00820_si_001.pdf (3.6MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES