Evaluation of Electronegativity Scales

Abstract

Scales of electronegativity values are used by chemists to describe numerous chemical features such as chemical mechanisms, bond polarity, band gap, atomic hardness, etc. While the many scales provide similar trends, all differ in their predictive quality. Confirmation of the quality of a new scale often uses a previous scale for comparison but does not use independent means to demonstrate the merits of the scale. Utilizing a table of binary compounds of known ionic, covalent, and metallic bonding characters, a means to evaluate electronegativity scales is developed here. By plotting the electronegativity values of the two bonded atoms in binary compounds of a known bonding character, a tripartite separation results that generally divides the three bond types. Using the results of graphs of this sort, the success of bonding separations of 14 different scales of electronegativity has been evaluated on the basis of three quantitative parameters that can provide a measure of the quality of the scales. Three scales, those of Allen, Martynov and Batsanov, and Nagle, have been shown to be superior in their ability to predict the expected separation of bond types. Since this scheme successfully demonstrates the ability to evaluate the quality of electronegativity scales, it can be applied to other scales to establish their effectiveness in predicting bond types in binary compounds and thus the quality of the scales. This scheme is applied to a recently published electronegativity scale to evaluate the ability to determine its quality.

Introduction

The concept of chemical bonding is central to the field of chemistry. A conceptual basis for defining it was proposed by Pauling, in which he posited that chemical bonding arises from “the tendency of an atom to attract electrons in a bond”.¹ This tendency is termed electronegativity (EN). Pauling proposed an intuitive but quantitative table of ENs based on the thermodynamic values of compounds that provided a description of the ionic character in bonds. This definition was soon followed by papers by Mulliken who described EN as the average of ionization energy and electron affinity.^2,3 This scale has witnessed extensive development. Iczkowski and Margrave⁴ promoted it in terms of energy per electron and related it to the chemical potential. Hinze and Jaffe described it as a property of orbitals, not of the entire atom, calculatable as integratable polynomials.⁵ Parr and colleagues developed the EN definition as a function of electron density and employed density functional theory (DFT), providing a quantum mechanical basis for EN.⁶ Using DFT, Sen, Bohm, and Schmidt expanded the concept to incorporate the chemical concept of atomic hardness along with EN.⁷ Putz, Russo, and Sicillia have provided an alternative formulation using electronic density and softness to reformulate Mulliken EN in terms of DFT.⁸ More recently, Valone recognized hardness as a coefficient of the total ionic character, coming full circle by providing a quantum mechanical description of ionicity originally proposed by Pauling.⁹ During this development of the Mulliken model, other authors added insights and proposed additional definitions. Sanderson promoted the concept that EN was the driving force of bonding, which was derived from the EN equalization of interacting species.¹⁰ Gordy and others provided a relationship of EN that described it as an electrostatic potential related to the reciprocal of atomic radius,¹¹ and Allred and Rochow described EN as a force and related it to the reciprocal of the square of atomic radius.¹² Both scales have been re-evaluated by Ghosh who used Slater’s orbital radii and revised units to correspond to atomic units.^13,14 A unique quantum mechanical EN scale was presented by Allen, based on the average one-electron energies of the valence shell.¹⁵ Many other scales have been developed using various observables such as dipole moments, nuclear quadrupole resonance frequencies, atomic hardness, atomic volumes, and atomic polarizability. As Mullay noted, the development of the concept of EN has had two phases: the first was that of developing EN as an atomic property, searching for the proper definition of EN; the second included analyses of the effects of charge and hybridization, employing the concept of EN equalization on bond formation.¹⁶ This prolonged effort has been one of the developments of intuitive descriptions of EN progressing to works that provided a quantum mechanical basis for EN.

The various EN scales provide similar results, indicating that metals tend to lose electrons and nonmetals tend to accept electrons. Nevertheless, all scales exhibit significant differences. Recent literature demonstrates that the authors select from the myriad of scales for evaluating the applications of EN or devise new scales for use for particular purposes. For example, Poletti et al. chose to use Allen’s scale to evaluate solid solutions since it was the “most recent physically-based” scale.¹⁷ Leong et al. used four scales to perform a cluster analysis to separate crystal morphologies.¹⁸ Rahm et al. used a scale that their group developed to find orbital energy changes under pressure.¹⁹ Qteish used six scales to find the greatest degree of localized clustering of crystalline morphologies.²⁰ And Liang and Xue used a scale by their group to suggest better supercapacitors.²¹ There has been no generally accepted theoretical explanation of EN and no clear means by which the best scales can be ascertained. For want of a means to evaluate the quality of EN scales, they have often been compared to the scale of Pauling. However, this process is at least suspect and likely counterproductive since it relies on a scale of doubtful quality. In fact, the quality of the Pauling scale, often the touchstone of these comparisons, has been seriously questioned.²² Even the best form of Pauling’s bonding equations is appropriate for only a limited number of compounds.²³ For the concept of EN to be most useful, we need a means to evaluate and compare the quality of EN scales. It is the purpose of this paper to provide a generally applicable method that can be used to evaluate the quality of EN scales. Determination of an EN scale’s quality will use an independent means by which the quality of the scale can be measured.

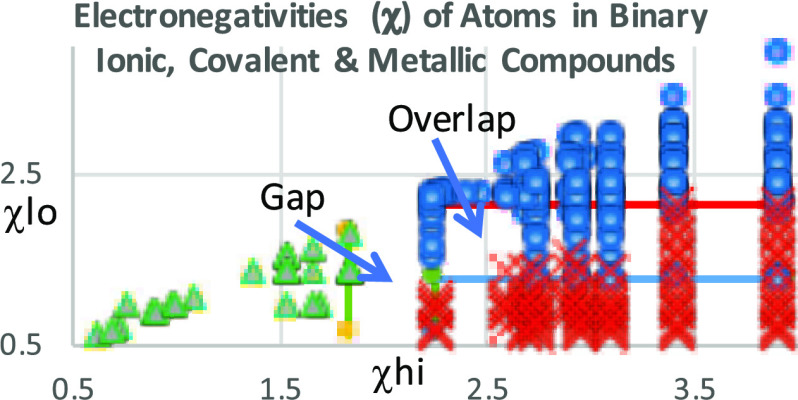
Strong chemical bonds are typically described as arising from ionic, covalent, or metallic forces. A previous publication by this author has shown that when binary compounds of a known bonding character are plotted in a two-dimensional graph of the EN values assigned to the two elements, a tripartite separation of these three bonding types results.²⁴ Various functions can serve to show this separation:²⁵ plotting Δχ (the difference between the higher and lower χ (EN) values (χ_hi) and (χ_lo), respectively) vs χ_avg (the average of the electronegativity values for the two binary elements) produces an isosceles triangle with metals located in a triangle in the lower left, ionic compounds in a parallelogram in the upper region, and covalent compounds in the lower right, and with homoatomic compounds along the baseline. Alternatively, a plot of the unfunctionalized lower EN (χ_lo) vs the higher EN (χ_hi) values produces a right triangle in which metallic compounds are located in a right triangle in the lower left, ionic compounds are in a rectangle in the lower right, and covalent compounds are in a right triangle in the upper region, and with homoatomic compounds found along the hypotenuse. Since this latter format uses the unfunctionalized values of EN and lines separating the three bonding types parallel the X and Y axes, it is natural to employ graphs using χ_lo and χ_hi axes to visualize bonding separations.²⁶ In such graphs, Δχ values are parallel to and offset from the hypotenuse (along which Δχ = 0).

To produce useful plots of EN scales that separate bonding types, it is necessary to use compounds of well-characterized bonding types. Except for homoatomic bonds, chemical bonds between atoms are never purely ionic, covalent, or metallic. However, many can be considered to be representatives of ideal bond types. A listing of binary compounds of well-characterized bond types that separates compounds of known bonding types from those of clearly mixed types is available²⁷ and is used here to provide graphs of electronegativity values for binary compounds of known bond types. While a different listing of binary compounds has been used previously by this author,²⁸ this more rigorously selected data set of binary compounds has provided interesting and useful graphical commonalities that were not obvious in the previous analyses. Graphs of these binary compounds using different EN scales can be used to compare different scales based on how effectively each scale separates binary compounds into three regions of like bonding character. Common characteristics of these graphs will be used to compare the relative quality of the scales. Besides evaluating parameters that indicate the effectiveness of separating bonding types, additional parameters will be identified that can be used to determine the utility of scales. These include the comprehensiveness of each scale and precision with which EN values are provided. Parameters will be normalized to enable comparisons. It is the hypothesis of this paper that by determining the quality of each scale in this manner, EN scales can be compared and the best ones determined. Conversely, the successful graphical separation of bonding type will confirm that EN values are directly related to the bonding character. Analyses using this process will enable the evaluation of extant and future scales.

Experimental Section

Fourteen EN scales were selected that cover a range of definitions of EN. These generally accepted EN scales were selected as representatives of the much more extensive literature of EN scales. These scales are those of Allen (Al),²⁹ Allred and Rochow (AR),³⁰ Batsanov (Ba),³¹ Gunnarsson and Lundquist (GL)¹³² as calculated by Robles and Bartolotti,³² Gordy (Go),³³ Gordy and Thomas (GT),³⁴ Martynov and Batsanov (MB),³⁵ Mulliken (Mk),³⁶ Mullay (My),³⁷ Nagle (Ng),³⁸ Pauling (Pa),^39,40 Robles and Bartolotti (RB),³² Sen, Böhm, and Schmidt (SBS),⁴¹ and Sanderson (Sn).⁴² A data set of binary compounds with well-defined bonding characteristics was obtained from the literature.²⁷ This set included representative elements through bismuth (#83), the zinc subfamily, but excluded noble gases. Using Microsoft Excel, a table of these compounds, separated by bonding types, was prepared for each EN scale listing the two elements with their ENs. Except for homoatomic compounds, each binary compound consisted of one element with a lower and one with a higher EN value. Using Excel X–Y graphing, plots for each of these scales were made, graphing lower EN vs higher EN values for compounds characterized as being essentially covalent, ionic, or metallic in character. Compounds of mixed bonding character were excluded. Additionally, a graph including all three bond types was prepared for each EN scale. Graphs that included the three basic bonding types were generally divided into tripartite regions, and the maximum and minimum EN values for each of the three bonding types were recorded using χ_lo and χ_hi axes (Table 1). In all tripartite plots, with negligible exceptions, a gap appeared between the metallic region (M, 36 compounds) and the combined covalent (C, 213 compounds) and ionic (I, 109 compounds) regions along the χ_hi axis. Conversely and in every case, an overlap occurred between the covalent and ionic regions along χ_lo for all EN scales. Since the M–CI gap appears along the χ_hi axis, it is the elements of higher EN that determine the locations of gaps. Determination of an M–CI boundary line was straightforward, lying half-way between the metallic element with maximum EN (along χ_hi) and the covalent or ionic element with the lowest value of EN (also along χ_hi). On the other hand, since the overlap between the ionic and covalent compounds appeared along the χ_lo axis, the C–I overlap was determined by elements with the lower EN values. The C–I boundary lines within overlap regions were determined in two ways: by listing increasing EN values of the elements within overlap regions and by listing all compounds whose element of lower EN fell within the overlap region. Because the number of compounds for any given element ranged from 1 to over 20, there was considerable bias in establishing compound boundary lines. Because of this bias, boundary lines using compounds were not considered any further.

Table 1. Gaps, Overlaps, and Dividing Lines^a.

author	Al	AR	Ba	GL	Go	GT	MB	Mk	My	Ng	Pa	RB	Sn	SBS	RZHb
χmax (F)	24.80	4.10	3.9	10.76	3.94	3.95	3.78	3.91	4.00	4.23	3.98	9.85	4.00	16.16	23.3
χmin (Cs)	3.89	0.86	0.35	2.13	0.78	0.75	0.77	0.62	0.66	0.80	0.79	1.29	0.22	2.33	3.9
gap min on χhi	10.79	1.82	1.4	4.86	1.83	1.8	1.88	1.83	1.86	1.70	2.04	4.47	2.34	7.90	–12.8
gap max χhi	13.33	2.06	2.0	5.41	2.17	2.1	2.32	2.25	1.99	2.22	2.18	4.79	2.52	8.03	–16.1
M–CI gap width	2.54	0.24	0.6	0.55	0.34	0.3	0.44	0.42	0.13	0.52	0.14	0.32	0.18	0.13	–3.3
M–CI boundary line	12.06	1.94	1.7	5.14	2.00	1.95	2.10	2.04	1.93	1.96	2.11	4.63	2.43	7.97	10.8
overlap min on χlo	9.32	1.44	1.1	3.18	1.12	1.34	1.45	1.28	1.36	1.46	1.57	2.48	1.49	4.60	9.1
overlap max on χlo	10.79	1.82	1.5	4.86	1.83	1.8	1.88	2.15	1.86	1.70	2.33	4.86	2.42	7.90	16.1
C–l overlap width	1.47	0.38	0.4	1.68	0.71	0.46	0.43	0.87	0.50	0.24	0.76	2.38	0.93	3.30	7.0
C–l boundary line	9.79	1.57	1.36	3.70	1.48	1.51	1.64	1.74	1.71	1.55	1.92	3.52	2.14	6.45	12.6
fractionalized M–CI line	0.486	0.473	0.436	0.478	0.508	0.494	0.556	0.522	0.483	0.463	0.530	0.470	0.608	0.493	0.464
fractionalized C–l line	0.395	0.383	0.349	0.344	0.376	0.382	0.434	0.445	0.428	0.366	0.482	0 357	0.535	0.376	0.541
M–CI/C–I boundary ratio	1.232	1.236	1.25	1.389	1.351	1.291	1.28	1.172	1.129	1.265	1.099	1.315	1.136	1.313	0.857
	avg ratio	1.247	0.087

^aLocations of EN boundary lines for 14 EN scales; M–CI divides metallic from the ionic/covalent regions along χ_hi, while C–I generally separates the covalent from ionic regions along χ_lo.

^bThere is no gap; negative values indicate overlap.

Elemental boundary lines were established at the midpoint of a listing of elements within the overlap region. If a boundary line were found to be at the EN value of one or more species, a fraction of those species was divided commensurately to count partially on each of the covalent and ionic sides of the line. This occurred frequently in those EN sets with limited significant figures.

Six parameters were determined that could be used to determine the utility of EN scales. They were functionalized such that lower values of each would provide better values. These parameters are intended to provide a means of evaluating the efficacy or practicality of scales. Three of these parameters were established based on the common characteristics of the EN graphs that led to the successful separation of bonding types. These three parameters were the ones used to determine the Quality of EN scales since they served to separate bonding types. To indicate the width of gap regions, a function of the gap distance between the highest metal EN along χ_hi and the lowest of either ionic or covalent EN values along χ_hi was determined. To generate a function of the gap distance in which lower values reflect better separation, for each scale, the EN of fluorine was divided by the gap distance, forming the parameter G. The number of outliers (O, substances misplaced in the triangular graph based on their recognized bonding type) were found within the overlap region but incorrectly located. The third quality parameter S was the summed EN distances from the boundary of elements on the “wrong side” of boundary lines fractionalized to the EN of fluorine. The first of three additional parameters for use in determining the utility of scales was the number of undefined elements within an EN scale, N, of a maximum of the 37 elements considered. The second ancillary parameter was the number of duplicated EN values, D. The parameter P evaluated the precision in EN values. The value of P was determined by dividing the implied error of EN values (0.1 or 0.01) by the EN of fluorine.

Since these parameters varied widely in numerical range and to be able to compare them, each was functionalized such that lower values demonstrated better values, and these were normalized to a scale from 1 to 10 and designated by the primed variables G′, O′, S′, N′, D′, and P′. These normalized values could then be compared with one another, as well as combined in various ways. Various functions were considered to determine the overall quality scores among the first three parameters, and the overall utility scores were found by selecting various of the six parameters. Quality and utility scores were found by simply adding selected primed parameters. Linear regression correlations between the parameters were assessed by determining the R² values for pairs of different parameters. Correlations between selected pairs of EN scales were also determined graphically to find their R² values.

Results

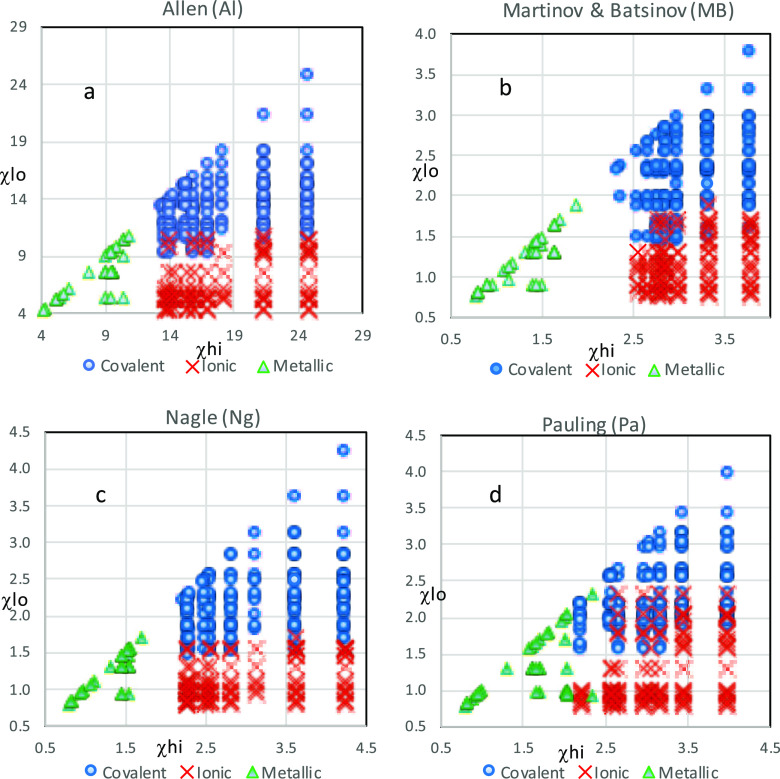
Tripartite plots of χ_lo vs χ_hi of the 14 EN scales were broadly similar (see Figure 1 for examples). Each had an obvious vertical gap on the χ_hi axis between the metallic and the combined covalent and ionic regions (separable by an M–CI line), with essentially no overlap between the metallic region and either the covalent or the ionic regions; only two EN scales had one or two metallic species falling outside the metallic region. On the other hand, all scales had a region of overlapping ionic and covalent compounds (roughly separable by a C–I line) along the χ_lo axis, with covalent compounds falling within the presumed ionic regions and ionic compounds lying within the covalent regions.

Figure 1.

Four tripartite plots examples of χ_lo vs χ_hi for EN scales of Allen (a), Martinov and Batsanov (b), Nagle (c), and Pauling (d), each showing a characteristic gap along χ_hi and overlap along χ_lo axes.

Dividing lines for the M–CI boundary were located at the midpoint of the gap region and for the C–I boundary at a point along the χ_lo axis that evenly divided the numbers of overlapped elements of lower EN. When M–CI boundary lines were fractionalized to the value of fluorine (EN of fluorine ranges from 3.78 to 24.8 among the scales used), these values ranged from 0.436 to 0.608 with an average of 0.50 ± 0.04 for the 14 scales. When C–I boundary lines were fractionalized to that of fluorine, they ranged from 0.344 to 0.535, averaging 0.40 ± 0.05. Within this group of scales, that of SBS had a small EN gap of 0.13 and one of the largest EN ranges, which, when fractionalized, produced a very large value for G′′. The ratios of the fractionalized M–CI to C–I boundary lines ranged from 1.10 to 1.35, averaging 1.25 ± 0.09 (Table 1). Despite the general similarities among EN scales, the significant differences in these scales were apparent and evaluated.

In graphs of each of the 14 EN scales, there was a very clear maximum EN of metallic elements. When the metallic elements that produced this separation were cataloged, tin was found to be by far the most prevalent element limiting the metallic character. Of the 14 scales of EN, four had tin as the element with the highest EN for this boundary, five had tin as the second-most common element, and two had tin as the third or fourth element. Bismuth was also represented as the cutoff metal, but only half as frequently. This observation correlates with that of Murphy et al. who stated that “All metals must have χ values which are less than or equal to that of Si”²² since the EN of silicon has the lowest EN of the metalloid elements.

To develop a means of comparing various scales, several parameters that characterize the nature of EN scales were considered. They were functionalized so that lower values indicated better EN scales. Three of these were determined from the results of graphing the several EN scales, which could be used to evaluate the quality of the scales—the ability of the scales to successfully separate the three bonding types. Gap distances between the metallic and covalent/ionic regions produce fractionalized G′′ values ranging from 6.5 to 124 with an average of 24.3, with the scale of SBS having a value of 124. The number of outliers (O, substances misplaced in the triangular graph based on their bonding type) ranged from 7 to 21 along the χ_lo axis; only two EN scales had a one or two metallic outliers in a bonding region other than where they were expected; all of the remaining outliers were covalent or ionic compounds found within the ionic/covalent overlap regions. The third quality parameter S was the summed EN distances from the boundary of elements on the wrong side of boundary lines; when fractionalized to the EN of fluorine, these ranged from 0.069 to 0.810. These three parameters constitute variables used for evaluating the quality of scales. In conjunction with the three quality parameters, there were three additional parameters applicable for determining utility of scales. The number of undefined elements within an EN scale, N, varied from 27 to 37, out of a maximum of the 37 elements considered. All but one scale had values of 4 or lower, but the scale of My had only 27 elements defined, with N = 10. The number of duplicated EN values, D, ranged from zero to 18, with most scales having values of 3 or fewer; however, two had large values of 17 (Ba) and 18 (GT). The parameter P that evaluated the precision in EN values was generally provided to three places although two of the scales, those of Ba and GT, had values of EN to only two places. With these six variables placed on a normalized scale between 1 and 10, comparisons could be made among each of the values of G′, O′, S′, D′, N′, and P′ (Table 2).

Table 2. Quality Parameters^a.

	Al	AR	Ba	GL	Go	GT	MB	Mk	My	Ng	Pa	RB	Sn	SBS	RZH
χmax (F)	24.8	4.1	3.9	10.76	3.94	3.95	3.78	3.91	4.00	4.23	3.98	9.85	4.00	16.16	23.3
G	2.54	0.24	0.6	0.55	0.34	0.3	0.44	0.42	0.13	0.52	0.14	0.32	0.18	0.13
G″ fractionalized	9.76	17.08	6.5	19.56	11.59	13.2	8.59	9.31	30.77	8.13	28.43	30.78	22.22	124.31
G′	1.25	1.81	1.00	2.00	1.39	1.51	1.16	1.21	2.85	1.12	2.68	2.85	2.20	10.00
O	7	10	13	15	15	14	8	16	8	7	19	20	13	12	11
O′	1.00	3.08	5.15	6.54	6.54	5.85	1.69	7.23	1.69	1.00	9.31	10.00	5.15	4.46	3.77
S fractionalized	0.136	0.322	0.18	0.533	0.810	0.284	0.206	0.573	0.242	0.069	0.515	0.644	0.575	0.412	0.858
S′	1.81	4.07	2.35	6.64	10.00	3.61	2.66	7.12	3.10	1.00	6.42	7.98	7.15	5.17	10.58
D	0	4	17	1	2	18	3	1	2	4	3	4	1	1	3
D′	1.00	3.00	9.50	1.50	2.00	10.00	2.50	1.50	2.00	3.00	2.50	3.00	1.50	1.50	2.50
N	3	4	1	0	0	0	1	1	10	3	0	0	3	4	0
N′	3.7	4.6	1.9	1.0	1.0	1.0	1.9	1.9	10.0	3.7	1.0	1.0	3.7	4.6	1.0
P fractionalized	0.0004	0.0022	0.0282	0.0012	0.0032	0.0313	0.0033	0.0030	0.0031	0.0024	0.0031	0.0012	0.0026	0.0007	0.0041
P′	1.00	1.51	9.10	1.22	1.80	10.00	1.84	1.77	1.79	1.59	1.80	1.22	1.65	1.09	2.08
Q1 = G′ + S′	3.06	5.88	3.35	8.63	11.39	5.12	3.82	8.34	5.96	2.12	9.09	10.84	9.35	15.17
Q2 = G′ + O′ + S′	4.06	8.96	8.50	15.17	17.93	10.97	5.52	15.57	7.65	3.12	18.40	20.84	14.50	19.63
U1 = G′ + S′ + N′ + D′	7.76	13.48	14.75	11.13	14.39	16.12	8.22	11.74	17.96	8.82	12.59	14.84	14.55	21.27
U2 = G′ + O′ + S′ + N′ + D′	8.76	16.56	19.90	17.67	20.93	21.97	9.92	18.97	19.65	9.82	21.90	24.84	19.70	25.73

^aParameters G (gap width & G′′′ (χ(F)/gap width), O (number of overlapped elements), S (sum of overlapped offset distances/χ(F)), D (# duplicate EN values), N (number of absent EN values), and P (precision of EN scale/χ(F)) implied the error of EN scales; primed quantities are normalized to a scale of 1–10. Q are quality scores and U are utility scores.

Quality scores, Q, were calculated from these parameters using various combinations of normalized values. The summed quality values of the three variables, G′, O′, and S′, ranged from 3.12 to 19.63, while summed utility values of G′, O′, S′, N′, and D′ had a range of 8.76–24.84 (Table 2). Linear correlations among the six parameters are shown in Table 3 and had an R² of 0.3 or less with two exceptions. One correlated pair of parameters was O and S with R² = 0.88; the other was that of D and P, with R² = 0.95. Due to high correlation and comparatively lower dispersion, the parameter P was excluded from calculations of Q and U. With or without this adjustment, three EN scales afforded the best agreement with bonding types. The three scales of Al, MB, and Ng have Q scores between 3 and 6; all others had values up to 20. Comparisons of these three scales with each other as well as with the classical Pa scale using linear regression produced values of R² varying from 0.91 to 0.99 (Table 3). The Pauling scale, although often used as a benchmark for confirmation of other EN scales, is a poor choice for verification of other scales. Its quality score is among the highest, and it cannot adequately separate well-characterized bonding types.

Table 3. Correlations^a.

	pairs
parameters	N and D	N and G	N and O	N and S	N and P	D and G	D and O	D and S	D and P	G and O	G and S	O and P	O and S	O and P	S and P
R2 =	0.0621	0.0588	0.3436	0.0428	0.0533	0.0454	3.00E-05	0.0235	0.9531	0.0066	0.0216	0.0599	0.8778	0.0056	0.0345

EN scales	Al vs Ng	Al vs Pa	Al vs MB	Ng vs Pa	Ng vs MB	MB vs Pa	Al vs RZH
R2 =	0.9902	0.9813	0.9626	0.9565	0.9472	0.9107	0.9035

^aLinear correlations comparing pairs of quality parameters (N, D, G, O, S, and P) and selected pairs of EN scale.

Analysis of these different EN scales demonstrates the potential utility of this method for evaluating the quality of EN scales. To this end, other recent scales were considered, such as the one using ground-state binding energies⁴³ or another using X-ray scattering.⁴⁴ The scale of Rahm, Zeng, and Hoffmann⁴³ (RZH) was selected because it was described by the authors as being closely related to the scale of Al and to correlate with his scale with a standard deviation of 9.3%. As with the 14 scales initially evaluated to establish useful parameters, EN values were plotted and the values of parameters were calculated. Boundary lines and parameters were similarly determined, and the quality and utility values were established, as shown in Tables 1–3 under RZH. This scale showed an extensive overlap in the ionic/covalent region with an overlap of about 30%, and no obvious gap appeared between the metallic and ionic/covalent compounds, so no M–CI boundary line could be determined. Since this scale had no gap between metals and ionic/covalent compounds, the values of Q or U could not include a value for G′. The Pauling scale, although often used as a benchmark to confirm the veracity of other EN scales, is a poor choice. Its quality score is among the highest since it cannot adequately separate well-characterized bonding types.

Discussion

Two sets of binary compounds of described bonding character are available in the literature: one by this author²⁴ using compounds selected from the text by Wells,⁴⁵ and the second by Meek and Garner²⁷ with compounds selected from the text by Greenwood and Earnshaw.⁴⁶ Tabulation of binary compounds, separated into bonding types, is available in the supplementary materials connected to the Meek and Garner paper. In the earlier paper by this author, the tripartite separation of ionic, covalent, and metallic bonding types was apparent and discussed. However, only with the use of the more recent compilation by Meek and Garner did the characteristic gaps become obvious for all graphs of EN scales evaluated. This common characteristic among the 14 graphs indicates the likelihood that the Meek set is superior to that used previously by this author. Not only do nearly all of the graphs show a clean separation of metallic bonding from either the ionic or covalent bonding but also a limited overlap region between the ionic and covalent compounds. The reason for this will be discussed later. Since the separation of bonding types is such a fundamental concept in chemistry, it is surprising that the Meek and Garner listing of binary compounds has not been used by other authors; as far as this author has been able to ascertain, other than their 2005 article, no pertinent use of their compilation appears in the scientific literature.

The quality of EN scales to predict the three bonding types has been evaluated by two-dimensional plots of χ_lo vs χ_hi. Analysis of these shows certain characteristic features common to all 14 EN scales evaluated: gap regions in which no compounds are found between regions of metallic bonding and of ionic/covalent bonding and overlap regions between ionic and covalent bonding types within which both the covalent and ionic compounds are found. The gaps are usually relatively wide, on the order of 10% of the total χ_hi range. Obviously, since compounds of mixed bonding character have been excluded from the binary compound data set, there are many unplotted compounds of a mixed character, such as metalloids, that could fill this gap. Because of the need to select well-defined bonding types for the analysis of EN scales, compounds of mixed metallic bonding types were excluded. The origin of this gap likely arises because metals are easily characterized by having readily observable physical properties, such as luster, ductility, malleability, electrical conductivity, thermal conductivity, etc. On the other hand, covalent and ionic compounds do not have such well-defined physical characteristics; the bonding character of these is much more a chemical concept, based on chemical properties such as the existence of molecules (where the bulk properties are temperature- and pressure-dependent) or the presence of ions (which are difficult to detect as individual entities and are determined secondarily by such measurable quantities as solubility, aqueous conductivity, or melting point). Gap boundary lines can therefore be located vertically along the χ_hi axis and placed between the metallic substance of the highest EN and the ionic/covalent substance of the lowest EN. On the other hand, boundary lines separating ionic from covalent compounds occur within an overlap region. Overlap is likely due to the difficulty in our ability to definitively define the bonding character, whereas metallic compounds can be clearly identified by their physical properties, ionic and covalent compounds are not so readily differentiated. This results in gaps between metallic compounds and ionic/covalent compounds but in overlaps between ionic and covalent compounds. It seems likely that some of the bonding character of compounds within the overlap regions may have been misidentified as covalent or ionic when they should have more properly been described as mixed. Compounds containing the elements Be, Al, In, Ga, and Sn—elements in or near the semimetallic band—were frequently found in the C–I overlap region. Thus, in binary compounds, the element with a low enough higher EN value determines whether a compound will be metallic and separated by an M–CI boundary line from the covalent and ionic compounds by a gap along χ_hi, whereas for compounds that are not metallic, the element with a lower EN value determines whether the compound will be ionic or covalent, generally separated by the C–I line along the χ_lo axis.

Six variables were considered that could be used to help determine the quality of EN scales: G, O, S, N, D, and P. The gap parameter G evaluates the successful separation of metallic bonding from those of either ionic or covalent character. Since compounds of mixed metallic and either ionic and/or covalent character were intentionally removed from the data set, the width of this gap should indicate the successful dichotomy between the metallic and ionic/covalent characteristics. An exceptionally narrow gap could indicate either the poor definition of the bond type or of poor EN values, but since most scales have a wide gap, a narrow gap in an EN scale can be attributed to the poor EN definition of that scale. While all but one scale had G′′ values of about 30 or lower, that of SBS had a value of 124. The standard deviation of these scales was 30.0, so the value for SBS was 4σ, well above the average. This high value of SBS’s G value arises from the combination of having both the second-highest EN of fluorine and having a very small gap; the fractionalized ratio of these two produces a value 4 times that of the next highest G′′ value. In every EN scale evaluated, there was an overlap in the bonding character between ionic and covalent species. Counts of the number of species in the overlap regions, O, provide a gauge of the bond-type misfit for each scale. This value ranges from 7 to 20, a 3-fold difference. A quantity S is defined as the sum of EN separation distances of all outliers in overlapped regions from their boundary lines. Ranging from 0.11 to 1.61, there is a 15-fold difference in the S parameter. These three parameters, arising from similarities found in the graphs of χ_lo vs χ_hi, can be used to assess the quality of EN scales. In combination with three ancillary parameters, the utility of scales can be evaluated. The number of undefined EN values in each scale, N, is used to evaluate the completeness of each EN scale since the inclusion of all elements allows for the prediction of the bonding character only for included elements. Missing values would preclude predictions of their bonding properties; the more complete a scale of EN values, the more comprehensive its utility. Nearly all scales miss values for the EN of the noble gases, so noble gases were excluded from consideration. Since the scale of My has only 27 of the 37 possible elements’ EN values indicated, the N value for this scale is significantly higher than that of the other scales. Duplication of EN values, D, leads to the ambiguity of those elements with the same values, limiting the use of such EN values to make comparisons. While most scales have D (duplication) values of 4 or lower, those of Ba (17) and GT (18) are much higher. This disparity arises from EN values of these two scales that have been given only to two places rather than three found in the other scales. Finally, since some scales had better precision, P, in their definitions of EN values, it is useful to recognize why some scales lacked precision; this value ranged from 0.0004 to 0.031, a 78-fold difference. Two scales have EN values provided only to two digits (Ba and GT), which produced several elements having the same EN values. The lack of precision precludes the precise differentiation or determination of properties such as dipole moments between elements of the same EN values. Since these six parameters result in values that are of differing magnitudes and on different scales, all six were normalized to a range from 1 to 10, with lower values indicating higher-quality EN scales. Using the three parameters G′, O′, and S′, arising from the gap separation and overlap of bonding types, the quality of the 14 scales could be compared by providing a quantitative value arising from the effectiveness of the separation of substances into the three bonding types. Also, using all six parameters, the utility of scales could be compared to provide a measure of how useful the scales are.

The utility score, U, is used to evaluate the efficacy or practicality of EN scales and was calculated as a sum of various normalized values from among G′, O′, S′, N′, D′, and P′ (each on a scale of 1–10). Similarly, the quality scores, Q, were calculated using G′, S′, and O′. Determining which selection of the parameters provides the most meaningful test of quality is subjective and requires some evaluation as well as rationalization. Pairs of the six parameters were plotted to determine the extent of correlation by linear regression (Table 3). While most pairs had an R² of 0.3 or less, two pairs had a significant correlation. In the case of the D–P pair (R² = 0.95), D measures the duplication of EN values and P measures the numerical precision of these values. The origin of their correlation arises from having either well-defined or poorly defined EN values. As opposed to EN definitions listed to three places, with EN values provided only to two places, duplication and lack of precision occur, diminishing the ability of these scales to differentiate between elements of the same EN values. Since these two terms are so highly correlated, it is appropriate to use only one of them. The D parameter has a slightly higher dispersion of values and is therefore a somewhat better discriminator of this type of parameter and so was accepted for inclusion and P was excluded. The pair of O and S also exhibits some correlation, but R² is only 0.88. While some correlation is not surprising since O and S are both measures of elements lying within overlap regions, these terms still exhibit differences in what they measure. The variable O is an integral count of overlapped elements, while S is a sum of offset EN distances of the overlapped elements from boundary lines. The R² value indicates a significant correlation but also portrays significant differences. Since the overlap of ionic and covalent compounds seems the most critical of parameters used to demonstrate the effectiveness of the separation of ionic from covalent substances, both O and S can be included in calculations, serving essentially as a weighting factor for the extent of overlap. Q and U scores using different selections of parameters are shown in Table 2 for the 14 EN scales.

The Q parameters G′ + S′ and G′ + O′ + S′ have been used to identify scales with the greatest ability in separating bond types. Three (or four) scales, those of Al, MB, and Ng (and for Q1, Ba), have demonstrably better scores, with G′ + S′ ranging from 2.12 to 3.82 (3.12 to 5.52 for G′ + O′ + S′) compared with other scales where the other 11 G′ + O′ scores ranged from 5.12 to 15.17 (for G′ + O′ +S′, they range from 7.65 to 20.84). These three (or four) scales are therefore considered to provide the greatest accuracy of EN definitions and therefore the quality of scales. Utility of scales is correlated with a sum selected from the six quality parameters—those that include the quality (accuracy) of EN definition as well as those measuring the completeness of EN tables, the precision of values, and the uniqueness of EN values. Scores for U = N′ + D′ + G′ + O′ + S′ range from 7.76 indicating the best agreement with a bond character to 21.27 for the least descriptive scale. While the four utility scores range nearly continuously, it is obvious that the same three scales are superior. Al, MB, and Ng have U scores that are significantly lower, ranging from 7.76 to 8.82, while the other 11 range from 16.56 to 25.73. Interestingly, the three superior scales rely on entirely different types of EN definitions: the Al scale is calculated on valence shell spectroscopic energies, the MB scale is based on the atomic radius and effective nuclear charge, and the Ng scale is calculated from atomic polarizabilities. Of these, Al and Ng are defined on atomic models, while MB employs a molecular approach using oxidation numbers. It is curious that, from this limited survey, no particular method of defining an EN scale, whether quantum mechanical or observable, whether atomic or molecular, seems to be exceptional in determining the quality of an EN scale. While the very definition of EN remains unclear, the described means for determining the quality of scales may be useful in finding better scales that could provide a perspective that will foster a more satisfactory definition of EN.

The three scales with the best Q scores were evaluated against one another as well as against the scale of Pa using R² as a tool to compare them (Table 3). The highest correlation is that between Al and Ng with R² = 0.990, and the worst is that between Pa and MB with R² = 0.911. Averages of the correlation values for each of the four scales show that the correlation of Al against the other three scales has the highest average correlation, 0.978, decreasing to 0.965 for Ng, to 0.950 for Pa and 0.940 for MB.

Since the described process has been shown to be an effective tool for evaluating EN scales, it should be able to evaluate other scales. New scales of EN continue to be developed. For example, the scale of Rahm, Zeng, and Hoffmann⁴³ was selected to test the use of Q and U because the authors described this scale as being closely related to Allen’s scale and to correlate with his scale with a standard deviation of 9.3%. Results of analyzing the RZH scale show that it does not compare favorably with the three best scales. Unlike all of the 14 EN scales analyzed for developing this tool for determining the quality of scales, the RZH scale has an overlap rather than a gap between metallic and ionic/covalent compounds (Table 1 under RZH). Additionally, while the typical C–I overlap is about 10% of the full EN scale for the 14 EN scales used to establish the quality of EN scales, the C–I overlap of RZH is about 30%, 3 times larger than “normal”. The value of R² among pairs of the three best scales as well as the Pa scale ranged from 0.91 to 0.99 and that between the RZH and Al scales, which was the tool used by these authors to establish the validity of this scale, was only 0.90 (Table 3 under RZH). Since this scale had no gap between metals and ionic/covalent compounds, the values of Q and U could not include a value for G′ and so these values cannot include this term. Even with the exclusion of the G parameter, one can readily see that this scale does not compare well with the three best scales of Allen, Martynov, and Batsanov, or Nagle. Instead, it is comparable in its ability to identify bonding types to some of the least predictive of the analyzed scales. Although the authors selected a high-quality scale for comparison, the correlation with this scale was only 0.90, a value too low to demonstrate an adequate correlation. It should be pointed out that this scale was designed for a special purpose: analysis of high-pressure EN, which required a scale that could incorporate a pressure-sensitive term.

Chemists can consider using this tool to evaluate, among other things, the quality of EN scales as was just demonstrated with the RZH scale or to evaluate the categorization of the bonding character in binary compounds using one or more quality scales. For example, if one or more scales locate a presumed covalent compound as ionic, its bonding categorization could be questioned. Similarly, using a single high-quality scale, such as the scale of Allen, we could compare the bonding type with respect to the often used Δχ function. In Allen’s χ_hi vs χ_lo graph, there are 13 compounds in the overlap region. They include such substances as AlCl₃, AlBr₃, AlH₃, BeCl₂, BeBr₂, and InCl₃, classed as covalent but found in the ionic region, and InBr₃, GaBr₃, Ga₂O₃, and SnO₂, classified as ionic but found in the covalent region. With the Δχ function, which parallels the hypotenuse (where Δχ = 0) of χ_hi vs χ_lo graphs, a line that evenly divides misplaced compounds is found at a Δχ value of 9.50 on Allen’s EN scale that produces about equal numbers of substances classified as ionic (Δχ > 9.50) but found within the covalent region as substances classified as covalent (Δχ < 9.50) but found within the ionic region. When reviewing the compounds that fall outside the expected bonding regions, 30 compounds are misplaced, including CF₄, SF₂, SeF₂, PF₃, BF₃, SiF₄, CF₄, SnO, SnO₂, HgO, and HgO₂, which are classified as covalent but lie within the ionic region, while MgCl₂, HgBr₂, MgS, CaS, MgSe, CaSe, SrSe, Li₂Se, BaSe, and Na₂Se are classified as ionic but fall within the covalent region. A critical review of these “misplaced” binary compounds may lead a chemist to question any one of the three things: the definition of the EN scale, the characterization of bonding types for compounds lying outside the bonding region predicted, or the soundness of the defining function to categorize ionic vs covalent character. Although frequently employed, Δχ has had a limited critical review as a legitimate function for describing the bonding character.

Conclusions

Plotting lower vs higher values of electronegativity (EN) for binary compounds of a known bond character produces a general separation of metallic, covalent, and ionic bonding types into tripartite regions. Metallic compounds have been shown to be those whose element of low higher EN segregates them while, once metallic compounds have been separated, the element of lower EN generally separates ionic from covalent compounds. Using 14 EN data sets and well-defined bonding character of binary compounds, plots of EN values of the two elements in those compounds produced the tripartite separation of bonding types. Six quantitative parameters related to the utility of the EN scales have been selected, and three of these parameters have been used to quantify the quality or effectiveness of EN scales to correctly identify the bonding character. Correlations between pairs of parameters were calculated, and due to a high correlation between two parameters, one could be excluded. Using sums of selected parameters, quality scores for the 14 EN scales were calculated, and utility (usefulness) scores were found to range from 8.76 to 25.73 and for accuracy (ability to predict bond type) to range from 2.12 to 15.17, with lower scores indicating better quality scales. Three EN scales, those of Allen, Martynov and Batsanov, and Nagle, were found to be superior for both quality scores for accuracy in predicting the bond type and scores for the usefulness of EN scales. Correlations between pairs of these three EN scales along with that of Pa were determined, ranging from a high value of 0.99 for the best correlation. Using the proposed scoring of EN scales, a recently published EN scale was evaluated to exemplify the use of this procedure to assess its quality. The proposed analysis of EN scales provides an independent means for evaluating the quality of EN scales by assessing the effectiveness of separation of the binary compounds’ bonding character by graphical means.

The author declares no competing financial interest.