Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 28;36(20):5502–5509. doi: 10.1021/acs.langmuir.0c00393

Spatiotemporal Heterogeneity of κ-Carrageenan Gels Investigated via Single-Particle-Tracking Fluorescence Microscopy

Koen J A Martens †,‡, John van Duynhoven †,§, Johannes Hohlbein †,∥,*
PMCID: PMC7254830  PMID: 32343144

Abstract

graphic file with name la0c00393_0005.jpg

Hydrogels made of the polysaccharide κ-carrageenan are widely used in the food and personal care industry as thickeners or gelling agents. These hydrogels feature dense regions embedded in a coarser bulk network, but the characteristic size and behavior of these regions have remained elusive. Here, we use single-particle-tracking fluorescence microscopy (sptFM) to quantitatively describe κ-carrageenan gels. Infusing fluorescent probes into fully gelated κ-carrageenan hydrogels resulted in two distinct diffusional behaviors. Obstructed self-diffusion of the probes revealed that the coarse network consists of κ-carrageenan strands with a typical diameter of 3.2 ± 0.3 nm leading to a nanoprobe diffusion coefficient of ∼1–5 × 10–12 m2/s. In the dense network regions, we found a fraction with a largely decreased diffusion coefficient of ∼1 × 10–13 m2/s. We also observed dynamic exchange between these states. The computation of spatial mobility maps from the diffusional data indicated that the dense network regions have a characteristic diameter of ∼1 μm and show mobility on the second-to-minute timescale. sptFM provides an unprecedented view of spatiotemporal heterogeneity of hydrogel networks, which we believe bears general relevance for understanding transport and release of both low- and high-molecular weight solutes.

Introduction

Carrageenan is a collection of linear sulfated polysaccharides, which are widely used as thickeners or gelling agents in food products, personal care products, and healthcare.1−3 Gelation is induced by cooling down hot solutions of carrageenan, whereupon single helices are formed that can subsequently form double helices with other carrageenan strands under the assistance of cations such as potassium, sodium, or calcium.4−7 This double helix formation results in cross-linking and thus thickening or gelling behavior. Altering the precise chemical composition or concentration of carrageenan or the introduced cations results in different properties of the material.4−6 Cations are required to induce gelation, with low concentrations of cations leading to low-strength hydrogels. Increasing the concentration of potassium, on the other hand, results in an increasing presence of stiff fiber rods, while addition of sodium ensues more flexible superstructures.5 The degree of sulfonation dictates the exact type of carrageenan; κ, λ, and ι-carrageenans are the most common carrageenan variants, having one, two, and three sulfate ester groups, respectively.2 In this study, we focused on the industrially relevant κ-carrageenan, for which the gel properties can readily be manipulated by specific ion additions.1,2,8

Detailed knowledge of the structure of carrageenan hydrogels is desirable for rational design of food and personal care products. Analysis of carrageenan gels or solutions is usually performed via bulk techniques such as rheology,5 differential scanning calorimetry (used to study gel transition points6), scattering techniques (small angle X-ray scattering and small angle neutron scattering, used to elucidate strand thickness and behavior7), and pulsed field gradient nuclear magnetic resonance (PFG NMR, used to study self-diffusion of low- and high-molecular-weight solutes9−11). Although these methods provide a wealth of information on the structure, formation, and behavior of carrageenan gels, they generally do not provide spatial information on network heterogeneity.

Spatial heterogeneity is an important aspect of hydrogels: it influences rheological properties, plays an important role in the loading and releasing behavior of solutes, and may also modulate enzyme activity during digestion.12−14 Currently used imaging techniques [e.g. electron microscopy (EM),5,8 raster image correlation spectroscopy (RICS),10 or fluorescence recovery after photobleaching (FRAP)15,16] have indicated that dense network regions exist on a micrometer scale. However, these methods require invasive or destructive sample preparation (EM) or have limited power to quantitatively resolve spatial heterogeneity (RICS and FRAP).11,17 Quantitative nondestructive and noninvasive imaging techniques could prove to be valuable in confirming the existence and size of these regions. Here, we apply single-particle-tracking fluorescence microscopy18,19 (sptFM) to study κ-carrageenan networks with high spatiotemporal resolution and nondestructive sample preparation.

In subdiffraction-limited sptFM, the positions of small (<100 nm) fluorescent particles are determined with ∼10–40 nm accuracy by fitting the emitted point spread functions (PSFs) with a mathematical model.20,21 By assessing the position of these fluorescent particles at a high temporal resolution (∼100 Hz), the movement of the particles in the xy focal plane can be determined. While the 2D sptFM methodology can be extended to include z-positional information (3D sptFM) using engineered PSFs, this can be actually detrimental for diffusion analysis because of a lower localization accuracy in the xy plane.20,22 Because the behavior of the particles is directly influenced by the local environment,14,19,23−25 quantification and analysis of the movement leads to spatial characterization of the local surrounding medium. Recent sptFM performed on mixtures of ι- and κ-carrageenan gels19,24 focused on using larger fluorescent particles (∼100 nm), effectively probing larger spatial structures than intended here.

In this study, we will employ sptFM to obtain quantitative and spatially defined structural information on κ-carrageenan gels by infusing fluorescent nanoprobes of 28 nm diameter in fully gelated networks. First, we will investigate the existence and properties of κ-carrageenan gel heterogeneity and analyze the diffusional behavior of the nanoprobes. Next, we will determine the morphology of the gel heterogeneity by evaluating nanoprobe trajectories based on their spatial position with sub-μm resolution.

Our results show the existence of primarily two nanoprobe diffusional states, which we attribute to diffusion in the coarse bulk network and in dense network regions, along with occasional switching between these states. The relationship between nanoprobe diffusion in the bulk coarse network is consistent with Johnson’s obstruction model,10,26,27 describing the coarse network as consisting of 3.2 ± 0.3 nm diameter κ-carrageenan fibers independent of sodium ion concentration. Within this coarse network, regions of dense networks with ∼1 μm diameter are embedded, irrespective of the sodium ion or κ-carrageenan polymer concentration. These dense network regions occasionally show mobility on the second-to-minute timescale, which we directly observed with multiple techniques.

Materials and Methods

κ-Carrageenan Gel Creation

κ-Carrageenan (Sigma-Aldrich, Zwijndrecht, The Netherlands) was thoroughly mixed with Milli-Q water with various volumes of 1 M 0.2 μm-filtered NaCl and KCl solutions to obtain various κ-carrageenan gels (0.5–2.5% (w/v) κ-carrageenan, 20 mM KCl, and 100–200 mM NaCl). This mixture was then heated in a heat block (Dry Block Thermostat, Grant Instruments Ltd, Shepreth, UK) to 75 °C and was left at this temperature for at least 15 min while regularly vortexing the solution. Then, 20 μL of the hot κ-carrageenan solution was pipetted on a cleaned (oven-burned at 500 °C for 20 min to remove possible organic fluorescent impurities28) glass coverslip (Paul Marienfeld GmbH & Co. KG, Lauda-Königshofen, Germany; #1.5H, 170 μm thickness), where the sample was confined by silicone wells. The sample was then left to solidify for at least 5 min before any measurement.

Probe Infusion in κ-Carrageenan Gels

After solidification of the gel and directly (∼1–5 min) before imaging, 2 μL of  0.02% w/v 28 nm diameter nanospheres (FluoSpheres carboxylate-modified dark red, Thermo Fisher Scientific, Waltham, MA, USA) solution was added to the side of the gels (leading to 0.002% w/v nanosphere concentration in the final sample volume). Single-particle-tracking results shown in this study consist of two replicates with four areas characterized in every replicate.

Single-Particle Imaging

All imaging was performed on a home-build single-molecule microscope, fully described elsewhere.29 Briefly, a 642 nm laser line was employed for epifluorescent illumination to excite the nanospheres via a Nikon 100× 1.49 NA HP/SR objective. The emission light was then filtered via a 700 ± 75 nm bandpass filter and imaged at 200 Hz with a Zyla 4.2 plus sCMOS (at 2 × 2 pixel binning, 128 nm pixel size) controlled using the micromanager software.30 Occasionally, the emission light was guided via the bypass mode of a rescan confocal microscope, which reduced the pixel size to 122 nm (at 2 × 2 pixel binning). Four different fields of view of every gel were recorded for 8000 frames (40 s) each and analyzed.

Rescan Confocal Imaging

The home-build microscope described above was expanded with a rescan confocal microscope (RCM) unit (Confocal.nl, Amsterdam, The Netherlands).31 The RCM uses the same laser line, and scans the confocal excitation spot over the sample through the same objective. The resulting emission light is rescanned with a mirror with 2× the sweep length as the excitation scanning mirror, leading to a 43 nm pixel size on the sCMOS chip. In practice, RCM is capable of a ∼40% increase in resolution with respect to the classical resolution limit.

Single-Particle-Tracking Analysis

The raw recorded single molecule data were analyzed with the ThunderSTORM plugin32 with pSMLM functionality20 in FIJI.33,34 A β-spline wavelet filter with scale 2 and order 3 was used for identification of molecules, after which a threshold of 1.25 times the standard deviation of the wavelet F1 value was used to detect single point spread functions (PSFs). Then, a 2D pSMLM sub-pixel fitting routine was employed on a 7 × 7 pixel region of interest around the center of the PSF. These subpixel localizations were loaded in MATLAB (The MathWorks, Natick, MA, USA) 2018b for further analysis.

Tracking of the individual localizations was performed via the tracking methodology incorporated in the SMALL-LABS software package,35 with a minimum merit of 0.01, 5 ms integration time, a gamma of 1, a minimum track length of 2 frames, and a maximum step size of 5 pixels (0.6 μm). Then, for every track found in a movie, the mean jump distance (mjd) was calculated and a histogram of the mjd was produced, weighing the mjd on the number of localizations per track. The histograms were plotted on a logarithmic x-axis and fitted with a double log-Gaussian, constraining the peak position of the Gaussians between (7 and 148) nm, and between (55 and 1097), nm respectively. These bounds were never limiting the fitting peak positions.

The peak positions are plotted either directly as mjd, or recalculated as the diffusion coefficient: 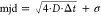Inline graphic, where σ is the localization uncertainty. The localization uncertainty was estimated by fitting a representative subset (∼4% of frames evenly spread over a single movie) of all localizations of all datasets with a maximum likelihood (MLE) Gaussian fitting model within ThunderSTORM,32 and extracting the calculated localization uncertainty.36 MLE-Gauss fitting is shown to have a ∼4% difference in localization uncertainty compared to the used phasor fitting.20 Over all localizations, a mean localization uncertainty of 22 nm was found, corrected for the difference in localization uncertainty.

Quantification of Probe State Switching

To have an indication of how many probes show behavior characteristic of switching from obstructed diffusion in the coarse network to largely immobilized diffusion in the dense network regions (e.g. Figure 1C bottom), all tracks from a single movie were tested as follows: first, tracks shorter than 20 frames were discarded, as these show insufficient information to assess switching behavior. Then, a 2-frame-moving average of the jumping distance plot was created. If this moving average plot had at least 5 consecutive frames (25 ms) of at least 150 nm jump distance (i.e. obstructed diffusion in the coarse network), along with at least 10 consecutive frames (50 ms) of at most 100 nm jump distance (i.e. largely immobile behavior), the track was indicated to be state-switching.

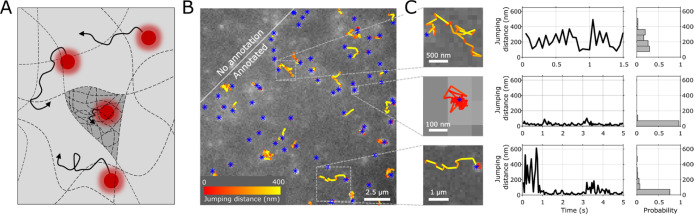
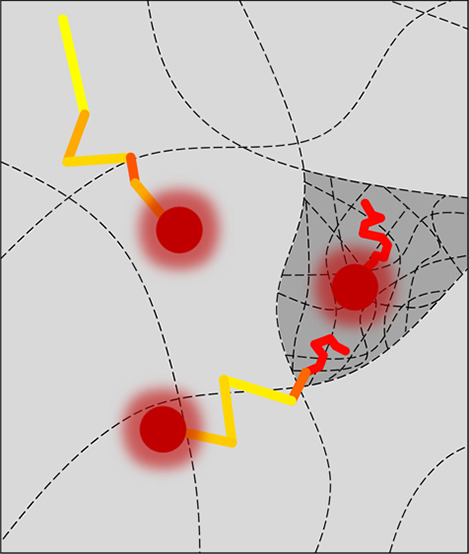
Figure 1.

Figure 1

Open in a new tab

sptFM in κ-carrageenan gels. (A) Schematic representation of fluorescent probes (red), embedded in a gel matrix (dotted lines). These probes are capable of diffusion in the gel matrix (arrows). A coarse network (light gray region) allows for obstructed diffusion of the fluorescent probes, while dense network regions (dark gray region) further decrease the mobility of the probes. (B) Typical localization (blue asterisks) and tracking (yellow-red colored lines) overlaid on a raw microscopy image. Shown here is single-particle-tracking of 28 nm diameter polymer probes in a 1% κ-carrageenan gel with 200 mM NaCl, 20 mM KCl. Highlighted regions are enlarged in (C). (C) Examples of obstructed diffusing (top), largely immobile (middle) or transitioning (bottom) particles. Left: the corresponding 2D movement of the single tracks. Middle: jump distance of this track plotted against the time of the track. Right: histogram created from the jump distances found in the track. Revealing network heterogeneity by the multimodal probe self-diffusion behavior.

Obstruction Model

Johnson’s obstruction model10,26 was calculated according to eq 1

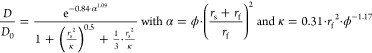graphic file with name la0c00393_m002.jpg 1

where D is the measured diffusion coefficient, D0 the diffusion coefficient of the probe in pure water, rs the nanosphere radius, rf the κ-carrageenan strand radius, and ϕ the polymer volume fraction. The κ-carrageenan strand radius is the only unknown parameter in this equation. This model is fitted to the obtained mjd log-Gaussian peak positions for both experimental conditions via a non-linear fitting procedure in MATLAB and a 95% confidence interval was obtained from this fit.

Johnson’s obstruction model assumes the following conditions: (1) the collisions between the probe and network are elastic; (2) the movement of the fibers is slow compared to the interaction times of the probes; (3) the entire volume is accessible except for the volume occupied by the probes and the fibers; (4) diffusive freedom of the probes in the polymer; and (5) non-negligible hydrodynamic drag of the probes. In our setting, the use of the Johnson model is justified, as (1) the probes and polymers are both hard structures, (2) only brief (elastic) interactions between the probes and polymers occur, and (3) the probes have no expected affinity to the polymer.

Mobility Maps

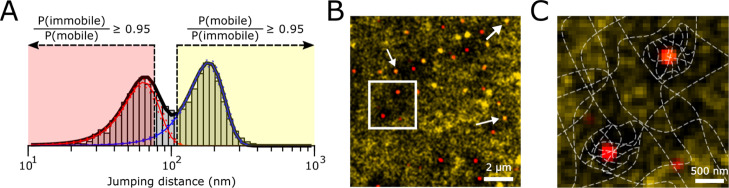
To create mobility maps, all localized particles were divided into three groups (immobile, mobile, or undefined) based on the mjd of the track to which the localizations belong. The double Gaussian fit of the mjd histograms of a single experiment (described above) was used to determine cut-off jump distances at which the ratio of the probability of the Gaussians was 0.95 for either P(mobile)/P(immobile) or for P(immobile)/P(mobile) (also see Figure 3A). Then, the localizations that correspond to tracks with jump distances lower than the jump distance found for P(immobile)/P(mobile) = 0.95 were termed “immobile”. A similar procedure was performed to find localizations that were termed “mobile”. Localizations that were neither “immobile” nor “mobile” were discarded for mobility mapping.

Figure 3.

Figure 3

Open in a new tab

Mobility mapping of immobile and mobile regions in κ-carrageenan gels. (A) Procedure to sort single localizations in immobile (red), mobile (yellow), or intermediate (discarded) groups based on the mjd of their corresponding track. (B) Representative image of a resulting pseudo-color-coded mobility maps. Red regions are locations consisting of solely immobile particles, yellow regions are locations consisting of solely mobile particles, and orange regions (arrows) are locations where both immobile and mobile probes are present. The outlined region is enlarged in (C). (C) Zoom-in from (B) with a proposed schematic network structure overlaid on the image. Dense network regions show translational migration in κ-carrageenan hydrogels.

Next, an average shifted histogram of only the “immobile” or “mobile” localizations was created via an algorithm identical to the ThunderSTORM32 average-shifted histogram visualization option with a magnification of 2 and a lateral shift of 2 pixels. These “immobile” and “mobile” mobility maps were colored and overlaid on each other.

Results and Discussion

κ-Carrageenan Gel Networks Probed using Fluorescent Probes

κ-Carrageenan solutions were prepared at varying polymer concentrations (0.5–2.5% w/v), varying NaCl concentrations (100–200 mM), and a fixed KCl concentration (20 mM). These compositions are commonly employed in food products37 and literature,4−6,10 and form gels throughout the parameter space. After cooling on a glass coverslip, 28 nm diameter carboxylate-modified fluorescent polymer nanospheres were infused into the gel. These probes were expected to move around in the gel network with a reduced diffusivity because of obstruction caused by the local network structure (Figure 1A).26 When we attempted to infuse nanospheres before gelation, we observed that a combination of residual salt and heating to 75 °C resulted in probe aggregation, and thus this procedure was not pursued further. Either the presence of residual salt or an increased temperature did not affect the diffusion of nanospheres, however.

Fluorescence emission from single probes could be observed using a 642 nm excitation laser light and a 5 ms camera frame time (Figure 1B). The PSFs were then identified and fitted (Methods; blue asterisks in Figure 1B,C). These positions were compared and potentially linked to those in the previous frames to create tracks. The diffusivity and jump distance of single tracks are shown as lines in Figure 1B,C.

Qualitatively, we could distinguish primarily two different mobilities of the fluorescent probes in the hydrogel network. We found that some of the probes were able to move around in the gel network slightly obstructed, leading to jumping distances in the order of several hundred nanometers (e.g. Figure 1C top). Other probes showed largely decreased self-diffusion over long time scales (>seconds; e.g. Figure 1C middle) in which the jumping distance is below ∼100 nm. Occasionally, probes showed interchanging behavior between these two previous states (e.g. Figure 1C bottom).

These results agree with earlier studies indicating the presence of spatial heterogeneity in the κ-carrageenan hydrogel networks.10,38,39 The coarse network bulk is expected to have a polymer concentration-dependent mesh size of ∼100 nm, allowing slightly obstructed diffusion of the 28 nm diameter probes, in agreement with our first observed species (Figure 1C top). Meanwhile, distinct regions in the network exist with a much denser network with mesh size <∼20 nm10, leading to hampered entry of the probes in the dense, but inherently flexible hydrogel network. This finding is in agreement with probes getting trapped and showing largely decreased self-diffusion (Figure 1C middle). Because probes are confined in both the coarse network bulk and the dense network regions, the diffusion coefficient obtained from jump distance analysis employed here is equally informative as mean squared displacement (MSD) analysis. Moreover, further quantification of the confinement effects via MSD would have to build on the assumption of spatial homogeneity,40 which is not present here.

Nonspecific chemical adsorption of the probes to network strands is unlikely because of repulsive negative charges. Moreover, similar experiments in a nongelated κ-carrageenan polymers (because of the absence of salt) showed only a single-diffusive population (Figure S1), suggesting that in those experiments, diffusion is determined solely by the viscosity of a semidilute polymer solution.41

The observation of occasional switching of the probe behavior from the trapped state to the obstructed diffusing state or vice-versa (Figure 1C bottom) indicates structural rearrangement of the dense network. This finding is strengthened by the presence of trapped probes in these experiments in general, as the probes were infused after network formation and became trapped in the already gelled dense network region.

3.2 nm Diameter κ-Carrageenan Network Fibers Hinder Probe Self-Diffusion in the Coarse Network

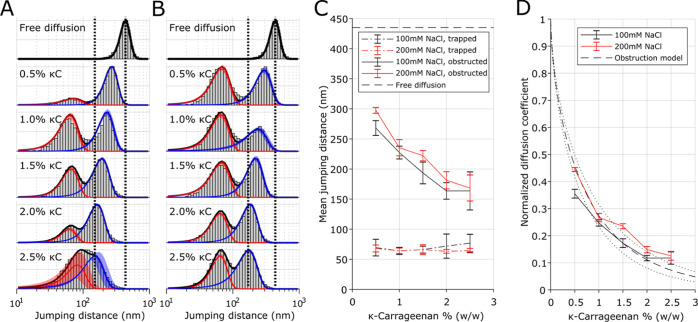
To quantify the probe diffusion profiles, we plotted the mjd of a single track weighted by their corresponding number of localizations as histograms (Figure 2A,B, Methods). These data can be well described by two populations;39 one corresponding to the probes trapped in the dense network (red outline in Figure 2A,B); and one corresponding to the probes showing obstructed self-diffusion in the coarse network (blue outline in Figure 2A,B). The state-switching behavior shown in Figure 1C bottom should be present in these histograms as a population with a convoluted mjd of the trapped and obstructed probes.29,42 However, this behavior is rare (<2% of all tracks longer than 20 frames likely show state-switching behavior; Methods), and is therefore not attempted to quantify. The mjd of each population was determined by fitting logarithmic Gaussian functions on the histogram (Figure 2A,B).

Figure 2.

Figure 2

Open in a new tab

Quantification of network obstruction experienced by fluorescent probes. (A,B) Histogram of mean jump distances, weighted on track length, found for freely diffusing 28 nm probes in water (top) and in 0.5–2.5% κ-carrageenan gels with 20 mM KCl and 100 mM NaCl (A) or 200 mM NaCl (B). The histograms are fitted with 2 Gaussian profiles shown in red (trapped population) and blue (obstructed population). Vertical black-dotted lines are added as a guide to the eye, shaded red/blue profiles show the standard deviation of the fit, derived from populations fitted to individual single-particle-tracking movies (each 12.5% of the complete data). (C) The mean trapped [red population in (A,B)] and obstructed [blue population in (A,B)] jump distance plotted vs the κ-carrageenan polymer content. Error bars represent the standard deviation of the fitted profile determined in (A,B). (D) Normalized diffusion coefficient corresponding to the mjd of the obstructed fraction as plotted in (C), assuming a 22 nm localization uncertainty. An obstruction model (dashed line, Methods, main text; dotted lines indicate 95% confidence interval of the fit) was fitted to the data and reveals a fiber diameter of 3.2 ± 0.3 nm.

The mjd plotted as a function of κ-carrageenan polymer and NaCl concentrations (Figure 2C) revealed that the population describing the trapped probes (red outline in Figure 2A,B) is unaffected by the polymer or NaCl concentration. The trapped probes had an average jump distance of ∼70 nm, which is higher than expected for fully immobile probes in which the measured jump distance is fully covered by the finite localization precision (22 nm; Methods). This trapped population had a self-diffusion coefficient of ∼1 × 10–13 m2/s, which is an inseparable convolution of probe self-diffusion and movement of the dense network region. We note that we observed a higher self-diffusion than shown previously for dendrimers trapped in κ-carrageenan gels observed via PFG NMR (10–14 m2/s).10 We attribute this to the coating of the dendrimers used in ref (10) with inert ethoxylate chains, which may entangle with polymer strands in the dense network.

The population describing the probes in the coarse network (blue outline in Figure 2A,B) shows a decreasing mjd with increasing κ-carrageenan polymer concentration, while it is mostly unaffected by the NaCl concentration. The mean diffusion coefficient of this obstructed population was ∼1 × 10–12 m2/s in 2.5% κ-carrageenan gels and increased to ∼5 × 10–12 m2/s in 0.5% κ-carrageenan gels. This relation between the probe self-diffusion coefficient and the polymer concentration can be accurately fitted by Johnson’s obstruction model10,26 (Figure 2D; Methods), indicating that the probe self-diffusion is obstructed by fibers of 3.2 ± 0.3 nm diameter in the coarse network. This finding agrees with earlier NMR studies in which a fiber diameter of ∼3 nm was found.10,27

Dense Networks Span 1 μm-Sized Regions

Next, we were interested in the spatial distribution of the network heterogeneity, which was not yet addressed in comparable experimental settings.25,39 To this end, the observed tracks were divided into three groups based on their respective mjd (Figure 3A). The first group (red) consists of tracks that have ≥95% probability of belonging to probes trapped in the dense regions. The second group (yellow) consists of tracks that have ≥95% probability of belonging to probes in the coarse network. The third group consists of tracks that cannot be attributed clearly to either the first or second group and where therefore discarded from further analysis.

Next, we created mobility maps (Methods) in which an image with a pixel size of 61 × 61 nm is pseudo-color coded based on the local probe behavior (Figure 3B). The map shows the existence of ∼1 μm sized regions characterized by the presence of immobile probe(s), while there are no nearby mobile probe(s). Probes are trapped in these regions (red), while probes present in the coarse network surrounding the dense regions (yellow) are unable to enter (Figure 3C), possibly resulting in black regions indicative of the absence of any probes. These dense network regions have similar length scales to those shown previously with EM.15

We confirmed the existence and size of these dense regions via rescan confocal microscopy (RCM).31 Here, the κ-carrageenan gels were infused with a higher concentration of fluorescent probes (0.03% w/v instead of 0.002%), causing fluorescence accumulation in the dense regions with respect to the coarse network.10 As a result, the dense regions with the trapped probes were very bright compared to the areas in which the obstructed diffusing particles cause a heterogeneous and noisy background fluorescence. The dense regions were identified by taking a temporal median average over multiple RCM images (Figure S2) and had a similar size to the ones determined via sptFM. Moreover, the size and distribution of the dense regions did not seem to depend on the tested κ-carrageenan polymer concentration range (Figure S2).

Two species of immobile particle regions could be distinguished in the single-particle-tracking derived mobility maps (Figure 3). First, there were regions that are characterized by the presence of immobilized probe(s) in the center and the absence of mobile probes in the direct periphery. We attributed these regions to stable dense network regions, as these mobility maps represent a temporal integration and are therefore averaged over 40 s of each recorded movie. Second, we observed immobilized probe(s) directly adjacent to and overlapped by mobile probes (i.e. orange regions, arrows in Figure 3B), which could not be attributed to stable dense network regions. We hypothesized that these occurrences are caused by temporal variations in the gel network, where the dense network regions themselves are mobile within the acquisition time (40 s).

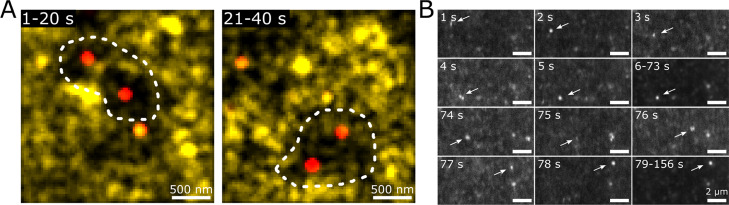
Therefore, we investigated the same mobility maps, but with a sliding temporal window. Similar dense network regions were observed, but some appear to migrate or disintegrate over time. We show an example in Figure 4A, where the same position in the gel is shown as a mobility map integrated over 0–20 s and 21–40 s of the same movie. During the first 20 s, a dense network region with a diameter of ∼1.5 μm is visible (dotted outline in Figure 4A). Later at the same position, however, only mobile particles are present. Meanwhile, a new dense region can be found ∼0.5 μm below the previous dense region. This finding suggests that dense network regions itself can migrate on the second to minute timescale even after full gelation. We note that by decreasing the temporal integration time, we are reducing the number of localizations used for creating the mobility maps. This effectively sets a lower limit to the time interval possible to be studied with mobility maps because of a decreasing signal-to-noise ratio.

Figure 4.

Figure 4

Open in a new tab

Movement of dense network regions in the coarse network. (A) Mobility maps of immobile (red) and mobile (yellow) probes in a 1% κ-carrageenan, 200 mM NaCl, and 20 mM KCl gel. The position of all particles found in the time range 1–20 s (left) or 21–40 s (right) are overlaid. The white-dotted outline represents the proposed outline of the dense region (B) RCM images show a migrating dense network region (indicated by arrows) in a 1% κ-carrageenan, 200 mM NaCl, and 20 mM KCl gel (also see Movie S.1). Images represent single RCMs, except for the 6–73 and 79–156 s images, where the median of the corresponding RCMs is shown.

We confirmed the migration of dense regions via rescan confocal microscopy operating at 1 Hz. While the presence of immobile regions is difficult to assess in single frames because of a low signal-to-noise ratio, assessment of multiple frames shows occasional and abrupt migration of dense network regions (Figure 4B, Movie S.1). This single migration event had a diffusion coefficient of ∼4 × 10–13 m2/s; this is faster than the trapped probe fraction determined earlier, but an order of magnitude slower than probes moving in the coarse network. This indicates that the migration is not caused by diffusion of the dense regions while normally embedded in the coarse network. Identical experimental conditions of solely mobile fluorescent probes revealed no observable immobile or migrating regions as these move too fast to be captured with a frame rate of 1 Hz (Movie S.2).

This dense network region migration is de facto different from the trapped fluorescent probe diffusion shown earlier. The trapped probe diffusion is a convolution of probes diffusing within single immobile dense network regions and possible movement of these dense network regions. Most observed dense network regions (Figure 3 and Movie S.1) are immobile on the micrometer scale, indicating that the trapped probe diffusion is governed by probe diffusion within dense network regions rather than dense network region migration. Contrarily, mobility maps and RCM movies show movement of the dense network regions themselves, as these methods are only sensitive to movement of the complete dense network regions rather than of single probes.

Migration of dense network regions can be explained by continuous slow reorganization of the bulk coarse network, whereupon at a certain critical reorganization level, the dense network is allowed to suddenly migrate within the bulk coarse network. Because of the rarity of these migrating dense network regions, along with poor signal to noise levels in both the temporally limited mobility maps and the RCM images, we did not attempt further quantification of the dense network region movement in this study.

Conclusions

In this study, we qualitatively and quantitatively visualized heterogeneity present in κ-carrageenan gels with sptFM. We observed bimodal self-diffusion of inert fluorescent probes embedded in the gels with occasional switching between the two states. By analyzing these states, we characterized κ-carrageenan gels as consisting of a coarse network with 3.2 ± 0.3 nm diameter fibers, in which ∼μm-sized dense network regions are present. These dense network regions showed rare and abrupt migration with a diffusion coefficient of ∼4 × 10–13 m2/s, suggesting continuous reorganization of the κ-carrageenan network even after full gelation. Quantitative information on the heterogeneity and reorganization kinetics is relevant for transport and release of low- and high-molecular-weight solutes in hydrogels, as well as for infusion and activity of digestive enzymes.

The existence and size of the dense network regions, as well as the size of the κ-carrageenan fibers, are in line with the results obtained from studies using either invasive or nonspatial techniques (nuclear magnetic resonance diffusometry or EM5,8,10). Our work indicates that the technique used here is reliable and has distinct advantages because of its noninvasive nature and spatial resolving power. Employment of sptFM, therefore, has potential to quantitatively and spatially assess the self-diffusion behavior of multiscale solutes in complex heterogeneous hydrogels.

Acknowledgments

K.J.A.M. is funded by a VLAG PhD-fellowship grant awarded to J.H.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.0c00393.

  • Histogram of probe jumping distances in nongelated κ-carrageenan polymer solutions; and probe infusion in varying κ-carrageenan concentration gels investigated with RCM; (PDF)

  • Movie of rescan confocal microscopy of probes in the 2% κ-carrageenan gel; and movie of rescan confocal microscopy of probes in water (ZIP)

The authors declare the following competing financial interest(s): J.v.D. is employed by a company that manufactures food products.

Supplementary Material

la0c00393_si_001.pdf (682.4KB, pdf)
la0c00393_si_002.zip (29.7MB, zip)

References

  1. Liu J.; Zhan X.; Wan J.; Wang Y.; Wang C. Review for Carrageenan-Based Pharmaceutical Biomaterials: Favourable Physical Features versus Adverse Biological Effects. Carbohydr. Polym. 2015, 121, 27–36. 10.1016/j.carbpol.2014.11.063. [DOI] [PubMed] [Google Scholar]
  2. Campo V. L.; Kawano D. F.; da Silva D. B.; Carvalho I. Carrageenans: Biological properties, chemical modifications and structural analysis—A review. Carbohydr. Polym. 2009, 77, 167–180. 10.1016/j.carbpol.2009.01.020. [DOI] [Google Scholar]
  3. Mihaila S. M.; Gaharwar A. K.; Reis R. L.; Marques A. P.; Gomes M. E.; Khademhosseini A. Photocrosslinkable κ-Carrageenan Hydrogels for Tissue Engineering Applications. Adv. Healthcare Mater. 2013, 2, 895–907. 10.1002/adhm.201200317. [DOI] [PubMed] [Google Scholar]
  4. Morris E. R.; Rees D. A.; Robinson G. Cation-Specific Aggregation of Carrageenan Helices: Domain Model of Polymer Gel Structure. J. Mol. Biol. 1980, 138, 349–362. 10.1016/0022-2836(80)90291-0. [DOI] [PubMed] [Google Scholar]
  5. Hermansson A.-M. Rheological and Microstructural Evidence for Transient States during Gelation of Kappa-Carrageenan in the Presence of Potassium. Carbohydr. Polym. 1989, 10, 163–181. 10.1016/0144-8617(89)90009-x. [DOI] [Google Scholar]
  6. Evageliou V. I.; Ryan P. M.; Morris E. R. Effect of Monovalent Cations on Calcium-Induced Assemblies of Kappa Carrageenan. Food Hydrocolloids 2019, 86, 141–145. 10.1016/j.foodhyd.2018.03.018. [DOI] [Google Scholar]
  7. Millane R. P.; Chandrasekaran R.; Arnott S.; Dea I. C. M. The Molecular Structure of Kappa-Carrageenan and Comparison with Iota-Carrageenan. Carbohydr. Res. 1988, 182, 1–17. 10.1016/0008-6215(88)84087-4. [DOI] [Google Scholar]
  8. Hermansson A.-M.; Eriksson E.; Jordansson E. Effects of Potassium, Sodium and Calcium on the Microstructure and Rheological Behaviour of Kappa-Carrageenan Gels. Carbohydr. Polym. 1991, 16, 297–320. 10.1016/0144-8617(91)90115-s. [DOI] [Google Scholar]
  9. Hu B.; Du L.; Matsukawa S. NMR Study on the Network Structure of a Mixed Gel of Kappa and Iota Carrageenans. Carbohydr. Polym. 2016, 150, 57–64. 10.1016/j.carbpol.2016.04.112. [DOI] [PubMed] [Google Scholar]
  10. de Kort D. W.; Schuster E.; Hoeben F. J. M.; Barnes R.; Emondts M.; Janssen H. M.; Lorén N.; Han S.; Van As H.; van Duynhoven J. P. M. Heterogeneity of Network Structures and Water Dynamics in κ-Carrageenan Gels Probed by Nanoparticle Diffusometry. Langmuir 2018, 34, 11110–11120. 10.1021/acs.langmuir.8b01052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. de Kort D. W.; van Duynhoven J. P. M.; Van As H.; Mariette F. Nanoparticle Diffusometry for Quantitative Assessment of Submicron Structure in Food Biopolymer Networks. Trends Food Sci. Technol. 2015, 42, 13–26. 10.1016/j.tifs.2014.11.003. [DOI] [Google Scholar]
  12. Singh H.; Ye A.; Ferrua M. J. Aspects of Food Structures in the Digestive Tract. Curr. Opin. Food Sci. 2015, 3, 85–93. 10.1016/j.cofs.2015.06.007. [DOI] [Google Scholar]
  13. Luo Q.; Boom R. M.; Janssen A. E. M. Digestion of Protein and Protein Gels in Simulated Gastric Environment. LWT–Food Sci. Technol. 2015, 63, 161–168. 10.1016/j.lwt.2015.03.087. [DOI] [Google Scholar]
  14. Stempfle B.; Große A.; Ferse B.; Arndt K.-F.; Wöll D. Anomalous Diffusion in Thermoresponsive Polymer-Clay Composite Hydrogels Probed by Wide-Field Fluorescence Microscopy. Langmuir 2014, 30, 14056–14061. 10.1021/la503571j. [DOI] [PubMed] [Google Scholar]
  15. Hagman J.; Lorén N.; Hermansson A.-M. Probe Diffusion in κ-Carrageenan Gels Determined by Fluorescence Recovery after Photobleaching. Food Hydrocolloids 2012, 29, 106–115. 10.1016/j.foodhyd.2012.02.010. [DOI] [Google Scholar]
  16. Lorén N.; Nydén M.; Hermansson A.-M. Determination of Local Diffusion Properties in Heterogeneous Biomaterials. Adv. Colloid Interface Sci. 2009, 150, 5–15. 10.1016/j.cis.2009.05.004. [DOI] [PubMed] [Google Scholar]
  17. Saalwächter K.; Seiffert S. Dynamics-Based Assessment of Nanoscopic Polymer-Network Mesh Structures and Their Defects. Soft Matter 2018, 14, 1976–1991. 10.1039/c7sm02444d. [DOI] [PubMed] [Google Scholar]
  18. Shen H.; Tauzin L. J.; Baiyasi R.; Wang W.; Moringo N.; Shuang B.; Landes C. F. Single Particle Tracking: From Theory to Biophysical Applications. Chem. Rev. 2017, 117, 7331–7376. 10.1021/acs.chemrev.6b00815. [DOI] [PubMed] [Google Scholar]
  19. Geonzon L. C.; Matsukawa S.. Phase Separated Structures of Mixed Carrageenan Gels Elucidated Using Particle Tracking. In NAC 2019; Murakami R.-I., Koinkar P. M., Fujii T., Kim T.-G., Abdullah H., Eds.; Springer Proceedings in Physics; Springer: Singapore, 2020; pp 41–48. [Google Scholar]
  20. Martens K. J. A.; Bader A. N.; Baas S.; Rieger B.; Hohlbein J. Phasor Based Single-Molecule Localization Microscopy in 3D (PSMLM-3D): An Algorithm for MHz Localization Rates Using Standard CPUs. J. Chem. Phys. 2018, 148, 123311. 10.1063/1.5005899. [DOI] [PubMed] [Google Scholar]
  21. Smith C. S.; Joseph N.; Rieger B.; Lidke K. A. Fast, Single-Molecule Localization That Achieves Theoretically Minimum Uncertainty. Nat. Methods 2010, 7, 373–375. 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Rocha J.; Corbitt J.; Yan T.; Richardson C.; Gahlmann A. Resolving Cytosolic Diffusive States in Bacteria by Single-Molecule Tracking. Biophys. J. 2019, 116, 1970–1983. 10.1016/j.bpj.2019.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Luo Q.; Sewalt E.; Borst J. W.; Westphal A. H.; Boom R. M.; Janssen A. E. M. Analysis and Modeling of Enhanced Green Fluorescent Protein Diffusivity in Whey Protein Gels. Food Res. Int. 2019, 120, 449–455. 10.1016/j.foodres.2018.10.087. [DOI] [PubMed] [Google Scholar]
  24. Geonzon L. C.; Bacabac R. G.; Matsukawa S. Network Structure and Gelation Mechanism of Kappa and Iota Carrageenan Elucidated by Multiple Particle Tracking. Food Hydrocolloids 2019, 92, 173–180. 10.1016/j.foodhyd.2019.01.062. [DOI] [Google Scholar]
  25. Aufderhorst-Roberts A.; Frith W. J.; Donald A. M. A Microrheological Study of Hydrogel Kinetics and Micro-Heterogeneity. Eur. Phys. J. E: Soft Matter Biol. Phys. 2014, 37, 44. 10.1140/epje/i2014-14044-y. [DOI] [PubMed] [Google Scholar]
  26. Johnson E. M.; Berk D. A.; Jain R. K.; Deen W. M. Hindered Diffusion in Agarose Gels: Test of Effective Medium Model. Biophys. J. 1996, 70, 1017–1023. 10.1016/s0006-3495(96)79645-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. de Kort D. W.; Van As H.; van Duynhoven J. P.. Estimating Microstructural Length Scales in κ-Carrageenan Hydrogels by PFG NMR Nanoprobe Diffusometry. Proceedings of the XIII International Conference on the Applications of Magnetic Resonance in Food Science; IM Publications Open, 2016; pp 73–76.
  28. Hübner C. G.; Renn A.; Renge I.; Wild U. P. Direct Observation of the Triplet Lifetime Quenching of Single Dye Molecules by Molecular Oxygen. J. Chem. Phys. 2001, 115, 9619–9622. 10.1063/1.1421382. [DOI] [Google Scholar]
  29. Martens K. J. A.; van Beljouw S. P. B.; van der Els S.; Vink J. N. A.; Baas S.; Vogelaar G. A.; Brouns S. J. J.; van Baarlen P.; Kleerebezem M.; Hohlbein J. Visualisation of DCas9 Target Search in Vivo Using an Open-Microscopy Framework. Nat. Commun. 2019, 10, 3552. 10.1038/s41467-019-11514-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Edelstein A. D.; Tsuchida M. A.; Amodaj N.; Pinkard H.; Vale R. D.; Stuurman N. Advanced Methods of Microscope Control Using μManager Software. J. Microbiol. Methods 2014, 1, 10. 10.14440/jbm.2014.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. De Luca G. M. R.; Breedijk R. M. P.; Brandt R. A. J.; Zeelenberg C. H. C.; de Jong B. E.; Timmermans W.; Azar L. N.; Hoebe R. A.; Stallinga S.; Manders E. M. Re-Scan Confocal Microscopy: Scanning Twice for Better Resolution. Biomed. Opt. Express 2013, 4, 2644–2656. 10.1364/boe.4.002644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ovesný M.; Křížek P.; Borkovec J.; Švindrych Z.; Hagen G. M. ThunderSTORM: A Comprehensive ImageJ Plug-in for PALM and STORM Data Analysis and Super-Resolution Imaging. Bioinformatics 2014, 30, 2389–2390. 10.1093/bioinformatics/btu202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Schindelin J.; Arganda-Carreras I.; Frise E.; Kaynig V.; Longair M.; Pietzsch T.; Preibisch S.; Rueden C.; Saalfeld S.; Schmid B. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Rueden C. T.; Schindelin J.; Hiner M. C.; DeZonia B. E.; Walter A. E.; Arena E. T.; Eliceiri K. W. ImageJ2: ImageJ for the next Generation of Scientific Image Data. BMC Bioinf. 2017, 18, 529. 10.1186/s12859-017-1934-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Isaacoff B. P.; Li Y.; Lee S. A.; Biteen J. S. SMALL-LABS: Measuring Single-Molecule Intensity and Position in Obscuring Backgrounds. Biophys. J. 2019, 116, 975–982. 10.1016/j.bpj.2019.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mortensen K. I.; Churchman L. S.; Spudich J. A.; Flyvbjerg H. Optimized Localization Analysis for Single-Molecule Tracking and Super-Resolution Microscopy. Nat. Methods 2010, 7, 377. 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Saha D.; Bhattacharya S. Hydrocolloids as Thickening and Gelling Agents in Food: A Critical Review. J. Food Sci. Technol 2010, 47, 587–597. 10.1007/s13197-010-0162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Bourouina N.; de Kort D. W.; Hoeben F. J. M.; Janssen H. M.; Van As H.; Hohlbein J.; van Duynhoven J. P. M.; Kleijn J. M. Complex Coacervate Core Micelles with Spectroscopic Labels for Diffusometric Probing of Biopolymer Networks. Langmuir 2015, 31, 12635–12643. 10.1021/acs.langmuir.5b03496. [DOI] [PubMed] [Google Scholar]
  39. Stempfle B.; Dill M.; Winterhalder M. J.; Müllen K.; Wöll D. Single Molecule Diffusion and Its Heterogeneity during the Bulk Radical Polymerization of Styrene and Methyl Methacrylate. Polym. Chem. 2012, 3, 2456–2463. 10.1039/c2py20268a. [DOI] [Google Scholar]
  40. Stracy M.; Kapanidis A. N. Single-Molecule and Super-Resolution Imaging of Transcription in Living Bacteria. Methods 2017, 120, 103–114. 10.1016/j.ymeth.2017.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. de Kort D. W.; Rombouts W. H.; Hoeben F. J. M.; Janssen H. M.; Van As H.; van Duynhoven J. P. M. Scaling Behavior of Dendritic Nanoparticle Mobility in Semidilute Polymer Solutions. Macromolecules 2015, 48, 7585–7591. 10.1021/acs.macromol.5b01530. [DOI] [Google Scholar]
  42. Vink J. N. A.; Martens K. J. A.; Vlot M.; McKenzie R. E.; Almendros C.; Estrada Bonilla B.; Brocken D. J. W.; Hohlbein J.; Brouns S. J. J. Direct Visualization of Native CRISPR Target Search in Live Bacteria Reveals Cascade DNA Surveillance Mechanism. Mol. Cell 2020, 77, 39–50.e10. 10.1016/j.molcel.2019.10.021. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la0c00393_si_001.pdf (682.4KB, pdf)
la0c00393_si_002.zip (29.7MB, zip)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES