Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 23;60(5):2605–2613. doi: 10.1021/acs.jcim.9b01176

Could Egg White Lysozyme be Solved by Single Particle Cryo-EM?

Y Zhang 1, R Tammaro 1, PJ Peters 1, RBG Ravelli 1,*
PMCID: PMC7254834  PMID: 32202786

Abstract

graphic file with name ci9b01176_0005.jpg

The combination of high-end cryogenic transmission electron microscopes (cryo-EM), direct electron detectors, and advanced image algorithms allows researchers to obtain the 3D structures of much smaller macromolecules than years ago. However, there are still major challenges for the single-particle cryo-EM method to achieve routine structure determinations for macromolecules much smaller than 100 kDa, which are the majority of all plant and animal proteins. These challenges include sample characteristics such as sample heterogeneity, beam damage, ice layer thickness, stability, and quality, as well as hardware limitations such as detector performance, beam, and phase plate quality. Here, single particle data sets were simulated for samples that were ideal in terms of homogeneity, distribution, and stability, but with realistic parameters for ice layer, dose, detector performance, and beam characteristics. Reference data were calculated for human apo-ferritin using identical parameters reported for an experimental data set downloaded from EMPIAR. Processing of the simulated data set resulted in a value of 1.86 Å from 20 214 particles, similar to a 2 Å density map obtained from 29 224 particles selected from real micrographs. Simulated data sets were then generated for a 14 kDa protein, hen egg white lysozyme (HEWL), with and without an ideal phase plate (PP). Whereas we could not obtain a high-resolution 3D reconstruction of HEWL for the data set without PP, the one with PP resulted in a 2.78 Å resolution density map from 225 751 particles. Our simulator and simulations could help in pushing the size limits of cryo-EM.

Introduction

Determining 3D structures from sub-100-kDa protein molecules has been a long-standing goal of the cryo-EM community, for which the first successes have been reported.1−3 Analysis of the size distribution of proteins in plants, animals, and fungal and microbial species4 shows that 90% of the plant and animal proteins are smaller than 100 kDa, and more than 50% of the proteins are smaller than 50 kDa. However, resolving a small (monomeric) protein in the electron microscope is difficult for multiple reasons. Electrons scatter much more compared to X-rays and neutrons,5 resulting in high amounts of energy being deposited in the sample for a relative small number of electrons per Å2 hitting the sample. Globular proteins of <50 kDa are smaller than 5 nm in size, whose signal can be easily swamped under thicker ice layers and ice imperfections. Protein molecules are likely to overlap when present in the bulk of the ice layer and can become (partly) damaged and preferentially oriented when attaching to the air–water interface.6 Sample heterogeneity, imperfect detectors, imperfect phase plates and optics, stage drift, and beam-induced motions all contribute to blurring of averages, which makes it challenging to achieve near-atomic-resolution structures of small macromolecules.7,8

The development of direct electron detectors with more stable microscopes and better data processing software has resulted in an increasing number of published high-resolution cryo-EM structures.9−11 Currently, the highest resolution of a single-particle cryo-EM structure is 1.54 Å for apo-ferritin.12 To date, the smallest protein solved by single-particle cryo-EM is 43 kDa.1 Structural determinations of proteins under the 38-kDa theoretical size limit have still not been resolved by single-particle analysis.1,5 The smaller a particle, the less scattering information that particle can provide. It is difficult to determine the five unknowns (shifts x and y and Euler angles α, β, and γ), which limits the alignment of the noisy protein images.5 The contrast transfer function (CTF), which is inherent with the mechanism of image formation in a microscope, oscillates the contrast of the particles as a function of resolution. It needs to be described accurately in order to be accounted for, which becomes more difficult at higher resolutions and at higher defoci. In conventional electron microscopy, contrast is enhanced by introducing a defocus: smaller particles are normally observed at a higher defocus. Spatial and temporal incoherence of the electron source dampens the high-resolution signal under strong underfocus conditions, which impedes reconstruction schemes. Researchers are trying different ways to overcome these limitations, such as high protein concentration, minimal ice thickness,1 and the use of scaffolds.3 A particularly promising route for small proteins seems to be the use of a phase plate (PP). An ideal PP would offer a π/2 phase shift without introducing any post-sample scattering. The Volta Phase Plate13 has made phase plates accessible to a wide community; however, it cannot offer a constant phase shift and generates undesired postsample scattering. Ongoing research aims to develop next-generation phase plates, such as a laser PP14,15 or electrostatic PP.16 Lower energy electron microscopy was proposed by Henderson et al.,17,18 as lower energy gives more information and has a somewhat better elastic/inelastic scattering ratio. Due to the faster damping of CTF at high spatial frequency at low energy, larger data sets and careful computational analysis would be required to recover high-resolution information.

Simulations could help identify and characterize the culprits preventing the 3D structural resolution of small proteins by single-particle cryo-EM. Furthermore, simulations facilitate the assessment of the new image processing methods and data collection techniques19 and could be used to evaluate the potential of new instrumentation improvements. Here, we adapted a TEM simulator developed by Vulović et al.,20 which is based on physical principles and considers the interaction between solvent, ions, and molecules. The simulator considers electron dose, which is important for the TEM of biological samples because biomolecular structures can be altered by radiation damage inflicted by higher electron doses.21,22 The radiation damage itself can be modeled by introducing a motion-blurring factor to all of the atoms.20 Other characteristics, such as ice layer thickness, beam parameters, CTF, and detector performance, are also accounted for in the simulator. Simulations were validated by comparing the simulated micrographs with real experimental data.19,20

First, we started with a subset of an experimental data set of mouse apo-ferritin (24-mer, 480 kDa) downloaded from EMPIAR-10216.23 Based on 29 224 particles extracted from this data set, we were able to obtain a 2 Å density map, faithful to the original experimental 1.64 Å map obtained with the full data set.23 We then simulated a data set based on the known structure of apo-ferritin (PDB: 2fha) with the exact same parameters as the ones used for the experimental data set and compared the two. We show that our simulations match the existing data. Data processing of the simulated data set resulted in a 1.86 Å density map obtained from 18 062 extracted particles using the program Relion,24 which is in good agreement with a 2 Å density map obtained from the experimental data.

Next, we examined how the simulations of a protein below the 38 kDa theoretical size limit (which still remains to be resolved by single-particle analysis) would look like. We selected the 14 kDa hen egg white lysozyme (HEWL, PDB: 1dpx), a protein standard among X-ray crystallographers. We simulated data sets with and without the ideal phase plate and tried to solve the HEWL structure from each data set. Whereas we could obtain a near-atomic resolution structure from the data set with ideal PP, we were unable to do so for the data set without PP.

Theory

Below, a summary is given of the theoretical framework used in this work. Most formulas have been described previously: the theory of image formation;20 whether one could align the particles;5 and how many particles are needed to achieve a certain resolution.25 We recapitulate certain formulas and describe some modifications.

Image Formation

The simulation of cryo-EM images of biological samples can be separated into four steps, (i) building of the specimen’s interaction potential, (ii) electron propagation through the specimen, (iii) influence of the optics of the electron microscope, and (iv) digital direct-electron detector response.20 Here, we only briefly introduce the theory.

(i) Interaction Potential

The interaction potential of the specimen can be calculated using the isolated atom superposition approximation (IASA). For biological specimens in cryo-EM, particles are always embedded in ice. The IASA model takes into account the solvent, ions, and molecular interactions. The total interaction potential of the specimen is described as the sum of inelastic scattering potential (Vab), which contributes to amplitude contrast, and elastic scattering potential Vint(r), which contributes to phase contrast.

graphic file with name ci9b01176_m001.jpg 1

where r = (x, y, z) is the position of the electron wave. The combination of Vatom(r) (“atom” contributions) and Vbond(r) (“bonds” contributions) gives the elastic interaction potential Vint(r) of the specimen. The “bond” contributions mainly come from the influence of solvent, ions, and molecular interactions. Vab is the inelastic part due to the interaction between the incident electrons with the free electrons in the specimen (ΔE ∼ 20 eV) and atom cores (ΔE > 100 eV). It was calculated as the imaginary part of the model.

The solvent interaction potential is calculated from known density of water molecule.20 The amorphousness of the solvent is modeled as a constant potential. Radiation damage was accounted for by applying a motion factor σM, which blurs the interaction potential of the atoms and bonds isotropically:20

graphic file with name ci9b01176_m002.jpg 2

where Ṽ(q) and Ṽint(q) are the Fourier transform of V(r) and Vint(r), respectively. The relation between the motion blur and B factor is26,27

graphic file with name ci9b01176_m003.jpg 3

(ii) Electron Propagation

A multislice algorithm was used to model the interaction between electrons and the specimen.28 Each slice was 2-nm-thick, which is a valid size for weak phase object approximation (WPOA), as it has multiple scattering events less than 5% at 300 keV.29 An incident plane wave Ψ0(x,y) = 1 was iteratively propagated though N slices with slice thickness Δz, such that an exit wave Ψexit(x,y) leaving the sample was calculated.

(iii) Optics of TEM

After the wave propagated through the specimen and before passing by the lower piece objective lens, we still have the exit wave Ψexit(x,y) in real space. To include the optics of a TEM in the simulation, we multiplied the CTF to the Fourier transformed exit wave function to simulate contrast of the image as a function of spatial frequency (k). Aberrations due to defocus and spherical aberration are included in CTF. The temporal coherence and the spatial coherence of the electron source which dampen the CTF are calculated in envelope functions which was corrected from ref (20) following:30

graphic file with name ci9b01176_m004.jpg 4
graphic file with name ci9b01176_m005.jpg 5

where the c and s represent the chromatic coherence and the spatial coherence of the electron source, respectively. The electron wavelength, calculated at relativistic speed, is given as λ.The spherical aberration is represented by Cs. The defocus value is Δf. The defocus spread δ is calculated as30

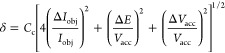graphic file with name ci9b01176_m006.jpg 6

where Cc is the chromatic aberration. The terms ΔIobj and ΔVacc indicate the instability of the objective lens current and the accelerating voltage. The term ΔE/Vacc is the intrinsic energy spread in the electron gun.

The PP was incorporated by introducing a phase shift eiΔϕ to the electron wave in reciprocal space and leaves the central transmitted beam unchanged. The electron intensity on the image plane I0(x,y) is given by

graphic file with name ci9b01176_m007.jpg 7

(iv) Detector Response

Contributions to the detector response in our simulation include conversion factor, modulation transfer function (MTF), and detective quantum efficiency (DQE). The final detected electron intensity, I(x, y), on the detector was calculated according to20

graphic file with name ci9b01176_m008.jpg 8

where Irn is the readout current and Idc is the dark current. CF is the conversion factor of the detector, in [ADU/e–]. Poiss describes the Poisson distribution and weights the probability of arrival of an electron for a given dose and expected intensity.20 NTF is the noise transfer function.20

What Is the Size Limitation of Particles That Can Be Aligned?

According to the theoretical calculation by Henderson,5 the protein orientation and position can be determined when Xsig > x. Here, Xsig is the signal-to-noise ratio of the image and describes whether the molecule can be detected or not. x is the multiple of sigma expected within the entire volume of five parameter space (shifts x and y and Euler angles α, β, and γ) to be examined:5

graphic file with name ci9b01176_m009.jpg 9
graphic file with name ci9b01176_m010.jpg 10

where Npix = D2/(d/2)2 is the number of pixels that corresponds to the area of one box containing the particle. The diameter of the particle is represented by D, and the resolution is expressed by d, both measured in Å.

The expression of x is given by the inverse complementary error function, which represents the standard deviation in Gaussian distribution. In other words, it is the lowest signal-to-noise ratio required for particle alignment. The cross-correlation coefficient for translation (shifts x and y) and rotation (Euler angles α, β, and γ) are (2D/0.2d)2 and (2πD/0.2d)3, respectively. The value of x will not change much. The key parameter that determines whether a single particle can be aligned is Xsig. The derivation of the equation according to Henderson5 can be found in the Supporting Information. Here, the expression of Xsig is given by

graphic file with name ci9b01176_m011.jpg 11

For a given electron energy, electron dose, diameter of the particles, and Nyquist frequency, a smaller number of d results in a larger value of Xsig. Therefore, the largest Xsig happens at the Nyquist frequency. Xsig at Nyquist is

graphic file with name ci9b01176_m012.jpg 12

This means for a microscope at a fixed energy and electron dose, the threshold of detecting a molecule is fixed. The value of Ne used in the calculations of Henderson5 was 5 e–/Å2, with which he arrived at a 38 kDa theoretical size limit. Assuming a spherical protein with a density of 0.8 Da/Å3, a 38 kDa protein has a diameter of 45 Å. With the incoming 5 e–/Å2 electron fluence, this protein is not able to be aligned as Xsig equals 6.5, which is smaller than the value of x which is 8.3. Henderson chose the value of Ne based on radiation damage studies using electron diffraction. Recently, it was shown that the best micro-electron diffraction data were obtained from lysozyme crystals at a fluence of 2.6 e–/Å2.31 However, in most modern SPA cryo-EM studies, the fluence is much higher than 5 e–/Å2. Dose-correction schemes account for the loss of signal at higher spatial frequencies as a function of dose. The first frames typically contain less high-resolution information, as one would expect based on the relatively pristine state of the biomolecule.7 This is probably due to beam-induced motions, whereas the latter frames within a movie contain less high-resolution features due to radiation damage to the particle of interest. For the low frequencies, all the frames contribute more or less the same. Overall, for imaging, an electron fluence greater than 5 e–/Å2 may still contribute to the signal up to Nyquist and surely helps with determining particle orientation and translation.25 In eq 12, when we use 50 e–/Å2 for Ne:

graphic file with name ci9b01176_m013.jpg 13

If we consider HEWL with a diameter of 32 Å, then Xsig equals 12.3. Using a pixel size of 0.5 Å/pixel, d at Nyquist frequency is 1 Å. So, x equals 8 and Xsig > x. This means that in theory we should be able to align the 14 kDa particles with a perfect detector and perfect image contrast. If we consider the contrast C of the micrographs,5 which varies from 0 to 1, the signal in eq 9 needs to be multiplied by C. Then, the question arises: can we still align particles as small as 14 kDa with current TEMs and detectors? Or would one need a(n ideal) phase plate in order to increase contrast C and obtain a meaningful alignment?

Number of Particles Needed to Reach a Certain Resolution

The number of particles required to build a density map with a certain resolution is given by Rosenthal and Henderson:25

graphic file with name ci9b01176_m014.jpg 14

where Ninproj is the number of images needed per projection. The term (πD)/d is given by the Crowther criterion,32 which describes the minimum number of unique projections needed for reconstructing a particle of diameter D to a resolution of d. Nasym is the number of asymmetric units that a molecule has. B is the temperature factor that describes the effect of contrast loss. Using an expression for Ninproj, we get (Supporting Information and ref (25)):

graphic file with name ci9b01176_m015.jpg 15

In order to determine what resolution one might expect given a certain number of particles, we take the natural logarithm of both sides in eq 15 and rewrite it:

graphic file with name ci9b01176_m016.jpg 16

In eq 16, ln(d) ≪ ln(Npart), therefore, we ignore ln(d). Thus, the final expression is

graphic file with name ci9b01176_m017.jpg 17

Methods and Results

Image Formation

Interaction potentials of the specimen were built using IASA. Nonoverlapping particles were randomly oriented and positioned to simulate micrographs of 4096 × 4096 pixels. A thin ice layer of 20 nm was used, and the particles were randomly positioned in all three dimensions within the ice layer. The electron propagation through the specimen was simulated via the multislice method. We simulated a 300 kV FEG TEM with a Falcon III33 detector used in counting mode. For the spherical and chromatic aberrations, a value of 2.7 mm was used and 4.7 mm for the focal distance. These parameters are typical for a Thermo Fisher Krios microscope. The size of the illumination aperture was 0.03 mrad, and the diameter of the objective aperture was 100 μm. We did not include objective astigmatism in our simulations. We used the DQE and MTF of Falcon III electron counting (EC) mode at 300 keV as given by Kuijper et al.33 We simulated micrographs of human H-chain ferritin (PDB: 2fha)34 and HEWL (PDB: 1dpx).35 For apo-ferritin, 166 micrographs (∼20 000 particles) were simulated with an underfocus in the range of 0.2 to 1.3 μm. For HEWL, 501 micrographs with PP and 866 micrographs without PP were simulated, each with 800 to 1100 particles per micrograph. A fluence of 50 e–/Å2 was used for each of the data sets. Power spectra of the micrographs were calculated with Gctf,36 and CTFs were fitted to these power spectra in the 30–2 Å resolution range. Data processing was done using Relion.9 The motion blur factor σM was 0.5 to approximate the beam induced movement of the specimen, which corresponds to a B factor of 19.7 Å2 according to eq 3. The quality of the simulated micrographs was compared to experimental ones from EMPIAR37 (Figure 1).

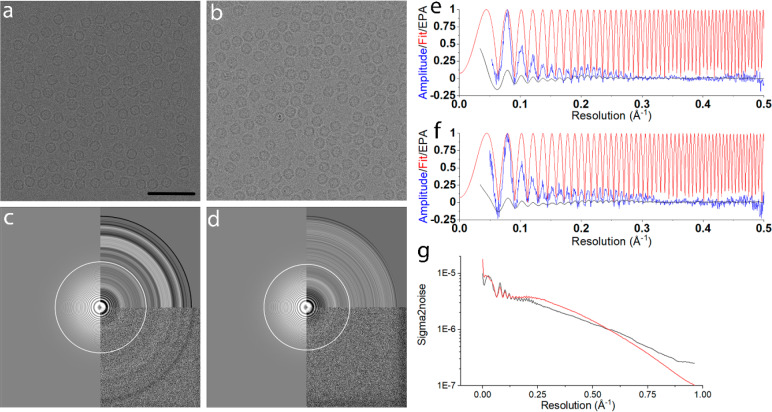
Figure 1.

Figure 1

Open in a new tab

(a) Simulated micrographs for apo-ferritin at 1220 nm underfocus (pixel size 0.5198 Å). (b) Experimental micrographs for apo-ferritin at 1210 nm underfocus (pixel size 0.5198 Å). (c) The Fourier transform of the micrograph shown in a, with equal-phase averaged and CTF fitted by Gctf. (d) The power spectrum of the real micrograph shown in b, CTF fitted by Gctf. (e) Background-subtracted amplitude spectrum (blue) and the fit (red) from the simulated micrograph, the same as c. (f) Background-subtracted amplitude spectrum (blue) and the fit (red) from the experimental micrograph, as in d. (g) Sigma to noise spectra of the particles picked from the simulated micrograph shown in a (black) versus those picked from the experimental micrograph b (red). Scale bar in a represents 50 nm and applies to b.

Data Processing

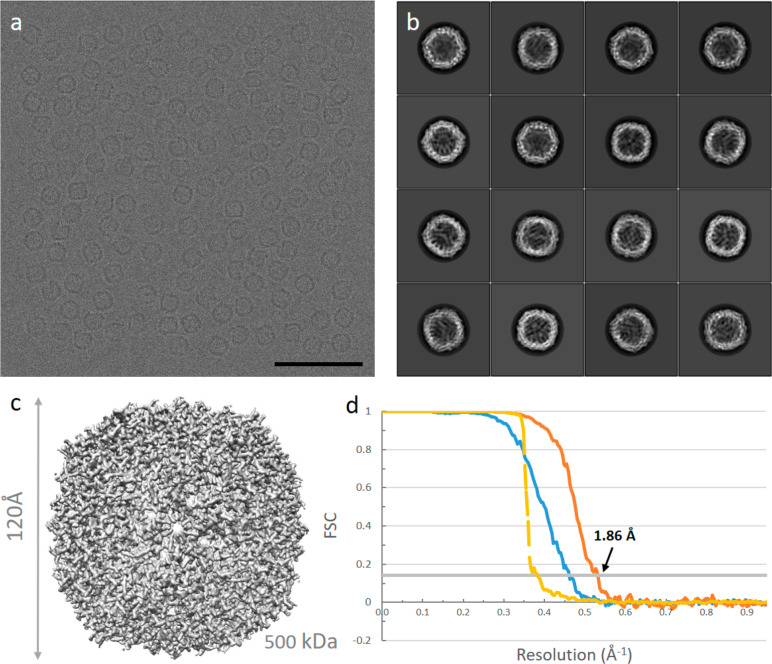
For the human apo-ferritin data set, 20 214 particles were picked from 166 micrographs (Figure 2a) with a pixel size of 0.5198 Å/pixel. Particles were extracted with a box size of 512 × 512 pixels. For 2D classification, we calculated 100 classes using a regularization parameter T of 2 (Figure 2b). As the data were simulated homogeneously from one model (PDB: 2fha), only very few picked particles and 2D classes had to be discarded. A total of 18 062 particles were selected for the initial 3D model building, and 3D classification could be skipped. In 3D refinement, the 3D initial model was low-pass filtered to 50 Å and used as the reference map, with octahedral (O) symmetry, which resulted in a 2.14 Å resolution map. The map was subsequently sharpened, and CTF refinement was performed.24 Finally, Refine3D was run again; the map was postprocessed and sharpened (B factor of −50 Å2), yielding a final 1.86 Å resolution map (Figure 2c).

Figure 2.

Figure 2

Open in a new tab

Single-particle analysis of a simulated human apo-ferritin data set. (a) A typical micrograph of apo-ferritin; the scale bar is 50 nm. (b) 2D class averages. (c) 3D reconstruction from 18 062 particles at 1.86 Å resolution. (d) Gold-standard Fourier shell correlation (FSC) before (blue line) and after (orange line) masking, and the phase randomized FSC (yellow line).

To compare our simulated micrographs with experimental micrographs, we downloaded 448 experimental micrographs from EMPIAR-1021637 (Figure S1a). The pixel size was 0.5198 Å/pixel. The reported defocus was in the range of 0.2 μm to 1.3 μm. From these 448 micrographs, 49 962 particles were picked, and extracted with a box size of 512 × 512 pixels. All the Relion processing procedures and parameters used for experimental data were the same as those for simulated data, except for an additional 3D classification step performed for the experimental data. In 3D classification, five classes were calculated using a regularization parameter T equals to 4. After 3D refinement and postprocessing, we obtained a 2 Å resolution map from 29 224 selected particles (Figure S1c).

For HEWL, we simulated micrographs both with and without PP. The PP used in simulation was an “ideal” PP, which brought no postsample scattering, introduced a fixed π/2 phase shift to the scattered electrons from the specimen, and had infinitely low cut-on frequency. The pixel size was 0.5 Å/pixel for both lysozyme data sets. Without PP, data were simulated with a 2.5 to 4 μm underfocus (Figure 3a). From 866 micrographs, 525 053 particles were picked and subjected to 2D classification with T equals to 2, using the “ignore CTFs until the first peak” option (Figure 3b). Hereafter, 484 137 particles were selected for 3D refinement using a reference map from the crystal structure (PDB: 1dpx), low-pass filtered to 20 Å, no symmetry. In our hands, building an initial 3D model de novo, as guided by Relion, failed. 3D refinement starting with a 15 Å low-pass filtered map from the known answer did not give any new information either, as it resulted in a 16 Å map (Figure 3c).

Figure 3.

Figure 3

Open in a new tab

Single-particle analysis of a simulated HEWL data set without PP. (a) A micrograph of HEWL at 4.0 μm underfocus; the scale bar is 50 nm. (b) 2D class averages. (c) The 3D reconstruction of HEWL without PP.

For HEWL with PP, the defocus ranged from 0.3 to 0.8 μm underfocus (Figure 4a). From 501 micrographs, 290 316 particles were picked and subjected to 2D classification with T equals to 2 with a mask diameter of 50 Å (Figure 4b). For this data, it was not needed to use the ‘ignore CTFs until the first peak‘ option in 2D classification. Then 225 751 particles were extracted in a 256 × 256 pixel box and used to build an initial 3D model. This initial model was used as a reference map in 3D refinement with a 15 Å low-pass filter, with selecting “ignored CTFs until the first peak” and no symmetry. The half maps of Refine3D were combined and sharpened using postprocessing, applying a B factor of −116 Å2, which resulted in a resolution map of 2.78 Å resolution based on gold-standard FSC25,38 (Figure 4c,d).

Figure 4.

Figure 4

Open in a new tab

Single-particle analysis of a simulated HEWL data set with PP. (a) A typical micrograph of HEWL with PP; the scale bar is 50 nm. (b) 2D class averages. (c) The 3D reconstruction of HEWL at 2.78 Å resolution from 225 751 particles. (d) Gold-standard Fourier shell correlation (FSC) before (blue line) and after (orange line) masking, and the phase randomized FSC (yellow line).

Discussion and Conclusion

We simulated single-particle micrographs from which high-resolution 3D density maps could be reconstructed. The simulated micrographs of apo-ferritin were similar to experimental micrographs recorded at a similar defocus, both in terms of intensity, noise, power spectra, background-subtracted radial average, CTF fit, and sigma-to-noise spectra of extracted particles (Figure 1). The B factor estimated by Gctf for the simulated micrographs equals ∼40 Å2, slightly greater than what was obtained from the experimental micrographs (∼30 Å2). The experimental data showed a somewhat stronger signal compared to the simulated one up to 0.5 Å–1 (Figure 1e vs f, Figure 1g), whereas the simulated data showed a slightly stronger signal beyond the resolution at which a 3D structure was obtained. These differences might be due to differences in ice as well as the specific detector as we used generic models in our simulations.

We obtained a 1.86 Å resolution density map for human apo-ferritin using 166 simulated micrographs with 18 062 particles. Circa 10% of the particles were discarded as we still found “imperfect particles” in the micrographs. The particles were placed at random positions within each micrograph taking a minimum interparticle distance into account. Retrospectively, this minimum distance was a bit too small. The simulator relocates the interaction potential of one particle when placing a second one too nearby, resulting in “damaged particles” in the simulated micrographs.

The B factor we calculated using eq 17 from the Guinier plots (Figure S3) was smaller for the simulated data (43 Å2) compared to the experimental data set (54 Å2). This could relate to the absence of large conformational differences between different particles. With 4260 simulated particles, we achieved a 2.04 Å resolution map, just slightly better than the 2.18 Å map from 4405 experimental selected particles (Figure S3). The identical conformation of simulated particles improved the determination of the five parameters (shifts x and y and Euler angles α, β, γ) and particle alignment during 3D refinement in Relion. The estimated accuracy of angles and offsets for the simulated data set with 4260 particles were 0.13° and 0.2 pixels, respectively, whereas they were 0.32° and 0.39 pixels for the experimental data with 4405 particles.

For HEWL, we observed clear differences between the data sets with and without PP after 2D classification. Without a phase plate, all particles collapsed in one 2D class unless we used the “Ignore CTFs to first peak” option in Relion. However, even then, most 2D classes were extremely blurred, reflecting the fact that the low spatial frequency information, which plays a dominant role in particle alignment, was extremely weak in these data. We were unable to obtain a good initial 3D starting map from the data itself. Starting the 3D refinement with a low-pass filtered map generated from the crystal structure 1dpx, we could not obtain a higher resolution map (Figure 3c). For the simulated HEWL data set in the presence of a PP, more than half of the 2D class averages (T = 2) converged into good 2D classes revealing clear details (Figure 4b), with high rotational and translational accuracy and high resolution (∼3 Å). Postprocessing revealed a B factor of −117 Å2, almost double the B factor used for apo-ferritin (−50 Å2). The higher B factor for HEWL compared to ferritin is probably due to inaccuracies in orientation and translation alignments which are 2.085° and 0.721 pixels in 3D refinement.

The distinct differences between data sets with and without an ideal PP would argue for the necessity of a PP for particle alignment in order to solve the structures of small proteins. Without PP, a density map of HEWL was not obtainable, at least in our hands. Simulations with and without PP of other small proteins, in particular those smaller than 50 kDa, would provide additional insight into the value of phase plates for single-particle reconstructions. An ideal phase plate would enhance the contrast of the low spatial frequency signal while maximizing the signal at high resolution as the envelope function will have less damping at lower defocus. The contrast in the images will strongly affect the quality of the alignment of particles and the number of particles that are needed to obtain a high-resolution 3D structure. If we take into account the contrast factor, the signal in eq 9 is degraded by a factor of C. Then, the total number of particles required to achieve a certain resolution will increase by a factor of 1/C2. Having an ideal phase plate would therefore decrease the number of particles needed to reach a certain resolution. The PP should be able to give a stable phase shift, preferably π/2, and introduce no or a small amount of postsample scattering. It has been shown that the variable phase shift provided by the Volta Phase Plate can be computationally accounted for; however, its postsample scattering will unavoidably dampen all signals, which will be detrimental, in particular at higher resolution. A laser PP or electrostatic PP holds the promise of constant phase shift with minimal postsample scattering.

While our simulation studies gave promising results, we note several caveats. A number of crucial factors in SPA cryo-EM were not accounted for in our simulations. We simulated particles with minimal overlap in a thin ice layer. Such layers have been described in the literature;1 however, these were most likely obtained by proteins attaching to an air–water interface,6 at which proteins can partly unfold, contributing to (an increase of) sample heterogeneity. In the simulations presented here, sample heterogeneity was not included. One could, for example, introduce heterogeneity within the biological assembly of ferritin, by having 24 slightly different copies per oligomer. Furthermore, each oligomer itself could be slightly different from the other ones. This would increase the estimated accuracy of angles and offsets reported during the refinements as well as the B-factor obtained from the Guinier plot. Another caveat is the way we modeled radiation damage, for which we employed a motion-blur factor. More advanced radiation damage models could certainly be envisioned, as well as higher motion-blur factors, than the one we used. An ideal phase plate does not exist yet: it should also be possible to integrate an existing phase plate in the simulator. We deposited all our data sets in EMPIAR and distribute the source code of the simulator via GitHub39 and hope that some of these caveats will be tackled in later versions.

Nevertheless, our simulations demonstrate that it should be possible to solve sub-50 kDa proteins with current image processing algorithms. We expect that with the development of better detectors, improved phase plates, and optimized sample preparation,40 one should be able to study a much larger percentage of all the known plant and animal proteins by SPA cryo-EM compared to what is possible nowadays.

Our simulations and simulation software can also be used for other purposes. First, it could help novel cryo-EM users in data processing training with the unique feature that all parameters are known a priori. It could help image processing developers to test novel algorithms, e.g., for improving initial 3D model algorithms for fewer numbers of particles. One could simulate focal pairs, to check procedures for combining high-resolution particle information collected close to focus with low-resolution information collected afterward at larger defocus. The potential benefits of better detectors, better beam source characteristics, and the use of different electron beam energies could all be explored computationally. Combined, it could help in pushing forward the already growing field of cryo-EM.

Acknowledgments

The authors acknowledge funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No. 766970 Q-SORT (H2020-FETOPEN-1-2016-2017). We like to thank Hang Nguyen for critical reading of the manuscript.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.9b01176.

  • Equations supporting the explanation in theory and extra figures and diagrams to support the validation of simulated data (PDF)

The authors declare no competing financial interest.

Supplementary Material

ci9b01176_si_001.pdf (523.8KB, pdf)

References

  1. Herzik M. A.; Wu M.; Lander G. C.. High-Resolution Structure Determination of Sub-100 KDa Complexes Using Conventional Cryo-EM. Nat. Commun. 2019, 10, 10.1038/s41467-019-08991-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Fan X.; Wang J.; Zhang X.; Yang Z.; Zhang J.-C.; Zhao L.; Peng H.-L.; Lei J.; Wang H.-W. Single Particle Cryo-EM Reconstruction of 52 KDa Streptavidin at 3.2 Angstrom Resolution. Nat. Commun. 2019, 10, 2386. 10.1038/s41467-019-10368-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Liu Y.; Huynh D. T.; Yeates T. O. A 3.8 Å Resolution Cryo-EM Structure of a Small Protein Bound to an Imaging Scaffold. Nat. Commun. 2019, 10, 1–7. 10.1038/s41467-019-09836-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Tiessen A.; Pérez-Rodríguez P.; Delaye-Arredondo L.. Mathematical Modeling and Comparison of Protein Size Distribution in Different Plant, Animal, Fungal and Microbial Species Reveals a Negative Correlation between Protein Size and Protein Number, Thus Providing Insight into the Evolution of Proteomes. BMC Res. Notes 2012, 5, 10.1186/1756-0500-5-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Henderson R. The Potential and Limitations of Neutrons, Electrons and X-Rays for Atomic Resolution Microscopy of Unstained Biological Molecules. Q. Rev. Biophys. 1995, 28, 171–193. 10.1017/S003358350000305X. [DOI] [PubMed] [Google Scholar]
  6. D’Imprima E.; Floris D.; Joppe M.; Sánchez R.; Grininger M.; Kühlbrandt W.. Protein Denaturation at the Air-Water Interface and How to Prevent It. eLife 2019, 8, 10.7554/eLife.42747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Scheres S. H. w. Beam-Induced Motion Correction for Sub-Megadalton Cryo-EM Particles. eLife 2014, 3, e03665 10.7554/eLife.03665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Li X.; Mooney P.; Zheng S.; Booth C. R.; Braunfeld M. B.; Gubbens S.; Agard D. A.; Cheng Y. Electron Counting and Beam-Induced Motion Correction Enable near-Atomic-Resolution Single-Particle Cryo-EM. Nat. Methods 2013, 10, 584–590. 10.1038/nmeth.2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zivanov J.; Nakane T.; Forsberg B. O.; Kimanius D.; Hagen W. J. H.; Lindahl E.; Scheres S. H. W.. New Tools for Automated High-Resolution Cryo-EM Structure Determination in RELION-3. eLife 2018, 7, 10.7554/eLife.42166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Tan Y. Z.; Aiyer S.; Mietzsch M.; Hull J. A.; McKenna R.; Grieger J.; Samulski R. J.; Baker T. S.; Agbandje-McKenna M.; Lyumkis D.. Sub-2 Å Ewald Curvature Corrected Structure of an AAV2 Capsid Variant. Nat. Commun. 2018, 9, 10.1038/s41467-018-06076-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bartesaghi A.; Aguerrebere C.; Falconieri V.; Banerjee S.; Earl L. A.; Zhu X.; Grigorieff N.; Milne J. L. S.; Sapiro G.; Wu X.; Subramaniam S. Atomic Resolution Cryo-EM Structure of β-Galactosidase. Structure 2018, 26, 848–856. 10.1016/j.str.2018.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hamaguchi T.; Maki-Yonekura S.; Naitow H.; Matsuura Y.; Ishikawa T.; Yonekura K. A New Cryo-EM System for Single Particle Analysis. J. Struct. Biol. 2019, 207, 40–48. 10.1016/j.jsb.2019.04.011. [DOI] [PubMed] [Google Scholar]
  13. Danev R.; Buijsse B.; Khoshouei M.; Plitzko J. M.; Baumeister W. Volta Potential Phase Plate for In-Focus Phase Contrast Transmission Electron Microscopy. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 15635–15640. 10.1073/pnas.1418377111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Schwartz O.; Axelrod J. J.; Campbell S. L.; Turnbaugh C.; Glaeser R. M.; Müller H. Laser Phase Plate for Transmission Electron Microscopy. Nat. Methods 2019, 16, 1016–1020. 10.1038/s41592-019-0552-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Müller H.; Jin J.; Danev R.; Spence J.; Padmore H.; Glaeser R. M. Design of an Electron Microscope Phase Plate Using a Focused Continuous-Wave Laser. New J. Phys. 2010, 12, 073011. 10.1088/1367-2630/12/7/073011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Tavabi A. H.; Beleggia M.; Migunov V.; Savenko A.; Öktem O.; Dunin-Borkowski R. E.; Pozzi G. Tunable Ampere Phase Plate for Low Dose Imaging of Biomolecular Complexes. Sci. Rep. 2018, 8, 5592. 10.1038/s41598-018-23100-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Peet M. J.; Henderson R.; Russo C. J. The Energy Dependence of Contrast and Damage in Electron Cryomicroscopy of Biological Molecules. Ultramicroscopy 2019, 203, 125–131. 10.1016/j.ultramic.2019.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Naydenova K.; McMullan G.; Peet M. J.; Lee Y.; Edwards P. C.; Chen S.; Leahy E.; Scotcher S.; Henderson R.; Russo C. J. CryoEM at 100 keV: A Demonstration and Prospects. IUCrJ 2019, 6, 1086–1098. 10.1107/S2052252519012612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Rullgård H.; Öfverstedt L. G.; Masich S.; Daneholt B.; Öktem O. Simulation of Transmission Electron Microscope Images of Biological Specimens. J. Microsc. 2011, 243, 234–256. 10.1111/j.1365-2818.2011.03497.x. [DOI] [PubMed] [Google Scholar]
  20. Vulović M.; Ravelli R. B. G.; van Vliet L. J.; Koster A. J.; Lazić I.; Lücken U.; Rullgård H.; Öktem O.; Rieger B. Image Formation Modeling in Cryo-Electron Microscopy. J. Struct. Biol. 2013, 183, 19–32. 10.1016/j.jsb.2013.05.008. [DOI] [PubMed] [Google Scholar]
  21. Weik M.; Ravelli R. B. G.; Kryger G.; McSweeney S.; Raves M. L.; Harel M.; Gros P.; Silman I.; Kroon J.; Sussman J. L. Specific Chemical and Structural Damage to Proteins Produced by Synchrotron Radiation. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 623–628. 10.1073/pnas.97.2.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ravelli R. B. G.; McSweeney S. M. The “Fingerprint” That X-Rays Can Leave on Structures. Structure 2000, 8, 315. 10.1016/S0969-2126(00)00109-X. [DOI] [PubMed] [Google Scholar]
  23. Patwardhan A.; Lawson C. L.. Databases and Archiving for CryoEM. In Methods in Enzymology; Academic Press Inc., 2016; Vol. 579, pp 393–412. 10.1016/bs.mie.2016.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Scheres S. H. W.Processing of Structurally Heterogeneous Cryo-EM Data in RELION. In Methods in Enzymology; Academic Press Inc., 2016; Vol. 579, pp 125–157, 10.1016/bs.mie.2016.04.012. [DOI] [PubMed] [Google Scholar]
  25. Rosenthal P. B.; Henderson R. Optimal Determination of Particle Orientation, Absolute Hand, and Contrast Loss in Single-Particle Electron Cryomicroscopy. J. Mol. Biol. 2003, 333, 721–745. 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
  26. Liu Q.; Li Z.; Li J. Use B-Factor Related Features for Accurate Classification between Protein Binding Interfaces and Crystal Packing Contacts. BMC Bioinf. 2014, 15, S3. 10.1186/1471-2105-15-S16-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Carugo O.How Large B-Factors Can Be in Protein Crystal Structures. BMC Bioinf. 2018, 19, 10.1186/s12859-018-2083-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kirkland E. J.Advanced Computing in Electron Microscopy, Second ed.; Springer: Boston, MA, 2010; 10.1007/978-1-4419-6533-2. [DOI]
  29. Vulović M.; Voortman L. M.; van Vliet L. J.; Rieger B. When to Use the Projection Assumption and the Weak-Phase Object Approximation in Phase Contrast Cryo-EM. Ultramicroscopy 2014, 136, 61–66. 10.1016/j.ultramic.2013.08.002. [DOI] [PubMed] [Google Scholar]
  30. Williams D. B.; Carter C. B.. Transmission Electron Microscopy A Textbook for Materials Science; Springer: New York, 2009; 10.1007/978-0-387-76501-3. [DOI] [Google Scholar]
  31. Bucker R.; Hogan-Lamarre P.; Mehrabi P.; Schulz E. C.; Bultema L. A.; Gevorkov Y.; Brehm W.; Yefanov O.; Oberthur D.; Kassier G. H.; Dwayne Miller R. J. Serial Protein Crystallography in an Electron Microscope. Nat. Commun. 2020, 11, 996. 10.1038/s41467-020-14793-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Crowther R. A. The Reconstruction of a Three-Dimensional Structure from Projections and Its Application to Electron Microscopy. Proc. R. Soc. London 1970, 317 (1530), 319–340. [DOI] [PubMed] [Google Scholar]
  33. Kuijper M.; van Hoften G.; Janssen B.; Geurink R.; De Carlo S.; Vos M.; van Duinen G.; van Haeringen B.; Storms M. FEI’s Direct Electron Detector Developments: Embarking on a Revolution in Cryo-TEM. J. Struct. Biol. 2015, 192 (2), 179–187. 10.1016/j.jsb.2015.09.014. [DOI] [PubMed] [Google Scholar]
  34. Hempstead P. D.; Yewdall S. J.; Fernie A. R.; Lawson D. M.; Artymiuk P. J.; Rice D. W.; Ford G. C.; Harrison P. M. Comparison of the Three-Dimensional Structures of Recombinant Human H and Horse L Ferritins at High Resolution. J. Mol. Biol. 1997, 268 (2), 424–448. 10.1006/jmbi.1997.0970. [DOI] [PubMed] [Google Scholar]
  35. Weiss M. S.; Palm G. J.; Hilgenfeld R. Crystallization, Structure Solution and Refinement of Hen Egg-White Lysozyme at PH 8.0 in the Presence of MPD. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2000, 56 (8), 952–958. 10.1107/S0907444900006685. [DOI] [PubMed] [Google Scholar]
  36. Zhang K. Gctf: Real-Time CTF Determination and Correction. J. Struct. Biol. 2016, 193 (1), 1–12. 10.1016/j.jsb.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Danev R.; Yanagisawa H.; Kikkawa M. Cryo-Electron Microscopy Methodology: Current Aspects and Future Directions. Trends Biochem. Sci. 2019, 44, 837–848. 10.1016/j.tibs.2019.04.008. [DOI] [PubMed] [Google Scholar]
  38. Scheres S. H. W.; Chen S. Prevention of Overfitting in Cryo-EM Structure Determination. Nat. Methods 2012, 9, 853–854. 10.1038/nmeth.2115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zhang Y.; Tammaro R.; Peters P. J.; Ravelli R. B. G.. M4I-Nanoscopy/InSilicoTEM: InSilicoTEM_v2.0.0; Zenodo, 2020; 10.5281/ZENODO.3693834. [DOI]
  40. Ravelli R. B. G.; Nijpels F. J. T.; Henderikx R. J. M.; Weissenberger G.; Thewessem S.; Gijsbers A.; Beulen B. W. A. M. M.; López-Iglesias C.; Peters P. J. Automated Cryo-EM Sample Preparation by Pin-Printing and Jet Vitrification. bioRxiv 2019, 651208. 10.1101/651208. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci9b01176_si_001.pdf (523.8KB, pdf)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES