Enhanced tES and tDCS computational models by meninges emulation

Abstract

Objective:

Understanding how current reaches the brain during transcranial Electrical Stimulation (tES) underpins efforts to rationalize outcomes and optimize interventions. To this end, computational models of current flow relate applied dose to brain electric field. Conventional tES modeling considers distinct tissues like scalp, skull, cerebrospinal fluid (CSF), gray matter and white matter. The properties of highly conductive CSF are especially important. However, modeling the space between skull and brain as entirely CSF is not an accurate representation of anatomy. The space conventionally modeled as CSF is approximately half meninges (dura, arachnoid, and pia) with lower conductivity. However, the resolution required to describe individual meningeal layers is computationally restrictive in an MRI-derived head model. Emulating the effect of meninges through CSF conductivity modification could improve accuracy with minimal cost.

Approach:

Models with meningeal layers were developed in a concentric sphere head model. Then, in a model with only CSF between skull and brain, CSF conductivity was optimized to emulate the effect of meningeal layers on cortical electric field for multiple electrode positions. This emulated conductivity was applied to MRI-derived models.

Main results:

Compared to a model with conventional CSF conductivity (1.65 S/m), emulated CSF conductivity (0.85 S/m) produced voltage fields better correlated with intracranial recordings from epilepsy patients.

Significance:

Conventional tES mpodels have been validated using intracranial recording. Residual errors may nonetheless impact model utility. Because CSF is so conductive to current flow, misrepresentation of the skull-brain interface as entirely CSF is not realistic for tES modeling. Updating the conventional model with a CSF conductivity emulating the effect of the meninges enhances modeling accuracy without increasing model complexity. This allows existing modeling pipelines to be leveraged with a simple conductivity change. Using 0.85 S/m emulated CSF conductivity is recommended as the new standard in non-invasive brain stimulation modeling.

1. Introduction

There is extensive literature on the usefulness of computational models of current flow in the study and optimization of transcranial Direct Current Stimulation (tDCS) and more generally transcranial Electrical Stimulation (tES) [1–3]. For example, models suggest that current flow during tDCS is between rather than only under electrodes, and that High-Definition tDCS can be used to focalize stimulation [4]. Models also predict that anatomical differences may explain inter-individual variability [5,6]. Acknowledging repeated and consistent experimental validation of model accuracy [7–12], there remains value in ongoing efforts to enhance model precision—especially as models support rational target engagement and personalized stimulation in expanding clinical trials [13].

A key advance in the creation of accurate and useful models was the development of gyri-precise models based on high-resolution MRI and the use of a priori information to correct models beyond image resolution [14]—notably ensuring continuity of the cerebrospinal fluid (CSF), which can be less than the MRI slice thickness. Subsequent studies have demonstrated the key role of CSF in shaping the delivery of current to the brain during transcranial electrical stimulation [15–18] as it presents a significantly higher conductivity than other tissue.

While CSF is represented as a homogenous mask spanning from the skull to the brain (the skull-brain interface), the anatomy in fact includes meningeal layers comprised of the dura mater, arachnoid mater, and pia mater. Meninges are relatively resistive and occupy a significant portion of the skull-brain interface — roughly 15 to 50%[19–22] of the skull-brain interface distance; this alters the effective conductivity skull-brain interface compared to a pure CSF mask [23]. Moreover, even the CSF compartment itself includes arachnoid trabeculae [21], increasing tortuosity and so in situ resistivity. While the anatomy is unequivocal, including meninges in tDCS / tES models is computationally restrictive. Computational models that are both high-resolution (e.g. 0.1 mm voxel) and large (e.g. span the entire head) can require intractably detailed meshes for numerical FEM solutions. To include the meninges within the volume conventionally modeled as homogenous CSF, upsampling to at least a resolution of ~0.05 mm (corresponding to half the thinnest layer thickness) would be required. Typical image-derived head models are created at 1 mm, some as low as 0.5 mm [2,5,18,24], but just a two-fold increase in isotropic resolution corresponds to an eight-fold increase in number of voxels (2³) and so of memory for each image volume (MRI and Masks) used to create the model.

As an alternative, we propose to continue modeling the skull-brain interface as a homogenous mask while assigning it a lower conductivity that provides a reasonable approximation specifically regarding underlying current flow in the brain. Such an approach not only maintains computational burden, but it allows seamless integration with all image-segmentation and modeling pipelines already developed for tES / tDCS [2,25–30]. To verify the practical impact of such an approach, and generally assess the role of the meningeal layers (pia, arachnoid, and dura), in tES / tDCS we first applied concentric sphere models. A 9-shell model (scalp, fat, skull, dura, arachnoid, CSF, pia, grey matter, white matter) was developed and compared to a conventional 6-shell model (scalp, fat, skull, CSF, grey matter, white matter) with the conductivity of the CSF compartment adjusted (“emulated”) to match cortical electric field in the 9-shell model. The emulated CSF was then simulated in a MRI-derived head models, including from a dataset of human subjects with intracranial recordings during tES. This allowed us to experimentally validate the accuracy of emulated CSF/meninges vs conventional CSF models.

2. Methods

2.1. Finite Element models of volume conduction

Finite element method (FEM) models were created in COMSOL multiphysics 5.1 (COMSOL, Inc., Burlington, MA, USA) using either Computer Aided Design (CAD) derived or image-derived meshes. Models were created using electrostatic volume conductor physics with material conductivities defined as follows (in S/m): air, 1 × 10⁻¹⁵; skin, 0.465; fat, 0.025; skull, 0.01; CSF, 1.65 (conventional conductivity) or 0.85 (emulated conductivity); gray matter, 0.276; white matter, 0.126; electrode, 5.8 × 10⁷; saline-soaked sponge or gel, 1.4. [15,31]. Boundary conditions were applied as ground (V = 0) on cathode surfaces, inward current density summating to 1 mA (n · J = 1 $\frac{1mA}{Area}$) on anode surfaces, and electrically insulated (n · J = 0) on all other exterior surfaces. The Laplace equation (∇ · (σ∇V) = 0) was solved and the resulting cortical electric field was interpreted as a correlate for neuromodulation [32].

2.2. Spherical Head Models with Meningeal Layers

CAD-derived spherical head models were developed to isolate the effect of meningeal layers. Geometries were defined and meshed in COMSOLc, material properties, and boundary conditions were applied, and cortical electric field was solved as in the image-derived head models (see above for FEM settings). Nine concentric spheres of 76.49, 72.76, 71.76, 64.03, 62.92, 62.72, 61.63, 61.53, 58.93 mm radii were modeled to represents the scalp, fat, skull, dura matter, arachnoid mater, CSF, pia mater, gray matter, and white matter. This corresponded to layer thicknesses of 3.73, 1, 7.73, 1.11, 0.2, 1.09, 0.1, 2.6, 58.93 mm respectively with white matter as the core [Fig. 1]. Layer thicknesses for scalp, fat, skull, CSF, grey matter, and white matter were based on previously published spherical head model dimensions for an adult head [4]. Meningeal layer (dura, arachnoid, pia) thicknesses were estimated from literature [19–22] noting references are varied due to the heterogeneous geometry of the layers themselves. Thickness of the skull-brain interface layers (Meninges and CSF) were estimated under constraints: (1) Thickness rank (largest to smallest) was CSF (sub-arachnoid space), dura, arachnoid, and pia, (2) total thickness of the skull-brain interface layers was maintained at the CSF thickness of previously published models [5], and (3) meningeal layers were modeled to the highest range of their respective possible thickness, as a worst case scenario. Conventional conductivities were as listed above with the additions of dura mater (0.100 S/m), arachnoid mater (0.125 S/m), and pia mater (0.150 S/m) [15,31]. Tissue conductivity of meningeal layers were similarly approximated from literature, and was modeled under the following constraints: (1) Conductivities of meninges were between that of scalp and skull, and (2) an assumed conductivity rank of lowest to highest from pia mater to dura mater was maintained.

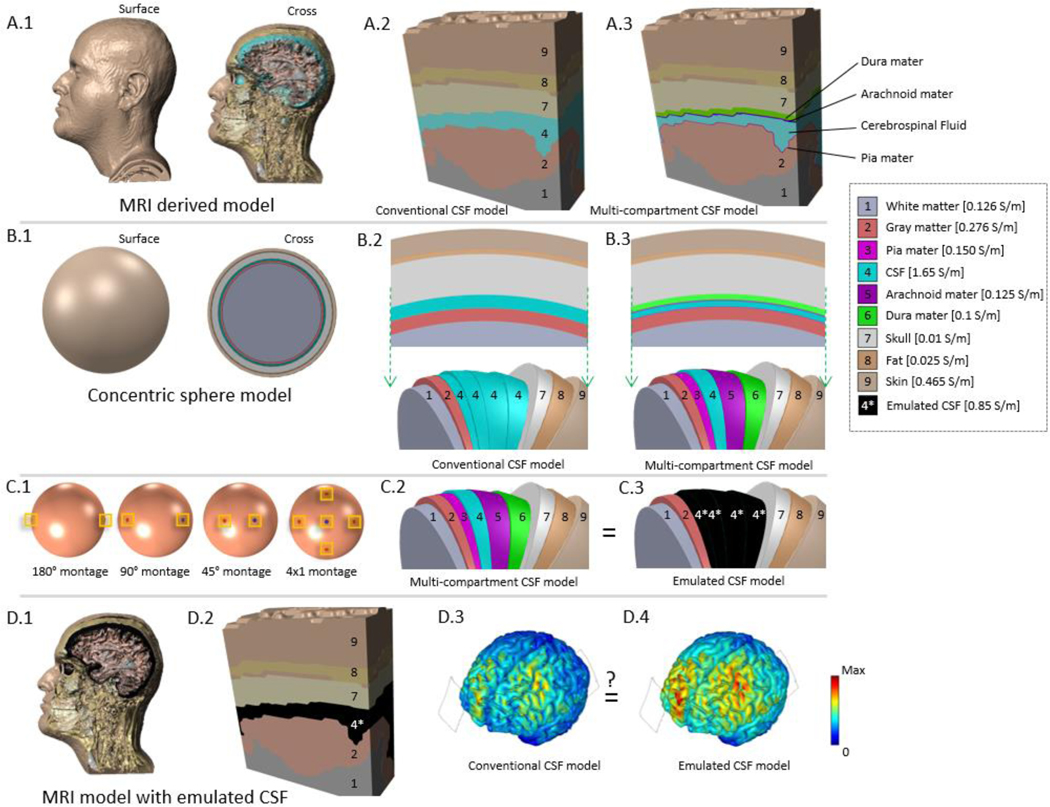
Figure 1: Workflow used to emulate the effect of individual meningeal layers on image-derived head models using spherical models.

Detailed image-derived (voxel-based) head models (A.1). Whereas image-derived models represent the skull-brain interface as pure CSF (A.2), in fact the space includes the meninges (A.3). Meninges are intractable to explicitly simulate in a full image-derived head model. Models were simplified to (B.1) a vector-based spherical head model where either pure CSF (B.2) or presence of meninges (B.3) can be modeled. The inclusion of individual meningeal layers within the conventional CSF volume was tested in four montages (C.1) to derive an emulated CSF conductivity (C.3) to mimic fully detailed (C.2) cortical electric field results. The effect of conventional CSF and emulated CSF conductivies were then compared in imaged-derived head models. While the skull-brain interface remains one compartment (D₁, D₂), assigning it an emulated conductivity is intended to approximate how the presence meninges would alter brain current flow (brain electric fields D₃, D₄).

Spherical head models were modeled across four tissue conductivity conditions, four electrode montages, and five skull-brain interface compositions. This produced a 4×4×5 table of conditions (Table 1). The four tissue conductivity conditions tested were to assess the relative impact of meningeal parameterization: (1) Conventional conductivities of skull, dura, arachnoid, CSF, and pia were modeled; (2) meningeal conductivities were doubled, (3) skull conductivity was increased to an extreme literature value (from 0.01 to 0.08 S/m) [33], and (4) both meningeal and skull conductivities were doubled. Within each of the previous tissue conductivity conditions, four montages were tested (anode-cathode 180°, anode-cathode 90°, anode-cathode 45°; and concentric 4×1 ring with 45° radius, Fig. 1.C) representing a span of potential electrode placements. Skull-brain interface composition was then assessed in the following five conditions (Fig. 1.C): 1. All layers were modeled as CSF per convention; 2. a layer of dura mater was introduced and the remainder was modeled as CSF; 3. dura and arachnoid mater were included and the remainder was modeled as CSF; 4. all layers (dura, arachnoid, CSF and pia) were modeled; or 5. all layers were modeled as a single tissue as in condition 1 but with a conductivity fitted to emulate the cortical electric field magnitude resulting from modeling all meningeal layers with CSF. The fifth composition was the basis for CSF emulation against the fourth full-detail composition.

Table 1: Comparison of electric fields produced in the brain using spherical models of varied precision (meninges layers represented) conductivity (skull and meninges) and montages (bipolar at 45, 90, and 180 and 4×1).

Minimum and maximum cortical (surface) electric fields, maximum electric field throughout the brain, and percent Area Half Max (AHM). The resulting emulated CSF conductivities ((A) 0.8 S/m, (B) 0.849 S/m, (C) 0.905 S/m, (D) 0.89 S/m) were used to arrive at the emulated CSF conductivity (0.85 S/m) used in the image-derived head models.

[A] Mo alterations	Min E Field V/m	Max E Reid V/m (surface)	Max E Reid V/m (across)	% Area Half Max	[C] Skull conductivity 0.08 S/m	Min E Field V/m	Max E Reld V/m (surface)	Max E Reld V/m (across)	% Area Half Max
CSF 180	0.198	0.320	0.522	100	CSF 180	0.221	0.800	1.181	18.0
CSF 90	0.086	0.380	0.500	28.1	CSF 90	0.087	0.850	1.170	18.2
CSF 45	0.042	0.429	0.430	7.5	CSF 45	0.041	0.950	1.100	6.5
CSF 4×1	0.003	0.260	0.375	11.9	CSF 4×1	0.001	0.750	1.046	7.9
CSF+dura 180	0.235	0.420	0.674	100	CSF+dura 180	0.257	1.000	1.452	16.5
CSF+dura 90	0.101	0.500	0.650	25.2	CSF+dura 90	0.100	1.100	1.441	15.9
CSF+dura 45	0.049	0.564	0.565	7.0	CSF+dura 45	0.048	1.200	1.361	6.1
CSF+dura 4×1	0.003	0.340	0.501	11.6	CSF+dura 4×1	0.001	0.900	1.298	8.2
CSF+dura+arach 180	0.244	0.440	0.712	100	CSF+dura+arach 180	0.265	1.100	1.523	14.2
CSF+dura+arach 90	0.104	0.500	0.688	27.9	CSF+dura+arach 90	0.103	1.100	1.513	17.2
CSF+dura+arach 45	0.050	0.599	0.599	6.8	CSF+dura+arach 45	0.049	1.300	1.423	5.7
CSF+dura+arach 4×1	0.003	0.400	0.534	10.0	CSF+dura+arach 4×1	0.001	1.000	1.365	7.4
CSF+dura+arach+pia 180	0.249	0.460	0.731	100	CSF+dura+arach+pia 180	0.270	1.100	1.560	17.0
CSF+dura+arach+pia 90	0.106	0.500	0.707	35.3	CSF+dura+arach+pia 90	0.105	1.100	1.549	19.5
CSF+dura+arach+pia 45	0.051	0.616	0.616	9.7	CSF+dura+arach+pia 45	0.050	1.300	1.465	8.5
CSF+dura+ara ch+pia 4×1	0.003	0.400	0.551	10.5	CSF+dura+arach+pia 4×1	0.001	1.000	1.402	7.8
CSF mod 180 (0.8 S/m)	0.249	0.460	0.732	1Q0	CSF mod 180 (0.905 S/m)	0.262	1.100	1.562	14.2
CSF mod 90 (0.8 S/m)	0.106	0.500	0.708	30.3	CSF mod 90 (0.905 S/m)	0.102	1.100	1.552	17.3
CSF mod 45 (0.8 S/m)	0.051	0.617	0.618	6.9	CSF mod 45 (0.905 s/m)	0.048	1.300	1.471	6.0
CSF mod 4×1 (0.8S/m)	0.003	0.400	0.552	10.4	CSF mod 4×1 (0.905 S/m)	0.001	1.000	1.410	7.5
[B] Dura, Arach, Pia Values Doubted	Min E Field V/m	Max E Reid V/m (surface)	Max E Reid V/m (across)	% Area Half Max	[D] Dura, Arach, Pia Values Doubled; Skull Conductivity 0.08 S/m	Min E Field V/m	Max E Reld V/m (surface)	Max E Reld V/m (across)	% Area Half Max
CSF 180	0.198	0.320	0.522	100	CSF 180	0.221	0.800	1.181	18.0
CSF 90	0.086	0.380	0.500	28.1	CSF 90	0.087	0.850	1.170	18.2
CSF 45	0.042	0.430	0.430	7.5	CSF 45	0.041	0.950	1.100	6.5
CSF 4×1	0.003	0.260	0.375	11.9	CSF 4×1	0.001	0.750	1.046	7.9
CSF+dura 180	0.233	0.420	0.665	100	CSF+dura 180	0.255	1.000	1.466	16.3
CSF+dura 90	0.100	0.500	0.641	24.5	CSF+dura 90	0.100	1.100	1.456	15.8
CSF+dura 45	0.04S	0.556	0.556	7.0	CSF+dura 45	0.047	1.200	1.376	6.2
CSF+dura 4×1	0.003	0.340	0.493	11.4	CSF+dura 4×1	0.001	1.000	1.315	6.8
CSF+dura+arach 180	0.240	0.440	0.699	100	CSF+dura+arach 180	0.261	1.100	1.535	14.0
CSF+dura+arach 90	0.103	0.500	0.674	26.8	CSF+dura+arach 90	0.102	1.100	1.524	17.0
CSF+dura+arach 45	0.050	0.586	0.587	6.9	CSF+dura+arach 45	0.04S	1.300	1.443	5.8
CSF+dura+arach 4×1	0.003	0.350	0.522	11.7	CSF+dura+arach 4×1	0.001	1.000	1.380	7.3
CSF+dura+arach+pia 180	0.245	0.440	0.716	100	CSF+dura+arach+pia 180	0.265	1.100	1.570	15.2
CSF+dura+arach+pia 90	0.105	0.500	0.691	31.0	CSF+dura+arach+pia 90	0.104	1.100	1.560	18.1
CSF+dura+arach+pia 45	0.050	0.602	0.602	7.7	CSF+dura+arach+pia 45	0.049	1.300	1.478	7.2
CSF+dura+arach+pia 4×1	0.003	0.400	0.538	10.1	CSF+dura+arach+pia 4×1	0.001	1.000	1.416	7.7
CSF mod 180 (0.849 S/m)	0.245	0.440	0.715	100	CSF mod 180 (0.890 S/m)	0.262	1.100	1.572	14.4
CSF mod 90 (0.849 s/m)	0.104	0.500	0.691	29.0	CSF mod 90 (0.890 S/m)	0.102	1.100	1.562	17.4
CSF mod 45 (0.849 S/m)	0.050	0.601	0.602	7.0	CSF mod 45 (0.890 S/m)	0.049	1.300	1.481	6.1
CSF mod 4×1 (0.849 S/m)	0.003	0.400	0.537	10.0	CSF mod 4×1 (0.890 S/m)	0.001	1.000	1.420	7.6

Model results were assessed using four metrics for brain electric field (EF): (1) minimum EF magnitude was calculated, (2) maximum EF magnitude was calculated on the cortical (grey matter) surface, (3) maximum EF magnitude was calculated within the brain (grey and white matter cross-section), and (4) EF spread on the cortical surface was quantified as the percent surface area at or above half the maximum surface EF (100 × ∫∫ (E ≥ $\frac{{\text{E}}_{\text{max}}}{2}$) dS/∫∫ dS), or percent Area Half Max (AHM). [34] These metrics were used to determine an effective emulated CSF conductivity to be applied to the entire skull-brain interface that could reproduce the effect of detailed meningeal layers for each tissue conductivity condition and each electrode montage (Table 1). The midrange emulated CSF conductivity from conditions 1–4 was selected and rounded to 2 significant figures.

2.3. Image-derived Head Models

The emulated CSF conductivity calculated from the spherical modeling was tested in image-derived models with two common montages. Cortical electric field was predicted in three neural typical heads of varying sizes (small, medium, large) using imaging data and segmentation from previous studies [5,6,24,35]. The head models were selected to be exemplary of high accuracy segmentation. S#, a large head size, has been a reference head model used in previous tDCS modeling [5,6,14,25]. (2) ICBM-NY head, medium size, was created more recently (2016) [24] to be a reference tES model base on averaged anatomy from 152 subjects (MNI / ICBM 152) [36]. S5, a small head, was used in tDCS models on inter-individual variability [5,37,38]. High resolution MRIs (1 mm³ isotropic) were segmented as scalp, fat, skull, air, CSF, grey matter, white matter. An automated segmentation pipeline based on algorithms in SPM8 [39] and updated for volume conduction models [30] was used to create initial image masks of scalp, skull, air, CSF, grey matter and white matter. Additional manual segmentation was applied to correct for noise, aliasing artifacts, and to add cortical detail. As in previous tES modeling studies dura, arachnoid, and pia matter were not individually segmented. Stimulation electrodes, sponge pads, and gels were modeled in SolidWorks (Dassault Systèmes Corp., Waltham, MA) and imported into ScanIP (Synopsys Simple ware, Mountain View, CA) for meshing. Two common montages were modeled: the M1-SO montage with an anode over the motor cortex (M1) and cathode over contralateral supra-orbital (SO) was modeled with 5×5 cm electrode and sponges, and the 4×1 montage with a center anode over M1 and surrounding electrodes 5 cm from center was modeled with small (1 cm radius) high-definition (HD) electrodes in a concentric ring configuration. In each case the position of M1 was chosen based on the 10–20 system for scalp electrodes [40]. An adaptive tetrahedral meshing algorithm was used in ScanIP to generate meshes between 6 × 10⁶ and 14 × 10⁶ quadratic elements. Results compared the effects of using emulated versus conventional CSF conductivity.

2.4. Validation in Subjects with Intracranial Recordings

The effect of the emulated CSF conductivity versus conventional CSF conductivity was assessed experimentally with intracranial recordings under TES from 10 subjects modeled and published in Huang, Liu, et al, 2017 (http://crcns.org/data-sets/methods/tes-1) [10]. Head models of 10 subjects (under 13 stimulation montages) were created from MRI’s acquired before and after a routine surgical evaluation for epilepsy. Pre-operative MRI’s were coregistered to post-operative MRI’s and segmented to avoid artifacts. Post-operative MRI’s informed electrode and craniotomy geometry and location. Subdural grid (8 × 8 contacts), strip (1 × 8 or 1 × 12 contacts), and depth electrode (1 × 8 or 1 × 12 contacts) on the lateral and medial frontal, parietal, occipital, and temporal cortex of the left and/or right hemisphere served as recording locations.

Head models were re-solved in an FEM package (Abaqus, Dassault Systèmes, Vélizy-Villacoublay, France) with both the emulated CSF conductivity (0.85 S/m) and the conventional conductivity (1.65 S/m). Models were parameterized as in sections 2.1 and 2.3, but without the inclusion of fat. The silicone rubber coated electrode grids and/or strips were modeled as effectively insulated (10⁻¹⁴ S/m). TES electrodes were modeled as they were experimentally, 2 × 2 cm on the forehead (Fpz) and occiput (Oz). One subject had three additional electrode montages with recordings (Fpz-shifted-left and Oz, Fpz and Oz-shifted-right, both Fpz-shifted-left and Oz-shifted-right). Other details specific to the experimental setup included the presence of craniotomies over the temporal lobe. Additional details on the experimental setup can found in Huang, Liu, et al, 2017 [10].

Experimental electric field was approximated as the difference of neighboring intracranial electrode voltages ((V_n+1 − V_n) / (x_n+1 − x_n), where V_n is electrode voltage and x_n is electrode location in meters). This calculation was repeated with FEM model predicted voltages sampled at intracranial electrode coordinates. Pearson correlation coefficients were calculated between the experimental and model electric fields at each electrode location for each subject. This calculation was repeated for each CSF conductivity model. A paired t-test was performed between the two CSF conductivity conditions for each subject correlation (Fig. 3).

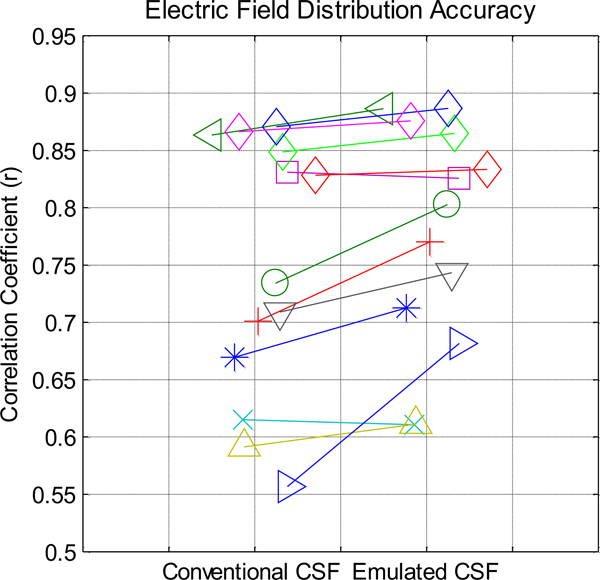
Figure 3: Across 13 trials in 10 subjects, correlations between model-predicted electric field using either conventional or emulated CSF values with in vivo recorded values.

Models using emulated CSF conductivity were better correlated to experimental measures compared to models using conventional CSF conductivity (p=0.008, t(12)=3.17). Each line represents a trial (montage and subject combination) and each marker represents a subject. One subject (diamond marker) was assessed under four different montages.

3. Results

Our principled approach started with concentric sphere models, where we evaluated if a 6-layered model with an emulated-CSF could reproduce brain current in a 9-layered model (that further includes the meninges). Precisely because a 9-layered image-derived model is not tractable, that concentric spheres are considered. And concentric-sphere analysis supports a principled strategy [4,41] as they are not biased by individualized anatomy inherent to image-derived analysis, and they allow comparison across assumptions and doses without compounding influence of idiosyncratic regional anatomy (e.g. skull thickness at different electrode locations). Moreover, we independently optimized emulated-CSF under 4 modeling assumptions (varying skull and meninges conductivity) and 4 montages selected to exemplify extremes; should a single emulated-CSF be effective across these 16 conditions, it would increase confidence in robustness.

Using 3 image-derived heads model and 2 exemplary montages we then compared predictions from standard and emulated-CSF. While illustrative, the scale of differences does not impugn the value of emulated-CSF: 1) the impact of changes is not definitive (e.g. how a 20% change in electric field in a given gyri relates to distinct behavioral outcomes;[42]); 2) if we show impact interacts with subject and montage tested, then ipso facto importance of emulated-CSF impact depends on individual anatomy and dose [5]; and 3) the impact will vary based on independent modeling assumptions (e.g. skull conductivity; [43]). However, the fundamental consideration here is that applying an emulated-CSF value has no methodological cost. So even a hypothetical benefit, deriving from any incremental changes in predicted brain current flow, can justify transition to emulated-CSF values. Also, for this reason we did not incorporate CSF anisotropy or consider individualized emulated-CSF values.

Finally, we compare predictions from standard and emulated-CSF values against previously collected intracranial recordings from epilepsy patients [10]. Blind parameter optimization inevitably enhances match; in our principled approach we tested the emulated-CSF value determined systematically in concentric-sphere. The application of this data set is not without noise and methodological nuance [44], and the method of segmentation and other modeling assumption [45] would impact the role of the CSF compartment. In any case, broader consideration of changing modeling pipelines is explicitly outside our scope. There are many open questions in tES modeling, but one of them is not if the compartment between brain and skull is in fact entirely occupied by CSF. And because any tissue (meninges) will have reduced conductivity relative to CSF, it follows that modeling this compartment as pure CSF must overestimate its effective conductivity. Our approach here was to develop a remedy for just thus issue.

3.1. Optimization of Emulated CSF in Concentric Spheres Modeling

In concentric sphere models, electric fields generally increased as more of the meningeal layers (from homogenous CSF, to CSF with dura, to CSF with dura and arachnoid, CSF with dura and arachnoid and pia) were added; absolute electric fields increased across the surface and depth of the brain, while relative focality increased (AHM decreased). To understand the sensitivity of these changes to model parameters several montages (2 electrodes at 180, 90, 45, and 5 electrodes in a 4×1 montage) and tissue property assumptions were evaluated (Table 1). Doubling the conductivities of the meningeal layers (Table 1.2) did not produce notable changes in measures of brain electric fields intensity or focally compared to conventional meninges conductivities (Table 1.1). Increasing skull conductivity from 0.01 to 0.08 S/m produced an increase in brain electric field amplitude and relative focality, with addition of meninges either with conventional (Table 1.3) or doubled conductivity (Table 1.4) further enhancing amplitude and relative focality.

For all the conditions noted above, cortical electrical fields were also predicted with a homogeneous CSF compartment (no explicit meninges) with emulated conductivity. A range of CSF layer conductivities in the 6-layered model (0.5 to 1.65 S/m) were simulated, and for each case compared to the corresponding 9-layered model. For absolute electric fields and relative focality, a 6-layered model CSF-compartment conductivity of ~0.85 S/m was found to provide a reasonable approximation of the 9-layered model across electrode montages and other tissue property assumptions. This was robust across conditions; an outcome that was not trivial and supporting the general use of 0.85 S/m as an emulated CSF-compartment approximation.

3.2. Emulated CSF in Image-derived Models

Starting with three exemplary MRI-derived models (large, medium, and small) and two montages (M1-SO and 4×1), cortical electric fields were predicted for conventional (1.65 S/m) and emulated (0.85 S/m) CSF-compartment conductivity. An incremental but notable increase in cortical electric field (ranging from 16–60%) was predicted across all subjects and montages when applying the emulated CSF-layer value in lieu of the conventional value (Fig. 2). There was no gross change in current flow patterns through the brain, such that the M1-SO montage produced diffused and clusters peaks between electrodes while the 4×1 Montage restricted current to inside the electrode rings. Nor was there a change in the ranking of subjects by peak brain electric field for each montage (i.e. the small and large heads had the highest and lowest electric field, respectively, for any given CSF conductivity and montage). Thus, these changes, while notable quantitative, do not necessarily challenge qualitative conclusions from past modeling efforts using conventional CSF conductivity.

Figure 2: Computational models in standard MRI-derived head models comparing brain electric fields using conventional and emulated CSF conductivity.

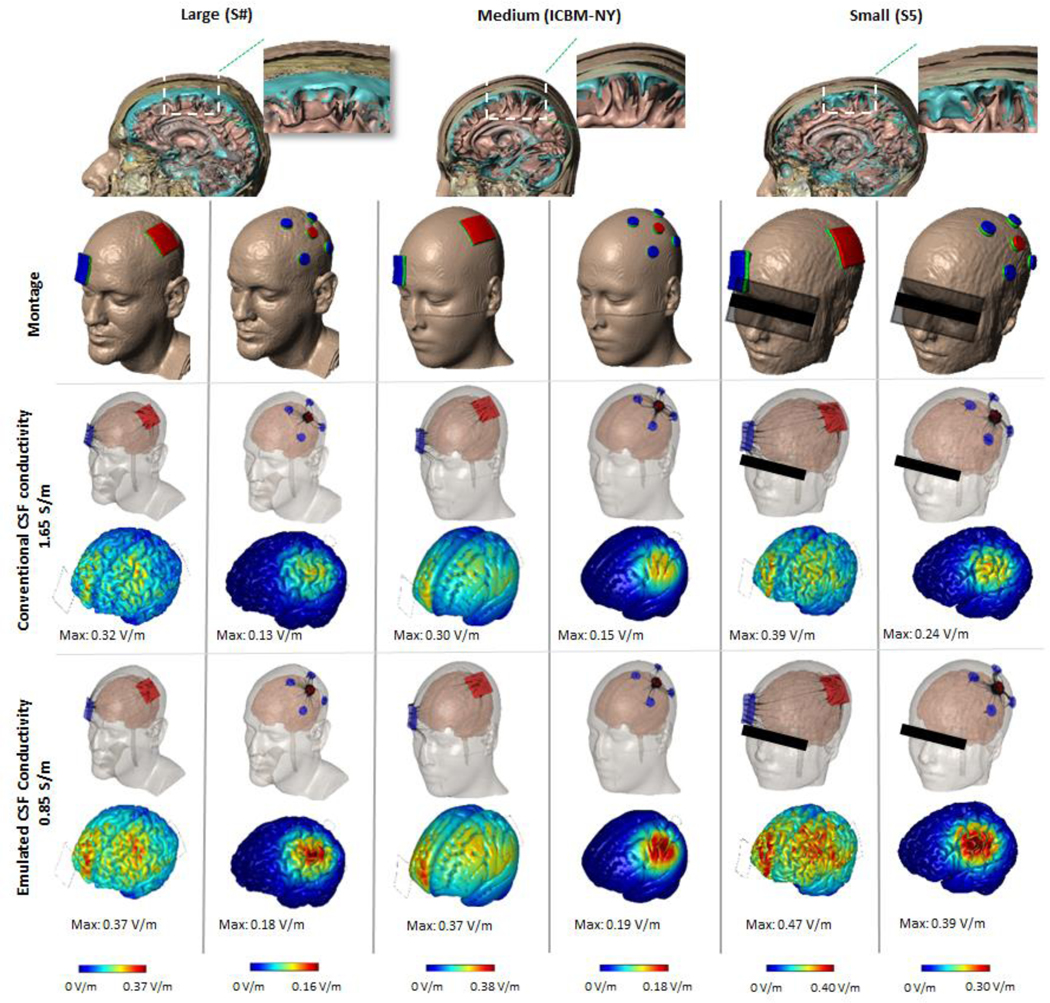
Segmentation masks showing the anatomical view of the layers of three individuals varying in age, gender, and head size. Two montages were modeled for each subject (M1-SO and 4×1). Cortical electric field was predicted using conventional CSF conductivity or emulated CSF conductivity. A more resistive emulated CSF layer raises the predicted electric field across all subjects and montages.

Finally, brain current flow was predicted in MRI-derived models of 10 subjects with epilepsy, where intra-cranial voltages were previously recorded during tES [10]. The accuracy of predicted voltage gradients using conventional (1.65 S/m) and emulated (0.85 S/m) CSF-compartment conductivity were compared. Correlation between model and experimental data significantly improved when using emulated CSF conductivity (Fig. 3).

4. Discussion

On the one hand, more sophisticated modeling techniques - notably the introduction and now standardized gyri-precise modeling workflow [14] - can advance understanding and practices of tES / tDCS. On the other hand, addition of modeling complexity that does not translate to human trials or clinical practice, may be only of “academic” value [46,47]. Modeling the skull-brain interface as pure CSF, which is highly conductive, is conspicuous since a substantial fraction of the space is occupied by meninges, which is relatively resistive. The explicit modeling of meningeal layers would dramatically increase computational burden (e.g. 0.05 mm voxel length), and so the cost of added complexity would need to be justified. However, our approach was to reproduce the relevant outcomes of the presence of meninges simply with an emulated-CSF value. This produced an incremental but validated increase in model accuracy. There is no added computational complexity cost and no impact on segmentation and modeling pipelines [2,27,29,48–51]. We argue that given emulated-CSF increases model accuracy (Fig. 3) with no added implementation cost, it can become the new standard in tDCS / tES modeling. We propose this correction would be equally useful for any models of transcranial brain stimulation that depends on electrical conductivity [41,52,53].

There is a general consensus on tissue properties used in tES / tDCS current flow models, [2,14,17,29,47,49–51,54,55]; with deviations [14,29,50,55] based on variation in assigned tissue conductivity [31,33,56–59]. CSF conductivity is not controversial — when isolated. However, this does not address in situ conductivity of the sub-arachnoid space nor correct for volume that should not be occupied by CSF [60–62]. The approach we develop here is akin to partial volume mixing formulas used to estimate the effective conductivity of heterogeneous mixtures. Partial volume formulas using MRI intensity to scale CSF conductivity is another possible technique [55], but qualitative features of typical T1 and T2 scans makes this approach less robust (image intensities are relative). Nor would such an approach allow levering of the extensively developed tools for tES modeling including automatic image segmentation for subject specific modeling. Rather, CSF-emulation can be immediately integrated into all modeling pipelines and software.

Given the present assumptions of modeling a continuous ~ 1 mm skull-brain interface (as CSF), the ease of implementation, and improved accuracy based on intra-cranial validation, we suggest the skull-brain interface be modeled at a conductivity of 0.85 S/m versus a more conductive pure CSF conductivity (1.65 S/m). There is no cost in regarded to complexity, no need to modify existing modeling tools, and therefore no evident rationale to not emulate CSF moving forward in models of tES techniques including tDCS.