On the benefits of flattening the curve: A perspective

Abstract

The many variations on a graphic illustrating the impact of non-pharmaceutical measures to mitigate pandemic influenza that have appeared in recent news reports about COVID-19 suggest a need to better explain the mechanism by which social distancing reduces the spread of infectious diseases. And some reports understate one benefit of reducing the frequency or proximity of interpersonal encounters, a reduction in the total number of infections. In hopes that understanding will increase compliance, we describe how social distancing (a) reduces the peak incidence of infections, (b) delays the occurrence of this peak, and (c) reduces the total number of infections during epidemics. In view of the extraordinary efforts underway to identify existing medications that are active against SARS-CoV-2 and to develop new antiviral drugs, vaccines and antibody therapies, any of which may have community-level effects, we also describe how pharmaceutical interventions affect transmission.

Highlights

• •Social distancing refers to non-pharmaceutical measures to mitigate pandemics.
• •These measures reduce the frequency or proximity of interpersonal encounters.
• •Their impact on daily and total numbers of new infections is commonly misrepresented.
• •We describe determinants of the magnitude and timing of the peak and the total number.
• •We also describe possible population-level effects of pharmaceutical interventions.

The most recent community mitigation guidelines for pandemic influenza [1] include a graphic illustrating the goals of non-pharmaceutical interventions, slowing the rate at which new infections occur (incidence), reducing the peak number of infected people (prevalence) and concomitant demands on healthcare facilities and personnel, and decreasing overall infections and deaths. Antimicrobial drugs generally are administered solely for the benefit of individual patients, but may also reduce the magnitude or duration of infectiousness, affecting transmission to others. Similarly, vaccines and monoclonal antibodies may reduce infectiousness as well as susceptibility. Accordingly, we include pharmaceutical interventions in our description of mechanisms underlying efforts to flatten the curve.

Plots of daily numbers of new infections, called epidemic curves, are affected by several factors, including under-reporting. Individual responses to infection by the same pathogen differ, and mild infections are less likely to be reported than those requiring medical attention. Absent widespread testing, few asymptomatic infections would be reported. In the ongoing pandemic, people with few if any symptoms may be infectious [2], diminishing the effectiveness of control measures based solely on symptomatic infections. Social distancing – increasing inter-personal distances, reducing the number of people attending meetings – involves everyone, reducing the risks of being infected if susceptible and of infecting others if infectious.

Assuming that infected people are infectious upon infection, other factors affecting epidemic curves are person-to-person contact rates (i.e., contacts per person per time period) and probabilities of infection on contact between infectious and susceptible people, or infectiousness. The sum of contacts by which susceptible people would be infected, which are products of these rates and probabilities [3], estimates the basic reproduction number, or average number of secondary infections per infected person.

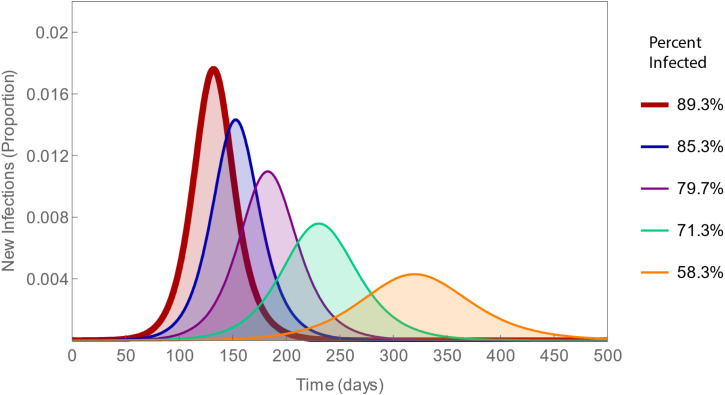
The areas beneath epidemic curves represent total numbers of infections. The onset, shape and area beneath these curves all depend on the basic reproduction number, which must be greater than one for epidemics to occur. The smaller this number, the longer the delay to peak incidence, the lower the peak, and fewer the total number of infections (Fig. 1). Both of the basic reproduction number’s constituents may be modifiable, contact rates by social distancing and infectiousness by medications, whereupon it would be termed an effective reproduction number.

Fig. 1.

Epidemic curves with varying contact rates. The contact rates decrease by 1 from 10 to 6 per day (left to right), corresponding to reproduction numbers ranging from 2.5 to 1.5. As these numbers decrease, the percent of the population infected decreases from 89% to 58%. Thus, social distancing not only delays and diminishes the peak number of infections, it also reduces the total number of infections.

While drugs are administered to cure infections or mitigate symptoms, they may also affect the magnitude or duration of infectiousness. Clinical trials of remdesivir and other promising antiviral drugs are underway (https://clinicaltrials.gov/ct2/results?cond=COVID-19), but none has yet been proven effective against SARS-CoV-2. This is the mechanism underlying the “treatment as prevention” approach to reducing HIV infection rates. Treatment of infected people with anti-retroviral drugs reduces their viral load, preventing their progression to AIDS. Authorities believe that it also reduces their infectiousness, which would lower the effective reproduction number. This is the rationale for the US national initiative, “Ending the HIV Epidemic: A Plan for America” (https://www.hiv.gov/federal-response/ending-the-hiv-epidemic/overview).

Similarly, unprecedented efforts to develop vaccines [4] or monoclonal antibodies (e.g., [5]) against SARS-CoV-2 also are underway. Should any prove safe and effective, they may reduce infectiousness as well as susceptibility to infection.

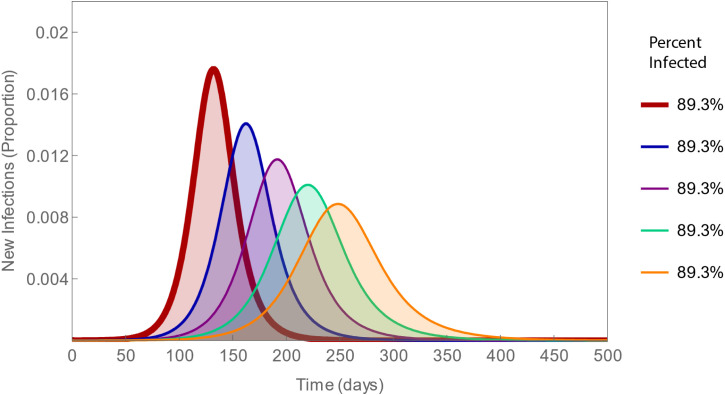
But the only way to flatten epidemic curves without also affecting the areas beneath them – as some figures in the media have suggested – is to change the mean interval between being infected and infecting others, or generation time. The pathogenesis of infectious diseases typically is characterized by replication prior to dissemination [6], so that people are not infectious for a while after being infected, called the latent period. Suppose – for sake of argument – that we could modify this period (Fig. 2).

Fig. 2.

Epidemic curves with varying latency. Intervals from infection to the onset of infectiousness or latent periods increase from 10 to 26 in 4-day increments (left to right), all corresponding to a basic reproduction number of 2.5. Note that the thick red curves are identical in both figures and that, in this one, while the curves differ in shape, the same total percent of the population, 89% is infected.

Should some infected people not live long enough to cause the average number of secondary infections, the basic reproduction number and generation time would no longer be independent. Be that as it may, the goal is not just to delay and reduce the peak number of infections, possibly below surge capacity as some figures in the media have suggested, it is also to reduce the total number of infections. Social distancing accomplishes all three objectives: (a) reducing the peak incidence of infections, (b) delaying the occurrence of this peak, and (c) reducing the total number of infections during epidemics.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

In the model that we used to generate these figures, the host population is partitioned into those who are susceptible to infection, S; who have been infected, but are not yet infectious, E; who are infectious, I; who have recovered and are immune, R; and who have died, D.

$$\begin{array}{c}{S}^{\prime }\left(t\right)=-\lambda \left(t\right)S\left(t\right),\hfill \\ E^{\prime }\left(t\right)=\lambda \left(t\right)S\left(t\right)-\epsilon E\left(t\right),\hfill \\ I^{\prime }\left(t\right)=\epsilon E\left(t\right)-\gamma I\left(t\right),\hfill \\ R^{\prime }\left(t\right)=p\gamma I\left(t\right),\hfill \\ D^{\prime }\left(t\right)=(1-p)\gamma I\left(t\right),\hfill \\ \text{where}\lambda \left(t\right)=a\beta \frac{I\left(t\right)}{N}\mathrm{and}N=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right).\hfill \end{array}$$

In this system of ordinary differential equations, $\lambda$ is the force or hazard rate of infection, $\epsilon$ is the rate of disease progression (its reciprocal is the latent period), $\gamma$ is the rate of recovery (its reciprocal is the infectious period), p is the proportion surviving (thus, disease-induced mortality is 1 – p), a is the contact rate (contacts per person per time period), $\beta$ is the probability of infection on contact between a susceptible and an infectious person, and N is the total population size.

The basic reproduction number, ${\Re }_0=a\beta ∕\gamma$, is equivalent to the more general definition in the text when the rates and probabilities are constant and infectious period is known. The number of new infections at time t is $\lambda \left(t\right)S\left(t\right)$ and total number or final size is ${\int }_0^{\infty }\lambda \left(t\right)S\left(t\right)dt$. For ease of interpretation, all numbers are plotted as fractions of the total population.

We solved this system numerically using Mathematica 12.1 (Wolfram Research, Champaign, Illinois) and evaluated the solution at times from 0 to 500 days. In both figures, $\gamma$ $=$ 1/5, $\beta$ $=$ 1/20, and $N=10^5$, with the contact rate, $a=10$ contacts per day and latent period, 1/$\epsilon =10$ days or having the values specified in the figure captions. The initial conditions are $S\left(0\right)=N-I\left(0\right)$, $I\left(0\right)=1$, and $E\left(0\right)=R\left(0\right)=D\left(0\right)=0$.