Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination?

Highlights

• •New COVID-19 mathematical model with lock-down effect.
• •New fractal-fractional differentiation.
• •New fractal-fractional integration.
• •Numerical scheme based on Newton polynomial.

Abstract

Countries around the world are implementing lock-down measures in a bid to flatten the curve of the new deadly COVID-19 disease. Our paper does not claim to have found the cure for COVID-19, neither does it claim that the suggested model have taken into account all the complexities around the spread of the disease. Nonetheless, the fundamental question asked in this paper is to know if within the conditions taken into account in this suggested model, the integral lock-down is effective in saving human lives. To answer this question, a mathematical model was suggested taking into account the possibility of transmission of COVID-19 from dead bodies to humans and the effect of lock-down. Three cases were considered. The first case suggested that there is transmission from dead to the living (medical staffs as they perform postmortem procedures on corpses, and direct contacts with during burial ceremonies). This case has no equilibrium points except for disease free equilibrium, a clear indication that care must be taken when dealing with corpses due to corona-19. In the second case we removed the transmission rate from dead bodies. This case showed an equilibrium point, although the number of deaths, carriers and infected grew exponentially up to a certain stability level. In the last case, we incorporated a lock-down and social distancing effect, using the next generation matrix. We could achieve a zero reproduction number, with number of deaths, infected and carriers decaying very rapidly. This is a clear indication that if lock-down recommendations are observed the threat of COVID-19 can be reduced to zero in few months.While our mathematical model agrees with the effectiveness of the lock-down, it is important to mention damaging effects of inadequate testing. The long waiting period of few days before confirmation of status, can only lead to more infections. The asymptomatic tested person could be positive and spread the infection, or could contact the virus in days after testing and will spread the disease further, after being given a false result. Testing kit that with immediate results are needed for more efficient measures. We used Italy’s Data to guide the construction of the mathematical model. To include non-locality into mathematical formulas, differential and integral operators were suggested. Properties and numerical approximations were presented in details. Finally, the suggested differential and integral operators were applied to the model.

1. Introduction

Humanity is in a state of unrest. Researchers from all fields of science, technology and engineering are awake since January 2020 with the aim to flatten the infection curve of COVID-19. Medical staffs from all over the world are working 24 hours as the spread has reached all the corners of the world. Governments around the globe are putting hands together to safe mankind from the heat of the COVID-19. Military forces and polices members all over the globe have embarked in a new war, as they aim to protect civilians from being exposed to the deadly disease. Streets and the sky are almost empty, the future of mankind is uncertain, economies, education, and many other sectors are affected. Businessmen and philanthropists around the world have donated part of their fortunes to help combat the spread. While up to now the bacteriological origin of the disease is unclear, the first cases were traced back to December 2019 in the city of Wuhan in China. Since then to the 14th of April 2020, 2,146,291 infected, 144,104 deaths and 545722 recovered, were recorded worldwide. It is worth noting however that these numbers are just an approximation of what has been made public, and cases that have been registered, one could postulate bigger numbers. What happened? What went wrong, where was this virus before, why 2019? The answers to these questions are still unknown. We shall recall that there exists in nature numerous mankind enemies in viruses, they only become harmful to humanity when they come in direct contact. In many ways mankind has violated the laws of nature, law of cohabitation, they went to the moon, which normally does not belong to them, they went underground in search of minerals, oil, they went under the sea is in the aquatic world. Mankind created artificial forms of life that could not be accepted by nature, modified the climate with heavy air pollution, polluted subsurface putting at risk all living beings within. Their great aim is perhaps to be in charge of their environment which could be right, as per many religious beliefs, they have been assigned the responsibility to be in control of the world under strict conditions of nature laws that do not need to be violated. No matter how strong technology has become, no matter how sophisticated weapons are, no matter how advanced the economy and knowledge are, humans still have to understand that as long as they violate laws of nature, covid-19 will not be the last outbreak.There’s going to be more outbreaks, more epidemics more pandemics. That is not a maybe, that is a fact, and it is a result of the way in which we humans interact with our planet.

Without loss of generality, while medical bodies, politicians, armies, law enforcement, businessmen, chemists, physicists, engineers, and many others are putting their efforts to help stop the spread of COVID-19, mathematicians are not left behind. New mathematical models that could be used for simulation, with the aim to predict the future behavior of the spread are developed. Few models of the spread of COVID-19 have been suggested so far, and are being used for some decision making [1], [2], [3], [4], [5], [6]. One key driver of the spread is direct contact with infected patients, object or corpses from COVID-19. While the world is still waiting for a possible vaccine, measures have been initiated in countries around the world and among them are lock-down and social distancing. In this paper, we suggest a mathematical model that takes into account the effect of lock-down. Noting that mathematical models rely on mathematical tools called differential and integral operators. Several have been suggested in the last decades as researchers recognized the complexity of nature and inadequacies of existing differential and integral operators. Fractal-fractional differential and integral operators are the result of combination of the so-called fractal derivative and fractional operators [7]. Questions aroused as the operators suffer limitations to handle initial conditions at the zero origin, although they have become powerful mathematical tools to the modeling of real world problems [8], [9], [10]. In this paper, we used a different fractal differential operators and construct different fractal-fractional operators.

The paper is structured as follows: Real data representing the spread of COVID-19 in Italy are presented statistically in compartmental categories of the pandemic infectious, recovered and deaths. The data does not provide a general representation for each country in the world, but are used for the sake of the theoretical study. A mathematical model including the effect of the lock-down is suggested, it can be seen as the extension of that suggested in [11]. Then, new differential and integral operators are introduced and some important results are presented. Finally, the novel differential and integral operators are applied to the suggested model.

2. Statistical analysis of some corona data

Without loss of generality, we present here Italy data. The data considered here are from January to 14 April 2020. We give some elementary statistical representation, as a guideline to construct the mathematical model. Data are put in histograms, line and pie charts for the number of deaths, recovered and infections. The figures show exponential growth of deaths and infected as depicted in Fig. 1, Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9 .

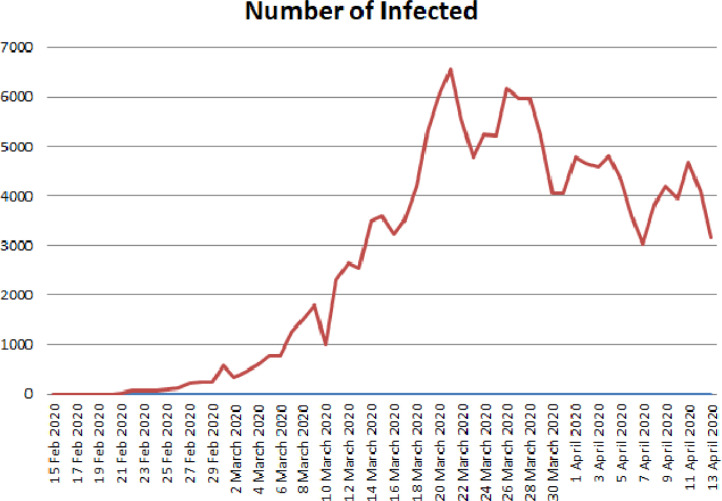
Fig. 1.

Number of infected in Italy from 15 February 2020 to 13 April 2020.

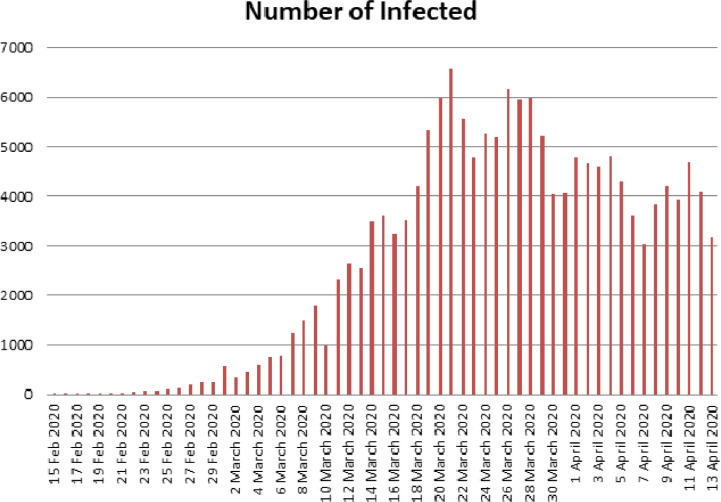
Fig. 2.

Number of infected in Italy from 15 February 2020 to 13 April 2020.

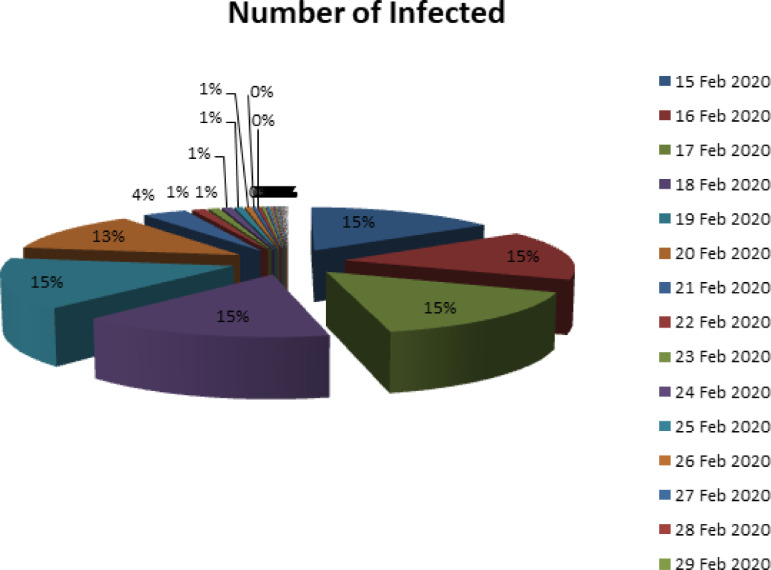
Fig. 3.

Number of infected in Italy from 15 February 2020 to 13 April 2020.

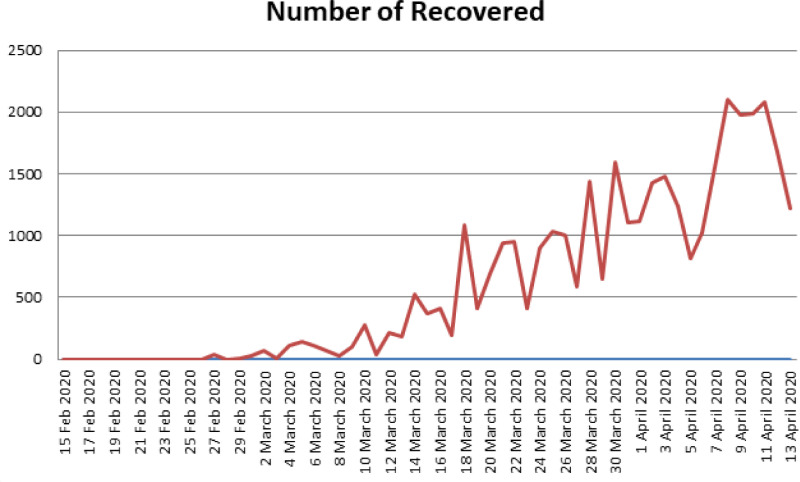
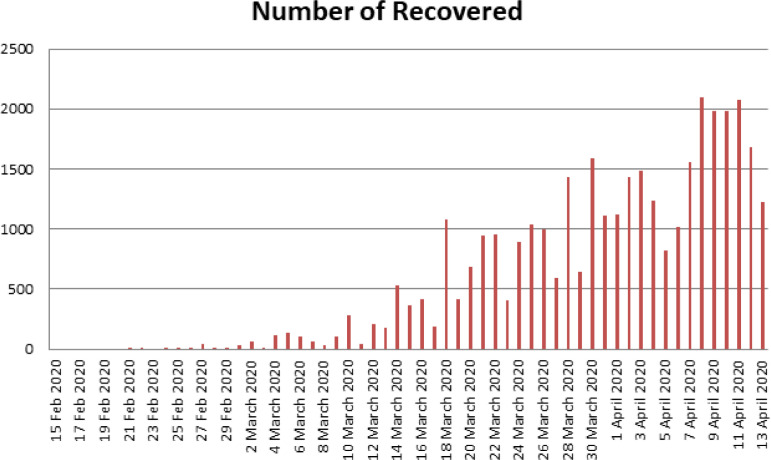
Fig. 4.

Number of recovered in Italy from 15 February 2020 to 13 April 2020.

Fig. 5.

Number of recovered in Italy from 15 February 2020 to 13 April 2020.

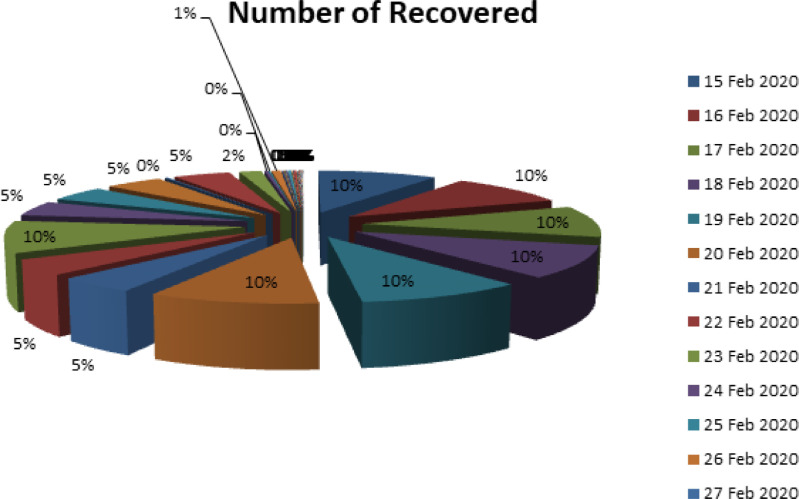
Fig. 6.

Number of recovered in Italy from 15 February 2020 to 13 April 2020.

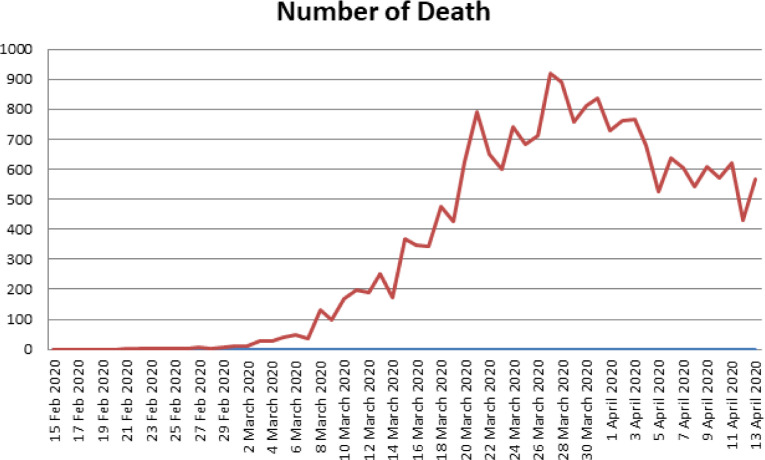
Fig. 7.

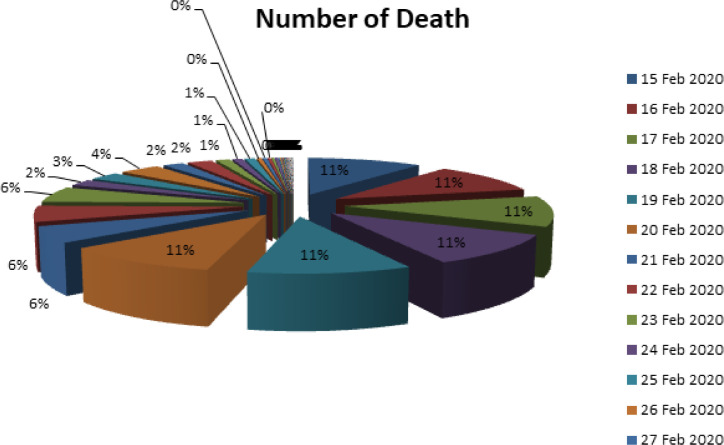
Number of death in Italy from 15 February 2020 to 13 April 2020.

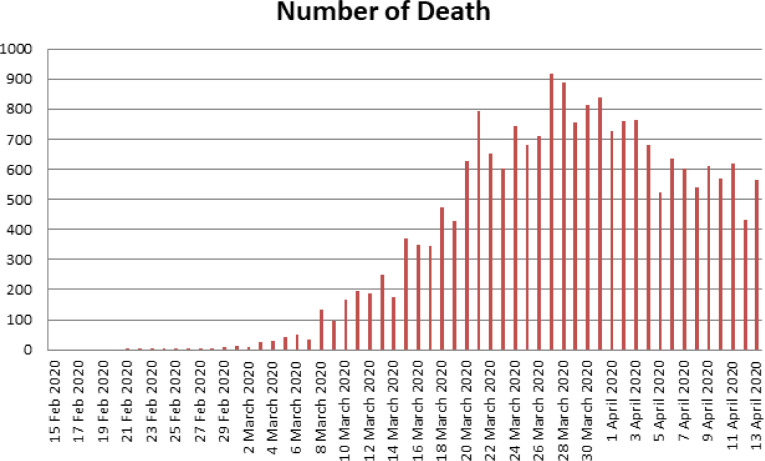
Fig. 8.

Number of death in Italy from 15 February 2020 to 13 April 2020.

Fig. 9.

Number of death in Italy from 15 February 2020 to 13 April 2020.

3. A mathematical model with lockdown effect

While the world is waiting for a vaccine that could be used to prevent the spread of COVID-19, while researchers are trying to develop a cure, governments around the world have introduced measures to help reduce the spread, these measures include, testing, isolation of infected patients, use of ventilators, social distancing and lock-down. In this section, we suggest a mathematical model that take into account the effect of lock-down and also the possibility of transmission from dead to susceptible populations. Of course the model does not take into account all the information regarding the spread, neither does the model is a cure of the COVID-19, but the model aims to confirm or dismiss the effect of lock-down as a possible adequate measure to help flatten the curve of deaths and infections.

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& \Lambda -\frac{\lambda SD}{N}-(\delta \left(x\right)+\mu )S+\eta R\hfill \\ \hfill \frac{dC}{dt}& =& \delta \left(x\right)\theta S+\frac{\lambda SD}{N}-(\beta +\mu +\pi )C\hfill \\ \hfill \frac{dI}{dt}& =& \delta \left(x\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill \frac{dR}{dt}& =& \beta C+\tau I-(\mu +\eta )R\hfill \\ \hfill \frac{dD}{dt}& =& \sigma I\hfill \end{array}$$ (1)

where the initial conditions are

$$S\left(0\right)=S_0,C\left(0\right)=C_0,I\left(0\right)=I_0,R\left(0\right)=R_0,N\left(0\right)=N_0,D\left(0\right)=D_0.$$ (2)

The function S(t) represents susceptible persons at risk of contacting COVID-19 at time t, the function C(t) represents carriers (dead corpse) that transmit the COVID-19 at time t, the function I(t) describes infective persons capable of transmitting the COVID-19 to persons at risk at time t, the function R(t) represents recovered persons who have been treated of COVID-19 and the function D(t) gives the total number of deaths at time t.

The parameters of the considered model are presented in Table 1 .

Table 1.

Parameters of the considered model.

Symbol	Interpretation
μ	Rate of natural death
Λ	Recruitment rate intoS(t)
θ	Probability of an S(t) class to join C(t) class
σ	Death rate induced by COVID-19
β	Recovery rate of C(t) class
δ(x)	Force of infection of class S(t)
τ	Recovery rate of I(t) class
π	Rate of which an C(t) class is recovered
η	Rate of which treated persons become C(t)class
δ	Rate of transmission
p	Proportion that a contact is efficient enough to cause infection
w	Transmission parameter for C(t) class
λ	Rate of infectivity betweenS(t) class and D(t) class
k	Rate of contact

For this model, we have

$$\delta \left(x\right)=\alpha \left(x\right)\left(\frac{I+wC}{N}\right)$$ (3)

where

$$\alpha \left(x\right)=k{e}^{-x}p$$ (4)

and

$$k=\{\begin{array}{cc}0\hfill & \text{if}x>1\hfill \\ >0\hfill & \text{if}x<1\hfill \end{array}.$$ (5)

We define the following norm

$${\parallel \phi \parallel }_{\infty }=\underset{t\in D_f}{\max }\left|\phi \left(t\right)\right|.$$ (6)

Owing to the biological correctness of the system, it is imperative to point out that

$$\forall t\ge 0,{\parallel S\parallel }_{\infty },{\parallel C\parallel }_{\infty },{\parallel I\parallel }_{\infty },{\parallel R\parallel }_{\infty },{\parallel D\parallel }_{\infty }<\infty .$$ (7)

We have the initial conditions

$$S\left(0\right)=S_0,C\left(0\right)=C_0,I\left(0\right)=I_0,R\left(0\right)=R_0,N\left(0\right)=N_0,D\left(0\right)=D_0.$$ (8)

They are biologically all positive.

Lemma 1

Let initial conditions be

$$\{S_0,C_0,I_0,R_0,D_0\}\subset \Omega .$$ (9)

Then if the solutions {S, C, I, R, D} exist, they are all positive for all ∀t ≥ 0.

Proof

We present the proof case by case starting with C.

$$\stackrel{.}{C}\left(t\right)=\delta \left(x\right)\theta S-(\mu +\beta +\pi )C+\frac{\lambda SD}{N}.$$ (10)

Since we assumed that all the solutions have the same sign, it is clear that

$$\frac{SD}{N}>0\text{also}\delta \left(x\right)S=k{e}^{-x}p\left(\frac{I+wC}{N}\right)S>0$$ (11)

Therefore

$$\stackrel{.}{C}\left(t\right)=-(\mu +\beta +\pi )C.$$ (12)

Which in turn leads to

$$C\left(t\right)>C\left(0\right)e^{-(\mu +\beta +\pi )t}.$$ (13)

This shows that C(t) is positive for ∀t ≥ 0. On the other hand, we have that

$$\begin{array}{ccc}\hfill \stackrel{.}{C}\left(t\right)& \le & \delta \left(x\right)\theta S+\frac{\lambda SD}{N}\hfill \\ & \le & k{e}^{-x}p\theta \left(\frac{IS+wCS}{N}\right)+\frac{\lambda SD}{N}\hfill \\ & \le & k{e}^{-x}p\theta \left(\frac{\left|I\right|\left|S\right|+w\left|C\right|\left|S\right|}{\left|N\right|}\right)+\frac{\lambda \left|S\right|\left|D\right|}{\left|N\right|}\hfill \\ & <& k{e}^{-x}p\theta \left(\begin{array}{c}\frac{{\max }_{t\in D_I}\left|I\right|.{\max }_{t\in D_S}\left|S\right|+wC{\max }_{t\in D_S}\left|S\right|}{{\max }_{t\in D_N}\left|N\right|}\\ +\frac{{\lambda \max }_{t\in D_S}\left|S\right|.{\max }_{t\in D_S}\left|D\right|}{{\max }_{t\in D_N}\left|N\right|}\end{array}\right)\hfill \\ & <& k{e}^{-x}p\theta (\frac{{\parallel I\parallel }_{\infty }{\parallel S\parallel }_{\infty }+wC{\parallel S\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }}+\frac{\lambda {\parallel S\parallel }_{\infty }.{\parallel D\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }})\hfill \\ & <& {\Pi }_1+C{\Pi }_2\hfill \end{array}$$ (14)

where

$$\begin{array}{ccc}\hfill {\Pi }_1& =& k{e}^{-x}p\theta (\frac{{\parallel I\parallel }_{\infty }{\parallel S\parallel }_{\infty }+wC{\parallel S\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }}+\frac{\lambda {\parallel S\parallel }_{\infty }.{\parallel D\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }})\hfill \\ \hfill {\Pi }_2& =& k{e}^{-x}p\theta \left(\frac{w{\parallel S\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }}\right).\hfill \end{array}$$ (15)

Thus

$$C\left(t\right)<c_0\exp \left({\Pi }_{2}t\right)+\frac{{\Pi }_1}{{\Pi }_2}\exp \left({\Pi }_{2}t\right).$$ (16)

We now consider the case of S(t)

$$\begin{array}{ccc}\hfill \stackrel{.}{S}\left(t\right)& =& \Lambda -(\delta \left(x\right)+\mu )S-\frac{\lambda SD}{N}+\eta R,\forall t\ge 0\hfill \\ & \ge & -\frac{\lambda SD}{N}-(\delta \left(x\right)+\mu )S,\forall t\ge 0\hfill \\ & \ge & -\frac{\lambda SD}{N}-k{e}^{-x}p\frac{(SI+wCS)}{N}-\mu S\hfill \\ & >& -\lambda S\frac{{\parallel D\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }}-k{e}^{-x}p\frac{({\parallel I\parallel }_{\infty }+w{\parallel C\parallel }_{\infty })}{{\parallel N\parallel }_{\infty }}S-\mu S\hfill \\ & >& {\Pi }_{3}S\hfill \end{array}$$ (17)

where

$${\Pi }_3=\lambda \frac{{\parallel D\parallel }_{\infty }}{{\parallel N\parallel }_{\infty }}+k{e}^{-x}p\frac{({\parallel I\parallel }_{\infty }+w{\parallel C\parallel }_{\infty })}{{\parallel N\parallel }_{\infty }}+\mu .$$ (18)

This leads to

$$S\left(t\right)>S\left(0\right)e^{-{\Pi }_{3}t}$$ (19)

which shows that S(t) is positive for ∀t ≥ 0. On the other hand,

$$\stackrel{.}{S}\left(t\right)\le \Lambda +\eta R\Rightarrow S\left(t\right)\le \Lambda t+\eta {\parallel R\parallel }_{\infty }t.$$ (20)

We next consider

$$\stackrel{.}{I}=\delta \left(x\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I.$$ (21)

Since S(t) and C(t) are positive, we can say that

$$\stackrel{.}{I}\ge -(\tau +\mu +\sigma )I,\forall t\ge 0.$$ (22)

This leads to

$$I\left(t\right)\ge I\left(0\right)e^{-(\tau +\mu +\sigma )t},\forall t\ge 0$$ (23)

which shows that

$$I\left(t\right)\ge 0\forall t\ge 0.$$ (24)

We consider

$$\stackrel{.}{R}=\beta C+\tau I-(\mu +\eta )R,\forall t\ge 0.$$ (25)

Since I(t) and C(t) are positive for ∀t ≥ 0, then

$$\stackrel{.}{R}\ge -(\mu +\eta )R,\forall t\ge 0.$$ (26)

This leads to

$$R\left(t\right)\ge R\left(0\right)e^{-(\mu +\eta )t},\forall t\ge 0.$$ (27)

Finally, if C(t) and I(t) are integrable,

$$\stackrel{.}{D}\left(t\right)=\sigma I.$$ (28)

Thus we have

$$D\left(t\right)=D\left(0\right)+\sigma {\int }_0^{t}I\left(\tau \right)d\tau >0.$$ (29)

 □

4. Well-posedness and biological feasibility

In this section, we investigate the interval and region within which the solution of our system will have perfect sense historically. We have already proved that ∀t all the solutions are positive also the suggested parameters. We know that ∀t > 0

$$\frac{dN\left(t\right)}{dt}=\Lambda -\mu N-\sigma I.$$ (30)

So in the absence of COVID-19

$$\frac{dN\left(t\right)}{dt}=\Lambda -\mu N.$$ (31)

We want that the function N(t) is a positively increasing function $\frac{dN\left(t\right)}{dt}>0.$

$$\frac{dN\left(t\right)}{dt}\ge N\left(t\right)<\frac{\Lambda }{\mu }.$$ (32)

The above inequality is referred in the literature as threshold population level. This leads us to conclude that the accepted set of solutions of the suggested model be confined within

$$\Omega =\{(S,C,I,R,D)\in {\mathbb{R}}_{+}^5:0\le S+C+I+R+D=N<\frac{\Lambda }{\mu }\}.$$ (33)

Here in biological terms ${\mathbb{R}}_{+}^5$ is the positive cone of ${\mathbb{R}}^5$ that also contains its lower dimensional faces. To be realistic, we exclude the case where $\frac{dN\left(t\right)}{dt}\ge 0$ which could mean that the host population could reduce asymptotically to the carrying capacity.

5. Equilibrium points and R₀

In this section, we derive the equilibrium points including disease free and endemic and finally we derive the reproduction number R ₀ using the next generation matrix approach. We recall that our system including α(x) is given as

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& \Lambda -\frac{\lambda SD}{N}-(k{e}^{-x}p\left(\frac{I+wC}{N}\right)+\mu )S+\eta R\hfill \\ \hfill \frac{dC}{dt}& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)\theta S+\frac{\lambda SD}{N}-(\beta +\mu +\pi )C\hfill \\ \hfill \frac{dI}{dt}& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill \frac{dR}{dt}& =& \beta C+\tau I-(\mu +\eta )R\hfill \\ \hfill \frac{dD}{dt}& =& \sigma I.\hfill \end{array}$$ (34)

The disease free equilibrium is given as

$$E_0=(\frac{\Lambda }{\mu },0,0,0,0).$$ (35)

We now define the matrices F and V as suggested by Van Den Driessche and Watmough [5]

$$F=\left[\begin{array}{cc}k{e}^{-x}p\theta w& k{e}^{-x}p\theta \\ k{e}^{-x}p(1-\theta )w& k{e}^{-x}p(1-\theta )\end{array}\right]$$ (36)

and

$$V=\left[\begin{array}{cc}\beta +\mu +\pi & 0\\ -\pi & \tau +\mu +\sigma \end{array}\right].$$ (37)

Thus

$$\begin{array}{ccc}\hfill F{V}^{-1}& =& \frac{1}{(\tau +\mu +\sigma )(\beta +\mu +\pi )}\hfill \\ & & \times \left[\begin{array}{cc}\delta \left(x\right)\theta w& \delta \left(x\right)\theta \\ \delta \left(x\right)(1-\theta )w& \delta \left(x\right)(1-\theta )\end{array}\right]\left[\begin{array}{cc}\tau +\mu +\sigma & 0\\ \pi & \beta +\mu +\pi \end{array}\right]\hfill \\ & =& \frac{1}{(\tau +\mu +\sigma )(\beta +\mu +\pi )}\hfill \\ & & \times \left[\begin{array}{cc}\delta \left(x\right)\theta w(\tau +\mu +\sigma )+\pi \left(\delta \left(x\right)\theta \right)& (\delta \left(x\right)\theta +\lambda )(\beta +\mu +\pi )\\ \delta \left(x\right)(1-\theta )w(\tau +\mu +\sigma )+\delta \left(x\right)(1-\theta )\pi & \delta \left(x\right)(1-\theta )(\beta +\mu +\pi )\end{array}\right].\hfill \end{array}$$ (38)

For simplicity let

$$\begin{array}{ccc}\hfill e& =& (\tau +\mu +\sigma )(\beta +\mu +\pi )\hfill \\ \hfill a& =& \delta \left(x\right)\theta w(\tau +\mu +\sigma )+\pi \left(\delta \left(x\right)\theta \right)\hfill \\ \hfill b& =& (\delta \left(x\right)\theta +\lambda )(\beta +\mu +\pi )\hfill \\ \hfill c& =& \delta \left(x\right)(1-\theta )w(\tau +\mu +\sigma )+\delta \left(x\right)(1-\theta )\pi \hfill \\ \hfill d& =& \delta \left(x\right)(1-\theta )(\beta +\mu +\pi ).\hfill \end{array}$$ (39)

Then

$$F{V}^{-1}=\frac{1}{e}\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=A.$$ (40)

Thus

$$\det (A-\lambda I)={\lambda }^2-\lambda \left(\frac{a+d}{e}\right)+\left(\frac{ad-bc}{e^2}\right).$$ (41)

So

$$\begin{array}{ccc}\hfill {\lambda }_1& =& \frac{\frac{a+d}{e}-\sqrt{{\left(\frac{a+d}{e}\right)}^2-4\left(\frac{ad-bc}{e^2}\right)}}{2}\hfill \\ \hfill {\lambda }_2& =& \frac{\frac{a+d}{e}+\sqrt{{\left(\frac{a+d}{e}\right)}^2-4\left(\frac{ad-bc}{e^2}\right)}}{2}\hfill \end{array}$$ (42)

under the condition that ad > bc. So the reproduction number is

$$R_0=\frac{\frac{a+d}{e}+\sqrt{{\left(\frac{a+d}{e}\right)}^2-4\left(\frac{ad-bc}{e^2}\right)}}{2}.$$ (43)

Thus we have

$$\begin{array}{ccc}\hfill R_0& =& \frac{1}{2(\tau +\mu +\sigma )(\beta +\mu +\pi )}\hfill \\ & & \times \left\{\begin{array}{c}\delta \left(x\right)\theta w(\tau +\mu +\sigma )+\pi \left(\delta \left(x\right)\theta \right)+\delta \left(x\right)(1-\theta )(\beta +\mu +\pi )+\\ {\left[\begin{array}{c}{(\delta \left(x\right)\theta w(\tau +\mu +\sigma )+\pi \left(\delta \left(x\right)\theta \right)+\delta \left(x\right)(1-\theta )(\beta +\mu +\pi ))}^2\\ -4\left(\begin{array}{c}(\delta \left(x\right)\theta w(\tau +\mu +\sigma )+\pi \left(\delta \left(x\right)\theta \right)\delta \left(x\right)(1-\theta )(\beta +\mu +\pi ))\\ -\left(\delta \left(x\right)\theta \right)(\beta +\mu +\pi )\delta \left(x\right)(1-\theta )w(\tau +\mu +\sigma )+\delta \left(x\right)(1-\theta )\pi \end{array}\right)\end{array}\right]}^{1/2}\end{array}\right\}.\hfill \end{array}$$ (44)

The suggested mathematical system does not contain another equilibrium point except for the disease-free equilibrium if there is a direct contact of class S(t) and class D(t). For example if in traditional burial ceremonies touching of corpses or contact with infected objects occur. However if susceptibles use sanitizer and are not in direct contact with corpses due to COVID-19 regulations then $\lambda =0.$ In this case, the new R ₀ is given as

$$R_0=\frac{k{e}^{-x}p}{(\tau +\mu +\sigma )(\beta +\mu +\pi )}\{(\beta +\mu +\pi )(1-\theta )+(w(\tau +\mu +\sigma )+\pi )\}$$ (45)

and the equilibrium points are given as

$$\begin{array}{ccc}\hfill S& =& \frac{N}{R_0},\hfill \\ \hfill C& =& \frac{\theta \Lambda (\tau +\mu +\sigma )(\mu +\eta )(R_0-1)}{\left\{\begin{array}{c}{R}_0\{(\tau +\mu +\sigma )(\beta +\mu +\pi )(\mu +\eta )-\eta \theta \beta -\eta \tau ((\beta +\mu +\pi )(1-\theta )+\pi \theta )\}\\ -\sigma (\mu +\eta )((\beta +\mu +\pi )(1-\theta )+\pi \theta )\end{array}\right\}},\hfill \\ \hfill I& =& \frac{\Lambda (\mu +\eta )((\beta +\mu +\pi )(1-\theta )+\pi \theta )(R_0-1)}{\left\{\begin{array}{c}{R}_0\{(\tau +\mu +\sigma )(\beta +\mu +\pi )(\mu +\eta )-\eta \theta \beta -\eta \tau ((\beta +\mu +\pi )(1-\theta )+\pi \theta )\}\\ -\sigma (\mu +\eta )((\beta +\mu +\pi )(1-\theta )+\pi \theta )\end{array}\right\}},\hfill \\ \hfill R& =& \frac{\Lambda (R_0-1)\{\beta \theta (\tau +\mu +\sigma )+\tau ((\beta +\mu +\pi )(1-\theta )+\pi \theta )\}}{\left\{\begin{array}{c}{R}_0\{(\tau +\mu +\sigma )(\beta +\mu +\pi )(\mu +\eta )-\eta \theta \beta -\eta \tau ((\beta +\mu +\pi )(1-\theta )+\pi \theta )\}\\ -\sigma (\mu +\eta )((\beta +\mu +\pi )(1-\theta )+\pi \theta )\end{array}\right\}}.\hfill \end{array}$$ (46)

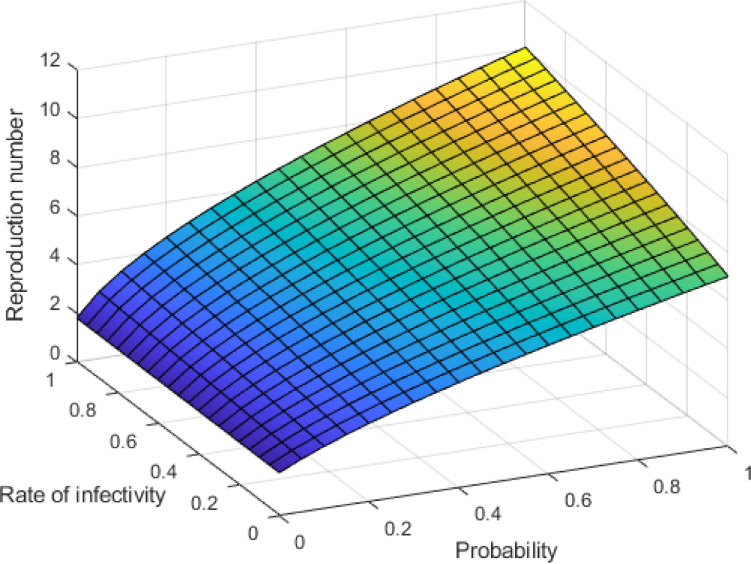
The numerical simulation is given for the reproduction number in Fig. 10

Fig. 10.

Reproduction number.

6. Model analysis under lock-down

The assumptions here are that citizens obey the lock-down rules. The medical personnel is not also exposed to COVID-19 from infected patients and dead bodies. Funerals are carried out in a manner that do not allow direct contact with corpses or infected objects. Citizens are not exposed to infected objects then, the following model is obtained

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& \Lambda -\mu S+\eta R\hfill \\ \hfill \frac{dC}{dt}& =& -(\beta +\mu +\pi )C\hfill \\ \hfill \frac{dI}{dt}& =& \pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill \frac{dR}{dt}& =& \beta C+\tau I-(\mu +\eta )R.\hfill \end{array}$$ (47)

Here we remove the death class due to COVID-19. The new model has positive solution as

$$S\left(t\right)\ge S\left(0\right)e^{-\mu t},C\left(t\right)\ge C\left(0\right)e^{-(\beta +\mu +\pi )t},I\left(t\right)\ge I\left(0\right)e^{-(\tau +\mu +\sigma )t},R\left(t\right)\ge R\left(0\right)e^{-(\mu +\eta )t}.$$ (48)

The disease free equilibrium is given as

$$(\frac{\Lambda }{\mu },0,0,0).$$ (49)

The next generation matrices are given as

$$F=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right],V=\left[\begin{array}{cc}\beta +\mu +\pi & 0\\ -\pi & \tau +\mu +\sigma \end{array}\right]$$ (50)

which means the reproductive number is $R_0=0.$ This implies no more infection, will be recorded.

7. New fractal-fractional differential and integral operators

Models with classical differentiation could be used to capture dynamical systems of infectious disease, when only initial conditions are used to predict future behaviors of the spread. However, when the situation is unpredictable maybe due to uncertainties associated to real world problems, classical differentiation and associated integral operators prove deficient. In the case of COVID-19, there are many uncertainties, many unknown and many misinformation making it very difficult to really provide a suitable mathematical model with classical differentiation. In general, non-local operators are more suitable for such situations, as they are able to capture non-localities and some memory effects depending if there are power law, fading memory or crossover effects. However, if in addition there are more complex behaviors that could not be replicated with power law, fading memory and crossover, the recently introduced fractal-fractional operators can be more suitable mathematical tools to handle such behaviors [12]. While these new operators have been recognized to be adequate in modeling complex problems, some questions were raised as the operators cannot handle time at the origin. In this section, we shall introduce a modified fractal-fractional operators, present their properties and their numerical approximations using already established techniques like Lagrange and Newton polynomial.

Definition 2

Let the function f(t) be a function not necessary differentiable. Let 0 < α ≤ 1 and 0 < β ≤ 1, where β is fractal dimension and α is a fractional order. A fractal-fractional derivative with order 0 ≤ α, β ≤ 1 with power-law kernel is defined as;

$${}_0^{FFP}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{1}{\Gamma (1-\alpha )}\frac{d}{d{t}^{\beta }}{\int }_0^{t}f\left(\tau \right){(t-\tau )}^{-\alpha }d\tau$$ (51)

where [12]

$$\frac{df\left(t\right)}{d{t}^{\beta }}=\underset{t\to t_1}{\lim }\frac{f\left(t\right)-f\left(t_1\right)}{t^{2-\beta }-t_1^{2-\beta }}(2-\beta ).$$ (52)

The fractal-fractional derivative with exponential decay kernel is defined as;

$${}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }\frac{d}{d{t}^{\beta }}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau .$$ (53)

The fractal-fractional derivative with Mittag-Leffler kernel is given as;

$${}_0^{FFM}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{AB\left(\alpha \right)}{1-\alpha }\frac{d}{d{t}^{\beta }}{\int }_0^{t}f\left(\tau \right)E_{\alpha }[-\frac{\alpha }{1-\alpha }{(t-\tau )}^{\alpha }]d\tau .$$ (54)

Remark 3

Let f be continuous, if ${}_0^{FFP}{D}_t^{\alpha ,\beta }f\left(t\right){,}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right)$ and ${}_0^{FFM}{D}_t^{\alpha ,\beta }f\left(t\right)$ exist, then for example

$${}_0^{FFP}{D}_t^{\alpha ,\beta }f\left(t\right)=\underset{t\to t_1}{\lim }\frac{F\left(t\right)-F\left(t_1\right)}{t^{2-\beta }-t_1^{2-\beta }}(2-\beta )$$ (55)

where

$$F\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_0^{t}f\left(\tau \right){(t-\tau )}^{-\alpha }d\tau .$$ (56)

Since F(t) is differentiable, we have

$${}_0^{FFP}{D}_t^{\alpha ,\beta }f\left(t\right)=\underset{t\to t_1}{\lim }\frac{F\left(t\right)-F\left(t_1\right)}{t-t_1}\frac{t-t_1}{t^{2-\beta }-t_1^{2-\beta }}(2-\beta )=F^{\prime }\left(t\right)\frac{1}{t^{1-\beta }}=\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}{\int }_0^{t}f\left(\tau \right){(t-\tau )}^{-\alpha }\frac{d\tau }{t^{1-\beta }}=\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}{\int }_0^{t}f\left(\tau \right){(t-\tau )}^{-\alpha }d(\tau ,t).$$ (57)

Thus

$${}_0^{FFM}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{AB\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)E_{\alpha }[-\frac{\alpha }{1-\alpha }{(t-\tau )}^{\alpha }]d(\tau ,t)$$ (58)

and

$${}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t).$$ (59)

Here $d(\tau ,t)=\frac{d\tau }{t^{1-\beta }}$ will be called the fractal-differential of variable τ and fractal representation $\frac{1}{t^{1-\beta }}.$

Corollary 4

The associated fractal-fractional integrals of order (α, β) are given as for power-law kernel;

$${}_0^{FFP}{J}_t^{\alpha ,\beta }f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}{\tau }^{1-\beta }f\left(\tau \right)d\tau .$$ (60)

For exponential kernel

$${}_0^{FFE}{J}_t^{\alpha ,\beta }f\left(t\right)=\frac{1-\alpha }{M\left(\alpha \right)}{t}^{1-\beta }f\left(t\right)+\frac{\alpha }{M\left(\alpha \right)}{\int }_0^t{\tau }^{1-\beta }f\left(\tau \right)d\tau .$$ (61)

and for the Mittag-Leffler kernel

$${}_0^{FFM}{J}_t^{\alpha ,\beta }f\left(t\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}^{1-\beta }f\left(t\right)+\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}{\tau }^{1-\beta }f\left(\tau \right)d\tau .$$ (62)

Remark 5

This version has no problem of singularity at the origin. Therefore boundary value problems with initial conditions at the origin can be handled.

7.1. Properties

We consider the space of continuous functions C. We defined the following norm

$${\parallel f\parallel }_{\infty }=\underset{t\in D_t}{\sup }\left|f\right|.$$ (63)

We assume that ∀t ∈ C, ‖f‖ < M, then

$$\begin{array}{ccc}\hfill \left|{}_0^{FFE}{D}_t^{\alpha ,\beta }\left(f\left(t\right)\right)\right|& =& \left|\frac{M\left(\alpha \right)}{(1-\alpha )}\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)\right|\hfill \\ & =& \left|\frac{M\left(\alpha \right)}{1-\alpha }[f\left(t\right)-\frac{\alpha }{1-\alpha }{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)]\right|\hfill \\ & \le & \frac{M\left(\alpha \right)}{1-\alpha }[\left|f\left(t\right)\right|+\frac{\alpha }{1-\alpha }\left|{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)\right|]\hfill \\ & \le & \frac{M\left(\alpha \right)}{1-\alpha }\left|f\left(t\right)\right|+\alpha M\left(\alpha \right){\int }_0^t\left|f\left(\tau \right)\right|\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)\hfill \\ & <& \frac{M\left(\alpha \right)}{1-\alpha }\underset{t\in D_t}{\sup }\left|f\left(t\right)\right|+\alpha M\left(\alpha \right){\int }_0^t\underset{\tau \in (0,t)}{\sup }\left|f\left(\tau \right)\right|\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)\hfill \\ & <& \frac{M\left(\alpha \right)}{1-\alpha }{\parallel f\parallel }_{\infty }+\alpha M\left(\alpha \right){\parallel f\parallel }_{\infty }{\int }_0^t\frac{1}{{\tau }^{1-\beta }}\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau \hfill \\ & <& \frac{M\left(\alpha \right)}{1-\alpha }{\parallel f\parallel }_{\infty }+\alpha M\left(\alpha \right){\parallel f\parallel }_{\infty }{\int }_0^t{\tau }^{\beta -1}\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau .\hfill \end{array}$$ (64)

One can find that

$${\int }_0^t{\tau }^{\beta -1}\sum _{k=0}^{\infty }\frac{{(-\frac{\alpha }{1-\alpha })}^k}{k!}{(t-\tau )}^{k}d\tau =\sum _{k=0}^{\infty }\frac{{(-\frac{\alpha }{1-\alpha })}^k}{k!}{\int }_0^t{\tau }^{\beta -1}{(t-\tau )}^{k}d\tau =\sum _{k=0}^{\infty }\frac{{(-\frac{\alpha }{1-\alpha })}^k}{k!}{t}^{\beta +k}\frac{\Gamma \left(\beta \right)\Gamma (k+1)}{\Gamma (\beta +k+1)}=\Gamma \left(\beta \right)t^{\beta }\sum _{k=0}^{\infty }\frac{t^k}{\Gamma (\beta +k+1)}{(-\frac{\alpha }{1-\alpha })}^k<\Gamma \left(\beta \right)t^{\beta }\sum _{k=0}^{\infty }\frac{t^k}{\Gamma (k+1)}{(-\frac{\alpha }{1-\alpha })}^k<\Gamma \left(\beta \right)t^{\beta }\exp (-\frac{\alpha }{1-\alpha }t).$$ (65)

Thus, we have

$$\left|{}_0^{FFE}{D}_t^{\alpha ,\beta }\left(f\left(t\right)\right)\right|<{\parallel f\parallel }_{\infty }[\frac{M\left(\alpha \right)}{1-\alpha }+\alpha M\left(\alpha \right)\Gamma \left(\beta \right)t^{\beta }\exp (-\frac{\alpha }{1-\alpha }t)].$$ (66)

Corollary 6

We have the following equality that can be obtained

$${}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right){=}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right)\frac{1}{t^{1-\beta }}+\frac{M\left(\alpha \right)}{1-\alpha }f\left(0\right)t^{\beta -1}\exp (-\frac{\alpha }{1-\alpha }t).$$ (67)

Proof

For proof, we write the following

$${}_0^{FFE}{D}_t^{\alpha ,\beta }f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }\frac{d}{d{t}^{\beta }}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau =\frac{M\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau \frac{1}{t^{1-\beta }}=\frac{M\left(\alpha \right)}{1-\alpha }{\int }_0^t\frac{d}{d\tau }[f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]+f\left(0\right)\exp [-\frac{\alpha }{1-\alpha }t]]d\tau \frac{1}{t^{1-\beta }}=\frac{M\left(\alpha \right)}{1-\alpha }{\int }_0^t\frac{d}{d\tau }f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d(\tau ,t)+\frac{M\left(\alpha \right)}{1-\alpha }f\left(0\right)\exp [-\frac{\alpha }{1-\alpha }t]t^{\beta -1}$$ (68)

which completes the proof. □

Remark 7

Let f ₁(t), f ₂(t) ∈ C.

$$\begin{array}{ccc}\hfill \left|{}_0^{FFE}{I}_t^{\alpha ,\beta }{f}_1\left(t\right){-}_0^{FFE}{I}_t^{\alpha ,\beta }{f}_2\left(t\right)\right|& =& |\frac{1-\alpha }{M\left(\alpha \right)}{t}^{1-\beta }(f_1\left(t\right)-f_2\left(t\right))+\frac{\alpha }{M\left(\alpha \right)}{\int }_0^t{\tau }^{1-\beta }(f_1\left(\tau \right)-f_2\left(\tau \right))d\tau |\hfill \\ & \le & \frac{1-\alpha }{M\left(\alpha \right)}\left|t^{1-\beta }(f_1\left(t\right)-f_2\left(t\right))\right|+\frac{\alpha }{M\left(\alpha \right)}\left|{\int }_0^t{\tau }^{1-\beta }(f_1\left(\tau \right)-f_2\left(\tau \right))d\tau \right|\hfill \\ & <& \frac{1-\alpha }{M\left(\alpha \right)}\left|t^{1-\beta }\right|\underset{t\in [0,t]}{\sup }|f_1\left(t\right)-f_2\left(t\right)|+\frac{\alpha }{M\left(\alpha \right)}\left|{\int }_0^t{\tau }^{1-\beta }\underset{\tau \in [0,t]}{\sup }|f_1\left(\tau \right)-f_2\left(\tau \right)|d\tau \right|\hfill \\ & <& \frac{1-\alpha }{M\left(\alpha \right)}\left|t^{1-\beta }\right|{\parallel f_1-f_2\parallel }_{\infty }+\frac{\alpha }{M\left(\alpha \right)}{\parallel f_1-f_2\parallel }_{\infty }\left|{\int }_0^t{\tau }^{1-\beta }d\tau \right|\hfill \\ & <& {\parallel f_1-f_2\parallel }_{\infty }[\frac{1-\alpha }{M\left(\alpha \right)}\left|t^{1-\beta }\right|+\frac{\alpha }{M\left(\alpha \right)}\frac{t^{2-\beta }}{{}^{2-\beta }}]\hfill \\ & <& {\parallel f_1-f_2\parallel }_{\infty }[\frac{1-\alpha }{M\left(\alpha \right)}\left|T^{1-\beta }\right|+\frac{\alpha }{M\left(\alpha \right)}\frac{T^{2-\beta }}{{}^{2-\beta }}]\hfill \\ & <& {\parallel f_1-f_2\parallel }_{\infty }K.\hfill \end{array}$$ (69)

Remark 8

Let β(t) and f(t) be differentiable, then

$$\frac{df\left(t\right)}{d{t}^{\beta \left(t\right)}}=\underset{t\to t_1}{\lim }\frac{f\left(t\right)-f\left(t_1\right)}{t^{2-\beta \left(t\right)}-t_1^{2-\beta \left(t_1\right)}}=\underset{t\to t_1}{\lim }\frac{f\left(t\right)-f\left(t_1\right)}{t-t_1}\frac{t-t_1}{t^{2-\beta \left(t\right)}-t_1^{2-\beta \left(t_1\right)}}=f^{\prime }\left(t_1\right)\underset{t\to t_1}{\lim }\frac{1}{\frac{t^{2-\beta \left(t\right)}-t_1^{2-\beta \left(t_1\right)}}{t-t_1}}=f^{\prime }\left(t_1\right)\frac{1}{t^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})}.$$ (70)

Therefore,

$${}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)\exp [-\frac{\alpha }{1-\alpha }(t-\tau )]d\tau \frac{1}{t^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})},$$ (71)

$${}_0^{FFP}{D}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)=\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}{\int }_0^{t}f\left(\tau \right){(t-\tau )}^{-\alpha }d\tau \frac{1}{t^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})},$$ (72)

and

$${}_0^{FFM}{D}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)=\frac{AB\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_0^{t}f\left(\tau \right)E_{\alpha }[-\frac{\alpha }{1-\alpha }{(t-\tau )}^{\alpha }]d\tau \frac{1}{t^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})}.$$ (73)

Corollary 9

If the functions β(t) and f(t) are differentiable, then the associated integral operators are given as: For the exponential kernel

$$\begin{array}{ccc}\hfill {}_0^{FFE}{J}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}{t}^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})f\left(t\right)\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_0^t{\tau }^{2-\beta \left(\tau \right)}(-{\beta }^{\prime }\left(\tau \right)\ln \tau +\frac{2-\beta \left(\tau \right)}{\tau })f\left(\tau \right)d\tau .\hfill \end{array}$$ (74)

For the power-law kernel

$${}_0^{FFP}{J}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\tau }^{2-\beta \left(\tau \right)}(-{\beta }^{\prime }\left(\tau \right)\ln \tau +\frac{2-\beta \left(\tau \right)}{\tau }){(t-\tau )}^{\alpha -1}f\left(\tau \right)d\tau .$$ (75)

and for the Mittag-Leffler kernel

$$\begin{array}{ccc}\hfill {}_0^{FFM}{J}_t^{\alpha ,\beta \left(t\right)}f\left(t\right)& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}^{2-\beta \left(t\right)}(-{\beta }^{\prime }\left(t\right)\ln t+\frac{2-\beta \left(t\right)}{t})f\left(t\right)\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^t{\tau }^{2-\beta \left(\tau \right)}(-{\beta }^{\prime }\left(\tau \right)\ln \tau +\frac{2-\beta \left(\tau \right)}{\tau }){(t-\tau )}^{\alpha -1}f\left(\tau \right)d\tau .\hfill \end{array}$$ (76)

8. Numerical scheme with exponential decay kernel

In this section, we consider Cauchy problem with the new differential operator which is given by

$$\begin{array}{ccc}\hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (77)

Applying the associate integral operator with exponential kernel, we can reformulate equation (77) as follows;

$$y\left(t\right)=\frac{1-\alpha }{M\left(\alpha \right)}{t}^{1-\beta }g(t,y\left(t\right))+\frac{\alpha }{M\left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right)){\tau }^{1-\beta }d\tau .$$ (78)

At the point $t_{\delta +1}=(\delta +1)\Delta t,$

$$y\left(t_{\delta +1}\right)=\frac{1-\alpha }{M\left(\alpha \right)}{t}_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))+\frac{\alpha }{M\left(\alpha \right)}{\int }_0^{t_{\delta +1}}g(\tau ,y\left(\tau \right)){\tau }^{1-\beta }d\tau$$ (79)

and at the point $t_{\delta }=\delta \Delta t,$ we have

$$y\left(t_{\delta }\right)=\frac{1-\alpha }{M\left(\alpha \right)}{t}_{\delta -1}^{1-\beta }g(t_{\delta -1},y\left(t_{\delta -1}\right))+\frac{\alpha }{M\left(\alpha \right)}{\int }_0^{t_{\delta }}g(\tau ,y\left(\tau \right)){\tau }^{1-\beta }d\tau .$$ (80)

If we take the difference of these equations, we obtain the following equation

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)-y\left(t_{\delta }\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }g(t_{\delta -1},y\left(t_{\delta -1}\right))\end{array}\right]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}g(\tau ,y\left(\tau \right)){\tau }^{1-\beta }d\tau .\hfill \end{array}$$ (81)

For brevity, we consider

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)-y\left(t_{\delta }\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}[G(t_{\delta },y\left(t_{\delta }\right))-G(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}G(\tau ,y\left(\tau \right))d\tau \hfill \end{array}$$ (82)

where

$$G(t,y\left(t\right))=g(t,y\left(t\right))t^{1-\beta }.$$ (83)

We shall recall that the Newton polynomial is given by;

$$\begin{array}{ccc}\hfill G(t,y\left(t\right))& \simeq & G(t_{\delta -2},y\left(t_{\delta -2}\right))+\frac{G(t_{\delta -1},y\left(t_{\delta -1}\right))-G(t_{\delta -2},y\left(t_{\delta -2}\right))}{\Delta t}(\tau -t_{\delta -2})\hfill \\ & & +\frac{G(t_{\delta },y\left(t_{\delta }\right))-2G(t_{\delta -1},y\left(t_{\delta -1}\right))+G(t_{\delta -2},y\left(t_{\delta -2}\right))}{2{\left(\Delta t\right)}^2}\hfill \\ & & \times (\tau -t_{\delta -2})(\tau -t_{\delta -1}).\hfill \end{array}$$ (84)

We now replace this polynomial into the equation (82), we get the following

$$\begin{array}{ccc}\hfill y^{\delta +1}-y^{\delta }& =& \frac{1-\alpha }{M\left(\alpha \right)}[G(t_{\delta },y\left(t_{\delta }\right))-G(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}{\displaystyle G(t_{\delta -2},y\left(t_{\delta -2}\right))\Delta t}\\ {\displaystyle +\frac{G(t_{\delta -1},y\left(t_{\delta -1}\right))-G(t_{\delta -2},y\left(t_{\delta -2}\right))}{\Delta t}{\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})d\tau }\\ {\displaystyle +\frac{G(t_{\delta },y\left(t_{\delta }\right))-2G(t_{\delta -1},y\left(t_{\delta -1}\right))+G(t_{\delta -2},y\left(t_{\delta -2}\right))}{2{\left(\Delta t\right)}^2}}\\ {\displaystyle \times {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})(\tau -t_{\delta -1})d\tau }\end{array}\right\}.\hfill \end{array}$$ (85)

We can calculate the integrals taken place on the right hand side of equation (85) as follows

$$\begin{array}{ccc}& & {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})d\tau =\frac{5}{2}{\left(\Delta t\right)}^2\hfill \\ & & {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})(\tau -t_{\delta -1})d\tau =\frac{23}{6}{\left(\Delta t\right)}^3.\hfill \end{array}$$ (86)

We can rearrange the above scheme as follows;

$$\begin{array}{ccc}\hfill y^{\delta +1}-y^{\delta }& =& \frac{1-\alpha }{M\left(\alpha \right)}[G(t_{\delta },y\left(t_{\delta }\right))-G(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}G(t_{\delta },y\left(t_{\delta }\right))\Delta t-\frac{4}{3}G(t_{\delta -1},y\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}G(t_{\delta -2},y\left(t_{\delta -2}\right))\Delta t\end{array}\right\}.\hfill \end{array}$$ (87)

If we replace G(t, y(t)) by its value, we can solve our equation numerically with the following scheme

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& y^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}[t_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))-t_{\delta -1}^{1-\beta }g(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))\Delta t-\frac{4}{3}{t}_{\delta -1}^{1-\beta }g(t_{\delta -1},y\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }g(t_{\delta -2},y\left(t_{\delta -2}\right))\Delta t\end{array}\right\}.\hfill \end{array}$$ (88)

9. Numerical scheme with Mittag-Leffler kernel

In this section, we solve the following problem

$$\begin{array}{ccc}\hfill {}_0^{FFM}{D}_t^{\alpha ,\beta }y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (89)

Applying the new fractional integral with Mittag-Leffler kernel, we transform the above equation into

$$\begin{array}{ccc}\hfill y\left(t\right)& =& y\left(0\right)+\frac{1-\alpha }{AB\left(\alpha \right)}{t}^{1-\beta }g(t,y\left(t\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right)){(t-\tau )}^{\alpha -1}{\tau }^{1-\beta }d\tau .\hfill \end{array}$$ (90)

At the point $t_{\delta +1}=(\delta +1)\Delta t,$ we obtain the following

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)& =& y\left(0\right)+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}g(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}{\tau }^{1-\beta }d\tau .\hfill \end{array}$$ (91)

For simplicity, we shall take as

$$G(t,y\left(t\right))=g(t,y\left(t\right))t^{1-\beta }.$$ (92)

We also have

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)& =& y\left(0\right)+\frac{1-\alpha }{AB\left(\alpha \right)}G(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (93)

As we did before, we replace the Newton polynomial into equation (93). Then the above equation can be organized as follows;

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& y\left(0\right)+\frac{1-\alpha }{AB\left(\alpha \right)}G(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})\Delta t{\int }_{t_{\mu }}^{t_{\mu +1}}{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})}{\Delta t}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})}{2{\left(\Delta t\right)}^2}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2})(\tau -t_{\mu -1}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (94)

For the integrals in equation (94), we can have the following calculations

$$\begin{array}{c}{\int }_{t_{\mu }}^{t_{\mu +1}}{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau =\frac{{\left(\Delta t\right)}^{\alpha }}{\alpha }[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau =\frac{{\left(\Delta t\right)}^{\alpha +1}}{\alpha (\alpha +1)}\left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2})(\tau -t_{\mu -1}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau =\frac{{\left(\Delta t\right)}^{\alpha +2}}{\alpha (\alpha +1)(\alpha +2)}\\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$ (95)

Replacing them into the equation (94) and substituting $G(t,y\left(t\right))=g(t,y\left(t\right))t^{1-\beta },$ we can get the following numerical scheme

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }[t_{\mu -1}^{1-\beta }g(t_{\mu -1},y^{\mu -1})-t_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})]\hfill \\ & & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }[t_{\mu }^{1-\beta }g(t_{\mu },y^{\mu })-2t_{\mu -1}^{1-\beta }g(t_{\mu -1},y^{\mu -1})+t_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})]\hfill \\ & & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (96)

10. Numerical scheme with power-law kernel

In this section, we deal with the following Cauchy problem

$$\begin{array}{ccc}\hfill {}_0^{FFP}{D}_t^{\alpha ,\beta }y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (97)

where the differential operator contains the new fractal-fractional derivative. Using new integral with power-law kernel, we convert the equation (97) into

$$y\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right)){(t-\tau )}^{\alpha -1}{\tau }^{1-\beta }d\tau .$$ (98)

At the point $t_{\delta +1}=(\delta +1)\Delta t,$

$$y\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$ (99)

where

$$G(\tau ,y\left(\tau \right))=g(\tau ,y\left(\tau \right)){\tau }^{1-\beta }.$$ (100)

Then we have

$$y\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\delta }}^{t_{\delta +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .$$ (101)

Placing the Newton polynomial in equation (101), we get the following

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& \frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})\Delta t{\int }_{t_{\delta }}^{t_{\delta +1}}{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})}{\Delta t}\hfill \\ & & \times {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\mu -2}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})}{2{\left(\Delta t\right)}^2}\hfill \\ & & \times {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\mu -2})(\tau -t_{\mu -1}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (102)

Putting $G(t,y\left(t\right))=t^{1-\beta }g(t,y\left(t\right))$ in the above equation, the following scheme can be obtained

$$\begin{array}{cc}{y}^{\delta +1}=\hfill & \frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})\hfill \\ & \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }g(t_{\mu -1},y^{\mu -1})\\ -t_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }g(t_{\mu },y^{\mu })\\ -2t_{\mu -1}^{1-\beta }g(t_{\mu -1},y^{\mu -1})\\ +t_{\mu -2}^{1-\beta }g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (103)

11. Numerical scheme with exponential decay kernel

In this section, we consider the following Cauchy problem

$$\begin{array}{ccc}\hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (104)

The above equation can be reformulated as follows;

$$\begin{array}{ccc}\hfill y\left(t\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}{t}^{2-\beta \left(t\right)}[-\beta \prime \left(t\right)\ln \left(t\right)+\frac{2-\beta \left(t\right)}{t}]g(t,y\left(t\right))\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right))[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\hfill \end{array}$$ (105)

We write the above equation as follows

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)-y\left(t_{\delta }\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})g(t_{\delta -1},y\left(t_{\delta -1}\right))\end{array}\right]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}g(\tau ,y\left(\tau \right))[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\hfill \end{array}$$ (106)

For simplicity, we take

$$G(t,y\left(t\right))=g(t,y\left(t\right))[-\beta \prime \left(t\right)\ln \left(t\right)+\frac{2-\beta \left(t\right)}{t}]t^{2-\beta \left(t\right)}$$ (107)

and we have

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)-y\left(t_{\delta }\right)& =& \frac{1-\alpha }{M\left(\alpha \right)}[G(t_{\delta },y\left(t_{\delta }\right))-G(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}G(\tau ,y\left(\tau \right))d\tau .\hfill \end{array}$$ (108)

If we put the Newton polynomial as the approximation of the function G(τ, y(τ)), one can write the following equation

$$\begin{array}{ccc}\hfill y^{\delta +1}-y^{\delta }& =& \frac{1-\alpha }{M\left(\alpha \right)}[G(t_{\delta },y\left(t_{\delta }\right))-G(t_{\delta -1},y\left(t_{\delta -1}\right))]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}G(t_{\delta -2},y\left(t_{\delta -2}\right))\Delta t\\ +\frac{G(t_{\delta -1},y\left(t_{\delta -1}\right))-G(t_{\delta -2},y\left(t_{\delta -2}\right))}{\Delta t}{\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})d\tau \\ +\frac{G(t_{\delta },y\left(t_{\delta }\right))-2G(t_{\delta -1},y\left(t_{\delta -1}\right))+G(t_{\delta -2},y\left(t_{\delta -2}\right))}{2{\left(\Delta t\right)}^2}\\ \times {\int }_{t_{\delta }}^{t_{\delta +1}}(\tau -t_{\delta -2})(\tau -t_{\delta -1})d\tau .\end{array}\right\}.\hfill \end{array}$$ (109)

If we do same routine and replace G(t, y(t)) by its value, we have the following numerical approximation

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& y^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})g(t_{\delta -1},y\left(t_{\delta -1}\right))\end{array}\right]\hfill \\ & & +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times g(t_{\delta },y\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times g(t_{\delta -1},y\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times g(t_{\delta -2},y\left(t_{\delta -2}\right))\Delta t\end{array}\right\}.\hfill \end{array}$$ (110)

12. Numerical scheme with Mittag-Leffler kernel

In this section, we handle our problem involving the new constant fractional order and variable fractal dimension

$$\begin{array}{ccc}\hfill {}_0^{FFM}{D}_t^{\alpha ,\beta \left(t\right)}y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (111)

If we integrate the equation (111) with the new integral operator including Mittag-Leffler kernel, the above equation can be converted to

$$\begin{array}{ccc}\hfill y\left(t\right)& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}^{2-\beta \left(t\right)}[-\beta \prime \left(t\right)\ln \left(t\right)+\frac{2-\beta \left(t\right)}{t}]g(t,y\left(t\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right)){(t-\tau )}^{\alpha -1}\hfill \\ & & \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\hfill \end{array}$$ (112)

At the point $t_{\delta +1}=(\delta +1)\Delta t,$ we have the following

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}g(\tau ,y\left(\tau \right)){(t_{\delta +1}-s)}^{\alpha -1}\hfill \\ & & \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\hfill \end{array}$$ (113)

For brevity, we consider

$$G(\tau ,y\left(\tau \right))=g(\tau ,y\left(\tau \right))[-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}$$ (114)

and we can write the following

$$\begin{array}{ccc}\hfill y\left(t_{\delta +1}\right)& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (115)

One can replace the Newton polynomial in equation (115) as follows

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})\Delta t{\int }_{t_{\mu }}^{t_{\mu +1}}{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})}{\Delta t}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})}{2{\left(\Delta t\right)}^2}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2})(\tau -t_{\mu -1}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (116)

Thus, we have the following scheme

$$\begin{array}{cc}{y}^{\delta +1}=\hfill & \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }[G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }[G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (117)

Replacing the function G(t, y(t)) by its value, we can present the following scheme for numerical solution of our equation

$$\begin{array}{cc}{y}^{\delta +1}=\hfill & \frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})g(t_{\delta },y\left(t_{\delta }\right))\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\hfill \\ & \times g(t_{\mu -2},y^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times g(t_{\mu -1},y^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times g(t_{\mu },y^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times g(t_{\mu -1},y^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (118)

13. Numerical scheme with power-law kernel

In this section, we deal with the following Cauchy problem with power-law kernel

$$\begin{array}{ccc}\hfill {}_0^{FFP}{D}_t^{\alpha ,\beta \left(t\right)}y\left(t\right)& =& g(t,y\left(t\right))\hfill \\ \hfill y\left(0\right)& =& y_0.\hfill \end{array}$$ (119)

where the new differential operator has constant fractional order and variable fractal dimension. Integrating the equation (119) with the new integral having power-law kernel, we transform it into

$$y\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t}g(\tau ,y\left(\tau \right)){(t-\tau )}^{\alpha -1}[-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .$$ (120)

At the point $t_{\delta +1}=(\delta +1)\Delta t,$ we can have the following

$$y\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$ (121)

where

$$G(\tau ,y\left(\tau \right))=g(\tau ,y\left(\tau \right))[-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}.$$ (122)

Then we have the following

$$y\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}G(\tau ,y\left(\tau \right)){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .$$ (123)

When we place the suggested polynomial in equation (123), we can write the following

$$\begin{array}{ccc}\hfill y^{\delta +1}& =& \frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})\Delta t{\int }_{t_{\mu }}^{t_{\mu +1}}{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})}{\Delta t}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \hfill \\ & & +\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }\frac{G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})}{2{\left(\Delta t\right)}^2}\hfill \\ & & \times {\int }_{t_{\mu }}^{t_{\mu +1}}(\tau -t_{\mu -2})(\tau -t_{\mu -1}){(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\hfill \end{array}$$ (124)

As we did before, we replace the associate calculations into above scheme, we have the following

$$\begin{array}{cc}{y}^{\delta +1}=\hfill & \frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }G(t_{\mu -2},y^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }[G(t_{\mu -1},y^{\mu -1})-G(t_{\mu -2},y^{\mu -2})]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }[G(t_{\mu },y^{\mu })-2G(t_{\mu -1},y^{\mu -1})+G(t_{\mu -2},y^{\mu -2})]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (125)

If we replace the function $G(t_{\mu -1},y^{\mu -1})$ by its value, the following numerical scheme is obtained;

$$\begin{array}{cc}& y^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\hfill \\ & \times g(t_{\mu -2},y^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times g(t_{\mu -1},y^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ & +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times g(t_{\mu },y^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times g(t_{\mu -1},y^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times g(t_{\mu -2},y^{\mu -2})\end{array}\right]\hfill \\ & \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\hfill \end{array}$$ (126)

14. Application of new operators to corona model

In this section, we apply the new differential and integral operators to the suggested mathematical model of COVID-19. Here, the classical differential operator will be replaced by the operator with power-law, exponential decay and Mittag-Leffler kernels. Additionally the variable order version will also be applied. We start with exponential decay kernel

$$\begin{array}{ccc}\hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }S& =& \Lambda -\frac{\lambda SD}{N}-(k{e}^{-x}p\left(\frac{I+wC}{N}\right)+\mu )S+\eta R\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }C& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)\theta S+\frac{\lambda SD}{N}-(\beta +\mu +\pi )C\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }I& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }R& =& \beta C+\tau I-(\mu +\eta )R\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }D& =& \sigma I.\hfill \end{array}$$ (127)

For simplicity, we write above equation as follows;

$$\begin{array}{ccc}\hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }S& =& S_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }C& =& C_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }I& =& I_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }R& =& R_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta }D& =& D_1(t,S,C,I,R,D)\hfill \end{array}$$ (128)

where

$$\begin{array}{ccc}\hfill S_1(t,S,C,I,R,D)& =& \Lambda -\frac{\lambda SD}{N}-(k{e}^{-x}p\left(\frac{I+wC}{N}\right)+\mu )S+\eta R\hfill \\ \hfill C_1(t,S,C,I,R,D)& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)\theta S+\frac{\lambda SD}{N}-(\beta +\mu +\pi )C\hfill \\ \hfill I_1(t,S,C,I,R,D)& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill R_1(t,S,C,I,R,D)& =& \beta C+\tau I-(\mu +\eta )R\hfill \\ \hfill D_1(t,S,C,I,R,D)& =& \sigma I.\hfill \end{array}$$ (129)

After applying fractal-fractional integral with exponential kernel, we have the following

$$\begin{array}{c}\hfill S\left(t_{\delta +1}\right)=S\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{S}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{S}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{S}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }d\tau \end{array}$$ (130)

$$\begin{array}{c}\hfill C\left(t_{\delta +1}\right)=C\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{C}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{C}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{C}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }d\tau \end{array}$$

$$\begin{array}{c}\hfill I\left(t_{\delta +1}\right)=I\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{I}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{I}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{I}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }d\tau \end{array}$$

$$\begin{array}{c}\hfill R\left(t_{\delta +1}\right)=R\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{R}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{R}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{R}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }d\tau \end{array}$$

$$\begin{array}{c}\hfill D\left(t_{\delta +1}\right)=D\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{D}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{D}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{D}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }d\tau .\end{array}$$

We can have the following scheme for this model

$$\begin{array}{c}\hfill S^{\delta +1}=S^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{S}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{S}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }{S}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{1-\beta }{S}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }{S}_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill C^{\delta +1}=C^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{C}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{C}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }{C}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{1-\beta }{C}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }{C}_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=I^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{I}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{I}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }{I}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{1-\beta }{I}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }{I}_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=R^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{R}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{R}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }{R}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{1-\beta }{R}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }{R}_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=D^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{1-\beta }{D}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{1-\beta }{D}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{1-\beta }{D}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{1-\beta }{D}_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{1-\beta }{D}_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}.\end{array}$$

For Mittag-Leffler kernel, we can have the following

$$\begin{array}{c}\hfill S\left(t_{\delta +1}\right)=S_0+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{S}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{S}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \end{array}$$ (131)

$$\begin{array}{c}\hfill C\left(t_{\delta +1}\right)=C_0+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{C}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{C}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \end{array}$$

$$\begin{array}{c}\hfill I\left(t_{\delta +1}\right)=I_0+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{I}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{I}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \end{array}$$

$$\begin{array}{c}\hfill R\left(t_{\delta +1}\right)=R_0+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{R}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{R}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau \end{array}$$

$$\begin{array}{c}\hfill D\left(t_{\delta +1}\right)=D_0+\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{D}_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{D}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .\end{array}$$

We can get the following numerical scheme

$$\begin{array}{c}{S}^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{S}_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\hfill \\ \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{S}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{S}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{S}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\hfill \end{array}$$ (132)

$$\begin{array}{c}\hfill C^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{C}_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{C}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{C}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{C}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{I}_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{I}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{I}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{I}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{R}_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{R}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{R}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{R}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{1-\beta }{D}_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{D}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{D}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{D}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

For power-law kernel, we can have the following

$$S\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{S}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$ (133)

$$C\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{C}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$

$$I\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{I}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$

$$R\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{R}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau$$

$$D\left(t_{\delta +1}\right)=\frac{1}{\Gamma \left(\alpha \right)}\sum _{\mu =2}^{\delta }{\int }_{t_{\mu }}^{t_{\mu +1}}{D}_1(\tau ,S,C,I,R,D){\tau }^{1-\beta }{(t_{\delta +1}-\tau )}^{\alpha -1}d\tau .$$

We can get the following numerical scheme

$$\begin{array}{c}{S}^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\hfill \\ \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{S}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{S}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{S}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{S}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\hfill \end{array}$$ (134)

$$\begin{array}{c}\hfill C^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{C}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{C}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{C}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{C}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{I}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{I}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{I}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{I}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{R}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{R}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{R}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{R}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^{\delta }{t}_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\\ \hfill \times [{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{1-\beta }{D}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{1-\beta }{D}_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{1-\beta }{D}_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{1-\beta }{D}_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

Now we do same routine for the fractal-fractional derivative with exponential kernel

$$\begin{array}{ccc}\hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}S& =& S_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}C& =& C_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}I& =& I_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}R& =& R_1(t,S,C,I,R,D)\hfill \\ \hfill {}_0^{FFE}{D}_t^{\alpha ,\beta \left(t\right)}D& =& D_1(t,S,C,I,R,D)\hfill \end{array}$$ (135)

where the operator has constant fractional and variable fractal dimension. The above equation can be reformulated as follows;

$$\begin{array}{c}\hfill S\left(t_{\delta +1}\right)=S\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times S_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times S_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{S}_1(\tau ,S,C,I,R,D)[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$ (136)

$$\begin{array}{c}\hfill C\left(t_{\delta +1}\right)=C\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times C_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times C_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{C}_1(\tau ,S,C,I,R,D)[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill I\left(t_{\delta +1}\right)=I\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times I_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times I_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{I}_1(\tau ,S,C,I,R,D)[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill R\left(t_{\delta +1}\right)=R\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times R_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times R_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{R}_1(\tau ,S,C,I,R,D)[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill D\left(t_{\delta +1}\right)=D\left(t_{\delta }\right)+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times D_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times D_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}{\int }_{t_{\delta }}^{t_{\delta +1}}{D}_1(\tau ,S,C,I,R,D)[\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\end{array}$$

If we do same routine, we have the following numerical approximation

$$\begin{array}{c}\hfill S^{\delta +1}=S^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times S_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times S_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times S_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times S_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times S_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$ (137)

$$\begin{array}{c}\hfill C^{\delta +1}=C^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times C_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times C_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times C_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times C_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times C_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=I^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times I_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times I_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times I_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times I_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times I_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=R^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times R_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times R_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times R_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times R_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times R_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=D^{\delta }+\frac{1-\alpha }{M\left(\alpha \right)}\left[\begin{array}{c}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times D_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ -t_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times D_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\end{array}\right]\\ \hfill +\frac{\alpha }{M\left(\alpha \right)}\left\{\begin{array}{c}\frac{23}{12}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \times D_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\Delta t\\ -\frac{4}{3}{t}_{\delta -1}^{2-\beta \left(t_{\delta -1}\right)}(-\frac{\beta \left(t_{\delta }\right)-\beta \left(t_{\delta -1}\right)}{\Delta t}\ln t_{\delta -1}+\frac{2-\beta \left(t_{\delta -1}\right)}{t_{\delta -1}})\\ \times D_1(t_{\delta -1},S\left(t_{\delta -1}\right),C\left(t_{\delta -1}\right),I\left(t_{\delta -1}\right),R\left(t_{\delta -1}\right),D\left(t_{\delta -1}\right))\Delta t\\ +\frac{5}{12}{t}_{\delta -2}^{2-\beta \left(t_{\delta -2}\right)}(-\frac{\beta \left(t_{\delta -1}\right)-\beta \left(t_{\delta -2}\right)}{\Delta t}\ln t_{\delta -2}+\frac{2-\beta \left(t_{\delta -2}\right)}{t_{\delta -2}})\\ \times D_1(t_{\delta -2},S\left(t_{\delta -2}\right),C\left(t_{\delta -2}\right),I\left(t_{\delta -2}\right),R\left(t_{\delta -2}\right),D\left(t_{\delta -2}\right))\Delta t\end{array}\right\}.\end{array}$$

For Mittag-Leffler kernel,

$$\begin{array}{c}\hfill S\left(t_{\delta +1}\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times S_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{S}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$ (138)

$$\begin{array}{c}\hfill C\left(t_{\delta +1}\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times C_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{C}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill I\left(t_{\delta +1}\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times I_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{I}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill R\left(t_{\delta +1}\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times R_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{R}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill D\left(t_{\delta +1}\right)=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times D_1(t_{\delta },S\left(t_{\delta }\right),C\left(t_{\delta }\right),I\left(t_{\delta }\right),R\left(t_{\delta }\right),D\left(t_{\delta }\right))\\ \hfill +\frac{\alpha }{AB\left(\alpha \right)\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{D}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\end{array}$$

Thus, we can present the following scheme for numerical solution of our equation

$$\begin{array}{c}{S}^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\hfill \\ \times S_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\hfill \\ \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times S_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\hfill \\ +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times S_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times S_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\hfill \\ \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\hfill \end{array}$$ (139)

$$\begin{array}{c}\hfill C^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times C_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times C_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times C_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times C_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times I_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times I_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times I_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times I_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times R_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times R_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times R_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times R_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=\frac{1-\alpha }{AB\left(\alpha \right)}{t}_{\delta }^{2-\beta \left(t_{\delta }\right)}(-\frac{\beta \left(t_{\delta +1}\right)-\beta \left(t_{\delta }\right)}{\Delta t}\ln t_{\delta }+\frac{2-\beta \left(t_{\delta }\right)}{t_{\delta }})\\ \hfill \times D_1(t_{\delta },S^{{}_{\delta }},C^{{}_{\delta }},I^{{}_{\delta }},R^{{}_{\delta }},D^{{}_{\delta }})\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{AB\left(\alpha \right)\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times D_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{\alpha {\left(\Delta t\right)}^{\alpha }}{2AB\left(\alpha \right)\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times D_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times D_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

For power-law kernel,

$$\begin{array}{c}\hfill S\left(t_{\delta +1}\right)=S_0+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{S}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$ (140)

$$\begin{array}{c}\hfill C\left(t_{\delta +1}\right)=C_0+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{C}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill I\left(t_{\delta +1}\right)=I_0+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{I}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill R\left(t_{\delta +1}\right)=R_0+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{R}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau \end{array}$$

$$\begin{array}{c}\hfill D\left(t_{\delta +1}\right)=D_0+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{t_{\delta +1}}{D}_1(\tau ,S,C,I,R,D){(t_{\delta +1}-s)}^{\alpha -1}\\ \hfill \times [-\beta \prime \left(\tau \right)\ln \left(\tau \right)+\frac{2-\beta \left(\tau \right)}{\tau }]{\tau }^{2-\beta \left(\tau \right)}d\tau .\end{array}$$

Thus, we can present the following scheme for numerical solution of our equation

$$\begin{array}{c}\hfill S^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times S_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times S_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times S_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times S_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\end{array}$$ (141)

$$\begin{array}{c}\hfill C^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times C_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times C_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times C_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times C_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

$$\begin{array}{c}\hfill I^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times I_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times I_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times I_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times I_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

$$\begin{array}{c}\hfill R^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times R_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times R_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times R_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times R_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

$$\begin{array}{c}\hfill D^{\delta +1}=\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +1)}\sum _{\mu =2}^n{t}_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \hfill \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})[{(\delta -\mu +1)}^{\alpha }-{(\delta -\mu )}^{\alpha }]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{\Gamma (\alpha +2)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times D_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ -t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }(\delta -\mu +3+2\alpha )\\ -{(\delta -\mu )}^{\alpha }(\delta -\mu +3+3\alpha )\end{array}\right]\\ \hfill +\frac{{\left(\Delta t\right)}^{\alpha }}{2\Gamma (\alpha +3)}\sum _{\mu =2}^{\delta }\left[\begin{array}{c}{t}_{\mu }^{2-\beta \left(t_{\mu }\right)}[-\frac{\beta \left(t_{\mu +1}\right)-\beta \left(t_{\mu }\right)}{\Delta t}\ln t_{\mu }+\frac{2-\beta \left(t_{\mu }\right)}{t_{\mu }}]\\ \times D_1(t_{{}_{\mu }},S^{\mu },C^{\mu },I^{\mu },R^{\mu },D^{\mu })\\ -2t_{\mu -1}^{2-\beta \left(t_{\mu -1}\right)}[-\frac{\beta \left(t_{\mu }\right)-\beta \left(t_{\mu -1}\right)}{\Delta t}\ln t_{\mu -1}+\frac{2-\beta \left(t_{\mu -1}\right)}{t_{\mu -1}}]\\ \times D_1(t_{{}_{\mu -1}},S^{\mu -1},C^{\mu -1},I^{\mu -1},R^{\mu -1},D^{\mu -1})\\ +t_{\mu -2}^{2-\beta \left(t_{\mu -2}\right)}[-\frac{\beta \left(t_{\mu -1}\right)-\beta \left(t_{\mu -2}\right)}{\Delta t}\ln t_{\mu -2}+\frac{2-\beta \left(t_{\mu -2}\right)}{t_{\mu -2}}]\\ \times D_1(t_{{}_{\mu -2}},S^{\mu -2},C^{\mu -2},I^{\mu -2},R^{\mu -2},D^{\mu -2})\end{array}\right]\\ \hfill \times \left[\begin{array}{c}{(\delta -\mu +1)}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(3\alpha +10)(\delta -\mu )\\ +2{\alpha }^2+9\alpha +12\end{array}\right]\\ -{(\delta -\mu )}^{\alpha }\left[\begin{array}{c}2{(\delta -\mu )}^2+(5\alpha +10)(\delta -\mu )\\ +6{\alpha }^2+18\alpha +12\end{array}\right]\end{array}\right].\end{array}$$

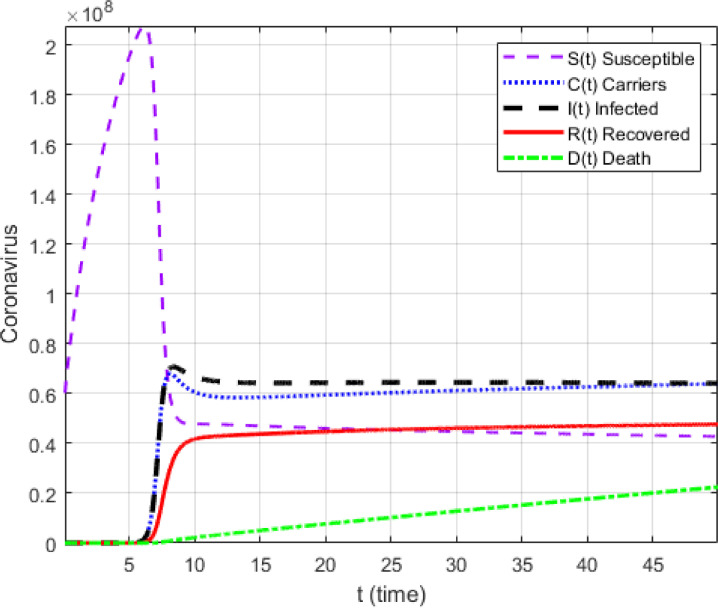
15. Numerical simulation

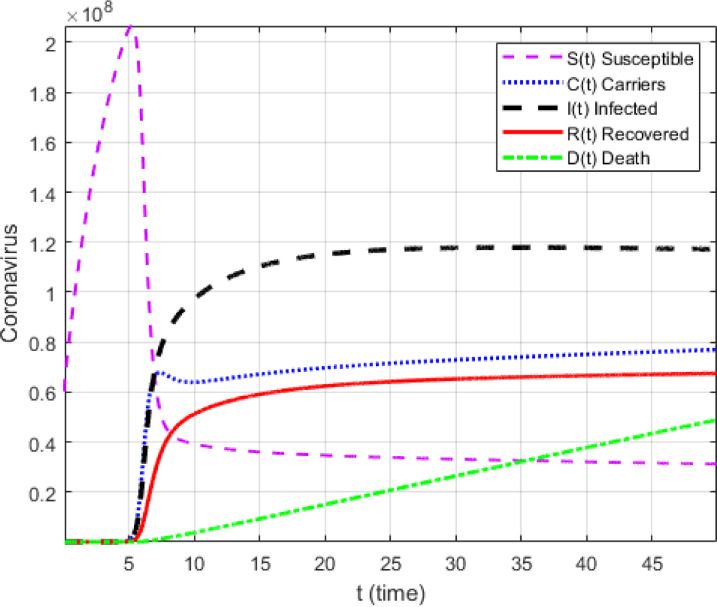
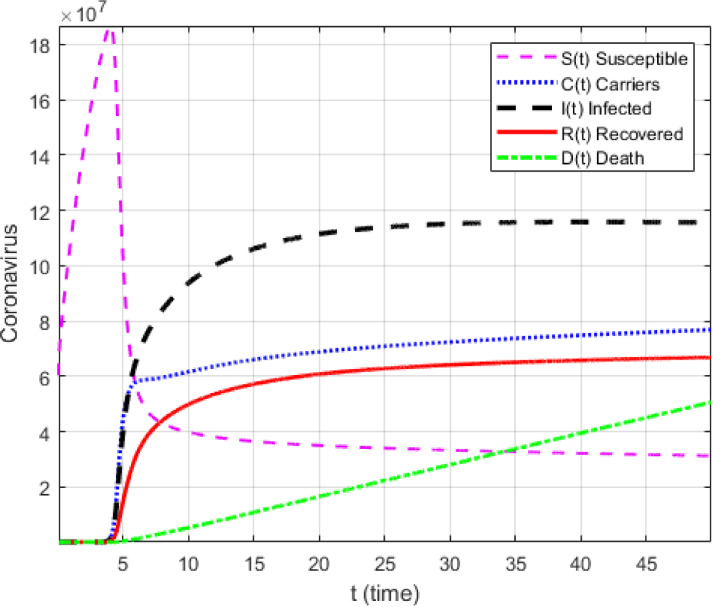
It is an old belief that an image or picture is worth a 1000 words. In this section, we use the suggested numerical scheme to present numerical simulations of the suggested model with the Mittag-Leffler kernel. To achieve this, we use the initial condition given in the early statistics. Two cases are presented, the first case without the effect of lock-down and the second with the lock-down effect where the contact parameter is reduced to zero. The simulations are presented in Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16 . In the first case where there is no lock-down, numerical simulations show an exponential growth of number of carriers, deaths and infected populations, a clear indication of the impact of no lock-down on the number of fatalities. The simulations are against those who believe that, all humans must be infected to get immunized. Such reasoning is very idealistic, immature and deadly. Humanity could disappear if such scenarios are fostered as the disease takes only around 14 or plus days to destroy human lungs and other parts. With implementation of lock-down the simulation shows a decline in deaths, carriers and infected numbers, a clear indication that while waiting for an adequate vaccine and cure, the lock-down is the perfect measure to help flatten the curves of death, carriers and infected. It is therefore important for humans to observe with great care measures put in place for the lock-down.

$$\begin{array}{ccc}\hfill D_t^{\alpha ,\beta }S& =& \Lambda -\frac{\lambda SD}{N}-(k{e}^{-x}p\left(\frac{I+wC}{N}\right)+\mu )S+\eta R\hfill \\ \hfill D_t^{\alpha ,\beta }C& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)\theta S+\frac{\lambda SD}{N}-(\beta +\mu +\pi )C\hfill \\ \hfill D_t^{\alpha ,\beta }I& =& k{e}^{-x}p\left(\frac{I+wC}{N}\right)(1-\theta )S+\pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill D_t^{\alpha ,\beta }R& =& \beta C+\tau I-(\mu +\eta )R\hfill \\ \hfill D_t^{\alpha ,\beta }D& =& \sigma I\hfill \end{array}$$

with the initial conditions

$$S\left(0\right)=6.03\times {10}^7,C\left(0\right)=20,I\left(0\right)=3,R\left(0\right)=0,D\left(0\right)=0.$$

Here the parameters can be taken as

$$\begin{array}{ccc}\hfill \Lambda & =& 6.04\times {10}^7,\lambda =0.5,k=2,x=0.3,p=.6,w=0.8,\mu =0.2,\hfill \\ \hfill \eta & =& 0.6,\theta =0.6,\beta =0.4,\pi =0.2,\tau =0.2,\sigma =0.01.\hfill \end{array}$$

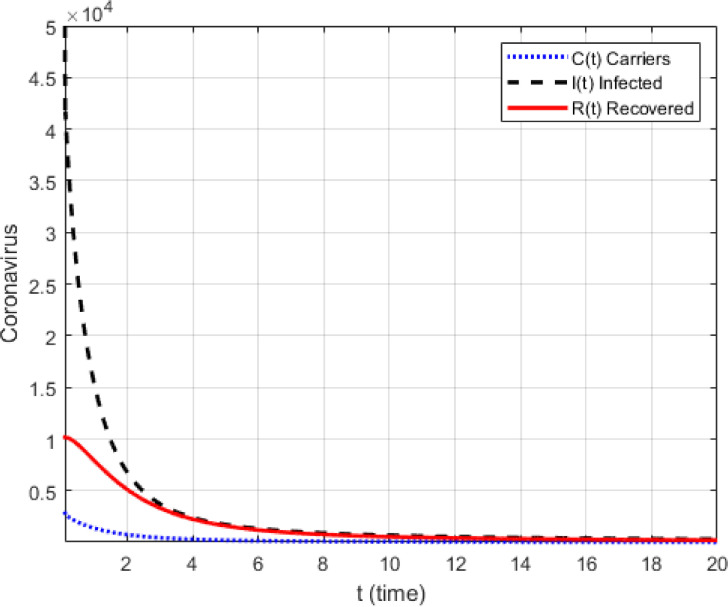
Fig. 11.

Numerical simulation for corona model with exponential kernel for $\alpha =0.88,\beta =0.92$.

Fig. 12.

Numerical simulation for corona model with Mittag-Leffler kernel for $\alpha =0.83,\beta =0.85$.

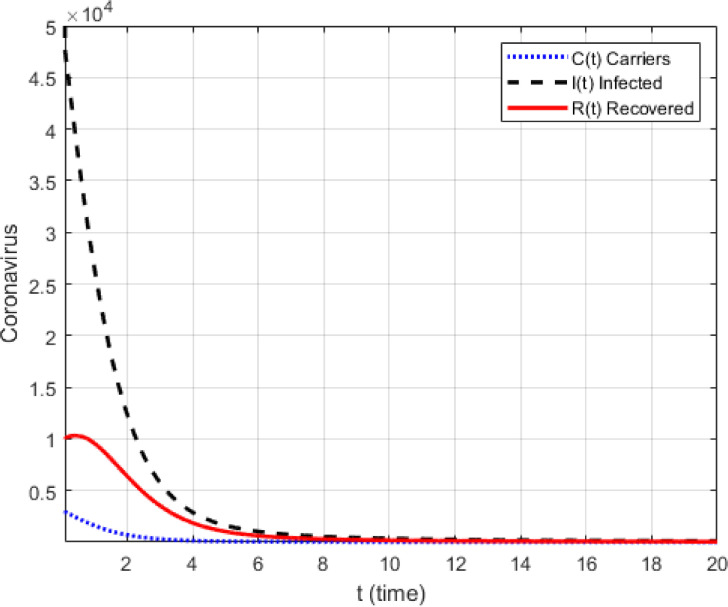
Fig. 13.

Numerical simulation for corona model with power-law kernel for $\alpha =0.8,\beta =0.91$.

Fig. 14.

Numerical simulation for corona model with exponential kernel for $\alpha =0.86,\beta =0.9.$

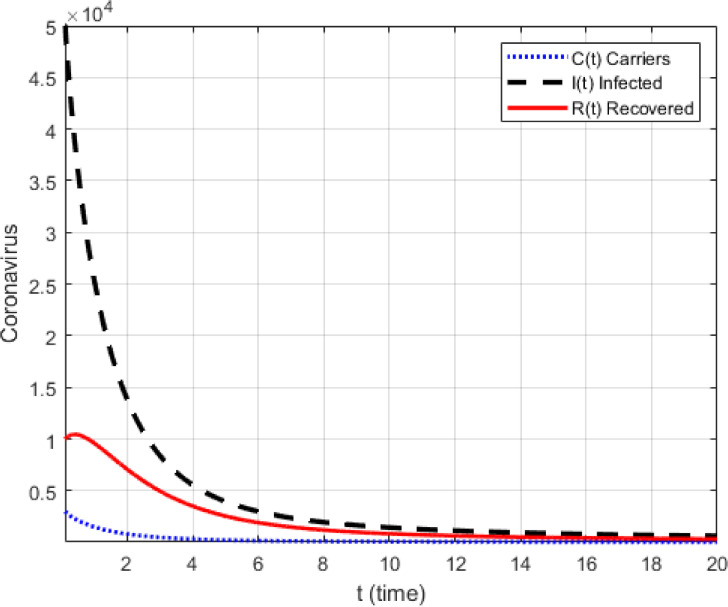
Fig. 15.

Numerical simulation for corona model with Mittag-Leffler kernel for $\alpha =0.9,\beta =0.51$.

Fig. 16.

Numerical simulation for corona model with power-law kernel for $\alpha =0.87,\beta =0.94$.

With lock-down, the following model is considered in Fig. 14, Fig. 15, Fig. 16.

$$\begin{array}{ccc}\hfill D_t^{\alpha ,\beta }S& =& \Lambda -\mu S+\eta R\hfill \\ \hfill D_t^{\alpha ,\beta }C& =& -(\beta +\mu +\pi )C\hfill \\ \hfill D_t^{\alpha ,\beta }I& =& \pi C-(\tau +\mu +\sigma )I\hfill \\ \hfill D_t^{\alpha ,\beta }R& =& \beta C+\tau I-(\mu +\eta )R\hfill \end{array}$$

where initial conditions are

$$S\left(0\right)=600000,C\left(0\right)=3000,I\left(0\right)=50000,R\left(0\right)=10000,D\left(0\right)=3000.$$

16. Conclusion

While mathematical models do not provide a cure for a given infectious disease,they are however used to replicate possible scenarios of the dynamic at hand. The new deadly COVID-19 outbreak in Wuhan China, has led to millions of infected, more than 150,000 deaths around the globe. Researchers and many other sectors have devoted their attention to flatten the curve of infection and deaths in the last past months. While humanity is waiting for a possible vaccine, they have introduced temporary measures including lock-down and social distancing to help control the spread and save lives from all corners of the globe. In this paper, using data from Italy, we presented some basic statistical figures to give an indication of the spread profile. These results helped to construct a mathematical model that takes into account the effect of lock-down. New fractal-fractional differential and integral operators were proposed and applied to the introduced mathematical model. Some numerical simulations indicated the efficiency of the lock-down. In our future work, we will include the effect of vaccine.

Credit Author Statement

I confirm that I am the sole author of this paper.

Declaration of Competing Interest

None.