An Advanced Deep Learning Model for Short-Term Forecasting U.S. Natural Gas Price and Movement

Abstract

Natural gas constitutes one of the most actively traded energy commodity with a significant impact on many financial activities of the world. The accurate natural gas price prediction and the direction of price changes are considered essential since these forecasts are utilized in energy sustainability planning, commodity trading and decision making, covering both the supply and demand side of natural gas market. In this research, a new deep learning prediction model is proposed for short-term forecasting natural gas price and movement. The proposed forecasting model exploits the ability of convolutional layers for providing a deep insight in natural gas data and the efficiency of LSTM layers for learning short-term and long-term dependencies. Additionally, a significant advantage of the proposed model is its abilities to predict the price of natural gas on the following day (regression) and also to predict if the price on the next day will increase, decrease or stay stable (classification) with respect to today’s price. The conducted series of experiments demonstrated that the proposed model considerably outperforms state-of-the-art deep learning and machine learning models.

Introduction

Crude oil and natural gas play strategic roles in socio-economic development around the world and global demand for energy is continuously rising because developed countries consume large amounts of energy, while demand in developing countries is increasing. They constitute the major energy sources for the global economy and price forecasting is significant for a variety of reasons including energy investment, policy decisions, portfolio diversification and hedging capabilities. Benchmarks for the crude oil include the Brent crude oil from four different fields in the North Sea, the Forties Blend, the Oseberg and Ekofisk, the Western Texas Intermediate extracted from U.S. wells and sent via pipeline to Oklahoma and the Dubai/Oman which consists a “basket” product from Middle East. Natural gas benchmark prices are the U.S. Henry hub natural gas, the Russian natural gas border price in Germany and the Indonesian Liquefied natural gas price in Japan.

Governments tighten up environmental regulations, seeking alternative energy sources to meet energy demand via reduction of the dependency on oil, with natural gas representing an economically viable alternative solution. While the three natural gas benchmarks exhibited a co-movement, there was a deviation (decoupling effect) of the U.S. natural gas [3, 9, 11], hereinafter referred as natural gas, after the Global Financial Crisis. The rapidly increasing demand for energy by emerging markets, along with the production decrease by the Organization of Petroleum Exporting Countries (OPEC) in Middle East, resulted in high oil and natural gas prices for three years. In U.S., the hydraulic fracturing (fracking) technique used to recover gas and oil from shale rocks reduced the overall production costs and therefore the natural gas price. This was reinforced by the locality of the market since unlike oil, natural gas is difficult to transport without a pipeline, unless it is liquefied which is costly. As a result, the prediction of natural gas price can potentially assist governments and financial investors for making their investment policies, gain significant profits and decrease their risks. Nevertheless, the accurate natural gas forecasting is generally considered, due to its chaotic nature, a complex and significantly challenging task.

During the last decade, significant deep learning techniques have been successfully applied in a variety of time-series forecasting problems [8, 13, 17]. These advanced techniques are probably the appropriate methods to extract knowledge from the noisy and chaotic nature of time-series data. Convolutional Neural Networks (CNNs) and LSTM networks constitute the most popular and widely utilized deep learning techniques. CNNs are based on convolutional layers which extract more valuable features by filtering out the noise of the input data while LSTM models are based on LSTM layers which capture sequence pattern information due to their distinct architecture. Nevertheless, classical CNNs are well suited to deal with spatial autocorrelation data, they are not usually adapted to correctly identify complex and temporal dependencies [1] while LSTM networks although they are dedicated to cope with temporal correlations, they manage only the features in the training set. Thus, a time-series prediction model which adopts the benefits of both techniques may significantly improve the forecasting performance.

In this work, we propose a new prediction model for short-term forecasting natural gas price which is based on the idea of exploiting the advantages of deep learning techniques. The proposed forecasting model exploits the capability of convolutional layers for learning the internal representation of the natural gas data and extracting useful patterns as well as the efficiency of LSTM layers for identifying short and long term dependencies. Additionally, the proposed prediction model has also ability of predicting the natural gas movement direction (increase, decrease or stay stable) of the next day with respect to today’s price. Our conducted numerical experiments illustrate that the proposed model considerably outperforms state-of-the-art deep learning and machine learning models for the prediction of the natural gas daily price and movement.

The remainder of this paper is organized as follows: Sect. 2 presents a survey of recent studies, regarding the application of machine learning techniques in natural gas forecasting. Section 3 presents a detailed description of the proposed advanced deep learning model. Section 4 presents the data collection and Sect. 5 presentes a series of numerical experiments. Section 6 discusses the findings of this research and presents our conclusions.

Natural Gas Forecasting: State of the Art

The recent developments of data mining and deep learning drew the attention of scientific community, attempting to gain significant insights on forecasting principal resources prices such as natural gas. During the last years, the problem of predicting the next day’s price of natural gas arises frequently, due to its significance as a profitable commodity. This led to the requirement and developement of new innovative forecasting models. In the sequel, we report the findings and outcomes from some rewarding studies regarding forecasting methodologies for natural gas price and movement.

Yu and Xu [16] proposed an improved back-propagation neural network model based on a combinational approach for short-term gas load forecasting. The proposed model was optimized by the real-coded genetic algorithm. They performed several modifications including an improved momentum factor and a self-adaptive learning rate as well as the determination of the initial weights and thresholds of the network by the genetic algorithm to avoid being trapped in local minimum. Such improvements exerted maximum performance of the neural network by accelerating the convergence speed and facilitating the forecasting efficiency. The data used in their research were recorded from Nov-2005 to Oct-2008 regarding natural gas load for Shanghai. Based on their preliminary numerical experiments, the authors stated that the proposed model was ideal for natural gas short-term load forecasting, presenting satisfactory prediction accuracy with a relatively small computation time.

Čeperić et al. [5] conducted a performance evaluation of traditional time-series models: Naive, AR and ARIMA as well as of the machine learning models: neural networks and strategic seasonality-adjusted support vector regression machines for short-term forecasting of Henry Hub spot natural gas prices. Additionally, they investigated the benefits of utilizing a feature selection technique as a pre-processing step. To evaluate the successfulness of the compated models in the short term forecasting of natural gas prices, they conducted a variety of numerical experiments ranging of different input variables and transformations, combinations of periods and window lengths. Their detailed experimental analysis illustrated the forecasting efficiency of machine learning models as well as the usefulness of feature selection techniques.

Merkel et al. [14] applied deep neural network methodologies for predicting natural gas short-term load. The authors utilized historical data from 62 operating areas from U.S. local distribution companies, covering a wide area of different geographical regions hence, represent a variety of climates. Their proposed model was evaluated against the traditional models: linear regression and artificial neural network. Their numerical experiments presented that the proposed deep learning model exhibited better short-term load forecasts on average. Moreover, they stated that even the much simpler linear regression model outperformed the proposed model, in some test cases. Finally, they concluded that although the deep learning techniques are a dominant option which usually outperforms simpler forecasting methods, it may not constitute the proper methodology for every operating area.

Nevertheless, none of the mentioned studies considered the adoption and combination of advanced deep learning techniques for natural gas price prediction and movement. Our contribution aims on imposing convolutional layers for learning the internal representation of the natural gas data and LSTM layers for efficiently identifying short-term and long-term dependencies. Moreover, in contrast to previous research studies, we provide performance evaluation of various deep learning and machine learning models for both regression and classification problems.

CNN-LSTM Model for Short-Term Forecasting Natural Gas

The main contribution of this research is the development of a forecasting model, named CNN-LSTM, utilizing advanced deep learning techniques for the short-term prediction of natural gas price and movement. The proposed model is based on of two main components.

The first component consists 2 convolutional layers of 32 and 64 filters of size (2, ), using same padding. Convolutional layers are specially designed data preprocessing layers which filter the input data for learning their internal representation. More specifically, the convolution kernel, called filter, can be considered as a tiny window which “slides” through each input instance and applies complex mathematical operations (convolutions) on each sub-region which this specified window “meets”. The application of several convolution kernels on the input data, results in the development of new convolved features which are usually more useful than the original ones.

The second component consists of a LSTM layer of 70 units and a dense layer of 16 neurons. LSTM layers process the generated features in order to identify short-term and long-term dependencies in the times series and provide an accurate prediction. Memory blocks and adaptive gate units constitute the major novelty of a LSTM layer. The former contain memory cells with self-connections for memorizing the temporal state while the latter control the information flow in the memory block. With the treatment of the hidden layer as a memory unit, LSTM can cope the correlation within time-series in both short and long term.

An overview of the proposed CNN-LSTM forecasting model architecture is depicted in Fig. 1.

Fig. 1.

CNN-LSTM forecasting model architecture

Data

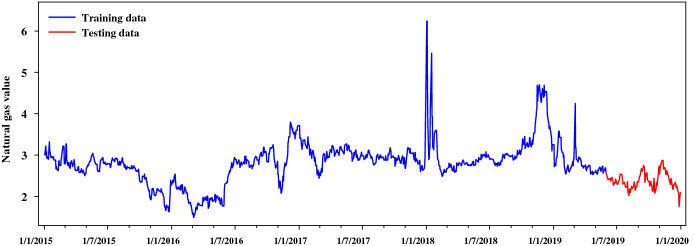
The data utilized in this research concern the daily natural gas prices in USD from Jan-2015 to Dec-2019 which were obtained from U.S. Energy Information Administration (www.eia.gov). Table 1 summarizes the descriptive statistics including the measures: Minimum, Mean, Maximum, Median, Standard Deviation (Std. Dev.), Skewness and Kurtosis.

Table 1.

Descriptive statistics for natural gas daily prices

Minimum	Mean	Maximum	Median	Std. Dev	Skewness	Kurtosis
1.49	2.75	6.24	2.78	0.37	0.98	5.25

The data were divided into training set and testing set. The training set consists of natural gas daily prices from 01-Jan-2015 to 31-Dec-2018 (1129 days) which ensures an adequate range of long and short-term trends. The testing set consists of daily prices from 01-Jan-2018 to 31-Dec-2019 (146 days) which ensures a substantial amount of unseen “out-of-sample” data for evaluating the compared forecasting models.

At this point, it is worth mentioning that in any attempt to increase the training dataset utilizing prices from past years, lead to the reduction of the performance of all evaluated forecasting models.

Fig. 2.

Daily natural gas prices trend from January 2015 to December 2019

Experimental Methodology

In this section, we evaluate the performance of the proposed forecasting model against LSTM forecasting models and the state-of-the-art machine learning models: Support Vector Regression (SVR) [7], Artificial Neural Network (ANN) [6] and Decision Tree Regression (DTR) [2]. For fairness and for performing an objective comparison, the hyper-parameters of all algorithms were selected in order to maximize their experimental performance. A brief description of the specification of each prediction model and its hyper-parameters is presented in Table 2.

Table 2.

Parameter specification of state-of-art machine learning and deep learning forecasting models

Model	Description
SVR	Kernel = RBF, ,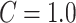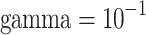
ANN	1 hidden layer with 20 neurons and an output layer of 1 neuron
DTR	Criterion = ‘mse’, max depth = unlimited, min samples split = 2
LSTM	LSTM layer with 70 units
	Output layer with 1 neuron
LSTM	LSTM layer with 70 units
	Dense layer with 8 neurons
	Output layer with 1 neuron
LSTM	LSTM layer with 70 units
	LSTM layer with 30 units
	Output layer with 1 neuron
LSTM	LSTM layer with 50 units
	LSTM layer with 20 units
	Dense layer with 8 neurons
	Output layer with 1 neuron

The implementation code was written in Python 3.4 on a PC (Intel(R) Core(TM) i7-6700HQ CPU 2.6GHz, 16 Gbyte RAM) while the deep learning and machine learning models were implemented using Keras library [10] and Scikit-learn library [15], respectively. Notice that all LSTM models, the ANN as well as the proposed CNN-LSTM model were trained utilizing Adaptive Moment Estimation (ADAM) algorithm for 100 epochs with a batch size equal to 128 and a mean-squared loss function which reported the best overall results.

The regression performance of all forecasting models was measured using the performance metrics: Root Mean Square Error (RMSE) metric and the Mean Absolute Error (MAE). Furthermore, regarding the classification problem of predicting whether the natural gas price on the next day would increase (Up), decrease (Down) or stay stable (−) with respect to today’s price, the performance of each model was evaluated using the performance metrics: Accuracy (Acc), Area Under Curve (AUC) and 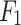-score (). In this research, we utilized three different prices for the forecasting horizon, namely 4, 6 and 12. The forecasting horizon F stands for the number of natural gas daily prices which are taken into consideration by each model for predicting the daily price on the following day. Its price is critical for the efficiency of an intelligent forecasting model [12].

Tables 3, 4 and 5 present the performance of the proposed CNN-LSTM forecasting model against the state-of-the-art prediction models, relative to forecasting horizon 4, 6 and 12, respectively. It is worth mentioning that for each performance metric the best performance was highlighted in bold. Regarding the natural gas price prediction problem, CNN-LSTM and SVR highlighted the lowest RMSE and MAE score, followed by ANN and LSTM models which exhibited similar regression performance. Regarding the classification problem of predicting if the price will increase, decrease or stay stable on the following day, CNN-LSTM exhibited the best performance considerably outperforming all other state-of-the-art models. More specifically, CNN-LSTM reported 55.25%, 55.03% and 53.97% accuracy for forecasting horizon equal to 4, 6 and 12, respectively, followed by LSTM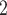 which reported 50.69%, 50.69% and 49.44%, in the same situations. Moreover, CNN-LSTM exhibited the best (highest) AUC for all prices of forecasting horizon and the best 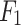-score for 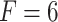and .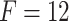

Table 3.

Performance comparison of the CNN-LSTM model against traditional regression models for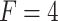

Model	RMSE	MAE	Acc	AUC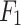
ANN	0.113	0.087	51.53%	0.651	0.584
SVR	0.093	0.067	50.69%	0.638	0.565
DTR	0.125	0.100	47.22%	0.578	0.473
LSTM	0.109	0.083	49.44%	0.632	0.557
LSTM	0.112	0.086	50.69%	0.656	0.638
LSTM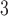	0.110	0.084	49.44%	0.618	0.532
LSTM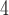	0.111	0.084	50.07%	0.605	0.508
CNN-LSTM	0.093	0.067	55.25%	0.680	0.571

Table 4.

Performance comparison of the CNN-LSTM model against traditional regression models for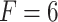

Model	RMSE	MAE	Acc	AUC
ANN	0.106	0.081	50.14%	0.651	0.579
SVR	0.092	0.067	48.61%	0.633	0.566
DTR	0.125	0.099	47.64%	0.578	0.472
LSTM	0.107	0.082	51.36%	0.643	0.566
LSTM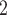	0.102	0.077	50.69%	0.631	0.553
LSTM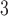	0.106	0.080	49.86%	0.634	0.561
LSTM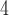	0.114	0.087	50.83%	0.618	0.527
CNN-LSTM	0.093	0.067	55.03%	0.674	0.589

Table 5.

Performance comparison of the CNN-LSTM model against traditional regression models for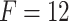

Model	RMSE	MAE	Acc	AUC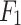
ANN	0.119	0.092	49.86%	0.629	0.550
SVR	0.094	0.069	48.39%	0.635	0.558
DTR	0.128	0.099	50.97%	0.592	0.482
LSTM	0.111	0.086	48.33%	0.632	0.563
LSTM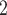	0.109	0.084	49.44%	0.628	0.551
LSTM	0.104	0.079	51.67%	0.649	0.579
LSTM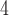	0.127	0.100	49.31%	0.624	0.545
CNN-LSTM	0.104	0.078	53.97%	0.670	0.620

Next, we demonstrate a deeper insight about the classification efficiency of the proposed forecasting model CNN-LSTM by presenting the confusion matrix regarding all forecasting horizons and compare it with that of the LSTM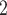 model which presented the best performance among state-of-the-art models. The confusion matrix can be considered as a complete evaluation methodology for describing and depicting in a compact way, valuable and useful information, regarding to a model’s forecasting performance.

Tables 6 and 7 present the confusion matrices of LSTM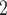 and CNN-LSTM, respectively. Notice that each row and each column of all confusion matrices represent the instances in an actual and in a predicted class, respectively. Firstly, based on the presented confusion matrices we can easily conclude that the exclusive prediction accuracy of the “Stable” class is very high for both compared prediction model. Additionally, the CNN-LSTM model managed to exhibit the best distribution of correctly identified instances per class for every forecasting horizon. This probably means that this model managed to keep a balance on learning the patterns which describe every class, consisting in total a more reliable and robust prediction model. In contrast, the LSTM model seems to be significantly biased since it misclassified most “Down” instances as “Up”. This implies that it ignored most data patterns and information which describe and seperate “Up” and “Down” classes.

Table 6.

Confusion matrices of LSTM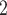 model for forecasting horizon 4, 6 and 12

Table 7.

Confusion matrices of CNN-LSTM model for forecasting horizon 4, 6 and 12

Summarizing, it is worth mentioning that the interpretation of Tables 3, 4, 5, 6 and 7 highlight that CNN-LSTM model is generally preferable for forecasting natural gas price and movement, considerably outperforming traditional state-of-the-art models in both regression and classification tasks.

In the sequel, we evaluate the forecasting reliability of the proposed model CNN-LSTM, by performing a test of autocorrelation in the residuals [4]. This test examines the presence of autocorrelation between the residuals (differences between predicted and actual prices) which in case it exists, implies that the forecasting model may be inefficient, since it did not manage to capture all the possible information contained in the training set. Two significant tools for testing the autocorrelation of the residuals are the Auto-Correlation Function (ACF) plot and the Ljung-Box Q-test. The ACF [4] is obtained from the linear correlation of each residual to the others in different lags and illustrates the intensity of the temporal auto-correlation. The portmanteau Ljung-Box Q-test [4] assesses the null hypothesis (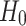) that “a series of residuals exhibits no autocorrelation for a fixed number of lags”.

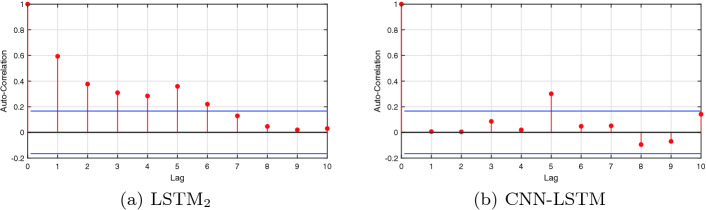
Figures 3, 4 and 5 present the Auto-Correlation Function (ACF) plot of LSTM and CNN-LSTM, for forecasting horizon equal to 4, 6 and 12, respectively. Notice that the confident limits (blue line) are constructed assuming that the residuals follow a Gaussian probability distribution. The ACF plot of CNN-LSTM are within 95% percent confidence interval for all lags regarding 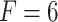, which verifies that the residuals have no auto-correlation while for 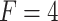and 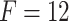the ACF plots present a small spike at lag 5, which reveal that there exists some negligibly autocorrelation in the residuals. In contrast, the ACF plots of LSTM indicated that the assumption of no auto-correlation in the errors is violated which suggests that the model’s forecasts may be inefficient, relative to all utilized prices of the forecasting horizon.

Fig. 3.

ACF plots on the residuals of LSTM and CNN-LSTM for

Fig. 4.

ACF plots on the residuals of LSTM and CNN-LSTM for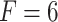

Fig. 5.

ACF plots on the residuals of LSTM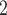 and CNN-LSTM for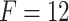

Table 8 reports the statistical analysis, performed by Ljung-Box Q-test for 10 lags with significance level 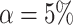. The portmanteau test suggests that the CNN-LSTM model does not violate the assumption of no autocorrelation in the errors for 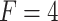and which implies that its forecasts may be efficient; while for the LSTM model, it suggests that there exists significant autocorrelation in the residuals at the 5% level.

Table 8.

Ljung-Box Q-test for 10 lags with significance level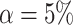

Model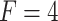
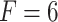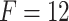	p-value		p-value		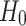p-value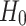
LSTM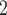	0.0001	Rejected	0.0270	Rejected	0	Rejected
CNN-LSTM	0.0974	Accepted	0.1072	Accepted	0.0207	Rejected

Discussion and Conclusions

In this section, we perform a discussion regarding the numerical performance of our proposed CNN-LSTM model for forecasting natural gas price and movement as well as the main findings and the limitations of this research.

The main contribution of this work is the development of a new forecasting model for the short-term prediction of natural gas price and movement. The proposed forecasting model exploits the capability of convolutional layers for learning the internal representation of the natural gas data and the efficiency of LSTM layers for identifying short-term and long-term dependencies. A significant advantage of the model is that it has the ability to predict the price of natural gas on the next day (regression) and also predicts if the price on the next day will increase, decrease or stay stable (classification) with respect to today’s price. The presented numerical experiments highlighted that although LSTM models constitute a wide and efficient choice for addressing time-series problems, their use along with convolutional layers could provide a significant boost in increasing the forecasting performance.

The problem of forecasting natural gas price and movement can be considered to belong on chaotic time series problems. This means that accurate and reliable predictions are almost impossible since these problems are close to random walk processes, while the identification of possible existing patters and their proper distinguishment among a large pool of noisy instances, seems to be a significantly challenging task.

The proposed forecasting model managed to achieve a noticeable performance increase in terms of accuracy, compared to traditional state-of-the-art prediction models, although the RMSE and MAE scores were slightly better. One possible reason is that the feature preprocessing stage, provided by the convolutional layers, managed to restrict the noise of each input sequence instance, extracting valuable and meaningful feature maps which assisted the LSTM model on its final prediction task.

It is worth mentioning that in real world applications such as the decision support for investment tasks regarding to natural gas stocks, a prediction model which achieves high classification accuracy would be considered much more efficient and valuable, compared to a model with better regression performance but lower accuracy score, since these investment decisions follow a “buy, hold, sell” strategy based on the price movement predictions “Up, Stable, Down”. Therefore, the proposed model has a potential to assist trading and investment decisions forming up a reliable natural gas price movement predictor.

Finally, a limitation of the prediction model that it is unable to efficiently identify and report possible input sequences which can actually lead to more accurate predictions. This ability could be crucial and significant in real world applications, since investment and trading decisions would be performed just only when the model identified reliable and accurate patterns, while noisy and uncertain input signals would be totally ignored, leading to safer decisions and probably higher returns. This constitutes an interesting and promising idea, which we intend to pursue in our future research.