Abstract
Durante la crisis de salud internacional provocada por la pandemia de COVID-19, además de conocer los datos sobre contagios, muertes y ocupación de camas hospitalarias también es necesario hacer predicciones que ayuden a la gestión de la crisis por parte de las autoridades sanitarias. El presente trabajo tiene como objetivo describir la metodología utilizada para la elaboración de modelos predictivos de contagios y defunciones para la epidemia de COVID-19 en España basados en curvas de Gompertz. La metodología se aplica al total del país y a cada una de sus comunidades autónomas. De acuerdo con los datos oficiales publicados a la fecha de realización de este trabajo, y a través de los modelos descritos, estimamos un total de alrededor de 240.000 contagiados y 25.000 fallecidos al final de la epidemia. Pronosticamos el final de la epidemia entre los meses de junio y julio de 2020.
Palabras clave: COVID-19, Predicción, Mortalidad
Abstract
During the international health crisis caused by the COVID-19 pandemic, it is necessary not only to know the data on infections, deaths and the occupation of hospital beds, but also to make predictions that help health authorities in the management of the crisis. The present work aims to describe the methodology used to develop predictive models of infections and deaths for the COVID-19 epidemic in Spain, based on Gompertz curves. The methodology is applied to the country as a whole and to each of its Autonomous Communities. Based on the official data available on the date of this work, and through the models described, we estimate a total of around 240.000 infected and 25.000 deaths at the end of the epidemic. At a national level, we forecast the end of the epidemic between June and July 2020.
Keywords: COVID-19, Forecasting, Mortality
Introducción
Durante la crisis de salud internacional provocada por la pandemia de COVID-19 se hace necesario no solo conocer los datos sobre contagios, muertes y ocupación hospitalaria, sino también hacer predicciones que ayuden a la propia gestión de la crisis por parte de las autoridades sanitarias.
El presente trabajo tiene como objetivo describir la metodología utilizada para la elaboración de modelos predictivos de contagios y defunciones para la epidemia de COVID-19 en España. Los datos utilizados, desde el 4 de marzo hasta el 22 de abril de 2020, fueron los datos oficiales que ofrecía diariamente el Ministerio de Sanidad de España1.?
Exposición del método
Para las modelizaciones se siguió el siguiente esquema, simplificación del descrito por Lega y Brown2:
-
•
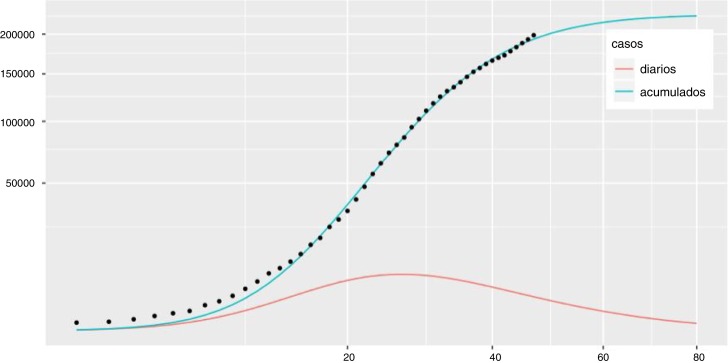
Paso 1: se ajustaron los valores acumulados a una curva G(t) (fig. 1 , curva de casos acumulados).
-
•
Paso 2: se calculó la primera derivada g(t) de la curva anterior (fig. 1, curva de casos diarios).
Figura 1.
Casos estimados en España según el modelo del día 19 de abril (día 47 de la serie de datos registrados). La curva de casos acumulados se corresponde con G(t) y la curva de casos diarios se corresponde con g(t). En el eje de abscisas aparece el día de la epidemia, considerando el inicio como el primer día de la serie de datos.
Con los datos acumulados diarios se calculó la curva de Gompertz3? de tres parámetros que mejor se ajustaba en cada caso a los datos:
Se utilizó el modelo de crecimiento de Gompertz en lugar de otros, como el logístico o el de Bertalanffy, por haber demostrado ser algo más preciso para predecir los casos acumulados fuera de la provincia china de Hubei4?, lugar donde se originó la pandemia de COVID-19.
Para el ajuste de la curva de Gompertz a los datos acumulados observados se usaron los algoritmos de Nelter-Mead5? implementados por Nash6. El software utilizado para los cálculos fue R 7? a través del paquete drc 8.
De esta manera obtuvimos modelizada la curva de casos acumulados, con la que pudimos estimar cuántos casos acumulados se observarían cualquier día determinado. Esta curva depende exclusivamente de los casos acumulados observados, ya que es la única información que la nutre.
El coeficiente a de la curva se corresponde con su asíntota superior, lo que puede interpretarse como el «horizonte» de la epidemia, esto es, el número de casos esperados al final de esta.
La primera derivada de la función anterior9, la interpretamos como la curva del número de casos diarios:
A través de ella se pueden calcular los valores esperados los días futuros. El punto donde esta función alcanza el máximo puede interpretarse como el pico de la epidemia.
Aplicación práctica
En el momento en que se publican nuevos datos diarios se vuelve a calcular un modelo según el esquema anterior para los contagios y otro para las defunciones en cada comunidad autónoma y para el total del país.
Para el presente trabajo se calcularon 50 modelos de contagios y 50 de fallecimientos para cada una de las comunidades autónomas (dos modelos diarios, desde el 4 de marzo hasta el 22 de abril, cada día un modelo).
Según esta metodología, el pico de contagios se alcanzó en España aproximadamente a finales de marzo, mientras que el pico de defunciones se estimó a primeros de abril de 2020. Los resultados concretos de los picos de las curvas, además de los horizontes, pueden consultarse en la app interactiva: https://www.easp.edu.es/data-apps/covid-easp/covid19_ESP/
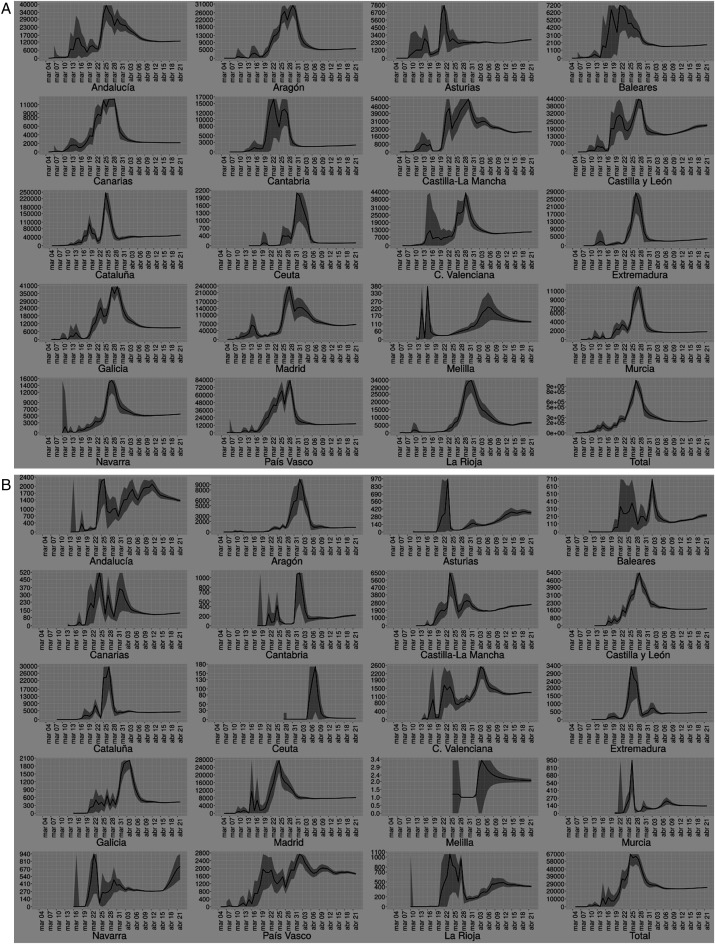
La figura 2 muestra la evolución de los horizontes (coeficientes a de los modelos) que se fueron calculando diariamente y a lo largo del tiempo. A modo de ejemplo, los modelos predecían más de 900.000 casos de contagio y unas 67.000 muertes en torno al 27 de marzo para el total de España, y a medida que se sucedieron los días estos horizontes estimados descendieron hasta situarse alrededor de 240.000 contagios y 25.000 fallecidos. A partir de los primeros días de abril, esas estimaciones permanecen estables a lo largo del tiempo. De manera general se observa que, en todos los casos, al principio el comportamiento de la serie de horizontes era algo errática, pero a medida que avanzaron los días el parámetro fue estabilizándose, lo cual se puede interpretar como medida de robustez de la estimación del número de contagiados y de fallecidos para cada comunidad autónoma.
Figura 2.
A). Evolución de los “horizontes” (coeficientes “a” de los modelos con los intervalos de confianza con un nivel de confianza del 95%) según se añadían nuevos datos diarios a las series estudiadas. Estos valores representan el número total de casos de contagio estimados al final de la epidemia para cada Comunidad Autónoma y para el total nacional.
A partir de las curvas de contagios diarios y de defunciones diarias (g(t)) se hizo una estimación de las fechas en que no se observarán más contagios ni más defunciones (tabla 1 ). Hay que hacer notar que tanto las predicciones de estas fechas como las de los horizontes son orientativas y no serán precisas si la situación epidemiológica varía sustancialmente.
Tabla 1.
Estimación de los coeficientes y de las fechas del fin de la epidemia según los datos a 22/4/2020
| Comunidad autónoma | Modelos de contagiados |
Modelos de fallecidos |
||||||
|---|---|---|---|---|---|---|---|---|
| b (IC95%) | a (IC95%) | c (IC95%) | Fecha fin | b (IC95%) | a (IC95%) | c (IC95%) | Fecha fin | |
| Andalucía | -0.102 (-0.106,-0.097) | 12701.872 (12449.056,12954.688) | 25.492 (25.204,25.78) | 10/06/20 | -0.084 (-0.088,-0.079) | 1375.354 (1322.365,1428.343) | 33.743 (33.179,34.307) | 05/06/20 |
| Aragón | -0.1 (-0.106,-0.095) | 5468.242 (5322.385,5614.099) | 27.084 (26.707,27.461) | 04/06/20 | -0.084 (-0.09,-0.079) | 880.491 (833.967,927.014) | 35.187 (34.43,35.944) | 01/06/20 |
| Asturias | -0.078 (-0.083,-0.073) | 2727.282 (2628.178,2826.386) | 25.458 (24.83,26.086) | 09/06/20 | -0.061 (-0.066,-0.056) | 351.555 (319.567,383.542) | 38.859 (37.219,40.5) | 05/06/20 |
| Baleares | -0.116 (-0.124,-0.107) | 1828.794 (1779.225,1878.363) | 23.256 (22.857,23.654) | 15/05/20 | -0.075 (-0.083,-0.067) | 223.425 (203.344,243.506) | 34.923 (33.49,36.356) | 18/05/20 |
| Canarias | -0.121 (-0.126,-0.116) | 2169.584 (2139.665,2199.502) | 22.922 (22.719,23.126) | 14/05/20 | -0.123 (-0.135,-0.112) | 123.78 (119.256,128.304) | 26.745 (26.271,27.22) | 23/04/20 |
| Cantabria | -0.113 (-0.125,-0.102) | 2140.596 (2056.683,2224.509) | 24.561 (24.002,25.12) | 18/05/20 | -0.081 (-0.089,-0.074) | 219.775 (203.95,235.599) | 34.6 (33.519,35.681) | 16/05/20 |
| Castilla-La Mancha | -0.088 (-0.092,-0.085) | 20389.014 (19938.915,20839.113) | 29.434 (29.107,29.762) | 29/06/20 | -0.083 (-0.086,-0.079) | 2619.466 (2538.272,2700.66) | 31.887 (31.413,32.362) | 12/06/20 |
| Castilla y León | -0.069 (-0.073,-0.064) | 22078.697 (20977.38,23180.014) | 31.945 (31.061,32.829) | 24/07/20 | -0.107 (-0.109,-0.105) | 1715.048 (1698.215,1731.88) | 29.785 (29.657,29.914) | 24/05/20 |
| Cataluña | -0.086 (-0.09,-0.081) | 49227.704 (47679.816,50775.591) | 27.969 (27.476,28.462) | 10/07/20 | -0.129 (-0.134,-0.123) | 4313.684 (4238.415,4388.953) | 27.729 (27.507,27.95) | 22/05/20 |
| Ceuta | -0.157 (-0.183,-0.131) | 115.651 (109.642,121.66) | 28.416 (27.846,28.987) | 21/04/20 | -0.262 (-0.393,-0.131) | 4.229 (3.926,4.533) | 30.558 (29.353,31.763) | 13/04/20 |
| C. Valenciana | -0.099 (-0.105,-0.094) | 11321.285 (11039.421,11603.15) | 25.324 (24.954,25.694) | 10/06/20 | -0.095 (-0.099,-0.091) | 1295.589 (1265.824,1325.353) | 30.546 (30.225,30.867) | 27/05/20 |
| Extremadura | -0.085 (-0.095,-0.074) | 3688.372 (3434.953,3941.79) | 26.766 (25.66,27.873) | 09/06/20 | -0.107 (-0.113,-0.102) | 446.697 (434.893,458.501) | 29.8 (29.454,30.146) | 11/05/20 |
| Galicia | -0.118 (-0.123,-0.113) | 8960.746 (8820.319,9101.173) | 26.091 (25.881,26.302) | 30/05/20 | -0.102 (-0.106,-0.097) | 429.271 (418.027,440.516) | 32.36 (32.024,32.697) | 15/05/20 |
| Madrid | -0.079 (-0.085,-0.074) | 67301.118 (64827.97,69774.266) | 26.79 (26.183,27.397) | 20/07/20 | -0.098 (-0.101,-0.096) | 8196.958 (8097.911,8296.005) | 26.119 (25.941,26.297) | 09/06/20 |
| Melilla | -0.086 (-0.095,-0.077) | 125.585 (119.102,132.067) | 24.356 (23.502,25.211) | 27/04/20 | -0.23 (-0.282,-0.177) | 2.059 (1.949,2.17) | 24.6 (23.781,25.42) | 13/04/20 |
| Murcia | -0.111 (-0.119,-0.103) | 1753.878 (1707.227,1800.529) | 23.685 (23.296,24.073) | 16/05/20 | -0.132 (-0.14,-0.125) | 131.682 (128.555,134.809) | 30.778 (30.505,31.051) | 27/04/20 |
| Navarra | -0.083 (-0.087,-0.08) | 5570.162 (5450.229,5690.095) | 26.716 (26.369,27.063) | 15/06/20 | -0.054 (-0.068,-0.04) | 717.719 (485.336,950.102) | 40.721 (34.291,47.151) | 25/06/20 |
| País Vasco | -0.089 (-0.093,-0.085) | 14460.898 (14126.727,14795.07) | 25.938 (25.58,26.296) | 21/06/20 | -0.063 (-0.065,-0.061) | 1714.421 (1662.367,1766.474) | 35.81 (35.261,36.36) | 26/06/20 |
| La Rioja | -0.057 (-0.063,-0.051) | 6587.953 (5963.087,7212.819) | 32.749 (30.823,34.675) | 23/07/20 | -0.074 (-0.078,-0.071) | 409.187 (392.912,425.462) | 34.138 (33.497,34.779) | 26/05/20 |
| Total | -0.085 (-0.089,-0.082) | 235897.171 (230282.564,241511.779) | 27.223 (26.849,27.596) | 28/07/20 | -0.094 (-0.096,-0.092) | 24582.574 (24249.75,24915.399) | 29.098 (28.903,29.293) | 26/06/20 |
IC95%: intervalo de confianza del 95%.
Coeficientes a, b y c de las curvas de Gompertz (G(t) y g(t)). La fechas de fin se calcularon resolviendo la ecuación g(t) = 0,75, esto es, el tiempo t en el que se esperaba menos de un caso en la curva de casos diarios g(t).
Conclusiones
Presentamos en este trabajo una metodología de fácil uso para modelizar epidemias como la de COVID-19. Consideramos que en esta sencillez radica su fortaleza, ya que se utilizan exclusivamente los datos sobre contagios y defunciones que después se predicen, sin contar con ningún tipo de covariable externa para su cálculo. Esto, por una parte, podría parecer una debilidad al no añadir más información a los modelos, pero así se evita el ruido que podrían introducir esas hipotéticas variables externas. Por otra parte, la ausencia de más información hace que la calidad de las predicciones dependa mucho de la calidad de los datos.
Hay que tener en cuenta que las predicciones de los modelos de contagios, sobre todo a partir de aproximadamente la tercera semana de abril de 2020, pueden sufrir grandes variaciones con respecto a los valores observados por los cambios en la definición de caso. No ocurre lo mismo con respecto a los modelos de defunciones, que son más robustos a lo largo del tiempo al no haber sufrido grandes cambios en su definición.
Con respecto a las fechas estimadas del fin de la epidemia en cada comunidad autónoma, hay que tener en cuenta que son estimaciones aproximadas y que pueden sufrir alteraciones si se producen cambios bruscos en las tendencias. De hecho, los modelos predecían horizontes de muchos más casos y defunciones a finales de marzo que a partir de la segunda quincena de abril, lo que puede deberse a las medidas de confinamiento tomadas por las autoridades, que tienen un efecto en las curvas de la epidemia a partir de al menos una semana desde su implantación10?.
En cuanto al fin de la epidemia, las fechas en las que se espera que no haya defunciones son anteriores a las fechas en las que se espera que no haya contagios, y esto tiene mucho sentido dado que no todas las personas contagiadas fallecerán y que el porcentaje de personas que sobreviven a la enfermedad es mucho mayor que el de las personas que fallecen.
En cualquier caso, en este trabajo presentamos una metodología utilizada para modelizar la epidemia de COVID-19 en España y en sus comunidades autónomas, y el valor que le damos es referente al contexto temporal de la epidemia, aunque somos conscientes de que pasada la crisis esta metodología puede ser matizada.
Editor responsable del artículo
Carlos Álvarez Dardet.
Contribuciones de autoría
Los dos autores han contribuido a la concepción del estudio, la redacción del manuscrito y la revisión de las distintas versiones. P. Sánchez Villegas realizó los análisis de los datos. Ambos se hacen responsables del contenido íntegro del trabajo.
Financiación
Ninguna.
Conflicto de intereses
Ninguno.
Bibliografía
- 1.Ministerio de Sanidad - Profesionales - Documentos técnicos para profesionales - Coronavirus. (Consultado el 24/4/2020.) Disponible en: https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov-China/documentos.htm.
- 2.Lega J., Brown H.E. Data-driven outbreak forecasting with a simple nonlinear growth model. Epidemics. 2016;17:19–26. doi: 10.1016/j.epidem.2016.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zwietering M.H., Jongenburger I., Rombouts F.M., et al. Modeling of the bacterial growth curve. Appl Environ Microbiol. 1990;56:1875–1881. doi: 10.1128/aem.56.6.1875-1881.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jia L., Li K., Jiang Y., et al. Prediction and analysis of coronavirus disease 2019. Cornell University; 2020 Disponible en: http://arxiv.org/abs/2003.05447. [Google Scholar]
- 5.Nelder J.A., Mead R. A simple method for function minimization. Comput J. 1965;7:308–313. Disponible en: https://academic.oup.com/comjnl/article-lookup/doi/10.1093/comjnl/7.4.308. [Google Scholar]
- 6.Nash J.C. Hilger; Bristol and New York: 1990. Compact numerical methods for computers: linear algebra and function minimisation. [Google Scholar]
- 7.R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria; 2019. Disponible en: https://www.r-project.org/.
- 8.Ritz C., Baty F., Streibig J.C., et al. Dose-response analysis using R. PLoS One. 2015;10:e0146021. doi: 10.1371/journal.pone.0146021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Clausen A., Sokol S. {Deriv}: R-based symbolic differentiation. 2019 Disponible en: https://cran.r-project.org/package=Deriv. [Google Scholar]
- 10.Figueiredo A., et al. Impact of lockdown on COVID-19 incidence and mortality in China: an interrupted time series study. Bull World Heal Organ. 2020 [Submitted]. Disponible en: https://www.who.int/bulletin/online_first/20-256701.pdf?ua=1. [Google Scholar]