Modeling COVID-19 epidemic in Heilongjiang province, China

Highlights

• •An adjusted model for Heilongjiang province, China
• •Large pool of asymptomatic patients is not identified
• •Strict interventions are needed to impede potential outbreak

Abstract

The Coronavirus Disease 2019 (COVID-19) surges worldwide. However, massive imported patients especially into Heilongjiang Province in China recently have been an alert for local COVID-19 outbreak. We collected data from January 23 to March 25 from Heilongjiang province and trained an ordinary differential equation model to fit the epidemic data. We extended the simulation using this trained model to characterize the effect of an imported ‘escaper’. We showed that an imported ‘escaper’ was responsible for the newly confirmed COVID-19 infections from Apr 9 to Apr 19 in Heilongjiang province. Stochastic simulations further showed that significantly increased local contacts among imported ‘escaper’, its epidemiologically associated cases and susceptible populations greatly contributed to the local outbreak of COVID-19. Meanwhile, we further found that the reported number of asymptomatic patients was markedly lower than model predictions implying a large asymptomatic pool which was not identified. We further forecasted the effect of implementing strong interventions immediately to impede COVID-19 outbreak for Heilongjiang province. Implementation of stronger interventions to lower mutual contacts could accelerate the complete recovery from coronavirus infections in Heilongjiang province. Collectively, our model has characterized the epidemic of COVID-19 in Heilongjiang province and implied that strongly controlled measured should be taken for infected and asymptomatic patients to minimize total infections.

1. Introduction

In December 2019, the coronavirus disease 2019 (COVID-19) occurred in Wuhan (Hubei province) and then unfolded in China and all over the world [1]. The novel coronavirus has been a serious threat to public health [2]. China has taken strict measures such as quarantine, social-distancing, suspicious isolation, community surveillance, to restrain COVID-19 outbreak by late February. However, Heilongjiang has now become the province with most diagnosed patients in China (i.e. even worse than Hubei province). Massive imported cases emerge and continue to increase. Specifically, a recent ‘super spreader’ or ‘imported escaper’ in Heilongjiang province has led to tens of diagnosed or asymptomatic cases [3]. Therefore, evaluating the epidemic of COVID-19 in Heilongjiang province may help provide effective strategies to restrict COVID-19 transmission.

Recently, many mathematical models have been constructed to investigate the epidemic of COVID-19. Some models have made modifications based on the conventional ‘SEIR’ model [4] and concluded that strictly controlled interventions are critically important to impede COVID-19 outbreak [5], [6], [7], [8], [9], [10], [11]. Several other model instead established a stochastic transition model to evaluate the transmission of COVID-19 and also emphasized the necessity of interventions such as social-distancing, isolation and quarantine [12,13]. Meanwhile, asymptomatic patients are covert cases which represent a serious threat to public health [14]. A few models have been developed to evaluate the role of coronavirus transmission based on asymptomatic cases [11,15,16]. However, all these models have ignored the COVID-19 transmission from bats and unknown hosts. A recently proposed novel model has characterized these interactions among bats, unknown hosts and people in details [17]. They estimated the basic reproduction number (R₀) to be ~2.4829 and indicated that model is locally asymptotically stable if R₀ < 1 [17]. These important models have greatly improved our understanding about the epidemic of COVID-19.

In current work, we developed a mathematical model to characterize imported escaper and asymptomatic patients. We trained our model based on COVID-19 epidemic in Heilongjiang province from January 23 to March 25, by which the last confirmed patient was cured in Heilongjiang province. Using this model, we performed stochastic simulations and found that partial relief in strictly controlled interventions may contribute to the occurrence of diagnosed patients recently (from April 9 to April 19) provided that there is only one imported patient without surveillance [3]. Meanwhile, we predicted that there is still an unidentified pool of asymptomatic patients. We suggested that strict or mild interventions should still be implemented to restrain a potential COVID-19 outbreak.

2. Materials and methods

2.1. Data and model construction

The number of experimentally confirmed patients and cured/recovered cases (January 23 to April 19) was obtained from Health Commission of Heilongjiang Province (http://wsjkw.hlj.gov.cn/, Table S1). Note that only domestic cases epidemiologically associated with the ‘super spreader’ between April 9 and April 19 were recorded and simulated. The total susceptible population was set to be the total population in Heilongjiang province from National Bureau of Statistics (37.71 million, http://www.stats.gov.cn/). Owing to closure of Wuhan on January 23, there are no Wuhan returnees to Heilongjiang province since then. The total population was divided into: susceptible population (S), closely observed population (C, individuals with public health intervention/close contacts), infected (I), recovered (R) and asymptomatic (A) patients. The equations were shown:

$$\begin{array}{c}dS/dt=\lambda C-{\beta }_{1}SC-{\beta }_{2}SA+\epsilon A-{\beta }_{3}SI\hfill \\ dC/dt={\beta }_{1}SC+{\beta }_{2}SA-{\nu }_{1}C-{\nu }_{2}C-\lambda C+{\beta }_{3}SI\hfill \\ dI/dt={\nu }_{2}C+{\nu }_{3}A-\mu \frac{K^n}{K^n+C^n+I^n}I\hfill \\ dR/dt=\mu \frac{K^n}{K^n+C^n+I^n}I\hfill \\ dA/dt={\nu }_{1}C-\epsilon A-{\nu }_{3}A\hfill \end{array}$$ (1)

λ describes the discharge rate from quarantine. β_i (i=1, 2, 3) describes the averaged contact rate between S and C, A or I, respectively. Specifically, β₁ is the average contact rate between susceptible population and close contacts. β₂ describes the average contact rate between susceptible population and asymptomatic patients. β₃ denotes the averaged contact between susceptible population and infected patients. ε denotes self-recovery rate for asymptomatic cases since specific asymptotic patients can recover without treatments [18], [19], [20]. ν₁ and ν₂ represent the transition rate from close contacts to asymptomatic and diagnosed ones, respectively. ν₃ is the transition from asymptomatic to diagnosed cases [18], [19], [20]. μ is the (maximum) average recovery rate. Since the health-care capacity in different provinces differ significantly owing to economic development, we further incorporated a threshold behavior for the recovery. We assumed that higher numbers of inpatients and quarantined cases will lower the average recovery rate. The health-care capacity will be improved if there are fewer diagnosed/quarantined patients. A Hill function was used to characterize the threshold behavior. The threshold was represented as a parameter K and the cooperativity effect was described by the parameter n (see model 1). Initial values for I and R were obtained from the official site (http://wsjkw.hlj.gov.cn/). The total susceptible population was set to be the total population in Heilongjiang province as described above. Other parameters and initial conditions (C and A) were estimated based on epidemic data from Heilongjiang province. For parameter estimation, 400 stochastic runs using Potterswheel toolbox [21] were implemented and the best fit parameter set was shown in Table 1 . Since the best fit for initial asymptotic population is <<1 (0.042736), we set initial value for A to be 0 since A should be an integer. We note that the parameter n in the best fit set was ~1.02545 suggesting that the threshold behavior in recovery rate has relatively low cooperativity.

Table 1.

Parameter values in Heilongjiang model.

Parameter	Value	Parameter	Value
λ	0.273779640898079	μ	0.250841001999977
ν3	0.0903757779355591	K	3182.81754858252
ε	0.0184478791005044	n	1.02545087428021
ν1	8.194638573622e-05	β3	8.156194101074e-10
β1	2.6897635132498e-9	S	37710000
β2	2.2831707485108e-9	C	1194356
ν2	2.8675525037598e-8	I	3

Parameters were estimated by PottersWheel using a trust-region method [21]. A χ² criteria was used for model identification (χ²/N<1, N is the number of data points) [21]. We did not incorporate death similar to recent assumptions [13,22].

2.2. Simulation

The τ-leap method was used for stochastic simulation [23]. Ordinary differential equations (ODEs) were numerically solved using ode23s in MATLAB (R2018b). The ‘ksdensity’ function in MATLAB was used for kernel estimation.

3. Results

3.1. Model training using epidemic data in Heilongjiang province

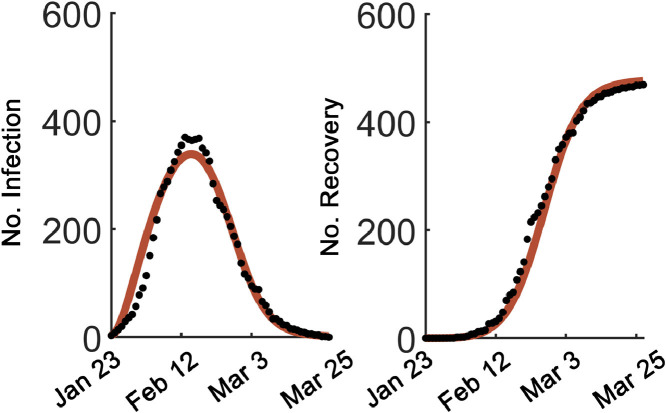
The model was first trained with epidemic data from Heilongjiang province. Using a reasonable initial guess, we performed unbiased parameter fitting by sampling parameters in logarithmic scale (totally, 400 sets). The top 200 fits were harvested. We noted that fitted initial values from 200 top fits for asymptomatic patient number ‘A’ approximated zero with mean value <0.1 and therefore the initial value ‘A’ for is set to be 0. The best fit was shown for infected and recovered patients by March 25 (Fig. 1 A). Notably, the fitted β_i (i=1, 2, 3) values were to the order of 10⁻¹⁰ to 10⁻⁹ suggesting that strong interventions were implemented to restrain mutual contacts (Table 1). Meanwhile, n is around 1 (1.02545) suggesting that the cooperativity was neglectable. The best fit parameter set was shown in Table 1. We further estimated a dynamic reproduction number based on ordinary differential equations [24]. The results showed that the reproduction number initially reached 5.0692 and then quickly dropped below 1 by Feb 14 and finally reached ~0.8702 (Fig. S1). Therefore, our model could faithfully match the epidemic data in Heilongjiang province and found that continuously strict measures indeed impeded the COVID-19 transmission.

Fig. 1.

Model training to epidemic data in Heilongjiang province. Model fitting to official data from Jan 23 to Mar 25. The model simulation was shown (brown). Infected patients (left, No. Infection) and cumulative recovered patients (right, No. Recovery) were shown. Solid dots: epidemic data.

3.2. Stochastic simulation matched the emerging patients

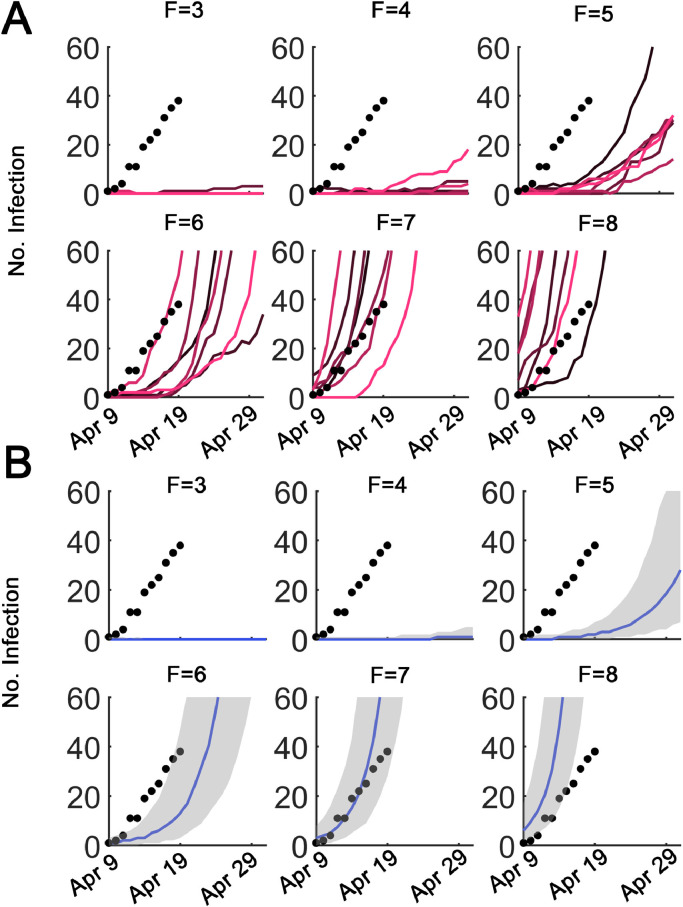
We then performed stochastic simulations using τ-leap method [23]. Since mutual contacts among different populations act as potential risk factors to COVID-19 outbreak [25], all β_i (i=1, 2, 3) values were multiplied by a contact factor F [β_i^’ =F∙β_i (i=1, 2, 3)]. Therefore, F=1 indicated strongly controlled interventions as implemented between late January and mid-March, while F>1 represented mild or relieved interventions. F>>1 was associated with strongly weakened or no interventions. The ‘imported escaper’ or ‘super spreader’ (the ‘super spreader’ here means that all recently confirmed patients can be associated with this ‘super spreader’ in an ongoing epidemiological study) arrived in Heilongjiang province at March 19 and was then subject to ‘home quarantine’ [3]. Therefore, the number of infected patients was increased by 1 at March 19 in the stochastic model. However, the ‘home quarantine’ was failed as reported possibly owing to accidental egress by escalator or stairs [3]. We modeled this by increasing F (from 3 to 8) and then performed stochastic simulations. Results suggested that even a moderate relief would not lead to the reported local outbreak (F=3,4 and 5, Fig. 2 A). Increasing F to 6-8, however, will result in possible matches between stochastic simulations and reported epidemic data (black dots, epidemic data; colored curves: stochastic simulations, Fig. 2A). The median values from 500 stochastic runs were shown for increasing F values (blue curves, Fig. 2B, the shaded areas denote 25% and 75% quartiles). Therefore, we predicted that the mutual contacts for the ‘super spreader’ was significantly elevated to around 7.

Fig. 2.

Stochastic simulations for ‘imported escaper’. (A) The reported numbers of infected patients since April 9 were shown as black dots. Stochastic simulations were displayed as colored curves. Different contact factor F values were indicated at top middle in each panel. (B) Same as in (A). The shaded areas denote 25% and 75% quartiles. The median was shown (blue curve).

3.3. Unravelling the covert pool of asymptomatic patients

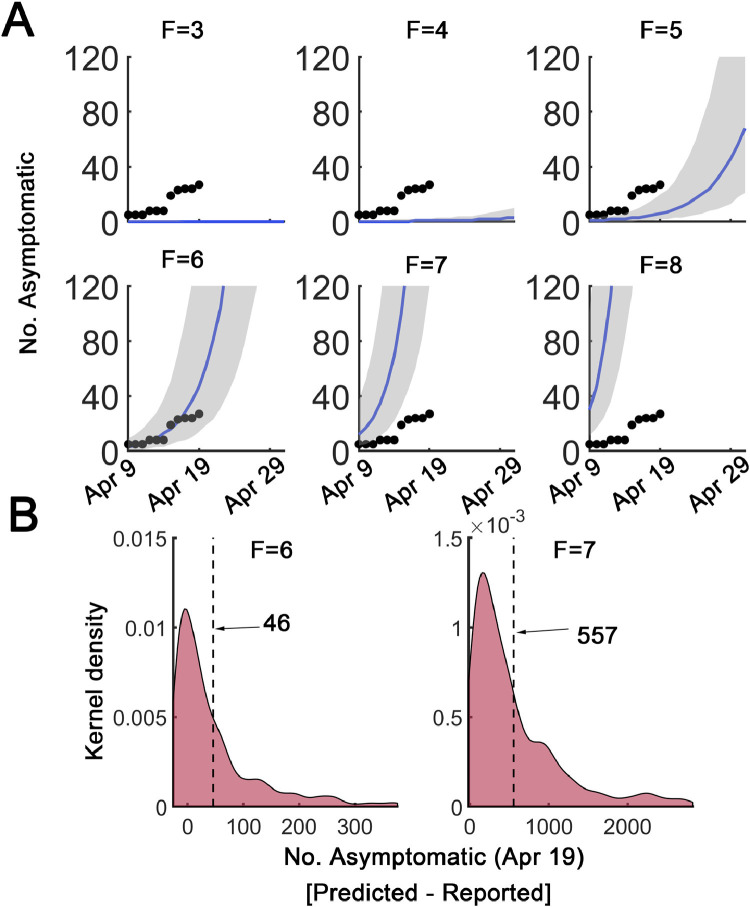
We further matched our simulations to the reported asymptomatic patients. Setting F=7, stochastic simulation could match the epidemic data (Fig. 2). However, we noted a large gap between the simulated number of asymptomatic patients to the reported cases (F=7, Fig. 3 A). Since asymptomatic patients usually do not seek medical tests owing to lack of symptoms, the reported number of asymptomatic cases may be lower than the actual number (Fig. 3A) [18], [19], [20]. The underestimation was significant for F=6 or F=7 on April 19 (dashed line: the mean value, Fig. 3B). The discrepancy seemed to grow if intervention strength was not altered (Fig. 3B). These simulations implied that the unidentified asymptomatic patients might be another serious concern since the asymptomatic cases can also be contagious [18], [19], [20].

Fig. 3.

Estimation of asymptomatic pool. (A) Estimated asymptomatic patient numbers from stochastic simulations. The reported data were shown as black dots. Median values from 500 stochastic runs were shown as blue curves. Shaded areas denote 25% and 75% quartiles. The contact factor F was indicated on top. (B) Distribution of differences in predicted and reported asymptomatic patient numbers ([predicted - reported]) from 500 stochastic runs in Heilongjiang model for F=6 (left) and F=7 (right) on April 19. The dashed line indicates the means. Kernel density estimation was used.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.4. Reestablishment of strict interventions is required to restrain outbreak

Since the confirmed patients have undergone an ongoing increase, we then evaluated the effect of establishment of strict interventions since April 20 (black dot, Fig. 4 A). Strict interventions were implemented (F=1 or 2) since April 20. We measured the time to peak and the recovery time since April 9, at which the first reported domestic patient occurs in Heilongjiang province [26]. We found that roughly ~33 days were used to reach the peak for F=1 whereas for F=2, the duration was increased to ~53 days (Fig. 4B and 4C, left). ~80 days were required for total recovery if F=1 whereas about 139 days were needed for F=2 (Fig. 4B and 4C, right). Therefore, these simulations suggested implementation of strict interventions is strongly required to impede a potential outbreak.

Fig. 4.

Effect of re-establishment of strict interventions. (A) Representative trajectory for implementation of strict intervention started on April 20. F was set to either 1 or 2 since April 20. Before April 20, F=7 because F=7 could better match the reported epidemic data. (B) Distribution of time to peak (left) and recovery time (right) since April 9 (when the first domestically diagnosed patient emerged). The dashed lines denote the mean values. The contact factor F=1. (C) Similar as in (B) for F=2. Kernel density estimation was used.

4. Discussion

In this study, we constructed a modified model which incorporated threshold behavior in recovery rate and asymptomatic patients with significant difference to ‘SEIR’ model [4]. However, ongoing importation into China especially in Heilongjiang province has been a serious threat recently. Furthermore, the asymptomatic patients are not easily identified owing to lack of obvious symptoms [20]. We estimated the influence of asymptomatic patients based on a data-driven model from Heilongjiang province. We anticipated that an area- or province-specific model may help unravel the underlying features of COVID-19 epidemic.

From simulation, we found that even one ‘imported patient’ or ‘super spreader’ reported recently can lead to up to ~ 40 infected patients and unpredictable pool of asymptomatic patients till April 19 [3]. We anticipated that the relaxed ‘home quarantine’ for this ‘imported patient’ [3] is unsuccessful and has initiated a local outbreak potentially. Simulation suggested that the mutual contacts from the relaxed ‘home quarantine’ might possibly increase to F=7 compared with F=1 for strictly controlled interventions. The occurrence of the ‘imported escaper’ might be ascribed to the significantly longer latent period [2], the weakened surveillance for COVID-19 inpatient transfer in specific hospitals and the murky mismanagement for COVID-19 tests [3]. All these deficiencies may possibly lead to a secondary blockage of some hospitals and communities for Haerbin City in Heilongjiang province. More seriously, the associated pool of asymptomatic patients was underestimated from official report. Since asymptomatic patients are also contagious, the potential impact of these covert cases should attract extensive attention. As least about one month is still required if strict measures are immediately implemented. Therefore, the ‘imported escaper’ argues for further epidemiological investigations as well as strongly controlled interventions. As more data are available, our model could be used for analyzing these novel epidemic data.

Liu et al. recently constructed a model with ‘asymptomatic patients’ [11]. However, asymptomatic populations in their model will eventually become diagnosed/confirmed patients with clear symptoms and are more likely to be ‘pre-symptomatic’ [14], which is in stark contrast to recent definition (i.e. asymptomatic patients were those who never develop symptoms) [18], [19], [20].

We modeled the COVID-19 epidemic induced by one imported patient without strict ‘quarantine’. Lessons from the emerging diagnosed patients recently in Heilongjiang province since April 9 should catch attention as they are epidemiologically associated with this ‘imported escaper’. Furthermore, we recommended that the strict measures such as isolation, home or centralized quarantine should be re-established especially in Haerbin City of Heilongjiang province to lower the risk of a potentially secondary outbreak. Finally, our model could also be applied elsewhere with adjusted parameters to monitor COVID-19 epidemic.

Ethical approval

Not required

CRediT authorship contribution statement

Tingzhe Sun: Conceptualization, Funding acquisition, Supervision, Methodology, Data curation, Writing - original draft, Visualization, Writing - review & editing. Yan Wang: Methodology, Data curation, Writing - original draft, Visualization, Writing - review & editing.

Declaration of Competing Interest

The authors declare no competing interests.