Monolithic Approach for Next-Generation Aircraft Design Considering Airline Operations and Economics

Abstract

Traditional approaches to design and optimization of a new system often use a system-centric objective that does not consider how the operator will use this new system alongside other existing systems. When the new system design is incorporated into the broader group of systems, the performance of the operator-level objective can be sub-optimal due to the unmodeled interaction between the new system and the other systems. Among the few available references that describe attempts to address this disconnect, most follow an MDO-motivated sequential decomposition approach of first designing an optimal system and then providing this system to the operator who decides the best way to use this new system along with the existing systems. This paper addresses this issue by including aircraft design, airline operations, and revenue management “subspaces”; and presents an approach that could simultaneously solve these subspaces posed as a monolithic optimization problem. The monolithic approach makes the problem an expensive MINLP problem and is extremely difficult to solve. We use a recently developed optimization framework that simultaneously solves the subspaces to capture the “synergy” in the problem. The results demonstrate that simultaneously optimizing the subspaces leads to significant improvement in the fleet-level objective of the airline when compared to the previously developed sequential subspace decomposition approach. The results also showcase that maximizing revenue and minimizing operating cost independently need not lead to a maximized profit solution for the airline.

I. Introduction and Motivation

A typical aircraft design process involves designing an aircraft for a particular design range and a payload capacity, or perhaps a set of payload-range combinations. An aircraft sizing analysis tool can size the aircraft (i.e., predict the aircraft size, weight, performance, cost, etc.) to meet the desired design mission range and seat capacity requirements. In reality, however, aircraft fly missions of different ranges with varying payloads to meet the needs of the operators. For example, an airline may allocate the new aircraft on short routes well below the aircraft’s design range to meet the high passenger demands on those routes. When the sizing process uses a single design range and payload, the resulting aircraft is not optimal for routes other than its defined payload-range combination. These sub-optimal “off-design” operations lead to increased operating costs (and likely reduced profit) on these short routes for the airlines. A profit-seeking airline would like to maximize the profit across the entire network it operates, thereby raising the need to formulate an optimization problem that accounts for design together with the operational and economic behavior of the airline. When an airline ponders acquisition of a new aircraft to operate alongside its existing fleet, that new aircraft should work to maximize the profit of the airline. The framework presented in this paper seeks to describe a new aircraft design approach that directly influences the airline level objective taking into consideration the operations and economics of the airline as decision variables into the optimization problem formulation. The figure below shows how the design, operations and economics “subspaces” interact, demonstrating the need for the monolithic formulation that would improve the fleet-level objective of the airline.

The engineering system shown in Fig 1, also referred to in this paper as the aircraft design optimization subspace, designs the wing geometry and the engine size, and then flies the aircraft on routes decided by the operation subspace with the number of passengers on-board driven by the economic subspace. Similarly, the operations subspace uses the new aircraft performance data along with the existing aircraft performance data and merges the load factor information from the economics subspace to allocate aircraft on different routes. The economic subspace receives the total available capacity (seats) on a given route from the operation subspace and seeks to sell these seats to customers by setting the fare values. Finally, the fleet-level profit of the airline is computed using the cost and the revenue information. The approach maximizes the airline profit by addressing all of these subspaces simultaneously.

Fig. 1.

Overview of the design, allocation, and the revenue management problem, showing their interactions.

Individually, these subspaces may be solved in sequence, posing them as separate optimization problems as demonstrated in the initial and previous efforts to address this type of problem [1–3]. Solving the problem in sequence makes it computationally tractable because this sequential decomposition breaks down the large mixed-integer non-linear programming (MINLP) problem into smaller subproblems. However, doing so omits some of the interactions between the subspaces (see Fig. 1) that could lead to sub-optimal solutions with respect to the fleet-level profit. In this sequential approach, at the time of designing the new aircraft, no information exists about how the airline allocates this new aircraft, or how many passengers fly aboard this new aircraft on these allocated routes. This subspace decomposition strategy does not exploit the synergy that exists between the subspaces. As an example, solving the subspaces sequentially first involves the aircraft design optimization, often posed as a nonlinear programming (NLP) problem. The design variables associated with the aircraft design process are typically continuous variables that define the wing and the engine parameters, and the aircraft design is subjected to various performance constraints. Further, depending on the level of fidelity desired in the various disciplines of the aircraft design subspace (e.g., aerodynamics, structures, control, propulsion, etc.), this problem may become computationally very expensive. On the other hand, the airline allocation subspace as a simplistic representation of a typical airline operation is often posed as an integer linear programming (ILP) problem. The integer design variables of the allocation problem are the number of trips made by each aircraft type on each route. This problem is the analog of setting the schedule for the airline by determining the number of trips each aircraft type in the airline’s fleet makes on each route. Once the schedule has been set, the airline tries to sell the available seats to the passengers at fares decided by the economic (revenue management) subspace. The revenue management subspace decides the ticket price for advance purchase of a fare class and the booking limit imposed on that fare class with the objective of maximizing the revenue on that route. The booking limit protects a number of seats for the subset of passengers who are willing to pay a higher price for last-minute booking. Deciding the right price for a fare class and the corresponding booking limit is in itself an optimization problem, often solved using nonlinear programming, with the ticket prices and the booking limits as the continuous type design variables of the problem.

In this paper we present an approach to solve the challenge problem: design-allocation-revenue management (DARM) posed as a single monolithic optimization problem that captures the interactions between the subspaces (also appears in Ref. [4]). Combining these subspaces makes this a MINLP problem and is very hard, if not impossible, to solve with available solvers. With recent advancement in the field of operations research, newer algorithms can solve MINLP problems [5], but their application to simultaneously solving the design, allocation, and revenue management problem is limited by the computationally expensive and sophisticated aero-structure-propulsion modules used by the aircraft design companies.

To address this challenge problem, we use the recently developed optimization framework AMIEGO [6], A Mixed Integer Efficient Global Optimization, available as a driver within NASA’s OpenMDAO [7]. AMIEGO employs a hybrid approach combining features from several different optimization algorithms. The optimization framework leverages the efficiency of a gradient-based optimizer to exploit the large-scale continuous design space together with the efficient global exploration capability of EGO [8] to explore the integer design space. In doing so, it combines the benefits that these individual optimization approaches are able to provide, i.e., the ability to handle a very large-scale design optimization problem in the continuous space with expensive analysis models using a gradient-based approach, while globally exploring the integer design space using the EGO framework, and limiting the expensive continuous optimization runs to as few as possible. The framework also employs Kriging with Partial Least Square (KPLS) [9], to address the curse of dimensionality issue of surrogate-based approaches [10].

II. Literature Review

There exists much literature that has advanced the state of the individual subspace problems. However, to the best of the authors’ knowledge, no literature exists that has posed and solved the design, allocation, and revenue management as a monolithic optimization problem. Most of the early and recent studies that combine the aircraft design and allocation subspaces have done so within the context of system-of-systems[1–3, 11–13]. One of the first steps was the MDO-motivated decomposition approach by Mane et al. [1], where they decomposed the large MINLP problem into two smaller subspace problems, with a top level driver that decides on the design range and seating capacity of the new “yet-to-be-developed” aircraft, as appears in Fig. 2.

Fig. 2.

Sequential decomposition approach (adapted from Ref. [1])

The aircraft design subspace problem sizes the new, “yet-to-be-developed” aircraft for a specific design mission range and payload (these information come from the top level) via an NLP problem formulation. The newly designed aircraft along with the existing aircraft in the fleet are, then, allocated to the route network via an MILP problem formulation that maximizes the airline-level profit. This profit value then becomes the solution to the top-level problem. The top-level subspace then generates a new set of requirements for the “yet-to-be-developed” aircraft (a new seat-range combination) and re-solves the aircraft design optimization and airline allocation problem sequentially.

This sequential subspace decomposition approach gets around the challenges and hurdles of an MINLP problem and solves two relatively easier subproblems — an NLP problem (design) and an MILP problem (allocation). This sequential approach reduces the computational cost and can solve a small-scale aircraft design optimization problem and a moderate-scale airline allocation problem leveraging the mixed integer linear programming (MILP) formulation of the allocation subspace. This approach has been applied to include multiple airlines, where the new yet-to-be-developed aircraft is designed to serve two airlines [14]. A follow-up effort using the same subspace decomposition framework addresses uncertainties in the design and the allocation subspace for military and commercial application [15, 16]. Although a significant amount of work has been done using the decomposition framework, the subspaces are inherently coupled and this subspace decomposition approach could not capture the synergy that exists between the various subspaces. It could only capture the one-way coupling i.e., based on how the new aircraft is designed affects the allocation subspace, however the allocation solution does not impact the new aircraft design. To address this shortcoming of the subspace decomposition approach, we investigate if there is an alternate way to approach this problem that would capture the interactions between the subspaces, leading to a better fleet-level solution.

As a starting step, the effort focused on establishing the interactions between the aircraft design and the airline allocation subspace while ignoring the top-level driver. We assume, as though through some prior analysis, that the seating capacity and the design range of the “yet-to-be-developed” aircraft is known and seeks to solve the design-allocation subspaces posed as a monolithic optimization problem (only aircraft design and airline allocation subspace in Fig. 2).

The first attempt to demonstrate the combined problem uses a form of branch-and-bound (BB) algorithm that enforces the integer constraints and solves only the mission-allocation problem (i.e., it ignores the aircraft design) for a simplistic three-route airline network problem [17]. For this three-route example problem, the simultaneous approach showed an improvement in the airline profit compared to the sequential approach. However, the BB had issues converging to a local solution without showing promises for global exploration. Further, the problem might get computationally very expensive with high-fidelity aircraft design and an increased size of the airline network, as observed earlier by Mane et al. [1], thereby establishing the need for a better approach. Follow-up efforts [18, 19] extended the three-route allocation-mission problem to consider a more realistic 128-route network and leverage a parallel computing framework. This work demonstrates the benefits of simultaneous optimization of the design-allocation subspace but makes a major assumption in the process, because it relaxes the integer constraints on the allocation variables. Relaxing the integer constraints on the problem makes it a classic continuous NLP problem and is solved using a gradient-based approach. This relaxing of the integer variables yields no practical meaning to the number of trips made by an aircraft type. One could round-off the continuous solution to the nearest integer value to address the integrality constraints; however, that may lead to infeasible or sub-optimal solutions [20]. Table 1 summarizes the pros and cons of the previously developed approaches that seek to combine design and the allocation.

Table 1.

Summary of the previous efforts that combine aircraft design and airline allocation

Methods	Approach	Pros	Cons
Sequential design-allocation with a top-level subspace	One MINLP (top-level) using complete/pseudo enumeration, one NLP (design) using gradient-based approach, and one MILP (allocation) using linear integer programming	Breaks the large problem into smaller easy-to-solve problems via subspace decomposition	Could capture only one-way coupling i.e. design affects allocation but not vice-versa, leads to sub-optimal solution
Simultaneous mission-allocation	one MINLP using branch-and-bound and gradient-based approach	Captures two-way coupling	Difficult to obtain a valid upper bound of the problem objective, limited global exploring capability, computationally inefficient
Simultaneous allocation-mission-design	One NLP using gradient-based approach within a computational analysis framework	Captures two-way coupling, capable of solving a larger network problem	Treats integer types variables as continuous – yields very little useful information to the allocation solution

Presence of highly nonlinear objective and constraints, large number of design variables together with the integer type design variables, makes the problem very challenging to solve. In an attempt to address the shortcomings of the previous approaches, Roy and Crossley[21] proposed a new MINLP approach. This new approach uses an Efficient Global Optimization or EGO-like framework to handle the integer and continuous type design variables using two different optimization algorithms. The framework leverages the global exploration capability of EGO-like approach to efficiently explore the integer design space and uses the capability of gradient-based methods to efficiently exploit the large-scale continuous design space. The paper demonstrates a small-scale aircraft design-allocation problem posed as an MINLP problem and solved using the EGO-like approach. The study used a simplistic Raymer-based [22] aircraft sizing tool to size the aircraft and obtain the aircraft performance data. The result using the EGO-like framework shows the simultaneous optimization yields an aircraft design solution that leads to slightly better fleet-level profit compared to the sequential decomposition approach for the three-route problem.

The work here builds upon this effort with an added revenue management model to better capture the airline economics and seek to solve the aircraft design, airline allocation, and revenue management posed as a monolithic optimization problem using FLOPS [23] as a sizing tool within the NASA’s OpenMDAO framework. To provide a basis for comparison and demonstrate the benefits of coupling, the results of this monolithic approach are also compared against the previously developed subspace decomposition technique.

III. Methodology

A. Problem description and formulation

The goal is to design an advanced version of a passenger aircraft with 162 seats and a design range with maximum payload of 2940 nmi that is yet-to-be-acquired by a hypothetical airline that has a defined route network and demand structure. We also seek to identify the right operational and economic strategy for the airline that aligns with its fleet-level goal. The seating capacity and design range with full passenger load of this new aircraft is based upon that of the Boeing 737-800; the popularity of this aircraft on current US domestic routes led to this choice. Our approach captures the operational and economic characteristics of the airline via a simple allocation model and a revenue management model, respectively, and treats aircraft design, airline allocation, and revenue management as three separate disciplinary subspaces that we seek to optimize simultaneously.

1. Aircraft Design Formulation:

In the aircraft design subproblem, the study assumes the design range and the maximum number of seats onboard are the same as that of a B737-800 type aircraft. Given the fixed design range and seat capacity, the objective is to size the aircraft by varying its wing geometry and engine parameters. The study here uses the Flight Optimization System (FLOPS) [23] developed at NASA LaRC as the sizing tool.

The design variables of the aircraft sizing problem along with their design bounds appear below. The first five variables define the wing geometry, and the last design describes the amount of static thrust per engine. This choice of design variables and their bounds for this work is based upon the previous efforts on aircraft design optimization [24–26].

The performance constraints that need to be satisfied in this problem are the take-off and the landing distance. The study sets the limit based on Ref. [24, 25] as 8500ft for take-off field length and 7000ft for landing field length. The effort described here created a Python wrapper for FLOPS that acts as an interface between OpenMDAO (also implemented in Python) and FLOPS.

2. Airline Allocation Formulation:

The work here uses the 11-route airline network that Mane et al. [1] used to demonstrate the sequential decomposition approach. To provide some resemblance to an actual airline’s operations, the description of this problem relies upon Bureau of Transportation Statistics (BTS) data [27]. Figure 3 shows the 11-route structure of the hypothetical airline network. The network represents a hub at Boston connecting the eleven airports on the spokes. Table 3 shows the distance of each route from the hub in nautical miles and the corresponding one-way daily demand. The BTS provides passenger travel data that are nearly symmetric, i.e., the number of passenger from A to B is nearly equal to passengers from B to A. In this representation, the “one-way” daily demand is the larger value of the number of passengers carried from A to B or B to A.

Fig. 3.

Eleven route airline network with hub at Boston

Table 3.

Table showing destination city from the hub at Boston (BOS), the route distance and the daily demand (one-way).

Route no.	O-D pair	Destination city	Distance (nmi)	Daily demand
1	BOS-JKF	New York, NY (JFK)	162	41
2	BOS-ORD	Chicago, IL (ORD)	753	1009
3	BOS-MCO	Orlando, FL (MCO)	974	89
4	BOS-MIA	Miami, FL (MIA)	1094	661
5	BOS-DFW	Dallas, TX (DFW)	1357	1041
6	BOS-SJU	San Juan, Puerto Rico (SJU)	1455	358
7	BOS-SEA	Seattle, WA (SEA)	2169	146
8	BOS-SAN	San Diego, CA (SAN)	2249	97
9	BOS-LAX	Los Angeles, CA (LAX)	2269	447
10	BOS-SJC	San Jose, CA (SJC)	2337	194
11	BOS-SFO	San Francisco, CA (SFO)	2350	263

For this problem, the airline is assumed to have two different types of existing aircraft already in operation. These include 10 B757-200 type aircraft and 14 A320-200 type aircraft. The cost and the performance data for these existing aircraft are obtained beforehand via FLOPS across all the 11 routes in the network at various load factor settings starting from 0 to 100% in steps of 10% increment. This data acts as a lookup table during the optimization preventing the need to rerun FLOPS for these existing aircraft data during the search and saves some computational time. Additionally, using FLOPS to predict cost and performance data for these aircraft maintains consistency with using FLOPS to predict cost and performance for the yet-to-be-acquired aircraft.

Given a fleet of aircraft and their cost and performance data, the airline allocates them across its routes in the network to meet the daily demand. The design variables involved in the allocation problem are the number of trips trip_a,j made by aircraft type a on route j. These are integer type design variables. This subproblem is subject to two types of operational constraints. The first is the demand constraint, mathematically represented as,

$$\sum _{a=1}^A(tri{p}_{a,j}\cdot pa{x}_{a,j})\le de{m}_j,\forall j=1,..,J$$ (1)

where, trip_a,j,pax_a,j represents the total number of trips made by aircraft type a on route j and the total number of passengers carried per trip by aircraft type a on route j respectively. The variable dem_j is the maximum demand on route j (as appears in the right-most column in Table 3). This constraint ensures the total number of passengers carried on a given route never exceeds the maximum demand on that route. The variable pax_a,j comes from the revenue management subspace for the simultaneous approach. The second is the aircraft count constraint, mathematically expressed as

$$2\sum _{j=1}^{J}tri{p}_{a,j}\cdot [B{H}_{a,j}(pa{x}_{a,j})+M{H}_{a,j}+1]\le 24\cdot flee{t}_a,\forall a=1,..,A$$ (2)

This constraint ensures the total number of aircraft of a particular type utilized within a 24 hours time frame never exceeds the maximum number of available aircraft type. Note, the block hour BH_a,j is also a function of the load factor and is decided by the revenue management subspace.

3. Revenue Management Formulation:

Revenue Management, typically, is treated as an independent domain from the scheduling and the aircraft design domains. Most studies in literature seek to find optimal fare class given a schedule (see, for instance Ref. [28]). The current study combines the revenue management subproblem with the design and the allocation subspaces. Combining these domains can lead to a better-coupled solution and, hence an improved airline profit. Revenue management, treated by itself, involves an optimization problem, where the airline needs to decide the proper ticket price for a particular fare class and then impose a booking limit on that particular fare class to protect seats to sell to high-paying last-minute business travelers. If the booking limit is set too high, then the airline may lose money by not being able to accommodate the high-paying business travelers. If the booking limit is too low, then the aircraft may fly with the majority of the seats being empty. Besides, revenue management also requires accurate prediction of demand forecast of the leisure and business type passengers. Also, deciding on the price for a fare class and the seat allocation that protects seats for future demands is a joint optimization problem, and there is a need to address them simultaneously [28]. The work here combines design, allocation, and the joint optimization of the class fare and booking limit considering the fleet level objective of the airline. This version of the revenue management problem is similar to what Cizaire and Belobaba [28] proposed. However, this study intentionally omits the uncertain aspect of the demand and assumed the demand to be deterministic. This is to develop a thorough understanding of the coupled DARM problem and to understand the interactions between the disciplines better. There is nothing in the model for revenue management that should prevent addressing uncertain demand, and future work will consider this uncertain aspect of the passenger demand. Further, the approach cited by Cizaire and Belobaba is for a single point-to-point flight. The work here extends the concept at a network level of the airline. The figure below shows the example problem of Ref. [28] with two fare classes and two booking limit periods.

For each route, the airline offers two classes of fare priceX and priceY. The fare class priceX is more expensive; and hence, it is less restrictive than the fare class priceY. The airline also sells these two fare classes across two different time windows. Time window 1 seeks to capture the leisure travelers and requires advance purchasing. Time window 2 is basically for the last minute business travelers, who are less flexible with their schedule but are willing to pay a higher price. The revenue management also needs to decide on the booking limit for fares during the time window one and protect seats for the fares offered in the time window two. To pose this as an optimization problem, the decision variables are priceX_t,j, priceY_t,j and z_1,j. The variables priceX_t,j, priceY_t,j are the non-restrictive and restrictive class fares respectively for the time window t on the route j. The variable z_1,j is the booking limit imposed on the number of seats available for purchase in the time window one on route j. The remaining seats are protected for the two classes of fares during the second time window. This subproblem is essentially an unconstrained Non-Linear Programming (NLP) problem; however, when integrated with the allocation discipline, the total accepted booking across both the time window is constrained to be less than or equal to the actual demand on that route.

The total demand in each time window is assumed independent of each other and is assumed to be a linear function of the less expensive fare class [29, 30]. These modeling assumptions are common in the literature of revenue management [28, 30].

$$\begin{gathered} n_{total,t,j}={\mu }_{t,j}(price{Y}_{t,j})={\alpha }_{t,j}-{\beta }_{t,j}\cdot price{Y}_{t,j} \\ \mathrm{where},{\alpha }_{t,j},{\beta }_{t,j}\ge 0 \\ \mathrm{and}price{Y}_{t,j}\in \left[0\frac{{\alpha }_{t,j}}{{\beta }_{t,j}}\right] \end{gathered}$$ (3)

One a given route j, Eq. (3) shows the total demand n_total,t,j on route j in the time window t is a linear function of the lesser expensive (restrictive) fare class priceY_t,j. The linear relationship between the demand and price requires the values of α_t,j and β_t,j. However, with the lack of widely available data on airline pricing, obtaining these values is difficult. The work here estimates the value of α_t,j and β_t,j using the daily demand data of Table 3 and an average ticket price obtained using Purdue-developed tool FLEET [31]. This ticket price is assumed to be the average fare the airline would have charged to all its passenger to have a realization of the daily demand as presented in Table 3. However, the daily demand data and the ticket price data are for a given route, with no information of how the passengers are segregated across the two time windows, i.e., how many people purchased tickets in time window 1 and how many purchased tickets in the time window 2. To split this demand and the price across the two time windows, the approach here assumes the airline charges 1.2 times the average fare and expects 40% of the daily demand [32] for the time window 2. This assumption gives us only one data point for each time window, but the demand-price relationship needs two data point to establish the linear relationship. Further, the ticket price should also factor in the distance of the city-pair route capturing the sensitivity in the price-demand model due to the presence of alternative modes of travel. For instance, passengers may be more sensitive to price changes on shorter routes, because there is also the option to consider an alternate mode of transportation. A price-elasticity sensitivity plot as a function of range appears in Fig. 5 below. With the one data point and the slope information (for this work, all routes are assumed to have alternate modes of transport, so the blue curve in Fig 5 provides the elasticity value), it is now possible to obtain both α_t,j and β_t,j for the time window t on route j.

Fig. 5.

Price-demand elasticity as a function of distance between the cities [31, 33].

The total revenue across both the time window on route j is given by

$$R_{total,j}=\sum _{t=1}^2{R}_{t,j}\mathrm{and}{R}_{t,j}=n_{accepted,t,j}\cdot [p_{t,j}\cdot price{X}_{t,j}+(1-p_{t,j})\cdot price{Y}_{t,j}]$$

where,

$$n_{accepted,1,j}=\{\begin{array}{ll}{n}_{total,1,j}& \mathrm{if}{n}_{total,1,j}<z_{1,j}\\ z_{1,j}& \mathrm{otherwise}\end{array}$$ (4)

$$n_{accepted,2,j}=\{\begin{array}{l}{n}_{total,2,j}\mathrm{if}{n}_{total,2,j}<[Capacity-\mathit{min}(n_{total,1,j},z_{1,j})]\\ [Capacity-\mathit{min}(n_{total,1,j},z_{1,j})]\mathrm{otherwise}\end{array}$$

The values p_1,j and p_2,j are the probabilities a passenger chooses a non-restrictive, expensive fare, given the two fare class options to choose from and the computation of these uses the binary logit model of Ref. [28]. The probabilities are modeled as utility functions of the priceX_t,j and priceY_t,j variables and are given by:

$$p_{t,j}=\frac{1}{1+\exp (a_t-b_t\cdot price{Y}_{t,j}+c_t\cdot price{X}_{t,j})}$$ (5)

The variable n_accepted,t,j is the accepted booking by the revenue management system at time window t for the route j. This accepted booking across both the time windows is the actual number of people that contribute to the revenue on that route.

Scenario Setup

To have a basis for comparison and demonstrate the benefits of coupling, the work here solves the above problem for the following three scenarios: baseline, sequential, and simultaneous approach.

Baseline:

In this scenario, there is no aircraft design optimization subproblem. The airline brings in five new 737-800 aircraft to the existing fleet composition that has ten B757-200 and fourteen A320-200 type aircraft. This scenario then solves the allocation problem (set the schedule), followed by the revenue management problem (set the fares) in sequence as appears in Fig 6. The problem formulations appear below.

Fig. 6.

Baseline scenario

Set the schedule (base:alloc-MILP).

Minimize	Fleet-level total operating cost
With respect to	flights per day*
(design variables)	passengers per aircraft type per route
Subject to	demand constraints
	aircraft count constraints
	capacity constraints

^*integer type

Mathematically,

$$\underset{tri{p}_{a,j},pa{x}_{a,j}}{\mathrm{Minimize}:}\sum _{a=1}^A\sum _{j=1}^{J}tri{p}_{a,j}\cdot {\mathit{cost}}_{a,j}$$

Subjected to:

$$\begin{gathered} \sum _{a=1}^{A}pa{x}_{a,j}=de{m}_j\forall j=1,2,\dots ,J \\ 2·\sum _{a=1}^{A}tri{p}_{a,j}\cdot (B{H}_{a,j}+M{H}_{a,j}+1)\le 24\cdot nu{m}_a{\forall }_a=1,2,..,A \\ pa{x}_{a,j}\le tri{p}_{a,j}\cdot sea{t}_a\forall a=1,2,\dots ,A\mathrm{and}j=1,2\dots ,J \end{gathered}$$ (6)

The variable pax_a,j represents the total number of passengers carried by aircraft type a on route j and is a decision variable to this allocation subproblem (base:alloc-MILP). The passenger variables are treated as continuous to reduce the computational burden. This assumption appears justified from the weight (payload) standpoint, because two passenger have different weights. This allocation problem in the baseline scenario is a Mixed Integer Linear Programming (MILP) problem, given the linear objective and constraints and we used the CPLEX solver available within the GAMS commercial package [34] to solve this subproblem. In reality, both cost_a,j and BH_a,j is a function of the number of passengers onboard or the load factor. However, to pose as a Mixed-Integer Linear Programming (MINLP) problem, this subproblem evaluates the cost and the block hour performance data at 80% load factor value. Note, the variable pax_a,j in Eq. (1) represents the number of passengers carried per trip compared to the variable pax_a,j in Eq. (6) that represents the total number of passengers carried by the aircraft type a on route j to pose and solve as a linear programming problem.

After allocation, the revenue management decides the ticket price for two fare classes for both the time windows on each route in the network. This is an unconstrained non-linear programming problem with design variables as described in the revenue management section. The revenue management decides how many bookings to accept in each time window (Eq. (4)), that affects the actual operating costs to fly these many passengers. These operating costs are different from the cost values used in the allocation formulation that assumes a fixed 80% load factor value on each route. With allocation results that describe trip_a,j decides the total available seats on a given route j. The revenue management subspace, then, decides the ticket price and the booking limit for these available seats that maximizes the total revenue. The total accepted passenger demand n_accepted,j that actually flies on the allocated aircraft determines the actual fleet-level operating cost. Then the airline’s profit is the total revenue less the updated total operating cost.

Decide fares (base:rms-NLP).

Maximize	Fleet-level revenue
With respect to	fare class per route
(design variables)	booking limit per route

Mathematically,

$$\underset{price{X}_{t,j},price{Y}_{t,j},z_{1,j}}{\mathrm{Maximize}:}\sum _{j=1}^J\sum _{t=1}^2{R}_{t,j}$$ (7)

Sequential Approach

This scenario considers the new aircraft design optimization subspace and solves the design, allocation, and revenue management subproblem in sequence as appears in Fig. 7.

Fig. 7.

Sequential scenario

For the 11 route DARM problem, the scenario first solves the aircraft sizing subproblem and sizes the new ‘yet-to-be-developed’ aircraft for a particular design mission range and payload combination. This subproblem uses a Non-Linear Programming (NLP) solver, the Sequential Quadratic Programming (SQP) [35] algorithm available within the SNOPT [36] solver. The aircraft design optimization problem minimizes the Total Operating Cost (TOC) for a specific design mission range and payload combination by varying the wing and engine parameters (aspect ratio, wing sweep, engine thrust, etc.), subject to the performance constraints, like take-off and landing distance. The problem formulation for this subproblem appears below.

Size the aircraft (seq:des-NLP).

Minimize	Total operating cost (TOC)
	(at a defined payload-range combination)
With respect to	wing shape variables
(design variables)	engine thrust
Subject to	aircraft performance constraints

Mathematically,

$$\begin{array}{l}\underset{x_{C-des}}{\mathrm{Minimize}:}\mathrm{Cos}t(x_{C-des})\\ \mathrm{Subject\; to}:TOFL(x_{C-des})\le 8500ft\\ LDFL(x_{C-des})\le 7000ft\end{array}$$ (8)

The optimized aircraft then computationally “flies on the routes” in the airline network to provide the off-design cost and performance coefficient data using FLOPS for these calculations. The airline then adds in five of these newly-designed aircraft to its existing fleet and allocates all of its aircraft to minimize the fleet-wide total operating cost subject to the allocation constraints (as appears in Eq. (9)).

This subproblem is again a Mixed Integer Linear Programming (MILP) problem (like the baseline case) and is solved using the CPLEX solver. The revenue management formulation is also the same as the baseline case. The allocation and the revenue management formulations for the sequential approach appears below.

Set the schedule (seq:alloc-MILP).

Minimize	Fleet-level total operating cost
With respect to	passengers per aircraft type
(design variables)	flights per day*
Subject to	demand constraints
	aircraft count constraints

^*integer type

Mathematically,

$$\underset{tri{p}_{a,j},pa{x}_{a,j}}{\mathrm{Minimize}:}\sum _{a=1}^A\sum _{j=1}^{J}tri{p}_{a,j}\cdot \cos t_{a,j}$$

Subjected to:

$$\begin{gathered} \sum _{a=1}^{A}pa{x}_{a,j}=de{m}_j\forall j=1,2,\dots ,J \\ 2·\sum _{a=1}^{A}tri{p}_{a,j}\cdot (B{H}_{a,j}+M{H}_{a,j}+1)\le 24\cdot nu{m}_a{\forall }_a=1,2,..,A \\ pa{x}_{a,j}\le tri{p}_{a,j}\cdot sea{t}_a\forall a=1,2,\dots ,A\mathrm{and}j=1,2\dots ,J \end{gathered}$$ (9)

Decide the fare (seq:rms-NLP).

Maximize	Fleet-level revenue
With respect to	fare class prices per route
(design variables)	booking limit per route

Mathematically,

$$\underset{price{X}_{t,j},price{Y}_{t,j},z_{1,j}}{\mathrm{Maxmize}:}\sum _{j=1}^J\sum _{t=1}^2{R}_{t,j}$$ (10)

Simultaneous Approach

Finally, the above DARM problem is posed and solved as one big monolithic problem (see Fig. 1). This problem has a total of 94 design variables including 33 integer type variables of the allocation subspace (3 aircraft types × 11 routes), 6 continuous type variables of the aircraft design subspace and 55 continuous design variables of the revenue management subspace (5 revenue variables × 11 routes). The monolithic problem formulation appears below.

Simultaneously, size the aircraft, set the schedule, and decide the fare (sim:MINLP).

Maximize	Fleet-level profit
With respect to	wing shape variables
(design variables)	engine thrust
	flights per day*
	fare class prices per route
	booking limit per route
Subject to	aircraft performance constraints
	demand constraints
	aircraft count constraints

^*integer type

Mathematically,

$$\underset{x_{C-des},tri{p}_{a,j},price{X}_{t,j},price{Y}_{t,j},z_{1,j}}{\mathrm{Maximize}:}\sum _{j=1}^J\sum _{t=1}^2{R}_{t,j}-\sum _{a=1}^A\sum _{j=1}^{J}tri{p}_{a,j}\cdot \cos t_{a,j}(x_{C-des})$$

Subject to:

$$\begin{array}{l}TOFL(x_{C-des})\le 8500ft\\ LDFL(x_{C-des})\le 7000ft\\ \sum _{a=1}^A{\mathit{trip}}_{a,j}·pa{x}_{a,j}\le de{m}_j\forall j=1,2,\dots ,J\\ 2·\sum _{a=1}^{A}tri{p}_{a,j}\cdot (B{H}_{a,j}({\mathit{pax}}_{a,j})+M{H}_{a,j}+1)\le 24\cdot nu{m}_a{\forall }_a=1,2,..,A\end{array}$$ (11)

B. Solving the problem

As mentioned earlier, the combined design-allocation-revenue management is an MINLP problem and is very difficult to solve given the presence of both integer and continuous type design variables and expensive and sophisticated analysis tools. The work here uses the recently developed EGO-like optimization algorithm AMIEGO, named as A Mixed Integer Efficient Global Optimization [4, 6], to solve the aircraft design-allocation-revenue management problem in a simultaneous manner. Preliminary results demonstrate [4, 6, 37] that AMIEGO has been successful in addressing several MINLP test problems of varying difficulty levels. An overview of the AMIEGO algorithm appears in Fig.8. The red ovals use the EGO-like surrogate-based approach that explores the integer design space, while the blue oval leverages the use of a gradient-based approach to explore the large-scale continuous design space. A detailed description of the AMIEGO algorithm appears in Ref. [4, 6, 38].

Fig. 8.

An overview of AMIEGO optimization framework

AMIEGO Setup:

AMIEGO’s initialization process (step 0: pre-processing), requires the upper and lower bound of the integer type design variables of the problem. To keep the computational budget as low as possible, it is desirable to have very accurate and tight variable bounds (as in narrow range between the upper and the lower limits). For the DARM problem, these bounds are not readily available because the variable trip_a,j may take any positive integer value. An arbitrary bound assignment may increase the computational cost due to an increased integer design space. The upper bound of the integer variables are estimated using the demand constraints of Eq. (1) of the allocation subproblem. The approach considers the case that if a particular route j is served only by a single aircraft type a, then the maximum number of trips that type of aircraft can make to meet the demand on that route is obtained using the Eq. (1) assuming a load factor of 80% per trip. Taking the maximum value across all the aircraft types a provides the upper bound for the integer variable trip_a,j. AMIEGO starts with 67 (2xI + 1, where xI = [trip_a,j]) initial points in step 1, generated using Latin Hypercube Sampling (LHS) from the set of integer-valued variables. Also, the baseline allocation solution that uses only existing aircraft to satisfy the allocation constraints replaces the integer point from the LHS set of integer points that is closest to this baseline solution. This provides a very good integer starting point for AMIEGO and helps bring down the computational cost. The idea here is to find an integer solution to the allocation problem under a limited computational budget using the AMIEGO algorithm that would result in increased profit when compared to the baseline (or even the sequential) case.

IV. Analysis and Discussion of Results

The allocation-revenue management only approach (aircraft design variables fixed to represent a B737-800) found solutions to the “baseline” scenario, while the sequential and the simultaneous approach find solutions to the DARM problem. In each of these cases, the airline-level goal is to maximize profit while satisfying the constraints across each disciplines.

The figure below shows the normalized airline profit ^* as solutions to the three scenarios. The simultaneous approach shows a 57.2% improvement in the fleet-level profit as compared to the baseline scenario, whereas the sequential approach shows only a marginal improvement in the airline profit (0.11% increase).

Starting with the aircraft sizing subspace, Table 4 below shows the difference in the wing plan form for the three scenarios. The sequential approach yields a higher aspect ratio wing and a reduced swept wing design solution. On the other hand, the simultaneous approach yields a design solution with a reduced aspect ratio, wing area and thrust per engine.

Table 4.

Aircraft design and performance data for the three scenarios (sized for design mission range of 2940 nmi)

	Baseline	Sequential	Simultaneous
Design variables
Aspect ratio	9.4	11.99	8.32
Taper ratio	0.159	0.1	0.158
Thickness-to-chord ratio	0.1338	0.091	0.1338
Wing area [sq.ft]	1345.5	1343.3	1309.8
Sweep [deg]	25.0	13.98	24.98
Thrust per engine [lbs]	24200	24200	24172.3
Performance data
Gross weight [lbs.]	169,028	163,612	170,099
Total operating cost [$]	67,418	66,449	67,533
Empty weight [lbs.]	79,593	83,272	87,043
Fuel burn [lbs.]	46,967	37,884	49,197
Thrust-to-weight ratio	0.286	0.296	0.284
Wing loading [lbs./sq.ft.]	125.6	121.8	129.9

Table 4 also shows the performance data of the “new” aircraft at the design mission range of 2940 nmi for the three scenarios. The aircraft is sized for a 2940 nmi design mission range with 162 seats onboard. The results in the table show that the sequential approach yields a lighter gross weight aircraft, that generally indicates a better performing aircraft for this design mission range. These results are intuitive, because the sequential approach solves the aircraft design problem to minimize the aircraft total operating cost at the design mission range and payload, and hence, we expect the best performance of the aircraft at this payload-range combination. However, when assessed from the airline operations perspective, this aircraft solution when combined with operations and economics leads to a lower airline profit value than the simultaneous scenario problem. From an acquisition practitioner standpoint, the airline (operator) may not care much about the values of the design variables for the new aircraft; however, they may care more about whether the new aircraft helps improve their fleet-level objective.

Figure 10 shows the net profit per day^† (one-way) on each route for the three scenarios. Overall the simultaneous approach yields higher profit across the majority of the routes. Figure 11 shows the allocation results. The new aircraft gets allocated on route 2, 3, and 4 for the simultaneous case while it is allocated on route 2, 4, and 5 for the sequential and the baseline case. Note, for the baseline case there is no new aircraft; instead, it has five B737-800-like aircraft as represented by the blue bars in the figure. Generally, the simultaneous approach makes fewer trips per day on the routes than the baseline and the sequential scenarios, thereby a lower total revenue, but also at a reduced total operating cost. This increases the net profit. Intuitively, one may think flying more passengers directly yields more profit, but this is not true in this case. Flying more flights (in the baseline and sequential results) does result in higher revenue. However, the airline incurs additional costs for making these extra trips. The baseline and the sequential approach generate more revenue but also incurs an additional cost at the same time. Baseline and sequential scenarios have similar revenue but sequential yields a slightly lesser operating cost due to a better aircraft design. On average, solution to the simultaneous scenario ends up with close to 100% load factor across majority of the profit-making routes, whereas the baseline and sequential solutions allocate aircraft and booked passengers at about 75-85% load factor per trip.

Fig. 10.

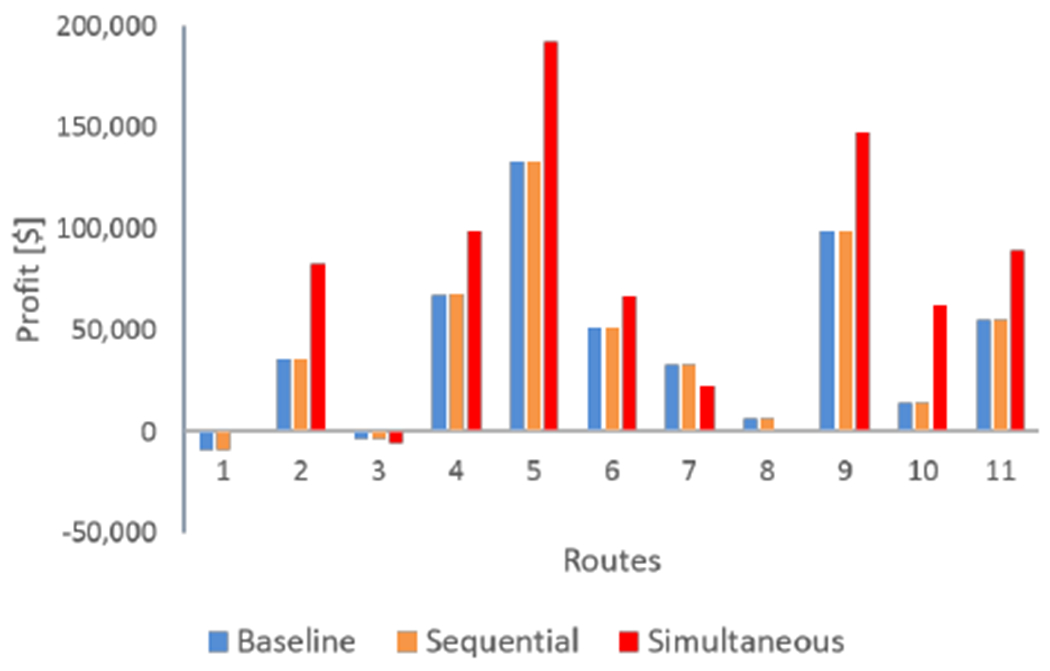
Profit on each route for the three scenarios.

Fig. 11.

Results showing allocation of different aircraft types for the three scenarios together with the fleet-level revenue and cost.

Although it was not apparent from Table 4 how the new aircraft contributes towards the improvement in profit for the simultaneous scenario, further investigation revealed that the new aircraft designed in conjunction with the operation and the economic subspace yields a more economical aircraft compared to the other two cases. Figure 12 below shows the cost to operate per nautical mile per actual passenger flown on the new aircraft across the three scenarios. The “hand-off” between how the aircraft is designed and how it is operated by the airline becomes obvious here. The simultaneous approach, at the time of optimizing the new aircraft, takes into account how the airline allocates this new aircraft (also how the revenue management subspace sets the ticket price) and accordingly, the approach yields an unified solution leading to a reduced cost per passenger nautical mile on the routes, which in turn contributes to the improvement in the airline profit.

Fig. 12.

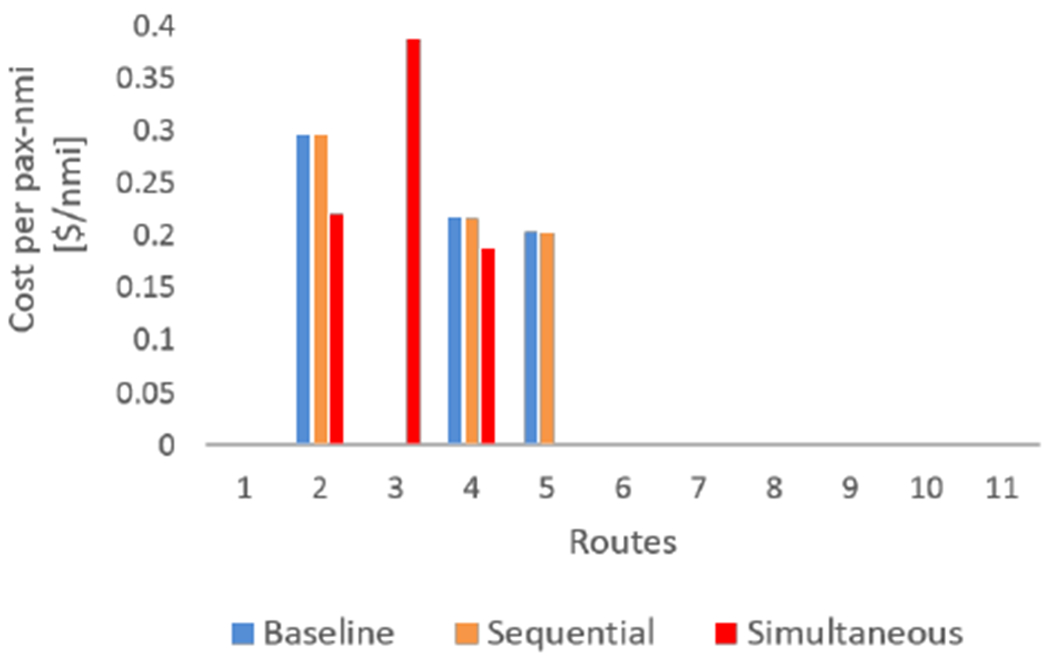
Comparison of the cost per passenger nautical mile of the new aircraft

Coupling sensitivity analysis:

The studies in the previous section demonstrate the benefits of capturing the interactions between the subspaces of aircraft design, airline allocation, and revenue management. In this section, the authors investigate which subspace contributes the most towards improving the fleet-level profit of the airline. Considering the baseline (or even the sequential) allocation solution and solving only the aircraft design and revenue management subspaces simultaneously (i.e., the airline allocation result is kept fixed at the baseline solution, and the design and the revenue management variables are made to vary simultaneously), there is only a marginal increase in the airline profit. Figure 13 compares the normalized profit using the three scenarios while keeping allocation solution of the simultaneous approach fixed at the baseline case.

Fig. 13.

Normalized profit comparison with the allocation variables kept fixed at the baseline solution

Figure 13 reveals that the allocation subspace plays a very important role towards the airline profit improvement for the simultaneous approach. This, in turn, attests to the global exploring capability of the AMIEGO framework to identify the right set of integer type allocation variables that improves the profit over the other approaches to this problem (as seen in Fig. 9). Without accounting for the integer type decision variables of the allocation problem, merely performing a simultaneous optimization of the design and revenue management subspace (both have continuous type decision variables) starting from the baseline or the sequential allocation result does not lead to as much improvement in the airline profit as evident from the Fig. 13.

Fig. 9.

Airline profit for the three scenarios

However, the optimization framework does not guarantee global convergence( see Fig. 10). For route 3, the airline takes a loss in all three scenarios. Using the simultaneous approach, one would expect the airline not to fly this route and improve the profit further. However, the improvement in profit for not flying those routes would have been insignificant over the already improved profit (compared to sequential and baseline case), and AMIEGO overlooks this enhancement. The framework is expected to lead to a near-global solution with a limited computational budget. The results discussed in this paper do show that, for the DARM problem of interest here, AMIEGO is able to find very good — but does not guarantee global optimal — solutions to the mixed integer nonlinear programming problem, and does so with acceptable computational cost.

Addressing Computational Cost

AMIEGO solves the above DARM problem in as few as 68 full “expensive” continuous optimization runs (step 2 of AMIEGO in Fig. 8). Figure 14 shows the computational cost associated with each AMIEGO iteration and the improvement in the solution quality as compared to the baseline solution.

Fig. 14. Computational cost and the corresponding improvement in the solution quality.

(a) The total number of expensive continuous optimization runs by AMIEGO (step2). Red dots represent continuous analysis using cheap evaluation tool. At iteration 0 there are 66 red dots stacked on top of each other.

(b) Percentage improvement with iteration from the baseline solution.

AMIEGO brings down the computational cost drastically by exploiting the problem formulation of the DARM problem. This exploitation of the mathematical structure is an ad-hoc implementation to significantly reduce the computational burden for this problem. Revisiting the allocation constraints of Eq. (1) & (2) (also reappear below), the demand constraints (the first expression in Eq. (12)) can always be satisfied for any value of trip_a,j. This is because the limiting value of the variable pax_a,j = 0 always satisfies the demand constraints irrespective of the value of trip_a,j.

$$\begin{array}{l}\sum _{a=1}^A({\mathit{trip}}_{a,j}·pa{x}_{a,j})\le de{m}_j,\forall j=1,..,J\\ 2\sum _{j=1}^{J}tri{p}_{a,j}\cdot [B{H}_{a,j}({\mathit{pax}}_{a,j})+M{H}_{a,j}+1]\le 24\cdot {\mathit{fleet}}_a,{\forall }_a=1,..,A\end{array}$$ (12)

However, this is not the case for the aircraft count constraints (represented by the second expression in Eq. (12)). If the value of block hours of an aircraft type on each route is assumed to be independent of the number of passengers carried (since there is not much deviation in block hours as a function of the number of passengers carried), then this is a linear function of only the integer valued variables trip_a,j. The resulting equation is very fast to evaluate for any given value of the integer type variable trip_a,j. Then, any value of trip_a,j, that does not satisfy the count constraints need not go to the step 2 of AMIEGO for the continuous optimization runs. Because this value of trip_a,j is infeasible with respect to the count constraints; sending it over for the continuous optimization is a waste of computational effort because varying only the continuous design variables does not help satisfying these count constraints. This implementation can be seen as a multi-fidelity-like approach where, if the feasibility check fails, the outcome of the expensive continuous optimization are evaluated using an inexpensive tool. This ad-hoc implementation within the AMIEGO framework for this specific problem appears in Fig. 15.

Fig. 15.

AMIEGO framework with the pre-optimization feasibility check

This simple check right before step 2 in AMIEGO, saves enormous computational effort. However, for these pre-checked infeasible points, AMIEGO still needs the objective function value (airline profit) and the constraint values. These values of the objective and constraints are evaluated at ${\mathbf{x}}_C^0$ (the default starting point for the continuous optimization). Because majority of the starting initial set of integer points belongs to the infeasible design space, a crude estimate is sufficient for this application. To AMIEGO, it appears as if these points came from the expensive continuous optimization runs in step 2. To evaluate the count constraints, we substitute the value of the block hours in Eq. (2) of the existing and the new aircraft. Note, block hour is a function of the number of passengers onboard. With no information about the number of passengers that fly in this “pre-check”, the authors use the minimum possible block hour value for that aircraft type on the given route. Investigation shows block time is monotonely decreasing as the load factor increases. Using this information, one can use the lowest possible block hour value (corresponding to a load factor of 100%) to evaluate the count constraints as a part of the feasibility check. This ensures that if this minimum possible value of block hour (fastest trip) does not satisfy the count constraints, no other block hour value does.

From Fig. 14(a), it appears that 66 out of the 67 initial integer points only required a few seconds for the continuous optimization runs. This shows that these are all points that failed the feasibility pre-check and the remaining efforts for this iteration uses the quick estimation to compute the objective and the constraints. The only expensive run at the start is the baseline allocation solution that replaces one of the 67 points from Latin Hypercube Sampling. After that, AMIEGO performs 67 more expensive continuous optimization runs (blue dots). Note, the infill point identified at iteration 3 also fails the feasibility check, so the required time for this iteration is only a few seconds. Similar failed cases appear as red dots in the figure. Overall, AMIEGO sees a total of 142 (67 initial points followed by 75 AMIEGO iterations) points to represent the profit surrogate, when only 68 came from the actual expensive continuous optimization runs. The idea behind this implementation is to represent the vast majority of the infeasible region using a fast approximation technique and model the feasible region with the actual expensive run results, thereby saving a significant amount of expensive continuous optimization runs where these runs are not expected to contribute to the search.

On the other hand, the sequential approach is computationally cheap. It requires solving only two expensive optimization problems (aircraft design and revenue management, where aircraft design is more on the expensive side) and one relatively fast mixed-integer linear programming problem for the allocation subspace.

V. Conclusion and Future Research Directions

Considering the design of a new aircraft together with the operations and economics of the airline is a challenging task just from the problem formulation and solution perspective. The effort presented herein identified the design requirements of a new aircraft yet-to-be-acquired by the airline. To address this challenge, we developed a process that considers the operational and economic characteristics of the airline as decision variables at the time of performing design optimization of the new aircraft. This consideration of operational and economics factors at the time of designing the new aircraft leads to a tightly coupled problem formulation that improves the fleet-level objective of the airline. However, the combined approach leads to a Mixed Integer Nonlinear Programming problem formulation and is difficult to solve. Leveraging the recently developed optimization framework AMIEGO, along with the computational framework and the parallel computing tools, the problem now is computationally tractable, with good, but not globally-optimal solutions.

The results reveal the presence of “synergism” between the subspaces. One may not be able to analyze the whole problem starting from a single subspace for these type of problems. Every subspace works in unison to contribute towards improving the airline-level objective. The simultaneous approach performs better than its sequential decomposition counterpart due to the fact that the simultaneous approach finds for an aircraft design, a fleet allocation, and revenue management ticket pricing that maximize airline profit. In the sequential approach, the aircraft is first sized to minimize total operating cost for its design mission range with no information how the airline operates this new aircraft. Then, the allocation subspace allocates all the aircraft (both new and existing), with no information on how the revenue management subspace sets the ticket price and how much demand the ticket price attracts. In the simultaneous approach, the aircraft design affects airline operational and economics, this in turn affects the design variables in the aircraft sizing subspace. The baseline and sequential approach results carry more passengers (satisfies more demand) and, hence, have higher revenue compared to the simultaneous approach but at the expense of higher total operating cost, thereby reducing the net profit for the airline. On the other hand, the simultaneous approach suggests airline to make fewer trips that reduces both cost and revenue in a way that yields a higher overall profit. The sensitivity analysis reveals operational subspace plays an important role in improving the fleet-level profit of the airline.

The demonstrations solving the combined new aircraft design-airline allocation-revenue management problem uses rather low fidelity representations of all three subspaces. This low level of fidelity allowed demonstration of posing and solving the design-allocation-revenue management as a monolithic optimization problem and of the potential improvement available when capturing the coupling amongst design, allocation, and revenue management. However, the usefulness of the results obtained in this effort is limited by the analyses and models. The authors would like to improve upon the existing fidelity in all subspaces and replace them with higher fidelity analysis tools. The current application problem used FLOPS as the aircraft sizing tool and employed a simplistic representation of a typical airline operation. The effort to replace FLOPS with a high-fidelity aircraft design tool is underway [6], and then, as part of future work, we intend to solve the above DARM problem with the high-fidelity aircraft design analyses using the proposed approach within the OpenMDAO framework. Another scope for improving the fidelity would be the airline operational side of the combined problem. The current study did not include passenger demand uncertainty; instead, it assumed a deterministic value for demand on the routes. However, in reality, the passenger demands are uncertain in nature. Further, the fluctuation in fuel price also plays a vital role in driving the operating cost of the airlines. Treating passenger demand, fuel price and other similar operational characteristics as uncertain parameters could potentially to lead to a more robust solution and we intend to consider this as part of future work.

Fig. 4.

Revenue management problem

Table 2.

Aircraft Design Variables.

Design Variables	Lower Bound	Upper Bound
Aspect ratio	8	12
Taper ratio	0.1	0.5
t/c ratio	0.009	0.17
Wing area [sq.ft]	1000	2000
Sweep [deg]	0.5	40
Thrust per engine [lbs]	20,000	30,000

Nomenclature

BH_a,j

Block hours of aircraft type a on route j

dem_j

Daily passenger demand on route j

fleet_a

Number of aircraft type a

MH_a,j

Maintenance-hours per block hour of aircraft type a on route j

MILP

Mixed-Integer Linear Programming

MINLP

Mixed-Integer Non-Linear Programming

NLP

Non-Linear Programming

pax_a,j

Number of passengers per flight on aircraft type a on route j

priceX_t

Non-restrictive fare class on time window t

priceY_t

Restrictive fare class on time window t

trip_a,j

Number of trips by aircraft type a on route j

x_C⁰

Vector of starting point for the continuous type design variables

x_I

Vector of integer type design variables

z_1,j

Booking limit on time window 1 on route j