On the Interpretability of Artificial Intelligence in Radiology: Challenges and Opportunities

Abstract

As artificial intelligence (AI) systems begin to make their way into clinical radiology practice, it is crucial to assure that they function correctly and that they gain the trust of experts. Toward this goal, approaches to make AI “interpretable” have gained attention to enhance the understanding of a machine learning algorithm, despite its complexity. This article aims to provide insights into the current state of the art of interpretability methods for radiology AI. This review discusses radiologists’ opinions on the topic and suggests trends and challenges that need to be addressed to effectively streamline interpretability methods in clinical practice.

Supplemental material is available for this article.

© RSNA, 2020

See also the commentary by Gastounioti and Kontos in this issue.

Summary

Interpretability methods hold the potential to improve understanding, trust, and verification of radiology artificial intelligence systems; active involvement of the radiology community is necessary for their development and evaluation.

Essentials

• ■ Radiology artificial intelligence (AI) systems often have numerous computational layers that can make it difficult for a human to interpret a system’s output.

• ■ Interpretability methods are being developed such that AI systems can be explained by using visualization, counterexamples, or semantics.

• ■ By enhancing their interpretability, AI systems can be better verified, trusted, and adopted in radiology practice.

Introduction

Artificial intelligence (AI) technologies for applications in radiology are continually gaining interest among health care providers (1). The topic of interpretability of machine learning is not new, but it has received increasing attention in the last few years, arguably because of the increased popularity of complex approaches such as deep learning (DL). The interpretability of an AI program is generally defined as the ability of a human to understand the link between the features extracted by an AI program and its predictions. Because DL applications have multiple hidden layers, it is difficult for humans to understand how they reach their conclusions, which is commonly known as the “black-box problem” of AI technology. As an example, simple and imperceptible changes can be added within input images to “fool” DL approaches (2); because we do not know how they were fooled, the perception of DL approaches as black boxes is increased.

We believe it is essential to involve the radiology community in the research and development of AI interpretability methods. In this article, we aim to introduce the topic of interpretable AI, describe the main approaches of interpretability, and provide insights into the current trends and challenges that need to be addressed to effectively streamline these methods in clinical practice. (A glossary of commonly used terms is available in Appendix E1 [supplement].)

Interpretability in Machine Learning

Several attempts have been made to create a formal definition of AI interpretability (3). An interpretable machine learning algorithm can be described as one in which the link between the features used by the machine learning system and the prediction itself can be understood by a human (4). Other definitions converge toward producing explainable models to end users while preserving high levels of accuracy (5). For example, a simple linear regression model that predicts the likelihood of cancer using a few features, such as smoking status, age, and family cancer history, would be classified as an interpretable machine learning algorithm because a human expert can use his or her domain knowledge to interpret how the AI model is using the information (ie, in the form of weights for each feature) to make predictions.

It is worth noting that a linear model is not necessarily interpretable. Similarly, a machine learning model based on hand-crafted features, such as a decision tree, is not necessarily interpretable just because the individual features are based on specific domain knowledge and are understandable by a human. The number and complexity of the model’s features directly affect the interpretability of the model (3). A linear model with thousands of parameters can be hard to understand, as can a model that uses inscrutable features.

DL is a subfield of machine learning concerned with methods that rely on deep neural networks as prediction models. DL models are currently the least interpretable machine learning models because of their large number of model parameters. For example, a DL network that predicts a diagnosis based on radiographic images of a patient’s lungs would not be considered interpretable. It is very difficult for a human, without the help of dedicated computational tools, to understand the interactions among the vast number of neurons within such a model. However, the neural networks used in DL are based on a well-defined mathematical formulation. Although it is not practical, it would be theoretically possible for a human to comprehend every computation performed in a deep neural network.

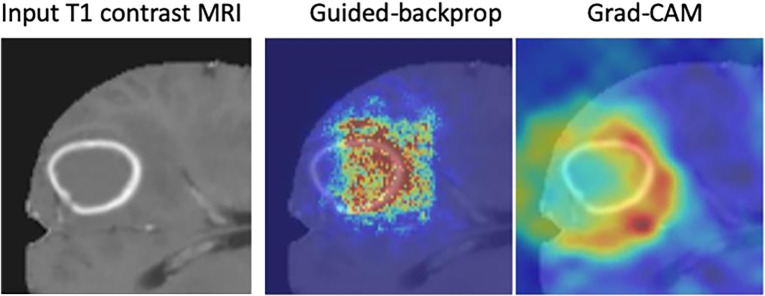
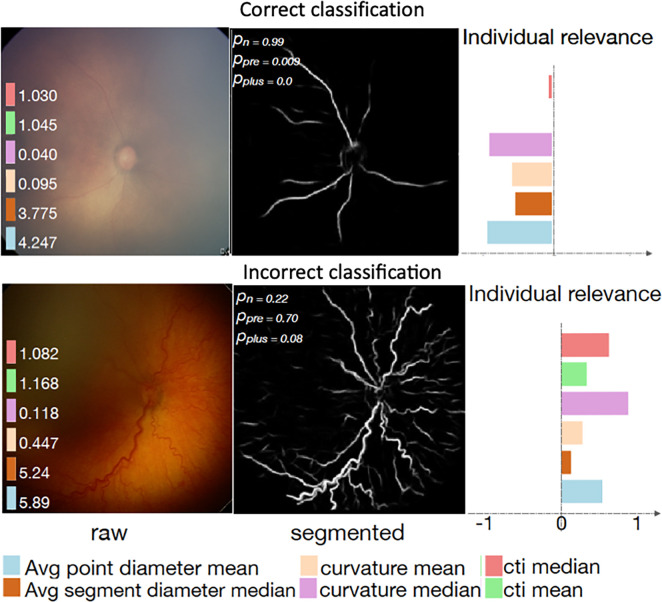
Interpretability methods are approaches designed to explicitly enhance the interpretability of a machine learning algorithm, despite its complexity. Figure 1 (6,7) shows examples of popular interpretability techniques applied on medical images, such as guided backpropagation (8), gradient-weighted class activation mapping (Grad-CAM) (9), and regression concept vectors (6), which are described in detail below. (A web-based demonstration of interpretability approaches is available at https://www.imimic-workshop.com/demo.) Different categorizations have been proposed for interpretability methods. For more detailed discussions of these taxonomies, the reader is pointed to Lipton (3) and Doshi-Velez and Kim (10). In the next sections, a summary is provided for a variety of different interpretability methods.

Figure 1a:

Examples of interpretability methods used on medical images. (a) Guided backpropagation and gradient-weighted class activation mapping (Grad-CAM) used on MRI to interpret areas of a brain image used by a deep learning model classifying the input image as a high-grade glioma. (Adapted and reprinted, with permission, from reference 7). Importance of pixels are color-coded as red = high importance, blue = low importance. (b) Regression concept vectors used to assess relevance of selected features describing curvature, tortuosity, and dilatation of retinal arteries and veins from retinal images, analyzed by a deep convolutional neural network. In b, examples of a correctly and wrongly classified image are shown, allowing the interpretation that the network is more sensitive to curvature and dilatation concepts for the classification of normal images, while being more sensitive to tortuosity for disease images. (Adapted and reprinted, with permission, from reference 6). Avg = average, cti = cumulative tortuosity index, Pn, Ppre, Pplus = network probabilities for normal, pre, and pre-plus classes.

Black Boxes versus White Boxes

Interpretability approaches can be categorized by whether they need the internal information and structure of a model (eg, model parameters and architecture for DL models) to operate, which is also referred to as the level of transparency, or level of accessibility to the internal information of a model. Interpretability methods that require access to the model’s internal information are referred to as methods operating on “white boxes.” For example, in convolutional neural networks (CNNs), a radiologist may use the flow of the gradients to a given layer of the network to yield a map, which can be overlaid on a radiographic image, that is informative of which anatomic regions are important for predicting a given class or disease (eg, Selvaraju et al [9]; see also examples in Fig 1a).

Interpretability methods operating on black boxes (also referred to as model-agnostic methods) do not require access to the internal information of the analyzed model. Instead, they operate directly on the input and output of a model and typically analyze how changes (ie, perturbations) to the input affect the output of the model (11). In practice, interpretability approaches that operate on black-box models are much easier to integrate with systems in which internal access to a prediction model is limited, such as in commercial AI solutions.

Global versus Local

Global interpretability methods seek to assess the common patterns in the overall population that drive a model’s predictions (12,13). For example, by analyzing a model on an entire set of medical images, global interpretability methods provide explanations of which patterns in the data are most important for the model’s predictions. Hence, global interpretability is suited during development and validation of AI solutions to verify that the learned patterns, extracted from the population, are coherent with existing domain knowledge. Furthermore, global interpretability methods can be used to detect biases in the training data that a model might be using to make predictions (14).

In contrast, local interpretability methods seek to explain why a prediction model makes a specific prediction for a given input (ie, “everyday explanations,” as stated by Miller [15]). Local interpretability enhances explanations for a given sample, which can be an image voxel, a complete image volume, or a set of patient-specific data.

Explanations through Visualizations

Visualization techniques provide powerful means to generate and convey insights into the behavior of machine learning models that are useful for model interpretation. Basic approaches to visualize the importance of input features to a model’s output include partial dependence plots (PDPs) and individual conditional expectation (ICE) plots (16), which are both methods for black-box models that aim to show the dependency between a model’s features and predictions. PDPs and ICE plots are assessed using the training set of a machine learning model by varying the value of one predictor at a time and reporting how the model’s predictions change over a population average (global) or individual (local) contribution of a feature, respectively. Conceptually, an important feature is expected to influence the model’s predictions when its value is changed. In radiology applications in which features are hand-crafted and based on prior knowledge (contrary to data-driven features that are generated by an algorithm), PDPs and ICE plots could be used to visualize the impact of that feature and validate the prior knowledge they represent. One main disadvantage of these methods is that they assume uncorrelated features, which might invalidate generated descriptions when applied to data in which correlations among features do exist. For example, in brain morphometry in which a patient’s age is correlated with cortical-thickness measurements, an ICE plot would create data points combining unrealistic age and cortical-thickness values.

Image-specific saliency maps (eg, Simonyan et al [13], Zhou et al [17]) were among the first local interpretability methods. The basic principle of these methods is to highlight areas of an image that drive the prediction of a model. The importance of these areas can be obtained by investigating the flow of the gradients of a DL model calculated from the model’s output to the input image or by analyzing the effect of a pixel (or region) to the output when that pixel (or region) is perturbed. This type of visualization facilitates interpretability of a model but also serves as a confirmatory tool to check that machine-based decisions align with common domain knowledge.

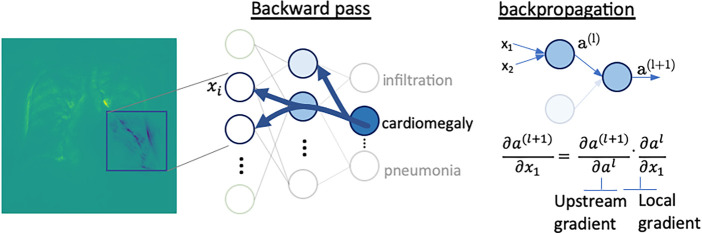
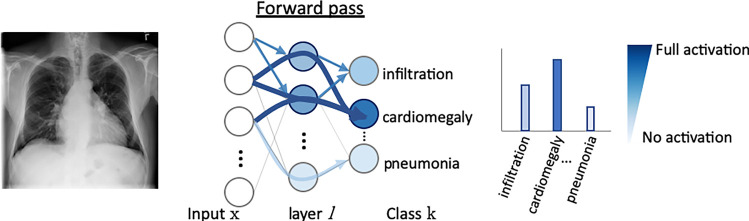
In radiology, saliency maps can be integrated easily into the radiology workflow because they work at the voxel level; hence, these visualization maps can be fused or merged with patient images and computer-generated results. The main concept of gradient-based saliency maps for DL models is illustrated in Figure 2. The main mechanism of these methods consists of calculating the gradient from the output of the DL model to the input image space, which yields so-called reconstruction saliency maps that show image regions that mostly activate a given class, k. Figure 2c shows example areas activating class “cardiomegaly.” The underlying idea of gradient-based approaches is that the magnitude of the gradient reflects the attribution of voxels (or pixels for two-dimensional images) to the prediction output of a model. Depending on the type of layer employed, different approaches have been proposed to calculate the gradient at layer l from layer (l + 1). For linear layers, the same process of backpropagation, used during the optimization of the network during the training phase, can be used to compute the reverse gradient (Fig 2c). For layers with nonlinearities, different approximations to the reverse gradient have been proposed (see Fig E1 [supplement]) and are described below in more detail. Simonyan et al (13) consider positive activations during the forward pass (Fig 2b), whereas the deconvolution network (DeconvNet) by Zeiler and Fergus (18) only considers positive reconstructed outputs at layer (l + 1). Both approaches were designed specifically for CNNs, and DeconvNet is specific to the rectified-linear-unit type of layer (see Fig 2a for examples of activation functions); hence, they are limited in the type of model on which they can be used.

Figure 2a:

Gradient-based saliency maps for image classification. (a) Basic concepts of neuron activation. A neuron is activated via a weighted combination of inputs and application of an activation function, g. (b) Gradient-based methods rely on a forward and a backward pass. Given an input image x, a class k is maximally activated through forward passing throughout all layers of the network. All positive forward activations are recorded for later use during the backward pass. To visualize the contribution of pixels in the image to the class k, all activations are set to zero except for the studied class k, and then (c) backpropagation uses the chain rule to compute gradients from the output to the input of the network. ReLU = rectified linear unit, tanh = hyperbolic tangent.

Figure 2c:

Gradient-based saliency maps for image classification. (a) Basic concepts of neuron activation. A neuron is activated via a weighted combination of inputs and application of an activation function, g. (b) Gradient-based methods rely on a forward and a backward pass. Given an input image x, a class k is maximally activated through forward passing throughout all layers of the network. All positive forward activations are recorded for later use during the backward pass. To visualize the contribution of pixels in the image to the class k, all activations are set to zero except for the studied class k, and then (c) backpropagation uses the chain rule to compute gradients from the output to the input of the network. ReLU = rectified linear unit, tanh = hyperbolic tangent.

Figure 2b:

Gradient-based saliency maps for image classification. (a) Basic concepts of neuron activation. A neuron is activated via a weighted combination of inputs and application of an activation function, g. (b) Gradient-based methods rely on a forward and a backward pass. Given an input image x, a class k is maximally activated through forward passing throughout all layers of the network. All positive forward activations are recorded for later use during the backward pass. To visualize the contribution of pixels in the image to the class k, all activations are set to zero except for the studied class k, and then (c) backpropagation uses the chain rule to compute gradients from the output to the input of the network. ReLU = rectified linear unit, tanh = hyperbolic tangent.

Guided backpropagation (8) combines these two approaches and considers positive forward activations and positive reconstructed outputs at layer (l + 1). Grad-CAM (9) is another gradient-based method proposed to overcome the lack of specificity observed in previously proposed methods and was proposed as a generalization of class activation maps (17) for CNN models. The basic idea of Grad-CAM is that image pixel attributions can be better visualized when calculating the gradient from the output to a given deeper layer (as opposed to calculating the gradient until the input layer of the model). Grad-CAM reconstructs maps as a weighted combination of forward neuron activation, with weights based on global average pooling and backpropagation outputs to a target layer. See Fig E1 (supplement) for formulation and Figure 1a for an example of guided backpropagation and Grad-CAM, highlighting the contrast-enhancing rim as an important area to classify the input T1-weighted contrast-enhanced MR image as a high-grade glioma.

In the approaches presented above, one important rationale of their design is that of discarding negative gradient values, which are assumed to not contribute with relevant information to the saliency map. In subsequent studies, this assumption has been countered with the rationale that negative gradient information (eg, absence of information) can contribute to the interpretability along with positive gradient information. This has been supported through experiments by Ancona et al (19), in which it was shown that occlusion of negative evidence produces an increase in the target output. Some of these recently proposed approaches making a distinction between negative and positive gradient information are presented below.

DL important features (DeepLIFT) is another saliency method based on backpropagating an output activation through layers of a DL model (20). DeepLIFT works by first measuring reference activation values of each neuron of the DL model during the forward pass (see Fig 1b). These reference activation values are obtained on a given reference input and then are used to measure the relative effect of activations produced by the input image being interpreted. Unlike gradient-based approaches, DeepLIFT uses a reference state to measure input contributions, even when its gradient is zero or when the gradient has discontinuities.

Figure 1b:

Examples of interpretability methods used on medical images. (a) Guided backpropagation and gradient-weighted class activation mapping (Grad-CAM) used on MRI to interpret areas of a brain image used by a deep learning model classifying the input image as a high-grade glioma. (Adapted and reprinted, with permission, from reference 7). Importance of pixels are color-coded as red = high importance, blue = low importance. (b) Regression concept vectors used to assess relevance of selected features describing curvature, tortuosity, and dilatation of retinal arteries and veins from retinal images, analyzed by a deep convolutional neural network. In b, examples of a correctly and wrongly classified image are shown, allowing the interpretation that the network is more sensitive to curvature and dilatation concepts for the classification of normal images, while being more sensitive to tortuosity for disease images. (Adapted and reprinted, with permission, from reference 6). Avg = average, cti = cumulative tortuosity index, Pn, Ppre, Pplus = network probabilities for normal, pre, and pre-plus classes.

Layer-wise relevance propagation (21) was proposed to overcome the problem of shattered gradients, which affects the stability of the gradient calculation and worsens with the depth of a DL model. Layer-wise relevance propagation decomposes the output activation as a sum of layer-wise relevance values, which describe the importance (or relevance) of each layer to the output prediction of a model. By recursively backpropagating layer-wise relevance values, it is possible to map the contribution of each pixel in the input image to the output prediction.

The reliability of saliency maps has been investigated by Adebayo et al (22), motivated by a lack of quantitative evaluation metrics for visualization-based interpretability methods. In this study, two types of tests (or sanity checks) were proposed to evaluate the reliability of visualization interpretability methods: a model parameter randomization test (eg, randomizing weights of a trained DL model) and a data randomization test (eg, retraining a model with randomly permuted class labels). For both types of perturbation, it is expected that changes to the model and training data should yield different saliency maps, as the saliency map should reflect how a given model interprets an input image. Results of this study showed that for some methods, such as guided backpropagation and guided Grad-CAM, the tests failed because the saliency maps were insensitive to these perturbations. As stated by Adebayo et al (22), explanations that do not depend on model parameters or training data might still provide useful information about prior information incorporated in the model architecture (eg, a specific DL model mostly driven by edge information on an image). We note that these findings need to be corroborated for medical images.

Interpretability methods producing saliency maps have been developed mainly for classification tasks in which the output of the model is a class label. These methods could, in practice, be extended to segmentation tasks (ie, highlighting areas of the image of importance to the segmentation result) by performing pixel-wise saliency mapping and then fusing all pixel-wise saliency maps into a single map that explains which areas of the image are important for the segmentation result. However, this approach does not account for potential neighboring interpixel correlations and might artificially produce larger pixel attribution values in central areas of a segmentation result, as a consequence of a spatial accumulation of pixel attributions as opposed to a higher importance of a given pixel to a segmentation result.

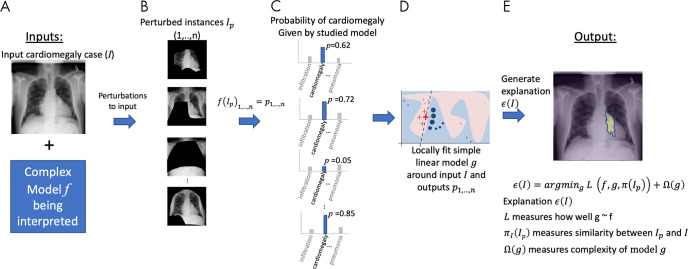
Local interpretable model-agnostic explanations (LIME) (11) is a local interpretability method (explanations at the sample level) that operates on black-box (model-agnostic) models. The main idea of LIME is to produce explanations of a complex model (eg, a DL model) by locally approximating it with a simple one (eg, a linear model) around the input sample being interpreted and then producing explanations of the simple model that are understandable to a human. The main concept of LIME for disease classification of chest radiographs is illustrated in Figure 3. Given an input sample (Fig 3, A), LIME first creates a set of perturbed versions (or instances) of the input. For images, this can be done by generating masks occluding regions of the image (Fig 3, B). The complex model is then used on the set of perturbed versions to generate output predictions (Fig 3, C). A simple model is then fitted on the basis of the set of perturbed input versions, weighted by their similarity to the input sample, and corresponding output predictions (Fig 3, D). The weights reflect the intuition that heavily perturbed instances are dissimilar to the input sample and therefore should receive a low weight so that the local simple model is more truthful around the input under interpretation. Finally, LIME generates an explanation by finding a perturbation (image mask in Fig 3, D) that minimizes the disagreement between the complex and simple model (ie, how well the simple model approximates the complex one) while keeping the complexity of the perturbation low (for images, the size of the image mask used to perturb the input). Figure 3, E, shows the result of LIME highlighting, in which pixels are most important for the classification of the input image as a cardiomegaly case.

Figure 3:

A, Local interpretable model-agnostic explanations (LIME) method approximates a complex model f (eg, a neural network) with a simplified model g (eg, linear model) around the input case I being interpreted. B, Perturbed instances (I_p)_1,...,n are produced, and C, predictions f(I_p)_1,...,n = p_1,...,n are obtained. D, The similarity π_I(I_p)_1,...,n between the input image I and each perturbed instance (I_p)_1,...,n is measured, and these values are used as weights to fit a simpler (eg, linear) model g, in a weighted fashion. The size of red crosses and blue circles illustrates weights. E, An explanation, ϵ(I), is generated by minimizing the disagreement between f and g (ie, how well g approximates f) while keeping the complexity of model g, as measured by Ω(g), low. Note: Perturbations can be of any type; in this example, image regions are blacked out. The similarity metric π_I as well as the model g can be selected by the user.

Explaining through Counterexamples or Influence Functions

Another group of interpretability approaches belongs to the family of influence functions, which at their core aim at understanding which training data points have a high impact on model predictions. This type of approach works by answering the question “What would happen if we did not have this training image, or if the values of this training image were changed slightly?” (23). The work of Koh and Liang (23) proposes a computationally efficient approach to assess which training images are most influential for a model by approximating leave-one-out retraining (ie, assessing change in model performance when leaving a sample out of the training set). These methods can also provide a framework to identify training images that are responsible for a potential domain shift (ie, training distribution mismatches the testing distribution) or to identify potentially mislabeled images during the training process, hence enabling a quality-control process of the training set. Once deployed, an AI system can be used in conjunction with influence-function methods to show which samples from the training images are driving a specific model’s prediction. We remark that this area of research and application has not yet received much attention for medical images.

Explanations through Semantics

Semantics offer a unique way of enhancing interpretability. Rather than outputting numbers or producing saliency maps on image regions, these methods output text explanations describing algorithmic predictions (24–26). For example, for a breast MRI scan, instead of outputting a single probability (eg, 85% probability of presence of breast cancer), this type of algorithm would, for example, output “high texture irregularity, and hyperintense T2-weighted rim” (24).

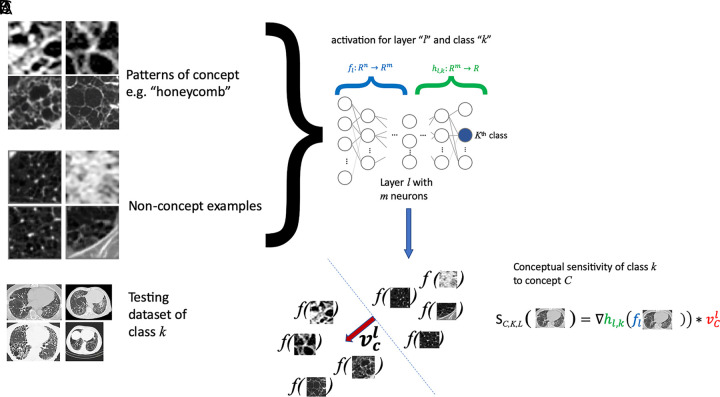
This family of methods includes testing with concept activation vectors (TCAV) (26) and has been presented to test the sensitivity of a neural network to a defined concept of interest. The main idea of TCAV is to quantify how responsive a DL model is to input patterns characterizing a concept (eg, Fig 4, A, “honeycomb pattern”) associated with the prediction output of the DL model (eg, Fig 4, C, idiopathic pulmonary fibrosis). Given concept and nonconcept examples (Fig 4, A), the DL model is employed to produce predictions for each example (see Fig 4, D) via forward passing them until reaching selected layer l with m neurons (Fig 4, C). With the produced set of examples and corresponding predictions, a linear model is built to separate both concept and nonconcept examples (see dotted line in Fig 4, D), which also defines a concept direction, v_c^l (red arrow in Fig 4, D). The sensitivity of class k (eg, k = idiopathic pulmonary fibrosis) to concept C (eg, C = honeycomb) of the DL model can be tested on new cases (Fig 4, B) and quantified by measuring changes to activations (Fig 4, E, green color-coded gradient term) when moving in the direction of the concept (Fig 4, E, red color-coded term).

Figure 4:

A, Testing with concept activation vectors (TCAVs) requires a set of samples characterizing the concept (eg, “honeycomb pattern,” a set of “nonconcept” examples, which are not related to the concept being studied), B, a testing dataset of the class k of interest (eg, idiopathic pulmonary fibrosis), and, C, a complex model f (eg, neural network) that one desires to interpret, and which has been trained to perform classification of these classes. D, A linear model is built from the concept and nonconcept samples using model f, by employing model f to generate classification labels for the concept and nonconcept samples. E, From the resulting linear model, separating concept from nonconcept examples (dotted line in D), its main perpendicular direction v_c^l (red arrow in D) can be obtained to assess the sensitivity of model f to concept C at layer l by quantifying changes to the activations of model f in the v_c^l direction.

In TCAV, it is then important to create a database of concept and nonconcept examples that represent the studied concept well and are not related to it, respectively. In practice, though, it is advisable to select nonconcept examples that do not differ too much from the concept examples.

Uncertainty Estimates of Machine Learning Models

Assessing the uncertainty of machine learning results can be used to enhance model interpretability by understanding which specific images, or areas of an image, the model identifies as being difficult (14). Uncertainty estimation has been proposed to assess voxelwise confidence levels of a DL model trained to segment structures on an image and to use these estimates to drive user corrections (27) or eliminate unconfident areas from further quantification tasks (28,29). Uncertainty estimation has also been used to assist in the referral of wrongly classified medical images for disease detection (30). Although uncertainty estimates can arguably be seen as being more closely related to auditability and system verification than to interpretability purposes, uncertainty estimates can in fact act as a proxy to enhance trust in a system, as a radiologist can verify whether the generated confidence levels of a computer-generated result match with their own assessment (ie, “Is the computer correctly pointing out areas of potential mistakes?”).

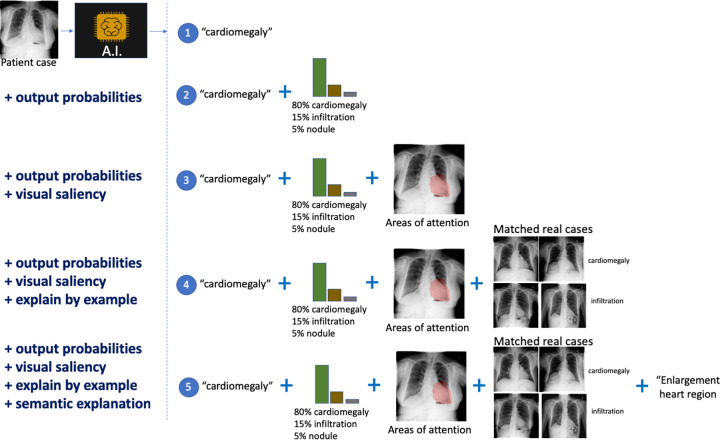
Because of the complexity of the decision process in radiology, we expect that a time-effective combination of interpretability modalities may be better suited for the analysis of AI systems. The different modalities that can be used for model interpretability in radiology are shown in Figure 5, which uses as an example the case of automatically diagnosing chest radiographs.

Figure 5:

Different modalities for model interpretation. For example, an artificial intelligence (AI) system that predicts the condition from a patient’s chest radiograph is shown. From top to bottom, interpretability information is added to the decision: (1) no interpretability information, (2) added output probabilities, (3) added visual saliency information describing areas of the image driving the prediction, (4) added matched real cases used during training of the AI solution influencing the prediction (ie, influential functions), and (5) added computer-generated semantic explanation.

In the following, we summarize the state of the art of interpretability methods used in radiology and medical imaging applications.

Interpretability Methods in Radiology and Medical Imaging Applications

Gallego-Ortiz and Martel (24) propose a rule-extraction approach to enhance the interpretation of nodes of a classification-tree model used to diagnose breast cancer using multiparametric MRI. Extracted rules are then displayed on a graph in the form of text to the user (eg, “high morphologic irregularity on T1-weighted image”).

The work of Kim et al (26) introduces a white-box global interpretability approach for diabetic retinopathy (among other applications) from retina fundus images. The approach can be classified under the semantics category, as it analyzes the complex internal relationships of a model and high-level concepts, such as “microaneurysms” or “pan-retinal laser scars.” In Pereira et al (14), global and local interpretability is performed for brain tumor segmentation and penumbra estimation in stroke lesions using multiparametric MRI. The authors demonstrate the usefulness of interpretability approaches to verify learned patterns of an AI system against common domain knowledge, as well as to identify potential bias introduced by a preprocessing step. In Zech et al (31), the authors used saliency maps on chest radiographs to validate the learned patterns of a DL system classifying patients as having pneumonia. Interestingly, through interpretability, the authors reported on the risks that a DL model can learn to recognize a specific clinical center or imaging system by capturing non–disease-related imaging features, such as metal tokens placed during scanning, that correlate with disease prevalence (eg, patients imaged with a bedside scanner had a higher prevalence of pneumonia). The work of Gale et al (25) used interpretability methods based on semantic text descriptions to explain pelvic fractures from frontal radiographs and showed the benefits of combining visual saliency and textual information for interpretability purposes.

Interpretability Methods for Machine Learning Models Are Needed in Radiology

As described previously, interpretability methods can be used for many different purposes, depending on the criticality of the task and whether an AI solution is being evaluated or requires system verification before deployment in clinical routine. In this section, we focus on describing the potential of interpretability methods for auditability, system verification, enhancing trust, and adoptability, as well as ethical and regulatory aspects.

Auditability, System Verification, Enhanced Trust, and User Adoption

Interpretability methods potentially can be used to audit an AI imaging solution. Auditing is an assessment of an AI solution’s conformance to applicable regulations, standards, and procedures, conducted independently from the solution’s developers. Auditing could be done by submitting the AI solution to thorough benchmarking and interpretability schemes, which aim to better understand how a system has learned the patterns of the data that drive its predictions. In this sense, the interpretability approaches explained above could be seen as one part of the set of tools available to an auditor.

Quality assurance of an AI solution also can benefit from interpretability approaches to identify a system’s potential weaknesses. For example, an interpretability approach identifying that a given imaging sequence, within a multisequence imaging setup, is the most important for the prediction performance of an AI solution can yield valuable insights as to how sensitive that solution might be to protocol changes of that particular sequence (eg, Pereira et al [14] and Eaton-Rosen et al [32]).

During development of an AI solution, interpretability methods, such as the influence functions explained above, could be used on the training dataset to unveil any potential bias in the data that might affect the learning patterns of an AI solution. As an example, Zech et al (31) found that an AI system was learning to recognize a marker, which was introduced by the imaging device into the patient images, to boost its diagnostic performance through an interpretability method based on the visualization of attention areas.

In general, interpretability approaches could have the potential to bring valuable insights to quality control of training sets and quality assurance and auditing protocols of AI systems, especially when considering recent findings showing how easy it is to induce system errors of DL approaches, by making targeted, visually imperceptible pixel changes to an image (33). Similarly, as recent findings by Geirhos et al (34) suggest that modern CNNs are biased to textural information, interpretability methods based on activation concepts, such as TCAV, offer means to quantify such potential biases. These findings still need to be shown for medical images.

As these technologies become mainstream in radiology practice, interpretability approaches can be used to enhance trust by creating evidence that demonstrates the robustness and underlying functioning. Together, it is apparent that by enhancing the interpretability of a system, trust from an expert user will also be enhanced, and thus the interpretability will promote effective adoption in practice (15).

Regulatory and Ethical Aspects

The need for regulations of AI technologies in radiology is well recognized, and recently more attention has been given to establishing standards and structured protocols to ensure a safe and streamlined integration of these technologies (35). The U.S. Food and Drug Administration is making important steps toward a new regulatory framework to improve the standardization and a streamlined integration of AI technologies in health care (36). In Europe, with the launch of the new General Data Protection Regulations, new challenges exist for the development of automated decision-making systems that require a “right to explanation” (37). In this sense, interpretability approaches are a fundamental asset to ensure regulatory conformance, and in doing so, it is vital to foster developments in a transdisciplinary approach. Further efforts are being conducted by the International Telecommunication Office, which promoted a workshop called Artificial Intelligence for Health, held in Switzerland in 2018, as well as the first International Organization for Standardization meeting, with their First International Standard committee for the entire AI ecosystem.

The ethical aspects of AI in radiology have recently been documented through the multisociety statement supported by the American College of Radiology, “Ethics of AI in Radiology: Summary of the Joint European and North American Multisociety Statement” (38), in which interpretability of AI systems has been highlighted as an important component for the radiology community. Notably, the multisociety statement signals the need to create guidelines to explain, test, and assess AI models. Several questions have been raised in this multisociety statement, including how much of an AI solution’s inner workings radiologists need to assess before applying the AI in patient care and how transparent AI vendors should be regarding the internal functioning of their products. Furthermore, it is debatable how much transparency an AI system should have while not compromising it against malicious attacks or intellectual-property breaches. In this sense, research and developments from the areas of security and cryptography, in which “security through obscurity” is generally discouraged, could leverage insights to improve these guidelines. Beyond transparency of the AI system itself, enhanced transparency of the evaluation procedures of AI technologies in biomedical imaging has also been highlighted by proposing guidelines and best-practice recommendations (39). In this sense, interpretability methods could be used by software quality-management teams not only to benchmark and analyze the accuracy of AI solutions but also to unveil their internal mechanisms. In relation to new regulatory frameworks being discussed, by the U.S. Food and Drug Administration and other bodies, to facilitate the evaluation and approval of AI systems that learn over time through continuous retraining cycles (active learning), we believe that interpretability methods can be used to ensure that observed system improvements do not stem from bias or confounders’ effects in the new data used for retraining of the AI system. We remark that this is particularly important when DL systems are confronted with updates of the imaging technology, changes to the imaging protocol, and other aspects that can change the training data over time.

As AI systems evolve, we expect their autonomy and interconnections with other AI systems to increase, leading to several questions related to how much autonomy they are actually permitted or which actions need to be taken when an AI solution disagrees with a human operator. Similarly, as the ubiquity of AI systems increases, interpretability methods can help in alleviating the increase in automation bias, in which human operators fail to notice or disregard AI failures or erroneously accept a machine’s decision despite contrary evidence.

Areas of Clinical Practice That Would Benefit from AI Interpretability Methods

In general, we remark that the goal of interpretability is not to understand every part of an AI system but to have enough information for the task at hand. As pointed out by Doshi-Velez and Kim (10), interpretability, in general, is not needed when there are no significant consequences for unacceptable results or when the problem at hand is well understood. In radiology, one can argue that both situations exist: a wrong diagnosis can have severe consequences for a patient, and clinical diagnosis is, in many clinical scenarios, not a trivial task and is prone to interpretation errors.

As the research area of interpretability grows, many different interpretability approaches are being proposed. However, we remark that many of them have not yet been explored for radiology.

In the following sections, we make potential links between current interpretability methods and some of the common tasks in radiologic practice.

Image Segmentation

Current visualization approaches based on uncertainty estimation can be used to leverage the trustworthiness of a segmentation algorithm. However, visualizing an explanation as to why a voxel receives a given class label is more difficult because many factors might influence its prediction, including, but not limited to, voxel position, neighboring and long-range intensity, and texture patterns. Textual explanations, on the other hand, can better leverage explanations for voxel classification tasks, through human-friendly concepts summarizing the imaging information driving voxel classifications.

Lesion and Organ Detection

Similar to image segmentation, visualization and textual explanations could potentially be used to understand how an AI system locates a specific target structure.

Image Registration

Visualization interpretability methods are suitable to interpret the results of an AI-based image-registration technology, as visualization methods can highlight image regions driving image-registration results. For nonrigid registration, in which the output of an AI-based registration model has many degrees of freedom, visualization techniques combined with user interactions could be used to enable an operator to specify a voxel or region on an image and visualize dynamically which areas of the image drive the voxelwise matching process. This area of research and application has not yet been explored.

Computer-assisted Diagnosis and/or Staging

For these tasks, visualization, textual explanations, and influence functions could potentially be used to enhance the interpretability of AI decisions. Particularly, we note that influence functions could be an effective approach in explaining a diagnosis by showing similar cases with the same diagnosis from an existing training database, as well as by showing counterexamples (“Why did the AI system not diagnose it as type X instead?”).

Prognosis

For these tasks, visualization, textual explanations, and influence functions are well suited to enhance the interpretability of AI-based predictions. Prognosis is arguably among the hardest tasks for an AI model, as many factors occurring in between imaging time and time to prediction can affect the final patient status. Interpretability methods can be of particular help to leverage understanding of potential non–disease-related imaging information (eg, a center-specific marker on an image [40]) that correlates with a given prognostic status.

Radiation Therapy Planning

An AI-based system for radiation therapy planning would involve image segmentation of tumors and healthy structures that need to be spared, followed by a voxelwise predictor of the radiation dose. Hence, producing explanations to voxelwise radiation-dose estimations is considered difficult with current state-of-the-art interpretability methods, as there are many factors to consider, such as the absolute and relative location of a voxel in relation to neighboring structures, clinical margins, the patient’s clinical information and records, the therapy regimen, and so forth. Conversely, visualization techniques could be used here to verify that radiation-dose predictions do consider neighboring organs that must be spared from radiation.

Computer-assisted Monitoring of Disease Progression

Visualization and textual explanations could potentially be used to enhance interpretability in these tasks, by, for example, visualizing temporal changes that explain an AI-based system classifying a patient as having a “response to therapy” or “progressive disease.”

Triaging

Triaging refers to the task of automatically classifying imaging cases by their level of severity of a given condition, and images are then subject to further processing and/or radiologic inspection. Visualization, textual, and influence-function interpretability methods could potentially be useful to audit the automated triaging process and ensure that radiologic clinical correlates are driving the triaging process and that spurious imaging features (eg, patient motion, incomplete field of view, metal artifacts, etc) are not.

Image Reconstruction

AI-based image reconstruction approaches are being proposed that incorporate fast and image quality–enhancing mechanisms, operating directly from k-space (41) or in combination with new techniques for MR fingerprinting (42). Ensuring quality and reliability of these data-driven reconstruction approaches is highly demanding, as it boils down to ensuring high generalization capability. Interpretability of AI-based reconstruction would be highly demanding because of the complex nature of the underlying inverse problem. However, basic interpretability approaches, based on occlusion tests of the temporal signal (fingerprints), have been recently reported in one study (42), enabling verification of the expected parts of the fingerprint signal contributing to reconstructed MR maps.

Discussion

Interpretability of machine learning is not a new topic of research; however, with the advent of an increasing number of DL technologies, the need for interpretability methods has gained more attention in recent years. Arguably, this stems from the high complexity of DL technologies, with typically millions of parameters being optimized during the training process, enabling DL models to scrutinize training datasets and automatically extract data patterns correlating to a target system’s output (eg, imaging patterns correlating with disease classification, prognosis, etc). Additionally, with such large parameter pools being optimized during training, DL models are enabled to potentially identify and use spurious data correlates, which leads to observable system performance improvements but lower levels of system reliability. This effect is further exacerbated when considering the large data pools needed to train DL models and, hence, the increased efforts needed to perform quality control of training datasets. In this sense, as the performance of AI-based systems currently relies on large, curated training datasets, we emphasize the potential of interpretability approaches not only to leverage explanations of such AI-based models but also to provide means for more scalable quality control of the data used for their training (eg, Koh and Liang [23]). Similarly, toward a more scalable performance improvement of AI-based systems, visualization schemes that combine uncertainty estimates of computer predictions could be used to target computer results that require human feedback (eg, Jungo et al [29] and Mahapatra et al [43]). Yet, we remark that more research efforts are needed to ensure that uncertainty estimates calculated from modern DL approaches are reliable and can effectively be used in the clinical routine (44,45).

The field of the interpretability of machine learning is being investigated for medical imaging applications. The set of currently available interpretability approaches is growing, although we notice that a majority of methods focus on providing saliency maps for classification tasks. In radiology practice, we hence remark on the importance of investigating and developing interpretability methods that cover a large variety of tasks. Furthermore, as AI systems begin to combine different types of patient information (eg, imaging, molecular pathways, clinical scores, etc [46]), we believe that interpretability methods that are able to handle such heterogeneity of information hold great potential.

In performing interpretability analysis, all of the methods described above typically require a radiology expert to validate whether the explanations make sense or align with common domain knowledge (ie, “Would a human use the same features to perform the task?”). In this regard, assessing levels of interpretability is highly dependent on user experience, and, hence, some subjectivity and user bias might be present in the design and evaluation of interpretability approaches. As pointed out by Poursabzi-Sangdeh et al (47) and Doshi-Velez and Kim (10), assessing good or bad interpretability is ultimately defined by human decision-making, not algorithms, and there are many factors influencing the assessment, including, for example, the complexity of a model, its level of transparency, and its number of features; even a user interface can affect the evaluation of interpretability methods.

Future research will be required to design standard and reproducible ways of assessing and comparing interpretability-enhancing methods. In this sense, assessing their reliability via simple yet effective tests (22), understanding their common patterns and unique strengths (19), and seeking to unify them into a theoretically sound framework (48) are important research avenues to ensure that interpretability methods can be trusted when analyzing AI technologies. Ultimately, we want safety and reliability from the AI systems we use in radiology. Therefore, if we employ interpretability methods, we need to ensure that those interpretability methods can be trusted in the first place. Toward this goal, it is important to involve researchers, practitioners, radiology end-users, machine learning engineers, and human-machine interfacing communities. In relation to the work of Doshi-Velez and Kim (10), laying down groundwork to define and evaluate interpretability, we remark on the importance of focusing on task-oriented interpretability methods in radiology that account for time constraints (ie, “How much time is there for interpretability purposes?”), required performance (ie, “What is the balance between model performance and its interpretability level?”), and scope of the interpretability (global vs local).

Conclusion

Interpretability of AI systems is a quickly growing field that has been highlighted by the radiology community as an important area of development, with much potential for the development of safe and intelligible AI technologies. However, the diversity of tasks in the radiology field requires task-specific interpretability solutions and tailored, interdisciplinary, clinically oriented validations of tasks critical to the patient’s safety, time constraints, and scope.