Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming

Highlights

• •Genetic Evolutionary Programming (GEP) has been used to analyze and predict COVID-19 in India.
• •Two Prediction models for confirmed cases and death cases for India and three most effected states are designed.
• •The models presents prediction data for next 10 days till 25 May 2020.
• •Mathematical formulations for the prediction models have been added.
• •GEP models are highly reliable and provide better predictions.

Abstract

COVID-19 declared as a global pandemic by WHO, has emerged as the most aggressive disease, impacting more than 90% countries of the world. The virus started from a single human being in China, is now increasing globally at a rate of 3% to 5% daily and has become a never ending process. Some studies even predict that the virus will stay with us forever. India being the second most populous country of the world, is also not saved, and the virus is spreading as a community level transmitter. Therefore, it become really important to analyse the possible impact of COVID-19 in India and forecast how it will behave in the days to come. In present work, prediction models based on genetic programming (GP) have been developed for confirmed cases (CC) and death cases (DC) across three most affected states namely Maharashtra, Gujarat and Delhi as well as whole India. The proposed prediction models are presented using explicit formula, and impotence of prediction variables are studied. Here, statistical parameters and metrics have been used for evaluated and validate the evolved models. From the results, it has been found that the proposed GEP-based models use simple linkage functions and are highly reliable for time series prediction of COVID-19 cases in India.

1. Introduction

Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) or coronavirus disease 2019 (COVID-19) is a global pandemic outbreak, the world is facing today. The virus, which migrated from Bats to human, originating from Wuhan, the capital of Hubei province of China, has influenced more than 180 countries of the world. The first patient was reported on 8 December 2019, in Wuhan by the Chinese administration [1]. A month later, the first death from the virus was reported on 9 January 2020. On the same day, world health organization (WHO) declared that a novel coronavirus diseases has been identified and is expanding multi-laterally everyday [2]. The virus which started from China, migrated to the third world and first case in Thailand was reported on 13 January 2020 [3]. The Chinese authorities tried to contain the virus by imposing certain strict actions including airport closures, highway closures, railway interruptions, public gathering suspension, halting public transport, closure of shops, mass activities and any other activity which accounts for social gatherings were brought to an immediate halt. All of these measures where employed to minimize the effect of community level transmission of the disease [4]. The Chinese authorities took over the control of the situation and collected data from 2018 International Air Transport Association (IATA) to identify and check the infectious disease vulnerability indexes (IDVIs) in new countries where the virus might have transmitted outside China [5]. It should be noted that IDVI has a range of [0, 1], higher the value of IDVI, lower is the risk of disease transmission and vulnerability. The vrius affected more than 85,000 Chinese population and the initial destinations affected were Hong Kong, Bangkok, Tokyo and Taipei, all having an IDVI above 0.65 [6].

Though numerous efforts have been brought into place, but still the virus was not controlled and by 19 January 2020, numerous cases across the world were reported [3]. WHO declared the disease as an emergency situation for the whole world on 31 January 2020 and by 11 March 2020, it was declared as a new threatening global pandemic [4]. As of 12 May 2020, almost 4,006,257 have been reported across the globe with a total death count (DC) of 278,892 amounting for a daily increase of 26% and 28% increase in confirmed cases (CC) to deaths per day [6]. The worst affected country being USA, the second most affected country is Russian Federation, followed by United Kingdom, Spain, Italy, Germany, France and Turkey. The virus which started from China, has engulfed almost every country of the world, with the most affected region being the European continent [7]. Average estimates have also been drawn to calibrate and design COVID-19 transmission models, before further investigation and pandemic control measures can be implemented [8]. It can also be noted that the virus started from a single individual but it migrated to cluster level and in present situation, is enormously increases as a community level transmission system [11].

India the second most populous country of the world with 1.3 billions people to serve, having an average household income ranked at 112th out of 164 countries by the world bank and with a 150th rank in global health care by world economic forum. This critical condition was under the scanner of the whole world, when the COVID-19 pandemic first set foot on Indian soil [9]. The first case was reported on 30 January 2020 and it was expected that India will not be able to survive the heat and due to lack of essential services, life of millions of people will be at stake. Its more than three months since the first case and the total number of confirmed cases have reached a level of 70756 as of 12th May 2020. With a recovery rate of 31.7%, a total of 22455 people have been recovered and discharged whereas 2293 people suffered from death [10]. If we compare the same figures with the third world, USA has a total number of confirmed cases amounting to 1,271,645 with an increase rate of 25,000 persons per day and a death count of 76,916 in the same period. Spain with a total of 224,390 confirmed cases versus 26,621 deaths, Russian Federation having 221,344 confirmed cases versus 2009 death cases and a daily increase of more than 10,000 cases. United Kingdom stands at fourth place with 219,187 confirmed cases versus 33,854 deaths, and China where the pandemic began is amounts for 84,450 confirmed cases versus a death count of 4643 people [6]. The major reason for such little affect of COVID-19 on India, is due to the timely response from the respective central and state governments.

Since the first day of the outbreak in India, the Indian govt. has been scanning each and every person coming to the country from China and people who had any Chinese travel history in the past few days. The first nation wide lockdown for 21 days was announced by the government on 23 March 2020 and was further extended by another 21 days till 3 May 2020, which has been further extended till 17 May 2020 (can be extended to 30 May 2020). Important measures included timely response to provide health care facilities, contact tracing, extensive testing, community mobilization and others have helped to contain virus and keep a low mortality rate. Different states have already recovered from various adversaries and that have helped them to keep a check on the new situation. Odisha, Kerela and Tamil Nadu has a long history of natural disasters and precautionary measures have already been taken by the government. Maharashtra on a whole uses drones to monitor social distancing and lockdown. A cluster containment strategy has also been employed to diagnose and contain the virus. This has been done by surveying, detecting and contact tracing of about 3 km of area where more than three patients are diagnosed [9].

The potential effect of COVID-19 have prompted various studies on the characteristics of the coronavirus and a large number of studies are under processing to estimate the possible devastation by the virus and to derive a vaccine for its cure. It has also been found that the virus has an adverse effect on elderly people as well as for people who are suffering from some kind of infectious diseases such a heart attacks, respiratory diseases, and others, and it a big concern for the authorities to keep a check on the virus so that minimum harm can be done [12]. Various studies have been conducted by researchers across the world to estimate the possible impact of coronavirus. The major studies include stochastic simulations [13], Weibull distribution model [14], exponential growth model [16], lognormal distribution [15] and others [17]. The studies were able to predict an average incubation period of 5.1 days and a total of 14 days quarantine necessary for analysing the virus within a person [13]. But none of these studies could estimate the exact reproduction rate and hence not much has been done to predict how the virus will effect in the coming weeks or so. Also, all of the studies have been done on China and not much work has been done with respect to the Indian sub-continent.

In present work, a new genetic programming based model (GP) [18] for times series prediction of the COVID-19 scenarios in India has been proposed to estimate the possible spread of the virus. The dataset for evaluation is taken from [19]. GP is an enhanced version of genetic algorithm (GA) [20], in which new solutions are generated as computer based programs rather than simple binary strings [21]. GP ore more precisely gene expression programming (GEP), is the most recent version of GP and has been analysed by various researchers to make prediction models, linear regression models and others [22], [23], [24]. The GEP model has been used to predict the total number of cases in India based on two major parameters, these include confirmed cases (CC), and death count (DC). Note that these time series have been developed from the date after first lockdown that is from 24 March 2020. Apart from that, the combined data set used in present work is available at. A major reason for using GEP modeling is that this approach is more efficient as compared to classical techniques and are more stable in comparison to artificial neural networks. Also, GEP based models generate simple prediction equations which can be optimized as per the end user requirements. Another reason for using GEP, is that these models do not need any prior information to develop prediction equations. Overall, it can be said that prediction models proposed by GEP based modeling have better calibration and can analyse the results in a much effective way [25], [26]. Thus in present work, GEP models are proposed based on the raw data taken from authentic sources since 24 March 2020.

The paper is organized into 4 sections, first section include the introduction as discussed above. In section 2, technical preliminaries and model analysis is presented, providing details on the basics of GEP and proposed GEP model. Section 3, provides the various results and discussion related to different scenarios of COVID-19. Here it should be noted that three most affected states of India have been taken under consideration and GEP models for all the states have been proposed. These states include Maharashtra, Gujarat and Delhi. This section further includes the model validation, comparative study and variable importance of all the component, for all the states, which are required for the accurate performance of the proposed GEP model. Apart from that, analysis with respect to percentage humidity, effect of temperature and variables on COVID-19 has also been discussed. Finally insightful conclusions and future recommendations are drawn in the final section.

2. Technical Preliminaries and Model Calibration

GEP is a highly effective evolutionary algorithm and has proved its worth in comparison to GA. The algorithm produces new equations instead of binary strings and hence has the direct advantage of mathematical formulations for higher dimensional problems which otherwise is not possible with a standard GA. In order to formulate the GEP model for India, it is really very important to investigate existing models and analyse if the proposed GEP models will be significant enough or not. Various models such as AceMod (Australian Census-based Epidemic Model) [27], neural network based models [28] and others have been employed to access the situation and provide exact predictions. Though these models are a bit significant but the first AceMod model has been used for influenza prediction [27] and has little relevance to COVID-19. The other neural network based model uses shallow long term memory (LSTM) method along with the fuzzy rule based model to predict the present scenario. A very high root mean square error (RMSE) and correlation (R ²) values have been found making the model little vulnerable to uncertainties. Both these methods discussed are basic and discrete in nature and require more sets of data values to provide exact predictions. Also these are classical techniques and pose very challenging implementation when compared to simple GEP based modelling. GEP allows for a system to be calibrated easily and even predict accurate as well as reliable solution under minimal constraints [25]. In present work, two major time series including CC and DC have been taken into consideration to access and predict the possible impact of COVID-19 in major states across India as well as India on a whole. The states which are taken into consideration are Maharashtra with the highest number of 23,401 CC versus 868 DC, Gujarat with 8541 CC versus 513 DC and Delhi with 7233 CC versus 73 DC. A detailed methodology for the GEP based models in presented in subsequent subsections.

2.1. Gene Expression Programming

GP on a whole is an extension of GA and is based on the same principle of Darwin’s theory of natural selections or survival of the fittest. Here new equations or simply computer based programming models are created in order to find a relationship between the input and output variables. It is basically a computer based program and creates a tree like structure commonly referred to as bree-based GP model and are declared in a functional programming language [22]. Overall, GP is a hierarchical structure with functions and terminals. The latest version of GP modelling is the GEP, which uses a fixed length character string instead of classical tree representation of a GP model. The new structure consists of five major components namely function set, control parameters, terminal condition, fitness function and a terminal set. All these components collectively form a simple para tree and is known as an expression tree (ET). The major advantage of using this kind of methodology is that it is extremely simple and works at chromosome level. It also consists of multi-genic properties and can be used for evolution of complex and nonlinear sub-programming models [29]. Each GEP model consists of a list of fixed length symbols, a function set (e.g.+,-, × , /,Log) and a terminal set (e.g.a,b,c,3). Thus in terms of both terminal set and function set, a GEP can be an invention of multiple chromosomes which are capable of representation in the form of any parse tree. To decode this information, Karva language is used at chromosome level [30] and a simple gene in Karva language is given by

$$/Log++c3ab$$ (1)

where a, b and c are variables and 3 is a constant. The expression in 1 is called as a K-expression or generally a Karva notation. The above formulated model can then be evolved in the form of a simple ETs as given by Figure 1 . The expression in Equation 1, can be converted into a k-expression. This expression is the root of ET, which reads through the functional node and finally to the terminal node. This type of interpretation allows for a quicker understanding of the complex mathematical intricacies [31]. Thus, a simplified k-expression is presented in the form of mathematical equations as given by

$$Log(a+b)/(c+3)$$ (2)

Fig. 1.

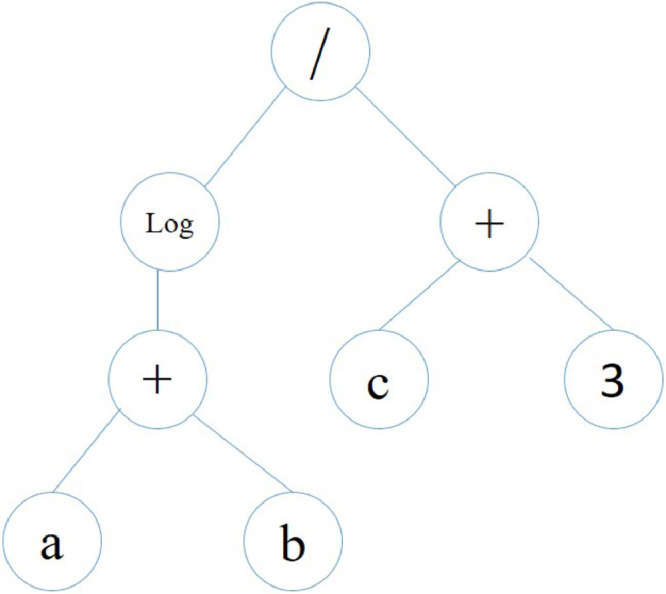
Representation of an ET.

Note that the above discussed k-expression it can be estimated that the total length of genes in a GEP model remains same but the total number of ETs keep changing with respect to the problem under consideration [22]. The GEP model thus formulated further finds that certain redundant elements are present in the notation which are not significant for genetic mapping. So for a GEP model to be an efficient model, the total length of a k-expression should be equal to or less than the total length of the GEP gene. Here it should be noted that a random head-tail methodology is followed by a GEP to select a gene. The head might have both the function symbol and the terminal symbol but the tail has only one terminal symbol [22].

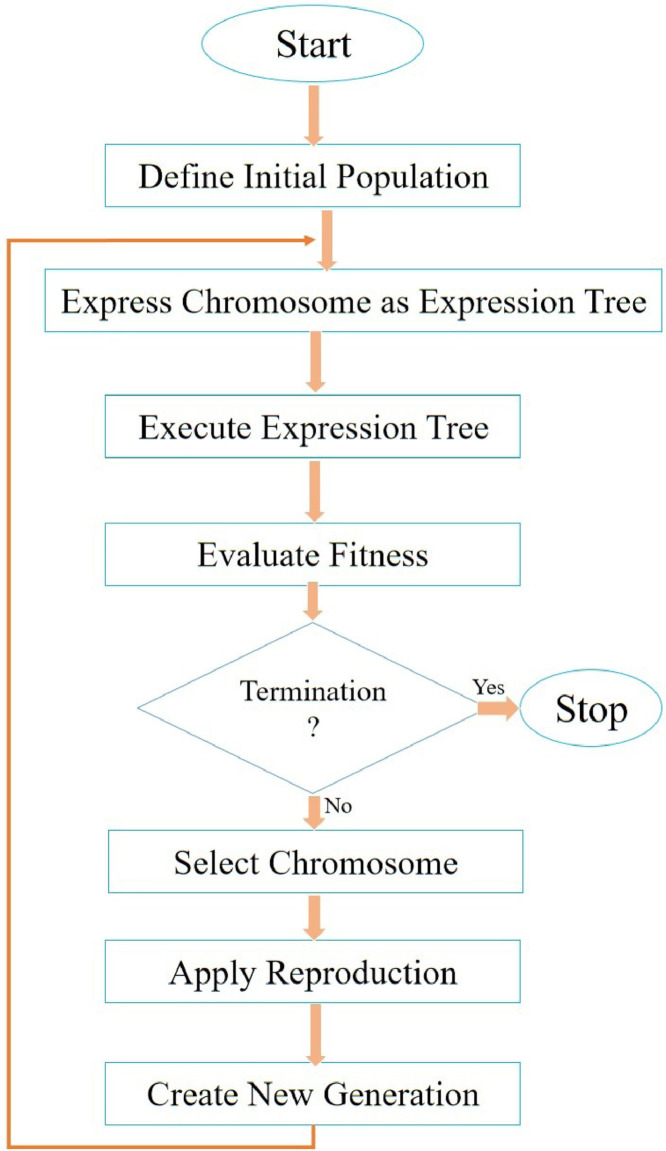
For a uniformly distributed randomly initialized population, a GEP model consists of fixed length chromosome for each and every member of the population. The next step is to evaluate the fitness of the chromosome as per the problem requirement, then evaluate the solution using roulette wheel selection with elitism and finally find the best solution based on fitness to reproduce new individuals with certain modifications. Note that a termination criteria, in terms of number of generation or some acceptable error value, is also defined. Here the final solution thus obtained after the termination criteria is met, is considered as the possible solution of the problem under test. The schematic diagram for the fundamental steps of a GEP model is given by Figure 2 . The algorithm because of the presence of roulette wheel selection mechanism, is very effective in optimizing and cloning the best individual with respect to changing iterations and finally finding the best solution [25].

Fig. 2.

Representation of a GEP algorithm.

2.2. Proposed GEP Model

To have a clear understanding of the total number of COVID-19 cases across India, two major parameters are taken into consideration including CC and DC. Both of these parameters are taken in order to accurately access and predict the effect of COVID-19. For performance evaluation, eight former records are used in the time series and best GEP model based on them is selected. The numerical data set used is divided into two sub data sets and are equivalently used for training as well as testing/validation phase. Also, it is a well-known fact that performance of an evolutionary algorithm can not be judged by using single run and hence multiple runs of the data set were performed to reduce the error and predict a near optimal output [25]. Here multiple runs of the same data set were simulated, thus helping the algorithm in providing exact output even if the total instances for experimentation are limited in number. As a further evaluation step, 70% data was used to perform training tasks and rest 30% was used to perform testing/validation. Here it should be further noted that the training data uses gene evolution and best model is predicted using correlation coefficient. Thus a new model has been proposed having better performance for training and can somehow work good enough for testing phase.

Apart from this, the GEP model is greatly affected by the choice of parameter. In order to have a fair model multiple runs have been conducted to find global solution by changing the parametric settings. The initial parametric setting was based on the previously introduced model as given by [22]. Further, for the best performance, the fitness function is evolved with respect to mean squared error (MSE) and the new fitness function can be mathematically formulated as

$$Fitness=\left(\frac{1}{1+MSE}\right)\times 1000$$ (3)

The fitness function formulated in equation 3, is used for all the cases under investigation. A detailed discussion on the model validity and comparative study is presented in consecutive section.

3. Numerical Results and Comparative Study

The GEP algorithm to devise new model for COVID-19 in India was implemented using GeneXpro Tool [31]. For genetic operators, the parameter settings are as given in Table 1 . The algorithm was run for a certain set of parameter and simulations were performed until no further improvement can be noticed in the GEP model. Here head size and total gene count helps in evolving the general architecture of GEP model. Gene count for each chromosome in the model determines the total number of terms in the GEP model and each gene further corresponds to each sub-ET. In present case, the total optimal levels for head size and genes is taken as 4 and 5 respectively. For gene size greater than 1, mathematical models can be linked by using linkage functions. Also, the linking functions used in present work are very basic in formulation and hence a simple yet optimal GEP model has been devised. The statistical parameters for the proposed GEP model are given in Table 2 . The next section details about the results and discussion corresponding to the proposed GEP model.

Table 1.

Parameter Settings for GEP algorithm.

Parameter	Settings
General
Chromosome	30
Gene	5
DC size	5
Head size	4
Tail size	5
Gene size	14
Linking function	Addition/Minimum
Genetic operator	+, -,  × , ÷,
Mutation rate	0.00206
Inversion rate	0.00546
IS and RIS transposition rate	0.00546
One-point and two-point recombination rate	0.00277
Gene recombination and transposition rate	0.00277
Numerical Constants
Constant per gene	10
Data type	Floating-Point
Range	[-10, 10]

Table 2.

Statistical Parameters of GEP model for external validation.

Item	Formula	Condition	GEP CC	GEP DC
1	R	0.8 < R	0.9999	0.9997
2	$k=\left[{\sum }_{i=1}^n(h_i\times t_i)\right]/h_i^2$	0.85 < k < 1.15	0.9996	0.9994
3	$k^{{}^{\prime }}=\left[{\sum }_{i=1}^n(h_i\times t_i)\right]/t_i^2$	$0.85<k^{{}^{\prime }}<1.15$	1.0000	0.9998
4	$m=(R^2-R{o}^2)/R^2$	|m| < 0.1	-0.00036	-0.00154
5	$n=(R^2-R{o}^{{}^{\prime }2})/R^2$	|n| < 0.1	-0.00026	-0.00155
6	$R_m=R^2\times (1-\sqrt{|R^2-{Ro}^2|})$	0.5 < Rm	0.9837	0.9592
where	${Ro}^2=1-\left[{\sum }_{i=1}^n{(t_i-h_i^0)}^2\right]/\left[{\sum }_{i=1}^n{(t_i-\overline{t_i})}^2\right]$	$h_i^0=k\times t_i$	1.0000	0.9999
	$R{o}^{{}^{\prime }2}=1-\left[{\sum }_{i=1}^n{(h_i-t_i^0)}^2\right]/\left[{\sum }_{i=1}^n{(h_i-\overline{h_i})}^2\right]$	$t_i^0=k^{{}^{\prime }}\times h_i$	1.0000	1.0000

Here two models based on CC and DC are devised and the parameter settings for their evaluation is given in Table 2. Here it should be noted that root mean square error (RMSE)and correlation coefficient (R) metrics are taken into consideration to evaluate the model, which are calculated as

$$RMSE=\frac{{\sum }_{i=1}^n|h_i-t_i|}{n}$$ (4)

$$R=\frac{{\sum }_{i=1}^n(h_i-\overline{h_i})(t_i-\overline{t_i})}{\sqrt{{\sum }_{i=1}^n{(h_i-\overline{h_i})}^2{\sum }_{i=1}^n{(t_i-\overline{t_i})}^2}}$$ (5)

where n is the total number of samples, h_i and t_i are the actual and intended outputs, $\overline{h_i}$ and $\overline{t_i}$ are averages of the actual and intended outputs for the ith output. Further, it is a well-known fact that only R values cannot be considered as good evaluation metrics. This is because R values do not change significantly by shifting the output of any predictive model. So there is requirement of some other parameters or indicators which can evaluate the proposed algorithm. In present work, RMSE has also been taken into consideration. Here RMSE is an error function and lower values of this parameter indicate that more precise model can be devised. Further, Smith et. al, [32] stated that for a model to be reliable and accurate, the correlation coefficient between the desired and intended values must be strong. Thus, it can be said that any model with lower value of RMSE and higher values of R has the capability of providing reliable time series predictions [33].

In order to externally validate the GEP model, criteria used by [34] has also been employed. The main feature of this criteria is that the regression slopes (k or $k^{{}^{\prime }}$) should be close to 1 and must be around the origin. The value of parameters n and m ought to be lower than 0.1 whereas external predictability R_m should be greater than 0.5 [35]. Also, the squared correlation coefficient ($R{o}^{{}^{\prime }2}$) and the coefficient (Ro ²) should be close to 1. Here it should be noted that value of $R{o}^{{}^{\prime }2}$ lies between the predicted and desired values where as Ro ² lies between desired and predicted values respectively [25]. More details on other parameters for external validation is given in Table 2. All of these parameters plays an important part in ensuring good prediction probability of each proposed model and also analysing the strong validity of the model.

3.1. GEP model for whole India

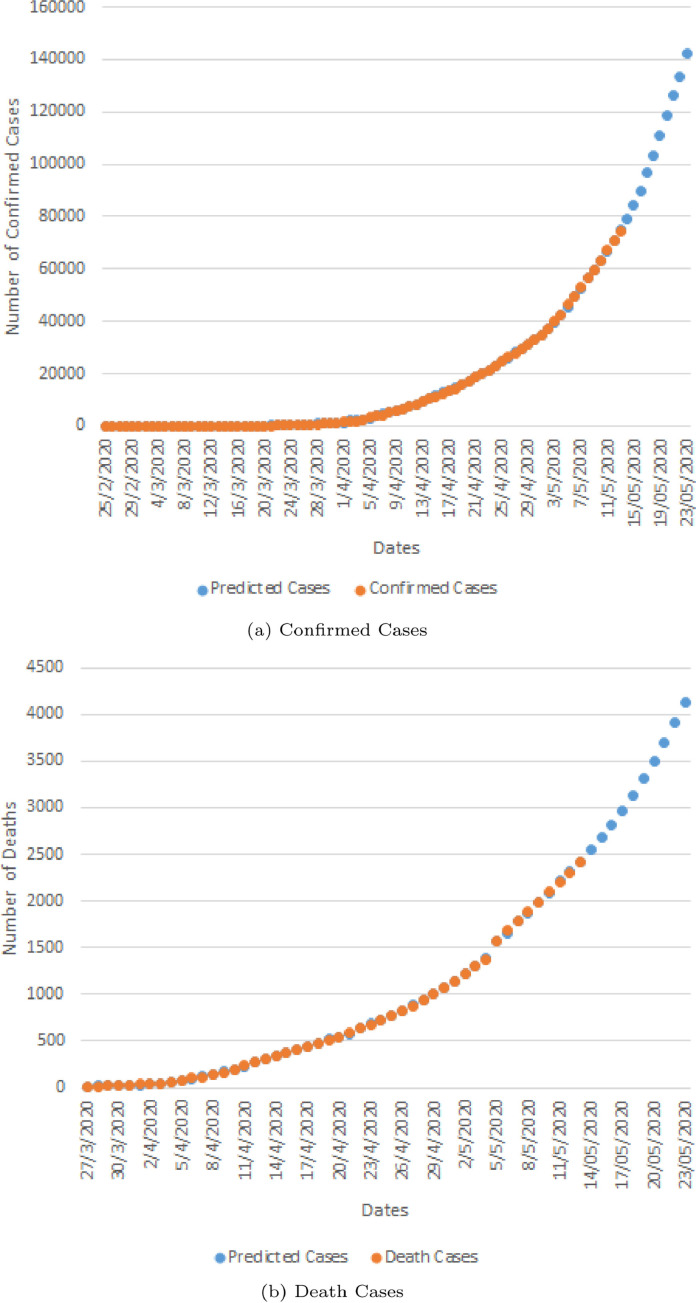
A comparison of actual to intended or predicted values for CC and DC are given in Figure 3 . The mathematical formulations discussed above, represent a complex organization of constant, operators and variables to predict the output. From Figure 3, it is evident that both the prediction models give almost equivalent results as that of the original CC and DC. Also, from the models, it can be seen that till 13 May 2020, there are total number of CC and DC is around 80,000 and 2500 respectively. The original values versus predicted values for the same period are almost similar. The Figure 3, also shows the predicted outputs for these models and it has been found that in the next 10 days that is by 23 May 2020, the total number of CC and DC will approximately become 142,000 and 4200 respectively.

Fig. 3.

Experimental versus predicted cases for COVID-19 in India using GEP model.

3.1.1. The Expression Tree based Validation

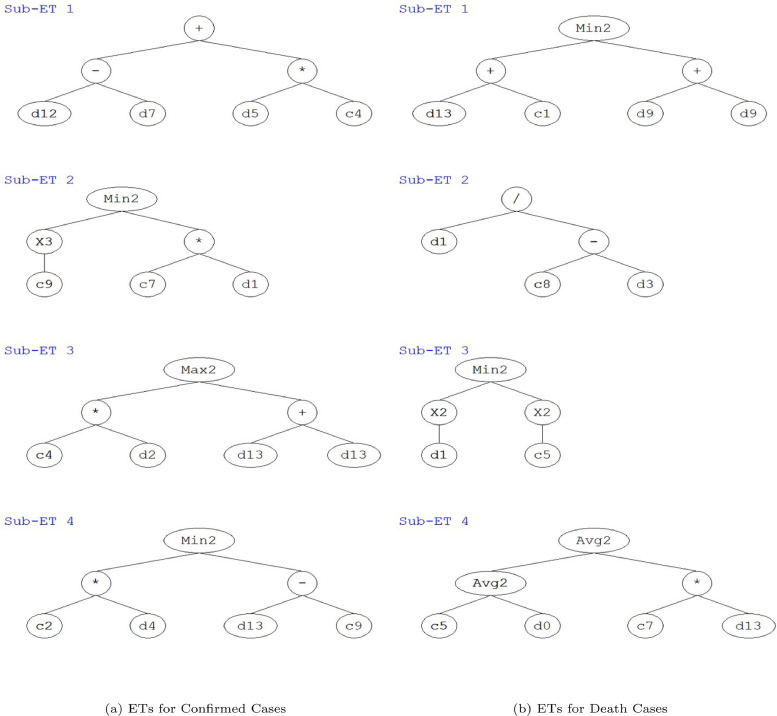
The expression trees for whole India is given in Figure 4 in terms of both CC and DC. Based on these, mathematical equations can be formulated and new prediction analysis can be drawn. From the Figure 4, it can be said that the proposed ETs can be consecutively divided into four subprograms. Each of the proposed subprograms represent individual aspects of the problem under consideration and meaningful information can be derived to get the overall desired solutions [25]. Here it can be indicated that each of the newly evolved sub-function from ETs consists of potential information about the basic psychology and architecture for a certain facet of the problem. This kind of information, ultimately paves way for evaluation at chromosomal level [31]. From the sub-ETs in Figure 4, it can be seen that the linkage function for CC is addition where as for DC, it is minimum function. From these sub-ETs, mathematical equation can be drawn and equivalent model for further predictions can be formulated. The time series model pseudo-code for whole India is given in Algorithm 1 for CC and in Algorithm 2 for DC. Here it should be noted that the model has been generated based on 91 training records for CC and 48 training records for DC.

Fig. 4.

Expression trees (ETs) for the modelling of COVID-19 in India.

Algorithm 1.

Time Series prediction model generated for CC across India.

Algorithm 2.

Time Series prediction model generated for DC across India.

3.1.2. Variable Importance

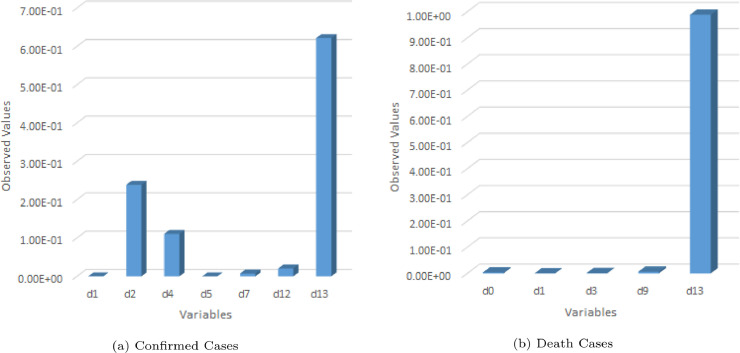
Predictor variables are an important and integral part of a GEP model [36]. These parameters help in understanding the contribution of all the variables in the model. Here a randomization phenomena is followed for each input values in order to analyse the importance of each variable and then finding the average reduction in R ² between the predicted value and the desired output. The results obtained for all the prediction variables are normalized such that the addition of all the variables amounts to 1. From the results in Figure 5 , it can be seen that for whole India as of 13 May 2020, the variable d13 greatly effects the algorithms and is the most important variable for both CC and DC. In case of CC, the model is highly sensitive to two other variables namely d2 and d4. In the next subsections, three major states of India have also been studied and performance of proposed GEP models of CC and DC for these three states has been analysed. Note that basic details about the ETs, variable importance and statistical values has not be referred again in order to avoid repetition.

Fig. 5.

Contribution of predictor variables for COVID-19 in India.

3.2. GEP model for Indian State: Maharashtra

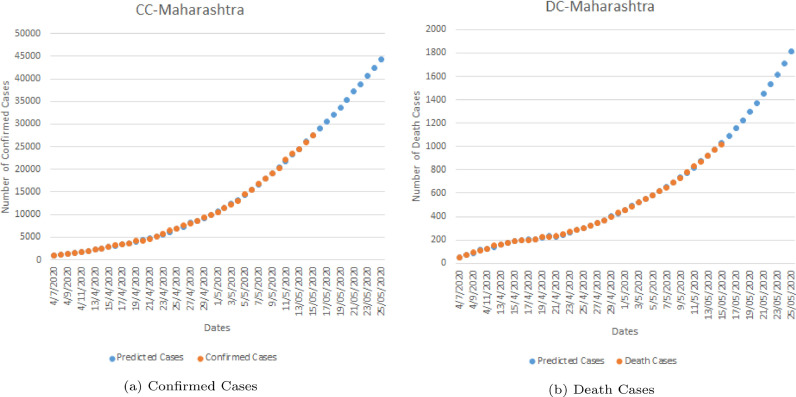
Maharashtra is the third largest state of India having an area of 604.5 square kms with a population of more than 110 million people. The state being the second largest in terms of population has various small areas where thousands of people live in small chunk of land. Dharavi, the largest slum of the world, is also located in Mumbai and is currently a COVID-19 hotspot. So it becomes necessary to analyse the possible impact of virus in Maharashtra and predict how it will behave in the near future. This section provides details on all the three aspects including statistical results for Maharashtra, India. The results of prediction models in comparison to actual CC and DC across the state is presented in Figure 6 . It has been found the GEP based prediction model proposed in present work provide very reliable results for both CC and DC till 15 May 2020. The GEP models further predicts that by 25 May 2020, the total number of CC will reach almost 45,000 and in the same period, the total DC will reach nearly 1800. Thus a sharp rise can be noticed in the COVID-19 cases across Maharashtra in the coming days.

Fig. 6.

Experimental versus predicted cases for COVID-19 in Maharashtra using GEP model.

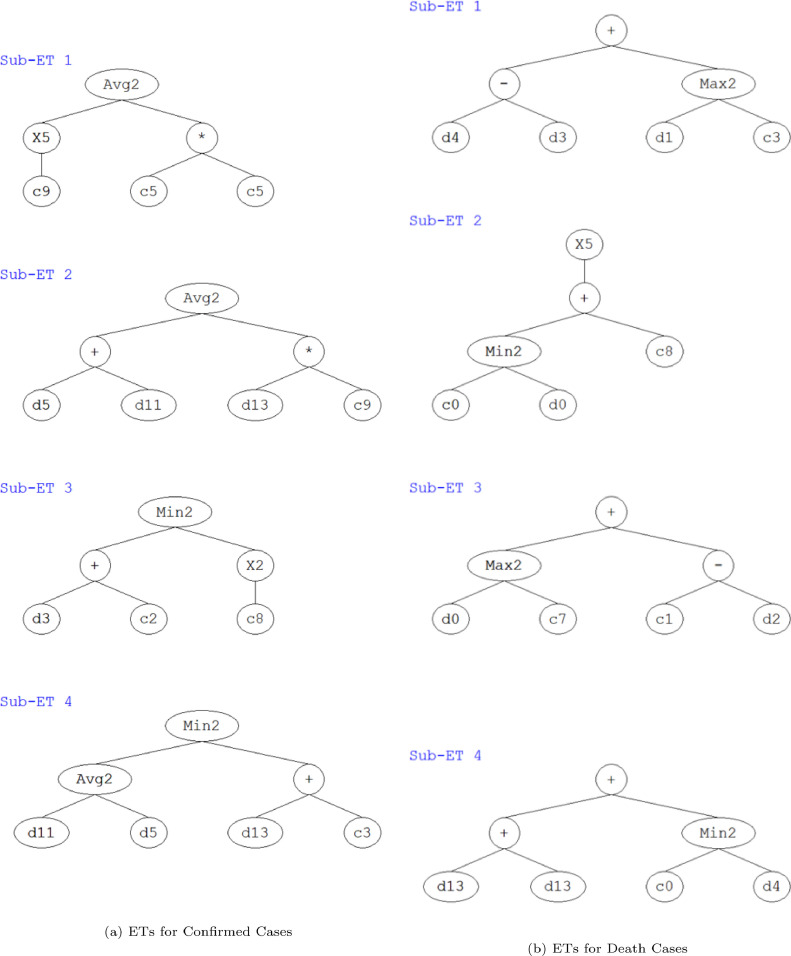
3.2.1. The Expression Tree based Validation

ET is another important parameter and is helpful in mathematical formulation of the problem under consideration. From the Figure 7 , it can be seen that the ETs for both CC and DC in Maharashtra consists of four independent levels (genes or subprograms) sub-ETs. For CC, the linking function used is the average function where as for DC, addition linking function is used. A generalized formulation of the ETs in terms of simulation program is presented in Algorithm 3 for CC and Algorithm 4 for DC.

Fig. 7.

Expression trees (ETs) for COVID-19 in Maharashtra.

Algorithm 3.

Time Series prediction model generated for CC in Maharashtra.

Algorithm 4.

Time Series prediction model generated for DC in Maharashtra.

3.2.2. Variable Importance

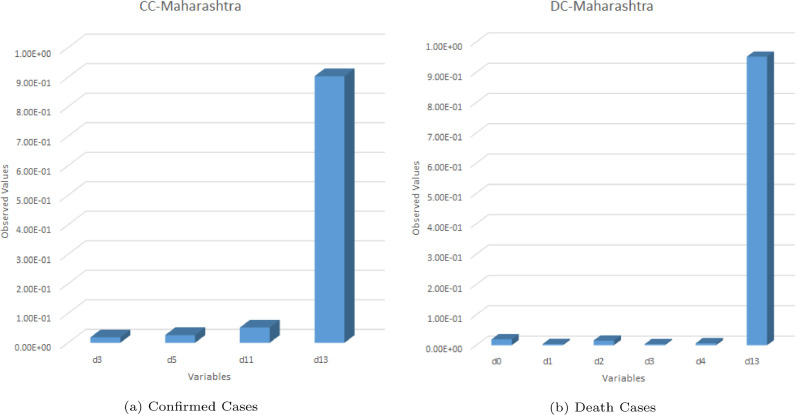
This parameter follows a randomization phenomena for each of the input values in order to analyse the importance of each variable. Here average reduction in R ² between the predicted and desired output is taken into consideration and variable importance is calculated. The results in Figure 8 show that the variable d13 plays a very significant role and is the most important parameter for COVID-19 in Maharashtra for both CC and DC. Apart from that, no other variable pose any major importance.

Fig. 8.

Contribution of predictor variables for COVID-19 in Maharashtra.

3.3. GEP model for Indian State: Gujarat

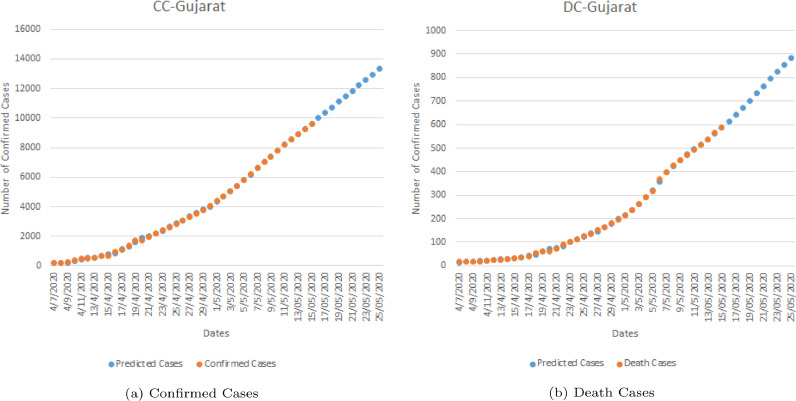
Gujarat is the second most affected state of India after Maharashtra and COVID-19 cases are rising at a higher pace. This section proposes two new GEP models for CC and DC in Gujarat. The results of prediction model with respect to actual cases for both CC and DC are given in Figure 9 . From the results, the total number of CC to DC as of 15 May 2020, is around 10,000 to 600 respectively and as per the GEP prediction models, it is expected to increase upto 14,000 and 900 respectively for CC and DC. The projected values further indicate that the possible spread of COVID-19 in Gujarat is an alarming factor and needs to be kept in check. The ETs based validation is presented in the next subsection.

Fig. 9.

Experimental versus predicted cases for COVID-19 in Gujarat using GEP model.

3.3.1. The Expression Tree based Validation

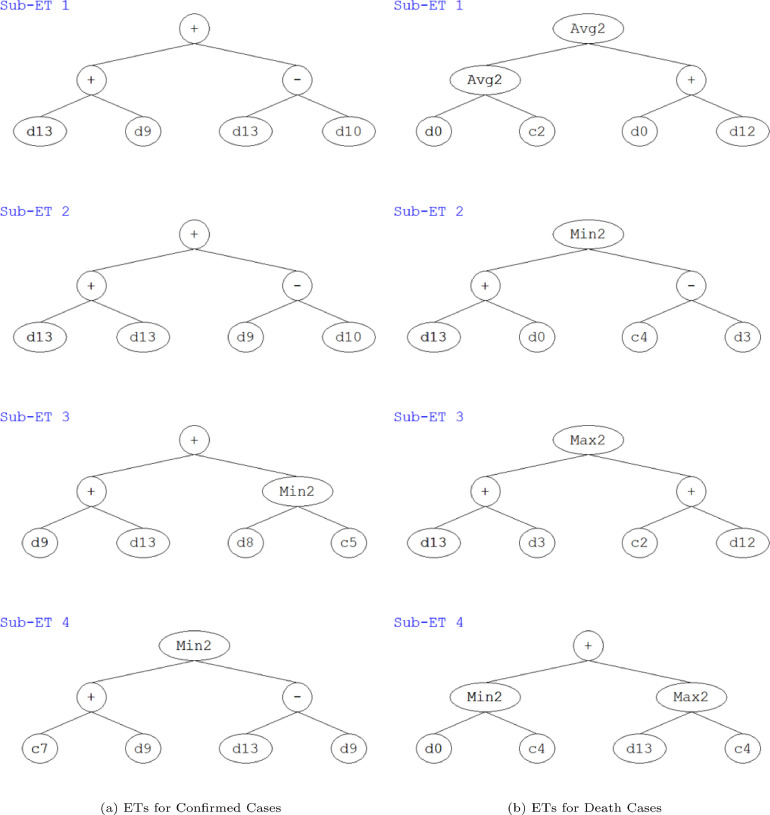
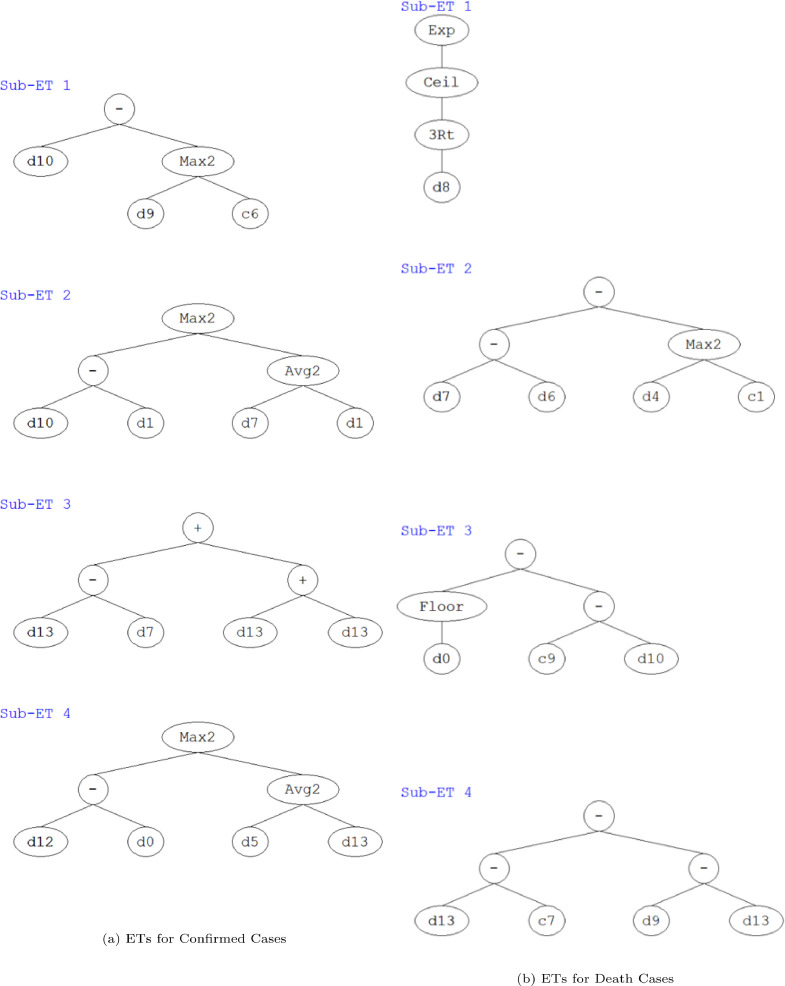
The ETs for both CC and DC in Gujarat are given by Figure 10 . It can be seen that the ETs for both the cases consist of four subprograms or chromosomes or simply four sub-ETs. All the sub ETs are connected by addition linking function for CC whereas for DC, average linking function is used. Also, from these ETs, mathematical equations can be formulated as per the end users requirement and further evaluation at chromosomal level. The general time series prediction models for Gujarat in case of CC is given in Algorithm 5 and for DC is given by Algorithm 6 . Here it should be noted that the model has been generated based on 39 training records for both CC and DC respectively.

Fig. 11.

Contribution of predictor variables for COVID-19 in Gujarat.

Fig. 10.

Expression trees (ETs) for COVID-19 in Gujarat.

Algorithm 5.

Time Series prediction model generated for CC in Gujarat.

Algorithm 6.

Time Series prediction model generated for DC inn Gujarat.

3.3.2. Variable Importance

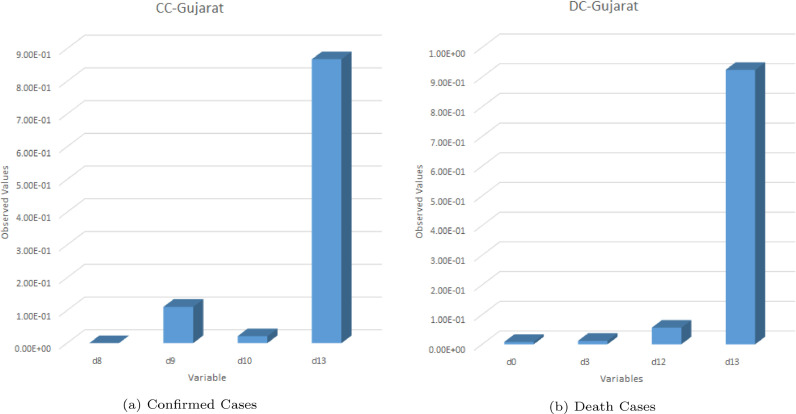
From Figure 13, it can be seen that the most significant variables in case of Gujarat is d13 for both CC and DC as of 15 May 2020. Note that the results obtained for reduction model in terms of R ² are normalized such that their addition makes the count 1. Apart from d13, for CC d9 also plays a very significant role where as for DC no other parameter post any significance. Thus overall we can say that the GEP model for Gujarat in case of CC is sensitive to two variables d13 and d9, while for DC only d13 pose significant challenge. In the next subsection, the GEP model for Delhi are proposed.

Fig. 13.

Expression trees (ETs) for COVID-19 in Delhi.

3.4. GEP model for Indian State: Delhi

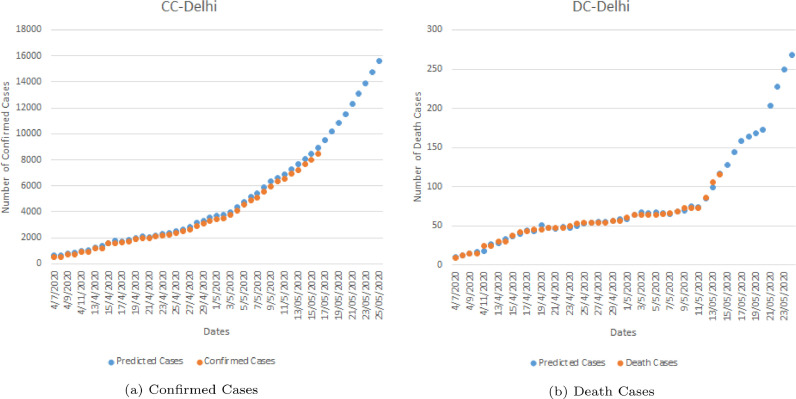
Delhi is one among the most populous city in the country, with a 1.48 square kms and a population of almost 20 million people. Thus a wide diversity of population lives in such compact living space. And with the onset of COVID-19, it becomes really very important to analyse and predict, how the virus will behave and spread across the state in the coming days. With a total of more than 8,000 CC and close to 120 DC as of 15 May 2020, a model such as GEP can be considered as an important factor in predicting the extent of the virus. From the results in Figure 12 , it can be seen that the virus is expected to increase at an alarming rate with a total expected rise in the CC to about 16,000 and DC to around 275 by 25 May 2020. The curve is rising exponentially and required measures need to be taken to stabilize the same. The ET based validation for CC and DC in Delhi is presented in the next subsection.

Fig. 12.

Experimental versus predicted cases for COVID-19 in Delhi using GEP model.

3.4.1. The Expression Tree based Validation

The ETs in case of Delhi are also grouped into four sub-ETs. Here subtraction linking function is used for both CC and DC and are presented in Figure 13. Along with the subtraction linkage function, in case of DC, the exponential linkage function also plays a significant role. Based on these ETs, the mathematical equations can be formulated and new predictive analysis can be presented. The time series prediction models thus generated for both CC and DC is given by Algorithm 7 and Algorithm 8 respectively. The variable importance of each of the prediction variables is presented in the next subsection.

Algorithm 7.

Time Series prediction model generated for CC in Delhi.

Algorithm 8.

Time Series prediction model generated for DC in Delhi.

3.4.2. Variable Importance

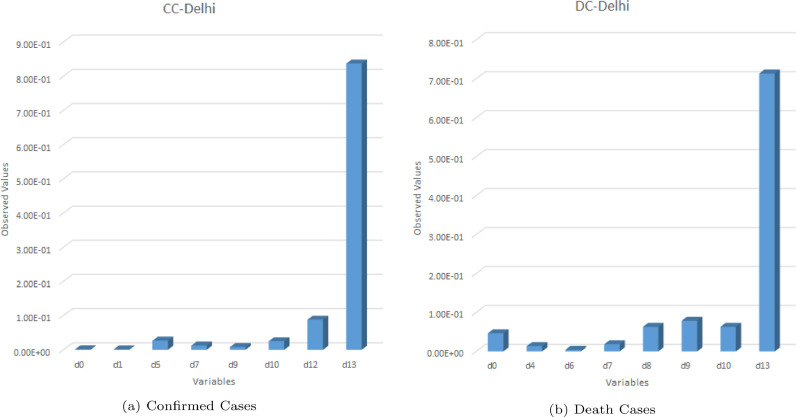
Predictor variables in case of Delhi play very significant role. Here d13 plays the most significant role for both CC and DC GEP models. Along with that, d5 and d12 also has little impact on the prediction model for CC whereas d8, d9 and d10 pose little significant knowledge for DC model. The results are presented in Figure 14 and it can be said that the prediction variables for Delhi two to three prediction variables affect the GEP models. Here also, the results from the prediction model are normalized so that the addition of all the variable amounts to 1. The next subsection details about the statistical results for all the cases under consideration.

Fig. 14.

Contribution of predictor variables for COVID-19 in Delhi.

3.5. Statistical Results for all the cases

The models calibrated in the above sections using ETs, GEP modeling and variable importance parameters are only acceptable if they are statistically significant. Since this is one among the first studies on COVID-19 dataset, a comparison with respect to other techniques is not available in the literature. So in present work, a comparative study for both CC and DC for all the three states and whole India is taken into consideration. The results are presented in terms of RMSE and R. It has already been discussed in the previous sections that RMSE should be higher and R must be close to 1. The results for comparison are presented in Table 3 . Here it can be seen that for almost all the cases, a higher RMSE has been found and the value of R for almost every case is close to 1. The lowest values of R is found to be 0.9881 which corresponds to the DC in Delhi whereas the highest value is 0.9999 which corresponds to the CC across whole India. Thus from the statistical results, it is evident that the proposed GEP models are highly reliable and new prediction can be derived based on these models. Further, the proposed models can be optimized using algorithms such as krill herd algorithms [37], naked mole-rat algorithm [38] and others.

Table 3.

Overall Performance of GEP model for CC and DC across India and major States.

	Whole India		Indian States
			Maharashtra		Gujarat		Delhi
	CC	DC	CC	DC	CC	DC	CC	DC
RMSE	5.5574	90.1863	7.1419	157.7254	19.5200	223.0803	11.8590	284.9057
R	0.9999	0.9997	0.9996	0.9996	0.9997	0.9996	0.9998	0.9881

4. Conclusion

A robust and reliable variant of GEP was used to model the confirmed cases and death cases of COVID-19 in India. New accurate empirical models were designed for prediction of CC and DC across whole India and three major states which are highly affected by the COVID-19 pandemic. These states include Maharashtra, Gujarat and Delhi. The proposed models were developed from the daily situation reports of COVID-19 cases published by the Ministry of Home Affairs, Govt. of India since the onset of first lockdown in the country that is 24 March 2020. The following conclusions have been formulated based on the proposed models:

• •The GEP models proposed in this work are highly reliable in predicting both confirmed cases and death cases across India. They also satisfy all the requirements of external validation and hence can be used for predicting future cases.
• •The RMSE and R values for all the cases is higher and close to 1 respectively. Thus verifying the solution quality of the proposed models and hence higher the chances of reliable predictions.
• •The ETs derived are very simple and basic mathematical equations can be formulated from them without any time-consuming laboratory implementations. These mathematical equations can be further used to optimize the proposed models using different optimization techniques such as differential evolution, cuckoo search algorithm and others.
• •The prediction variables of all the proposed models play very significant role and it has been found that apart from Delhi, all other models have effect of only one or two prediction variables. Thus making the models less sensitive to variables.
• •Apart from that, from the experimental results, it can be said that GEP models are highly reliable as they are based on experimental data rather than just basic assumptions, as in case of conventional models. Another salient feature of GEP modeling is that it can work on less time series data and still provide reliable results.

Thus overall, it can be said that GEP based models are highly reliable and can be treated as benchmark for time series predictions. The concern arises when the total number of cases increases many fold. In those cases, GEP models need to be optimized. So, mathematical equations derived from the GEP models are optimized using highly effective state-of-the-art evolutionary algorithms. As a future direction, these equations can be derived and algorithms such as Krill herd algorithm, naked mole-rat algorithm and others can be used to optimize the prediction models. Also, the prediction models shows CC and DC for the next 10 days show that strict measures need to be taken to keep the virus under check. Here lockdown and social distancing should be strictly followed so that the virus can be controlled and refrained to particular areas only.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.