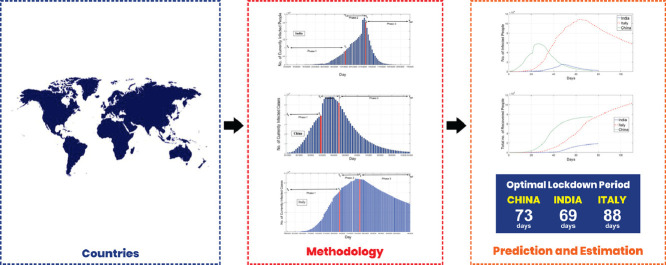
Highlights
-
•
The very first model to predict the minimum optimal time of the lockdown.
-
•
Deliberates salient features like silent carriers, sociability of newly infected person and unregistered deaths of coronavirus infectious people along with SIR model.
-
•
Based on the awareness and sustainability of disease, the number of suspected person varies with respect to time of spreading of virus. Hence, three phases are formed to define the suspected rate as it will not grow exponentially all the time.
-
•
At first Phase, when the awareness of newly discovered virus is at initial phases, the suspecting rate will grow exponentially. Suspected rate depends on sociability of infected person.
-
•
Second Phase is during lockdown when the social distancing is followed. In this phase, death cases are more as number of current infected person are at peak. Simultaneously, the number of recovered person per day will increase.
-
•
Third Phase is when there is reduction in number of active cases. Number of suspected cases will reduce depending upon the testing speed of medical team.
-
•
In order to calculate the optimal lockdown time Topt, the approach of proposed model is to find a situation when the number suspected people starts to reduce w.r.t. time, number of infected people increases for a while but start reducing with respect to time, and also the number of recovered people rises w.r.t. time.
-
•
The model is tested on China data and is efficient enough to propose a model very close to their actual figures of infected people, recovered people, died and active cases. The model predicts the optimal lockdown period as 73 days for China which is very close to their actual lockdown period (77 days).
-
•
Also, the model is implemented to predict the optimal lockdown period of India and Italy.
-
•
The programming part is done in C++ language with Linux OS.
Keywords: COVID-19, SIRD Model, Pandemic, Lockdown, Silent Carriers
Graphical abstract
Abstract
This paper proposes a three-phase Susceptible-Infected-Recovered-Dead (3P-SIRD) model to calculate an optimal lockdown period for some specific geographical regions that will be favorable to break not only the transmission chain but also will help country’s economy to recover and support infrastructure in a fight against COVID-19. Proposed model is novel since it additionally includes parameters i.e. silent carriers, sociability of newly infected person and unregistered died coronavirus infected people along with the infection rate, suspected rate and death rate. These parameters contribute a lot to figure out the more clear model, along with essential parameters. The model takes the testing rate of suspected people into consideration and this rate varies with respect to phase of the epidemic growth. Proposed 3P-SIRD model is divided into three-phases based on the awareness and sustainability of disease. Time is divided into different periods as rate of infection and recovery fluctuates region to region. The model is tested on China data and is efficient enough to propose a model very close to their actual figures of infected people, recovered people, died and active cases. The model predicts the optimal lockdown period as 73 days for China which is very close to their actual lockdown period (77 days). Further, the model is implemented to predict the optimal lockdown period of India and Italy.
Notations for Proposed Model
- S(t):
Susceptible persons at time t
- I(t):
Active infected cases at time t
- R(t):
Total person recovered from infection at time t
- D(t):
Total person died from infection at time t
- Sc(t):
Silent carrier at time t
- Itotal:
Total number of infected cases
- α:
Variable incubation rate of susceptible person
- αc:
Variable incubation rate of silent carrier
- β:
Probability of a susceptible person resulting in a new infected person (suspected to infected)
- γR, γD:
Recovery and Death rate of infected person
- γT:
Testing rate of susceptible person provided by government or agencies
- μ:
Number of infected person as a silent carrier, having no symptoms of infection
- u:
Death rate of unregistered infected people
- m:
Mobility factor
- P:
Number of person met with infected person before isolated or being detected
- tsl:
Start day of lockdown
- t0, t1, t2:
Start day of phase 1, phase 2 and phase 3
- ta, tb:
First and fifth day of phase 2
- tc, td:
First and fifth day of phase 3
- topt:
Last day of phase 3
- Topt:
Optimal lockdown period
- TS, TE:
Start and End day of evaluation
- NI, NS, NR, NS:
Number of Infected, Suspected, Recovered and Died people from TS to TE
1. Introduction
The surfacing of severe acute respiratory disorder coronavirus 2 (SARS-CoV-2; formerly provisionally entitled 2019 novel coronavirus or 2019-nCoV) disease (COVID-19) in China at the end of 2019 has triggered an enormous worldwide outbreak and is a major public health concern. COVID-19 outbreak was first reported in Wuhan, China on 31 December, 2019. The COVID-19 pandemic is surging around the world and is accelerating at an exponential rate.
Outside of China, on 13 January 2020, the first Coronavirus case was reported in Thailand [1] and since then COVID-19 outbreak has now spread rapidly all over the world [2]. On 30 January 2020, World Health Organization (WHO) has declared COVID-19 as a Public Health Emergency of International Concern (PHEIC) [3]. Most people infected with the Coronavirus experience mild to moderate respiratory ailment and get well without demanding special treatment. Older people and those with medical problems like chronic respiratory disease, cardiovascular disease, diabetes, and cancer are more likely to develop serious infection. The COVID-19 spreads mainly through droplets of saliva or discharge from the nose when an infected person coughs or sneezes, so it is essential that every people also practice respiratory protocol. As of April 2020, there are over 1,848,439 confirmed cases all over the world [2]. Thus, there is a need of immediate actions to prevent the disease at the community level. At this time, there are no specific vaccines or treatments for COVID-19. Though, there are several on-going clinical trials evaluating potential treatments. The recent dissemination of the COVID-19 has reintroduced the concern of the scientific and political community in the mathematical models for epidemic. Many researchers are making efforts for suggesting new refined models to examine the current situation and foresee possible future scenarios. SIR model where SIR refers to Susceptible, Infected and Removed, was proposed by Kermack and MacKendrick [4] which is based on a system of initial values problems of ordinary differential equations (ODEs). The SIR model and its later variations, such as Susceptible-Exposed-Infected-Removed (SEIR) [5] are generally used by the epidemic medical community in the study of outbreaks dissemination. With this paper it is expected to contribute to the ongoing exploration on this topic. Compared to earlier outbreaks, such as SARS-CoV or MERS-CoV [6], when the infection had been stopped after a relatively small number of infected people, researchers are now investigating a different situation. Undoubtedly the figure of infected people rises exponentially, and seemingly, it can be clogged only by a complete lockdown of the affected areas, as proven by the COVID-19 outbreak in the Wuhan, China in December 2019. Similarly, in case of Italy, to limit the virus dissemination all over the Italian area, the government has started to impose more severe constraints since 9 March 2020 [7]. Optimistically, these actions will affect the spread of the Coronavirus dropping down the number of infected people. Governments of many countries are keeping their population under lockdown, while hunting every suspect case for testing and treating and quarantining those who test positive. But the question arises that how a coronavirus lockdown does last because this shutdown brutally kicks the country’s economy and long shutdown can arise a survival issues in front of lower-class people and labors who work on daily payment basis. The introduction of various levels of lockdown requires an adaptation of the typical epidemic representations to this new situation. Some examples about the Chinese outbreak can be found in [4], [8], [9]. In the currently evolving Italian situation, it is possible to model the introduction of restricting measures by introducing a non-constant infection rate [10].
In this paper some further parameters are added to represent the infection rate, suspected rate and death rate. These parameters contribute a lot to figure out the more clear model. The essential parameters which are included in this paper are silent carriers, sociability of newly infected person, undefined deaths of coronavirus infected people that are not registered anywhere. As there is no vaccination available for COVID-19, the only solution to control the dissemination, apart from personal hygiene, is lockdown strictly followed by every citizen. Once this virus starts spreading one to another person in any crowded region or highly populated cities it is very difficult to handle the situation. That’s why lockdown is strictly imposed. Contrary, the long lockdown also led to an unprecedented evacuation of workers from their workplace to their homes in far-flung villages all over the country. Additionally, long-term lockdown could cripple country’s economy. Therefore, there is a need to estimate the lockdown time in such a way that the spreading rate of infection is under control as well as the country’s economy mend up the loss that has had during the lockdown period. Hence, this paper, for the very first time, proposes a three-phase Susceptible-Infected-Recovered-Dead (3P-SIRD) model to find a minimum optimal lockdown period in a manner that the spreading rate of infection is under control. The countries taken under the case study for obtaining the optimal lockdown period are China, India and Italy.
The organization of the paper is as follows: Section 1 gives introduction and details about seriousness of COVID-19. Section 2 describes the proposed 3P-SIRD model. Section 3 presents the case study for China, India and Italy. The result analysis is performed in section 4 followed by conclusion in Section 5.
2. Proposed 3P-SIRD Model
In the situation of COVID-19 when there is no authentic medication available and the only precaution to control the spreading of disease is lockdown. Proposed model provides solution by predicting optimal lockdown period. The approach is based on the analysis of data and to use it for training the data to find the minimum time period of lockdown when infection rate of disease is under control. The minimum time period is referred as the optimal lockdown period.
In the absence of lockdown, the rate of change in number of suspected people is proportional to the social meeting of infected person, which is known as P in our model, that is the number of person met with infected person (not yet detected) before isolated or being detected. As per analysis of data, infected people need considerable time to recover after getting medication, so recovery rate is also low in initial days. Once lockdown is implemented, the social meetings of infected person (not yet detected) become restricted. So in the lockdown period suspected rate due to new infected person, which are being infected after lockdown becomes lesser than previous infected period. This results in reduction of suspected rate at time t 1. Our model tracks this time t 1 and checks the parameters values after this time t 1. These new parameters values are used in determining the minimum optimal time as lockdown period Topt.
Proposed model is divided into three-phases based on the awareness and sustainability of disease. Input data are collected from authorized links followed by analysis and categorization (clustered) [10]. Time is divided into different periods as rate of infection and recovery fluctuates from region to region. From initial time to lockdown time, infection rates are calculated from the given data.
2.1. Details of the Model
There are following assumptions that are made to model the mathematical background:
-
•
Social distancing is followed consistently during the lockdown period.
-
•
Unreported infected people (who are not registered) are not considered in the model. It is therefore assumed that the number of registered infected people form a representative group for the actually real infected and is not limited by the test capacities or variable test behaviour or other factors.
-
•
In the model, a mobility factor m is considered. As if the lockdown is not so strict then the movement of citizens remains to fulfil the daily basic needs.
-
•
In the model, Silent carrier (Sc) is also considered for those who are actually Corona infectious but show delayed or no symptoms. These carriers also play a major role in spreading the disease.
-
•
The term total infected stands for the sum of current infected, total recovered and total death.
-
•
The term suspected people stand for the people who either have pre-symptoms or come in contact with infected.
-
•
Infection rate calculation is mutating in the proposed model. Sociability of the infected person has been considered proportional to the summation of total number of person came in contact with infected person after being infected. This can also be considered in phase 1 of COVID-19.
-
•
Vaccination of COVID-19 is not available till date.
-
•
Lockdown can expose most of the infected cases and also controls the dissemination of the virus.
-
•
Under lockdown period a phase will come when number of current suspected people will either become constant or get reduced with time. The starting of this phase is time t 1. The difference between suspected people as par their current state is seen because of the test results, which will further consider suspected people either as infected or not infected. So these assumptions say that difference in suspected people depends upon the rate of testing of COVID-19.
-
•
It is assumed that at time t 2, where t 2 is greater than t 1, number of current infected people starts getting reduced. This time is named as recovery time. According to assumption this reduction in number of infected people is due to either higher recovery rate of infected people or death of infected people.
-
•
The recovered person are no longer susceptible of infection (which is apparently not yet proved, or disproved for COVID19).
-
•
The criteria of optimality (for obtaining Topt) is either S tends to zero or S forms an asymptote to X-axis. This means number of suspected people becomes negligible or near to zero.
In this paper, the population is divided into four categories namely Suspected (S), Infected (I), Recovered (R) and Dead (D) the equation is given as:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
In SIR model and its further variations [4], [5], [11], dS(t)/dt depends on number of suspected and infected people. In this paper, it is considered that actual suspected rate is dependent upon the sociability of the newly infected person if the strict social distancing is not there and also in contrast of previous versions of models [4], [5], [11], a factor Sc is added for the silent carriers in dI(t)/dt. Silent carriers are those infected people who don’t show symptoms and in the past history of China suffers a lot of these carriers [12], [15]. The range of μ is taken in the interval 0 to 0.25 [18].
In order to consider the lockdown imposed by the government, the whole time interval [t 0, t 1] is divided in two sub-intervals [t 0, tsl] and [tsl, t 1], where tsl represents the starting time when lockdown imposed by the government and t 1 represents time when the shutdown start to yield an appreciated changes in the data trend. Furthermore, meanwhile the applied constraints should decline the number of contacts between Infected and Suspected, coefficient β is modeled in Eq. (1) as a decreasing time dependent function β(t). A similar model for the infection rate of SEIRD equations can be found in [11], where the function is assumed to have decreasing rational function.
In order to calculate the optimal lockdown time Topt, a situation is required to be found after t 1 time when the number of suspected people starts getting reduced w.r.t. time, number of infected people increases for a while but starts reducing with respect to time, and also the number of recovered people rises w.r.t. time. It was analysed that Coronavirus growth take place in three-phases in any specific geographical area [14].
First Phase
At first Phase, when the awareness of newly discovered virus is at initial phases, then it will grow exponentially. As it can spread 10 times more than other existing most dreadful epidemics. Additionally, because of late symptoms, an infected person helps virus to spread. In the same phase lockdown implies by the authorities at time tsl, which can reduce infection growth rate after a certain time period. Without lockdown an infected person can infect more than 10 person in a day if the person is social. In the absence of lockdown and lack of social distancing, suspected rate depends on sociability of infected person. Therefore, the growth in number of infected cases is exponent:
| (6) |
here, k is a variable that represents newly detected infected person in first phases, a coefficient accounting for the susceptible person get infected by contagious person. The range of P is taken in the interval 3 to 10 [16], [17].
Second Phase
Second Phase is during lockdown when the social distancing is followed. Policies of authority helped to find a large number of infected people in the area. At time t 1 number of suspected cases growth would either decrease or remain constant. Now no new infected cases arise, as most of the infected person was from suspected person whose test report become positive. In this phase, current number of active cases will be:
| (7) |
In this phase, death cases are more as number of current infected person are at peak. Simultaneously, the number of recovered person per day will increase and the range of P will become in the interval 0 to 4. With low increment rate of active cases and high recovery, third phase will start within some days.
Third Phase
Third phase is the phase of epidemic when there is reduction in number of active cases. Number of suspected cases will reduce depending upon the testing speed of medical team. As less number of infected cases, active cases can be managed at high proficiency with proper isolation. Once it is analysed that the number of suspected person is reduced significantly i.e. current suspected cases graph becomes asymptotic to X-axis or when S tends to zero, then the process of opening the lockdown may get started. Current infected count is still non-zero, but decreasing as infected patients either become recovered or dead.
| (8) |
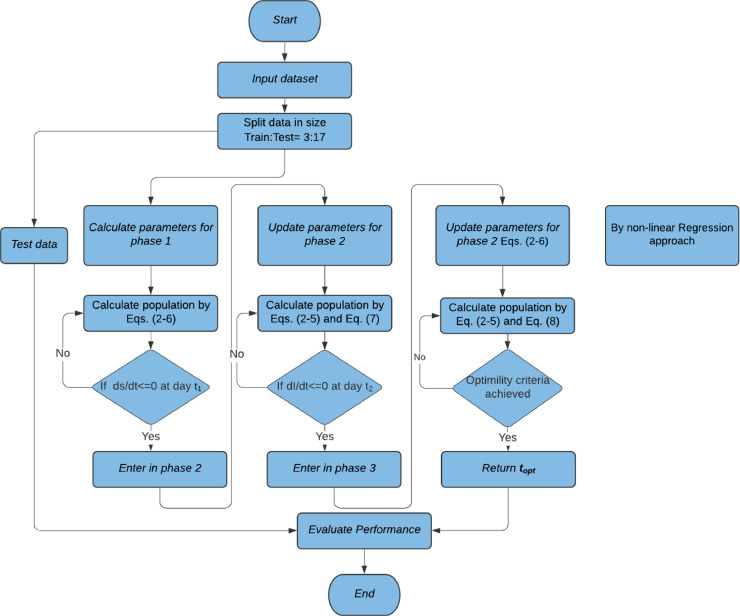
2.2. Process and Flowchart
The step-wise process and corresponding flowcharts are depicted in this section. Here Topt is a function of NI, NS, NR, ND, TS, TE, tsl. The flowchart presented by Fig. 1 represents the complete stepwise process of proposed 3P-SIRD model, which is further elaborated by Pseudo-codes of Phase 1-3. Since proposed model works with differential equations and adopted method is regression model, it works on linear as well as non-linear models, which is achieved by transforming the system of differential equations [Eqs. (2–8)] into a system of integral equations and treating the transformed system as a statistical model for a collection of regressions with covariates which approximate the integrals. On solving Eq. (6), the result becomes:
| (9) |
Fig. 1.
Stepwise process of proposed 3P-SIRD model.
Here, c 1 and K are constants with K is equal to . Similarly, Eq. (3) produces following result:
| (10) |
where,
Equation (8) produces following results:
| (11) |
Similarly, on solving Eqs. (2,4-5) following solutions are obtained respectively:
| (12) |
| (13) |
| (14) |
here, c 2, c 3, c 4, c 5, c 6 and c 7 are constants. It can be very clearly observed from Eq. (9) that the number of suspected people at time t is dependent over the number of infected people at time t. Number of infected people at time t grows exponentially as can be observed from Eq. (10). S grows exponentially with reference to time t as can be observed in Eq. (11). It can be observed from Eq. (11) that, S(t) will not be zero ever, or one should say S(t) will be zero at infinite time. Hence, the criteria of optimality (for obtaining Topt) is either S tends to zero or S forms an asymptote to X-axis. This means it will be parallel to X-axis and will cut X-axis at infinite.
Since proposed model is dividing growth of COVID-19 in three-phases and each phase has different value of parameters. This can be achieved by regression approach and to obtain parameters least square method is applied on Eqs. (9-(11), (13)-14) taken as in the following way:
| (15) |
| (16) |
here, y is dependent variable and x is independent variable. The coefficients a and b are trained by the least square method so as to obtain best fit regression curve. Train data is taken based on boundary value approach, which covers maximum variation in parameters value. In each phase, model have different formulation for difference in suspected cases at time t. Thus rather than using single model, formulation of parameter performed by each phase independently. Resultant line equation and respective slope and intersection values are used for calculation of values at new points.
Algorithm 1.
Pseudo-code for Phase 1
Algorithm 2.
Pseudo-code for Phase 2
Algorithm 3.
Pseudo-code for Phase 3
3. Case Study of China and Prediction for India and Italy
This section explains the details of all the case studies performed. Since, the lockdown period has got completed for China, the model has got tested for prediction accuracy for China. Other countries i.e. India, Italy and many more are still under lockdown, hence proposed model predicts the optimal lockdown period for these countries.
3.1. Case Study of China
The case study for training of proposed model, the data related to COVID-19 facts of China are considered [13]. Since, this is the only country whose phase-3 of epidemic growth has been achieved. Facts are taken from 22 January 2020 to 14 April 2020. Number of suspected person is calculated on the bases of formula given in proposed model. Here tsl represents the lockdown date which is 23 January 2020. Number of suspected person are calculated by Eq. (6).
Step 1: Initially the data got splitted i.e. data ta from 22 January to 13 February is taken as train data. Parameters are calculated using Eqs. (1–8). Data from 14 February to 24 April is used as test data to evaluate performance of model.
Step 2: Phase 2 starting point is recognized by the algorithm and that is 11 February, earlier than the normal cases may happen in case of high number of testing and awareness of public before lockdown. Here the point to be noticed that if the mobility in society is present under the lockdown conditions, then span of phase 1 will be more.
Step 3: Parameters values calculated in step 1 and step 2 are used as input to predict number of active cases, suspected cases, total death and total recovered person, until the total active cases have started to reduce.
Step 4: This point is starting of phase-3 which is 23 February Now the suspected person rate will depend on testing rate as shown in Eq. (8). The number of total recovered person rate will be reduced as variation in immune system variation.
Step 5: From this point, parameters values are used as input to predict number of active cases, suspected cases, total deaths, and total recovered person till number of suspected person become negligible using Eqs. (1–8). Hence, optimal lockdown period Topt is obtained.
3.2. Prediction for India and Italy
Step 1: Initially the data is collected and parameters are calculated using Eqs. (1–8).
-
•
For India data from 03 March to 20 April is taken as train data. Lockdown start date is 25 March, 2020.
-
•
For Italy data from 15 February to 20 April is taken as train data. Lockdown start date is 9 March, 2020.
Step 2: Phase-2 starting point is recognized by the algorithm. Here the point to be noticed that if the mobility in society is present under the lockdown conditions, then span of phase 1 will be more. For India phase-2 starting point is 14 April, 2020; for Italy it is 2 April, 2020.
Step 3: Parameters values calculated in step 1 and step 2 are used as input to predict number of active cases, suspected cases, total death and total recovered person, until the total active cases have started to reduce.
Step 4: This point is starting of Phase-3 which is 29 April for India and 20 April for Ital. Now the suspected person rate will depend on testing rate as shown in Eq. (8). The number of total recovered person rate will be reduced as variation in immune system variation.
Step 5: From this point, parameters values are used as input to predict number of active cases, suspected cases, total deaths, and total recovered person till number of suspected person become negligible using Eqs. (1–8). At this point Topt provides the optimal lockdown period.
4. Experimental Setup and Result Analysis
The countries taken as the case study are China, India and Italy. COVID-19 data of Infected, Recovered, Died person for all countries are taken from reference [13]. The programming part is done in C++ language with Linux OS. Since the lockdown period of China is over and it is considered as recovered. Hence, the complete actual and predicted data are available for the comparison and for testing the accuracy of proposed model to predict the lockdown period. Whereas, other three countries are facing the lockdown in current situations, so the actual lockdown data available till date are taken for comparison with the predicted data. The predicted data provides the prediction till the optimal date of the lockdown completion. The results of all the three countries are evaluated at the criteria of number of infected, recovered and died people, predicted by proposed model compared with actual data as shown by Figs. 2 -5. The impact of increasing the test rate is also discussed for all the countries. The optimal lockdown period and dates of start of all the three phases is presented in results.
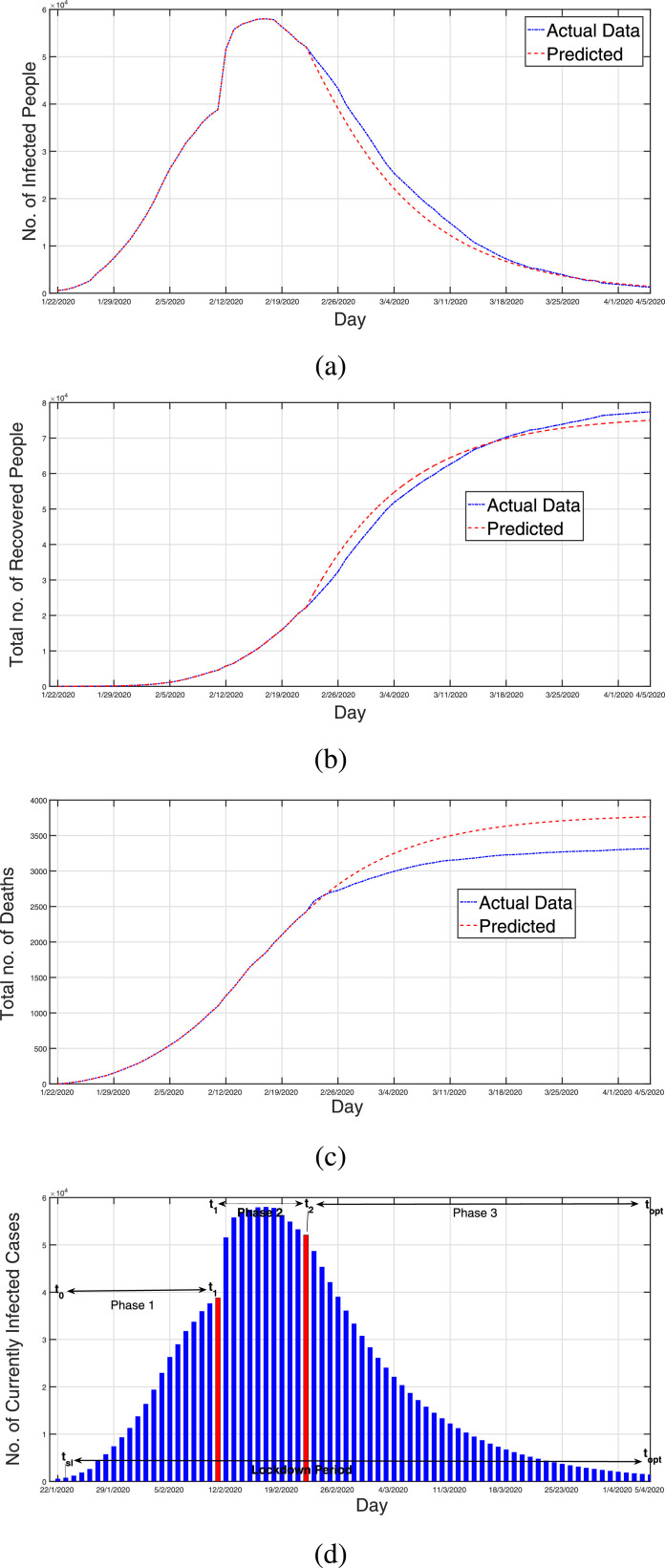
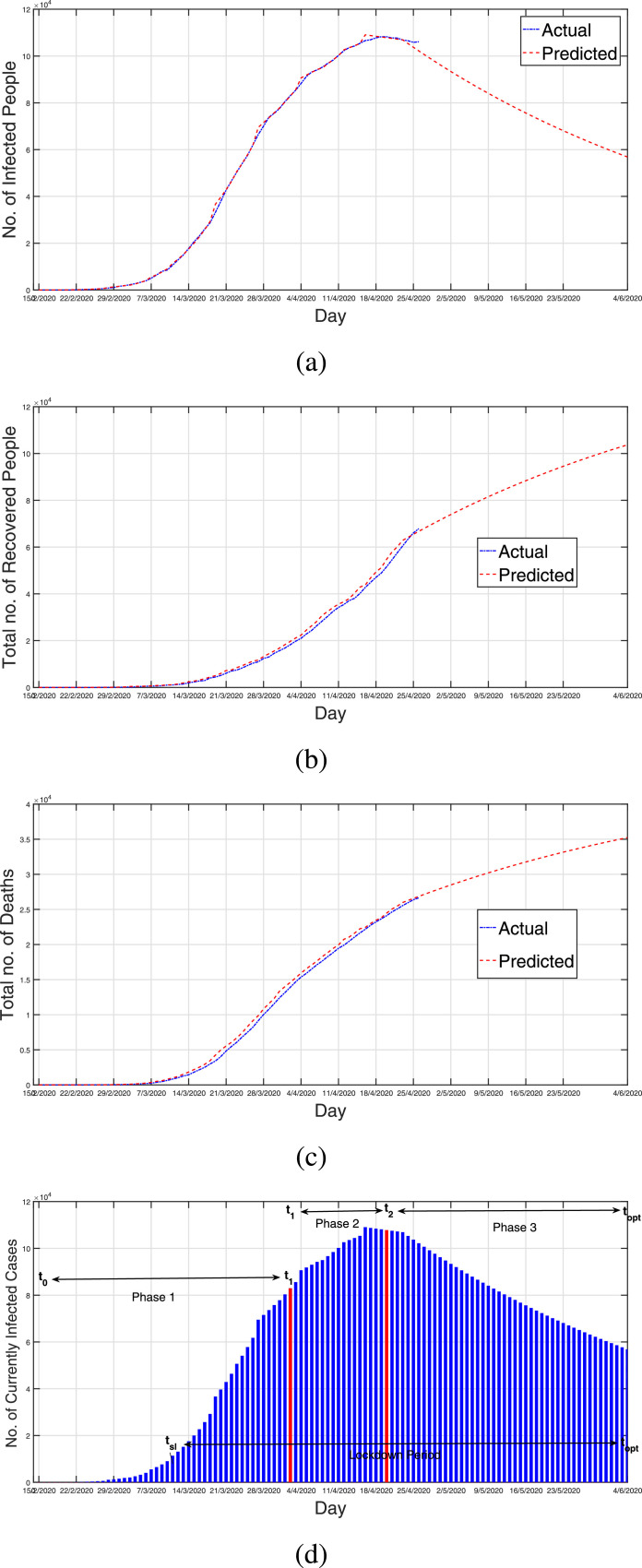
Fig. 2.
Comparison between actual vs calculated of China for (a) Infected people, (b) Recovered people, (c) Number of deaths, (d) Active infected cases.
Although, the infection growth rate is expected to be exponential but it may depend upon country’s population density, type of lockdown, social status, peoples’ seriousness and precautionary measures about the epidemic, mobilty and many more parameters discussed in previous sections. Hence, the curve may not have the expected exponential shape at some places.
The results of case study of China are shown by Figs. 2 (a-d). It can be observed by the figures that proposed model fits well for the data of infected people (Fig. 2(a)), as well as with the data of recovered people (Fig. 2(b)). The model initially fits well with the data of died people (Fig. 2(c)) as well. Figs. 2(a) and 2(b) shows that by the time number of infected people becomes negligible. It can be observed from Fig 2(a) that the rate of infection grows at exponential rate and decreases at quadratic rate. Further, number of active case is shown by Fig 2(d). The orange lines show the Phase-2 and Phase-3. Phase-2 starting date was 11 February, 2020; Phase-3 starting date was 23 February, 2020. The total duration of the study is 22 January, 2020 to 14 April, 2020. The optimal lockdown period in the case of China is 23 January, 2020 to 5 April 2020 (73 days).
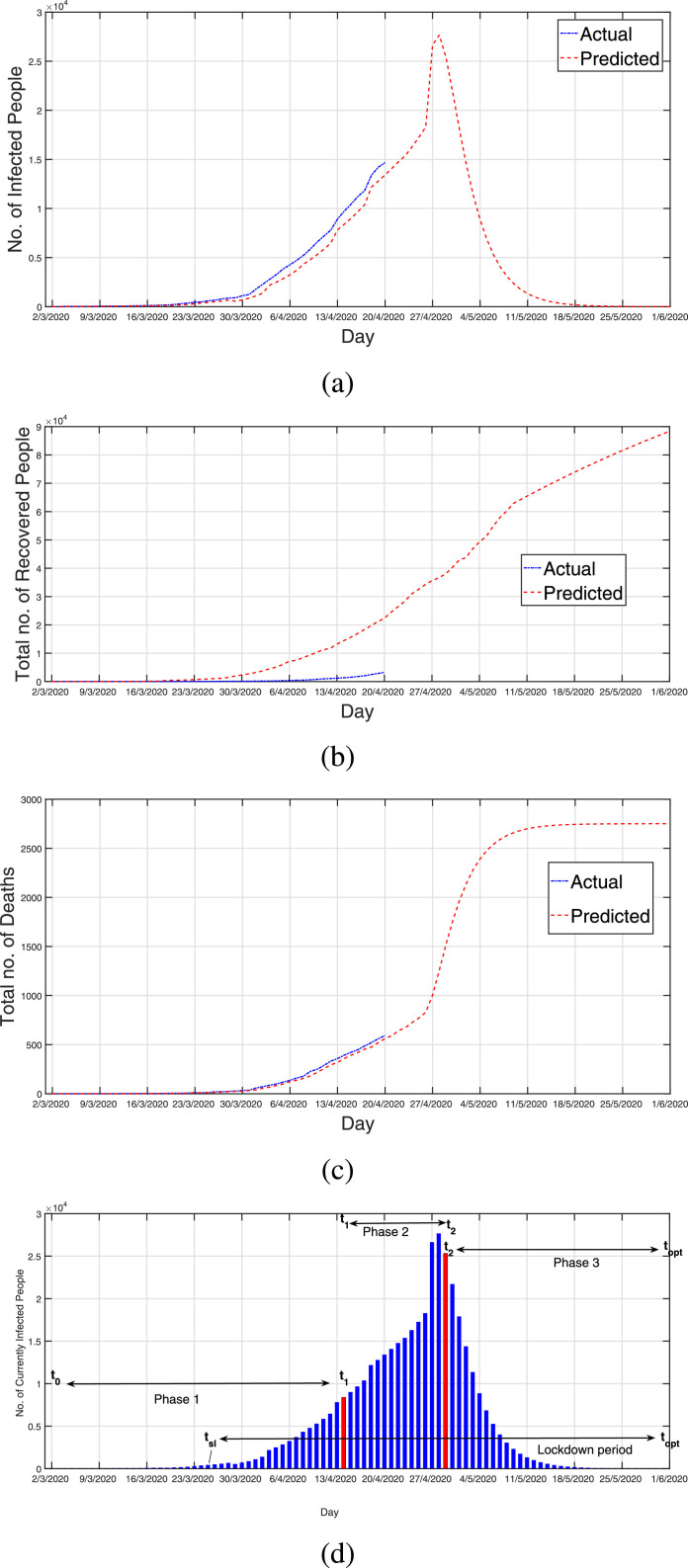
The prediction results of India are shown by Figs. 3 (a-d). The total duration of the study for prediction is 2 March, 2020 to 24 May, 2020. Phase-2 starting date is 14 April, 2020; Phase-3 starting date is 29 April, 2020. Predicted optimal lockdown period of India is 25 March, 2020 to 1 June 2020 (69 days).
Fig. 3.
Prediction statistics of India for (a) Infected people, (b) Recovered people, (c) Number of deaths, (d) Active infected cases.
Similarly, the prediction results of Italy are shown by Figs. 4 (a-d) with predicted optimal lockdown period between 9 March, 2020 to 4 June, 2020 (88 days). The total duration of the study for prediction is 15 February, 2020 to 4 June, 2020. Phase-2 starting date is 2 April, 2020; Phase-3 starting date is 20 April, 2020.
Fig. 4.
Prediction statistics of Italy for (a) Infected people, (b) Recovered people, (c) Number of deaths, (d) Active infected cases.
Also it is observed that by increasing number of tests per day for suspected cases Topt can be reduced as shown by Table 1 for P=10. If social distancing and lockdown is strictly followed then Phase-2 can be achieved soon and number of suspected people start getting reduced and Topt can be achieved earlier. The optimal lockdown period for India and Italy are 69 days and 88 days respectively, with reference to their testing rate.
Table 1.
Change in Topt with reference to γT.
| γT | Country (Topt) |
||
|---|---|---|---|
| Italy | India | China | |
| 0.21 | 97 | 77 | 83 |
| 0.23 | 92 | 72 | 77 |
| 0.25 | 88 | 69 | 73 |
| 0.27 | 84 | 66 | 69 |
| 0.29 | 81 | 63 | 66 |
| 0.31 | 78 | 61 | 63 |
5. Conclusion and Future Scope
In this paper, a three-phase Susceptible-Infected-Recovered -Dead (3P-SIRD) model is developed to estimate the optimal time of lockdown due to COVID-19. Additionally, we have updated previously developed models by considering some parameters like Silent Carriers, unregistered deaths, mobility factor so that more accurate modelling of data can be performed. Further, it is considered that the number of suspected person varies with respect to time of dispersal of virus. Therefore, three-phases are formed to define the suspected rate as it will not grow exponentially all the time. Finally, proposed model takes China, India and Italy as case study and the result shows the approximate lockdown time as 73 days for china (which is very near to actual lockdown period i.e. 77 days). Also, it is tried to make the prediction for optimal lockdown period for India and Italy: that is 69 days for India and 88 days for Italy. Proposed model can be extended by defining different levels of lockdown according to the severity. In this case infection rate will vary as per strictness level during lockdown. Also, the variation in lockdown period with reference to the testing rate is studied.
Proposed model can be applied to estimate the optimal lockdown time for any pandemic disease whose vaccine is not available, after which infection can also be controlled without affecting local communities.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests.
Acknowledgment
We are thankful to Dr. Krishna Mohan from Birla Institute of Scientific Research, Jaipur, India for his valuable suggestions throughout the work.
References
- 1.Hui D. The continuing 2019-ncov epidemic threat of novel coronavirus to global health - the latest 2019 novel coronavirus outbreak in Wuhan. China, International Journal of Infectious Diseases. 2020;91:264–266. doi: 10.1016/j.ijid.2020.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World Health Organization (WHO) Situation Report-35, WHO. 2020. Coronavirus disease 2019 (COVID-19) [Google Scholar]
- 3.World Health Organization (WHO), Statement on the second meeting of the International Health Regulations (2005) Emergency Committee regarding the outbreak of novel coronavirus (2019-nCov), WHO, 2020.
- 4.Kermack W.O., McKendrick A.G. Proceedings of the Royal Society of London; vol. A. 1927. A contribution to the mathematical theory of epidemics; p. 700-721. [Google Scholar]
- 5.Boujakjian H.. Modeling the spread of ebola with seir and optimal control. 2016. SIAM UG Research Online, No. 9 299–310.
- 6.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sjodin H., Wilder-Smith A., Osman S., Farooq Z., Rocklv J. Only strict quarantine measures can curb the coronavirus disease (COVID-19) outbreak in Italy, 2020. Eurosurveillance. 2020;25(13):2000280. doi: 10.2807/1560-7917.ES.2020.25.13.2000280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wu J., Leung K., Leung G. Nowcasting and forecasting the potential domestic and international spread of the 2019-ncov outbreak originating in Wuhan. China: A modelling study, Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tang Z., Li X., Li H. Prediction of new coronavirus infection based on a modified SEIR model. medRxiv. 2020 [Google Scholar]
- 10.Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in china, italy and france. Chaos, Solitons & Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Piccolomini E.L., Zama F.. Preliminary analysis of COVID-19 spread in italy with an adaptive SEIRD model. ArXiv (2020) arXiv-2003.
- 12.https://www.scmp.com/news/china/society/article/3076323/third-coronavirus-cases-may-be-silent-carriers-classified.
- 13.https://www.worldometers.info/coronavirus/#countries.
- 14.Tian L., Li X., Qi F., Tang Q.Y., Tang V., Liu J., Cheng X., Li X., Shi Y., Liu H., Tang L.H.. Pre-symptomatic transmission in the evolution of the COVID-19 pandemic. ArXiv preprint (2020) arXiv:2003.07353.
- 15.https://science.thewire.in/health/covid-19-mortality-india-civil-registration-deaths/.
- 16.https://economictimes.indiatimes.com/news/international/world-news/new-report-on-138-coronavirus-cases-reveals-disturbing-details/articleshow/74022946.cms?from=mdr.
- 17.https://www.nature.com/articles/d41586-020-00760-8.
- 18.https://www.vox.com/future-perfect/2020/4/3/21206392/presymptomatic-coronavirus-spread-symptoms.