A bioinspired stretchable membrane-based compliance sensor

Significance

The human skin is capable of identifying compliance of touched materials using pressure and strain-sensing mechanoreceptors. This multitude of sensation requirement has been a grand challenge preventing the development of compact devices capable of compliance sensing. The compliance sensor presented here is developed by integrating a strain and a pressure sensor with a unique design. The thin form factor of the proposed method, along with easy fabrication, enables integration to robotics in high spatial resolution. Thus, the compliance sensor presented here is expected to enable humanlike compliance sensation to robots and machines.

Abstract

Compliance sensation is a unique feature of the human skin that electronic devices could not mimic via compact and thin form-factor devices. Due to the complex nature of the sensing mechanism, up to now, only high-precision or bulky handheld devices have been used to measure compliance of materials. This also prevents the development of electronic skin that is fully capable of mimicking human skin. Here, we developed a thin sensor that consists of a strain sensor coupled to a pressure sensor and is capable of identifying compliance of touched materials. The sensor can be easily integrated into robotic systems due to its small form factor. Results showed that the sensor is capable of classifying compliance of materials with high sensitivity allowing materials with various compliance to be identified. We integrated the sensor to a robotic finger to demonstrate the capability of the sensor for robotics. Further, the arrayed sensor configuration allows a compliance mapping which can enable humanlike sensations to robotic systems when grasping objects composed of multiple materials of varying compliance. These highly tunable sensors enable robotic systems to handle more advanced and complicated tasks such as classifying touched materials.

A fundamental property often associated with the perception of compliance is the measure of compliance. Our human skin can sense compliance, thus allowing us to classify and discriminate touched objects. Mechanoreceptors within our human skin are responsible for our touch sensation. These receptors can capture different types of forces, such as pressure, texture, and vibration (1, 2). Among these receptors slowly adapting (SA) receptors, SA-I (Merkel cell) and SA-II (Ruffini organ) play a crucial role in compliance sensation. The former measures static pressure applied on the skin with high resolution while the latter is able to detect skin stretch. As a result, we can distinguish compliant objects. Current technological advances can now allow some of these important elements of human sensations incorporated into robotic and medical applications. There has been an increased demand to develop artificial skin that can mimic human touch sensations (3–7). One of the goals of the artificial skin concept is to provide a variety of sensations using electrical devices. With the advances in stretchable materials and microfabrication, there are reports regarding flexible sensors capable of sensing temperature (8–10) and both static and dynamic forces (11–13). These reported sensors demonstrated their potentials toward wearable device applications, such as prosthetic devices (14–16), pulse-wave sensing (17–19), and force-sensitive mapping (20–23). We anticipate that in the near future, “compliance” sensors will be a vital part of artificial skin because a combination of compliance sensor with other sensors will enable us to differentiate materials and to provide important feedback during manipulation of objects. Usually, deformation of the grasped objects is related to their degree of compliance (24, 25). Therefore, compliance sensor is an important sensing block that needs to be developed and integrated to artificial skins to provide humanlike sensations for prosthetic arms or robotic systems.

There are several types of sensing mechanisms to transduce compliance of the touched material to an electrical signal that can be read digitally: 1) Cutometer is a commercial tool used in clinical settings for measurement of elasticity of skin by applying a negative air pressure to the skin and measuring deformation via an optical measurement system (26, 27). 2) A handheld device was proposed that utilizes a tactile resonance sensor for detecting compliance of skin (28). The device utilizes piezoceramic structures to be used as sensing and actuating terminals that are used to identify compliance and modulus of the touched material using structural dynamic relations. The advances in material science and microfabrication led to the development of flexible devices that were used to classify compliance of touched materials. 3) An electronic whiskerlike sensor was proposed that is composed of strain sensors and able to identify compliant materials when a known deformation is applied to substrate material (29). 4) A soft prosthetic hand with integrated optical waveguides was reported. By controlling the compliance of the fingers, compliance of touched objects was classified (30). Other types of devices include flexible piezoelectric devices (31), microelectromechanical systems (MEMS)-based sensors (32), pressure sensors (33), and optical sensors (34).

Despite the above progress, however, it remains highly challenging to implement these sensors to applications that require compact form factor (35–37) due to their bulky external components, such as pneumatic systems and precise optical measurement components, high-voltage requirement for actuation, and integration issues. The reason for the compliance-sensing apparatus being complex is that it requires two parameters to be simultaneously measured, that is, both applied pressure and deformation information are needed to detect compliance of an object. It is thus challenging to integrate two sensors into a single compact unit. On the other hand, even though pressure and strain sensors are widely studied in the literature as individual sensing elements, it is challenging to integrate them without coupling effects. To develop a compliance sensor that can be integrated into artificial skin or robotic systems, the requirements are 1) it should have a compact form factor that can be easily integrated, 2) it should not require large external components such as pumps and moving stages, or a considerable structural change in the integrated system, and 3) sensors should be decoupled for reliable performance.

In this work, we describe a bioinspired thin compliance sensor that simultaneously detects pressure and deformation similar to SA-I and SA-II in human skin without the need for any bulky external components and does not occupy a considerable volume. In order to mimic the stretch and pressure sensation capability of SA-I and SA-II, we coupled a membrane-based strain sensor (MBSS) to a pressure sensor for compliance identification of touched materials. As a result, the sensor can capture both the surface deformation of the touched material and the applied pressure, simultaneously. We developed two different sensing methods for the MBSS by utilizing resistive and capacitive-based sensors. For instance, the resistive sensor yielded a sensitivity of 11 Ω/N and 104 Ω/N when materials with modulus of 75 GPa and 20 kPa were tested, respectively. Similarly, the capacitive sensor resulted in a sensitivity of 80 fF/N (femtofarad Newton) and 1,280 fF/N for similar materials, respectively. We also demonstrated the easily tunable sensitivity of the sensor by reducing the membrane thickness, which is useful when higher resolution is needed. The thin and small form factor of the sensor enables it to be applied in different applications. First, we integrated the sensor to a robot finger and identified compliance of grasped objects; second, by building arrayed sensors, we were able to map surface an object made up of different materials. This is useful to detect irregular objects inside tissues, such as tumors.

Results

Compliance and Modulus Measurement.

Quantitatively, compliance is reciprocal of stiffness, and for a bar structure under normal pressure the equation governing the deflection is given by

$$F=kx,$$ [1]

where k is the stiffness of the structure, and x is the deformation. k is dependent on geometrical and material parameters, and for a bar in compression it can be written as

$$k=EA/L,$$ [2]

where E is Young’s modulus, A is area, and L is length of the bar along the pressure direction. Therefore, both geometrical and material properties play an important role in our understanding of compliance.

When a material is touched, compliance sensing can provide tactile information occurring due to the nature of contact as well as kinesthetic information (24). Furthermore, following Eqs. 1 and 2, modulus information can also be inferred if geometric dimensions of the touched materials are available (i.e., during robotic finger grasping). From Eq. 1, two terms need to be measured to identify compliance of the object: 1) applied force (or pressure), and 2) deformation in response to the applied force. Therefore, these parameters need to be measured simultaneously for compliance sensing.

Sensor Structure and Output.

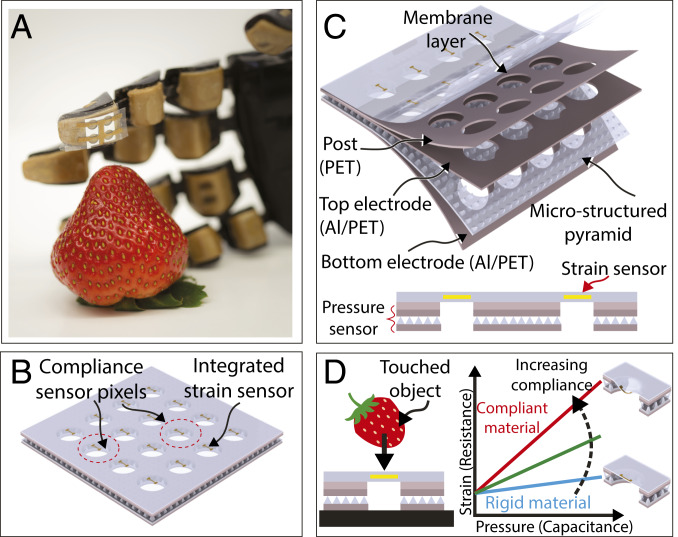
It is desirable to have a compliance sensor that has a thin form factor be easily deployed on small areas in an array configuration (Fig. 1A), operate without a bulky external component, and does not require a structural modification on the mounted device. To achieve such a compact compliance sensor, a bilayer sensing method is proposed where the first layer consists of a stretchable membrane to detect surface deformation of the touched material and the second layer consisting of a pressure sensor. The sensor array can be fabricated by alignment and lamination of flexible layers (Fig. 1 B and C). Each pixel consists of a post structure with a circular opening to allow the MBSS to deform together with the material when pressure is applied (SI Appendix, Fig. S1 A and B). On the other hand, conventional strain sensors respond to extensions while pressure sensors respond to normal pressure only (SI Appendix, Fig. S1 C and D). The MBSS consists of a capacitive or resistive-based strain sensor aligned with respect to the circular openings on the post structure. When the MBSS contacts to a material, it deforms as contact pressure increases (Fig. 2 A and B). This deformation per unit pressure depends on geometrical parameters such as membrane radius and thickness as well as material compliance. The smaller deformation translates as a higher sensitivity for compliant materials. Meanwhile, the applied pressure is measured by the pressure sensor. Combining the outputs of the MBSS and the pressure sensor a sensitivity value, S, is calculated for each object which is the ratio of the strain response to the pressure response. S is then used to distinguish materials of different compliance (i.e., a larger S for more compliant materials) (Fig. 1D).

Fig. 1.

Detecting compliance of materials. (A) A robotic hand with integrated compliance sensor array touching a strawberry. (B) Illustration of the compliance sensor array. (C) Exploded view of the arrayed configuration showing laminated layers. Bottom subset figure shows a cross-sectional view of two sensor pixels. (D) An exemplary output plot of the proposed sensor. The strain sensor provides y-axis data as either resistive or capacitive change, while the pressure sensor provides x-axis force/pressure data as capacitance change.

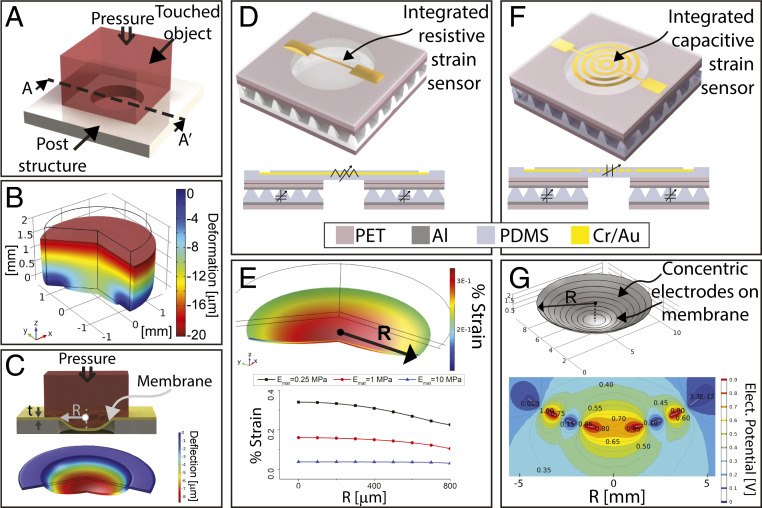
Fig. 2.

FE models of standalone compliance sensing units. (A) Schematic view of a post structure with a circular opening that generates deformation on a specific region on the touched material when pressure is applied. Mechanical FE simulation results showing (B) deformation contour plot when a cylindrical object having 2 mm thickness, 3 mm diameter, and Young’s modulus of 100 kPa placed on a post structure with a 2-mm-diameter circular opening under 1-kPa pressure; (C) contour plot of a membrane with Young’s modulus of 1 MPa placed on post with 1-mm radius opening contacted with a material having Young’s modulus of 100 kPa under 1-kPa applied pressure. (D) Illustration of an RMB sensor. The cross-sectional image shows resistive and capacitive sensor components. (E) Mechanical FE simulation results showing strain on the membrane when materials with different modulus touch the sensor under 1 kPa. (F) Illustration of a CMB sensor that has circular interdigitated electrodes to generate a fringe-field electric field on the membrane. Both RMB and CMB have pressure sensors with microstructured pyramids with 50-µm base length and 20-µm height sandwiched in between Al/PET films. (G) Electromechanical FE simulation results showing electric field lines on the membrane during deformation.

Finite-Element Modeling.

To identify important geometrical and material features of the sensor and its response to materials with different compliance, we developed a finite-element (FE) model. There are different structural designs that can force a material to deform around a predefined region. We focused on a design with a circular opening because of uniform stress regions around the edges under pressure. The surface deformation of the touched object is dependent on its thickness, the applied pressure, and the radius of the opening. Fig. 2 B and C show FE results where a 2-mm-thick material is applied against the block with a circular opening. SI Appendix, Fig. S2A shows the profile of the deformation around the circular opening for materials with different modulus.

Next, we developed an FE model to identify the geometrical parameters of the MBSS. Fig. 2C shows the cross-sectional view of the device structure with the MBSS and deformation contour plots of the MBSS when a material is placed on top and pressure is applied. SI Appendix, Fig. S2B shows the effect of radius on the deformation and suggests that it is especially important for detecting compliant materials with high sensitivity. When the radius is increased from 0.5 to 2 mm, the deflection of the MBSS increased more than 4×. As seen in SI Appendix, Fig. S2C, by varying modulus of the MBSS from 0.25 to 2 MPa, there is not a considerable difference in the displacement. Identifying less compliant material is more challenging because of the decrease in membrane deflection. That would require optimization of geometrical parameters. This can be explained by considering the flexural rigidity of a membrane, D, defined as

$$D=\frac{E{t}^3}{12\left(1-{\vartheta }^2\right)},$$ [3]

where t is the thickness of the membrane and ν is Poisson’s ratio. Thus, for further sensitivity enhancement, a thinner structure is needed with a larger radius. By simply changing these geometrical parameters, we can adjust the mechanical properties of the membrane and identify different materials, without the need to change the membrane material.

We utilized resistive and capacitive strain sensors for the MBSS and the pressure sensor. Fig. 2D shows the resistive membrane-based (RMB) sensor and its cross-sectional view. To understand the responses of the strain sensors, we simulated strain on the membrane when pressured by the object (Fig. 2E). For instance, when a 1-mm-radii and 50-µm-thick polydimethylsiloxane (PDMS) membrane is used to identify materials with modulus of 0.25 and 1 MPa, respectively, it results in almost twofold increase in sensitivity, while a material with 10 MPa has almost no responses in radial strain. Fig. 2F shows the capacitive membrane-based (CMB) sensor by utilizing circular interdigitated electrodes. The gap between consecutive electrodes determines the capacitance of this fringe-field capacitor. To understand the behavior of the CMB, an electromechanical FE model is developed (Fig. 2G). In the small deformation regime, an increase in deformation increases the curvature of the membrane which results in an increase in capacitance. Further deforming the membrane, gaps between the electrodes increase due to stretching and dominate the effect of curvature. Therefore, capacitance starts decreasing.

Fabrication and Characterization of the Sensors.

Here, we fabricated a compliance sensor that can measure two parameters simultaneously and in a decoupled manner by laminating several flexible layers. The pressure sensor fabrication was completed following our previous work (23). We used PDMS (10:1) as the dielectric elastomer layer, which had microstructured tapered pyramids with 50-µm base length and 20-µm height stacked in between 50-nm aluminum-coated polyethylene terephthalate (PET) films with 25-µm thickness (SI Appendix, Fabrication).

RMB Sensor.

The RMB sensor was built by patterning a gold microcrack-based strain-sensing layer. It was previously shown that microcracks can be induced Cr/Au layer by controlling deposition conditions and work as a resistive strain sensor (38, 39). These cracks change film resistance with applied strain and high sensitivity can be achieved. Critical geometrical features of the sensor, such as length and width, are defined by a shadow mask during evaporation.

The experimental setup described below was utilized to apply cyclic loads through materials of different modulus. We utilized a widely known and available elastomer, PDMS, with different cross-linker ratios that yielded materials with different modulus. In addition to the glass, which resembles a low-compliance material, three different PDMS ratios were tested, namely PDMS (10:1), PDMS (25:1), and PDMS (50:1). The materials have a thickness of 3 mm and Young’s modulus of 2.02 ± 0.18 MPa, 0.39 ± 0.038 MPa, and 0.0247 ± 0.0017 MPa, respectively, determined by uniaxial compression testing (SI Appendix, Fig. S4). Fig. 3A shows the automated high-precision vertical stage and force gauge that was used to control applied pressure on the sensor. Materials were placed on top of the sensor and contacted to the force gauge to measure applied force during loading.

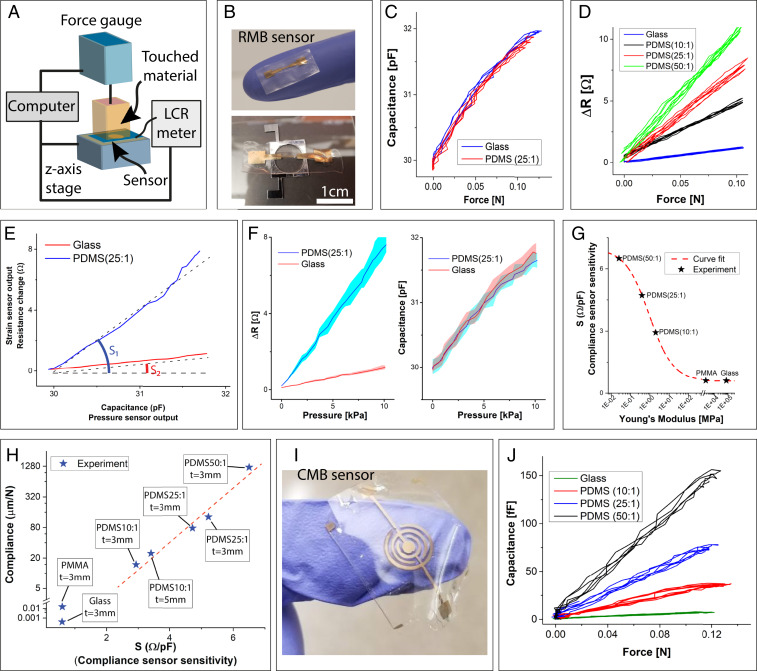
Fig. 3.

Characterization of RMB and CMB sensors. (A) Schematic view of characterization setup. A glass backing support was used to provide uniform pressure to the object. (B) Fabricated resistive membrane layer with a strain sensor width of 500 µm and length of 4 mm within 32-µm-thick PDMS (10:1). RMB sensor has a footprint of 1 × 1 cm². (C) The output of the capacitive pressure sensor showing similar outputs for glass and PDMS (25:1). (D) The output of the resistive strain sensor to materials of different modulus. Compliant materials result in higher resistance change and vice versa. (E) Compliance sensor measurements for two different materials, PDMS (25:1) and glass. Sensitivity, S, is the parameter that characterizes the output of the compliance sensor (strain sensor output per pressure sensor output) and is a measure of the object’s compliance. (F) Multimodal sensing operation of the compliance sensor: Resistive strain sensor (Left) and capacitive pressure sensor response (Right) were recorded simultaneously. The strain sensor response of PDMS (25:1) and glass has a sensitivity of 0.745 and 0.118 Ω/kPa, respectively, while both have similar pressure sensor response. (G) Sensor output can be related to Young’s modulus when objects of the same geometrical dimensions are measured. A curve was fit and R² of >0.99 was achieved using a symmetrical sigmoidal function (S = a + (b − a)/(1 + (x/c)^d)) where a = 6.97, b = 0.702, c = 0.931, and d = 0.586. (H) Compliance sensor S versus calculated compressive compliance of objects (SI Appendix, Table S1). (I) Optical image of the fabricated stretchable strain sensor layer with circular interdigitated electrodes to form a planar capacitor. Characterization results showing (J) output of capacitive strain sensor with a PDMS (10:1) layer thickness of 35 µm and electrode gap and width of 450 and 500 µm, respectively; materials yield higher sensitivity in strain sensor response whereas pressure sensor output yields similar response.

We characterized the RMB sensors with a PDMS membrane with 4-mm-long and 0.5-mm-wide strain sensor on the pressure sensor with 6-mm-diameter circular opening with a footprint of 1 × 1 cm² (Fig. 3B). We used PDMS (10:1) of 32 µm thickness as the membrane and laminated on the pressure sensor. Fig. 3 C and D show the obtained characterization results. As expected, when the sensor was in contact with more compliant materials sensor responded with higher sensitivity (resistance change per applied pressure). For the most compliant material tested, PDMS (50:1), almost a 2× more change in resistance was observed compared to PDMS (10:1). S values of 104 ± 7.8 Ω/N, 75 ± 6.1 Ω/N, 47 ± 2.4 Ω/N, and 11 ± 0.94 Ω/N were measured for PDMS (50:1), PDMS (25:1), PDMS (10:1), and glass, respectively. SI Appendix, Fig. S5A shows the time response of the RMB sensor for three different materials under the same cyclic pressure profile. Even though different materials yielded different sensitivities, the pressure sensor beneath yielded similar responses during loading cycles. Fig. 3E shows compliance sensor measurement for different materials which yields higher sensitivity, S, for more compliant materials. This observation confirms the potential of the sensor to be used as a standalone compliance sensor. Long cyclic tests of the sensor with different materials for 500 cycles show the repeatability of the sensor output (SI Appendix, Fig. S3 A and B).

The geometrical parameters of the sensor can be adjusted to tailor the sensor for accommodating a specific range of compliance. In this case, we demonstrated the tunability of the RMB sensor by adjusting the membrane thickness from 25 to 35 µm. SI Appendix, Fig. S5B shows the resistance change under the loading cycle of sensors with different membrane thicknesses when touched with PDMS (50:1) and glass. The sensitivity was increased from 85 to 120 Ω/N for PDMS (50:1) for sensors with a membrane thickness of 35 and 25 µm, respectively. The close-up view of the response when the glass is touched shows a higher sensitivity with the sensor having a thinner membrane (SI Appendix, Fig. S5C). This demonstrated that the sensitivity of the RMB can be further tuned using geometrical parameters up to a certain pressure, which is limited to 10 kPa in this case. However, after the maximum operational pressure, due to gap spacing below the MBSS and nonlinear material behavior during large-deformation regime, the compliance sensor cannot provide decoupled strain sensor and pressure sensor responses (Fig. 3F and SI Appendix, Discussion 1). Fortunately, the simultaneous reading of these sensors up to the operational pressure is enough to generate the required sensitivity parameter for material compliance identification. We tested various objects of the same thickness (3 mm) all supported on rigid substrates and were able to show a significant difference in sensitivity, S, according to material Young’s modulus (Fig. 3G). Therefore, in case the material dimensions are unknown, the sensor output S can be used to classify them according to their compliance (Fig. 3H).

CMB Sensor.

The CMB sensor was developed by integrating a single-layer membrane-type capacitor with the pressure sensor (Fig. 2C). To develop a planar capacitive strain sensor, we utilized fringe-field effects and considered circular interdigitated electrodes on the membrane. Fig. 3J shows the fabricated design which usually has lower sensitivity compared to double-plate capacitors. However, it can be built by depositing a single metal layer and prevents stress-related artifacts due to additional layers. The characterized sensor had a 35-µm-thick PDMS (10:1) membrane with an electrode gap and a width of 450 and 500 µm, respectively. As shown in Fig. 3I, S values of 1,280 ± 79 fF/N, 680 ± 52 fF/N, 270 ± 18 fF/N, and 80 ± 6.2 fF/N were measured for PDMS (50:1), PDMS (25:1), PDMS (10:1), and glass, respectively. Pressure sensor response for different tested materials is shown in SI Appendix, Fig. S5D. Even though the capacitive sensor seemed to provide better sensitivity for the identification of compliant materials, the effect of further membrane deformation resulted in a decrease in sensitivity, thus allowing for only a low applied force. This limits further usage in the identification of compliant materials when higher force or larger radius is needed to provide a better resolution.

Robot Finger with Compliance Sensation.

With the development of the artificial-skin concept, many research groups have proposed various sensors for robotic and prosthetic applications (5, 6), including pressure sensors to give the sense of touch to the robot. Here, our bioinspired compliance sensor unit can be advantageously used to add another dimension for the robot’s sensing capability. For example, the sensor can be placed on a robot finger without changing the structure of the finger, which then can identify the compliance of touched materials. To assess the feasibility of its application, we fabricated a standalone sensing unit that consists of an RMB sensor with a footprint of 1 × 1 cm² and integrated on one side of a robot finger, as shown in Fig. 4A. A feedback loop was programmed using the pressure sensor readings of the sensor, as shown in the block diagram in SI Appendix, Fig. S6A. The resistance of the RMB sensor was recorded using an inductor-capacitance-resistance meter (SI Appendix, Fig. S6B). Different materials were placed in between the robot finger to test the ability of the robot to classify touched materials. Once the capacitance reaches the maximum limit, the robot finger stops and restarts moving in the opposite direction to release the grasped material (Movie S1). Fig. 4B shows the setup. In order to test materials other than glass, PDMS blocks were attached to the glass block to allow contact to the sensor. SI Appendix, Fig. S6C shows simultaneous capacitance and resistance recordings from the compliance sensor. Fig. 4C shows resistance readings of the sensor for three different materials grasped by the robot finger. For compliant materials, maximum resistance value increases under a similarly applied force. With this result, we have successfully demonstrated the ability of the sensor to be used as a compliance sensor on robot fingers.

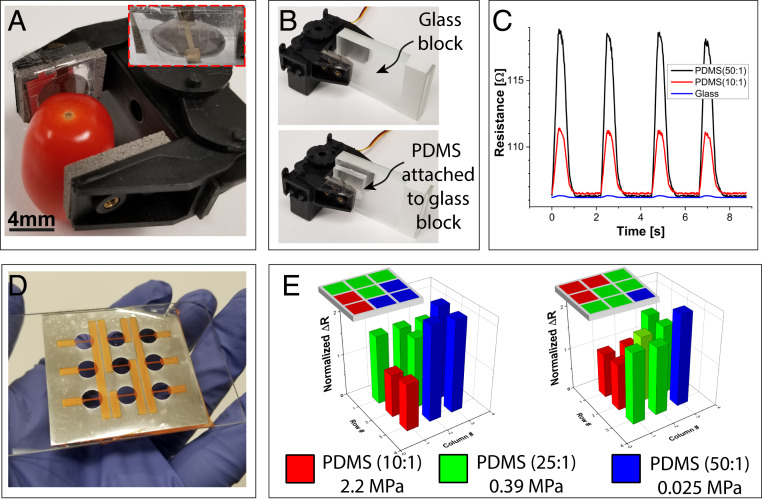
Fig. 4.

Integration of compliance sensor to a robotic gripper and demonstration of compliance mapping. (A) Optical image of the robotic finger holding a fresh tomato with integrated compliance sensor. The subset image shows the mounted sensor. (B) Optical image of the robotic finger contacting the glass and PDMS materials. (C) Resistance output of RMB sensor while grasping objects with different modulus. (D) Fabricated 3 × 3 sensor array on the palm. (E) The output of the strain sensor when an object with three different materials contacted to the sensor with 10-kPa pressure. Subset shows combination of materials (Scenario 1: normalized resistance changes in ascending order 1.00, 1.04, 1.56, 1.57, 1.62, 1.62, 2.18, 2.22, and 2.23; Scenario 2: normalized resistance changes in ascending order 1.00, 1.02, 1.02, 1.52, 1.55, 1.62, 1.62, 1.63, and 2.25). Results show normalized average resistance change of 10 loading cycles. Each RMB sensor pixel has a circular opening of 5 mm with a strain sensor 3.2 mm long and 450 µm wide.

Compliance Mapping.

In our daily lives, we touch “hybrid” items made up of multiple materials with different degrees of compliance. Developing a realistic compliance sensation requires sensors to possess high spatial resolution (Fig. 1A). In addition to our single sensor mounted on the robotic finger, a multimaterial sensing platform is needed, especially for prosthetic and surgical applications, to mimic or enable real-life experiences (35–37). To realize such a platform, multiple sensors need to be integrated into a smaller footprint, similar to mapping devices. We developed two different compliance mapping devices to show the applicability of the sensor for prosthetic applications. The first device has a 3 × 3 array (Fig. 4D). Each sensor pixel has a circular opening of 5 mm with a 3.2-mm-long strain sensor and a pitch of 8.3 mm. Two different scenarios were tested by placing three different materials on a glass slide. First, four out of nine sections of the glass slide were covered with PDMS (25:1), while the remaining areas were covered with more compliant PDMS (50:1) and less compliant PDMS (10:1) (Fig. 4 E, Inset). Then, five out of nine sections of the area were covered with PDMS (25:1); three and one out of nine sections were covered with PDMS (10:1) and PDMS (50:1), respectively. The glass slide holder was then placed on to the sensing platform with materials touching the sensors, and a uniform pressure was applied through the glass backing substrate. Fig. 4E shows the responses of the sensor pixels due to an applied force of 0.12 N through the multimaterial holder. For both tests, pixels touching the more compliant material have relatively higher S values. For the first case, average normalized resistance changes of 1.00, 1.04, 1.56, 1.57, 1.62, 1.62, 2.18, 2.22, and 2.23 were observed for each pixel. For the second case, a similar trend was observed for the same materials with average normalized changes of 1.00, 1.02, 1.02, 1.52, 1.55, 1.62, 1.62, 1.63, and 2.25. For both cases, the compliance sensor was able to classify materials’ compliance demonstrating the capability of the device as a potential prosthetic sensor. In some cases, we observed slight variations in the pixels’ responses, even if the same material is in contact. This could be due to variations in the center alignment of strain sensors with respect to circular openings of post structure. The pixel variations can be further improved with more precise alignment of the layers during the lamination process. We anticipate that such high-resolution compliance sensors can be useful in future prosthetic and robotic applications, where skinlike features are desired. To show the high spatial resolution capability of the proposed sensor, we fabricated a small form factor 2 × 2 compliance sensor array with a footprint of 1.2 × 1.2 cm² with openings of 4.2-mm diameter and 6.8-mm pitch (SI Appendix, Fig. S7). Such small form-factor devices will enable next-generation human–machine interactions. Furthermore, mapping tools can also be used to monitor compliance of tissues for various medical applications, such as the detection of tumors for breast cancer (40–42).

Discussion

We have successfully fabricated a compliance sensor, which can simultaneously measure surface deformation of the touched material and the applied pressure in a decoupled manner. Even though pressure sensing is widely studied in the literature, progresses in wearable compliance sensors for robotics or prosthetics remain lacking due to the requirement of multidimensional sensing (i.e., force and deformation) in a small footprint and thin form factor to enable compliance sensing. Here, we addressed these limitations by employing an MBSS to detect surface deformation of touched material. Then, integrating a pressure sensor comprising a microstructured pyramid layer, the sensor was realized. We investigated capacitive and resistive sensing mechanisms as a strain sensor and confirmed the operation of the integrated device as a compliance sensor. Our sensors were tested in different applications to validate their applications toward humanlike sensing capabilities. First, the sensor was integrated into a robotic finger, and materials of varying compliance were identified. Next, to illustrate humanlike sensation for grasping items with materials of different compliance, an array of sensors was developed. We showed that with our fabricated high-spatial-resolution sensor, items with materials of different compliance could be electrically identified. However, our results indicate that an increase in the applied pressure results in large deformations in the membrane, which prevents correct pressure measurements via pressure sensor yielding uncorrelated results. Hence, a pressure calibration is required prior to using the sensor to understand the critical pressure range for measurements. Taken together, high tunability of geometrical and materials properties, the low cost of the materials used, and the ease of manufacturing and integration to robotic systems enable our proposed compliance sensing device highly viable and attractive for various artificial-skin applications.

Materials and Methods

Details of fabrication can be found in SI Appendix, Fabrication. Details of characterization of the sensors can be found in SI Appendix, Characterization.

Data and Materials Availability.

All data needed to evaluate the conclusions in the paper are present in the paper or SI Appendix.