Significance
Applying magnetic fields is a powerful strategy to study the electronic properties of inorganic materials and paramagnetic organic systems due to their straightforward Zeeman interactions. We demonstrate with magnetic fields almost 1 million times stronger than that of Earth (up to 25 T) that we can perturb the optoelectronic properties of model “nonmagnetic” organic chromophores. These perturbations arise from the induction of ring currents in these aromatic molecules, which explains the increased relative magnetic sensitivity of the molecular aggregates in comparison to molecules in solution, in analogy to a molecular solenoid. Our results hint that magnetic fields may provide a new handle to control the optoelectronic properties of molecular systems to make new multifunctional and magnetosensitive organic devices.
Keywords: magnetic fields, ultrafast spectroscopy, aromatic ring currents
Abstract
The properties of organic molecules can be influenced by magnetic fields, and these magnetic field effects are diverse. They range from inducing nuclear Zeeman splitting for structural determination in NMR spectroscopy to polaron Zeeman splitting organic spintronics and organic magnetoresistance. A pervasive magnetic field effect on an aromatic molecule is the aromatic ring current, which can be thought of as an induction of a circular current of π-electrons upon the application of a magnetic field perpendicular to the π-system of the molecule. While in NMR spectroscopy the effects of ring currents on the chemical shifts of nearby protons are relatively well understood, and even predictable, the consequences of these modified electronic states on the spectroscopy of molecules has remained unknown. In this work, we find that photophysical properties of model phthalocyanine compounds and their aggregates display clear magnetic field dependences up to 25 T, with the aggregates showing more drastic magnetic field sensitivities depending on the intermolecular interactions with the amplification of ring currents in stacked aggregates. These observations are consistent with ring currents measured in NMR spectroscopy and simulated in time-dependent density functional theory calculations of magnetic field-dependent phthalocyanine monomer and dimer absorption spectra. We propose that ring currents in organic semiconductors, which commonly comprise aromatic moieties, may present new opportunities for the understanding and exploitation of combined optical, electronic, and magnetic properties.
The interplay between organic molecules and magnetism is a budding field of study with diverse applications in the physical sciences, ranging from chiral sorting (1, 2) to molecular circuitry (3–6) and quantum computing (7, 8). The magnetic field effects (MFEs) that most physical chemists consider have their origins in the spin-Zeeman effect, where paramagnetic states with nonzero spin multiplicity have magnetic field-dependent state energies. These Zeeman effects can in some cases play a critical role in the photophysical dynamics and properties of a wide variety of systems, most notably recently observed in organic semiconductor thin films for organic electronics applications as well as in bird magnetoreception (9–18). The cases where organic molecules have magnetic field interactions that are not derived from the spin-Zeeman effect are underexplored, but if they are discovered on general molecular platforms they can have a wide-ranging impact on our ability to tune the electronic properties of molecules by utilizing noninvasive fields. In this context, magnetism is already a powerful tool for looking at excited-state processes involving paramagnetic states, but the further exploration into diamagnetic field effects on organic molecules could lead to the development of new multifunctional organic devices with integrated electrical, optical, and magnetic properties.
This perspective in many ways is inspired by some of the salient features that govern the magneto-optical responses in magnetic circular dichroism (MCD) spectroscopy. While best known for its ability to interrogate the degeneracy of electronic states, many electronic transitions will display a weak MCD due to the magnetic field-induced mixing of electronic states that gives rise to the B-terms, even in diamagnetic systems (19). In these cases, it is a weak Zeeman effect on a state’s orbital angular momentum that causes certain transitions to be differentially sensitive to circularly polarized light, although one can imagine that Zeeman perturbations to a chromophore’s Hamiltonian should affect its linear absorption properties or photophysics more broadly (20). Unfortunately, the ability to observe MCD even at high magnetic fields is due to the high sensitivity of the differential absorption measurement, as opposed to arising from strong MFEs like in the case of spin-Zeeman interactions. This MCD effect on molecular electronic transitions does suggest, though, a possible avenue by which magnetic fields can directly interact with the wavefunction of an organic molecule.
Our search for a stronger magnetically induced perturbation of optical properties led us to an exceptionally common MFE in chemistry, namely the aromatic ring current (21–23). Simply put, the ring current effect can be understood as the induction of circular electronic motion in an aromatic π-system, akin to how the application of a magnetic field on a macroscopic conducting wire ring gives rise to a directional current. Despite the prevalence of ring currents in chemical systems, a detailed understanding of what effect the applied magnetic field has on molecular electronic orbitals is still an active area of investigation (24–28). The effects of these induced currents in aromatic organic molecules are commonly seen in NMR spectroscopy, where the induced magnetic field arising from the circular current can either enhance or detract from the Zeeman splitting of 1H nuclei, resulting in modified chemical shifts in the NMR spectrum as compared to the absence of the ring current (29, 30).
The advent of molecular electronics and single-molecule conductance experiments have reinvigorated our understanding of circular currents from a quantum mechanical perspective. Of particular interest is the proposal that an applied magnetic field on a single aromatic molecular wire between two contacts not only incites a circular current but also physically changes the electronic structure of the molecule; this is thought to occur due to the extra vector potential term in the π-electron kinetic energy operator due to the magnetic field, which in turn affects the resultant molecular orbitals (6). Such an effect has not been directly verified in organic molecules, likely because of the requirement to reach high magnetic fields in order to generate such a current, on the order of teslas, as well as the likelihood that the perturbations to the electronic structure readouts, like optical properties for example, are expected to be small for most porphyrinoid aromatic systems, on the order of nanoamperes per tesla (23, 31). However, the possibility of perturbing the electronic structure of aromatic molecules with high magnetic fields is attractive. If successfully demonstrated, this MFE could be applied to several aspects of chemistry and organic optoelectronics, where the electronic structures of organic aromatic molecules can dominate their photophysical properties and even their chemical reaction selectivity.
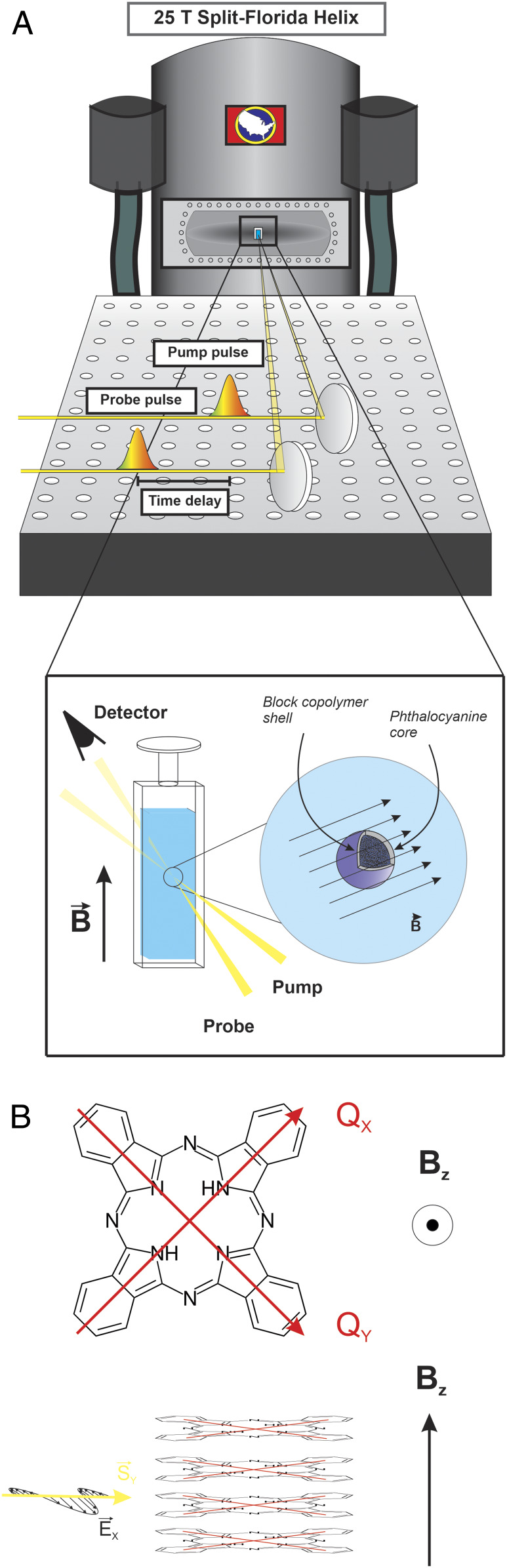
Here we explore how high magnetic fields affect the optical properties of model aromatic systems, specifically phthalocyanines and their aggregates, by using steady-state and time-resolved electronic spectroscopy. For this study we developed a unique optical spectroscopy setup at the National High Magnetic Field Facility using the 25-T Split-Florida Helix magnet with the construction of a home-built broadband transient absorption setup around it (shown schematically in Fig. 1), described in our previous work (32). Phthalocyanines, which are cyclic organic chromophores (Fig. 2B), are known for having strong and distinct magneto-optical responses like in MCD due to the degeneracy of the two lowest unoccupied molecular orbitals in most fourfold symmetric phthalocyanines (21, 33, 34). By working in the Voigt geometry instead of the Faraday geometry, that is, orienting the relative polarization of light perpendicular to the direction of the applied magnetic field, we minimize contributions from magneto-optical effects and look explicitly for magnetic field-induced changes to the linear absorption spectra. We find that not only can the application of the magnetic field reproducibly affect the photophysics of phthalocyanines in a fashion measurable by optical spectroscopy but also that the observed changes are consistent with molecular ring currents as the effects scale with the degree of π-stacking in phthalocyanine nanoparticles.
Fig. 1.
Optical spectroscopy at high magnetic fields. (A) A graphical schematic of the crux of the experimental setup, with emphasis on the orientation of the applied magnetic field with respect to the sample position. (B) Orientation of the lowest energy transition dipole moments in a model free base phthalocyanine (i.e., metal-free) molecule and a plane perpendicular applied magnetic field in the z-direction (Top). A model of phthalocyanine aggregates (Bottom) with the applied magnetic field perpendicular to the plane of a subset of isotropically distributed aggregates in solution, as well as to the Poynting vector and electric field polarization of the incoming light.
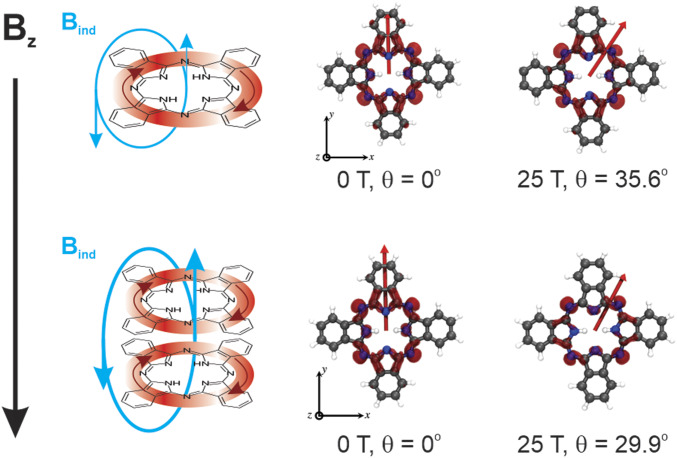
Fig. 2.
(Left) A representation of the application of a magnetic field (Bz) perpendicular to the plane of a phthalocyanine monomer (Top) and phthalocyanine stacked dimer (Bottom). The strength of the induced magnetic field (Bind) depends on the magnitude of the applied magnetic field via the induced circular current of π-electrons in the aromatic systems. (Right) TD-DFT calculations of a free base phthalocyanine monomer (Top) and dimer (Bottom) at 0 and 25 T with the magnetic field oriented perpendicular to the plane of the molecule. The red line indicates the direction of the transition dipole moments of the lowest energy monomer and most optically bright excitonic transitions, while the colored surfaces indicate their associated spatial transition densities. A complete set of magnetic field strengths for these calculations can be found in SI Appendix as well as the tabulated magnitudes of their transition dipole moments.
Results and Discussion
Time-Dependent Density Functional Theory and Magnetic Field-Dependent Steady-State Spectroscopy.
As a proof of principle, we first performed time-dependent density functional theory calculations on an unmodified free base (i.e., metal-free) phthalocyanine in the presence and absence of a magnetic field using a real-time propagation method within time-dependent density functional theory (TD-DFT) as implemented in the Octopus code (35–37), shown in Fig. 2. This approach serves to modify the Hamiltonian according to a Zeeman interaction with the angular momentum operator and allows straightforward visualization of the chromophore’s resultant transition density as opposed to the approach in ref. 6, allowing simple calculations of the resultant absorption spectrum. We find that the transition density of the QY electronic excitation, the lowest energy transition in the free base phthalocyanine, is modulated not only in amplitude but also in spatial distribution upon increasing application of a magnetic field normal to the molecular plane (SI Appendix, Figs. S1 and S2), to the effect that at 25 T the transition dipole moment rotates into the x axis by 35.6°. The rotation of the transition dipole moments of the model phthalocyanine QY transition is not particularly unexpected—related work on porphyriniod magneto-optical excitonic effects has suggested that this rotation occurs from the mixing of the QX character into the QY, although in the specific reference the QX and QY states are degenerate (38). On the other hand, the decrease in the amplitude of the transition density is more surprising, as it reflects a change in overall molecular orbital structure as a response to the applied magnetic field. Since the QX and QY generally have similar oscillator strengths, the transition amplitude decrease is likely not due to the transition mixing.
A similar calculation was then performed on a free base phthalocyanine dimer, where the second phthalocyanine was situated such that the interplanar distance was 4 Å without any lateral offset. Our hypothesis is that due to the strong electronic interactions between the two aromatic systems their electrons might interact with the applied magnetic field jointly and thereby amplify the MFE. Surprisingly, while the direction of the transition dipole moment at 25 T did not rotate to the same extent in the dimer as in the monomer, the spatial distribution and the amplitude of the transition density was predicted to be significantly perturbed. Calculations of the dimer electronic transitions in the presence of the magnetic field indicate a larger-magnitude change of its transition dipole moments compared to the predictions for the monomer. The exact changes in the magnitude of the transition dipole moments with applied magnetic field are explored in depth in consideration of the resultant computed absorption and are also tabulated in SI Appendix, Figs. S1 and S2.
We measured the magnetic field-dependent absorption spectra of copper (CuPc) and free base (H2Pc) phthalocyanines both in toluene solution as well as in the aggregated nanoparticle form. The phthalocyanines themselves have well-known spectroscopic signatures, consisting of sharp resonances in the red edge of the visible electromagnetic spectrum as shown for CuPc in Fig. 3. Upon nanoparticle formation using flash nanoprecipitation (39, 40), the CuPc spectrum starkly blue-shifts by 70 nm and broadens, giving rise to a new excitonic absorption band due to the strong intermolecular interactions concomitant with molecular aggregation, characteristic of H-aggregates. This absorption spectrum differs from the absorption spectra of many recorded CuPc thin films and single crystals because of the lack of crystallinity in the nanoparticle samples (41). The absorption spectra for H2Pc in toluene and in nanoparticle form can be found in SI Appendix, Figs. S3 and S4, and interestingly the H2Pc nanoparticle has almost the same absorption spectrum as that of the CuPc nanoparticle, exemplifying their matching excitonic properties coming from the phthalocyanine π-stacking intermolecular geometries in their aggregate form. For clarification, the blue-shifted absorption feature present for the phthalocyanine nanoparticles is the bright upper exciton according to molecular exciton theory, with the lower dark exciton transition likely located energetically at 780 nm, but hidden by its lack of oscillator strength.
Fig. 3.
Linear absorption at high magnetic fields. (A) Magnetic field dependent absorption spectra of CuPc in toluene solution and in nanoparticle form. (B) A magnified view of the CuPc molecule absorption at 677 nm. (C) Plotted values of the Q band absorption maximum for H2Pc, CuPc, and their respective nanoparticles normalized at the 0-T values.
With application of the magnetic field, we see clear differences in the absorption properties of the CuPc solution and nanoparticle form, although the effect on the nanoparticle is much stronger. We see the maximum effect at 25 T, where the absorption cross-section of the CuPc nanoparticle excitonic transition decreases by more than 10%, while that of the CuPc in solution changed only by a maximum of 3%. Importantly, this is an effect that is similarly reflected in H2Pc, which has almost the same sensitivity in nanoparticle form as the CuPc nanoparticle system, while also having a relatively muted effect on the molecules in solution. This MFE is distinct from other steady-state absorption MFEs like MCD for the following reasons. Foremost, we use plane-polarized light in the Voigt geometry, whereas MCD arises in the Faraday geometry, where the Poynting vector of circularly polarized light is parallel to the magnetic field direction. Further, the magnitude of changes in the MCD spectrum even at high magnetic fields is orders of magnitudes weaker than the decreases in absorption we report above for phthalocyanines (34). The decrease in oscillator strength for the nanoparticles appears to be linear with respect to the applied magnetic field, which minimizes the likelihood that this effect may be coming from the quadratic Zeeman effect (42). Similarly, there appears not to be any shift in the absorption maxima of any phthalocyanine investigated, and thus we do not expect this to be due to any explicit spin–orbit coupling interaction as observed in inorganic semiconductors or in carbon nanotubes (43, 44).
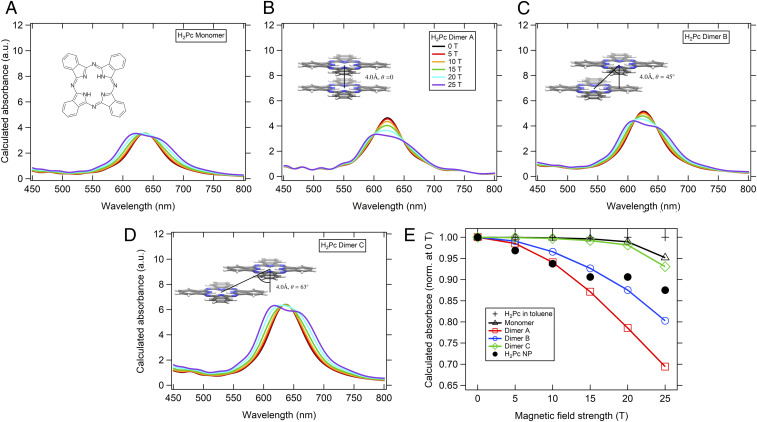
We reason that the photophysics of phthalocyanine aggregates might be more sensitive to the applied magnetic fields than their molecular counterparts due to electronic interactions between neighboring phthalocyanine π-systems. Since this electronic interaction gives rise to the excitonic transitions in the phthalocyanine nanoparticles, the perturbation of the initial molecular orbitals, even to a minor degree, might affect that of their interactions with one another to a greater extent. Since the electronic coupling resulting from orbital overlap is sensitive to intermolecular orientation, we used TD-DFT to model the absorption spectrum of a free base phthalocyanine monomer and compared its absorption spectrum to that of a range of simulated dimers, keeping the interplanar distance fixed but translating one phthalocyanine relative to another, shown in Fig. 4.
Fig. 4.
TD-DFT calculations of the magnetic field-dependent absorption spectra of a model free base phthalocyanine. (A) Monomer and (B) dimer A with an interplanar distance of 4 Å with no slip-stack angle. (C) Dimer with the same interplanar distance as dimer A, but a slip-stack angle of 45°. (D). Dimer with the same interplanar distance as the previous two but with a slip stack angle of 60°. (E) Plotted magnetic field dependent absorption spectrum maxima of the calculated free base phthalocyanine monomer and dimers with the experimental values presented for reference.
Although the calculated absorption spectrum of the phthalocyanine monomer does not closely match that of the experimental absorption spectrum, the predicted magnetic field dependence of the monomer spectrum compared to that of the dimer is in accord with our experiments shown in Fig. 3. We find that the simulation of the monomer shows a much weaker magnetic field sensitivity compared to each dimer calculated. The dimer with no slip-stack angle displays the greatest decrease in oscillator strength at 25 T, reaffirming our hypothesis that this MFE is most apparent when there is a strong electronic interaction between the molecules. As the molecular slip-stack angle increases, calculations predict a decrease in magnetic field sensitivity to the point that the molecular dimer with the highest slip-stack angle has an MFE almost identical to the phthalocyanine monomer. Looking at how the experimental results from the H2Pc nanoparticle compare to the computational ones gives a predicted slip-stack angle closest to the 0° and 45° conditions, which is in good agreement with the observed slip-stack angles in various crystalline forms of free base phthalocyanines (45). Further, the observed changes in the simulated absorption spectra are expected to be somewhat reduced in our nanoparticle systems, since in the latter the transition dipole moments of the excitons are isotropically distributed with respect to the direction of the applied magnetic field. The fact that there are possible intermolecular configurations for which this MFE severely drops off is in good agreement with our supplementary experiments on ZnPc nanoparticles, which not only exhibit much weaker electronic coupling but also exhibit a negligible MFE (SI Appendix, Fig. S5). This can be reasoned from the observation that the ZnPc and CuPc molecules have almost identical steady-state absorption spectra in solution and magnetic field-dependent steady-state spectra, meaning that resultant differences in their absorption properties in the nanoparticle result from differences in intermolecular electronic coupling. Since the absorption spectra for the ZnPc and CuPc nanoparticles are distinct, it follows that the neighboring CuPc and ZnPc nanoparticle aggregates must have different arrangement, with ZnPc aggregate less electronically coupled. This could be a consequence of intermolecular slip-stack angle as shown above, or due to an increase in the interplanar distance.
The ZnPc nanoparticle results, coupled with the magnetic field sensitivity, bring up an important distinction between this work and the known MFEs in these kinds of organic aromatic molecules. First, the electronic transitions in ZnPc and CuPc are for the most part identical with regard to the phthalocyanine ring itself, so if what we were observing were a Zeeman effect of the angular momentum state, which in MCD serves to split degenerate orbitals resulting in circular dichroism, then it should be apparent in both metal-coordinated phthalocyanine systems. It is likely that this effect serves to split the absorption band of all of the free base phthalocyanine absorption spectra calculated in Fig. 4 to roughly the same degree, which we observe to be both a disparate effect to the decrease in oscillator strength and not reflected in our experimental absorption spectra, although likely related to the predictions in ref. 38. If this was an effect of spin–orbit coupling, then not only would we expect as drastic of an MFE for the CuPc in solution as compared to that in nanoparticle form, we would also expect negligible MFE from both H2Pc systems, for which we observe an identical steady-state MFE as compared to the CuPc nanoparticles.
Observation of Ring-Current Effects in NMR Spectroscopy.
The steady-state results above can be explained by the existence of interacting aromatic ring currents in the phthalocyanine aggregates. As shown in Fig. 2, aromatic ring currents are the molecular equivalent of magnetic induction of current in a conductive ring, where in the phthalocyanine case the delocalized π-electrons that compose the highest occupied molecule orbital are the charges of interest. While ring currents are generally quite weak (for phthalocyanines on the order of nanoamperes per tesla), the circulation of electrons in the molecular plane may affect the optical transitions of the molecule itself, similarly to how the application of a magnetic field to a benzene molecular wire is proposed to change its electronic properties (6). In this case, then, the enhancement of the optical MFE would increase with aggregation and π-stacking of the molecular rings, in analogy to a molecular solenoid, with electronic interactions between nearby aromatic molecules increasing the local amount of circulating electron density.
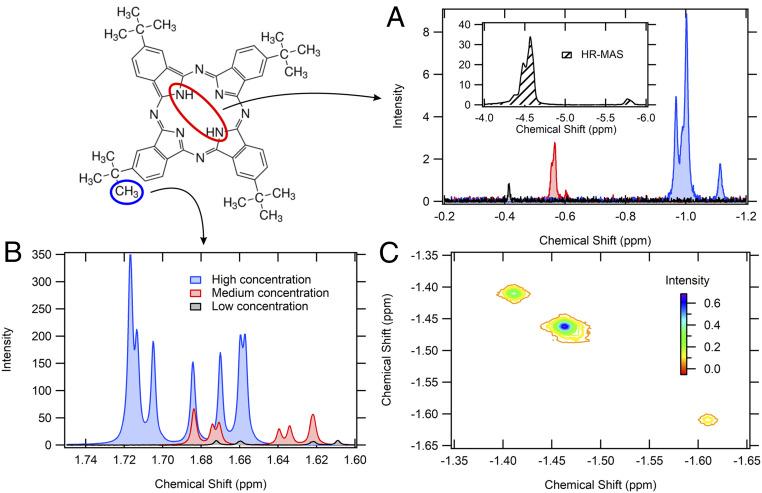
Aromatic ring currents have been historically investigated using NMR spectroscopy. NMR spectroscopy measures the Zeeman splitting of nuclear spins by observing modified proton resonances in a magnetic field, where the Zeeman splitting of a nucleus of interest depends additionally on its electronic environment. However, in the case of a molecule with an aromatic ring current, this will also depend on the proton’s location with respect to the aromatic ring. For an aromatic ring current, protons on the inside of the molecular ring will be upfield shifted (to more negative parts per million, or ppm) and those on the outside of the ring will be downfield shifted (to more positive ppm). Since we are interested in whether the strength of the ring currents increases with aggregation, we can track the NMR spectrum of H2Pc at various concentrations in d8-toluene to look for shifts in both the central protons and in the peripheral tert-butyl groups, shown in Fig. 5.
Fig. 5.
NMR measurements showing that the strength of the ring currents increases with increasing aggregation. Concentration-dependent NMR spectra of H2Pc, with attention paid to (A) central protons and (B) the tert-butyl protons, which show opposite shifts with increasing concentration. (C) Two-dimensional NOESY spectrum at the central proton resonances which show a lack of cross-peaks between the multiple peaks that arise at the highest concentrations.
The initial value of −0.4 ppm of the H2Pc inner protons at the lowest concentration (∼10−6 M) serves as a baseline for understanding the strength of the ring currents in individual phthalocyanine monomers, since the resonance appears more upfield than the tetramethylsilane standard as well as most protonated functional groups in organic chemistry, including amines. Increasing the concentration to 10−5 and 10−4 M further shifts these peaks upfield to −1.0 ppm, and this upfield shift does not saturate even at the high-resolution magic angle spinning (HR-MAS) limit at −4.5 ppm, where the concentration likely best resembles that inside the phthalocyanine nanoparticles. Such strong upfield shifts with concentration reflect greater degrees of aggregation which, from the perspective of ring currents, can be understood as an increased number of circulating π-electrons generating a magnetic moment that the central proton resonances are sensitive to. In other words, for an aggregate structure like an H2Pc dimer, the induced magnetic field as a result of the two stacked individual phthalocyanine ring currents is greater than for only one, resulting in a shift in the NMR peak. The fact that this peak shifts further upfield with higher concentrations is partially due to an increase in relative concentration of dimers and higher aggregates; however, the fact that it is nonsaturating even in the pseudocondensed phase HR-MAS experiment must mean that higher aggregates (trimers, tetramers, etc.) and their ring currents also generate successively stronger induced magnetic field. This is further recapitulated in nucleus-independent chemical shift (NICS) calculations shown in SI Appendix for various dimer configurations, which show ring-current effects which strongly depend on the interplanar orientation of the phthalocyanine dimer (SI Appendix, Fig. S14). NICS calculations are useful in assessing the presence of ring currents as compared to calculations of the expectation value of the ground-state wavefunction’s electron current operator since the NICS values are experimentally verifiable via NMR spectroscopy, whereas wavefunction-based calculations would provide direct computational support of the magnetic field-generated circular currents. Calculations of the NMR shifts for the phthalocyanine monomer, dimer, and trimer not only reproduce the observed experimental shift but also the observed splitting (SI Appendix, Fig. S16). The observation of a concomitant downfield shift of the tert-butyl proton resonances in the 1.6 to 1.7 ppm range is completely consistent with the observation of the upfield shifts for the central protons; stronger induced ring currents in aromatic systems give rise to stronger copropagating induced magnetic fields at the ring’s periphery, increasing the proton Zeeman splitting and giving rise to further upfield shifts of the tert-butyl protons.
The observation of multiple peaks in the upfield portion of the NMR spectrum also reflects the generation of aggregates with distinct intermolecular interactions or number of monomers, instead of usually being the result of NMR splitting due to the proximity of protons to neighboring protons. Two-dimensional (2D) nuclear Overhauser effect spectroscopy (NOESY) experiments easily confirm our hypothesis of distinct morphological populations because of the lack of cross-peaks between the various proton resonances, meaning that each peak likely represents a different intermolecular orientation or aggregate size. Since phthalocyanine crystals are also known to assemble in various polymorphs, it is unsurprising that their aggregates in deuterated toluene solution also come with specific intermolecular distances. It is also unsurprising that the furthest upfield peak is not composed of the largest fraction of morphologies, since again the phthalocyanine crystal structures reported so far do not exist with slip-stack angles close to 0°.
Importantly, these NMR results depend on the aggregation state of the phthalocyanines, consistent with our theoretical and experimental results on the steady-state properties of the phthalocyanine nanoparticles. This supports our hypothesis that the observed magnetic field sensitivities in steady-state optical spectroscopies can be attributed to electronic states perturbed by molecular ring currents. The perturbed electron densities at high magnetic fields then result in modified photophysical properties of the molecule, giving rise to our magnetic field-dependent linear absorption spectra.
Magnetic Field-Dependent Ultrafast Spectroscopy.
On the basis that these ring-current states have modified optical properties, we hypothesize that the steady-state properties are not the only ones that should be altered. The photophysical properties of the excited states, such as their time evolution and interconversion between states, may similarly be altered by the magnetic field. Time-resolved spectroscopies have previously been used to investigate the effects of magnetic fields on the photophysical dynamics of organic molecules; however, they almost always focus on the effect that the magnetic field has on the energies of the paramagnetic states in the system, whether they are triplet excited states or radical ion pairs (11, 46, 47). These Zeeman effects are small even with large magnetic fields for most organic molecules, which in turn affects only their long time (tens of picoseconds to microseconds) dynamics (48, 49). Thus, perturbations of subpicosecond dynamics are likely not to originate from Zeeman interactions, allowing the specific study of the dynamics associated with perturbed photophysical properties from magnetic field-induced ring currents, with extremely rare exceptions (49).
We focus on the ultrafast dynamics of our CuPc system in both solution and in nanoparticle form, as the dynamics of H2Pc in nanoparticle form show complex internal conversion dynamics, likely due to some nonadiabatic population of the ground state from the lower excitonic state (50). The photoinduced dynamics of CuPc in both solution and in nanoparticle are governed by an ultrafast intersystem crossing (ISC) from the singlet to the triplet manifold. This transition can easily be tracked at 0 T using ultrafast pump–probe spectroscopy, shown in Fig. 6, which in both situations results in a decrease in amplitude of the blue-side excited-state absorption (ESA) at 640 and 560 nm for the solution and nanoparticles cases, respectively. In the solution case, there is an added indicative feature in the decrease of the stimulated emission component of the positive signal at 680 nm. Although the electronic transitions in the visible region for CuPc stem mostly from the π–π* transitions from the phthalocyanine rings, the reason that ISC is on the subpicosecond timescale for both the solution and nanoparticle forms is due to the spin–orbit coupling arising from the coordinated Cu(II) ion at the center of the phthalocyanine. Reverse ISC back to the ground state occurs on the nanosecond to tens of nanosecond timescales for both systems and are outside the experimental range of our magnetic field-dependent pump–probe setup.
Fig. 6.
Ultrafast spectroscopy at high magnetic fields. (A) Two-dimensional false-color plots of the transient absorption measurements of CuPc in toluene solution (Top) and CuPc nanoparticles (Bottom) at 25 T. (B) Comparison of global analysis between experiments on CuPc in toluene (Top) and CuPc nanoparticles (Bottom) at 0- (Left) and 25-T (Right) applied magnetic field. In each case, the initial spectrum (black) evolves to the final spectrum (red) with a time constant indicated in the legend.
The results from the ultrafast spectroscopy reflect to a large degree the same general trend as the rest of our computed and experimental results; the CuPc nanoparticles exhibit a more drastic MFE than its molecular counterpart in solution. Specifically, the ISC rate from the lowest singlet excitonic state of the CuPc nanoparticle accelerates to 250 fs−1 from 325 fs−1 when brought to 25 T. However, in the CuPc solution the ISC rate barely increases, within the temporal resolution of our experiments and the challenging level of signal-to-noise ratio associated with high-magnetic-field ultrafast experiments. Therefore, we do not ascribe this change to an MFE. An intermediate field of 15 T on the CuPc nanoparticle system is shown in SI Appendix, Fig. S9 and has an ISC rate of 300 fs−1, consistent with an upward-trending ISC rate with the magnetic field strength, although limited by our signal-to-noise ratio. Assignment of the subtle differences in the shapes of the EAS spectra extracted from global analysis is also limited by our signal-to-noise ratio, although the relative intensity of the ground state bleach as compared to the ESA between 0 and 25 T qualitatively reflects the decrease in ground-state oscillator strength observed in our steady-state experiments.
In general, the electronic states of molecular systems like CuPc have two major ways of interacting with external magnetic fields: 1) a Zeeman effect on the spin degrees of freedom, which in this case likely acts on the triplet sublevels, or 2) a Zeeman effect on degenerate electronic states with nonzero orbital angular momentum, like is seen in MCD. While the latter MFE is generally a steady-state absorption effect for circularly polarized light, the Zeeman effect on triplet sublevels can have important consequences on photophysical dynamics, as described previously. This Zeeman effect, however, is likely not the cause of the observed MFEs in both the steady-state and time-resolved experiments, since it would affect the molecular and nanoparticle CuPc systems similarly, which is clearly not what is experimentally observed. We also know that the radical pair mechanism, which has been shown to modify electron transfer rates on timescales as short as picoseconds in some cases, should not be operative in the CuPc nanoparticles because of the lack of polaron formation.
These standard MFEs are ruled out as the cause for the increased ISC rate, and thus we are left with the interpretation that the same MFE that perturbs the steady-state absorption spectrum is responsible for the changes in ultrafast dynamics. In consideration of how the rate of ISC might be generally affected, it is instructive to write the rate of ISC in the Fermi Golden Rule form:
| [1] |
where VSO is the spin–orbit coupling of the singlet and triplet states between which ISC occurs and ΔEST is the energy difference between those same states. The exponential term of the above relation is the one that usually has a magnetic field-dependent influence over the rates of ISC, since the Zeeman splitting of triplet or doublet states decreases the energy gap between the triplet manifold and the initial singlet state. In the case of CuPc, where the gap between the singlet and triplet state can be estimated to be 550 meV using literature values for the phosphorescence energy and by approximating the energy of the lower energy excitonic state, the Zeeman splitting even at 25 T is on the order of 1 meV, which works to barely affect the energy gap (51, 52).
Ruling out changes in the energy gap leaves modification of the spin–orbit coupling as the likely cause of the increased ISC rate at 25 T. This fits well within our presented picture of the phthalocyanine aggregates having perturbed electron density at high magnetic fields due to their enhanced aromatic ring currents as compared to their molecular analogs. Since the spin–orbit coupling depends entirely on the electronic properties of the interacting singlet and triplet states, it follows that perturbed electronic states arising from the aggregate ring currents would have different spin–orbit couplings at high fields. Thus, the ultrafast ISC in the CuPc nanoparticle system continues to reaffirm the proposal of enhanced ring-current electronic states, which have the effect to perturb the electronics and photophysics of aromatic molecular chromophores.
Considering the photophysical and computational investigations together brings us to the following physical picture for the observed MFEs in this work. We have discovered that phthalocyanines in solution have weak, but detectable, magnetic field-sensitive electronic properties as predicted by TD-DFT and confirmed by absorption spectroscopy. This magnetic field sensitivity can be enhanced or diminished depending on the aggregation state of the phthalocyanine, suggesting cooperative MFEs between phthalocyanine monomers dependent on their relative orientation. This orientation-dependent sensitivity is consistent with the generation of aromatic ring currents in neighboring phthalocyanines, since they are expected to exist in individual molecules as well as become stronger or weaker depending on the alignment of the aromatic rings, in analogy to a solenoid. Thus, a picture arises that electronic states of phthalocyanines are modulated by magnetic fields due to the induction and strength of aromatic ring currents. While this MFE may be too weak to affect the energies of diamagnetic electronic states, the electronic character of these states is perturbed enough by the induction of aromatic ring currents to spectroscopically investigate their photophysical differences.
Conclusions
We reported steady-state and ultrafast optical experiments together with TD-DFT simulations on a range of phthalocyanine samples that suggest the role of magnetic field-induced aromatic ring currents perturbing the photophysical properties of these systems. We found that the phenomena were more pronounced in aggregated systems. We reasoned that the strong electronic interactions between π-stacked phthalocyanine molecules in the aggregates lead to an enhancement of the ring-current strength in analogy to a molecular solenoid.
Our discovery of optical readouts for the presence of aromatic ring currents adds an additional method for the molecular spintronics and single-molecule electronics communities to characterize the photophysical properties of various relevant organic systems. The stacked π-system structure in the phthalocyanine nanoparticles may lend comparison to the understanding of magnetoconductance properties of carbon nanotubes, which have been previously investigated as a molecular solenoid (53). Our paper should inspire the continued development of magneto-electronics in condensed-phase organic semiconductor systems, where we motivate that quantum effects in aromatic ring currents may modulate the molecular orbital interactions that govern electronic properties.
Experimental
Sample Preparation.
CuPc, H2Pc, and ZnPc were used as acquired (Sigma-Aldrich) for toluene solution experiments. In order to form the phthalocyanine nanoparticles, the phthalocyanines and an amphiphilic stabilizer, here polystyrene blocked in this work with polyethylene glycol (PS-b-PEG, 5k–1.6k) were codissolved in THF, a water-miscible organic solvent. Through micromixing of the phthalocyanine-block copolymer solution with Milli-Q deionized water using a confined impinging jet reactor, the phthalocyanines precipitate in the aqueous environment and are stabilized by the amphiphilic block copolymer to form organic nanoparticles, in a process known as flash nanoprecipitation (39, 40, 54, 55). The mixed streams were then diluted 10-fold into an aqueous collecting solvent and used after dialysis to remove the remaining THF. Sizes and polydispersity indexes were characterized by dynamic light scattering, which can be found in SI Appendix, Fig. S12.
TD-DFT Simulations.
The electronic Hamiltonian of a molecule under a static magnetic field B in the z direction is
| [2] |
where is the Kohn–Sham Hamiltonian in the absence of the magnetic field, is the angular momentum operator, and is the Bohr magneton. The system is subsequently perturbed by a small time-dependent potential in the shape of a Dirac delta pulse (56):
| [3] |
where is the Hamiltonian given by Eq. 2, is the amplitude of the electric field, is the direction of the incident electric field, and is the dipole moment operator. In the linear response regime, when the applied electric field pulse is small, the response is linear and the dipole moment is
| [4] |
where is the permanent dipole moment of the system in the absence of an external electric field and is the linear polarizability tensor along the axis over which the external field is applied. In the frequency domain, Eq. 4 can be rewritten as
| [5] |
where we have defined as the induced dipole moment. Finally, the absorption cross-section tensor σ can be calculated as
| [6] |
where is the average of the polarizability tensor given by
| [7] |
where Tr [.] is the trace operator that takes the sum of the diagonal elements of the polarizability tensor. The equation above takes into account the random orientation of the molecule. The full polarizability tensor at all frequencies is obtained from three independent simulations in which the initial field is applied in three mutually orthogonal directions. In all of our simulations we have employed real-time TD-DFT at the generalized gradient approximation level of theory using the Perdew–Burke–Ernzerhof exchange-correlation functional in its spin-polarized form and corrected using the averaged-density self-interaction method proposed by Legrand et al. (57). The core electrons were represented by Troullier–Martins pseudopotentials (58). The system was discretized on a 0.2-Å grid, and the simulation box was constructed by adding spheres of 4-Å radii around each atom. The time-dependent equations are integrated using a time step of 0.0023 fs and propagated for 20.0 fs. The Fourier transform was performed using an exponential damping, corresponding to a Lorentzian-shaped spectrum (37). The Octopus package which we used to implement our TD-DFT calculations is freely available on the web.
NICS Calculations.
Using ground-state DFT methods, the ring-current shifts were analyzed based on the simulation of the NICS for the H2Pc and ZnPc monomers and their corresponding three types of dimers with various slip-stack angles. The NICS values at different points along the z axis of these compounds were obtained at B3LYP/6-311+G(d,p) level of theory with the using the gauge-including atomic orbital method as implemented in Gaussian 09/E.01 (59, 60). The NMR shielding tensors for the H2Pc monomer, dimer, and trimer were calculated using the gauge-independent atomic orbital method as implemented in the Gaussian 16 software package (61). The shielding constants were taken as a weighted average for the methyl groups.
Steady-State Absorption Spectroscopy.
A Xenon lamp (Oriel) generated white light that was focused into the center of the magnet using an achromatic lens after passing through a Glan–Taylor polarizer such that the polarization of the incoming light was perpendicular to the applied magnetic field. The light was transmitted through samples in a 1-mm quartz cuvette (Starna) and either directed onto a spectrometer (Acton 2750i) that dispersed the transmitted light onto a back-illuminated Si charge-coupled device (CCD) (Spec-10; Princeton Instruments) or a portable universal serial bus-based spectrometer (Ocean Optics). Reference experiments in solvent only showed no magnetic field dependence on their transmission. For magnetic field-dependent steady-state absorption measurements, the field was ramped at 7 T per minute until the magnetic field strength reached the target, the absorption measurement was taken, and then the field increased until 25 T was reached, where we then ramped the field down, replicating all of the magnetic field measurements in reverse. No difference was found in the steady-state absorption measurements taken when the field was ramping up versus ramping down. The temperature at the sample position is estimated to be 298 K, since the part of the magnet which surrounds the sample is actively cooled with a chilled water system to maintain operation. Due to the active cooling, we estimate that the fluctuation in temperature at the sample position is at most 20 K; we see very little fluctuation of our spectroscopic readouts either via steady-state or time-resolved methods overall which would report on temperature fluctuations at the sample position.
Ultrafast Pump–Probe Spectroscopy.
The pump–probe setup has been described in detail in our earlier work. Briefly, a 1-kHz Ti:sapphire laser with 25-fs pulse duration (Coherent) was fed into a home-built noncollinear optical parametric amplifier, generating broadband visible pulses from 530 to 750 nm, which simultaneously covers the optical transitions in both the phthalocyanine nanoparticles and toluene solutions. These pulses were then compressed to <20 fs using two chirped mirror pairs in succession and split to generate the pump and probe beams. The polarization and power of the pump and the probe beams were controlled with λ/2 waveplates and wire-grid polarizers on each arm, and the pump power was limited such that there was no exciton–exciton annihilation at short times in the H2Pc nanoparticle system.
The pump beam was directed into a mechanical delay line in order to acquire pump–probe delay resolved dynamics, while a portion of the probe was sent onto a photodiode for balanced detection with boxcar integration. Time steps were collected for the first picosecond with 10-fs steps and then to the end of the stage limit (1 ns) with 100 steps set exponentially longer than the previous, beginning at 10 fs. The pump was chopped at a frequency of 250 Hz, corresponding to two on, two off pump–probe cycles. The pump and probe beam were focused to the center of the bore, where a 1-mm quartz cuvette housed the liquid-phase sample, using 100-cm and 75-cm focal length optical lenses, respectively. The transmitted signal from the probe is directed into a spectrometer-camera pair (Andor Shamrock spectrograph and Andor Newton CCD camera) to resolve the wavelength access in our pump–probe experiments. Care was taken to direct the beam away from the water cooling pipes, as the humidity changes with the magnet in operation were found to affect the performance of electronics. This issue has since been resolved by the National High Magnetic Field Laboratory by the insulation of those pipes.
NMR Spectroscopy.
Proton NMR experiments were done with a 500-MHz NMR spectrometer (Bruker) using d8-toluene solvent suppression with up to 500 scans. For HR-MAS experiments, 5 mg of H2Pc were placed in an HR-MAS capillary with a few microliters of d8-toluene. Two-dimensional NOESY experiments were performed on an 800-MHz NMR spectrometer (Bruker).
Data Availability.
All data needed to support the conclusions of this paper are included in the main text and SI Appendix.
Supplementary Material
Acknowledgments
We acknowledge financial support by the National Science Foundation, MRI program (DMR-1229217), and by Princeton University through the Innovation Fund for New Ideas in the Natural Sciences. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement DMR-1157490 and the State of Florida. M.M. acknowledges financial support by European Community (H2020 Marie Skłodowska-Curie Actions), Project 655059. M.B.O. acknowledges financial support by the National Science Foundation - Institute for Complex Adaptive Matter (NSF-ICAM) and the National Science Foundation for the use of supercomputing resources through the Extreme Science and Engineering Discovery Environment, Project TG-CHE140097 and acknowledges financial support by the Agencia Nacional de Promoción Científica y Tecnológica fondo para la Investigación Científica y Tecnológica (ANPCyT-FONCyT, Grant PICT-2017-0795). B.M.W. acknowledges support from the US Department of Energy, Office of Science, Early Career Research Program under Award DE-SC0016269. B.K. acknowledges support by the National Science Foundation Graduate Research Fellowship under Grant DGE-1656466 as well as the Princeton Environmental Institute Walbridge Fund. B.K. thanks Istvan Pelczer for guidance and discussion with regard to the NMR spectroscopy and Kyra Schwarz and Bo Fu for careful reading of this manuscript.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1918148117/-/DCSupplemental.
References
- 1.Banerjee-Ghosh K., et al. , Separation of enantiomers by their enantiospecific interaction with achiral magnetic substrates. Science 360, 1331–1334 (2018). [DOI] [PubMed] [Google Scholar]
- 2.Naaman R., Waldeck D. H., Chiral-induced spin selectivity effect. J. Phys. Chem. Lett. 3, 2178–2187 (2012). [DOI] [PubMed] [Google Scholar]
- 3.Tagami K., Tsukada M., Current-controlled magnetism in T-shape tape-porphyrin molecular bridges. Curr. Appl. Phys. 3, 439–444 (2003). [Google Scholar]
- 4.Jo M. H., et al. , Signatures of molecular magnetism in single-molecule transport spectroscopy. Nano Lett. 6, 2014–2020 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Rai D., Hod O., Nitzan A., Magnetic field control of the current through molecular ring junctions. J. Phys. Chem. Lett. 2, 2118–2124 (2011). [Google Scholar]
- 6.Rai D., Hod O., Nitzan A., Magnetic fields effects on the electronic conduction properties of molecular ring structures. Phys. Rev. B 85, 1–21 (2012). [Google Scholar]
- 7.Hod O., Rabani E., Baer R., Magnetoresistance of nanoscale molecular devices. Acc. Chem. Res. 39, 109–117 (2006). [DOI] [PubMed] [Google Scholar]
- 8.Coronado E., Epsetin A. J., Molecular spintronics and quantum computing. J. Mater. Chem. 19, 1670–1671 (2009). [Google Scholar]
- 9.Wang F. J., Bässler H., Vardeny Z. V., Magnetic field effects inπ -conjugated polymer-fullerene blends: Evidence for multiple components. Phys. Rev. Lett. 101, 1–4 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Gautam B. R., Nguyen T. D., Ehrenfreund E., Vardeny Z. V., Magnetic field effect on excited-state spectroscopies of π-conjugated polymer films. Phys. Rev. B 85, 1–7 (2012). [Google Scholar]
- 11.Huynh U. N. V., Basel T. P., Ehrenfreund E., Vardeny Z. V., Transient magnetic field effect of photoexcitations in donor-acceptor organic semiconductors. J. Phys. Chem. Lett. 9, 4544–4549 (2018). [DOI] [PubMed] [Google Scholar]
- 12.Khachatryan B., et al. , Magnetophotocurrent in organic bulk heterojunction photovoltaic cells at low temperatures and high magnetic fields. Phys. Rev. Appl. 5, 1–9 (2016). [Google Scholar]
- 13.Baniya S., et al. , Magnetic field effect in organic light-emitting diodes based on electron donor-acceptor exciplex chromophores doped with fluorescent emitters. Adv. Funct. Mater., 10.1002/adfm.201601669 (2016). [DOI] [Google Scholar]
- 14.Bayliss S. L., et al. , Site-selective measurement of coupled spin pairs in an organic semiconductor. Proc. Natl. Acad. Sci. U.S.A. 115, 5077–5082 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weiss L. R., et al. , Strongly exchange-coupled triplet pairs in an organic semiconductor. Nat. Phys. 13, 176–181 (2017). [Google Scholar]
- 16.Xu H., Wang M., Yu Z. G., Wang K., Hu B., Magnetic field effects on excited states, charge transport, and electrical polarization in organic semiconductors in spin and orbital regimes. Adv. Phys. 68, 49–121 (2019). [Google Scholar]
- 17.Rodgers C. T., Hore P. J., Chemical magnetoreception in birds: The radical pair mechanism. Proc. Natl. Acad. Sci. U.S.A. 106, 353–360 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Maeda K., et al. , Chemical compass model of avian magnetoreception. Nature 453, 387–390 (2008). [DOI] [PubMed] [Google Scholar]
- 19.Hughes J. L., Pace R. J., Krausz E., The exciton contribution to the Faraday B term MCD of molecular dimers. Chem. Phys. Lett. 385, 116–121 (2004). [Google Scholar]
- 20.Piepho S., Schatz P., Group Theory in Spectroscopy with Applications to Magnetic Circular Dichroism (Wiley-Interscience, 1983). [Google Scholar]
- 21.Pople J. A., Molecular orbital theory of aromatic ring currents. Mol. Phys. 1, 175–180 (1958). [Google Scholar]
- 22.Lazzeretti P., Ring currents. Prog. Nucl. Magn. Reson. Spectrosc. 36, 1–88 (2000). [Google Scholar]
- 23.Janson T. R., Kane A. R., Sullivan J. F., Knox K., Kenney M. E., The ring-current effect of the phthalocyanine ring. J. Am. Chem. Soc. 91, 5210–5214 (1969). [Google Scholar]
- 24.Peeks M. D., Claridge T. D. W., Anderson H. L., Aromatic and antiaromatic ring currents in a molecular nanoring. Nature 541, 200–203 (2017). [DOI] [PubMed] [Google Scholar]
- 25.Kanno M., Kono H., Fujimura Y., Laser-control of ultrafast π-Electron ring currents in aromatic molecules: Roles of molecular symmetry and light polarization. Appl. Sci. (Basel) 8, 2347 (2018). [Google Scholar]
- 26.Valiev R. R., Benkyi I., Konyshev Y. V., Fliegl H., Sundholm D., Computational studies of aromatic and photophysical properties of expanded porphyrins. J. Phys. Chem. A 122, 4756–4767 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Peeks M. D., et al. , Aromaticity and antiaromaticity in the excited states of porphyrin nanorings. J. Phys. Chem. Lett. 10, 2017–2022 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rodriguez J. J., Mukamel S., Probing ring currents in Mg-porphyrins by pump-probe spectroscopy. J. Phys. Chem. A 116, 11095–11100 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wannere C. S., Schleyer P. V. R., How do ring currents affect (1)h NMR chemical shifts? Org. Lett. 5, 605–608 (2003). [DOI] [PubMed] [Google Scholar]
- 30.Schleyer P. V. R., Maerker C., Dransfeld A., Jiao H., van Eikema Hommes N. J. R., Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 118, 6317–6318 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Valiev R. R., Cherepanov V. N., The influence of benzene rings on aromatic pathways in the porphyrins. Int. J. Quantum Chem. 113, 2563–2567 (2013). [Google Scholar]
- 32.Maiuri M., et al. , High magnetic field detunes vibronic resonances in photosynthetic light harvesting. J. Phys. Chem. Lett. 9, 5548–5554 (2018). [DOI] [PubMed] [Google Scholar]
- 33.Hollebone B. R., Stillman M. J., Assignment of absorption and magnetic circular dichroism spectra of solid, α phase metallophthalocyanines. J. Chem. Soc. Faraday Trans. II 74, 2107 (1978). [Google Scholar]
- 34.Rawat N., et al. , Spin exchange interaction in substituted copper phthalocyanine crystalline thin films. Sci. Rep. 5, 16536 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Andrade X., et al. , Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems. Phys. Chem. Chem. Phys. 17, 31371–31396 (2015). [DOI] [PubMed] [Google Scholar]
- 36.Marques M. A. L., Castro A., Bertsch G. F., Rubio A., Octopus: A first-principles tool for excited electron-ion dynamics. Comput. Phys. Commun. 151, 60–78 (2003). [Google Scholar]
- 37.Castro A., et al. , Octopus: A tool for the application of time-dependent density functional theory. Phys. Status Solidi Basic Res. 243, 2465–2488 (2006). [Google Scholar]
- 38.Yuen-Zhou J., Saikin S. K., Yao N. Y., Aspuru-Guzik A., Topologically protected excitons in porphyrin thin films. Nat. Mater. 13, 1026–1032 (2014). [DOI] [PubMed] [Google Scholar]
- 39.Kudisch B., et al. , Binary small molecule organic nanoparticles exhibit both direct and diffusion-limited ultrafast charge transfer with NIR excitation. Nanoscale 11, 2385–2392 (2019). [DOI] [PubMed] [Google Scholar]
- 40.Johnson B. K., Prud’homme R. K., Mechanism for rapid self-assembly of block copolymer nanoparticles. Phys. Rev. Lett. 91, 118302 (2003). [DOI] [PubMed] [Google Scholar]
- 41.Caplins B. W., Mullenbach T. K., Holmes R. J., Blank D. A., Femtosecond to nanosecond excited state dynamics of vapor deposited copper phthalocyanine thin films. Phys. Chem. Chem. Phys. 18, 11454–11459 (2016). [DOI] [PubMed] [Google Scholar]
- 42.Schiff L. I., Snyder H., Theory of the quadratic zeeman effect. Phys. Rev. 55, 59–63 (1939). [Google Scholar]
- 43.Walck S., Reinecke T., Exciton diamagnetic shift in semiconductor nanostructures. Phys. Rev. B 57, 9088–9096 (1998). [Google Scholar]
- 44.Stier A. V., McCreary K. M., Jonker B. T., Kono J., Crooker S. A., Exciton diamagnetic shifts and valley Zeeman effects in monolayer WS2 and MoS2 to 65 Tesla. Nat. Commun. 7, 10643 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yim S., Heutz S., Jones T. S., Model for the α→β1 phase transition in phthalocyanine thin films. J. Appl. Phys. 91, 3632–3636 (2002). [Google Scholar]
- 46.Piland B., Burdett J. J., Kurunthu D., Bardeen C. J., Magnetic field effects on singlet fission and fluorescence decay dynamics in amorphous rubrene. J. Phys. Chem. C 117, 1224–1236 (2013). [Google Scholar]
- 47.Musewald C., et al. , Magnetic field dependence of ultrafast intersystem-crossing: A triplet mechanism on the picosecond time scale? J. Am. Chem. Soc. 121, 8876–8881 (1999). [Google Scholar]
- 48.Oviedo-Casado S., Urbina A., Prior J., Magnetic field enhancement of organic photovoltaic cells performance. Sci. Rep. 7, 4297 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gilch P., Magnetic field effect on picosecond electron transfer. Science 281, 982–984 (2011). [DOI] [PubMed] [Google Scholar]
- 50.Caplins B. W., Mullenbach T. K., Holmes R. J., Blank D. A., Intermolecular interactions determine exciton lifetimes in neat films and solid state solutions of metal-free phthalocyanine. J. Phys. Chem. C 119, 27340–27347 (2015). [Google Scholar]
- 51.Van Bree J., Silov A. Y., Koenraad P. M., Flatté M. E., Pryor C. E., G factors and diamagnetic coefficients of electrons, holes, and excitons in InAs/InP quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 85, 165323 (2012). [Google Scholar]
- 52.Vincett P. S., Voigt E. M., Rieckhoff K. E., Phosphorescence and fluorescence of phthalocyanines. J. Chem. Phys. 55, 4131–4140 (1971). [Google Scholar]
- 53.Tsuji N., Takajo S., Aoki H., Large orbital magnetic moments in carbon nanotubes generated by resonant transport. Phys. Rev. B Condens. Matter Mater. Phys. 75, 1–4 (2007). [Google Scholar]
- 54.Lu H. D., Lim T. L., Javitt S., Heinmiller A., Prud’homme R. K., Assembly of macrocycle dye derivatives into particles for fluorescence and photoacoustic applications. ACS Comb. Sci. 19, 397–406 (2017). [DOI] [PubMed] [Google Scholar]
- 55.Lu H. D., et al. , Narrow absorption NIR wavelength organic nanoparticles enable multiplexed photoacoustic imaging. ACS Appl. Mater. Interfaces 8, 14379–14388 (2016). [DOI] [PubMed] [Google Scholar]
- 56.Yabana K., Bertsch G. F., Time-dependent local-density approximation in real time. Phys. Rev. B 54, 4484–4487 (1996). [DOI] [PubMed] [Google Scholar]
- 57.Legrand C., Suraud E., Reinhard P. G., Comparison of self-interaction-corrections for metal clusters. J. Phys. At. Mol. Opt. Phys. 35, 1115–1128 (2002). [Google Scholar]
- 58.Troullier N., Martins J. L., Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B Condens. Matter 43, 1993–2006 (1991). [DOI] [PubMed] [Google Scholar]
- 59.Wolinski K., Hinton J. F., Pulay P., Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 112, 8251–8260 (1990). [Google Scholar]
- 60.Frisch M. J., et al. , Gaussian 09 (Revision E.01, Gaussian Inc., Wallingford CT, 2009).
- 61.Frisch M. J. et al., Gaussian 16, (Gaussian, Inc., Wallingford, CT, 2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data needed to support the conclusions of this paper are included in the main text and SI Appendix.