A machine learning forecasting model for COVID-19 pandemic in India

Abstract

Coronavirus disease (COVID-19) is an inflammation disease from a new virus. The disease causes respiratory ailment (like influenza) with manifestations, for example, cold, cough and fever, and in progressively serious cases, the problem in breathing. COVID-2019 has been perceived as a worldwide pandemic and a few examinations are being led utilizing different numerical models to anticipate the likely advancement of this pestilence. These numerical models dependent on different factors and investigations are dependent upon potential inclination. Here, we presented a model that could be useful to predict the spread of COVID-2019. We have performed linear regression, Multilayer perceptron and Vector autoregression method for desire on the COVID-19 Kaggle data to anticipate the epidemiological example of the ailment and pace of COVID-2019 cases in India. Anticipated the potential patterns of COVID-19 effects in India dependent on data gathered from Kaggle. With the common data about confirmed, death and recovered cases across India for over the time length helps in anticipating and estimating the not so distant future. For extra assessment or future perspective, case definition and data combination must be kept up persistently.

Introduction

As of date confirmed COVID-19 cases1 across the globe are 1,498,833 and mortality approximately 5.8%. Gradually the mortality rate is increasing and it’s an alarming factor for the whole world. Transmission is categorized into 4 stages based on the mode of spread and time. Every nation imposed different methodologies starting from staying in-home, using masks, travel restrictions, avoiding social gatherings, frequently washing hands and sanitizing the places often in the case of a common effort to combat the outbreak of this disease. Many countries imposed a lockdown state that prevents the movement of the citizens unnecessarily. Due to this social distancing factor and movement restrictions, the wellbeing and economy of the various nations are being under jeopardy. GPD of the entire world dropped drastically. When the person is found infected, he is isolated and treatment is given for recovery. But based on the severity it will cause death and also people left with a higher level of depression.

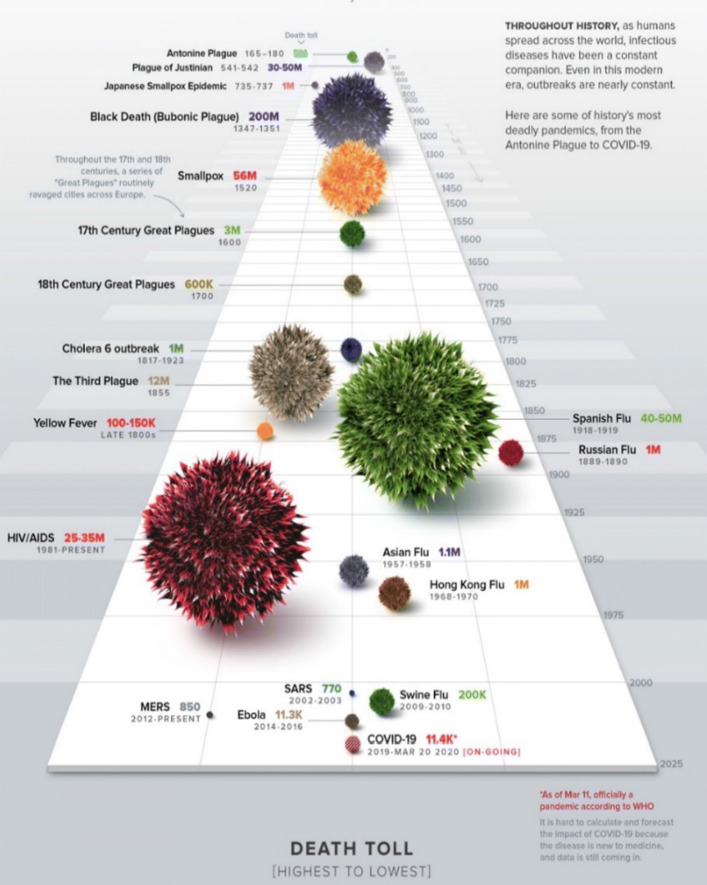
In India, the outbreak of coronavirus as disturbed the functioning of life as a whole. all were pushed to stay back to safeguard from the dreadful transmission. In the initial stages, the confirmed cases are those returned from oversees followed by transmission via local transmission. More caution is given to the elderly and immunity fewer people. The demographic of the infected people in India indicates that 39 years is the median. Comparatively, people between 21 and 40 years are being affected more. The everyday predominance information of COVID-2019 from January 22, 2020, to April 10, 2020, was gathered from the website of Kaggle.2 Weka 3.8.43 and Orange4 is utilized to decipher the information. LR, MLP, and VAR are applied on the Kaggle dataset having 80 instances for anticipating the future effects of COVID-19 pandemic in India. Forecasting is the need of an hour that helps to device a better strategy to tackle this crucial hour across the globe because of this infectious disease. As mentioned by the visual capitalist, the human race as crossed several outbreaks because of the several microbes that were invisible and invincible. COVID-19 is the current threat in the highly sophisticated twenty-first century. Figure 1 is a snapshot of the visual capitalist.5

Fig. 1.

History of pandemic

Artificial intelligence (AI) can assist us in handling the problems that need to be addressed raised by the COVID-196 pandemic. It isn't simply the innovation, however, that will affect yet rather the information and inventiveness of the people who use it. Without a doubt, the COVID-19 emergency will probably uncover a portion of the key shortages of AI. Machine learning (ML), the present type of AI, works by recognizing designs in chronicled training information. People have a preferred position over AI. We can take in exercises from one situation and apply them to novel circumstances, drawing on our dynamic information to make the best speculations on what may work or what may occur. Computer-based intelligence frameworks, conversely, need to gain without any preparation at whatever point the setting or assignment changes even marginally.

The COVID-19 emergency, hence, will feature something that has consistently been valid about AI: it is a device, and the estimation of its utilization in any circumstance is dictated by the people who structure it and use it. In the present emergency, human activity and development will be especially basic in utilizing the intensity of what AI can do. One way to deal with the novel circumstance issue is to assemble new training information under current conditions. For both human leaders and AI frameworks the same, each new snippet of data about our present circumstance is especially significant in advising our choices going ahead. The more viable we are at sharing data, the more rapidly our circumstance is not, at this point novel and we can start to see a way ahead. AI can assist us in handling the problems that need to be addressed raised by the COVID-19 pandemic. It isn't simply the innovation, however, that will affect yet rather the information and imagination of the people who use it. To be sure, the COVID-19 emergency will probably uncover a portion of the key setbacks of AI. Machine learning, the present type of AI, works by recognizing designs in verifiable training information. People have a preferred position over AI. We can take in exercises from one setting and apply them to novel circumstances, drawing on our theoretical information to make the best theories on what may work or what may occur. Simulated intelligence frameworks, interestingly, need to gain without any preparation at whatever point the setting or undertaking changes even somewhat. The COVID-19 emergency, along these lines, will feature something that has consistently been valid about AI: it is an apparatus, and the estimation of its utilization in any circumstance is dictated by the people who plan it and use it. In the present emergency, human activity and development will be especially basic in utilizing the intensity of what AI can do. One way to deal with the novel circumstance issue is to accumulate new training information under current conditions. For both human chiefs and AI frameworks the same, each new snippet of data about our present circumstance is especially important in illuminating our choices going ahead. The more compelling we are at sharing data, the more rapidly our circumstance is not, at this point novel and we can start to see a way ahead.

Related work

Sujatha and Chatterjee (2020) proposed a model that could be useful to foresee the spread of COVID-2019 by using linear regression, Multilayer perceptron and Vector autoregression model on the COVID-19 kaggle data to envision the epidemiological example of the malady and pace of COVID-2019 cases in India. Yang et al. (2020) introduced dynamic SEIR model for anticipating the COVID-19 pestilence pinnacles and sizes. They utilized an AI model prepared with respect to past SARS dataset additionally shows guarantee for future expectation of the scourges. Barstugan et al. (2020) presented early stage location of COVID-19, which is named by World Health Organization (WHO), by machine learning strategies actualized on stomach Computed Tomography pictures. Elmousalami and Hassanien (2020) presents a correlation of day level guaging models on COVID-19 influenced cases utilizing time series models and numerical detailing. Rizk-Allah and Hassanien (2020) acquainted another guaging model with examine and gauge the CS of COVID-19 for the coming days dependent on the announced data since 22 Jan 2020. Rezaee et al. (2020) introduced a mixture approach dependent on the Linguistic FMEA, Fuzzy Inference System and Fuzzy Data Envelopment Analysis model to ascertain a novel score for covering some RPN inadequacies and the prioritization of HSE dangers. Navares et al. (2018) introduced an answer for the issue of anticipating every day medical clinic confirmations in Madrid because of circulatory and respiratory cases dependent on biometeorological markers. Cui and Singh (2017) created and applied the MRE hypothesis for month to month streamflow prediction withspectral power as a random variable. Torky and Hassanien (2020) introduced a blockchain incorporated structure which research the chance of using peer-to peer, time stepping and decentralized storage points of interest of blockchain to construct another framework for confirming and distinguishing the obscure contaminated instances of COVID-19 infection. Ezzat and Ella (2020) a novel methodology called GSA-DenseNet121-COVID-19 dependent on a hybrid CNN structure is proposed utilizing an optimization strategy.

Methods and materials

In statistics, Linear Regression7 (LR) is a direct way to deal with demonstrating the connection between a dependent variable and at least one independent variable. LR was the main kind of regression analysis to be concentrated thoroughly and to be utilized widely in useful applications (Yan and Su 2009). LR shows the connection between two variables by fitting a straight condition to based information. One variable is viewed as an independent and the other is viewed as a dependent. An LR1 line has a condition of the structure:

$$Y=bX+a$$ 1

here X is the independent and Y is the dependent variable. The slope of the line is b and a is the intercept (the value of y when x = 0).

A multilayer perceptron8 (MLP) is a type of feedforward artificial neural network (FANN). The term MLP is utilized vaguely, now and then freely to indicate any FANN, now and then carefully to allude to systems made out of various layers of the perceptron. An MLP9 is a perceptron that is generally used for complex issues. The formula for MLP2 is:

$$y=\phi \left(\sum _{i=1}^n,w_i,x_i,+,b\right)=\phi \left(w^{T}x+b\right)$$ 2

here w is for the vector of weights, x is for the vector of inputs, b is for bias and phi are the non-linear activation function.

A Vector Autoregression10 (VAR) is a prediction calculation which is utilized when at least two-time series impact one another, i.e., the connection between the time arrangements included is bi-directional. The formula for VAR is:

$$Y_t=\alpha +{\beta }_1{Y}_{t-1}+{\beta }_2{Y}_{t-2}+\cdots +{\beta }_p{Y}_{t-p}+{ϵ}_t$$ 3

where α is the intercept, a constant and β1, β2 till βp are the coefficients of the lags of Y till order p.

Order ‘p’ means, up to p-lags of Y is utilized and they are the predictors in the equation. The ε_t is the error considered as white noise.

Experimental results

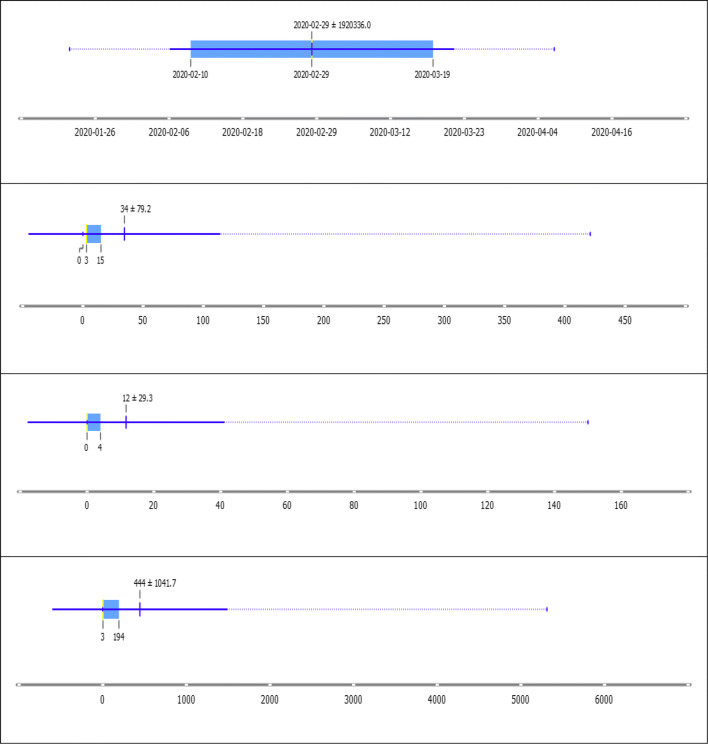
The structure of data based on date, confirmed, recovered and death are shown in Fig. 2 with the boxplots, and it's very clear that several cases are in so primitive stages. As mentioned by WHO, right now India is in the second phase indicating very few cases and forecast of this same is the potential work that is required at this juncture (Tareen et al. 2019).

Fig. 2.

Boxplot of India COVID-19

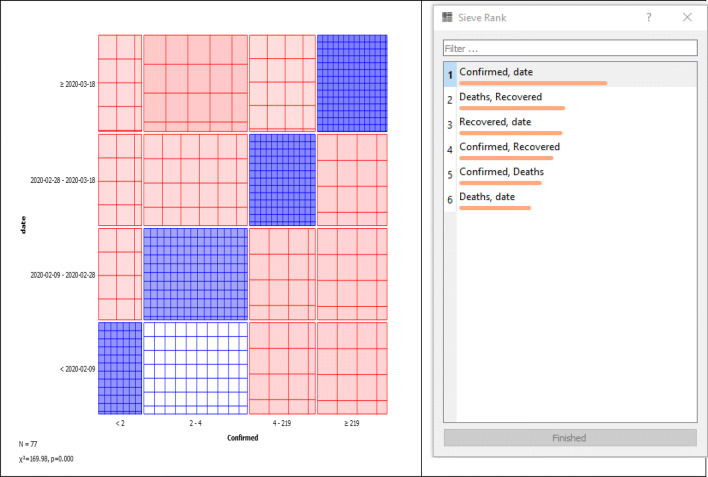
Sieve diagram provides the visualization of the dataset along with that showing the sieve rank. Figure 3 illustrates attributes that have a strong relationship with the dark shades. The interestingness of the pair of attributes is represented via this contingency table. It's a very graphical way of frequency visualization.

Fig. 3.

Sieve diagram for INDIA COVID-19

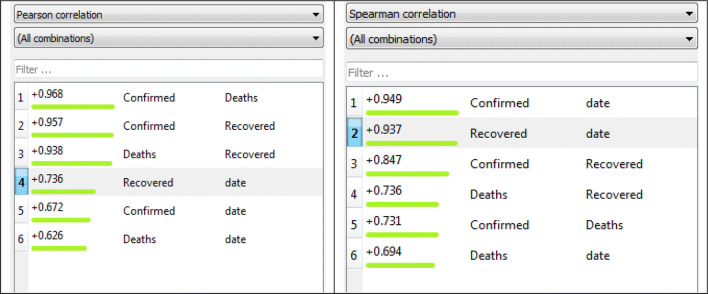
Correlation plays a great role in finding the dependency among the features of the dataset. Our dataset revolves around the confirmed, recovered, and death of cases because of the COVID-19 outbreak over the time frame of around 2 months in India. From the Spearman correlation, it's very evident that based on progressive of the day (date) the possibility of getting prone to sickness is very high and that is given with thE+0.949 correlation value. Figure 4 provides a glance at the correlation between Pearson and the spearman process. Appreciably the date attribute is holding a higher level of importance and that's is reason globally the measures have been taken for social distancing (Mu et al. 2018; Gautheir 2001). Normally the spread happens just in contact with the person by a handshake is the big brother in case of COVID-19. Correlation provides the signal about the impact and necessary countermeasures to be taken into consideration. Across the globe, leaders of the nation are carrying out various trial and error methods to combat the seriousness of the disease.

Fig. 4.

Pearson and spearman correlation

Forecasting gives pertinent and consistent input about the past, present, and future happenings with certain statistical and scientific approaches. Helps in string decision making in all perspectives. Broadly classified into qualitative and quantitative approaches. Steps involved in forecasting is the deciding factor of the task. Initial understanding of the problem with complete analysis, making a strong foundation, collecting data based on the previous two steps followed by future estimation. Comparison between actual and estimated with followup actions. Various applications like economic and sales prediction, budget, census and stock market analysis, yield projections and many more fields. The medical field also a potential area to deploy the forecast and predication to serve the number of people in need (Hajirahimi and Khashei 2019; Yamana and Shaman 2019). Our work carried out with linear regression, multilayer perceptron, and VAR model over the time series dataset to provide the forecast.

VAR model is a more suitable analysis model in the multivariate time series. It helps in inferencing and analysis of policy. It is used more in a practical forecasting scenario but it is hading superior forecasting performance. Technically narrating about the VAR, it is an m-equation, m-variable model in which individual variable explains on its own based on current, past values. Various parameters of VAR begins with maximum auto-regression order. Various information criteria that help in optimize autoregressive order are Akaike's information criterion (AIC), Bayesian information criterion (BIC), Hann-Quinn and Final prediction error (FPE). By adding and varying trends from constant, linear, and quadratic with forecast steps ahead and confidence intervals (Billio et al. 2019; Portet 2020; Zhang and Krieger 1993). The formula for calculating AIC, BIC and HQ is as follows:

$$\mathit{AIC}\left(p\right)=ln\left|{\mathrm{\Sigma }}^{\prime }\right|+\frac{2{\left(n\right)}^{2}p}{X}$$ 4

$$\mathit{BIC}\left(p\right)=ln\left|{\mathrm{\Sigma }}^{\prime }\right|+\frac{{\left(n\right)}^{2}p\mathit{ln}X}{X}$$ 5

$$HQ\left(p\right)=ln\left|{\mathrm{\Sigma }}^{\prime }\right|+\frac{{\left(n\right)}^{2}p2lnlnX}{X}$$ 6

where n is the number of attributes in the system, X is the sample size, and $\mathrm{\Sigma }{}^{\prime }$ is an estimate of the covariance matrix $\mathrm{\Sigma }$.

Sitational forcast in India

In our forecast work the maximum auto-regression order of 6 followed by an average of information criterion is used for visualization. The trend of constant, linear, and quadratic along with 1 step ahead and 95% confidence interval (CI) is introduced (Tapia 2020). In Figs. 5, 6, 7, 8 and 10, 11, 12, 13 and 14) the X-axis shows the days and the Y-axis shows the number of cases.

Fig. 5.

Prediction of confirmed, deaths and recovered case of COVID-19 in India

Fig. 6.

Prediction of confirmed, deaths and recovered case of COVID-19 in India

Fig. 7.

Prediction of confirmed case of COVID-19 in India

Fig. 8.

Prediction of confirmed cases of COVID-19 in India

Fig. 10.

Prediction of confirmed, deaths and recovered case of COVID-19 in India

Fig. 11.

Prediction of deaths case of COVID-19 in India

Fig. 12.

Prediction of deaths case of COVID-19 in India

Fig. 13.

Prediction of recovered case of COVID-19 in India

Fig. 14.

Prediction of recovered case of COVID-19 in India

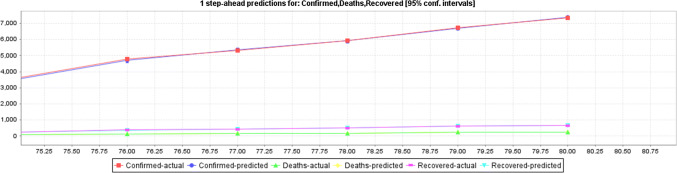
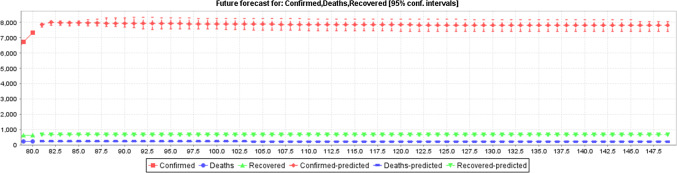
Figure 5 shows the COVID-19 predicted confirmed cases; death cases and recovered cases based on actual confirmed, death and recovered data with a 95% CI with LR.The graph can be interpreted that cases are going to be increased in future as per the existing case data.

Figure 6 shows the COVID-19 predicted confirmed cases; death cases and recovered cases based on actual confirmed, death and recovered data with a 95% CI with MLP. The graph using MLP can be interpreted that cases are going to be increased in future as per the existing case data.

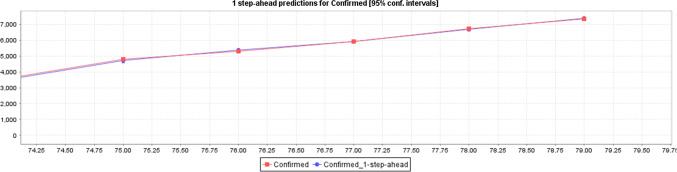
Figure 7 shows the predicted confirmed cases based on the actual confirmed case data with a 95% CI with LR. The graph using can be interpreted that confirmed cases are going to be increased in future as per the existing case data by utilizing LR.

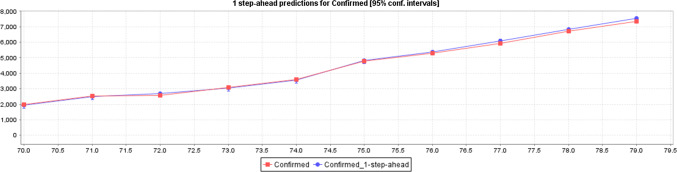
Figure 8 shows the predicted confirmed cases based on the actual confirmed case data with a 95% CI with MLP. The graph using MLP shows prediction of confirmed cases in a incremental range based on the existing data of 80 days.

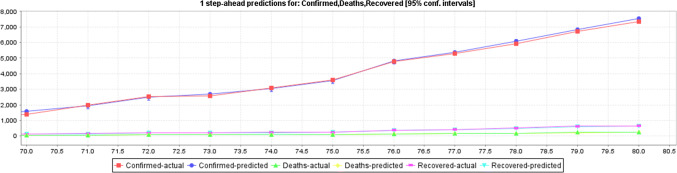
Figure 9 shows the predicted impacts of COVID-19 based on the actual data of confirmed, death and recovered cases with 95% CI via LR. In this figure also it is showing that the confirmed cases will be increasing day by day based on the input data, system shows this prediction.

Fig. 9.

Prediction of confirmed, deaths and recovered case of COVID-19 in India

Figure 10 predicts the impacts of COVID-19 based on the actual data of confirmed, death and recovered cases with 95% CI through MLP. This graph shows the confirmed cases will go down with a very slow rate and the recovered and death records will fluctuate (i.e. some times more some times less) as per prediction with MLP.

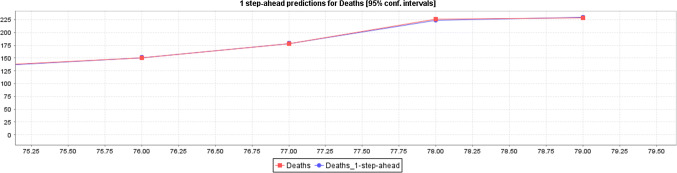
Figure 11 shows the predicted impacts of COVID-19 death based on the actual data of death cases with 95% CI through LR. The graph can be interpreted that cases are going to be increased in future as per the existing case data.

Figure 12 shows the predicted impacts of COVID-19 death based on the actual data of death cases with 95% CI through MLP. The Fig. 12 can be interpreted that cases are going to be increased in future as per the existing case data.

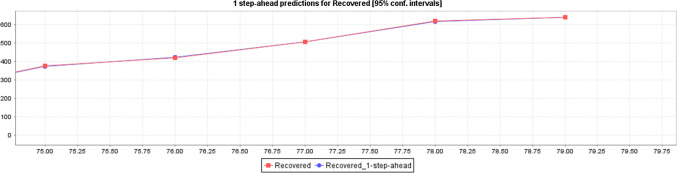
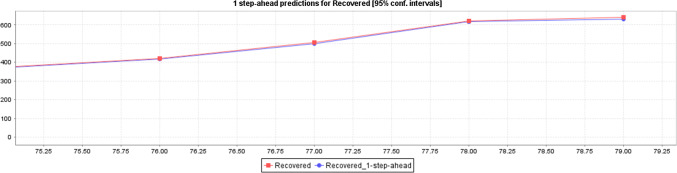
Figure 13 shows the predicted impacts of COVID-19 recovered based on the actual data of recovered cases with 95% CI through LR. By analyzing the Figs. 13 and 14 we can understand the cases are going to increase in future.

Figure 14 shows the predicted impacts of COVID-19 recovered based on the actual data of recovered cases with 95% CI with MLP.

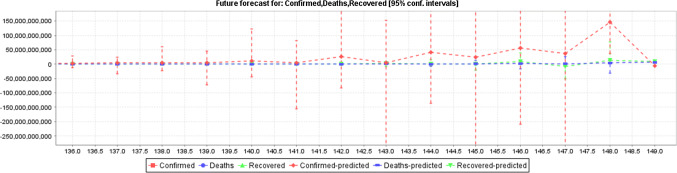
Figure 15 shows the forecast of next 69 days in the VAR model, where auto regression order is 10, with AIC optimize information criteria with constant and linear trend vectors and CI of 95% for the confirmed, recovered and death cases are illustrated in perfect manner.

Fig. 15.

Forecast of confirmed, deaths and recovered cases of COVID-19 using VAR model

We have given data of cases till the 80th day i.e. 10th April 2020. Table 1 shows the predicted values of cases (confirmed, death, recovered) by using the LR method from the 81st day i.e. 11th April 2020 for the next 69 days, i.e. 18th June 2020.These are the predicted values as per the actual values given in the system as an input. The Figs. 5,7,9,11,13 are generated based on the predicted values of Table 1.

Table 1.

Shows the predictions based on LR method

Day	Confirmed	Death	Recovered	Day	Confirmed	Death	Recovered
81*	7808.92	302.19	700.13	116*	22,104,623.27	491,914.12	1,832,867.82
82*	11,917.99	376.67	905.87	117*	12,262,871.21	824,095.54	297,887.88
83*	12,305.59	467.58	989.58	118*	32,223,941.03	907,747.97	2,883,964.11
84*	19,453.07	549.53	1377.01	119*	26,088,053.5	1,287,627.26	888,706.29
85*	18,735.18	712.15	1498.23	120*	45,318,195.77	1,546,165.90	3,910,095.79
86*	28,397.71	737.36	2008.82	121*	54,270,550.5	2,061,914.87	2,539,226.34
87*	26,173.88	1047.01	2211.58	122*	59,663,263.01	2,781,901.17	5,430,282.76
88*	40,693.32	1057.98	3010.66	123*	110,115,023.1	3,000,087.83	4,623,105.04
89*	33,589.51	1585.92	3068.47	124*	76,564,011.72	5,338,945.62	8,908,021.65
90*	58,063.80	1494.88	4390.64	125*	208,913,310.2	4,407,109.34	8,437,084.42
91*	40,907.15	2391.34	4007.60	126*	105,018,921.6	9,184,659.21	11,316,096.25
92*	89,552.70	2136.28	6300.44	127*	376,179,905.9	7,977,681.74	21,693,542.93
93*	56,788.32	3703.99	5452.63	128*	147,903,976.7	14,566,390.58	8,248,606.34
94*	150,798.48	3209.93	10,169.88	129*	678,769,292.3	13,945,117.80	44,782,374.75
95*	84,839.09	5786.47	7729.75	130*	206,994,172.5	26,395,041.51	15,096,328.41
96*	245,521.95	4756.97	16,783.85	131*	1,175,630,806	20,155,810.16	61,306,415.72
97*	110,746.31	8962.08	10,547.63	132*	421,594,206.9	48,380,620.38	43,388,724.32
98*	379,351.00	6708.71	25,592.98	133*	1,789,529,536	37,486,842.02	105,515,960.70
99*	136,377.15	14,375.22	14,343.03	134*	1,126,792,896	68,783,982.59	26,769,355.21
100*	598,986.64	9748.22	39,795.53	135*	2,580,310,966	90,083,114.30	267,434,162.00
101*	170,331.70	22,784.25	18,615.60	136*	2,401,726,195	95,456,946.49	− 18,098,564.29
102*	971,945.81	14,914.70	66,243.59	137*	4,155,239,685	155,874,755.40	376,863,037.50
103*	209,563.81	35,443.29	22,243.92	138*	4,596,816,690	204,946,361.70	295,475,200.70
104*	1,582,344.50	22,716.37	108,988.04	139*	5,870,415,755	213,046,626.20	134,340,612.00
105*	273,441.95	57,045.16	29,503.02	140*	11,389,299,953	365,128,230.40	876,857,511.40
106*	2,554,815.59	34,492.39	173,119.92	141*	4,443,897,350	513,873,083.10	518,780,412.90
107*	392,236.07	92,077.13	39,887.79	142*	26,615,311,366	318,858,077.70	315,344,811.50
108*	4,055,694.90	55,634.96	281,763.93	143*	4,794,077,579	1,258,132,358.00	2,388,354,024.00
109*	621,204.29	143,073.14	38,787.96	144*	40,877,363,141	546,815,772.40	642,559,825.80
110*	6,384,538.94	94,691.93	469,386.54	145*	24,332,062,371	1,478,635,685.00	169,239,745.10
111*	1,186,337.43	223,901.79	45,310.66	146*	56,499,628,059	2,480,287,744.00	9,428,815,852.00
112*	9,940,794.97	156,602.73	741,368.58	147*	37,206,760,856	1,242,023,613.00	− 7,853,630,454.00
113*	2,527,199.24	359,381.03	115,300.62	148*	1.47E+11	3,855,234,852.00	14,455,120,851.00
114*	15,004,728.39	263,425.62	1,132,663.46	149*	− 5,379,178,982	6,269,977,109.00	8,869,259,975.00
115*	5,562,688.14	555,114.01	206,747.76

* System generated symbol for future case prediction

We have given data of cases till the 80th day i.e. 10th April 2020. Table 2 shows the predicted values of cases (confirmed, death, recovered) by using MLP method from the 81st day i.e. 11th April 2020 for the next 69 days, i.e. 18th June 2020. These are the system predicted values as per the actual values given as an input.

Table 2.

Shows the predictions based on MLP method

Day	Confirmed	Death	Recovered	Day	Confirmed	Death	Recovered
81*	7868.83	236.43	661.55	116*	7852.39	233.64	658.98
82*	8002.83	234.33	655.87	117*	7849.97	233.62	658.91
83*	7993.54	234.73	658.10	118*	7847.64	233.61	658.84
84*	7983.92	234.54	660.42	119*	7845.40	233.60	658.78
85*	7977.48	233.99	658.43	120*	7843.25	233.59	658.72
86*	7964.45	234.59	662.30	121*	7841.18	233.58	658.67
87*	7962.95	234.54	662.87	122*	7839.19	233.57	658.62
88*	7958.09	234.76	664.45	123*	7837.27	233.56	658.57
89*	7955.03	234.71	664.34	124*	7835.44	233.55	658.53
90*	7950.54	234.61	663.84	125*	7833.68	233.54	658.49
91*	7944.50	234.55	663.55	126*	7831.99	233.54	658.45
92*	7940.39	234.45	663.11	127*	7830.38	233.53	658.41
93*	7934.87	234.40	662.82	128*	7828.83	233.52	658.38
94*	7930.32	234.33	662.52	129*	7827.35	233.52	658.35
95*	7925.56	234.28	662.25	130*	7825.93	233.51	658.32
96*	7921.09	234.23	662.00	131*	7824.57	233.51	658.30
97*	7916.78	234.17	661.75	132*	7823.28	233.50	658.28
98*	7912.50	234.13	661.52	133*	7822.04	233.50	658.25
99*	7908.35	234.08	661.30	134*	7820.86	233.49	658.23
100*	7904.26	234.04	661.08	135*	7819.73	233.49	658.22
101*	7900.27	234.00	660.88	136*	7818.65	233.49	658.20
102*	7896.38	233.97	660.70	137*	7817.63	233.48	658.18
103*	7892.59	233.93	660.52	138*	7816.65	233.48	658.17
104*	7888.89	233.90	660.35	139*	7815.72	233.48	658.15
105*	7885.30	233.87	660.19	140*	7814.83	233.47	658.14
106*	7881.81	233.84	660.04	141*	7813.99	233.47	658.13
107*	7878.42	233.81	659.90	142*	7813.19	233.47	658.12
108*	7875.13	233.79	659.77	143*	7812.42	233.47	658.11
109*	7871.95	233.76	659.65	144*	7811.70	233.46	658.10
110*	7868.86	233.74	659.53	145*	7811.01	233.46	658.09
111*	7865.87	233.72	659.42	146*	7810.36	233.46	658.09
112*	7862.98	233.70	659.32	147*	7809.74	233.46	658.08
113*	7860.19	233.69	659.23	148*	7809.15	233.46	658.07
114*	7857.50	233.67	659.14	149*	7808.59	233.46	658.07
115*	7854.90	233.65	659.06

* System generated symbol for future case prediction

Figure 15 gets its waves of the different cases from the Table 3 values for the next 69 days. It depends on the various parameters mentioned in the VAR model part.

Table 3.

Shows the predictions based on VAR model

Day	Confirmed	Death	Recovered	Day	Confirmed	Death	Recovered
81*	10,601.4	332.18	976.70	116*	2.89E+06	78,492.7	240,238
82*	13,682.6	411.19	1042.98	117*	4.80E+06	145,552	309,526
83*	14,583.5	466.62	1308.17	118*	9.40E+06	297,229	758,623
84*	15,670.2	428.87	1309.26	119*	8.11E+06	235,470	692,976
85*	17,289.3	492.20	1241.68	120*	6.04E+06	193,805	745,716
86*	26,698.6	810.59	2056.95	121*	6.85E+06	233,995	442,027
87*	31,760.5	953.46	2386.76	122*	9.54E+06	307,906	709,591
88*	35,231.7	1072.63	3411.28	123*	2.18E+07	622,641	1.84E+06
89*	39,492	1273.61	3265.65	124*	2.27E+07	690,473	1.71E+06
90*	38,830	1315.47	3508.82	125*	1.77E+07	667,861	2.09E+06
91*	57,657.9	1709.69	5079.78	126*	1.01E+07	281,826	919,611
92*	74,883.1	2177.42	5717.68	127*	1.76E+07	478,183	1.27E+06
93*	90,441.8	2909.22	7926.20	128*	5.75E+07	1.78E+06	4.03E+06
94*	88,489.4	2678.05	7646.36	129*	5.71E+07	1.78E+06	4.50E+06
95*	81,119.5	2391.89	7367.93	130*	4.28E+07	1.35E+06	5.84E+06
96*	144,087	4490.57	11,003.00	131*	2.25E+07	726,654	1.44E+06
97*	182,798	5795.74	13,562.70	132*	3.65E+07	1.43E+06	2.60E+06
98*	220,192	6739.28	21,021.00	133*	1.25E+08	3.53E+06	9.28E+06
99*	219,219	6673.90	18,613.50	134*	1.46E+08	4.05E+06	1.11E+07
100*	203,958	6921.17	17,655.90	135*	1.43E+08	5.05E+06	1.56E+07
101*	304,566	9356.79	25,456.60	136*	3.29E+07	1.38E+06	3.15E+06
102*	396,012	10,950.90	29,537.20	137*	2.68E+07	620,297	4.73E+06
103*	578,127	18,324.10	50,406.70	138*	3.00E+08	8.46E+06	1.75E+07
104*	544,025	17,748.50	45,620.00	139*	4.05E+08	1.29E+07	2.85E+07
105*	408,893	13,309.40	45,703.90	140*	3.75E+08	1.21E+07	4.57E+07
106*	691,638	20,597.70	55,518.50	141*	3.53E+07	519,601	6.14E+06
107*	1.00E+06	31,899.50	67,072.50	142*	4.49E+07	3.59E+06	6.05E+06
108*	1.43E+06	44,894.90	131,165.00	143*	6.30E+08	1.85E+07	3.30E+07
109*	1.27E+06	35,749.80	108,128.00	144*	9.33E+08	2.54E+07	7.16E+07
110*	1.06E+06	35,896.80	106,105.00	145*	1.18E+09	3.69E+07	1.20E+08
111*	1.54E+06	49,980.20	113,224.00	146*	1.71E+08	1.03E+07	1.80E+07
112*	2.02E+06	58,017.90	153,112.00	147*	− 2.69E+08	− 4.59E+06	1.51E+07
113*	3.61E+06	108,192.00	315,139.00	148*	1.12E+09	2.51E+07	4.03E+07
114*	3.52E+06	115,126.00	273,612.00	149*	2.62E+09	8.07E+07	1.68E+08
115*	2.42E+06	88,497.50	301,755.00

* System generated symbol for future case prediction

Conclusion

Information and communication technology help in the decision-making process based on the past data with the data analytics and data mining perspective. The size of data available is huge and gathering information and getting an interesting pattern out of the cumulated data is a challenging task. With the prevailing data about confirmed, recovered and death across India for over the time duration helps in predicting and forecasting the near future. The correctness of the model could be increased by introducing related attributes like several hospitals, the immune system of the infected person, age of the patient, gender of the patient, steps taken to combat the proliferation of the virus, and so on to make it completely informative. As of now, it's very prudent that yards to carry needs to be stringent and vigil in nature to handle this crucial situation by social distancing, lockdown, curfew, quarantine, and isolation to prevent the transmission. By seeing the predicted values and matching with cases from John Hopkins University11 data we can conclude that the MLP method is giving good prediction results than that of the LR and VAR method using WEKA and Orange. In future we can work with some deep learning methods for forcasting time series data for getting better predictions.

Author contributions

All the authors have made substantive contributions to the article and assume full responsibility for its content.

Compliance with ethical standards

Conflict of interest

The authors declare that we don’t have any conflict of Interest.