Abstract
The SARS-CoV-2 virus causes the disease COVID-19, and has caused high morbidity and mortality worldwide. Empirical models are useful tools to predict future trends of disease progression such as COVID-19 over the near-term. A modified Incidence Decay and Exponential Adjustment (m-IDEA) model was developed to predict the progression of infectious disease outbreaks. The modification allows for the production of precise daily estimates, which are critical during a pandemic of this scale for planning purposes. The m-IDEA model was employed using a range of serial intervals given the lack of knowledge on the true serial interval of COVID-19. Both deterministic and stochastic approaches were applied. Model fitting was accomplished through minimizing the sum-of-square differences between predicted and observed daily incidence case counts, and performance was retrospectively assessed. The performance of the m-IDEA for projection cases in the near-term was improved using shorter serial intervals (1–4 days) at early stages of the pandemic, and longer serial intervals at mid- to late-stages (5–9 days) thus far. This, coupled with epidemiological reports, suggests that the serial interval of COVID-19 might increase as the pandemic progresses, which is rather intuitive: Increasing serial intervals can be attributed to gradual increases in public health interventions such as facility closures, public caution and social distancing, thus increasing the time between transmission events. In most cases, the stochastic approach captured the majority of future reported incidence data, because it accounts for the uncertainty around the serial interval of COVID-19. As such, it is the preferred approach for using the m-IDEA during dynamic situation such as in the midst of a major pandemic.
Keywords: Forecasting/methods, Models, Statistical, Communicable diseases/epidemiology, SARS coronavirus-2, COVID-19
1. Introduction
The SARS-CoV-2 virus causes the disease COVID-19, and has caused high morbidity and mortality worldwide (WHO, 2020; Wu, Zhao, et al., 2020, Wu, Leung, et al., 2020). COVID-19 was first reported in Canada on January 25, 2020 (COVID-19 Canada Open Data Working Group, 2020). This case, and many subsequent cases over the following weeks, were linked to international travel (COVID-19 Canada Open Data Working Group, 2020). The WHO declared COVID-19 as a pandemic on March 11, 2020—the same day that the case total reported in Canada exceeded 100 (Government of Canada, 2020). It might never be known precisely when community transmission of the disease originally occurred in Canada, but the first documented case was reported on March 1, 2020 (COVID-19 Canada Open Data Working Group, 2020). However, it is likely that community transmission had occurred at some point before this date.
As of May 15, 2020, cumulative cases of COVID-19 continue to climb in Canada, with variations in the trends of reported cases among provinces and territories (Government of Canada, 2020). There is a need for mathematical models to provide projections of future incidence and cumulative cases in Canada to assist with decision-making. During the early-to mid-stages of a novel epidemic or pandemic, very little is known of the specific mechanisms of transmission of disease—this is a global issue for COVID-19. Empirical models are useful tools to predict future trends of disease progression such as case counts over the near-term. Many empirical models are available for such projections, with varying degrees of success in projecting cases in past outbreaks of infectious disease (e.g. Chowell et al., 2016; Xiao et al., 2013).
The Incidence Decay and Exponential Adjustment (IDEA) model was first published in 2013 as a simple phenomenological model to predict the progression of infectious disease outbreaks (Fisman, Hauck, Tuite, & Greer, 2014). It has since been shown to perform comparably to other approaches for projecting case counts of Ebola (Tuite & Fisman, 2018), and has fit well to observed case counts of Middle East Respiratory Syndrome (Fisman, Rivers, Lofgren, & Majumder, 2014), Zika virus (Majumder et al., 2016; Ogden et al., 2017), and animal diseases (Gardner, Ali, Kayali, Kelton, & Greer, 2016; Greer, Spence, & Gardner, 2017). The IDEA model was developed on the premise of the interaction of the basic reproduction number of the disease (R0) and d, the latter of which is discount factor that can represent, for example, interventions implemented to curb the spread of disease (Fisman, Hauck, et al., 2014; Fisman, Rivers, et al., 2014). In part because it does not require detailed mechanistic information on disease transmission, it has recently been suggested for “quick and dirty” forecasting in the face of an infectious disease epidemic (Tuite & Fisman, 2018). While the model has several limitations, it can provide a complement to mechanistic approaches, with the advantage of being easily and rapidly applied by public health officials (Tuite & Fisman, 2018).
The IDEA model is parameterized on the basis of the serial interval of the disease in question. The serial interval of an infectious disease describes the period of time between successive cases. Specifically, it is defined as the interval between the clinical onset (onset of symptoms) in a primary case and the clinical onset in a secondary case (Fine, 2003; Moghadas & Milwid, 2016; Nishiura, Linton, & Akhmetzhanov, 2020b; Vink, Bootsma, & Wallinga, 2014). Biological variables determining the serial interval include the time needed for disease transmission to occur, relative to the time of clinical onset in the primary case, and the incubation period in the secondary case, which is the period of time between infection and clinical onset (Fine, 2003). The serial interval can be calculated as the sum of these two values (Fine, 2003). Serial intervals shorter than the median incubation period often result when transmission is possible prior to the development of symptoms in the primary case (Fine, 2003). This is the case with infections such as human immunodeficiency virus/acquired immunodeficiency syndrome (HIV/AIDS) and hepatitis A (APHA, 2000).
Given that the IDEA model is one tool used for producing near-term projections of cases of COVID-19 (Smith et al., 2020, submitted), the goal of this study was to explore the impact of the assumed serial interval for COVID-19 on projection accuracy using a retrospective analysis. This was accomplished by producing projections of cases seven days into the future at various stages of the pandemic in Canada. The modified IDEA (m-IDEA) model approach was developed from the original IDEA model described by (Fisman, Hauck, et al., 2014) to instead project incident cases on a daily basis.
2. Methods
The modified Incidence Decay and Exponential Adjustment model approach
The original IDEA model (Fisman, Hauck, et al., 2014) is dependent on the serial interval for the disease:
| (1) |
Where represents the incidence of disease in one generation of the disease (defined by the serial interval), R0 is the reproduction number, d is a discount factor that can represent the impact of public health measures to limit the impact of the disease spread, and g represents the disease generation (the original IDEA model classified this as t, but it is referred to as g herein to avoid confusion with subsequent equations). While the IDEA model compares predicted cases versus reported cases aggregated by serial interval (g has historically been an integer value), the approach was modified to provide case projections on a daily basis.
The generation of the disease, g, is defined as:
| (2) |
Where t represents time in days, and SerInt represents the serial interval of the disease in days. This parameterization allows for g to represent continuous rather than discrete values, dependent on SerInt. I(g) is calculated at each day, t, and returns the number of cases occurring between t - SerInt and t. Cumulative cases at time t is then determined by summing each I(g) calculated every corresponding serial interval from t = 0 through t:
| (3) |
Where represents the first determination of since the beginning of the pandemic, and represents the most recent determination of to date. Finally, daily incidence was calculated as:
| (4) |
In what follows, the m-IDEA model is defined to be the collection of Equations (1)–(4). The m-IDEA model is a re-parameterization of the IDEA model and uses an approach that allows for calculation of precise daily estimates. For example, if one assumes a serial interval of seven days for a given disease, the original IDEA model returns estimates of incidence for each week-long period. So, the IDEA model calculates the total cases aggregated by disease generation, that is, total cases occurring between Days 0–6, 7–13, 14–20, etc. As a result, it is impossible to determine the precise number of cases predicted for a single day. The modified approach allows for g to comprise intra-generational values, and precise daily estimates are determined through Equations (3), (4).
The m-IDEA model was used to project daily case incidence using a range of serial intervals given the lack of knowledge on the true serial interval of COVID-19 at this time. It is unknown precisely when the first community-acquired case of COVID-19 occurred in Canada. It was assumed for this analysis that community transmission was occurring on or before March 11, 2020 simply (and subjectively) because it was the day when reported cumulative cases in Canada exceeded 100. A simple back-calculation from this date, assuming an a priori R0 of 2, was conducted to anchor the model so that March 11, 2020 corresponded to generation 6 of the disease in Canada. The assumed occurrence of the first case of community-acquired COVID-19 in Canada was therefore dependent on the serial interval used.
The m-IDEA model was implemented in Microsoft Excel with the add-ins @Risk version 8.0 and Evolver version 8.0 (Palisade Corporation, New York, USA) to allow for Monte Carlo simulation using Latin Hypercube Sampling and optimization of model parameters. Optimization of R0 and d parameters was accomplished through minimizing the sum-of-square differences between predicted and observed daily incidence case counts. This least-squares fitting method was performed using the past twenty days of observed data, aside from the first three projection days, which only used 5, 10, and 15 days worth of data, respectively, since that was all that was available from March 11 onwards. Near-term projections using the m-IDEA model were made every five days using data from projection day (PD) 0 (March 11, 2020) through to PD 55 (May 4, 2020). The first projection occurred on PD 5, and considered data reported from March 11, 2020 through March 15, 2020, whereas the last projection is referred to as PD 55 and considered data reported from April 15, 2020 through May 4, 2020. Case data were downloaded from www.Canada.ca on May 11, 2020. On May 3, 2020, the Quebec government announced that new case totals reported that day included 1,317 previously unreported cases from April. Therefore, incidence on May 3, 2020 was reduced by 1,317 cases to account for this reporting error. Model parameter solutions were derived for a range of discrete integer serial interval values on each PD using the OptQuest optimization function in Evolver such that optimization results remained stable, defined as within 0.01% for 20,000 consecutive trials. The OptQuest engine uses methods of tabu search, scatter search, integer programming, and neural networks in a novel algorithm.
To provide a comparative visual of projections produced by both the original IDEA model and the m-IDEA, fitting was performed as described above, except it was performed on all data reported from March 11, 2020 through May 10, 2020, arbitrarily assuming a five day serial interval. The entire dataset was used because limiting data to only the past 20 days of reporting resulted in too few data points to fit the IDEA model.
Following analysis of the deterministic serial interval values, a stochastic approach was considered. Fitting was generally performed using the same procedure as for deterministic serial intervals. However, the serial interval used on each PD was allowed to range uniformly from either 1–4 days or 5–9 days, given the results of the deterministic approach. To derive 90% prediction intervals and minimum and maximum estimates, a Poisson error structure in the reported data was assumed. Monte Carlo simulations with Latin Hypercube Sampling were performed for 1,000 iterations to consider both the impact of total uncertainty of the serial interval of COVID-19 as well as the reported case data; for computational practicality the parameter values were considered stable if they remained within 0.01% for 500 trials (rather than the 20,000 trials used for deterministic simulations).
For each PD, daily incident cases projected for seven days in the future were compared with actual case counts reported since the date of projection (e.g., PD 5 projections made using data up to March 15, 2020 were compared with cases reported on March 16 through March 22, 2020) using the root mean square error (RMSE):
| (5) |
Where is the reported value at time t, is the model projection at time t, and n is the number of observations.
3. Results
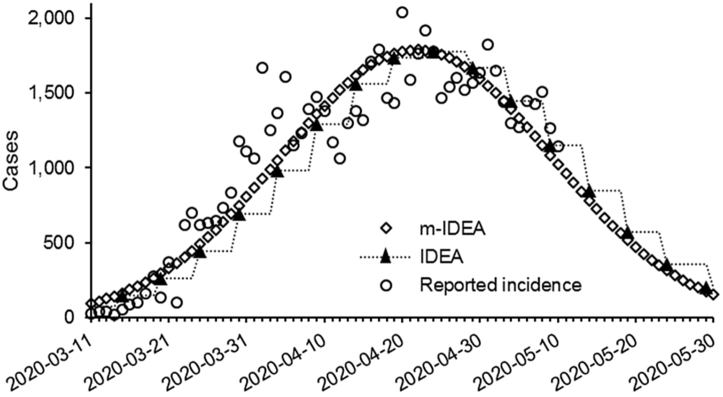
A plot of predicted incidence produced by the original IDEA and m-IDEA models using a five day serial interval and reported incidence through May 10, 2020 is provided in Fig. 1. The re-parameterization of the IDEA model to the m-IDEA approach results in a smooth fit between whole number generations of the disease. Predicted values by the IDEA model are interpolated using a step-wide function to allow for clear visualization of differences between the two curves (rather than linear interpolation, which would obscure the curves). R0 and d values were 3.43 and 0.043, respectively, for both models. Both models indicated a decline in new cases of COVID-19 in Canada through May 2020.
Fig. 1.
A comparison of the IDEA versus the m-IDEA model results assuming a serial interval of five days for COVID-19, and fit to reported case data from March 11, 2020 through May 10, 2020. See text for full description on modelling procedure.
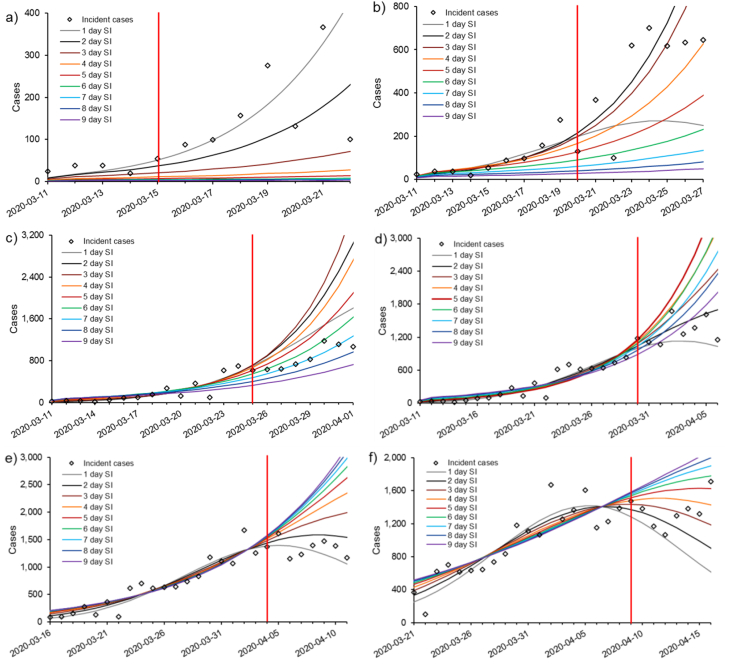
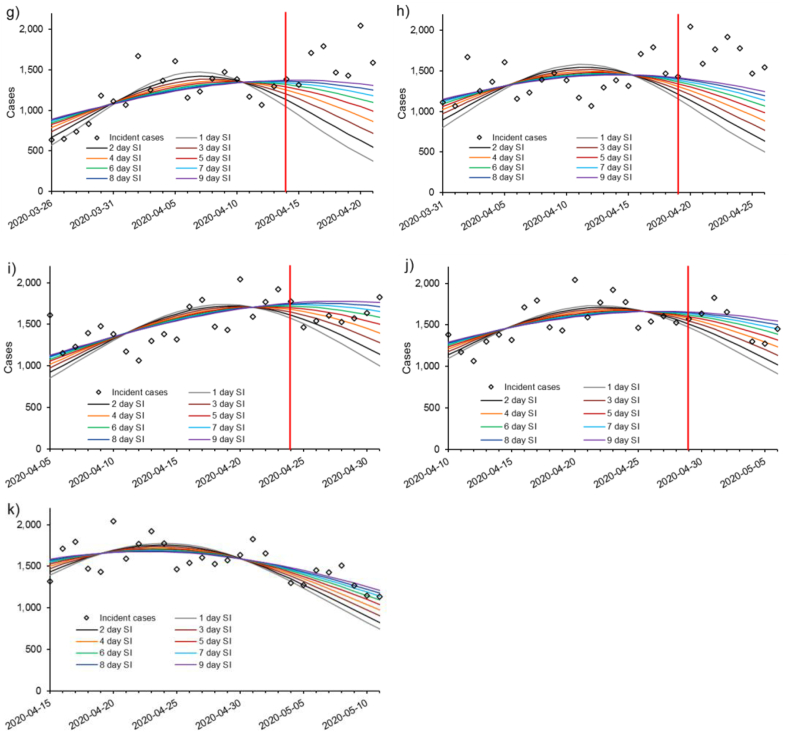
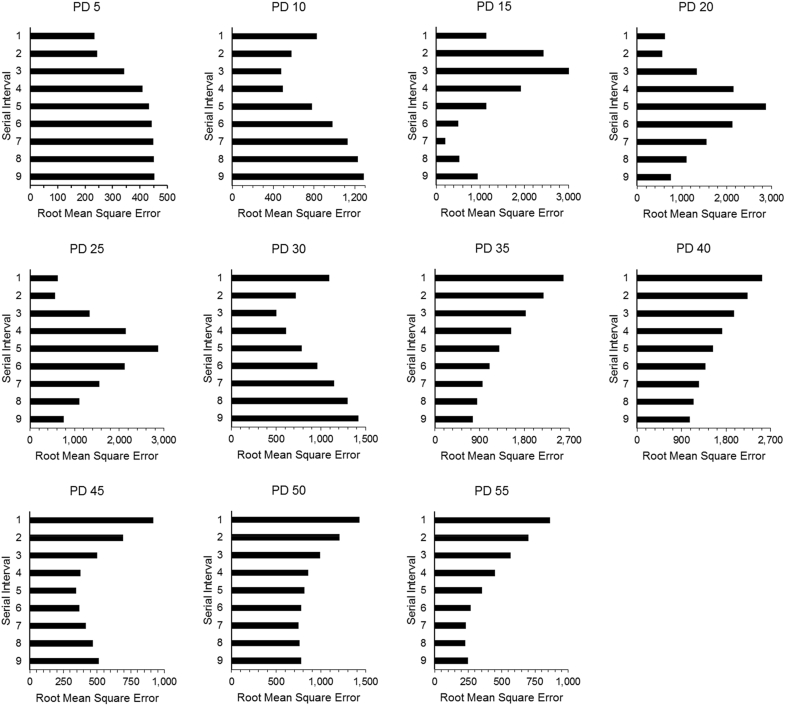
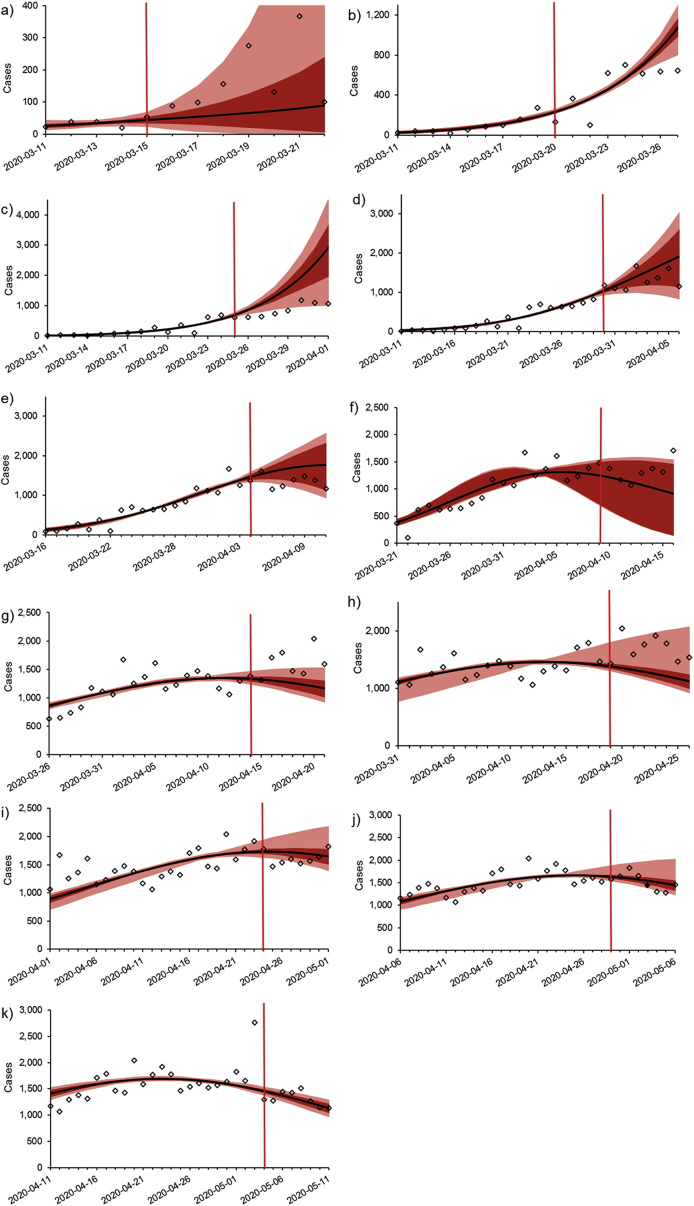
Best fit seven-day projections for each serial interval produced each PD are plotted in Fig. 2. The associated R0 and d values are provided in Table 1, and model performance in Fig. 3. Estimated R0 parameters tended to increase with serial interval; however, in most cases, the control parameter, d, also increased with serial interval (Table 1). Generally, the serial intervals that provided the best fits were variable throughout the first two weeks of the projection period. Once a full 20 days of data had accumulated for fitting, lower serial intervals (1–4 days) provided better predictive capability through PD 30. However, from PD 35 onward, in most cases higher serial intervals (5–9 days) were associated with better projection performance (Fig. 3), and serial intervals ranging from 1 to 4 days considerably under-predicted future incidence in the near-term.
Fig. 2.
Best-fit curves of the m-IDEA model at various stages of the pandemic in Canada. See text for full details on the fitting procedure. Projected trajectory was dependent on the serial interval used on the model. Projections were made every five days using data reported since March 11, 2020. All incidence data up to and including the vertical red line were used to fit the model. Incidence data reported since the projections were made are plotted to the right of the vertical red line. See the online version of this article for colour. a) projection day (PD) 5; b) PD 10; c) PD 15; d) PD 20; e) PD 25; f) PD 30; g) PD 35; h) PD 40; i) PD 45; j) PD 50; k) PD 55.
Table 1.
Best fit parameters for each discrete serial interval (SerInt) used in the m-IDEA model for each projection day (PD). See text for details on the fitting procedure used and reported case data considered for each projection. Corresponding charts are available in Fig. 2.
| PD 5 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.56 | 1.69 | 1.71 | 1.68 | 1.64 | 1.60 | 1.57 | 1.55 | 1.54 |
| D | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PD 10 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.77 | 1.88 | 1.99 | 2.13 | 2.21 | 2.22 | 2.20 | 2.16 | 2.11 |
| D | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PD 15 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.60 | 1.93 | 2.01 | 2.23 | 2.40 | 2.54 | 2.63 | 2.70 | 2.73 |
| D | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PD 20 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.63 | 2.16 | 2.43 | 2.46 | 2.35 | 2.51 | 2.65 | 2.77 | 2.87 |
| D | 0.01 | 0.02 | 0.02 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PD 25 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.60 | 2.20 | 2.67 | 3.01 | 3.23 | 3.34 | 3.38 | 3.36 | 3.29 |
| D | 0.01 | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 |
| PD 30 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.59 | 2.25 | 2.86 | 3.39 | 3.84 | 4.20 | 4.49 | 4.71 | 4.87 |
| D | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 |
| PD 35 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.56 | 2.23 | 2.91 | 3.57 | 4.19 | 4.77 | 5.30 | 5.79 | 6.23 |
| D | 0.01 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.09 |
| PD 40 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.48 | 2.08 | 2.71 | 3.35 | 3.99 | 4.61 | 5.21 | 5.79 | 6.33 |
| D | 0.01 | 0.02 | 0.03 | 0.04 | 0.06 | 0.07 | 0.08 | 0.09 | 0.09 |
| PD 45 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.40 | 1.87 | 2.38 | 2.89 | 3.39 | 3.88 | 4.34 | 4.78 | 5.19 |
| D | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.07 |
| PD 50 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.37 | 1.81 | 2.29 | 2.79 | 3.29 | 3.79 | 4.27 | 4.75 | 5.20 |
| D | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.07 |
| PD 55 | |||||||||
| SerInt (days) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R0 | 1.35 | 1.78 | 2.27 | 2.78 | 3.32 | 3.88 | 4.44 | 5.01 | 5.58 |
| D | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 |
Fig. 3.
Measure of fits for m-IDEA model 7-day projections using discrete serial intervals. See text for details on the fitting procedure used and reported case data considered for each projection day (PD). Corresponding charts are available in Fig. 2. A lower root mean square error is indicative of relatively better projection performance.
Results from the stochastic approach to incorporate uncertainty in the serial interval used in the m-IDEA are provided in Fig. 4. Serial intervals were allowed to range uniformly from 1 through 4 days for PDs 5 through 30, and 5 through 9 days for PDs 35 through 55, because these ranges generally included the best fit discrete serial intervals in Fig. 3. This approach provides large prediction intervals and ranges between minimum and maximum values due to the incorporation of a range of serial intervals. In most cases, this approach captures the majority of future reported incidence data, with some notable exceptions on PD 10, 15, and 35.
Fig. 4.
Mean seven-day projections using a stochastic m-IDEA model at various stages of the pandemic in Canada. See text for full details on the fitting procedure. Projections were made every five days using data reported since March 11, 2020. All incidence data up to and including the vertical red line were used to fit the model. Incidence data reported since the projections are plotted to the right of the vertical red line. a) projection day (PD) 5; b) PD 10; c) PD 15; d) PD 20; e) PD 25; f) PD 30; g) PD 35; h) PD 40; i) PD 45; j) PD 50; k) PD 55. Plots for PDs 5 through 30 (a-f) were derived with a uniformly distributed serial interval ranging from one to four days, and assuming a Poisson error structure in reported data. Plots for PDs 35 through 55 reflect a serial interval ranging from five through nine days, also assuming a Poisson error structure in reported data. 90% prediction intervals and minimum and maximum predicted values are indicated in shaded red and pink, respectively.
4. Discussion and conclusion
Producing daily projections using the IDEA equation previously required simplifying assumptions of the inter-generational trend of cases. A step-wise approach was used in Fig. 1 to better illustrate the differences between the IDEA and m-IDEA models, but it is also possible to scale inter-generational values assuming an equivalent daily incidence within each serial interval (Tuite & Fisman, 2018). Regardless, the scaling of the IDEA model in whole number “generation times” has been previously recognized as a limitation that results in staggered forecasts (Tuite & Fisman, 2018). The m-IDEA model precludes these simplifying assumptions and produced daily incidence estimates using the IDEA model function. This allows for prediction of daily confirmed cases, which are critical during a pandemic of this scale for planning purposes.
The IDEA model operates under the premise that an epidemic follows first-order exponential growth with simultaneous second-order decay (Fisman, Hauck, et al., 2014; Fisman, Rivers, et al., 2014). Prior studies using the original IDEA model have determined that the model fit is impacted by the serial interval used (Ogden et al., 2017). This is the first approach, however, where the impact of serial interval over time has been examined, particularly in the midst of an epidemic (or pandemic, in this case). The assumed serial interval of COVID-19 had an impact on accuracy of near-term projections of reported cases using the m-IDEA model. A range of serial intervals were examined herein to reflect possible values gleaned from the literature. Reported serial intervals of COVID-19 ranged from 1 to 8.9 days, with the majority of values between 4 and 6 days (Bi et al., 2020; Böhmer et al., 2020; Du, Wang, et al., 2020; Du, Xu, et al., 2020; Fan, Liu, Pan, Douglas, & Bao, 2020; Gan et al., 2020; Ganyani et al., 2020; Huang et al., 2020; Ji et al., 2020; Ki, 2020; Klausner, Fattal, Hirsch, & Shapira, 2020; Li, Chen, Yuan, Song, & Ma, 2020; Li, Guan, et al., 2020; Liao et al., 2020; Liu, Liao, et al., 2020; Liu, Wu, et al., 2020; Liu, Li, et al., 2020; Liu, Bi, et al., 2020; Lytras, Panagiotakopoulos, & Tsiodras, 2020; Ma et al., 2020; Mizumoto & Chowell, 2020; Nishiura, Linton, & Akhmetzhanov, 2020a; Nishiura et al., 2020b; Ping, 2020; Pung et al., 2020; Qian et al., 2020; Sun et al., 2020; Tindale et al., 2020; Wang & Teunis, 2020; Wu, Zhao, et al., 2020; Wu, Leung, et al., 2020; Xu et al., 2020; You et al., 2020; Zhang et al., 2020; Zhao, Cao, Chong et al., 2020; Zhao, Cao, Gao et al., 2020; Zhao, Gao et al., 2020). In studies specific to countries other than China, the serial interval ranged from 4 to 6.34 days (Böhmer et al., 2020; Bui, Nguyen Thanh, & Nguyen Ngoc, 2020; Ganyani et al., 2020; Ki, 2020; Klausner et al., 2020; Pung et al., 2020; Tindale et al., 2020; Zhao, Cao, Gao et al., 2020).
The performance of the m-IDEA for projection cases in the near-term was improved using shorter serial intervals (1–4 days) at early stages of the pandemic, and longer serial intervals at mid to late-stages (5–9 days). Correspondingly, studies examining pooled data from multiple countries reported median serial intervals ranging from 4 to 4.6 days between December 12, 2019 and February 5, 2020, and 6.7 days from February 20 to March 3, 2020 (Ma et al., 2020; Nishiura et al., 2020b). However, it is possible that other factors such as the exposure period of infectees and sample size could have contributed to the finding of a longer serial interval in the second time frame studied by Ma et al. (2020) and Nishiura et al. (2020b). This suggests that the serial interval of COVID-19 might increase as the pandemic progresses, which is rather intuitive and corresponds to the observations using the m-IDEA model. Increasing serial intervals can be attributed to gradual increases in public health interventions such as facility closures, public caution and social distancing, thus increasing the time between transmission events. From January 21 through February 8 2020, longer median serial intervals of 7.5–8.8 days were reported for Wuhan, China, whereas regions of China other than Wuhan reported 3.96 days. During this period, Wuhan’s lockdown measures were comparatively stricter (Du, Wang, et al., 2020; Lytras et al., 2020; Nishiura et al., 2020a). Best-fit projections at later PDs considered herein were associated with greater control parameter (d) values (but also greater R0 values) compared to shorter serial intervals.
The best-fit parameters for the m-IDEA model were dependent on the serial interval used. Generally, the estimated R0 and d parameters both increased with serial interval (Table 1). Projections made in mid-April (PD 35) were associated with the highest R0 values across the projection period when using serial intervals ranging from three to eight days. On its own, this could mistakenly be interpreted as an indication of increased disease transmission—which is contrary to expectations given that these projections were made approximately one month following implementation of public health measures across Canada. However, in most cases, d values were also greater compared to earlier PDs. This emphasizes that the m-IDEA is not a tool intended to produce R0 values in a vacuum, and R0 must be presented and considered hand-in-hand alongside its associated d value.
Given a lack of knowledge of the actual pandemic start date in Canada, March 11, 2020 was chosen as an anchoring point for COVID-19 community transmission in Canada for the m-IDEA model, corresponding to generation 6 of the disease. There is considerable uncertainty around the start date of community transmission in Canada. With this approach, the calculated start date varied with serial interval (i.e., a serial interval of 1 day corresponded with a start date of March 5, 2020, whereas a serial interval of 9 days corresponded with a start date of Jan 17, 2020), as well as the assumed R0 of the disease (a R0 of 2 was assumed a priori for this analysis). The impact of the assumed start date of the pandemic can have an influence on m-IDEA model projections: when March 11, 2020 was instead anchored to lower or higher generations relative to generation 6, resulting near-term projections for PD 55 (the only PD for which this was explored) were also lower and higher, respectively (results not shown). It is also likely that best fit serial intervals for each PD would vary with differing generation numbers anchored to March 11, 2020. Future work could explore these impacts more thoroughly.
Implementations of the IDEA model for Ebola were better able to predict the epidemic peak in West Africa compared to producing accurate short-term projections (Tuite & Fisman, 2018). The m-IDEA was unable to produce accurate short-term projections at early stages for the pandemic in Canada, which is unsurprising given the rapidly changing landscape of public health intervention and testing strategies during these early stages, as well as the lack of time-series data for fitting at early stages. The best fit serial intervals appeared to stabilize somewhat from PD 25 onwards. A comparison of three phenomenological models (the generalized Richard’s model, logistic, and stochastic m-IDEA models), showed that none of the models provided reasonable accurate projections in early March of 2020 (Smith et al., 2020, submitted).
The stochastic approach used can account for the uncertainty around the serial interval of COVID-19, and is preferred for the m-IDEA during a dynamic situation such as in the midst of a major pandemic. Various distributions of serial intervals coupled with a Poisson error structure in reported case data were implemented, and resultant distributions of case incidence were projected. This approach inherently accounts for correlation between m-IDEA parameters R0 and d. Through iterative fitting procedures, the incidence curves represent the 90% prediction intervals (and minimum and maximum) for each data point of each projection associated with specific solutions of R0 and d. This is more realistic than simply calculating the 5th and 95th percentiles of R0 and d across simulations and deriving prediction intervals, which would result in highly unlikely to impossible combinations of parameters.
It was shown here that the serial interval associated with the best fit of the m-IDEA model changes throughout the course of the COVID-19 pandemic in Canada. It is proposed that the serial interval used in the m-IDEA model be frequently updated through retrospective analysis of model performance, and modified where necessary for future projections. For example, here it was shown that lower and higher serial intervals produced more accurate projections at earlier and later stages, respectively, of the COVID-19 pandemic in Canada. Low serial intervals (1–4 days) projected considerably lower incidence than reported for future cases at the later stages of this study period. Although the IDEA model was not developed as a tool to predict the actual serial interval of a disease, the use of the m-IDEA provides evidence that the serial interval of COVID-19 at the national level in Canada has increased over the course of the pandemic. While the RMSE was used to assess model performance, it is possible that results could vary when using alternate error metrics. Caution is advised before adopting these same serial intervals for application of phenomenological models to other datasets, at the regional (e.g. provinces and territories) or international scale. A similar analysis should be conducted in other regions to determine the serial interval(s) that provides the best fit to date in an iterative manner.
It has been previously proposed that the IDEA model could implement “multiple time-specific control parameters” to improve forecasting (Tuite & Fisman, 2018). Until then, incorporating uncertainty through a stochastic approach to parameterize the serial interval is preferred, as it has been shown that the serial interval associated with more accurate near-term projections varied throughout the study period. Although this is somewhat akin to trying to “hit a moving target”, it is nevertheless preferable and more biologically plausible compared to assuming an identical, discrete value serial interval throughout the pandemic.
Declaration of competing interest
I have no conflicts of interest to declare.
Acknowledgments
I would like to thank the Knowledge Synthesis team members within the Public Health Risk Sciences Division of Public Health Agency of Canada. Their daily literature scans and summarization of Sars-CoV-2 publications contributed to the quick preparation of the work presented here. Thanks to Charly Phillips (Public Health Risk Sciences Division of Public Health Agency of Canada) for her assistance summarizing serial interval values from the literature.
Handling editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
References
- American Public Health Association (APHA) In: Control of communicable diseases manual. 17th ed. Chin J., editor. American Health Association; Washington, DC: 2000. [Google Scholar]
- Bi Q., Wu Y., Mei S., Ye C., Zou X., Zhang Z. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: A retrospective cohort study. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30287-5. 0(0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böhmer M.M., Buchholz U., Corman V.M., Hoch M., Katz K., Marosevic D.V. Outbreak of COVID-19 in Germany resulting from a single travel-associated primary case. SSRN Electronic Journal. 2020 doi: 10.2139/ssrn.3551335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bui L., Nguyen Thanh T., Nguyen Ngoc H. Early estimation of reproduction number of covid-19 in Vietnam. Medrxiv. 2020 doi: 10.1101/2020.03.28.20046136. 2020.03.28.20046136-2020.03.28.20046136. [DOI] [Google Scholar]
- Chowell G., Hincapie-Palacio D., Ospina J., Pell B., Tariq A., Dahal S. Using phenomenological models to characterize transmissibility and forecast patterns and final burden of Zika epidemics. PLoS Currents. 2016;8 doi: 10.1371/currents.outbreaks.f14b2217c902f453d9320a43a35b9583. ecurrents.outbreaks.f14b2217c902f453d9320a43a35b9583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- COVID-19 Canada Open Data Working Group Epidemiological data from the COVID-19 outbreak in Canada. 2020. https://github.com/ishaberry/Covid19Canada Retrieved from.
- Du S., Wang J., Zhang H., Cui W., Kang Z., Yang T. Predicting COVID-19 using hybrid AI model. SSRN Electronic Journal. 2020 doi: 10.2139/ssrn.3555202. [DOI] [PubMed] [Google Scholar]
- Du Z., Xu X., Wu Y., Wang L., Cowling B.J., Meyers L.A. Serial interval of COVID-19 among publicly reported confirmed cases. Emerging Infectious Diseases. 2020;26(6) doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J., Liu X., Pan W., Douglas M.W., Bao S. Epidemiology of 2019 novel coronavirus disease-19 in Gansu province, China, 2020. Emerging Infectious Diseases. 2020;26(6) doi: 10.3201/eid2606.200251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine P.E. The interval between successive cases of an infectious disease. American Journal of Epidemiology. 2003;158(11):1039–1047. doi: 10.1093/aje/kwg251. [DOI] [PubMed] [Google Scholar]
- Fisman D.N., Hauck T.S., Tuite A.R., Greer A.L. An IDEA for short term outbreak projection: Nearcasting using the basic reproduction number. PloS One. 2014;8(12) doi: 10.1371/journal.pone.0083622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisman D., Rivers C., Lofgren E., Majumder M.S. Estimation of MERS-coronavirus reproductive number and case fatality rate for the spring 2014 Saudi Arabia outbreak: Insights from publicly available data. PLoS Currents. 2014 doi: 10.1371/currents.outbreaks.98d2f8f3382d84f390736cd5f5fe133c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganyani T., Kremer C., Chen D., Torneri A., Faes C., Wallinga J. Estimating the generation interval for COVID-19 based on symptom onset data. Euro Surveillance. 2020;25(17) doi: 10.2807/1560-7917.ES.2020.25.17.2000257. 2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan H., Zhang Y., Yuan M., Wu X.Y., Liu Z.R., Liu M. Epidemiological analysis on 1 052 cases of COVID-19 in epidemic clusters. Zhonghua Liu Xing Bing Xue Za Zhi = Zhonghua Liuxingbingxue Zazhi. 2020;41(5) doi: 10.3760/cma.j.cn112338-20200301-00223. E027-E027. [DOI] [PubMed] [Google Scholar]
- Gardner E.G., Ali M., Kayali G., Kelton D., Greer A. Using the incidence decay and exponential adjustment (IDEA) model to understand transmission dynamics of MERS-CoV in a camel herd. International Journal of Infectious Diseases. 2016;53:126. [Google Scholar]
- Government of Canada Coronavirus disease (COVID-19): Outbreak update. 2020. https://www.canada.ca/en/public-health/services/diseases/2019-novel-coronavirus-infection.html Retrieved from.
- Greer A.L., Spence K., Gardner E. Understanding the early dynamics of the 2014 porcine epidemic diarrhea virus (PEDV) outbreak in Ontario using the incidence decay and exponential adjustment (IDEA) model. BMC Veterinary Research. 2017;13(1):8. doi: 10.1186/s12917-016-0922-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L., Zhang X., Zhang X., Wei Z., Zhang L., Xu J. Rapid asymptomatic transmission of COVID-19 during the incubation period demonstrating strong infectivity in a cluster of youngsters aged 16-23 years outside Wuhan and characteristics of young patients with COVID-19: A prospective contact-tracing study. Journal of Infection. 2020 doi: 10.1016/j.jinf.2020.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji T., Chen H., Xu J., Wu L., Li J., Chen K. Lockdown contained the spread of 2019 novel coronavirus disease in Huangshi city, China: Early epidemiological findings. Clinical Infectious Diseases. 2020. https://academic.oup.com/cid/advance-article/doi/10.1093/cid/ciaa390/5816958 ciaa390 Retrieved from. [DOI] [PMC free article] [PubMed]
- Ki M. Epidemiologic characteristics of early cases with 2019 novel coronavirus (2019-nCoV) disease in Korea. Epidemiology and Health. 2020;42 doi: 10.4178/epih.e2020007. e2020007-e2020007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausner Z., Fattal E., Hirsch E., Shapira S.C. A single holiday was the turning point of the COVID-19 policy of Israel. Medrxiv. 2020 doi: 10.1101/2020.03.26.20044412. 2020.03.26.20044412-2020.03.26.20044412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao J., Fan S., Chen J., Wu J., Xu S., Guo Y. Epidemiological and clinical characteristics of COVID-19 in adolescents and young adults. The Innovation. 2020;1(1):100001. doi: 10.1016/j.xinn.2020.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M., Chen P., Yuan Q., Song B., Ma J. Transmission characteristics of the COVID-19 outbreak in China: A study driven by data. Medrxiv. 2020 doi: 10.1101/2020.02.26.20028431. 2020.02.26.20028431-2020.02.26.20028431. [DOI] [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. New England Journal of Medicine. 2020;382(13):1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Bi L., Chen Y., Wang Y., Fleming J., Yu Y. Active or latent tuberculosis increases susceptibility to COVID-19 and disease severity. Medrxiv. 2020 doi: 10.1101/2020.03.10.20033795. 2020.03.10.20033795-2020.03.10.20033795. [DOI] [Google Scholar]
- Liu J., Liao X., Qian S., Yuan J., Wang F., Liu Y. Community transmission of severe acute respiratory syndrome coronavirus 2, Shenzhen, China, 2020. Emerging Infectious Diseases. 2020;26(6) doi: 10.3201/eid2606.200239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.F., Li J.M., Zhou P.H., Liu J., Dong X.C., Lyu J. Analysis on cluster cases of COVID-19 in tianjin. Zhonghua Liu Xing Bing Xue Za Zhi = Zhonghua Liuxingbingxue Zazhi. 2020;41(5):654–657. doi: 10.3760/cma.j.cn112338-20200225-00165. [DOI] [PubMed] [Google Scholar]
- Liu X., Wu J., Liu M., Dai Y., Zhou D., Li W. Presymptomatic transmission of COVID-19 in a cluster of cases occurred in confined space: A case report. Infectious Diseases. 2020 doi: 10.21203/RS.3.RS-18053/V1. [DOI] [Google Scholar]
- Lytras T., Panagiotakopoulos G., Tsiodras S. Estimating the ascertainment rate of SARS-CoV-2 infection in Wuhan, China: Implications for management of the global outbreak. Medrxiv. 2020 doi: 10.1101/2020.03.24.20042218. 2020.03.24.20042218-2020.03.24.20042218. [DOI] [Google Scholar]
- Majumder M.S., Santillana M., Mekaru S.R., McGinnis D.P., Khan K., Brownstein J.S. Utilizing nontraditional data sources for near real-time estimation of transmission dynamics during the 2015-2016 Colombian Zika virus disease outbreak. JMIR Public Health and Surveillance. 2016;2(1) doi: 10.2196/publichealth.5814. e30-e30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma S., Zhang J., Zeng M., Yun Q., Guo W., Zheng Y. Epidemiological parameters of coronavirus disease 2019: A pooled analysis of publicly reported individual data of 1155 cases from seven countries. Medrxiv. 2020 doi: 10.1101/2020.03.21.20040329. 2020.03.21.20040329-2020.03.21.20040329. [DOI] [Google Scholar]
- Mizumoto K., Chowell G. Transmission potential of the novel coronavirus (COVID-19) onboard the Diamond Princess cruises ship, 2020. Infectious Disease Modelling. 2020;5:264–270. doi: 10.1016/j.idm.2020.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moghadas S., Milwid R. Glossary of terms for infectious disease modelling: A proposal for consistent language. 2016. https://nccid.ca/publications/glossary-terms-infectious-disease-modelling-proposal-consistent-language/ Retrieved from.
- Nishiura H., Linton N.M., Akhmetzhanov A.R. Initial cluster of novel coronavirus (2019-nCoV) infections in Wuhan, China is consistent with substantial human-to-human transmission. Journal of Clinical Medicine. 2020;9(2) doi: 10.3390/jcm9020488. 488-488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. International Journal of Infectious Diseases. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogden N.H., Fazil A., Safronetz D., Drebot M.A., Wallace J., Rees E.E. Risk of travel-related cases of Zika virus infection is predicted by transmission intensity in outbreak-affected countries. Parasites & Vectors. 2017;10(1):41. doi: 10.1186/s13071-017-1977-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ping K. Medrxiv; 2020. Epidemiologic characteristics of COVID-19 in Guizhou, China. 2020.03.01.20028944-2020.03.01.20028944. [DOI] [PubMed] [Google Scholar]
- Pung R., Chiew C.J., Young B.E., Chin S., Chen M.I.C., Clapham H.E. Investigation of three clusters of COVID-19 in Singapore: Implications for surveillance and response measures. The Lancet. 2020;395(10229):1039–1046. doi: 10.1016/S0140-6736(20)30528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian G., Yang N., Ma A.H.Y., Wang L., Li G., Chen X. COVID-19 transmission within a family cluster by presymptomatic carriers in China. Clinical Infectious Diseases. 2020 doi: 10.1093/cid/ciaa316. ciaa316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith B.A., Bancej C., Fazil A., Mullah M., Yan P., Zhang S. 2020. The performance of phenomenological models in providing near-term Canadian case projections in the midst of the COVID-19 pandemic. Submitted. [DOI] [PubMed] [Google Scholar]
- Sun W.W., Ling F., Pan J.R., Cai J., Miao Z.P., Liu S.L. Epidemiological characteristics of 2019 novel coronavirus family clustering in Zhejiang province. Zhonghua Yu Fang Yi Xue Za Zhi [Chinese Journal of Preventive Medicine] 2020;54 doi: 10.3760/cma.j.cn112150-20200227-00199. E027-E027. [DOI] [PubMed] [Google Scholar]
- Tindale L., Coombe M., Stockdale J.E., Garlock E., Lau W.Y.V., Saraswat M. Transmission interval estimates suggest pre-symptomatic spread of COVID-19. Medrxiv. 2020 doi: 10.1101/2020.03.03.20029983. 2020.03.03.20029983-2020.03.03.20029983. [DOI] [Google Scholar]
- Tuite A.R., Fisman D.N. The IDEA model: A single equation approach to the Ebola forecasting challenge. 2018. [DOI] [PubMed]
- Vink M., Bootsma M., Wallinga J. Serial intervals of respiratory infectious diseases: A systematic review and analysis. American Journal of Epidemiology. 2014;180(9):865–875. doi: 10.1093/aje/kwu209. [DOI] [PubMed] [Google Scholar]
- Wang Y., Teunis P.F.M. Strongly heterogeneous transmission of COVID-19 in mainland China: Local and regional variation. Medrxiv. 2020 doi: 10.1101/2020.03.10.20033852. 2020.03.10.20033852-2020.03.10.20033852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO WHO director-general’s remarks at the media briefing on 2019-nCoV on 11 February 2020. 2020. https://www.who.int/dg/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020 Retrieved from.
- Wu J.T., Leung K., Bushman M., Kishore N., Niehus R., de Salazar P.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nature Medicine. 2020;26(4):506–510. doi: 10.1038/s41591-020-0822-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F., Zhao S., Yu B., Chen Y., Wang W., Song Z. A new coronavirus associated with human respiratory disease in China. Nature. 2020;579(7798):265–269. doi: 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y., Patel Z., Fiddler A., Yuan L., Delvin M., Fisman D.N. Estimated impact of aggressive empirical antiviral treatment in containing an outbreak of pandemic influenza H1N1 in an isolated First Nations community. Influenza and Other Respiratory Viruses. 2013;7(6):1409–1415. doi: 10.1111/irv.12141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu x., Liu X., Wang L., Ali S.T., Du Z., Bosetti P. Household transmissions of SARS-CoV-2 in the time of unprecedented travel lockdown in China. Medrxiv. 2020 doi: 10.1101/2020.03.02.20029868. 2020.03.02.20029868. [DOI] [Google Scholar]
- You C., Deng Y., Hu W., Sun J., Lin Q., Zhou F. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. International Journal of Hygiene and Environmental Health. 2020;228:113555. doi: 10.1016/j.ijheh.2020.113555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J., Litvinova M., Wang W., Wang Y., Deng X., Chen X. Evolving epidemiology of novel coronavirus diseases 2019 and possible interruption of local transmission outside Hubei province in China: A descriptive and modeling study. The Lancet. 2020 doi: 10.1016/S1473-3099(20)30230-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S., Cao P., Chong M.K.C., Gao D., Lou Y., Ran J. Cambridge University Press; 2020. The time-varying serial interval of the coronavirus disease (COVID-19) and its gender-specific difference: A data-driven analysis using public surveillance data in Hong Kong and Shenzhen, China from January 10 to February 15, 2020. [DOI] [Google Scholar]
- Zhao S., Cao P., Gao D., Zhuang Z., Chong M.K.C., Cai Y. Epidemic growth and reproduction number for the novel coronavirus disease (COVID-19) outbreak on the Diamond Princess cruise ship from January 20 to February 19, 2020: A preliminary data-driven analysis. SSRN Electronic Journal. 2020 doi: 10.2139/ssrn.3543150. [DOI] [Google Scholar]
- Zhao S., Gao D., Zhuang Z., Chong M., Cai Y., Ran J. Estimating the serial interval of the novel coronavirus disease (COVID-19): A statistical analysis using the public data in Hong Kong from January 16 to February 15, 2020. Medrxiv. 2020 doi: 10.1101/2020.02.21.20026559. 2020.02.21.20026559-2020.02.21.20026559. [DOI] [Google Scholar]