Mathematical modeling of COVID-19 fatality trends: Death kinetics law versus infection-to-death delay rule

Abstract

The COVID-19 pandemic has world-widely motivated numerous attempts to properly adjust classical epidemiological models, namely those of the SEIR-type, to the spreading characteristics of the novel Corona virus. In this context, the fundamental structure of the differential equations making up the SEIR models has remained largely unaltered—presuming that COVID-19 may be just “another epidemic”. We here take an alternative approach, by investigating the relevance of one key ingredient of the SEIR models, namely the death kinetics law. The latter is compared to an alternative approach, which we call infection-to-death delay rule. For that purpose, we check how well these two mathematical formulations are able to represent the publicly available country-specific data on recorded fatalities, across a selection of 57 different nations. Thereby, we consider that the model-governing parameters—namely, the death transmission coefficient for the death kinetics model, as well as the apparent fatality-to-case fraction and the characteristic fatal illness period for the infection-to-death delay rule—are time-invariant. For 55 out of the 57 countries, the infection-to-death delay rule turns out to represent the actual situation significantly more precisely than the classical death kinetics rule. We regard this as an important step towards making SEIR-approaches more fit for the COVID-19 spreading prediction challenge.

Nomenclature

C

recorded number of total (cumulated) infections

ΔC

recorded number of change in total (cumulated) infections per time step

$E_{\mathrm{del}}^{\mathrm{F}}$

absolute error between recorded fatalities and fatalities predicted by infection-to-death delay rule based on arbitrary values of $f_{\text{F}}$ and $T_{\text{F}}$

$〈E_{\mathrm{del}}^F〉$

time-averaged absolute error between recorded fatalities and fatalities predicted by infection-to-death delay rule based on arbitrary values of $f_{\text{F}}$ and $T_{\text{F}}$

${〈E_{\mathrm{del}}^F〉}^{\text{est}}$

time-averaged absolute error between recorded fatalities and fatalities predicted by infection-to-death delay rule based on optimized estimates for $f_{\text{F}}$ and $T_{\text{F}}$

$E_{\mathrm{kin}}^F$

absolute error between recorded fatalities and fatalities predicted by death kinetics model based on arbitrary values of ${\beta }_{\text{F}}$

${〈E_{\mathrm{kin}}^F〉}^{\text{est}}$

time-averaged absolute error between recorded fatalities and fatalities predicted by death kinetics model based on optimized estimates for ${\beta }_{\text{F}}$

$E_{\mathrm{kin}}^{\Delta F}$

absolute error between recorded fatality changes and fatality changes predicted by death kinetics model based on arbitrary values of ${\beta }_{\text{F}}$

$〈E_{\mathrm{del}}^{\Delta F}〉$

time-averaged absolute error between recorded fatality changes and fatality changes predicted by death kinetics model based on arbitrary values of ${\beta }_{\text{F}}$

${〈E_{\mathrm{kin}}^{\Delta F}〉}^{\text{est}}$

time-averaged absolute error between recorded fatality changes and fatality changes predicted by death kinetics model based on optimized estimate for ${\beta }_{\text{F}}$

ΔE

relative change of prediction error between death kinetics model and infection-to-death delay rule

$f_{\text{F}}$

apparent fatality-to-case ratio

$f_{\text{F}}^{\text{est}}$

optimized estimate for the apparent fatality-to-case ratio

F

recorded number of fatalities

ΔF

recorded number of changes in fatalities per time step

F_del

fatalities predicted by infection-to-death delay rule

F_kin

fatalities predicted by death kinetics model

I

recorded number of infected people

ΔI

recorded number of change in infected people per time step

N_t

number of time points considered in a specific country

R

recorded number of recoveries

ΔR

change per time, of recorded recoveries

${\mathcal{R}}_{\mathrm{del}}^{\mathrm{F},\text{est}}$

relative time-averaged absolute error between recorded fatalities and fatalities predicted by infection-to-death delay rule based on the optimized estimates for $f_{\text{F}}$ and $T_{\text{F}}$

${\mathcal{R}}_{\mathrm{kin}}^{\mathrm{F},\text{est}}$

relative time-averaged absolute error between recorded fatalities and fatalities predicted by death kinetics model based on the optimized estimate for ${\beta }_{\text{F}}$

t

time since first recording

Δt

time step

$T_{\text{F}}$

characteristic infection-to-death period

$T_{\text{F}}^{\text{est}}$

optimized estimate for the characteristic infection-to-death period

β_F

death transmission coefficient

${\beta }_{\text{F}}^{\text{est}}$

optimized estimate for death transmission coefficient

1. Introduction

It is generally agreed on that mathematical models, and in particular agent-based epidemic simulation models, may help in combating COVID-19. Such models have underlined the importance of quarantining infected individuals and their family members, workplace distancing, closing of educational institutions and effective case management; as practically proven very successful in Singapore [1].

As concerns predictions of infection and death kinetics, the SEIR model type (taking into account populations of Susceptible, Exposed, Infectious, and Removed individuals; with removal being associated to recovery or death) enjoys particular popularity [2], [3], [4], [5]. However, reliable SEIR-supported mid- to long-term prognoses remain a formidable, largely unsolved challenge: E.g., SEIR-predicted numbers from March 11, 2020, such as a peak of 26,000 infected people in Italy foreseen for March 21, 2020 [6], did not match the reality seen a few weeks later. In fact, this peak was actually recorded in Italy only on April 19, 2020, when Italy reported more than 108,000 active infections, and around 24,000 fatalities [7]. On the one hand, these large deviations between model predictions and the actually recorded numbers stem from the uncertainty of the underlying SEIR model parameters: they may not be sufficiently well known for the novel COVID-19 pandemic yet. On the other hand, one may ask to which extent the standard SEIR models are actually applicable to the COVID-19 pandemic, or more precisely, if the structure of the involved differential equations might need some adaptations, so as to convincingly and reliably predict the future spreading of COVID-19 as well as the related fatalities, for different boundary conditions arising from social behavior and improvements in the health care system.

In this paper, we address this open, and highly relevant question. To that end, we consider, for 57 countries, the recordings of total (cumulated) COVID-19 infections, active COVID-19 infections, and COVID-19-related fatalities (described in Section 2.1). On this basis, we assess both the traditional death kinetics law (see Section 2.2), and a new infection-to-death delay rule (see Section 2.3). A comprehensive comparison of the two methods is presented in Section 3, as to their capabilities to predict the fatality trends recorded in each of the considered countries based on the respectively recorded infections. The paper is concluded by a discussion on the potential implications of the revealed results, see Section 4.

2. Data and methods

2.1. Data base

We use the data provided on the reference website Worldometer [7], namely the developments over time, of the country-specific total numbers of cases of people infected with COVID-19 (being the cumulated numbers of people infected until the respective dates), of the active cases of infected people (being the numbers of people currently infected at the respective dates), as well as of the total deaths related to COVID-19 (being the cumulated numbers of deceased people until the respective dates). Importantly, our focus is on countries where the reported numbers of fatalities are statistically relevant, and where the related death kinetics follow more or less smooth trends. As of April 26, 2020, this applies to the following 57 countries (given in alphabetical order): Algeria, Argentina, Australia, Austria, Bangladesh, Belgium, Brazil, Canada, Chile, China, Colombia, Croatia, Czech Republic, Denmark, Dominican Republic, Ecuador, Egypt, Finland, France, Germany, Greece, Hungary, Iceland, India, Indonesia, Iran, Iraq, Ireland, Israel, Italy, Japan, Luxembourg, Malaysia, Mexico, Morocco, Netherlands, New Zealand, Norway, Pakistan, Panama, Peru, Philippines, Poland, Portugal, Romania, Russia, Saudi Arabia, Serbia, South Africa, South Korea, Spain, Sweden, Switzerland, Turkey, Ukraine, United Kingdom, and the United States of America.

Since the data available on [7] are, from time to time, slightly corrected, all raw data used in the present study (up to date on April 26, 2020) are explicitly documented in this paper. For the sake of demonstration, the data recorded in Austria are shown in Table 1 , while the data for all other countries are provided in the Supplementary Material. Thereby, it is noted that the total (cumulated) numbers of confirmed cases, C, the numbers of active infections, I, and the total (cumulated) numbers of fatalities, F, are directly extracted from [7]. All other quantities given in Table 1, namely the total (cumulated) number of recoveries, R, as well as the daily changes ΔC, ΔI, ΔF, and ΔR can be straightforwardly computed.

Table 1.

Date-specific COVID-19 data recorded in Austria, according to [7], namely the numbers of confirmed cases of infected people, C, the numbers of active infections, I, the numbers of fatalities, F, and the numbers of recovered individuals, R; as well as the corresponding changes per day, i.e., ΔC, ΔI, ΔF, and ΔR.

Date	C	ΔC	I	ΔI	F	ΔF	R	ΔR
Feb 25	2	2	2	2	0	0	0	0
Feb 26	2	0	2	0	0	0	0	0
Feb 27	5	3	5	3	0	0	0	0
Feb 28	7	2	7	2	0	0	0	0
Feb 29	10	3	10	3	0	0	0	0
Mar 1	14	4	14	4	0	0	0	0
Mar 2	18	4	18	4	0	0	0	0
Mar 3	24	6	24	6	0	0	0	0
Mar 4	29	5	29	5	0	0	0	0
Mar 5	43	14	41	12	0	0	2	2
Mar 6	66	23	64	23	0	0	2	0
Mar 7	81	15	79	15	0	0	2	0
Mar 8	104	23	102	23	0	0	2	0
Mar 9	131	27	129	27	0	0	2	0
Mar 10	182	51	178	49	0	0	4	2
Mar 11	246	64	242	64	0	0	4	0
Mar 12	361	115	356	114	1	1	4	0
Mar 13	504	143	497	141	1	0	6	2
Mar 14	655	151	648	151	1	0	6	0
Mar 15	860	205	853	205	1	0	6	0
Mar 16	1018	158	1007	154	3	2	8	2
Mar 17	1332	314	1319	312	4	1	9	1
Mar 18	1646	314	1633	314	4	0	9	0
Mar 19	2179	533	2164	531	6	2	9	0
Mar 20	2649	470	2634	470	6	0	9	0
Mar 21	2992	343	2975	341	8	2	9	0
Mar 22	3582	590	3557	582	16	8	9	0
Mar 23	4474	892	4444	887	21	5	9	0
Mar 24	5283	809	5246	802	28	7	9	0
Mar 25	5588	305	5548	302	31	3	9	0
Mar 26	6909	1321	6748	1200	49	18	112	103
Mar 27	7697	788	7414	666	58	9	225	113
Mar 28	8271	574	7978	564	68	10	225	0
Mar 29	8788	517	8223	245	86	18	479	254
Mar 30	9618	830	8874	651	108	22	636	157
Mar 31	10,180	562	8957	83	128	20	1095	459
Apr 1	10,711	531	9129	172	146	18	1436	341
Apr 2	11,129	418	9222	93	158	12	1749	313
Apr 3	11,524	395	9334	112	168	10	2022	273
Apr 4	11,781	257	9088	−246	186	18	2507	485
Apr 5	12,051	270	8849	−239	204	18	2998	491
Apr 6	12,297	246	8614	−235	220	16	3463	465
Apr 7	12,639	342	8350	−264	243	23	4046	583
Apr 8	12,942	303	8157	−193	273	30	4512	466
Apr 9	13,244	302	7709	−448	295	22	5240	728
Apr 10	13,560	316	7177	−532	319	24	6064	824
Apr 11	13,806	246	6865	−312	337	18	6604	540
Apr 12	13,945	139	6608	−257	350	13	6987	383
Apr 13	14,041	96	6330	−278	368	18	7343	356
Apr 14	14,226	185	6209	−121	384	16	7633	290
Apr 15	14,350	124	5859	−350	393	9	8098	465
Apr 16	14,476	126	5080	−779	410	17	8986	888
Apr 17	14,595	119	4460	−620	431	21	9704	718
Apr 18	14,671	76	4014	−446	443	12	10,214	510
Apr 19	14,749	78	3796	−218	452	9	10,501	287
Apr 20	14,795	46	3694	−102	470	18	10,631	130
Apr 21	14,873	78	3411	−283	491	21	10,971	340
Apr 22	14,925	52	3087	−324	510	19	11,328	357
Apr 23	15,002	77	2786	−301	522	12	11,694	366
Apr 24	15,071	69	2669	−117	530	8	11,872	178
Apr 25	15,148	77	2509	−160	536	6	12,103	231
Apr 26	15,225	77	2401	−108	542	6	12,282	179

2.2. Traditional approach: death kinetics law

The death kinetics law usually used in SEIR models reads as [8], [9]

$$\frac{\text{d}{F}_{\text{kin}}\left(t\right)}{\text{d}t}={\beta }_{\text{F}}I\left(t\right),$$ (1)

with F _kin as the death kinetics law-predicted number of fatalities, I as the number of (actively, or currently) infected people, t being the time variable, and ${\beta }_{\text{F}}$ denoting the death transmission coefficient (also referred to as death rate or mortality rate). Clearly, the idea expressed mathematically by Eq. (1) is that the increase of fatalities at time instant t is proportional to the number of people infected at time instant t.

Next, we aim at finding, country-specifically, the optimal value of ${\beta }_{\text{F}},$ such that the model-predicted fatality changes according to Eq. (1) agree as well as possible with the recorded data; i.e., with ΔF, as seen for Austria in the seventh column of Table 1. For that purpose, it is necessary to discretize Eq. (1), yielding

$$\Delta F_{\mathrm{kin}}\left(t_i\right)=F_{\mathrm{kin}}\left(t_i\right)-F_{\mathrm{kin}}\left(t_{i-1}\right)={\beta }_{\text{F}}I\left(t_{i-1}\right).$$ (2)

Hence, time is now split into intervals $\Delta t=t_i-t_{i-1},$ with the interval limits indicated by index i, $i=1,\cdots ,N_t,$ N_t standing for the number of time points considered. Furthermore, ΔF _kin denotes the increase of fatalities per time interval. As for Table 1, the time interval amounts to $\Delta t=1$d, and the number of time steps amounts to $N_t=56$. For a specific value of ${\beta }_{\text{F}},$ the absolute error between model-predicted and recorded fatality steps associated with time instant t_i is given by

$$E_{\mathrm{kin}}^{\Delta F}({\beta }_{\text{F}};t_i)=|\Delta F_{\mathrm{kin}}({\beta }_{\text{F}};t_i)-\Delta F\left(t_i\right)|.$$ (3)

The corresponding average over the entire recording period reads as

$$〈E_{\mathrm{kin}}^{\Delta F}〉\left({\beta }_{\text{F}}\right)=\frac{1}{N_t}\sum _i^{N_t}{E}_{\mathrm{kin}}^{\Delta F}({\beta }_{\text{F}};t_i).$$ (4)

Minimizing $〈E_{\mathrm{kin}}^{\Delta F}〉\left({\beta }_{\text{F}}\right)$ yields the country-specific, optimized estimate for the death transmission coefficient, ${\beta }_{\text{F}}^{\text{est}}$; hence

$$\forall {\beta }_{\text{F}}\in [{\beta }_{\text{F,low}},{\beta }_{\text{F,up}}]:〈E_{\mathrm{kin}}^{\Delta F}〉\left({\beta }_{\text{F}}\right)\ge 〈E_{\mathrm{kin}}^{\Delta F}〉\left({\beta }_{\text{F}}^{\text{est}}\right)={〈E_{\mathrm{kin}}^{\Delta F}〉}^{\text{est}}.$$ (5)

The optimization task described by Eqs. (2)–(5) was implemented by numerically scanning the relevant range of values for ${\beta }_{\text{F}},$ given through ${\beta }_{\text{F,low}}=0$ and ${\beta }_{\text{F,up}}=3\times {10}^{-2}{\text{d}}^{-1},$ considering thereby a variation step size of $\Delta {\beta }_{\text{F}}=1\times {10}^{-6}{\text{d}}^{-1}$. Notably, for all studied data sets, a distinct minimum of $〈E_{\mathrm{kin}}^{\Delta F}〉\left({\beta }_{\text{F}}\right)$ could be found within the above-defined parameter rang. This minimum is denoted by ${〈E_{\mathrm{kin}}^{\Delta F}〉}^{\text{est}}$ and associated with the optimized estimate for ${\beta }_{\text{F}},$ ${\beta }_{\text{F}}^{\text{est}},$ see Eq. (5). Furthermore, the optimization was performed for $\Delta t=0.1$d, with ΔF(t_i) being computed from linear interpolation of the total fatality numbers F(t_i) (which are available on [7] with $\Delta t=1$d, see Table 1).

2.3. Alternative approach: infection-to-death delay rule

As an alternative to Eq. (1), we adopt a more “microscopic” description, which takes into account the actual course of the disease at the patient level. There, after some time of illness, it turns out whether an infected person recovers or dies. Mathematically, this can be expressed as follows:

$$F_{\mathrm{del}}\left(t\right)=f_{\text{F}}C(t-T_{\text{F}}),$$ (6)

where F _del is the delay rule-predicted fatality number, $f_{\text{F}}$ is the apparent fatality-to-case fraction, and C is the total (cumulated) number of recorded cases of infections at time point $(t-T_{\text{F}}),$ $T_{\text{F}}$ being the characteristic time of fatal illness.

Again, we introduce a discretized version of Eq. (6), for the sake of finding the parameters yielding the best-possible agreement between the model-predicted and the country-specifically recorded fatalities, reading as

$$F_{\mathrm{del}}\left(t_i\right)=f_{\text{F}}C(t_i-T_{\text{F}}).$$ (7)

Assigning specific values to $f_{\text{F}}$ and $T_{\text{F}}$ and evaluating Eq. (6) accordingly allows for computing the absolute error between model-predicted and recorded fatalities, reading as

$$E_{\mathrm{del}}^F(f_{\text{F}},T_{\text{F}};t_i)=|F_{\mathrm{del}}\left(t_i\right)-F\left(t_i\right)|.$$ (8)

The corresponding average over the entire recording period reads as

$$〈E_{\mathrm{del}}^F〉(f_{\text{F}},T_{\text{F}})=\frac{1}{N_t}\sum _i^{N_t}{E}_{\mathrm{del}}^F(f_{\text{F}},T_{\text{F}};t_i).$$ (9)

Minimizing $〈E_{\mathrm{del}}^F〉(f_{\text{F}},T_{\text{F}})$ yields the country-specific, optimized estimates for the apparent fatality-to-case fraction and of the characteristic time of fatal illness, $f_{\text{F}}^{\text{est}}$ and $T_{\text{F}}^{\text{est}}$; hence

$$\begin{array}{ccc}& & \forall f_{\text{F}}\in [f_{\text{F,low}},f_{\text{F,up}}]\wedge \forall T_{\text{F}}\in [T_{\text{F,low}};T_{\text{F,up}}]:\hfill \\ & & 〈E_{\mathrm{del}}^F〉(f_{\text{F}},T_{\text{F}})\ge 〈E_{\mathrm{del}}^F〉(f_{\text{F}}^{\text{est}},T_{\text{F}}^{\text{est}})={〈E_{\mathrm{del}}^F〉}^{\text{est}}.\hfill \end{array}$$ (10)

In more detail, we considered parameter ranges defined by $f_{\text{F,low}}=0$ and $f_{\text{F,up}}=0.6,$ with a variation step size of $\Delta f_{\text{F}}=0.001,$ as well as by $T_{\text{F,low}}=0$ and $f_{\text{F,up}}=30$ d, with a variation step size of $\Delta T_{\text{f}}=0.1$ d. These parameter ranges allowed for finding unique error minima for all studied countries. Analogously to the optimization routine described in Section 2.2, a time step of $\Delta t=0.1$d was considered, requiring respective linear interpolation of the recorded fatality numbers.

2.4. Comparison of models

In order to quantitatively compare the alternative approach introduced in Section 2.3 to the classical death kinetics model described in Section 2.2, an additional error measure is required for the quantification of the predictive capability of the death kinetics approach. Thus, analogously to Eq. (8), we introduce the absolute error between the total number of fatalities predicted by the death kinetics model when considering the optimized estimate for the death transmission coefficient, and the total number of recorded fatalities. Mathematically, it reads as

$$E_{\mathrm{kin}}^F({\beta }_{\text{F}}^{\text{est}};t_i)=|F_{\mathrm{kin}}({\beta }_{\text{F}}^{\text{est}};t_i)-F\left(t_i\right)|.$$ (11)

The corresponding average over the entire recording period reads as

$${〈E_{\mathrm{kin}}^F〉}^{\text{est}}=\frac{1}{N_t}\sum _i^{N_t}{E}_{\mathrm{kin}}^F({\beta }_{\text{F}}^{\text{est}};t_i).$$ (12)

Based on this error measure, we assess the predictive capability of the alternative, delay-based approach with respect to the predictive capability of the traditional death kinetics approach. To that end, we compute the relative change in the time-averaged absolute errors, denoted by ΔE, and defined through

$$\Delta \mathrm{E}=\frac{{〈E_{\mathrm{del}}^F〉}^{\text{est}}-{〈E_{\mathrm{kin}}^F〉}^{\text{est}}}{{〈E_{\mathrm{kin}}^F〉}^{\text{est}}}.$$ (13)

If, for a particular country, ΔE < 0, then the new infection-to-death delay rule describes the fatality trend of this country better than the death kinetics model. If, in turn, ΔE > 0, then the death kinetics model describes the fatality trend of this country better than the new infection-to-death delay rule.

3. Results

The analyses described in Sections 2.2–2.4 were applied to the data recorded in all 57 countries mentioned in Section 2.1, see also the Supplementary Material for detailed, country-specific lists. The results of those analyses, namely the optimized estimates for the parameter governing the death kinetics model, ${\beta }_{\text{F}}^{\text{est}},$ as well as of the parameters governing the infection-to-death delay rule, $f_{\text{F}}^{\text{est}}$ and $T_{\text{F}}^{\text{est}},$ are listed in Table 2 .

Table 2.

Country-specific optimized estimates for the death transmission coefficient, ${\beta }_{\text{F}}^{\text{est}},$ for the apparent fatality-to-case fraction, $f_{\text{F}}^{\text{est}},$ and for the characteristic time of fatal illness $T_{\text{F}}^{\text{est}}$; together with corresponding absolute error measures ${〈E_{\mathrm{kin}}^F〉}^{\text{est}}$ and ${〈E_{\mathrm{del}}^F〉}^{\text{est}},$ the maximum number of fatalities, $F_{\text{max}},$ the relative error measures ${\mathcal{R}}_{\mathrm{kin}}^{\mathrm{F},\mathrm{est}}$ and ${\mathcal{R}}_{\mathrm{del}}^{\mathrm{F},\mathrm{est}},$ as well as relative error change associated to the comparison of the death kinetics model with the infection-to-death delay rule, ΔE.

Country	${\beta }_{\text{F}}^{\text{est}}\left[{10}^{-3}{\mathrm{d}}^{-1}\right]$	$f_{\text{F}}^{\text{est}}[-]$	$T_{\text{F}}^{\text{est}}\left[\mathrm{d}\right]$	${〈E_{\mathrm{kin}}^F〉}^{\text{est}}[-]$	${〈E_{\mathrm{del}}^F〉}^{\text{est}}[-]$	$F_{\text{max}}[-]$	${\mathcal{R}}_{\mathrm{kin}}^{F,\mathrm{est}}[-]$	${\mathcal{R}}_{\text{del}}^{F,\mathrm{est}}[-]$	$\Delta E[-]$
Algeria	10.633	0.164	3.5	42.34	11.44	425	0.0996	0.0269	−0.73
Argentina	3.765	0.062	6.9	6.11	2.57	192	0.0318	0.0134	−0.58
Australia	0.631	0.011	8.3	3.52	2.96	83	0.0424	0.0357	−0.16
Austria	2.242	0.035	10.9	25.60	13.63	542	0.0472	0.0251	−0.47
Bangladesh	2.900	0.032	0.0	17.65	6.22	145	0.1217	0.0429	−0.65
Belgium	11.507	0.207	9.0	216.58	71.00	7094	0.0305	0.0100	−0.67
Brazil	8.695	0.112	7.2	100.49	20.47	4271	0.0235	0.0048	−0.80
Canada	5.541	0.094	12.8	104.43	24.52	2560	0.0408	0.0096	−0.77
Chile	1.385	0.021	9.2	5.76	1.28	189	0.0305	0.0068	−0.78
China	1.858	0.040	5.9	489.99	245.85	4632	0.1058	0.0531	−0.50
Colombia	3.086	0.071	8.6	13.59	3.71	244	0.0557	0.0152	−0.73
Croatia	1.091	0.032	11.6	3.55	1.39	55	0.0646	0.0252	−0.61
Czech Republic	1.411	0.035	10.1	9.93	2.89	220	0.0452	0.0131	−0.71
Denmark	3.438	0.054	4.7	22.56	12.57	422	0.0535	0.0298	−0.44
Dominican Republic	2.263	0.049	0.2	42.81	4.83	278	0.1540	0.0174	−0.89
Ecuador	2.481	0.056	2.9	72.11	14.83	576	0.1252	0.0258	−0.79
Egypt	6.039	0.086	2.7	17.33	3.46	317	0.0547	0.0109	−0.80
Finland	2.131	0.061	16.6	9.55	4.59	190	0.0503	0.0242	−0.52
France	8.283	0.151	5.3	1779.10	254.42	22,856	0.0778	0.0111	−0.86
Germany	2.705	0.042	11.2	209.64	56.03	5976	0.0351	0.0094	−0.73
Greece	2.216	0.055	6.3	12.24	2.59	134	0.0913	0.0193	−0.79
Hungary	8.383	0.161	9.4	4.57	5.49	272	0.0168	0.0202	0.20
Iceland	0.000	0.006	10.6	3.59	0.39	10	0.3589	0.0393	−0.89
India	2.875	0.032	0.1	44.14	6.16	881	0.0501	0.0070	−0.86
Indonesia	5.449	0.087	0.1	84.27	6.71	743	0.1134	0.0090	−0.92
Iran	4.788	0.063	0.3	791.26	103.75	5710	0.1386	0.0182	−0.87
Iraq	2.336	0.056	0.0	24.85	4.58	87	0.2856	0.0527	−0.82
Ireland	3.473	0.083	9.6	25.01	11.44	1087	0.0230	0.0105	−0.54
Israel	0.740	0.016	9.1	6.05	2.67	201	0.0301	0.0133	−0.56
Italy	5.829	0.143	4.0	3782.04	69.12	26,644	0.1419	0.0026	−0.98
Japan	1.612	0.034	6.4	18.06	7.27	372	0.0485	0.0196	−0.60
Luxembourg	0.778	0.023	7.4	11.85	2.96	88	0.1346	0.0336	−0.75
Malaysia	0.974	0.018	3.6	10.14	2.04	98	0.1035	0.0208	−0.80
Mexico	14.165	0.293	13.4	41.13	8.19	1305	0.0315	0.0063	−0.80
Morocco	1.658	0.051	0.0	40.19	10.87	161	0.2496	0.0675	−0.73
Netherlands	5.544	0.134	4.8	471.05	40.25	4475	0.1053	0.0090	−0.91
New Zealand	0.000	0.015	17.5	3.25	0.51	18	0.1806	0.0281	−0.84
Norway	0.895	0.031	14.6	9.21	3.44	201	0.0458	0.0171	−0.63
Pakistan	1.508	0.041	10.6	9.73	5.14	281	0.0346	0.0183	−0.47
Panama	1.636	0.031	2.6	15.58	1.92	159	0.0980	0.0121	−0.88
Peru	4.082	0.027	0.0	24.63	12.84	728	0.0338	0.0176	−0.48
Philippines	2.956	0.072	2.9	54.15	10.05	501	0.1081	0.0201	−0.81
Poland	3.051	0.060	8.1	10.34	6.53	535	0.0193	0.0122	−0.37
Portugal	1.743	0.041	5.2	82.84	9.21	903	0.0917	0.0102	−0.89
Romania	3.889	0.062	3.9	35.15	5.18	619	0.0568	0.0084	−0.85
Russia	1.087	0.011	2.1	13.09	2.31	747	0.0175	0.0031	−0.82
Saudi Arabia	0.675	0.034	11.6	15.84	5.33	139	0.1139	0.0383	−0.66
Serbia	1.010	0.019	0.0	25.41	4.38	156	0.1629	0.0281	−0.83
South Africa	0.986	0.035	15.3	5.56	4.57	87	0.0639	0.0526	−0.18
South Korea	0.845	0.023	18.0	10.26	21.33	242	0.0424	0.0881	1.08
Spain	6.308	0.109	2.3	2845.25	109.89	23,190	0.1227	0.0047	−0.96
Sweden	8.092	0.212	13.1	47.64	35.49	2194	0.0217	0.0162	−0.26
Switzerland	3.837	0.058	9.5	37.77	17.95	1610	0.0235	0.0112	−0.52
Turkey	1.808	0.026	2.0	219.69	20.92	2805	0.0783	0.0075	−0.90
Ukraine	1.959	0.026	0.0	19.34	3.01	209	0.0925	0.0144	−0.84
United Kingdom	9.216	0.155	3.4	1090.41	176.30	20,732	0.0526	0.0085	−0.84
United States	3.802	0.069	5.9	1817.13	168.43	55,413	0.0328	0.0030	−0.91

This table also contains the average absolute errors associated with optimized model parameters of the death kinetics law and the infection-to-death delay rule, ${〈E_{\mathrm{kin}}^F〉}^{\text{est}}$ and ${〈E_{\mathrm{del}}^F〉}^{\text{est}},$ as well as the relative change of the error ΔE. In order to allow for better comparability between the countries, Table 2 also features the number of maximum fatalities per country (that is the number of fatalities on April 26, 2020), termed $F_{\text{max}},$ and the ratios ${\mathcal{R}}_{\mathrm{kin}}^{F,\mathrm{est}}={〈E_{\mathrm{kin}}^F〉}^{\text{est}}/F_{\text{max}}$ and ${\mathcal{R}}_{\mathrm{del}}^{F,\mathrm{est}}={〈E_{\mathrm{del}}^F〉}^{\text{est}}/F_{\text{max}},$ to be interpreted as characteristic relative errors associated with the kinetics law and with the delay rule, respectively. Furthermore, the results are also elaborated visually, with three distinct examples being included in this paper:

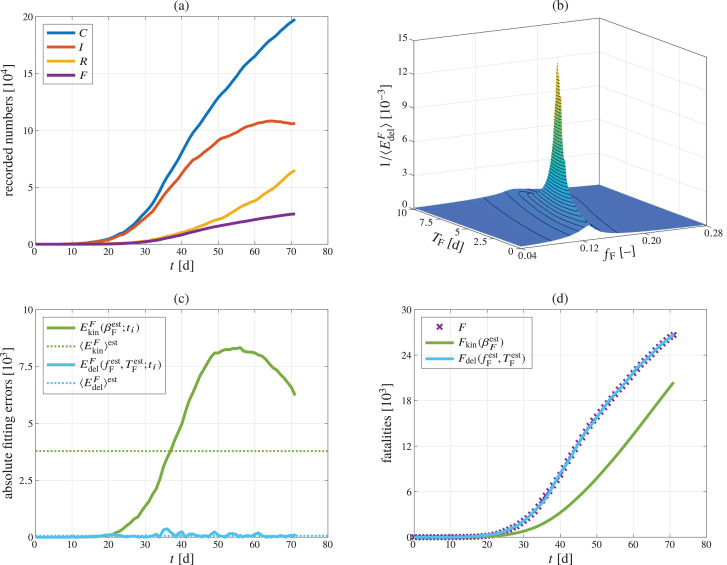
• •Italy, which was the first heavily hit European country, exhibiting the peak in active infections on April 19, 2020, see Fig. 1 ;
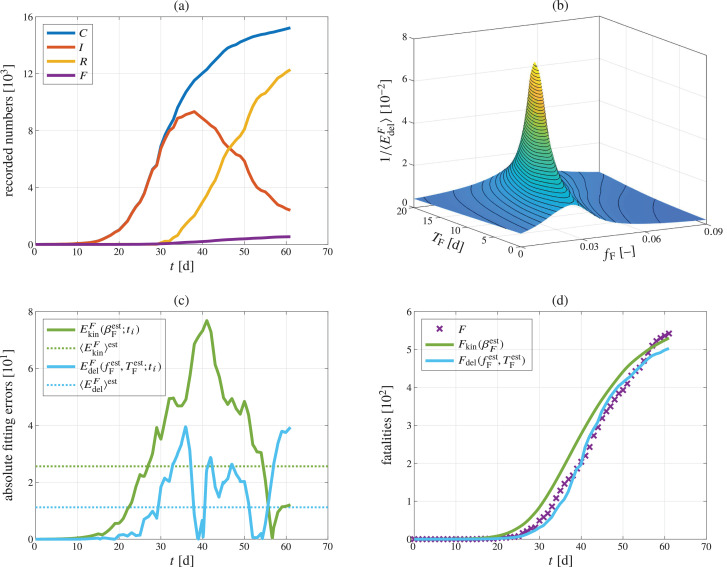
• •Austria, which has exhibited, already by April 26, 2020, an extended period of decreasing active infections (with the respective peak observed on April 3, 2020), see Fig. 2 ; and
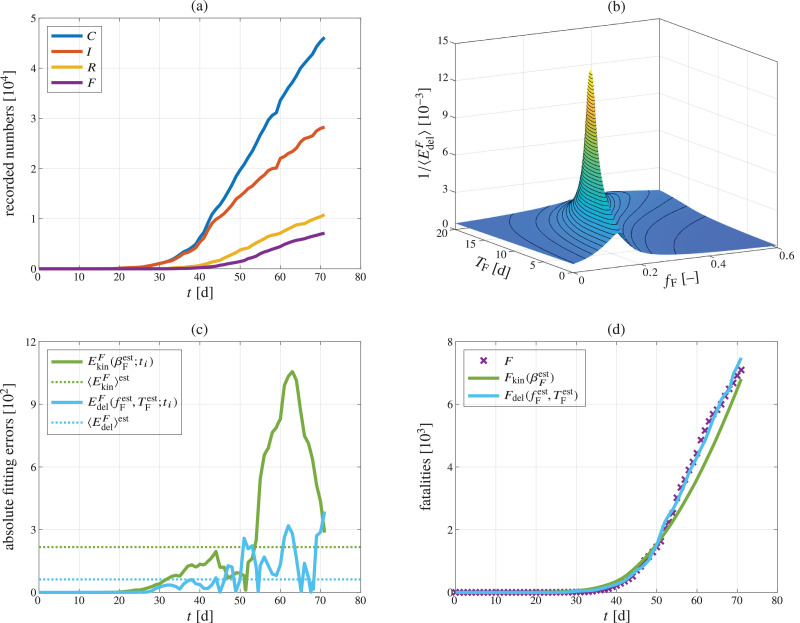
• •Belgium, which has been experiencing, as of April 26, 2020, a still increasing number of active infections, see Fig. 3 .

Fig. 1.

COVID-19 pandemic data and model predictions for Italy, comprising (a) time courses of total infections C, currently infected people I, recovered people R, and fatalities F, according to [7]; (b) inverse of the time average over the delay rule-related prediction error; (c) the absolute errors between model-predicted fatalities and the recorded fatalities, based on the death kinetics model, $E_{\text{kin}}^F,$ and based on the infection-to-death delay model, $E_{\text{del}}^F,$ considering the optimized estimates of parameters ${\beta }_{\text{F}},$$f_{\text{F}},$ and $T_{\text{F}},$ as well as their temporal averages; and (d) model-predicted versus recorded fatality trends.

Fig. 2.

COVID-19 pandemic data and model predictions for Austria, comprising (a) time courses of total infections C, currently infected people I, recovered people R, and fatalities F, according to [7]; (b) inverse of the time average over the delay rule-related prediction error; (c) the absolute errors between model-predicted fatalities and the recorded fatalities, based on the death kinetics model, $E_{\text{kin}}^F,$ and based on the infection-to-death delay model, $E_{\text{del}}^F,$ considering the optimized estimates of parameters ${\beta }_{\text{F}},$$f_{\text{F}},$ and $T_{\text{F}},$ as well as their temporal averages; and (d) model-predicted versus recorded fatality trends.

Fig. 3.

COVID-19 pandemic data and model predictions for Belgium, comprising (a) time courses of total infections C, currently infected people I, recovered people R, and fatalities F, according to [7]; (b) inverse of the time average over the delay rule-related prediction error; (c) the absolute errors between model-predicted fatalities and the recorded fatalities, based on the death kinetics model, $E_{\text{kin}}^F,$ and based on the infection-to-death delay model, $E_{\text{del}}^F,$ considering the optimized estimates of parameters ${\beta }_{\text{F}},$$f_{\text{F}},$ and $T_{\text{F}},$ as well as their temporal averages; and (d) model-predicted versus recorded fatality trends.

The corresponding recorded data can be found in Table 1 (for Austria) as well as in the Supplementary Material (for Italy and Belgium). Furthermore, the Supplementary Material contains the recorded data and the diagrams analogous to Figs. 1–3 for all other 54 investigated countries. We emphasize that the surface plots shown in Figs. 1(b), 2(b), and 3(b) show the inverses of the time-averaged delay rule-related absolute errors, rather than their actual values, as functions of the apparent fatality-to-case fraction and of the characteristic period of fatal illness. These surface plots testify to the uniqueness of the optimized parameter estimates within the studied parameter ranges. While Figs. 1(d), 2(d), and 3(d) unarguably illustrate how much better the infection-to-death rule represents the fatality trends recorded in these three countries than the death kinetics model, it is also clearly visible that the agreement between infection-to-death rule-predicted and recorded fatalities is not quite as convincing for Austria as it is for Italy and Belgium. This is probably caused by the fact that Austria has already entered a second phase of the pandemic, similar to South Korea, where this effect is much more pronounced, as discussed in more detail below and in Section 4.

For the large majority of all investigated country-specific data sets, namely for 55 out of 57 (i.e., for all countries except for Hungary and South Korea), the infection-to-death delay rule proposed in this paper represents the actually recorded fatality trends significantly better than the traditional death kinetics model known from the widely used SEIR-approaches. This improvement is underlined by relative error changes ranging from $-16\%$ to $-98\%,$ whereby the latter dramatic improvement relates to one of the countries which were hit very early and very hard: Italy, see also Fig. 1. Substantial modeling improvements thanks to the infection-to-death delay rule are also seen for other European countries with pronounced excess mortality due to the COVID-19 pandemic according to [10], such as Spain ($-96\%$), the Netherlands ($-91\%$), France ($-86\%$), the United Kingdom ($-84\%$), Sweden ($-26\%$), or Belgium ($-67\%$); for the latter, see Fig. 3. However, the significance of the infection-to-death delay rule is not restricted to countries exhibiting a particularly high death toll. In fact, this rule works equally well for countries such as Greece ($-79\%$), the Dominican Republic ($-89\%$), Iceland ($-89\%$), the United States of America ($-91\%$), or Germany ($-73\%$). When taking the mean error change over all 55 countries where the infection-to-death delay rule outperformed the death kinetics law, we still arrive at an impressive $\overline{\Delta \mathrm{E}}=-68\%$. It should be mentioned that, for the above-defined 55 countries, the infection-to-death delay rule allows for remarkable modeling precisions, quantified by relative average errors of only a few percent, see the ninth column of Table 2. In particular, across those 55 countries, the mean value of ${\mathcal{R}}_{\mathrm{del}}^{F,\text{est}}$ amounts to $\overline{{\mathcal{R}}_{\mathrm{del}}^{F,\text{est}}}=1.88\%,$ whereas the mean value of ${\mathcal{R}}_{\mathrm{kin}}^{F,\text{est}}$ amounts to $\overline{{\mathcal{R}}_{\mathrm{kin}}^{F,\text{est}}}=8.15\%$.

Keeping this in mind, we turn to the only two investigated countries where the traditional death kinetics law yields better representations of the recorded fatality trends than the here proposed infection-to-death delay rule, namely South Korea and Hungary. As for Hungary, we observe that the prediction errors of both the death kinetics law and the infection-to-death delay rule are low, amounting to  ≈ 2%. Hence, a particularly important role of the traditional approach cannot be argued in that case. The situation is different for South Korea. There, the data reflects a period of a significant fatality trend lasting for more than two months (which is much longer than, in some cases even about twice as long as reported for most of the other countries). Still, when applying the analysis described in Sections 2.2–2.4 to the first 35 days of the recorded fatality trend, the infection-to-death delay rule again outperforms the classical death kinetics model. In particular, for this reduced analysis period, the South Korea data yield the following error values: ${〈E_{\mathrm{kin}}^F〉}^{\text{est}}=12.17$ and ${〈E_{\mathrm{del}}^F〉}^{\text{est}}=4.49$; hence, $\Delta \mathrm{E}=-63\%$. A discussion on the possible reasons for these results is given in Section 4 of this paper.

The peculiarities observed for Hungary and South Korea do not apply to any other of the investigated countries, including those at the lower end of the spectrum of values estimated for $f_{\text{F}},$ such as Iceland ($f_{\text{F}}=0.006$), Australia ($f_{\text{F}}=0.011$), New Zealand ($f_{\text{F}}=0.015$), Croatia ($f_{\text{F}}=0.032$), the Czech Republic ($f_{\text{F}}=0.035$), or Austria ($f_{\text{F}}=0.035$); for the latter, see Fig. 2.

4. Discussion

By quantifying the extent of contact reduction necessary to bring down the COVID-19 reproduction number to values below one, stochastic transmission models [11] have proven as valuable mathematical tools for mitigating risks associated with COVID-19. By comparison, the prospects that classical SEIR-models can be successfully applied for combating the COVID-19 pandemic are less clear, as model calibration is usually an extremely challenging task, due to the potential non-identifiability of key model parameters [12].

The present contribution aims at elucidating the role of SEIR-models in a quantitative fashion, by comparing one of the key assumptions of the SEIR-models, namely the death kinetics law, to a somehow obvious alternative, taking into account the course of the disease, where the patient either recovers or dies after some characteristic time. Interestingly, the corresponding infection-to-death delay rule considering invariant, country-specific model parameters (i.e., the apparent fatality-to-case fraction and the characteristic fatal illness period) captures the data recorded in 55 out of the 57 studied countries significantly better than the traditional death kinetics law considering also an invariant, country-specific model parameter (i.e., the death transmission coefficient). As for the two remaining countries, the two models perform more or less equally well for Hungary, whereas South Korea deserves particular mention. There, it is instructive to closely examine the respective developments of infections and fatalities over time, as they reveal that in South Korea at least two distinct kinetics regimes have governed the fatality trend, see Figure 50(d) of the Supplementary Material. As stressed in Section 3, it turns out that the death kinetics of the first month can be satisfactorily described by means of the infection-to-death delay rule, whereas the entire period of roughly two months is better described by the death kinetics model. However, it should be emphasized that the related errors of both methods significantly increase with time. This may suggest that over time, more than one characteristic time of fatal illness governs the death kinetics; in the sense that one and the same infection wave may lead to two or more fatality waves. This is indicated by the prediction curve first underestimating and then overestimating the actually confirmed fatality numbers, see Figure 50(d) of the Supplementary Material. Interestingly, a very similar behavior, albeit in a much less pronounced fashion is seen for Austria, see Fig. 2(d) of this paper. This potential effect of two fatality waves seems to be consistent with the unusually high viral shedding period associated with COVID-19-affected patients, lasting up to 37 days in survivors [13]. Given the still limited knowledge on the various intricacies of the COVID-19 virus, this last proposition should be regarded as nothing more than a speculation; its verification, most likely requiring some sort of combination of more than just one infection-to-death delay term, goes beyond the scope of this paper.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/