Wintertime CO₂, CH₄ and CO emissions estimation for the Washington DC / Baltimore metropolitan area using an inverse modeling technique

Abstract

Since greenhouse gas mitigation efforts are being mostly implemented in cities, the ability to quantify emission trends for urban environments is of paramount importance. However, previous aircraft work has indicated large daily variability in the results. Here we use measurements of CO₂, CH₄ and CO from aircraft over five days within an inverse model to estimate emissions from the D.C./Baltimore region. Results show good agreement with previous estimates in the area for all three gases. However, aliasing caused by irregular spatiotemporal sampling of emissions is shown to significantly impact both the emissions estimates and their variability. Extensive sensitivity tests allow us to quantify the contributions of different sources of variability and indicate that daily variability in posterior emissions estimates is larger than the uncertainty attributed to the method itself (i.e. 17% for CO₂, 24% for CH₄ and 13% for CO). Analysis of hourly reported emissions from power plants and traffic counts shows that 97% of the daily variability in posterior emissions estimates is explained by accounting for the sampling in time and space of sources that have large hourly variability and, thus, caution must be taken in properly interpreting variability that is caused by irregular spatiotemporal sampling conditions.

Graphical Abstract

Introduction

As cities move toward mitigating their carbon footprints, estimating their emissions using atmospheric observations is a valuable way to assess the efficacy of mitigation policies. Recent work^1–7 has already demonstrated the capability of top-down (atmospheric measurement-based) estimation methods to inform bottom-up inventory methods for some greenhouse gases (GHGs). On regional and urban scales, top-down methods have been shown to be effective at estimating emissions using either tower-based or aircraft-based concentration measurements.^8–12

Atmospheric trace gas concentration measurements from airborne platforms have been used extensively to estimate emissions from a region. Both oil and gas basins and urban regions have been studied using mass balance methods,^13–17 including the Washington D.C./Baltimore metropolitan area.^11,12 Researchers have also used aircraft observations with transport models in an inversion framework to estimate emissions at regional,^18–21 urban^22,23 and local scales.²⁴

Several studies have investigated the source of daily variability in aircraft-based top-down emissions estimates for a given region. Variability in estimated emission rates has previously been attributed to uncertainty in the mass balance methodology, which would confound or obscure real emissions changes.^25,26 More recent work using airborne measurements over oil and gas fields has shown that temporal variability in emissions must be considered when interpreting estimates from single-day flights, however. Lavoie et al.²⁷ found significant temporal variability in single source emissions of methane (CH₄) from the Eagle Ford oil and gas production basin in Texas, while Schwietzke et al.²⁸ investigated the effect of episodic CH₄ emissions from natural gas facilities on the regional mass balance estimates in the Fayetteville Shale.

In this study, we use observations collected during five aircraft flights over a two-week period in February 2016 within a Bayesian inversion framework to: 1) estimate emissions of CO₂, CH₄ and CO from the cities of Washington D.C. and Baltimore, MD, (Fig. 1), 2) quantify the uncertainty, and its sources, in each day’s emissions estimate and, 3) explain the cause for the observed daily variability in the estimated emissions.

Figure 1:

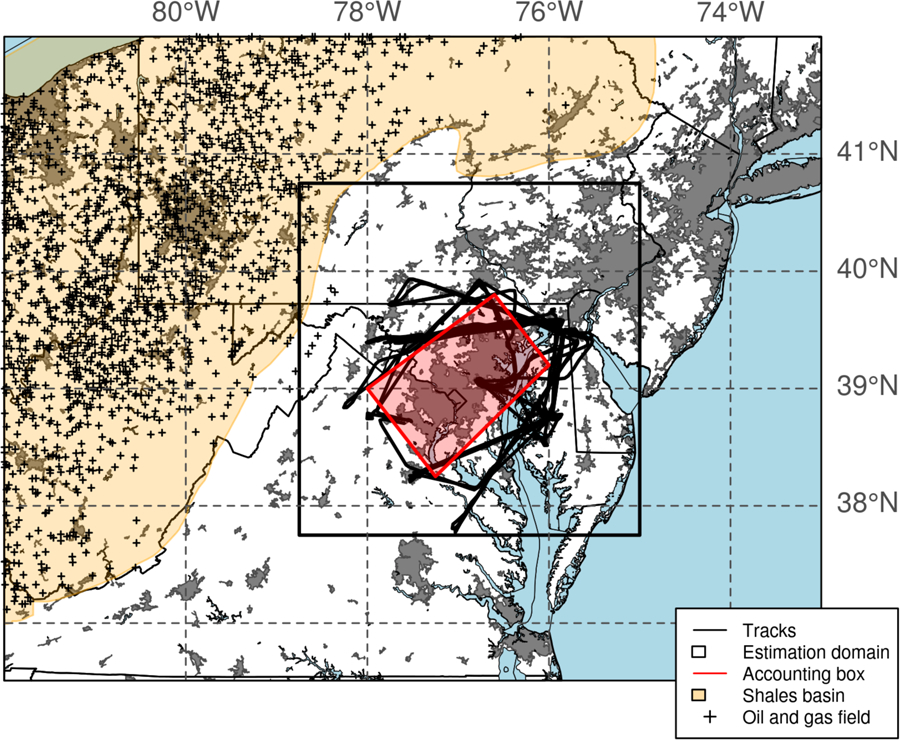
Computational domain (0.03° resolution) showing the inversion domain (black rectangle) and the outer domain (entire map) used to account for nearby outside sources. Flight tracks, Census-designated urban areas (gray shaded regions), the Marcellus, Devonian (Ohio) and Utica shale plays in the Appalachian basin and locations of the geometric center (centroid) of the oil and gas fields are also shown.²⁹ Total emissions are reported here within the accounting box (red polygon) defined by the corners: (39.80°N, 76.60°W), (39.00°N,78.00°W), (38.25°N, 77.25°W) and (39.20°N, 76.00°W).

To this end, we use an ensemble of inversions where prior emissions, transport model and observation dataset were varied. Ensemble spread and correlations between six transport models were used to construct the full model-data mismatch covariance matrix, and the background mole fraction was first estimated by using sensitivities to nearby outside sources and then further optimized within the inversion. Additionally, sensitivity tests were conducted investigating the impacts of background choice, omitting correlations in the transport error covariance matrix and changing the magnitude of the prior emission errors. We use the inversion ensemble and sensitivity tests to quantify the different sources of variability and, thus, understand the uncertainty inherent in the inverse methodology. We then investigate daily variability in estimated emissions and to what extent this variability can be explained by aliasing caused by irregular sampling of spatial and temporal variability in large sources within the study domain.

Methods

Observations

Trace gas observations from two airborne platforms were used in this study: Purdue University’s Beechcraft Duchess, housing the Airborne Laboratory for Atmospheric Research, or ALAR, (Purdue) and the University of Maryland’s Cessna 402B research aircraft (UMD). The two aircraft flew simultaneously for 5 days, mostly during afternoon hours, collecting trace gas mole fraction and meteorological data along transects at different altitudes that covered the full depth of the PBL (Fig. 1 and SI for further details). To determine the effect of withholding observations from the inversion system, we alternatively used CO₂ and CH₄ observations from both aircraft, the UMD aircraft alone, or the Purdue aircraft alone, as part of the ensemble of inversions. Purdue did not measure CO, thus the CO inversions used only UMD observations.

Bayesian Inversion Framework

We estimate trace gas emissions using a Bayesian inverse analysis^30,31 as in Lopez-Coto et al.³² Optimum posterior estimates of fluxes are obtained by minimizing the cost function J:

$$J\left(x\right)=\frac{1}{2}\left[{\left(x-x_b\right)}^T{\mathbf{P}}_b^{-1}\left(x-x_b\right)+{\left(\mathbf{H}x-y\right)}^T{\mathbf{R}}^{-1}\left(\mathbf{H}x-y\right)\right]$$ (1)

where x_b is the first guess or a priori state vector, P_b the a priori error covariance matrix which represents the uncertainties in our a priori knowledge about the fluxes and R the error covariance matrix, which represents the uncertainties in the observation operator H and the observations y, also known as model-data mismatch. The observation operator H is constructed using the sensitivity of observations to surface fluxes, or footprints (units: ppm µmol⁻¹ m² s) generated with a transport model. Here we modify the formulation to include optimization of the background in the inversion (see SI for details).

Transport Models

In order to generate an ensemble of transport models and therefore better represent the uncertainties, NOAA’s Hybrid Single-Particle Lagrangian Integrated Trajectory dispersion model (HYSPLIT)³³ was driven with 5 different meteorological products: the High Resolution Rapid Refresh (HRRR) NOAA operational forecast product³⁴ and 4 configurations of the Weather Research and Forecasting model (WRF³⁵) provided by the National Center for Atmospheric Research (NCAR) that included 4 different PBL parametrizations, 2 sources of initial and boundary conditions and the inclusion of the Building Energy Parameterization (BEP) urban canopy model in one of the configurations. In addition, the vertical mixing option in HYSPLIT also varied (Table S1 and SI for details).

Emissions Inventories

Nine CO₂ emissions inventories were used in the inversion to investigate the resultant variability in the posterior emissions (Table S2). Four of them (Vulcan (VU³⁶), ODIAC (OD³⁷), FFDAS (FF³⁸) and ACES (AC³⁹) are existing anthropogenic CO₂ inventories but for a different year; one provided only on-road emissions (DARTE (DA⁴⁰)); one is the mean of the previous five (EB); and the rest (flat (FL) and simple (SP³²)) are constructed here to complement the ensemble of prior fluxes. In addition, we use the ACES mean for February between 12 – 19 EST (AC2). Since DARTE only provided on-road emissions, a simple calculation of urban emissions was used to complement it. CH₄ prior emissions were represented using EPA’s gridded inventory (EP) for 2012,⁴¹ EDGAR v4.3.2⁴² for 2012 (EG), the mean of the previous two (EB), and a flat prior (FL). For CO we use EDGAR v4.3.2 (EG),⁴³ the National Emissions Inventory (NEI) for 2011 from EPA (NI,⁴⁴), the annual mean ACES inventory (AC as in the CO₂ case) scaled using the mean observed ∆CO: ∆CO₂ ratio (6.18 ppb/ppm) and, again, a flat prior (FL).

Background Determination

Properly accounting for the background is critical for the inversion as the flux correction is based on the observed enhancements above the background value. The impact of upwind sources can be important especially in areas such as the one under study here, where multiple sources exist in the surroundings (Fig. 1). Thus, we estimated the contribution from outside the domain using a Lagrangian approach by convolving footprints from a reduced set of our ensemble of transport models and prior fluxes. We extended the domain to the full extent shown in Fig. 1. The full background was then represented as the ensemble mean of the contribution from outside of the domain of interest (y_oc, time-varying along the track) plus the long-range background (y_lr, constant for a given flight). This methodology provided a time varying a priori background that included uncertainties that was then further optimized in the inversion (SI).

Error Covariances

i). Prior Flux Error Covariance

The prior flux error covariance represents the uncertainties in the prior estimation of the fluxes. Although bottom-up CO₂ emissions estimates are made on global and national scales with small uncertainties, considerable errors are introduced when the emissions are disaggregated to grid cells, due to the usage of proxies to spatially distribute emissions.⁴⁵ Reported errors at grid cell levels range from 4% to more than 190%, averaging about 120%.⁴⁶ For CH₄ and CO it is likely that the errors at grid cell levels are even larger than for CO₂ because of the less well-known characteristics of these species’ sources. Given these reported uncertainties at grid cell levels, we use a value of 100% of the grid cell emissions as uncertainty in this work for all the prior inventories and gases with the exception of FFDAS where we use a scaled up version of the provided uncertainties and the EB case for CO₂ where we use the standard deviation of the ensemble at each pixel to represent the uncertainties. In all cases, a covariance exponential model in space was assumed. (See SI for details)

ii). Outside Contribution (background) Prior Error Covariance

We consider a double exponential model, in space and time, to represent the error covariance of the outside contribution (y_oc) along the track. The diagonal is populated with the uncertainty of the initial guess outside contribution based on the variance from the different transport models and prior fluxes (SI).

iii). Model Error

The model-data mismatch error covariance was assumed to have three independent contributions: 1) uncertainty in the observations, 2) uncertainty in the long-range background concentration and 3) uncertainty in the transport model representation. The uncertainties in the observations have their origin in the measurement uncertainties and the representativity of the assigned mean to the averaging period (one minute in our case). This contribution is not correlated and thus the covariance was considered diagonal. The long-range background (y_lr) determination also introduces uncertainty into the system. This contribution was also assumed to be uncorrelated. Lastly, the transport model uncertainty is complex with several previously published methods for its determination. Here we tested two methods, both based on the ensemble of transport models. First, we tested a diagonal covariance populated with the inter-model variance simulated using the same surface fluxes (the prior emissions in each inversion case) in all the transport models similar to Engelen et al.⁴⁷ and Desroziers et al.⁴⁸ As stated in Engelen et al.,⁴⁷ this estimate can be too large for some models and too small for other models, thus, in order to better represent the fidelity of each model and for each observation, we weighted the inter-model standard deviation with the relative error computed by using the wind measurements from the aircraft. This definition of the transport model error covariance assumes there are no correlations in space and time which is unlikely to be true. Therefore, for the second method, which was used in the main ensemble of inversions, we computed the correlations between the different transport models and included them in the covariance matrix, leaving the first method as a sensitivity test (see SI for details).

Sensitivity Analysis

As described in the previous sections, the main inversion ensemble was composed by different prior emissions (9 for CO₂, 4 for CH₄ and 4 for CO), 6 transport models and 3 combinations of the observations for 5 flight days, totaling 1,290 inversions (810 + 360 + 120). This inversion ensemble was configured with the background and prior and transport error covariances choices that are most reasonable for the analysis. However, in order to additionally test the sensitivity of the posterior estimates to inversion setup choices that might not be as appropriate, we also investigated the effects of changing the background determination, the transport error covariance, and the prior flux error covariance, separately from the main inversion ensemble. Specifically, for the background test, we performed the inversion 1) without optimizing the Lagrangian background, 2) scaling the Lagrangian background, and 3) selecting a single constant value along the track as background defined by the 1^st, 5^th or 10^th percentile, to compare with our base case of optimizing the background (OBC1). For the scaled background case, a single scaling factor for each flight was applied to the background time series. This scaling factor was the ratio of posterior to prior emissions for the inversion case where the background was not optimized or scaled. We also tested the impact of using only a diagonal transport error covariance as well as reducing and increasing the uncertainty in the prior fluxes (50%, 100% and 200%). This sensitivity test resulted in a total of 12 cases with 15,480 individual inversions, (Table S3).

Both the main inversion ensemble and the sensitivity test were analyzed in the same fashion, grouping by cases (prior, transport, day, observation dataset or sensitivity case) and then computing the mean and quantiles as shown in Figs. 2, S7, S10, S13 and S16. The variability associated with each grouping was then computed as the standard deviation among each case’s mean value.

Figure 2:

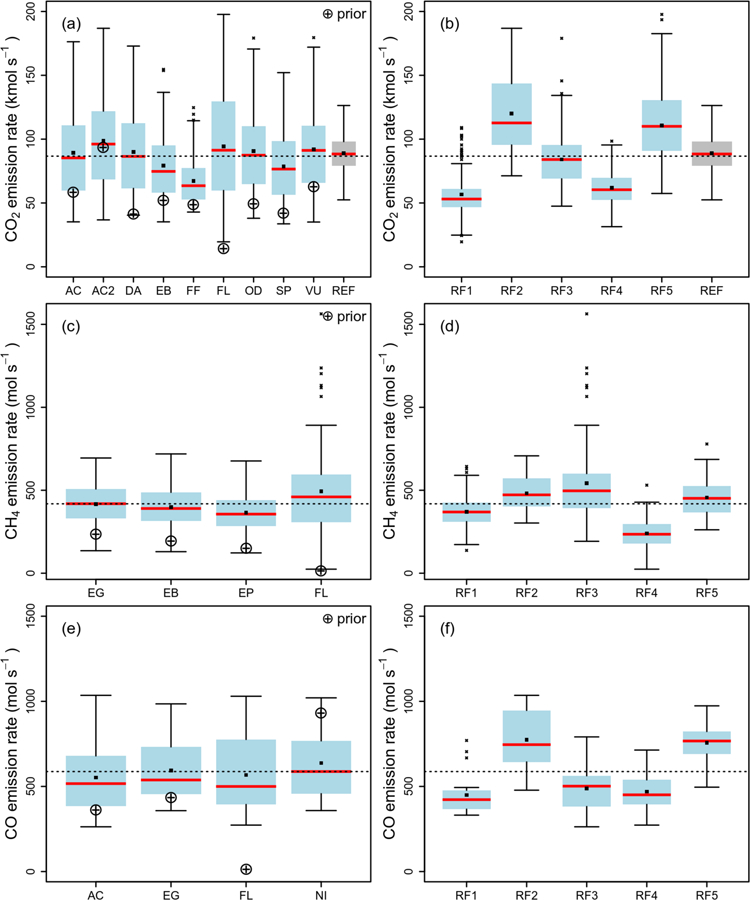
Boxplots of the total CO₂, CH₄ and CO estimated emission rate within the accounting box grouped by: (a,c,e) the different inventories used as priors and (b,d,f) the different research flights. The grey bar in panels (a,b) are the values provided by ACES, scaled to totals of 2016, for February between 12 – 19 EST (referred as REF). Blue bars indicate the 25^th to 75^th range, whiskers the range up to 1.5 times the IQR, x’s the outliers (> 1.5 x IQR), red line the median, square markers the mean and the dotted line the posterior mean. The circled pluses in panel (a,c,e) represent each prior’s total emissions. (See methods section and Tables S1 and S2 for abbreviations)

Normalized Observed Emissions

We construct an analysis to investigate whether the hourly variability of the energy generation and traffic sectors’ emissions, combined with the specific flight pattern on a given day, can explain the daily variability in the posterior CO₂ estimates. Both of these sources have publicly available data at the hourly level: Continuous Emissions Monitoring System (CEMS⁴⁹) data for power plants and Travel Monitoring Analysis System (TMAS⁵⁰) data for traffic counts. First, we sum all the power plant emissions and traffic counts within the footprint (we use the ensemble mean footprint as a mask) of each observation used in the inversion and within the defined accounting box. We match the hourly power plant emissions and traffic counts with the observation time, accounting for transport time to the point of the observation at hourly temporal resolution. Then we average this value (the sum of all traffic counts or powerplant emissions within each footprint) over all observations in each flight for each of the five flights. Using an average allows us to account for the difference in the number of observations per flight. Because traffic counts and power plant emission rates are in different units, we define the normalized observed emissions (nOE), allowing for the combination of the two sectors. We normalize counts and power plant emissions each to their respective campaign mean so that the campaign mean is equal to one. Furthermore, we use the relative contribution of the different sectors in the ACES 2011 annual mean³⁹ within the defined accounting box to construct the normalized observed emissions (nOE) for each flight as follows:

$$nO{E}_i=f_e\frac{CEM{S}_i}{\langle CEMS\rangle }+f_r\frac{TMA{S}_i}{\langle TMAS\rangle }+1-\left(f_e+f_r\right)$$ (2)

In the above definition, i is the index indicating the flight, f_e is the contribution of the electricity production sector (16%) and f_r is the contribution of the traffic emissions (46%) in ACES. The last term of Eq. 2 represents the remainder of anthropogenic CO₂ emission sectors. By this construction, the mean nOE for the campaign is also equal to 1.

Results

In the following subsections we present the main results of the analysis and discuss the variability and uncertainty of the emissions estimates. In this context, the terms variability and uncertainty are not used as synonyms. Rather, we use the term variability to describe how a property (posterior total emissions for the most part) changes (varies) with respect to different variables like time, space or model choices. The term uncertainty refers to the ability of the inverse method to represent the measurand, and it combines all sources of variability for a single day’s estimate.

Emissions Rates

Our mean estimates for the defined accounting box are 87 ± 28 kmol s⁻¹ for CO₂, 0.42 ± 0.12 kmol s⁻¹ for CH₄ and 0.59 ± 0.16 kmol s⁻¹ for CO (mean ± 1-σ) where the bounds presented here represent the posteriors’ daily variability. Ren et al.¹¹ using a mass balance method, estimated emission rates of 96 kmol s⁻¹ for CO₂, 0.57 ± 0.28 kmol s⁻¹ for CH₄ and 0.55 ± 0.27 kmol s⁻¹ for CO using the same flight observations as this study. In addition, Salmon et al.¹² estimated a CO emission rate (also using a mass balance method) of 0.54 ± 0.47 kmol s⁻¹ in February 2015. Our estimates are consistent with these within 1-σ uncertainties for both methods.

The applied inversion methodology corrected the prior inventories (Fig. 2a,c,e) by quite different amounts leading to consistent results in the posterior emissions, with variability due to choice of prior of 11%, 13% and 6% (or 9.6, 0.055 and 0.035 kmol s⁻¹) for CO₂, CH₄ and CO respectively (1-σ), significantly lower than the variability of the prior values themselves (flat prior included), 41%, 65% and 87% (or 20.8, 0.097 and 0.38 kmol s⁻¹). The flat (FL) prior led to the largest range and IQR for all of the three gases due to the loose constraint it imposed on the inversion. For CO₂, the FFDAS³⁸ prior (FF) resulted in the lowest posterior estimates as well as the lowest range and IQR due to the low prior uncertainty assigned, making it hard for the inversion to deviate from the prior values. For CH₄, the inversions using the 2012 EPA gridded inventory⁴¹ (EP) as a prior provided the lowest estimates, probably due to the lower prior emissions allocated into the urban areas and, therefore, lower prior uncertainties, making it harder to correct those areas. For CO, the scaled ACES inventory (AC) led to the lowest estimates. Variability due to transport model choice was 15% for CO₂, 13% for CH₄ and 16% for CO (1-σ), (Figs. S7c, S10c and S13c). We note that HR and MY2 provided the highest and lowest estimates respectively, while MY and BL had the most variable results. The observation dataset choice impacted the results the least, with only a 6 % standard deviation of the mean for CO₂ and 10% for CH₄ with very similar range and IQR for each of the three cases (Figs. S7d, S10d). In contrast to the relatively small effect of varying these three model choices (prior, transport model, and observation dataset), the daily variability of the estimates was 33% for CO₂ and 28% for CH₄ and CO (1-σ) (Figs. 2b,d,f). The mean estimates for each day do not overlap with the IQR of the other days and while the CO₂ and CO estimates follow a very similar pattern (as they have similar sources), they differ from that of CH₄. In addition, the coefficient of determination between the daily emission estimates for the three gases is r²=0.90 for CO vs CO₂, r²=0.40 for CO₂ vs CH₄ and r²=0.19 for CO vs CH₄. This suggests that the inversion is actually providing different estimates for each day, and that the posterior differences between days are not only the result of choices in the model set up.

The spatial distribution of the averaged CO₂ posterior emissions for each prior case shows that most of the emissions are coming from the urban areas, even in the flat prior case (Fig. S8). The results show that the roads (traffic emissions) and fine spatial scale features are only resolved in modeling results when high resolution inventories are used as the prior emissions. The inversion was able to spatially differentiate between the cities of Baltimore and Washington DC, correcting their emissions differently (Fig. S9): emissions from Washington, DC were adjusted upward in all cases while those from Baltimore were corrected downward in the cases of AC, AC2 and VU and only slightly upward for the rest.

The spatial distribution of the averaged CH₄ posterior emissions (Fig. S11) indicates that while some emissions are from urban areas, significant emissions occur NNE and NNW of the Washington - Baltimore metropolitan area as well, which is different than for CO₂. All the CH₄ priors were corrected upwards indicating an overall underestimation of emissions in the existing inventories (Fig. S12), with the strongest corrections applied to point sources outside urban areas. However, the urban areas were also corrected upward, with this correction being larger for EP than for EG or EB cases. Our posterior mean ratio to the 2012 EPA gridded inventory (EP),⁴¹ 2.73 ± 0.76, is in very good agreement with Ren et al.’s¹¹ estimate of 2.8 times the EPA values for the same region.

The spatial distribution of the mean posterior CO fluxes (Fig. S14) indicates that the CO emissions largely originate in the urban areas, as they do for CO₂. In addition, the correction (Fig. S15) is mostly applied in the urban cores, increasing the fluxes for AC, FL and EG while strongly decreasing the emissions for NI case. Due to the construction of AC for CO (using the ACES CO₂ inventory scaled by mean observed ∆CO: ∆CO₂ ratio), power plant emissions were present in the prior, while we expect the power plants ratio to be small compared to other sources. The inversion was able to correct down at least a few of them (blue dots in Fig. S15a). The NEI CO prior case was strongly corrected down over all urban areas, even in Philadelphia, indicating that the inversion is able to correct underestimation as well as overestimation in the prior. The NEI CO overestimation has been extensively reported in the literature;^22,23,51 specifically in the DC/Baltimore region a close to 50 % overestimation of the NEI CO inventory has been reported,^11,12 similar to our result of 58%.

Sensitivity Analysis

For all three gases, the diagonal model-data mismatch error covariance (EDC1) provided larger emissions estimates than the equivalent full covariance case (C1) (Fig. S16). In addition, the range and IQR within each case was larger with the diagonal covariance indicating that the off-diagonal terms played an important role in limiting the number of possible solutions. The background selection impacted both the mean estimates and the range and IQR indicating that incorrect background specification can bias the estimation results. The prior flux error sensitivity test showed that posterior emissions estimates were larger when prior uncertainties were doubled, and the range and IQR within each case was also larger indicating a potential over-fitting problem. When prior uncertainties were halved from the base case, the estimates were lower and less variable, indicating the solutions were more constrained by the prior fluxes than by the observations. This effect was similar to the FFDAS prior case for CO₂, for which the prior uncertainties were likely too small. Despite the differences described above, the variability of the mean across the sensitivity analysis cases remained relatively low, at 11% for CO₂, 17% for CH₄ and 8% for CO.

Special Case: Flat Prior

The inversions using a spatially flat prior (FL) were able to provide mean totals close to those in which an inventory prior was used for all three gases (Fig. 2). This result demonstrates the potential for using aircraft measurements to estimate an overall city-wide emission rate for a location where a spatially explicit inventory or other emissions information is unavailable. However, we have also shown that the range and IQR in the flat prior case was the greatest among all the prior cases, implying that when using a flat prior sampling more time periods (i.e. using more observations) is required to provide confidence in the estimates. The spatial distribution of the campaign-averaged posterior fluxes for CO₂, CH₄ and CO (Fig. S17) is consistent with the results obtained with the other priors as well. For example, CO₂ and CO show very similar spatial distributions with most of the emissions originating in the urban areas while CH₄ shows a broader spatial distribution. Note that these spatial patterns are a result of a campaign of 5 days with winds coming from different directions (Fig. S1), leading to a good triangulation of the source locations.

Discussion: Uncertainty and Sources of Variability

Method Combined Uncertainty

We were able to disentangle and quantify the different sources of variability present in the inversion-based emissions estimates and found that the largest source of variability in the retrieved emissions is the daily variability. In the following analysis, we omit the daily variability because the goal is to understand the uncertainty we expect in each day’s estimate and whether the daily variability is likely to be caused by general uncertainty in the method. Here we assume each source of variability is independent of the others, so that the variances can be summed to estimate the method uncertainty in each day’s estimate. We note that the assumption of independence is not likely to be true and therefore this uncertainty estimation might be biased due to not considering the correlations among them. In addition, the ensemble construction (transport, priors, observation dataset, covariances and background) might impact the ensemble spread and therefore might not be the true uncertainty in the method but it does, however, provide an indication of the likely variability introduced by the different model choices.

Three different cases are shown in Table 1 for estimating combined uncertainties. The Combined Uncertainty 1 case considers all sources of variability tested in the inversion. However, we believe that two transport models are outliers that suffer from improper mixing and resulted in biased estimations. The highest retrieved fluxes are obtained consistently using the HR configuration, suggesting that this configuration is too dispersive, although more research is needed to be more certain. The lowest posterior estimates consistently correspond to the configuration including the experimental vertical mixing parametrization (MY2), indicating that this method may under-predict vertical mixing. Removing these two outlier configurations reduces the variability due to transport model choice to 7% for CO₂, 10% for CH₄ and 8% for CO; these are used to calculate the Combined Uncertainty 2 case. Because the flight tracks are different for each aircraft, the variability due to the observation dataset may also be affected by the spatial and temporal distribution of the sources being measured, so we remove this variability to also calculate the Combined Uncertainty 3 case.

Table 1:

Sources of variability and combined uncertainty.

Source of uncertainty	ϵ CO2 (%)	ϵ CH4 (%)	ϵ CO (%)
daily	33	28	28
prior	11	13	6
transport	15	14	16
transport no outliers	7	10	8
observation dataset	6	10	6a
sensitivity	11	17	8
Combined Uncertainty 1 (prior, transport, dataset and sensitivity)	22	27	20
Combined Uncertainty 2 (prior, transport no outliers, dataset and sensitivity)	18	26	14
Combined Uncertainty 3 (prior, transport no outliers and sensitivity)	17	24	13

^aCO variability due to the observation dataset is assumed to be the same as for CO₂.

Daily Variability in Estimated Emissions: Aliasing

The daily variability in our posterior emissions from the inversion ensemble was 33% for CO₂ and 28% for CH₄ and CO (Table 1). This variability is larger than each individual source of variability as well as the three cases of the combined uncertainties as shown above, although for CH₄ the two are comparable. In order to better understand the origin of this variability in the estimates, we conducted an analysis of the temporal variability and spatial sampling of the two largest sources of CO₂ in the accounting box, according to the ACES inventory: energy generation and on-road traffic.³⁹ Thirteen power plants and 87 counting stations were used within the accounting box (Fig. S18). Both of these sources have significant variability throughout a single day, with traffic counts in the area varying by up to a factor of 20 between night time and evening rush hour depending on the location (Fig. S19, S20), and individual power plant reported emissions varying up to a factor of two within a single day, but even more between days as they sometimes shut down completely (Fig. S21). If daily means of these emissions are investigated, neither the average daily mean of powerplant emissions nor the average daily mean of traffic counts correlates with the daily mean emissions from our inversion posterior. However, the daily variability in the posterior estimates can indeed be explained using an analysis that considers the hourly variability of these two sectors’ emissions, combined with the specific flight pattern on a given day. We define each day’s normalized observed emissions (nOE, Eq. 2) using powerplant and traffic count data to conduct this analysis.

Fig. 3 shows the daily mean estimated CO₂ emissions from the inversion as a function of the normalized observed emissions (nOE), with error bars representing the 25^th and 75^th percentiles of the ensemble of inversions for each day. The correlation between the two is nearly perfect (r² = 0.97), implying that the daily variability observed by the inversion is caused by irregular spatiotemporal sampling (aliasing) of the rapidly changing underlying emissions.

Figure 3:

Estimated CO₂ emission rates (kmol s⁻¹) for each research flight as a function of the normalized observed emissions (nOE) computed using CEMS and TMAS hourly data. Errors bars correspond to 25^th and 75^th percentiles of the ensemble of inversions for each day. Red line indicates the linear fit.

These results, showing that aliasing of large hourly variability in emissions from large CO₂ sources can explain 97% of the variability in our CO₂ emissions estimate, suggest that similar spatiotemporal variability in CO and CH₄ sources could explain the variability in our estimates for those gases as well. We note that for CH₄ this is less clear due to the larger estimated uncertainty in the posterior emissions, but it is plausible given that large temporal variability in CH₄ source emissions has been reported in oil and gas production fields,^27,52 and likely exists in urban areas as well.

Path Forward

Flight campaigns are extremely useful for greenhouse gas (GHG) and pollutant emissions estimation because of the fast deployment and large spatial coverage that is provided by a moving platform. However, they are limited by the reduced temporal coverage as well as the difficulty of measuring all the areas at the same time. We have shown that this irregular sampling (in time and space) generates aliasing of the emissions impacting both the emissions estimates and the variability of those estimates. Therefore, moving forward, multiple flights over a region over different hours, days, months and seasons are recommended as well as multiple aircraft flying together with well-coordinated flight plans based on forecast back-trajectories so that the coverage of the cities can be maximized at all times. Addition of measurements from every platform (surface, aerial or from space) available should also help reduce the aliasing of emissions. This aliasing of emissions is likely not exclusive to aircraft campaigns but rather a ubiquitous problem to all monitoring systems based on spatiotemporally discrete sampling (aircraft, cars, polar orbiting satellites as well as sparse tower networks) and it must be considered when designing the measurements and interpreting the results.