Abstract
Background: Weight can be adjusted for height using the Benn parameter (kg/mB), where B is the power that minimises the correlation with height.
Aim: To investigate how the Benn parameter changes across age (10–65 years) and time (1956–2015) and differs between sexes.
Subjects and methods: The sample comprised 49,717 individuals born in 1946, 1958, 1970 or 2001. Cross-sectional estimates of the Benn parameter were produced and cohort differences at ages 10/11 and 42/43 years were examined using linear regression. Multilevel modelling was used to develop trajectories showing how the Benn parameter changed over age from childhood to mid-adulthood in the three older cohorts.
Results: The Benn parameter was closest to 2 in childhood but consistently lower across adulthood, particularly in females and the most recent cohort. At ages 10/11 years, the Benn parameter was greater than 3 in both sexes in the 2001 cohort but between 2.2 and 2.7 in the three older cohorts. This difference was estimated to be +0.67 (0.53, 0.81) in males and +0.53 (0.38, 0.68) in females, compared to the 1946 cohort, and was driven by a much higher weight SD in the 2001 cohort. Conversely, at ages 42/43 years, the Benn parameter was lowest in the 1970 cohort due to a slightly lower weight-height correlation. This difference was estimated to be −0.12 (−0.34, 0.10) in males and −0.15 (−0.42, 0.13) in females, compared to the 1946 cohort.
Conclusions: Changes over time in the obesogenic environment appear to have firstly reduced the Benn parameter due to a lowering of the weight-height correlation but secondly and more drastically increased the Benn parameter due to increasing weight variation.
Keywords: Benn parameter, Body mass index, birth year cohort, secular trend, trajectory
Introduction
The body mass index (BMI kg/m2) is an index of weight-for-height that works on the premise that weight increases proportionately to height squared, so that dividing weight by height squared results in an index that is uncorrelated with height. This is an attractive quality for researchers and clinicians who want to analyse or assess body weight while accounting for the fact that taller people are generally heavier and shorter people are generally lighter. The index was initially called the Quetelet Index after the Belgian scientist Lambert Adolphe Quetelet (Quetelet 1842). Over the following 100 or so years, numerous other formulae were proposed, including the Rohrer index (kg/m3) (Rohrer 1908; Keys et al. 1972). In a review of the published literature, Ancel Keys et al (1972) set out to decide which was the best index based on (1) the strongest correlation with weight and adiposity and (2) the weakest correlation with height. Quetelet’s Index was found to be the best “obesity index” and a change in name to the BMI was proposed. Keys’ work was, however, firmly aimed at adults. In the 1970s, weight-for-height was used in children without reference to age, partly due to convenience and also because no-one recognised the need to adjust for age as well as height. Cole’s (1979) seminal paper was the first to propose that BMI adjusted for age was a useful alternative to weight-for-height in children. By the 1980s, the BMI was used by many human biologists to adjust weight for height in both children and adults (Deutsch et al. 1985; Rosenbaum et al. 1985; Lasker and Mascie-Taylor 1989).
Today, the BMI is ubiquitous in obesity research and practice but is also widely criticised (Prentice and Jebb 2001) mainly for showing residual correlation with height and failing to distinguish between fat mass and fat-free mass (Romero-Corral et al. 2008), particularly in early-childhood (Demerath et al. 2006; Johnson et al. 2017). Note that solving this problem by measuring body composition simply transmits the dilemma of what powers of height to use to each of fat mass and fat-free mass (Wells et al. 2002; Nightingale et al. 2011). The BMI was never intended to assess obesity status in an individual but might be improved in any given sample by altering the height power to make the index truly uncorrelated with height. The Benn index does exactly this and can be calculated as kg/mB, where the Benn parameter (B) is the coefficient obtained from a general linear regression of log weight (kg) on log height (m). A coefficient of 2, as used in the calculation of BMI, would mean that as height increases by 1% weight increases by 2%. The coefficient can, of course, also be calculated as
where is the correlation between log weight and log height, is the standard deviation (SD) of log weight, and is the SD of log height (Stanton 2001).
When expressed this way, it is easy to see how the Benn parameter is influenced by variation in, and the correlation between, weight and height. Previous studies have investigated the value of the Benn parameter in different samples and at different ages, generally finding that values peak at 2.5–3.0 in puberty before declining into adulthood, where values are normally between 1.0 and 2.5 (Goldbourt and Medalie 1974; Lee et al. 1981; Garn and Pesick 1982; Cole 1986; Micozzi et al. 1986; Revicki and Israel 1986; Nevill and Holder 1995; Sperrin et al. 2016; Peterson et al. 2017). The peak occurs when it does because puberty leads to greater variation in weight and height, which stretches the weight–height ellipse along its major axis, increasing the weight–height correlation and therefore the Benn parameter. Despite there being a long history of research on this topic, no studies have modelled longitudinal data to produce trajectories showing how the Benn parameter changes with age from childhood to mid-adulthood. Previous studies have also consistently reported the Benn parameter to be lower in females than males (Goldbourt and Medalie 1974; Lee et al. 1981; Garn and Pesick 1982; Cole 1986; Micozzi et al. 1986; Revicki and Israel 1986; Nevill and Holder 1995; Sperrin et al. 2016; Peterson et al. 2017). This difference, at least in adulthood, has been explained by Burton as resulting from the fact that women have greater percentage body fat than men (Burton 2007; Flegal et al. 2009), which lowers the value of the Benn parameter because fat mass is highly variable yet has a very low correlation with height (Heymsfield et al. 2007; Burton 2015). Put differently, the greater the level of adiposity, the lower the correlation of total body weight with height (because fat mass has a very low correlation with height), and the lower the Benn parameter (Burton 2007, 2015). One might therefore have expected the Benn parameter in the general population to have declined over time, since the 1970s, alongside the development of the obesity epidemic (Flegal et al. 1998; Johnson et al. 2015). Alternatively, a secular increase in weight variation over time would have the opposite effect and increase the Benn parameter. How and why the Benn parameter has changed over time in response to shifts in the socio-political, behavioural, and nutritional landscape has not however previously been investigated.
Using longitudinal data from four large nationally-representative United Kingdom (UK) birth cohort studies, we aimed to investigate how the weight-height relationship, captured by the Benn parameter, changes across age (10–65 years), differs between sexes and varies according to time (1956–2015).
Subject and methods
Study samples
The 1946 Medical Research Council National Survey of Health and Development (1946 NSHD) is based on a sample (N = 5362) born in one week in March 1946 in England, Scotland, and Wales. The sample comprises all singleton births from women with husbands in non-manual and agricultural employment and a random selection of one in four singleton births to females with husbands in manual employment (Wadsworth et al. 2006; Kuh et al. 2011). The 1958 National Child Development Study (1958 NCDS) is based on 17,638 people born in one week in March 1958 in England, Scotland, and Wales; 920 immigrants born in the same week were incorporated during childhood (Power and Elliott 2006). A similar strategy was used in the 1970 British Cohort Study (1970 BCS), which is based on 17,287 people born in one week in April 1970, with the addition of 1814 individuals who were (1) born in Northern Ireland and included only in the birth sweep, (2) an immigrant who was incorporated into the study in childhood, or (3) never took part in any sweep (Elliott and Shepherd 2006). Finally, the 2001 Millennium Cohort Study (2001 MCS) is based on 18,818 people born between September 2000 and January 2002 who were living in England, Scotland, Wales, or Northern Ireland at age 9 months (Hansen 2012). All of the studies have received ethical approval and obtained informed parental and/or participant consent; this information is available from the study websites and/or cohort profiles.
For inclusion in the present study, participants were required to have at least one measurement of BMI during the studied age range. The resulting sample size in each study (1946 NSHD, N = 4724; 1958 NCDS, N = 16,307; 1970 BCS, N = 15,437; 2001 MCS, N = 13,249) represents more than 70% of the full cohort.
Data
In the 1946 NSHD, weight and height were assessed at data collection sweeps at target ages of 11, 15, 20 (self-reported), 26 (self-reported), 36, 43, 53, and 60–64 years. In the 1958 NCDS, weight and height were assessed at data collection sweeps at target ages of 11, 16, 23 (self-reported), 33, 42 (self-reported), 44, and 50 (self-reported) years. In the 1970 BCS, weight and height were assessed at data collection sweeps at target ages of 10, 16 (one-third self-reported), 26 (self-reported), 30 (self-reported), 34 (self-reported), and 42 (self-reported) years. In the 2001 MCS, weight and height were assessed at data collection sweeps at target ages of 11 and 14 years. These data have been collated and cleaned as part of the Cohort and Longitudinal Studies Enhancement Resources (CLOSER) initiative (Johnson et al. 2015). The data and supporting metadata are available from the UK Data Archive.
In total, there were 26,168 observations of BMI in the 1946 NSHD, 74,975 in the 1958 NCDS, 56,275 in the 1970 BCS, and 23,279 in the 2001 MCS. In the 1946 NSHD, 79% of the sample had four or more serial observations and 68% had observations spanning more than 30 years. In the 1958 NCDS, 81% of the sample had three or more serial observations and 69% had observations spanning more than 25 years. In the 1970 BCS, 72% of the sample had three or more serial observations and 62% had observations spanning more than 20 years.
Statistical analyses
BMI was computed as weight (kg)/height (m)2. Means and SDs for weight, height, and BMI at each sweep were produced stratified by sex and study. Correlations among height, weight, and BMI at each sweep were also produced stratified by sex and study.
The Benn parameter is the coefficient from the regression of log weight on log height (Benn 1971). Cross-sectional estimates were obtained by performing this regression for each study, sex, and sweep separately. All cohorts had a sweep at ages 10–11 years and three of the cohorts had a sweep at ages 42–43 years. Sex stratified regression models were applied to data pooled across the cohorts at each of the two ages. These models incorporated cohort × log height interaction terms to formally test for differences in the Benn parameter between cohorts.
Longitudinal analyses were then conducted in the 1946 NSHD, 1958 NCDS, and 1970 BCS to make use of the power of the serial data in these cohorts. For each sex and cohort separately, we modelled log weight against log height (centred at the mean) in a multilevel general linear regression framework (measurement occasion at level one and individuals at level two) with a random intercept (Equation (1) (Johnson et al. 2013a; Johnson 2015). Age was included as a fixed effect using a restricted cubic spline, with seven knots in the 1946 NSHD, six knots in the 1958 NCDS, and five knots in the 1970 BCS. Default knot locations were used based on Harrell’s (2001) recommended quantiles. The log height (or Benn) parameter was allowed to change over age through its interaction with the age spline terms. An adjustment was made for whether the data were measured or self-reported. Further, we allowed the level one variance (i.e. error) to differ according to whether the data were measured or self-reported. The model formula is given as
where and are the natural logged values at age of person is a restricted cubic spline of decimal age with up to seven knots. is a dummy variable contrasting self-reported data against measured data. are fixed effects. a random effect. is an error term for self-reported data and is an error term for measured data. The is assumed to be normally distributed with mean zero and variance The and are assumed to follow normal distributions with zero means, variances and and covariance zero.
The value of the Benn parameter at age is then calculated as
The models were used to estimate mean trajectories describing how the Benn parameter changes over age. Trajectories for the three cohorts were plotted together in a single figure, for each sex, in order to visualise secular differences in the Benn parameter.
All procedures were performed in Stata 15 (StataCorp LP, College Station, TX, USA). The command runmlwin was used for the multilevel models (Leckie G and Charlton C 2012).
Results
The mean values of weight, height, and BMI are shown in Table 1. Weight and BMI increased with age in each sex and study, while height was reassuringly stable across adulthood. Expected secular differences in BMI values were observed. For example, mean BMI at ages 10/11 years in males was 17.3 kg/m2 in the 1946 NSHD and 1958 NCDS, 16.7 kg/m2 in the 1970 BCS, and 19.1 kg/m2 in the 2001 MCS. Similarly, mean BMI at ages 42/43 years in males was 25.7 kg/m2 in the 1946 NSHD, 26.4 kg/m2 in the 1958 NCDS, and 27.5 kg/m2 in the 1970 BCS.
Table 1.
Weight, height, and BMI means.
| Males |
Females |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Age | Date | N | Weight (kg) | Height (cm) | BMI (kg/m2) | N | Weight (kg) | Height (cm) | BMI (kg/m2) | |
| 1946 NSHD | ||||||||||
| 2461 males | 11 | 1957 | 2050 | 34.3 | 140.6 | 17.3 | 1887 | 34.9 | 140.8 | 17.5 |
| 2263 females | 15 | 1961 | 1881 | 51.8 | 162.0 | 19.6 | 1700 | 51.9 | 158.4 | 20.6 |
| 20 | 1966 | 1802 | 70.9 | 176.9 | 22.6 | 1629 | 57.7 | 162.7 | 21.8 | |
| 26 | 1972 | 1822 | 73.6 | 177.1 | 23.4 | 1782 | 59.0 | 162.4 | 22.4 | |
| 36 | 1982 | 1631 | 76.5 | 175.3 | 24.8 | 1618 | 62.1 | 162.3 | 23.5 | |
| 43 | 1989 | 1612 | 79.0 | 175.3 | 25.7 | 1595 | 66.2 | 162.3 | 25.2 | |
| 53 | 1999 | 1451 | 83.7 | 174.6 | 27.4 | 1494 | 71.6 | 161.6 | 27.5 | |
| 60–64 | 2006–2010 | 1059 | 85.4 | 174.8 | 27.9 | 1155 | 72.9 | 161.7 | 27.9 | |
| 1958 NCDS | ||||||||||
| 8357 males | 11 | 1969 | 6381 | 36.0 | 143.9 | 17.3 | 6117 | 37.2 | 144.8 | 17.6 |
| 7950 females | 16 | 1974 | 5697 | 58.9 | 170.2 | 20.2 | 5342 | 54.4 | 160.9 | 21.0 |
| 23 | 1981 | 6124 | 72.7 | 177.3 | 23.1 | 6145 | 58.2 | 162.2 | 21.1 | |
| 33 | 1991 | 5379 | 79.8 | 176.8 | 25.5 | 5321 | 65.1 | 162.9 | 24.5 | |
| 42 | 2000 | 5465 | 83.3 | 177.3 | 26.4 | 5574 | 67.0 | 162.6 | 25.3 | |
| 44 | 2002 | 4576 | 86.3 | 175.9 | 27.8 | 4618 | 71.2 | 162.5 | 27.0 | |
| 50 | 2008 | 4139 | 87.0 | 176.2 | 28.0 | 4097 | 70.7 | 162.6 | 26.8 | |
| 1970 BCS | ||||||||||
| 7923 males | 10 | 1980 | 6251 | 32.2 | 138.7 | 16.7 | 5908 | 32.8 | 138.4 | 17.0 |
| 7514 females | 16 | 1986 | 3713 | 63.1 | 173.8 | 20.8 | 4213 | 56.5 | 162.8 | 21.3 |
| 26 | 1996 | 2576 | 74.9 | 175.3 | 24.4 | 4697 | 62.8 | 164.6 | 23.2 | |
| 30 | 2000 | 5313 | 81.4 | 178.5 | 25.5 | 5559 | 65.4 | 164.2 | 24.3 | |
| 34 | 2004 | 4521 | 84.6 | 178.5 | 26.5 | 4794 | 67.9 | 164.2 | 25.2 | |
| 42 | 2012 | 4298 | 87.7 | 178.6 | 27.5 | 4433 | 70.6 | 164.2 | 26.2 | |
| 2001 MCS | ||||||||||
| 6702 males | 11 | 2012 | 6342 | 40.9 | 145.9 | 19.1 | 6238 | 42.2 | 146.7 | 19.4 |
| 6547 females | 14 | 2015 | 5406 | 58.6 | 166.8 | 21.0 | 5293 | 57.1 | 161.0 | 21.9 |
The SDs for weight showed a similar pattern of between-cohort differences (Table 2). For example, the weight SD at ages 10/11 years in males was 6.0 kg/m2 in the 1946 NSHD, 6.9 kg/m2 in the 1958 NCDS, 4.9 kg/m2 in the 1970 BCS, and 9.9 kg/m2 in the 2001 MCS. Similarly, the weight SD at ages 42/43 years in males was 12.1 kg/m2 in the 1946 NSHD, 13.7 kg/m2 in the 1958 NCDS, and 15.7 kg/m2 in the 1970 BCS. Because the height SDs were approximately the same in each cohort (at comparable ages), the BMI SDs demonstrated a similar pattern of between-cohort differences as those for weight.
Table 2.
Weight, height, and BMI standard deviations.
| Males |
Females |
|||||||
|---|---|---|---|---|---|---|---|---|
| Age | Date | Weight (kg) | Height (cm) | BMI (kg/m2) | Weight (kg) | Height (cm) | BMI (kg/m2) | |
| 1946 NSHD | ||||||||
| 11 | 1957 | 6.0 | 6.7 | 2.1 | 7.1 | 7.1 | 2.6 | |
| 15 | 1961 | 9.6 | 8.9 | 2.4 | 8.8 | 6.3 | 3.0 | |
| 20 | 1966 | 9.2 | 6.8 | 2.5 | 8.4 | 6.3 | 2.9 | |
| 26 | 1972 | 10.0 | 6.5 | 2.8 | 9.2 | 6.4 | 3.2 | |
| 36 | 1982 | 11.4 | 6.6 | 3.2 | 11.3 | 6.1 | 4.1 | |
| 43 | 1989 | 12.1 | 6.6 | 3.5 | 12.8 | 6.0 | 4.8 | |
| 53 | 1999 | 13.6 | 6.6 | 4.0 | 14.3 | 6.0 | 5.5 | |
| 60–64 | 2006–2010 | 13.5 | 6.6 | 4.1 | 14.1 | 5.9 | 5.3 | |
| 1958 NCDS | ||||||||
| 11 | 1969 | 6.9 | 6.9 | 2.4 | 7.7 | 7.5 | 2.7 | |
| 16 | 1974 | 10.3 | 7.9 | 2.7 | 8.5 | 6.2 | 3.0 | |
| 23 | 1981 | 10.4 | 7.0 | 2.9 | 9.1 | 6.6 | 3.2 | |
| 33 | 1991 | 12.9 | 6.7 | 3.7 | 13.4 | 6.4 | 4.9 | |
| 42 | 2000 | 13.7 | 6.7 | 3.9 | 13.6 | 6.6 | 5.0 | |
| 44 | 2002 | 14.6 | 6.6 | 4.3 | 15.2 | 6.2 | 5.6 | |
| 50 | 2008 | 15.3 | 6.6 | 4.5 | 15.0 | 6.2 | 5.5 | |
| 1970 BCS | ||||||||
| 10 | 1980 | 4.9 | 6.2 | 1.9 | 5.7 | 6.4 | 2.3 | |
| 16 | 1986 | 10.4 | 8.5 | 3.0 | 8.8 | 6.7 | 3.1 | |
| 26 | 1996 | 11.1 | 5.2 | 3.4 | 11.2 | 6.8 | 4.0 | |
| 30 | 2000 | 13.5 | 7.2 | 3.8 | 13.0 | 6.9 | 4.7 | |
| 34 | 2004 | 14.6 | 7.2 | 4.2 | 14.1 | 6.8 | 5.1 | |
| 42 | 2012 | 15.7 | 7.1 | 4.6 | 15.3 | 6.9 | 5.6 | |
| 2001 MCS | ||||||||
| 11 | 2012 | 9.9 | 7.1 | 3.6 | 10.3 | 7.4 | 3.7 | |
| 14 | 2015 | 13.6 | 8.7 | 4.0 | 12.0 | 6.4 | 4.2 | |
As shown in Table 3, the weight–height correlations generally decreased over age and were lower in females than males. They also appeared to decrease over time, most noticeably in adulthood in males. For example, the correlation at ages 42/43 years in males was 0.46 in the 1946 NSHD, 0.44 in the 1958 NCDS, and 0.39 in the 1970 BCS. The BMI-height correlations were positive at age 10/11 years but switched to be negative at age 20 years in the 1946 NSHD, age 23 years for males and age 16 years for females in the 1958 NCDS, and age 16 years in the 1970 BCS. Further, the negative adulthood BMI-height correlations were consistently stronger for females than males.
Table 3.
Weight, height, and BMI correlations.
| Males |
Females |
|||||||
|---|---|---|---|---|---|---|---|---|
| Age | Date | Weight Height |
BMI Weight |
BMI Height |
Weight Height |
BMI Weight |
BMI Height |
|
| 1946 NSHD | ||||||||
| 11 | 1957 | 0.69 | 0.84 | 0.19 | 0.66 | 0.87 | 0.22 | |
| 15 | 1961 | 0.75 | 0.82 | 0.26 | 0.50 | 0.88 | 0.04 | |
| 20 | 1966 | 0.55 | 0.81 | −0.05 | 0.45 | 0.84 | −0.10 | |
| 26 | 1972 | 0.48 | 0.84 | −0.07 | 0.39 | 0.87 | −0.12 | |
| 36 | 1982 | 0.49 | 0.86 | −0.02 | 0.34 | 0.91 | −0.08 | |
| 43 | 1989 | 0.46 | 0.87 | −0.03 | 0.26 | 0.92 | −0.13 | |
| 53 | 1999 | 0.42 | 0.89 | −0.04 | 0.22 | 0.93 | −0.16 | |
| 60–64 | 2006–2010 | 0.39 | 0.88 | −0.09 | 0.26 | 0.92 | −0.12 | |
| 1958 NCDS | ||||||||
| 11 | 1969 | 0.68 | 0.87 | 0.23 | 0.68 | 0.87 | 0.24 | |
| 16 | 1974 | 0.65 | 0.86 | 0.17 | 0.44 | 0.87 | −0.06 | |
| 23 | 1981 | 0.49 | 0.83 | −0.07 | 0.39 | 0.85 | −0.14 | |
| 33 | 1991 | 0.43 | 0.88 | −0.04 | 0.29 | 0.92 | −0.10 | |
| 42 | 2000 | 0.44 | 0.88 | −0.02 | 0.29 | 0.91 | −0.12 | |
| 44 | 2002 | 0.41 | 0.89 | −0.04 | 0.27 | 0.93 | −0.09 | |
| 50 | 2008 | 0.40 | 0.90 | −0.03 | 0.27 | 0.93 | −0.10 | |
| 1970 BCS | ||||||||
| 10 | 1980 | 0.65 | 0.81 | 0.08 | 0.64 | 0.84 | 0.13 | |
| 16 | 1986 | 0.54 | 0.80 | −0.07 | 0.40 | 0.84 | −0.15 | |
| 26 | 1996 | 0.34 | 0.91 | −0.07 | 0.33 | 0.89 | −0.13 | |
| 30 | 2000 | 0.44 | 0.87 | −0.05 | 0.29 | 0.90 | −0.14 | |
| 34 | 2004 | 0.42 | 0.88 | −0.05 | 0.26 | 0.91 | −0.14 | |
| 42 | 2012 | 0.39 | 0.89 | −0.06 | 0.24 | 0.92 | −0.15 | |
| 2001 MCS | ||||||||
| 11 | 2012 | 0.64 | 0.92 | 0.30 | 0.65 | 0.92 | 0.30 | |
| 14 | 2015 | 0.57 | 0.90 | 0.16 | 0.43 | 0.93 | 0.07 | |
Cross-sectional estimates of the Benn parameter are presented in Table 4. At ages 10/11 years, the Benn parameter was greater than 3 in both sexes in the 2001 MCS but between 2.2 and 2.7 in the three older cohorts. Compared to the 1946 NSHD, this cohort difference was estimated to be +0.67 (0.53, 0.81) in males and +0.53 (0.38, 0.68) in females (Table 5). Conversely, at ages 42/43 years, the Benn parameter was lowest in the 1970 BCS. Compared to the 1946 NSHD, this cohort difference was, however, estimated to only be −0.12 (−0.34, 0.10) in males and −0.15 (−0.42, 0.13) in females.
Table 4.
Cross-sectional estimates of the Benn parameter.
| Age | Date | Males | Females | |
|---|---|---|---|---|
| 1946 NSHD | ||||
| 11 | 1957 | 2.44 | 2.58 | |
| 15 | 1961 | 2.60 | 2.12 | |
| 20 | 1966 | 1.87 | 1.70 | |
| 26 | 1972 | 1.77 | 1.56 | |
| 36 | 1982 | 1.95 | 1.67 | |
| 43 | 1989 | 1.90 | 1.39 | |
| 53 | 1999 | 1.82 | 1.21 | |
| 60–64 | 2006–2010 | 1.66 | 1.41 | |
| 1958 NCDS | ||||
| 11 | 1969 | 2.61 | 2.69 | |
| 16 | 1974 | 2.50 | 1.79 | |
| 23 | 1981 | 1.79 | 1.51 | |
| 33 | 1991 | 1.85 | 1.52 | |
| 42 | 2000 | 1.92 | 1.46 | |
| 44 | 2002 | 1.84 | 1.52 | |
| 50 | 2008 | 1.87 | 1.49 | |
| 1970 BCS | ||||
| 10 | 1980 | 2.20 | 2.36 | |
| 16 | 1986 | 1.86 | 1.51 | |
| 26 | 1996 | 1.71 | 1.48 | |
| 30 | 2000 | 1.84 | 1.39 | |
| 34 | 2004 | 1.81 | 1.32 | |
| 42 | 2012 | 1.78 | 1.24 | |
| 2001 MCS | ||||
| 11 | 2012 | 3.11 | 3.12 | |
| 14 | 2015 | 2.61 | 2.34 |
Table 5.
Estimated differences in the Benn parameter between cohorts at two ages.
| Males |
Females |
|||||
|---|---|---|---|---|---|---|
| B | 95% CI | p | B | 95% CI | p | |
| 10/11 years | ||||||
| 1946 NSHD (referent) | – | – | – | – | – | – |
| 1958 NCDS | 0.17 | 0.03, 0.31 | .02 | 0.10 | −0.05, 0.25 | .18 |
| 1970 BCS | −0.24 | −0.38, −0.10 | .001 | −0.22 | −0.38, −0.07 | .005 |
| 2001 MCS | 0.67 | 0.53, 0.81 | <.001 | 0.53 | 0.38, 0.68 | <.001 |
| 42/43 years | ||||||
| 1946 NSHD (referent) | – | – | – | – | – | – |
| 1958 NCDS | 0.02 | −0.20, 0.23 | .88 | 0.08 | −0.19, 0.35 | .57 |
| 1970 BCS | −0.12 | −0.34, 0.10 | .28 | −0.15 | −0.42, 0.13 | .30 |
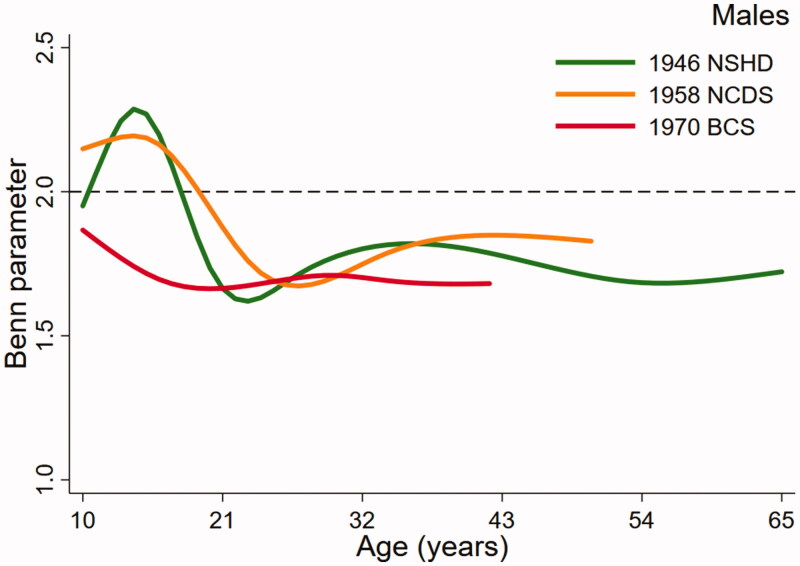
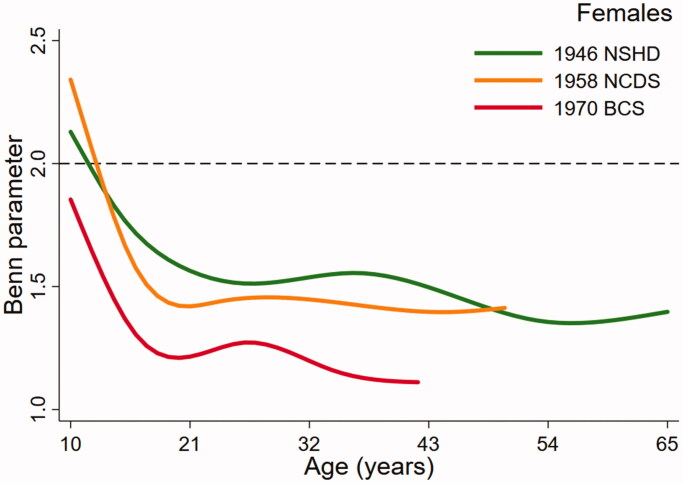
Figures 1 (males) and 2 (females), the key output from the multilevel models, present trajectories describing how the Benn parameter changes over age in study. The dashed reference line at 2 represents the height power for BMI (i.e. kg/m2). The Benn parameter for each sex and cohort was closest to 2 in childhood but was consistently lower than 2 across adulthood, particularly in females. For example, the estimated Benn parameter for females in the 1970 BCS was close to 1 at 42 years of age. There were also noticeable differences in the trajectories between the studies. Males in the 1946 NSHD demonstrated a clear peak in the Benn parameter in adolescence that was less obvious in the 1958 NCDS and not present at all in the 1970 BCS. For females, the shape of the trajectory was similar in each cohort, declining across adolescence before plateauing in adulthood. In both sexes, the trajectory for the 1970 cohort was generally lower than the trajectories for the 1946 NSHD and 1958 NCDS cohorts. A secular trend towards a lower Benn parameter trajectory was, however, clearer in females than males.
Figure 1.
Benn parameter trajectories for males, estimated using multilevel models.
Figure 2.
Benn parameter trajectories for females, estimated using multilevel models.
Discussion
In this paper, we demonstrate how the best power with which to raise height, termed the Benn parameter, changes over age and is lower in females compared to males. The key and novel findings, however, are that the Benn parameter was slightly lower in the 1970 cohort compared to the older cohorts because of a slightly lower weight-height correlation, but much higher in childhood in the 2001 cohort compared to the older cohorts because of much greater variation in weight.
Previous studies have derived age- and sex-specific height scaling powers for the computation of the Benn index. Cole (1986) reported that the optimal power is approximately 2 in pre-school children, increasing to a peak of around 3 in puberty that occurred 18-months earlier in girls than in boys, before decreasing into adulthood. The fact that we only observed a peak in adolescence in males in the 1946 NSHD is probably because we only had childhood/adolescent data at 10/11 and 15/16 years of age, so had no information to identify a peak in between these ages. Peterson et al (2017) similarly found limited evidence of a peak in a recent analysis of the 1999–2006 US National Health and Nutrition Examination Surveys (NHANES), perhaps owing to the data being cross-sectional and grouped into age bins (e.g. 12–13 years). Other studies have similarly investigated the Benn parameter at various ages and in different populations; values during adulthood are normally between 1.1 and 2.5 and typically lower in women than in men (Goldbourt and Medalie 1974; Lee et al. 1981; Garn and Pesick 1982; Micozzi et al. 1986; Revicki and Israel 1986; Nevill and Holder 1995). No studies have, however, modelled longitudinal data to produce trajectories of the Benn parameter spanning up to 55 years of life, as we have done in the present paper. Sperrin et al (2016) have produced trajectories based on serial cross-sectional Health Survey for England data and observed the Benn parameter to be fairly stable and approximate 2.0 for men and 1.5 for women between 20 and 70 years of age. They did not find any evidence that the Benn parameter had changed over time between 1991 and 2011 but did conclude that ‘longitudinal studies across a variety of cohorts samples’ are needed (Sperrin et al. 2016).
The proportion of a person’s weight that is fat, as opposed to lean tissue or bone, is on average higher among women than men (Heo et al. 2012). Fat has a lower correlation with height than muscle does (Burton 2007, 2015) resulting in a lower weight–height correlation in females compared to males, as documented in the present study. A lower weight–height correlation results in a lower Benn parameter, so it makes sense that height needs to be raised to a lower power for females compared to males. Fat is also more variable than fat-free mass (Burton 2007), which has an opposing effect and increases the Benn parameter. However, at least as far as sex differences are concerned, it appears that this opposing effect does not overpower the effect of the lower weight–height correlation.
Different levels of variation in, and correlation between, weight and height can help explain why the Benn parameter takes different values in different groups of individuals, be these morphological, geographical, or secular. Here, we demonstrate that the Benn parameter is not static over time but has altered in response to shifts in the socio-political, behavioural, and nutritional landscape. The obesity epidemic really started in the 1970s (Flegal et al. 1998; Johnson et al. 2012a; Johnson et al. 2015) and the 1970 BCS cohort has therefore experienced the worsening obesogenic environment across their entire lives. The Benn parameter tended to be slightly lower in the 1970 BCS compared to the older cohorts, because of a slightly lower weight–height correlation. This secular difference was clearer in females than males; this could be explained by a stronger positive secular trend in adiposity in females than males, although evidence to support this theory is mixed (Okosun et al. 2004; Li et al. 2006; Li et al. 2007; Johnson et al. 2013b; Freedman et al. 2017). The estimated difference in the Benn parameter between the 1970 BCS and the 1946 NSHD was larger at ages 10/11 years than 42/43 years, perhaps because at later ages, the environment was more obesogenic and this increased the weight SD (which has the opposite effect on the Benn parameter compared to the decreasing weight-height correlation). It, therefore, follows that the Benn parameter was much higher in childhood in the 2001 cohort compared to the older cohorts because of much greater variation in weight but only a marginally lower weight-height correlation. The finding that the Benn parameter was approximately 3 in contemporary pubertal children is in agreement with literature reporting the tri-ponderal mass index (kg/m3) to be a better indicator of body fat levels in modern-day adolescences than BMI (Peterson et al. 2017).
Despite the BMI not being computed using the power that best minimises its correlation with height, the index is ubiquitous in obesity research and practice. A different height scaling power has not been universally accepted and applied, perhaps because changing the Benn parameter apparently has little influence on the resulting index. For example, in males at age 60–64 years in the 1946 NSHD, the correlation between kg/m2 and kg/m1.5 is 0.99 and the percentage variation in each index explained by height is 0.4% and 0.07%, respectively. Such a high correlation does not, however, mean that BMI is not a biased weight-for-height index. Using the example above, the concordance (which incorporates a bias correction factor) is actually only 0.45 (Lin 1989). Even if there are no biases, the idea that the BMI should ideally be uncorrelated with height is questionable. As shown by Benn (1971), minimising the correlation of a weight-for-height index with height only maximises the association between the index and adiposity if height and adiposity are uncorrelated. This is not normally true, particularly during childhood and adolescence when there are strong temporal relationships between skeletal dimensions and tissue accretion during growth and development (Dunger et al. 2005; Johnson et al. 2012b; Cole et al. 2014; Bell et al. 2018). Garn and Haskell (1959, 1960) showed that children with greater levels of body fat were indeed taller and entered puberty earlier, and this finding has been replicated more recently in the EarlyBird study (Metcalf et al. 2011). This might explain why we observed small positive BMI–height correlations in childhood/adolescence in the present study. If the purpose of a weight-for-height index is to assess health risk, rather than weight independent of height per se, then making the index uncorrelated with height might not be the goal. Indeed, being tall in childhood/adolescence or short in adulthood are associated with various non-communicable diseases, independently of adiposity (Emerging Risk Factors Collaboration 2012; Grijalva-Eternod et al. 2013; Wells and Cole 2014). The idea that part of the risk apportioned by BMI is not due to adiposity is not often thoroughly considered but could be tested empirically in epidemiology papers (Wells 2014; Gracia-Marco et al. 2016).
An evolutionary perspective
Evolutionary life history theory assumes that the resources available to an organism in any environment are finite, and that each organism has been selected to allocate those resources in ways that maximise reproductive fitness (Stearns 1992). The four key functions are maintenance, growth, reproduction, and defence (Wells et al. 2017). Height is clearly a marker of growth, either ongoing or completed. Fat-free mass is a marker not only of growth but also of maintenance (given that it incorporates the vital organs) and reproduction (since muscle mass promotes sexual signalling in males, while fat-free mass is a stronger predictor of offspring birth weight in females). Fat mass can be considered a marker of defence, as adipose tissue contributes both energy and molecular precursors to immune function (Wells et al. 2019). Trade-offs between different life history functions may manifest at the level of these body components and this may explain why associations between height, fat mass, and fat-free mass may vary substantially between population sub-groups. In Peru, for example, the correlation between childhood height and waist circumference is negative in harsher high-altitude settings (indicating a trade-off between growth and defence) but positive in more favourable lowland settings (Pomeroy et al. 2014). These insights may help understand the variable values taken by the Benn index observed in the present study, where the emergence of the obesogenic niche is altering ways in which height growth is correlated with accretion of fat mass and fat-free mass. If both the numerator (the sum of fat mass and fat-free mass) and the denominator (height) not only respond similarly to ecological factors but also do so in coordinated ways that vary by age and setting, then a single statistical solution may be unrealistic.
Strengths and limitations
The key strength of this paper lies in the longitudinal analysis on the relationship of weight with height across age (10–65 years) and time (1956–2015) in 49,717 males and females with 180,697 serial observations. Attrition over follow-up was observed (e.g. 43% fewer observations at age 60–64 years compared to age 11 years in the 1946 NSHD), but this is handled by the multilevel models under a missing at random assumption. While the four birth cohort studies were designed to be nationally representative at initiation, ethnic diversity is low and even in the 1970 BCS sample only about 5% were non-white British. In the 2001 MCS sample approximately 15% were non-white British. The association of BMI with body fat differs between ethnicities (Hudda et al. 2017, 2018), but the extent to which this is because the weight-height relationship is not properly captured by raising height to a power of 2 in some ethic groups needs further investigation. Body composition data are limited in the studies, so we were not able to assess the relationship of BMI with body composition (over age, time, and sex) and how this might depend on the Benn parameter.
Conclusion
This paper demonstrates how the Benn parameter (the optimal height scaling power to create an index of weight that is minimally correlated with height) is not consistent because the degree to which weight and height vary and correlate with each other differs between sexes and changes across age and time. Changes over time in the obesogenic environment appear to have first reduced the Benn parameter due to a lowering of the weight–height correlation but second and more drastically increased the Benn parameter due to increasing weight variation. If population levels of obesity continue to rise as a result of the weight distribution becoming increasingly right skewed, the call to replace BMI with the tri-ponderal mass index (kg/m3) may become more valid.
Funding Statement
This work was supported by the UK Medical Research Council (WJ New Investigator Research Grant: MR/P023347/1). RH is Director of the CLOSER consortium which is supported by funding from the Economic and Social Research Council (ESRC) and the UK Medical Research Council. An initial grant for this work was awarded to CLOSER in 2012 and extended, by the ESRC, in 2017 (award reference: ES/K000357/1). RH was supported by the UK Medical Research Council (Programme code: MC_UU_12019/2). The UK Medical Research Council provides core funding for the MRC National Survey of Health and Development.
Acknowledgements
W. J. acknowledges support from the National Institute for Health Research (NIHR) Leicester Biomedical Research Centre, which is a partnership between University Hospitals of Leicester NHS Trust, Loughborough University, and the University of Leicester. All the funding sources had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author contributions
WJ conceptualised the study, carried out the analyses, and drafted the initial manuscript. All authors made substantial contributions to the interpretation of the data, revised the manuscript critically for important intellectual content, gave final approval of the version to be published, and agree to be accountable for all aspects of the work.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- Bell JA, Carslake D, Wade KH, Richmond RC, Langdon RJ, Vincent EE, Holmes MV, Timpson NJ, et al. 2018. Influence of puberty timing on adiposity and cardiometabolic traits: a Mendelian randomisation study. PLOS Med. 15(8):e1002641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benn RT. 1971. Some mathematical properties of weight-for-height indices used as measures of adiposity. Br J Prev Soc Med. 25(1):42–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton RF. 2007. Why is the body mass index calculated as mass/height2, not as mass/height3? Ann Hum Biol. 34(6):656–663. [DOI] [PubMed] [Google Scholar]
- Burton RF. 2015. Adult fat content: reinterpreting and modelling the Benn Index and related sex differences. Ann Hum Biol. 42(1):91–96. [DOI] [PubMed] [Google Scholar]
- Cole TJ. 1979. A method for assessing age-standardized weight-for-height in children seen cross-sectionally. Ann Hum Biol. 6(3):249–268. [DOI] [PubMed] [Google Scholar]
- Cole TJ. 1986. Weight/height compared to weight/height2 for assessing adiposity in childhood: influence of age and bone age on p during puberty. Ann Hum Biol. 13(5):433–451. [DOI] [PubMed] [Google Scholar]
- Cole TJ, Pan H, Butler GE. 2014. A mixed effects model to estimate timing and intensity of pubertal growth from height and secondary sexual characteristics. Ann Hum Biol. 41(1):76–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demerath EW, Schubert CM, Maynard LM, Sun SS, Chumlea WC, Pickoff A, Czerwinski SA, Towne B, et al. 2006. Do changes in body mass index percentile reflect changes in body composition in children? Data from the Fels Longitudinal Study. Pediatrics. 117(3):e487–e495. [DOI] [PubMed] [Google Scholar]
- Deutsch MI, Mueller WH, Malina RM. 1985. Androgyny in fat patterning is associated with obesity in adolescents and young adults. Ann Hum Biol. 12(3):275–286. [DOI] [PubMed] [Google Scholar]
- Dunger DB, Ahmed ML, Ong KK. 2005. Effects of obesity on growth and puberty. Best Pract Res Clin Endocrinol Metab. 19(3):375–390. [DOI] [PubMed] [Google Scholar]
- Elliott J, Shepherd P. 2006. Cohort profile: 1970 British Birth Cohort (BCS70). Int J Epidemiol. 35(4):836–843. [DOI] [PubMed] [Google Scholar]
- Emerging Risk Factors Collaboration. 2012. Adult height and the risk of cause-specific death and vascular morbidity in 1 million people: individual participant meta-analysis. Int J Epidemiol. 41(5):1419–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flegal KM, Carroll MD, Kuczmarski RJ, Johnson CL. 1998. Overweight and obesity in the United States: prevalence and trends, 1960–1994. Int J Obes. 22(1):39–47. [DOI] [PubMed] [Google Scholar]
- Flegal KM, Shepherd JA, Looker AC, Graubard BI, Borrud LG, Ogden CL, Harris TB, Everhart JE, et al. 2009. Comparisons of percentage body fat, body mass index, waist circumference, and waist-stature ratio in adults. Am J Clin Nutr. 89(2):500–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman DS, Zemel BS, Ogden CL. 2017. Secular trends for skinfolds differ from those for BMI and waist circumference among adults examined in NHANES from 1988–1994 through 2009–2010. Am J Clin Nutr. 105(1):169–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garn SM, Haskell JA. 1959. Fat and growth during childhood. Science. 130(3390):1711–1712. [DOI] [PubMed] [Google Scholar]
- Garn SM, Haskell JA. 1960. Fat thickness and developmental status in childhood and adolescence. Arch Pediatr Adolesc Med. 99:746–751. [DOI] [PubMed] [Google Scholar]
- Garn SM, Pesick SD. 1982. Comparison of the Benn index and other body mass indices in nutritional assessment. Am J Clin Nutr. 36(4):573–575. [DOI] [PubMed] [Google Scholar]
- Goldbourt U, Medalie JH. 1974. Weight-height indices. Choice of the most suitable index and its association with selected variables among 10,000 adult males of heterogeneous origin. Br J Prev Soc Med. 28(2):116–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gracia-Marco L, Moreno LA, Ruiz JR, Ortega FB, de Moraes AC, Gottrand F, Roccaldo R, Marcos A, et al. 2016. Body composition indices and single and clustered cardiovascular disease risk factors in adolescents: providing clinical-based cut-points. Prog Cardiovasc Dis. 58(5):555–564. [DOI] [PubMed] [Google Scholar]
- Grijalva-Eternod CS, Lawlor DA, Wells JC. 2013. Testing a capacity-load model for hypertension: disentangling early and late growth effects on childhood blood pressure in a prospective birth cohort. PLOS One. 8(2):e56078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen K. 2012. Millennium Cohort Study first, second, third and fourth surveys: a guide to the datasets, 6th ed. London (UK): Centre for Longitudinal Studies, University of London. [Google Scholar]
- Harrell FJ. 2001. Regression modeling strategies. New York, USA: Springer Publishing Company. [Google Scholar]
- Heo M, Faith MS, Pietrobelli A, Heymsfield SB. 2012. Percentage of body fat cutoffs by sex, age, and race-ethnicity in the US adult population from NHANES 1999–2004. Am J Clin Nutr. 95(3):594–602. [DOI] [PubMed] [Google Scholar]
- Heymsfield SB, Gallagher D, Mayer L, Beetsch J, Pietrobelli A. 2007. Scaling of human body composition to stature: new insights into body mass index. Am J Clin Nutr. 86(1):82–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudda MT, Nightingale CM, Donin AS, Fewtrell MS, Haroun D, Lum S, Williams JE, Owen CG, et al. 2017. Body mass index adjustments to increase the validity of body fatness assessment in UK Black African and South Asian children. Int J Obes. 41(7):1048–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudda MT, Nightingale CM, Donin AS, Owen CG, Rudnicka AR, Wells JCK, Rutter H, Cook DG, et al. 2018. Patterns of childhood body mass index (BMI), overweight and obesity in South Asian and black participants in the English National child measurement programme: effect of applying BMI adjustments standardising for ethnic differences in BMI-body fatness associations. Int J Obes. 42(4):662–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W. 2015. Analytical strategies in human growth research. Am J Hum Biol. 27(1):69–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Balakrishna N, Griffiths PL. 2013a. Modeling physical growth using mixed effects models. Am J Phys Anthropol. 150(1):58–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Choh AC, Lee M, Towne B, Czerwinski SA, Demerath EW. 2017. Is infant body mass index associated with adulthood body composition trajectories? An exploratory analysis. Pediatr Obes. 12(1):10–18. [DOI] [PubMed] [Google Scholar]
- Johnson W, Chumlea WC, Czerwinski SA, Demerath EW. 2013b. Secular trends in the fat and fat-free components of body mass index in children aged 8–18 years born 1958–1995. Ann Hum Biol. 40(1):107–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Li L, Kuh D, Hardy R. 2015. How has the age-related process of overweight or obesity development changed over time? Co-ordinated analyses of individual participant data from five United Kingdom Birth Cohorts. PLoS Med. 12(5):e1001828; discussion e1001828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Soloway LE, Erickson D, Choh AC, Lee M, Chumlea WC, Siervogel RM, Czerwinski SA, et al. 2012a. A changing pattern of childhood BMI growth during the 20th century: 70 y of data from the Fels Longitudinal Study. Am J Clin Nutr. 95(5):1136–1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Stovitz SD, Choh AC, Czerwinski SA, Towne B, Demerath EW. 2012b. Patterns of linear growth and skeletal maturation from birth to 18 years of age in overweight young adults. Int J Obes. 36(4):535–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keys A, Fidanza F, Karvonen MJ, Kimura N, Taylor HL. 1972. Indices of relative weight and obesity. J Chronic Dis. 25(6–7):329–343. [DOI] [PubMed] [Google Scholar]
- Kuh D, Pierce M, Adams J, Deanfield J, Ekelund U, Friberg P, Ghosh AK, Harwood N, on behalf of the NSHD Scientific and Data Collection Team, et al. 2011. Cohort profile: updating the cohort profile for the MRC National Survey of Health and Development: a new clinic-based data collection for ageing research. Int J Epidemiol. 40(1):e1–e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasker GW, Mascie-Taylor CG. 1989. Effects of social class differences and social mobility on growth in height, weight and body mass index in a British cohort. Ann Hum Biol. 16(1):1–8. [DOI] [PubMed] [Google Scholar]
- Leckie G, Charlton C. 2012. runmlwin: a program to run the MLwiN multilevel modeling software from within Stata. J Stat Soft. 52(11):1–40. [Google Scholar]
- Lee J, Kolonel LN, Hinds MW. 1981. Relative merits of the weight-corrected-for-height indices. Am J Clin Nutr. 34(11):2521–2529. [DOI] [PubMed] [Google Scholar]
- Li C, Ford ES, McGuire LC, Mokdad AH. 2007. Increasing trends in waist circumference and abdominal obesity among US adults. Obesity. 15(1):216–224. [DOI] [PubMed] [Google Scholar]
- Li C, Ford ES, Mokdad AH, Cook S. 2006. Recent trends in waist circumference and waist-height ratio among US children and adolescents. Pediatrics. 118(5):e1390–e1398. [DOI] [PubMed] [Google Scholar]
- Lin LI. 1989. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 45(1):255–268. [PubMed] [Google Scholar]
- Metcalf BS, Hosking J, Fremeaux AE, Jeffery AN, Voss LD, Wilkin TJ. 2011. BMI was right all along: taller children really are fatter (implications of making childhood BMI independent of height) EarlyBird 48. Int J Obes. 35(4):541–547. [DOI] [PubMed] [Google Scholar]
- Micozzi MS, Albanes D, Jones DY, Chumlea WC. 1986. Correlations of body mass indices with weight, stature, and body composition in men and women in NHANES I and II. Am J Clin Nutr. 44(6):725–731. [DOI] [PubMed] [Google Scholar]
- Nevill AM, Holder RL. 1995. Body mass index: a measure of fatness or leanness? Br J Nutr. 73(4):507–516. [DOI] [PubMed] [Google Scholar]
- Nightingale CM, Rudnicka AR, Owen CG, Cook DG, Whincup PH. 2011. Patterns of body size and adiposity among UK children of South Asian, black African-Caribbean and white European origin: Child Heart And health Study in England (CHASE Study). Int J Epidemiol. 40(1):33–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okosun IS, Chandra KM, Boev A, Boltri JM, Choi ST, Parish DC, Dever GE. 2004. Abdominal adiposity in U.S. adults: prevalence and trends, 1960–-2000. Prev Med. 39(1):197–206. [DOI] [PubMed] [Google Scholar]
- Peterson CM, Su H, Thomas DM, Heo M, Golnabi AH, Pietrobelli A, Heymsfield SB. 2017. Tri-Ponderal Mass Index vs Body Mass Index in estimating body fat during adolescence. JAMA Pediatr. 171(7):629–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomeroy E, Stock JT, Stanojevic S, Miranda JJ, Cole TJ, Wells JC. 2014. Stunting, adiposity, and the individual-level “dual burden” among urban lowland and rural highland Peruvian children. Am J Hum Biol. 26(4):481–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power C, Elliott J. 2006. Cohort profile: 1958 British birth cohort (National Child Development Study). Int J Epidemiol. 35(1):34–41. [DOI] [PubMed] [Google Scholar]
- Prentice AM, Jebb SA. 2001. Beyond body mass index. Obes Rev. 2(3):141–147. [DOI] [PubMed] [Google Scholar]
- Quetelet A. 1842. A treatise on man and the development of his faculties (Reprinted). New York (USA): Burt Franklin, 1968. [Google Scholar]
- Revicki DA, Israel RG. 1986. Relationship between body mass indices and measures of body adiposity. Am J Public Health. 76(8):992–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohrer F. 1908. Eine neue Formel zur Bestimmung der Körperfülle. Korrespondenze-Blatt der Deutschen Gesellschaft für Anthropologie. Ethnologie Und Urgeschichte. 39:5–7. [Google Scholar]
- Romero-Corral A, Somers VK, Sierra-Johnson J, Thomas RJ, Collazo-Clavell ML, Korinek J, Allison TG, et al. 2008. Accuracy of body mass index in diagnosing obesity in the adult general population. Int J Obes. 32(6):959–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum S, Skinner RK, Knight IB, Garrow JS. 1985. A survey of heights and weights of adults in Great Britain, 1980. Ann Hum Biol. 12(2):115–127. [DOI] [PubMed] [Google Scholar]
- Sperrin M, Marshall AD, Higgins V, Renehan AG, Buchan IE. 2016. Body mass index relates weight to height differently in women and older adults: serial cross-sectional surveys in England (1992–2011). J Public Health. 38(3):607–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanton JM. 2001. Galton, Pearson, and the Peas: a brief history of linear regression for statistics instructors. J Stat Educ. 9(3):1–13. [Google Scholar]
- Stearns SC. 1992. The evolution of life histories. New York (USA): Oxford University Press. [Google Scholar]
- Wadsworth M, Kuh D, Richards M, Hardy R. 2006. Cohort Profile: The 1946 National Birth Cohort (MRC National Survey of Health and Development). Int J Epidemiol. 35(1):49–54. [DOI] [PubMed] [Google Scholar]
- Wells JC. 2014. Commentary: the paradox of body mass index in obesity assessment: not a good index of adiposity, but not a bad index of cardio-metabolic risk. Int J Epidemiol. 43(3):672–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells JC, ALSPAC Study Team, Cole TJ, Steam A. 2002. Adjustment of fat-free mass and fat mass for height in children aged 8 y. Int J Obes. 26(7):947–952. [DOI] [PubMed] [Google Scholar]
- Wells JC, Cole TJ. 2014. Height, adiposity and hormonal cardiovascular risk markers in childhood: how to partition the associations? Int J Obes (Lond). 38(7):930–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells JCK, Cole TJ, Cortina-Borja M, Sear R, Leon DA, Marphatia AA, Murray J, et al. 2019. Low maternal capital predicts life history trade-offs in daughters: why adverse outcomes cluster in individuals. Front Public Health. 7:206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells JCK, Nesse RM, Sear R, Johnstone RA, Stearns SC. 2017. Evolutionary public health: introducing the concept. Lancet. 390(10093):500–509. [DOI] [PubMed] [Google Scholar]