Automated Grouping of Medical Codes via Multiview Banded Spectral Clustering

Abstract

Objective:

With its increasingly widespread adoption, electronic health records (EHR) have enabled phenotypic information extraction at an unprecedented granularity and scale. However, often a medical concept (e.g. diagnosis, prescription, symptom) is described in various synonyms across different EHR systems, hindering data integration for signal enhancement and complicating dimensionality reduction for knowledge discovery. Despite existing ontologies and hierarchies, tremendous human effort is needed for curation and maintenance – a process that is both unscalable and susceptible to subjective biases. This paper aims to develop a data-driven approach to automate grouping medical terms into clinically relevant concepts by combining multiple up-to-date data sources in an unbiased manner.

Methods:

We present a novel data-driven grouping approach – multi-view banded spectral clustering (mvBSC) combining summary data from multiple healthcare systems. The proposed method consists of a banding step that leverages the prior knowledge from the existing coding hierarchy, and a combining step that performs spectral clustering on an optimally weighted matrix.

Results:

We apply the proposed method to group ICD-9 and ICD-10-CM codes together by integrating data from two healthcare systems. We show grouping results and hierarchies for 13 representative disease categories. Individual grouping qualities were evaluated using normalized mutual information, adjusted Rand index, and F₁-measure, and were found to consistently exhibit great similarity to the existing manual grouping counterpart. The resulting ICD groupings also enjoy comparable interpretability and are well aligned with the current ICD hierarchy.

Conclusion:

The proposed approach, by systematically leveraging multiple data sources, is able to overcome bias while maximizing consensus to achieve generalizability. It has the advantage of being efficient, scalable, and adaptive to the evolving human knowledge reflected in the data, showing a significant step toward automating medical knowledge integration.

INTRODUCTION

With the advent of high-throughput gene sequencing technologies, rich genotypic data of high quality can be readily obtained in a cost-effective manner. The growing availability of this high-quality biologic data has shifted the clinical research bottleneck to a paucity on its phenotypic counterpart. Most traditional “-omics” studies have focused on a small number of pre-specified phenotypic outcomes, limiting the potential to discover associations for phenotypes not recorded in the study. Recently, tremendous efforts have been made to link biorepository data to electronic health records (EHR), which contains phenotypic information at an unprecedented granularity and scale.[1–3] These linked data enable large-scale next-generation omics studies (NGOS), significantly expanding opportunities for precision medicine research, such as individualized risk prediction with genetic and clinical profiles, pharmacogenomics studies inferring treatment effect heterogeneity, and discovery research to advance understanding of human diseases. One of such efforts that continues to prove invaluable is Phenome-Wide Association Study (PheWAS). [4] By screening for associations between genomic markers and a diverse range of phenotypes has PheWAS been able to unfold new therapeutic targets, side-effect predictions while deepening the understanding of diseases and prognosis.[5] Critical to the success of PheWAS that ultimately fulfils the promise of precision medicine is accurately and efficiently annotating patients with disease characteristics among millions of individuals.

Defining clinically relevant phenotypes accurately from the EHR in a scalable fashion, however, is a challenging task. A medical concept (e.g. diagnosis, laboratory test, prescription etc.) is often described with various “synonymous” terms in the EHR. For disease conditions, the International Classification of Disease (ICD) coding system uses many codes with slight variations to encode each disease condition. For example, ICD-9 codes “714.0”, “714.1”,”714.2” describe slight variations of rheumatoid arthritis (RA). For epidemiological or genetic association studies on RA, these codes are often preferred to be grouped together to represent the overarching concept on RA.[6] Here and thereafter, we use “synonymous codes” to refer to codes that describe the same phenotype but differ in minor details in the context of research studies on disease conditions”. Grouping near-identical features into a single one saves a great degree of freedom for inference and thus plays an indispensable role in ensuring reproducibility and maintaining power. This is particularly important when it comes to EHR utilization efficiency, as medical codes, not limited to ICD codes per se, are often used in slightly different ways across EHR systems due to heterogeneity in the healthcare system as well as how or when the encodings are performed.[7] Towards such efforts, Denny et al. developed a PheWAS catalog, providing valuable human annotations that define disease phenotypes based on groups of ICD-9 codes.[8] Recently, the grouping has been updated to also include ICD-10-CM codes.[9]

While the ICD hierarchy is highly informative, not all diseases have the same level of granularity in the ICD codes and hence no universal rule can be applied to group codes based on the hierarchy to properly represent distinct phenotypes. On the other hand, while the existing PheWAS-oriented grouping is no doubt a highly valuable asset to the research community, the manual curation approach has several major limitations. First, it lacks scalability as it requires substantial manual efforts when a new version or type of concept needs to be added. Updating the PheWAS catalog to include over 68,000 ICD-10-CM codes inevitably required substantial human effort. Second, manual efforts are potentially susceptible to subjective bias. Heavily resting on domain knowledge also refrains its generalizability. Third, due to the coding heterogeneity across healthcare systems, manually curated groups based on experience from one healthcare center may not be very portable to others. Although healthcare-center-specific groupings may be needed to best reflect the coding process, it is often desirable to employ a unified grouping structure to capture shared clinical knowledge. Deriving such a unified structure may require synthesizing information from multiple healthcare centers. This signifies the need for a generalizable data-driven approach to efficiently group medical concepts – one that is scalable and resonating in lockstep with the continuing expansion of the coding system as well as human knowledge evolution. Compared to a manual approach, a data-driven approach also has the advantage of portability that could systematically leverage multiple data sources to overcome bias and maximize consensus to achieve generalizability.

Existing unsupervised clustering methods such as hierarchical clustering, k-means clustering, matrix and tensor factorization based are useful data-driven algorithms for grouping related concepts. [10–15] For example, such clustering methods can be used to group ICD codes together with related procedure codes based on the low dimensional representations of medical concepts described in Choi et al. [16] However, these clustering methods are not effective when the goal is to only group near synonymous concepts. In this paper, we present a novel data-driven grouping approach – multi-view banded spectral clustering (mvBSC) – to group near synonymous medical codes using their co-occurrence patterns observed from m healthcare systems. By convention in the network analysis community, each data source can also be termed as a view.[17–22] The proposed mvBSC algorithm groups codes by constructing a shared network based on m independently acquired similarity matrices, with each similarity matrix learned from the corresponding healthcare system. Using a single data source, the mvBSC approach is able to create a healthcare-system-specific grouping structure that reflects its underlying characteristics. To showcase its utility, we apply the mvBSC algorithm to group ICD-9 and ICD-10-CM (ICD-10 for brevity hereafter) codes using data from the Veteran Health Administration (VHA) and Partner’s Healthcare Biobank (PHB). The automated approach results in group structures highly consistent with human annotation while having the advantage of being efficient, scalable, and adaptive to evolving human knowledge reflected in the observed data.

METHODS

Suppose there are a total of n ICD codes to be grouped. Let V = {v_i, 1 ≤ i ≤ n} denote the vertex set in which node v_i represents the i^th ICD code. The input of the mvBSC algorithm requires m similarity matrices defined on the involved ICD codes obtained independently from m healthcare centers. To assemble such a similarity matrix, we first construct semantic vectors for each code based on the word2vec algorithm using the skip-gram model.[23, 24] Although other algorithms such as the GloVe have been proposed, we use the word2vec algorithm for its simplicity in implementation and superior performance. [25–28] The word2vec only requires a co-occurrence table that records the frequency of an ICD pair co-occurring within a pre-specified time window, typically 7 or 30 days.[29, 30] The word2vec generates a semantic embedding vector for each of the ICD code within each healthcare system. For the s^th (s = 1, …, m) healthcare system, a cosine similarity matrix ${\mathit{W}}^s={\left[W_{ij}^s\right]}_{n\times n}$ is then computed in which the entry $W_{ij}^s$ represents the pairwise cosine similarity between the semantic vectors corresponding to v_i and v_i in this healthcare system.

To more effectively group ICD codes, we also leverage the existing knowledge on ICD hierarchical structure.[31]. It is well known that ICD codes that are ontologically further apart are less likely to be grouped together. To measure the distance between ICD codes, we let d: V × V ↦ [0, +∞) be a pre-defined distance metric. We employ a specific choice of d(∙,∙) for our grouping algorithm as discussed below although plenty of alternatives can be used. For example, pairwise distances among ICD-9 codes can be intuitively calculated through their numeric representations. It is worth mentioning that this distance metric only needs to conform non-negativity and symmetry but not necessarily the triangle inequality. We set a distance upper bound 2δ which serves as the maximal group length such that codes with pairwise distance beyond 2δ are never grouped. As detailed below in the algorithm, the mvBSC also introduces a banding parameter h ∈ (0, δ] that forces $W_{ij}^s, s=1,\dots ,m$ to 0 whenever d(v_i, v_j) > h. This banding operation can effectively reduce the chance of distant pairs being grouped.

The output of mvBSC is the grouping structure of all codes where codes in the same group are viewed as synonyms that collectively represent an ICD concept. The “ICD concept” is analogous to the “PheCode” in the PheWAS catlog and the “Concept Unique Identifier” (CUI) in the Unified Medical Language System (UMLS). A generic workflow is outlined in Figure 1.

Figure 1:

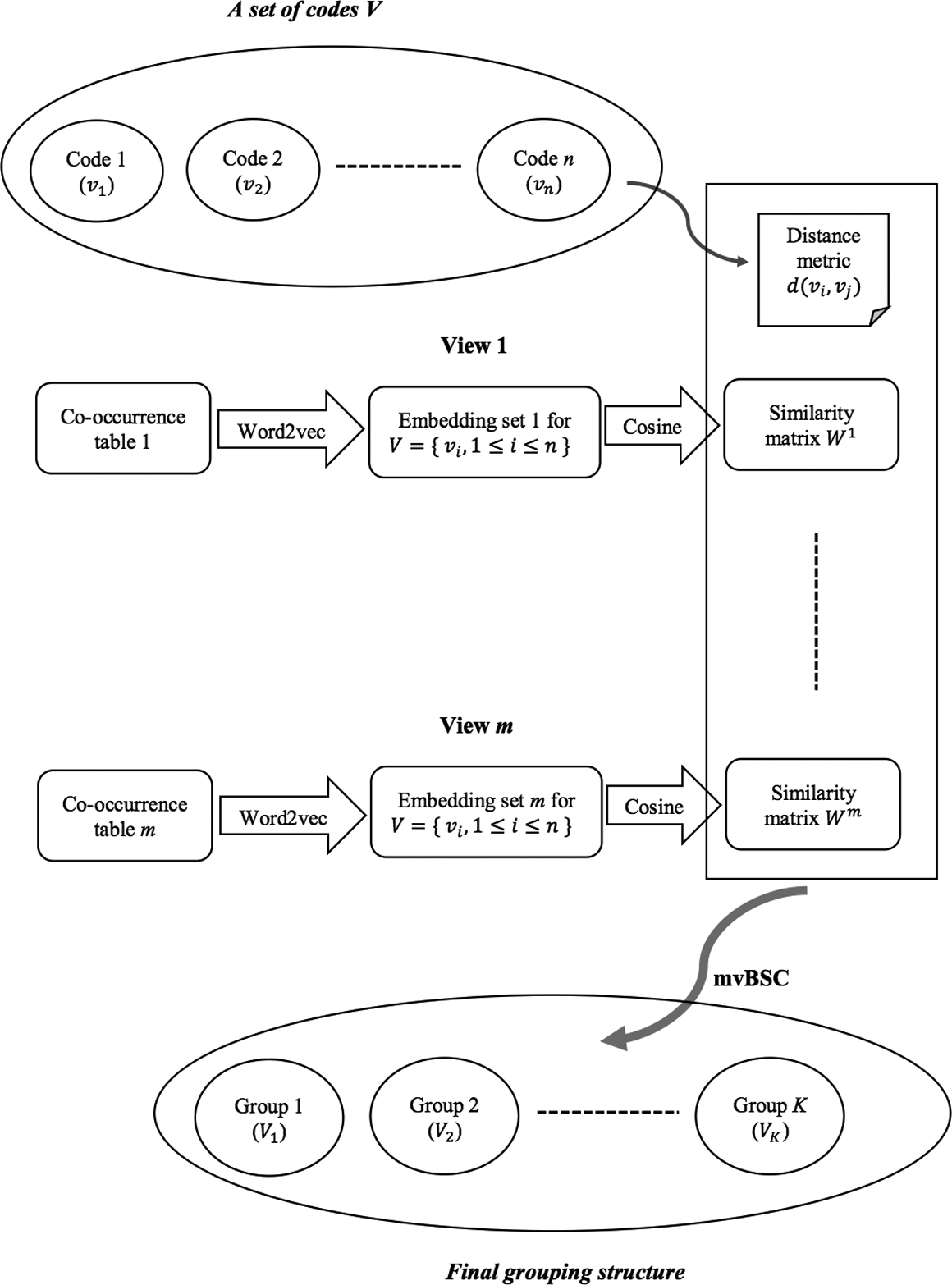
mvBSC algorithm work flow.

mvSBC algorithm

We group ICD codes into concept groups by creating a unique non-overlapping partition such that V = ∪_k V_k, V_k ∩ V_l = ∅, 1 ≤ k < l ≤ k where K is the total number of concept groups; in other words, every code v_i should belong to one and only one concept group V_k. Let Z* denote the associated group membership matrix in that $Z_{ik}^{*}=1$ if v_i ∈ V_k and 0 otherwise. To infer about group membership Z* based on the m similarity matrices {W^s, s = 1, …, m}, we propose the mvSBC algorithm which consists of the following four steps:

1. Banding: given a banding parameter h ∈ (0, δ], keep $W_{ij}^s$ if d(v_i, v_j) ≤ h and 0 otherwise. Run eigen-decomposition on W^s, and construct a matrix U^s whose columns are the eigenvectors of W^s corresponding to its first K largest singular values.

2. Combining: given ${\sum }_{s=1}^m{\lambda }_s=1, {\lambda }_s\ge 0, s=1,\dots , m$, run eigen-decomposition on ${\sum }_{\text{s}=1}^m{\lambda }_s{\mathit{U}}^s{\mathit{U}}^{s^{\prime }}$ whose eigenvectors corresponding to its first K largest singular values are concatenated to form a matrix $\overline{\mathit{U}}$.

3. Clustering: group the codes by performing k-means clustering on the rows of $\overline{\mathit{U}}$.

4. Trimming and Regrouping: given δ>0, calculate the group length l_k := max_{{vi, vj ∈ vk}} d (v_i, v_j), k = 1, …, K Repeat (1)-(3) on codes belonging to groups whose length is over δ until all group lengths are less than 2δ.

The banding step in step (1) enforces any pairwise similarity score to be 0 if the corresponding pairwise distance is larger than the given threshold h, as illustrated in Figure 2. This thresholding induces sparsity on the similarity matrix, which in turn not only serves as a denoising step but also greatly improves computational efficiency. More essentially, this banding operation discourages ontologically distant pairs being grouped together, ensuring alignment with prior knowledge. By performing a spectral decomposition on the banded similarity matrix for each view, we obtain U^s U^s′ whose eigenspace approximates Z*Z*′. We then synthesize information from m views by optimally combining these m eigenspace estimators in step (2) to yield a central K-dimensional eigenvector estimator $\overline{\mathit{U}}$. In step (3), we perform a simple k-means clustering algorithm on $\overline{\mathit{U}}$ to obtain the grouping structure. Considering k-means is a greedy algorithm that could potentially converge to a local minimum yielding a small number of groups with an extremely large group length exceeding the preset upper bound 2δ, in step (4) we repeat step (1)-(3) on codes within these overly stretched groups until all group lengths are well-behaved under 2δ. If m = 1 or let λ_s = 1 for s^th view, the mvBSC algorithm provides the optimal grouping for each specific healthcare center.

Figure 2:

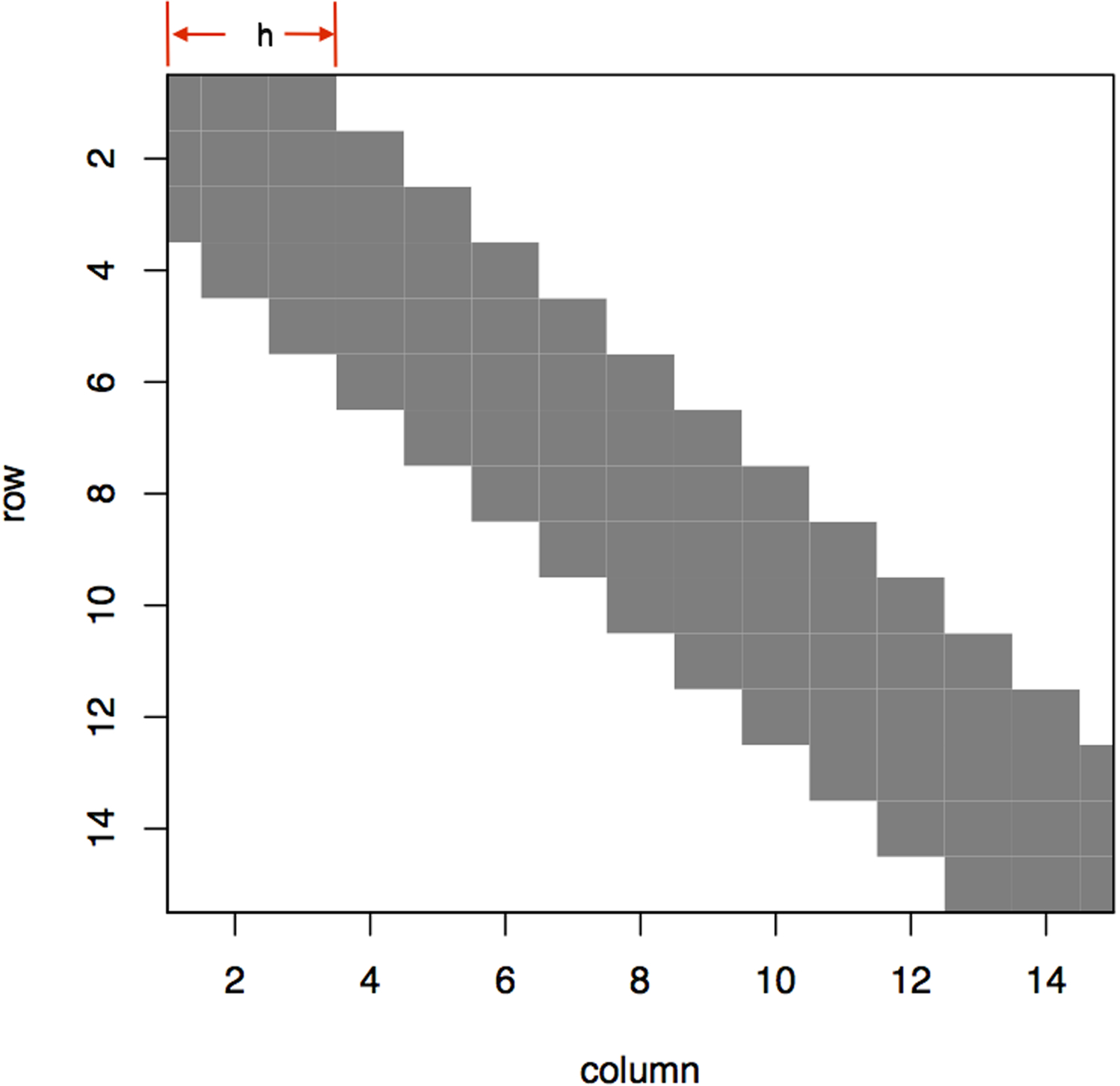
An example of banding a 15-by-15 similarity matrix. The banding parameter h decides the window size that only entries whose corresponding pairwise distance is inside this range would be kept colored in gray. Otherwise entries would be thresholded to 0. This banding operation discourages distant pairs being grouped. In general, banding would sparsify the similarity matrix but not necessarily result in this nicely tapering structure centering at the diagonals.

Hierarchy building via roll up after mvBSC

The PheWAS catalog developed by Denny et al. [8] is formatted in a three-layer hierarchy in which each PheCode as a leaf node can automatically fold its digit(s) to roll up so long as its associated Boolean variable “rollup” is 1. For example, an ICD-9 code that maps to PheCode “008.11” also maps to “008.1” and “008”. Since our “ICD concept” is analogous to “PheCode”, it is interesting to build a similar three-level hierarchy to reflect ICD concept closeness. Such hierarchy is useful for other types of medical codes including CPT codes and medications. To this end, we introduce a variable “roll-up” indicating the hierarchy level. More specifically, rollup being 0 means the initial groupings, rollup is 1 if the initial groups are rolled one level up and is 2 if rolled twice up. After grouping by mvBSC, we run agglomerative clustering algorithm as follows:

1. Calculate group-level cosine similarity matrix G = [G_kl]_{K × K} using $\overline{\mathit{U}}$ and convert to dissimilarity matrix D = [D_kl]_{K × K} where D_kl := G_kk + G_ll – 2G_kl.

2. Calculate group-level distance matrix R = [R_kl]_{K × K} where R_kl := median (d(v_i, v_j), v_i ∈ V_k, v_j ∈ V_l)

3. Run Agglomerative clustering algorithm on $\tilde{\mathit{D}}={\left[{\tilde{D}}_{kl}\right]}_{K\times K}$ where ${\tilde{D}}_{kl}:=D_{kl}*R_{kl}$. Cut at two desired heights along the dendrogram to produce a three-layer hierarchy.

Distance Metric d (∙,∙)

Since the ICD-9 and ICD-10 coding systems are not compatible, it is necessary to design a unified distance metric. To this end, we leverage the existing General Equivalence Mappings (GEM), in particular the ICD-9-to-ICD-10 mapping jointly developed by the Centers for Medicare & Medicaid Services (CMS) and the Centers for Disease Control and Prevention (CDC).[32] Mapping letters [A-Z] to [1–26], an ICD-10 code presents as an integer part followed by 1–3 digits. We then calculate all ICD-10 pairwise distances through their numeric representations. To reflect the fact that codes differing at the integer level are much more dissimilar than codes only differing among digits, we adopt a set of monotonically decreasing weights for distance calculation. A small constant number is assigned if an ICD-10 pair maps to the same ICD-9 code. Using the ICD-9-to-ICD-10 mapping, a pairwise distance involving an ICD-9 code is subsequently calculated based on distances involving all its mapped ICD-10 codes. For other medical codes such as CPT codes, distance metric can also be defined according to the numeric numbers representing the codes since the closer the numbers are the more similar the codes are. The explicit form of d(∙,∙) can be referred to in more details in the Supplementary Materials.

Parameter tuning and evaluation metric

The tuning parameters {h, λ_s, s = 1, …, m} as well as the total number of groups K are not known a priori in practice. We use the existing PheCodes on ICD-9 and ICD-10 codes as partial labels to tune these parameters. The evaluation metric for tuning we use is a composite score defined as the sum of the normalized mutual information (NMI) [33] and adjusted Rand index (ARI) [34], which are the two most commonly used metrics in the network analysis literature to evaluate the similarity between two partitions on the same vertex set. The range of NMI is [0,1], and that of ARI is [−1,1]; a higher value indicates a closer match between two partitions. Our experiments reveal that ARI tends to favor smaller K while NMI tends to favor larger K, so we use this composite score to render a more robust, consistent estimate of K. Optimal choices of the banding parameter h were tuned via a grid search where 100 equally-spaced values were considered between the minimal and maximal pairwise distance. Likewise, 11 equally spaced values between [0,1] were considered for λ_s. Since the number of PheCodes (K_PheWAS) is a reasonably good estimate for K, we examined all values for K on the approximate range [K_PheWAS, 2K_PheWAS]. We referred to the most recent PheWAS catalog that provides groupings on both ICD-9 and ICD-10 codes. A small portion of ICD-10 codes are mapped to multiple PheCodes, to avoid ambiguity, we only used uniquely PheCode labeled ICD-10 codes for tuning. For hierarchy building, enabling the “rollup” option in the PheWAS catalog, we were able to fold PheCodes with two digits into ones with a single digit, from which we could decide at what height of the tree the composite score reaches the maximum. Similarly, PheCodes were further collapsed into their integer representations to help cut the tree as the top layer. Figure 3 shows the hierarchical clustering dendrogram on disease category I00-I25, in which clusters given by mvBSC are leaf nodes and the second and first layer are obtained at the height colored in blue and red respectively.

Figure 3:

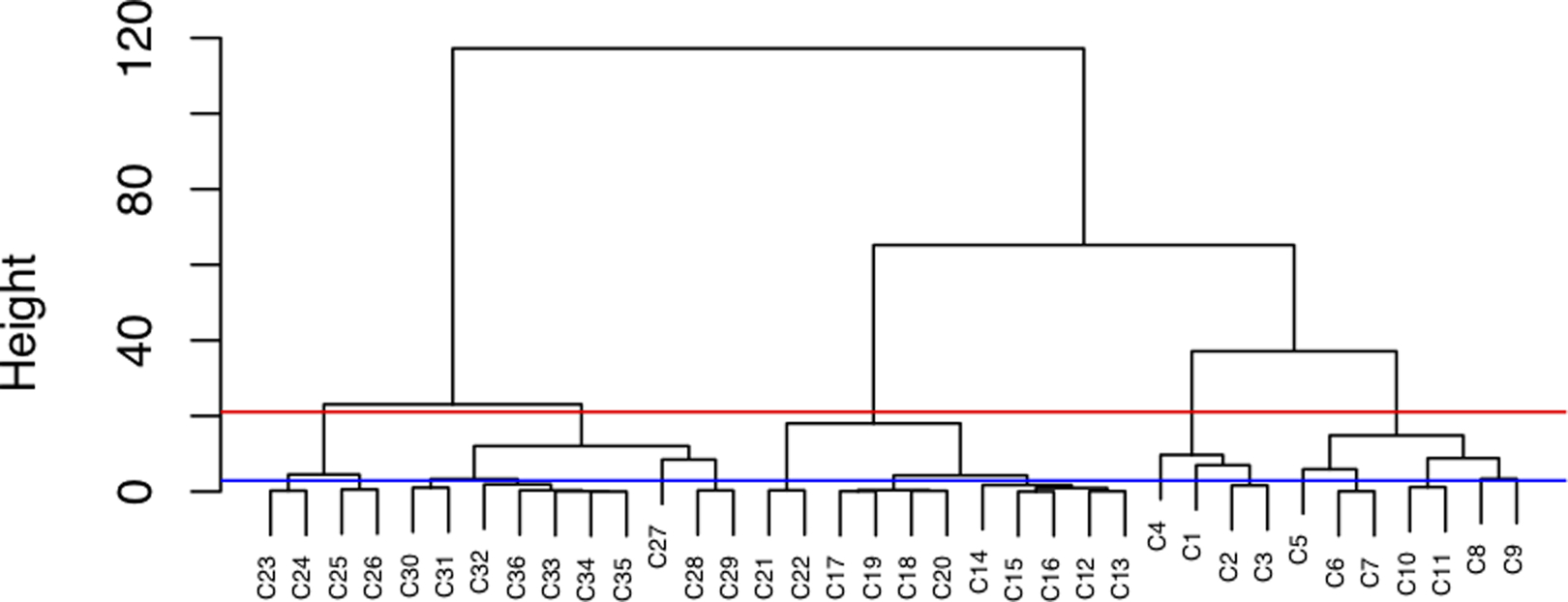
Clustering dendrogram on category I00-I25.

Training the Algorithm using PHB and VHA Data

To evaluate performance, we applied the proposed method (mvBSC) to group ICD-9 and ICD-10 codes by combining two sources: ICD data from a million subjects randomly selected from the Veterans Health Administration (VHA), and ICD data from patients in the Partners Healthcare Biobank (PHB). Two main factors contribute to the heterogeneity across these two healthcare systems. First, the underlying patient populations vary substantially. VHA serves the veteran population while PHS primarily consists of tertiary hospitals whose patients tend to have more complex and severe diseases. Second, the sample sizes are very different. VHA data has 1 million patients whereas PHB has only about 60,000.

An additional complication arises when grouping both ICD-9 and ICD-10 codes: these two sets of codes are adopted over non-overlapping time periods and hence nearly no co-occurrences occur between ICD-9 and ICD-10 codes within a short time window for any patient. To overcome this, we use the ICD-9 to ICD-10 mapping provided by the Centers for Medicare and Medicaid (CMS)[32] and identified the subsets of ICD-9 and ICD-10 codes in which the ICD-9-to-ICD-10 mapping is unique. These ICD9-codes are then replaced by their corresponding ICD-10 codes for co-occurrence matrix calculations. Sufficient co-occurrences between ICD-9 and ICD-10 codes are generated in this step, which in turn improves the training on the ICD embeddings.

We employ the mvBSC algorithm to create ICD concept groups based on (i) both VHA and PHB data; (ii) VHA data alone; and (iii) PHB data alone. The first set of groupings reflects the consensus knowledge and is expected to be more similar to the existing PheWAS groupings. Groupings based on data from individual healthcare systems are expected to reflect their unique patterns of coding behavior and patient population. Since ICD codes are organized by disease categories, groupings are performed within each of the categories. We focus on most common diseases and exclude categories that either lack sufficient EHR data due to rare prevalence or lack significance for grouping near-identical codes. Specifically, we demonstrate groupings for the following 13 disease categories: (1) Certain infectious and parasitic diseases (A00-B99); (2) Malignant neoplasms (C00-C97); (3) Diseases of the blood and blood-forming organs and certain disorders involving the immune mechanism (D50-D89); (4) Mental and behavioral disorders (F00-F99); (5) Nervous system (G00-G99); (6) Eye and adnexa (H00-H59); (7) Ear and mastoid process (H60-H95); (8) Certain diseases involving the circulatory system (I00-I25); (9) Digestive system (K00-K93); (10) Skin and subcutaneous tissue (L00-L99); (11) Arthropathies (M00-M25); (12) Genitourinary system (N00-N99); and (13) Pregnancy, childbirth and the puerperium (O00-O99).

Evaluation

We report the accuracy of grouping by the mvBSC algorithm against the PheWAS grouping based on the NMI, ARI as well as the F₁-measure defined as

$$F_1-\mathit{\text{measure}}= \frac{2*\mathit{\text{Precision}}*\mathit{\text{Recall}}}{\mathit{\text{Precision}}+\mathit{\text{Recall}}},$$

$$\mathit{\text{where}} \mathit{\text{Precision}}= \frac{\# \mathit{\text{PairsCorrectlyPredictedInSameCluster}}}{\#\mathit{\text{TotalPairsPredictedInSameCluster}}}and \mathit{\text{Recall}}= \frac{\# \mathit{\text{PairsCorrectlyPredictedInSameCluster}}}{\#\mathit{\text{TotalPairsInSameCluster}}} .$$

To further evaluate the grouping quality of our algorithm, we obtained an independent set of domain expert annotations of 698 pairs sampled from 5 disease categories that had been selected by domain experts according to their familiarity to guarantee relevancy. Out of these, we sampled 25 pairs randomly from each of category and 574 pairs from 15 groups of ICD codes. For each group, we sampled codes from one mvBSC cluster along with its two adjacent clusters and a cluster further apart. To ensure unbiasedness, the domain experts are blinded from the algorithm output during assessment and annotate whether a pair of ICD codes should be considered as “synonymous” for most clinical research studies. We report the F₁-measure of the algorithm output at different levels of roll-up against this set of annotated grouping and compare to the benchmark of the agreement between the PheWAS grouping and the additional annotation which quantifies the level of agreement between different human annotations.

Results

Table 1 summarizes mvBSC’s groupings similarity in terms of NMI, ARI and F₁-measure towards PheWAS at each hierarchy level for each ICD category detailed above by combining similarity matrices from both VHA and PHB. These results demonstrate that our data-driven groupings generally have high agreement with PheWAS groupings, and that our hierarchy follows closely with the one given by PheWAS and shows more resemblance as it is rolled up. Against the additional set of expert gold standard annotation, the F₁-measure of the mvBSC algorithm is 0.73 at roll-up level 0 and 0.79 at roll-up level 1. The level of agreement is comparable to the agreement between PheWAS against these annotations, which has an F₁-measure of 0.78 and 0.82 at roll-up levels of 0 and 1, respectively. This also suggests that domain experts may prefer level 1 roll-up groupings for clinical studies.

Table 1:

grouping result summary. Basic information on each specific disease category under consideration is displayed in the first two columns. The roll-up column indicates the level of hierarchy with 0 indicating no rollup, 1 indicating rollup once and 2 indicating rollup twice. The K_pheWAS and K_mvBSC columns indicate the total number of groups suggested by PheWAS and by mvBSC at each hierarchy level. The last three columns summarize the similarity evaluation to PheWAS groupings by NMI, ARI, F₁-measure.

Disease Category	ICD Category	# of codes (# w/ PheCode)	Roll-up	KpheWAS	KmvBSC	NMI	ARI	F1
(1) Certain infectious and parasitic diseases	A00–B99	849 (828)	0	77	180	0.74	0.22	0.27
			1	70	58	0.70	0.40	0.44
			2	34	44	0.70	0.51	0.54
(2) Malignant neoplasms	C00-C97	1081 (1081)	0	83	86	0.87	0.49	0.52
			1	70	70	0.89	0.58	0.61
			2	34	28	0.84	0.68	0.71
(3) Blood and blood-forming organs and certain disorders involving the immune mechanism	D50–D89	243 (241)	0	66	68	0.85	0.45	0.56
			1	49	48	0.84	0.54	0.61
			2	22	13	0.73	0.65	0.69
(4) Mental and behavioral disorders	F00–F99	843 (840)	0	62	132	0.73	0.17	0.20
			1	53	22	0.73	0.62	0.67
			2	24	21	0.73	0.66	0.72
(5) Nervous system	G00–G99	748 (748)	0	89	124	0.82	0.38	0.43
			1	80	64	0.86	0.62	0.65
			2	48	39	0.87	0.71	0.73
(6) Eye and adnexa	H00–H59	1096 (1092)	0	100	100	0.79	0.44	0.48
			1	85	58	0.81	0.51	0.54
			2	30	36	0.80	0.64	0.66
(7) Ear and mastoid process	H60–H95	458 (452)	0	31	36	0.76	0.58	0.62
			1	29	22	0.76	0.67	0.70
			2	14	6	0.75	0.62	0.69
(8)Circulatory diseases	I00–I25	208 (182)	0	26	28	0.80	0.50	0.56
			1	22	14	0.81	0.68	0.73
			2	8	4	0.89	0.92	0.95
(9) Digestive system	K00–K93	827 (782)	0	149	148	0.84	0.48	0.53
			1	131	79	0.85	0.58	0.62
			2	56	38	0.85	0.74	0.76
(10) Skin and subcutaneous tissue	L00–L99	738 (738)	0	84	145	0.77	0.47	0.50
			1	77	120	0.78	0.72	0.74
			2	38	84	0.70	0.53	0.58
(11) Arthropathies	M00–M25	1374 (1369)	0	59	114	0.83	0.43	0.45
			1	52	62	0.82	0.51	0.53
			2	18	16	0.79	0.65	0.70
(12) Genitourinary system	N00–N99	685 (676)	0	149	155	0.84	0.38	0.46
			1	118	70	0.84	0.45	0.50
			2	51	69	0.81	0.44	0.48
(13) Pregnancy, childbirth and the puerperium	O00–O99	608 (603)	0	52	128	0.78	0.33	0.39
			1	52	66	0.79	0.45	0.50
			2	39	64	0.77	0.42	0.47

Detailed grouping results for five representative categories can be found in supplementary materials; here, we only analyze a few representative findings for arthritis, cardiovascular disease, and anemia. Overall, our groupings tend to separate disease codes by coarse pathophysiological attributes at the highest level of the hierarchy and more minute differences at lower levels. Within each level, groups of codes enjoy both intuitive internal consistency and clear separation from other groups. For instance, our method differentiates arthritis at the coarsest level into such broad categories as septic arthritis, post-infective arthropathies (i.e. immune complex-mediated disease), rheumatoid arthritis, and osteoarthritis. Within the rheumatoid arthritis group, it further distinguishes codes by extra-articular involvement (i.e. rheumatoid lung, vasculitis) and presence of rheumatoid factor. Only at the lowest level of the hierarchy does the grouping distinguish by the joint affected – a granular disease attribute. By contrast, the current PheWAS divides all ICD-9 codes related to Rheumatoid Arthritis (RA) into three groups – rheumatoid arthritis, juvenile rheumatoid arthritis, and other inflammatory polyarthropathies – that can be rolled up to the broad group of P714 (rheumatoid arthritis and other inflammatory polyarthropathies). While these groups are certainly clinically meaningful, our grouping both achieves more clinically meaningful separation with ICD-10 and at the same time can be utilized at different levels of the hierarchy depending on the level of specificity desired.

In addition to finding a consensus grouping using both VHA and PHB data, individual groupings reflective of each unique healthcare system were also obtained. Figure 4 shows such an example: whereas rheumatic valvular disease is distinguished from non-rheumatic disease for PHB, no such differentiation is made for VHA. This may reflect differing coding practices or patient population characteristics between the two healthcare systems, though ultimately both groupings are clinically sensible.

Figure 4:

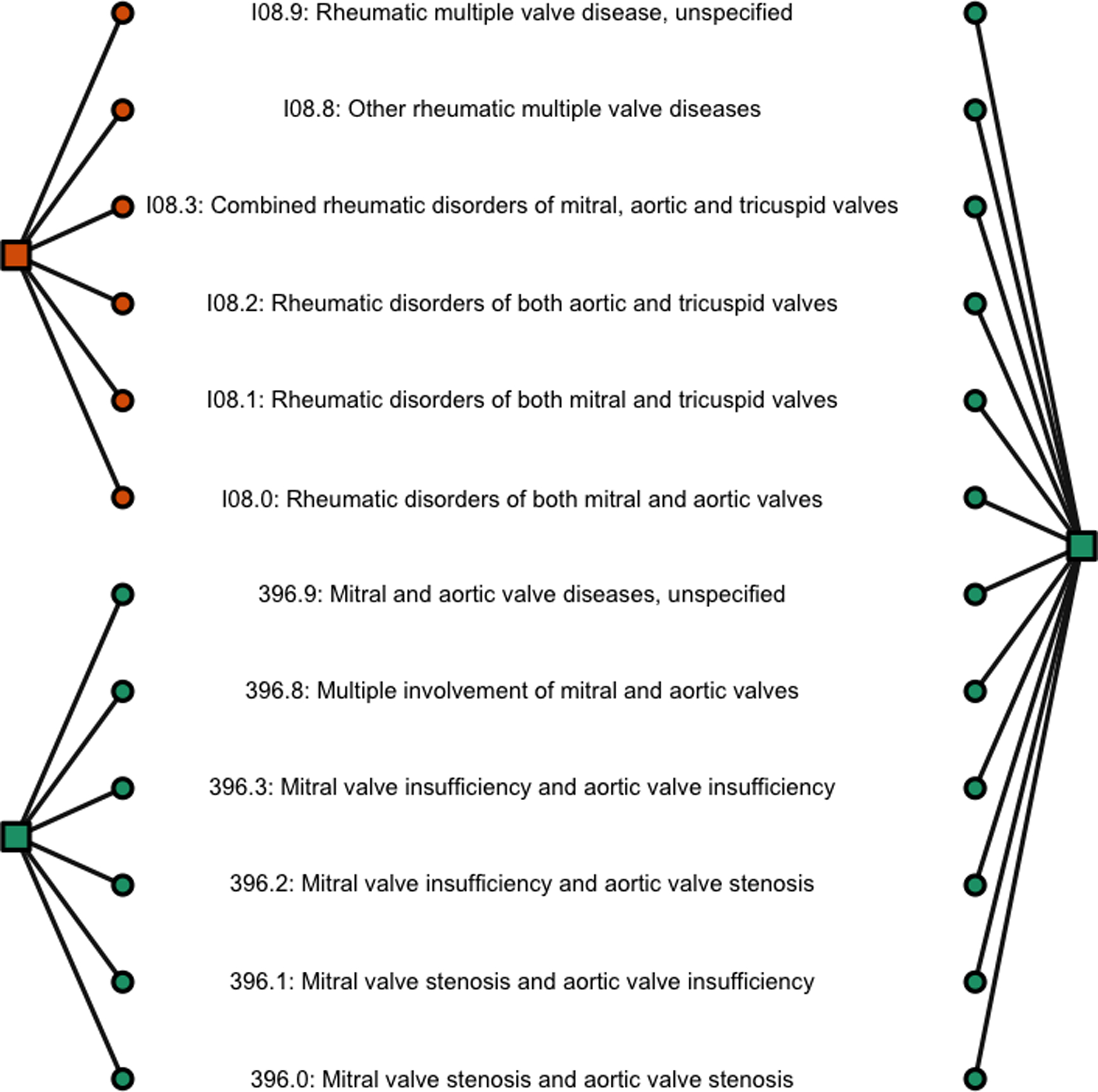
Grouping comparison within I08 given by mvBSC using data from PHB (left) and VHA (right) respectively. ICD codes (in circle) are colored according to their belonged groups (in square).

DISCUSSION

In this paper, we demonstrate the power of the proposed procedure through jointly grouping ICD-9 and ICD-10 codes in an unbiased manner of utilizing two data sources from the VHA and the PHB. Although the performance of the mvBSC method is only evaluated for grouping ICD codes in 13 disease categories against several sets of human annotations, these results suggest that the mvBSC produced grouping structure for the ICD codes that is highly consistent with human annotations. Our data-driven approach, however, has major advantages over manual approaches including scalability and transportability.

For the current ICD grouping analysis, we derived similarity matrices of the codes based on their co-occurrences observed in healthcare systems. It is also possible to additionally measure similarity between the codes based on the semantic similarities between the text strings associated with the codes, which can be achieved by deriving embeddings for the ICD text strings based on word or concept embeddings. The value of including such an additional source of similarity matrix warrants further research.

Results from the current ICD grouping analysis based on VHA and PHB data suggest that the mvBSC algorithm is generally capable of separating diseases into a clinically and physiologically meaningful hierarchy. Among the cardiovascular diseases, for instance, it broadly separates the cohort into rheumatic heart diseases, valvular disease, hypertensive heart (and kidney) disease, and coronary artery disease/ischemic heart disease (CAD/IHD). Within the CAD/IHD group, myBSC further distinguishes such clinically distinguishable groups as atherosclerosis, stable angina, unstable angina, myocardial infarction, and post-infarction complications. Conditions such as heart failure, which can occur as a result of different etiologies, were generally separated by their physiologic cause; for example, rheumatic heart failure is grouped with other sequelae of rheumatic heart disease whereas heart failure secondary to uncontrolled hypertension is grouped with other hypertensive heart diseases. Likewise, among the hematologic diseases, our method separates the anemias, coagulopathies, and malignancies. It further differentiates the anemias into the anemias as a result of nutritional deficiencies (i.e. iron, B12, folate deficiency etc.), hereditary production anemias (i.e. thalassemias, sickle-cell anemia, metabolic disorders etc.), hemolytic anemias (i.e. spherocytosis, autoimmune etc.), and aplastic anemias (i.e. drug induced, constitutional etc.). At further levels of the hierarchy it separates these subsets more finely, generally keeping very closely in line with the existing ICD hierarchies. Thus, across several different systems, our method develops a hierarchy that is internally consistent at every level, clinically meaningful, and easily interpretable using existing hierarchies as a standard.

While the data-driven grouping on ICD proposed in this paper are intended for research, it may inform updates on the existing GEM ICD-9 to ICD-10 mapping, which was developed for billing purposes. For example, it would be ideal to separate infectious arthropathies associated with bacteria (711.41 e.g.) from those associated with viruses, fungi or parasites (711.51, 711.71, 711.81 e.g.). Our method instead maps all of the above to PheCode “711.” due to the fact that the CMS ICD-9-to-ICD-10 mapping maps 711.41, 711.51, 711.71, and 711. to the same ICD-10 code (M01.X19). Consequently, their pairwise distances are too small to tease them apart. On the other hand, such a “flaw” can effectively mirror out what parts need further investigation and refinement of the current ICD-9-to-ICD-10 mapping. The grouping quality could potentially improve as more data on ICD-10 code usage and from additional healthcare centers become available.

Our proposed mvBSC method is readily applicable for grouping many other types of medical terms in the EHR, including lab codes and procedure codes that are truly in need of a data-driven grouping strategy. One limitation of the current mvBSC algorithm is the need for a distance measure that can distinguish highly similar codes from dissimilar codes. For ICD, the method relies on the ICD hierarchy to derive a distance measure. Such distance measures can also be naturally constructed for some other medical terminologies such as the CPT and LOINC codes. In addition, if the codes can be mapped to the UMLS, one may leverage the UMLS ontology and define distance using the graphical structure of the UMLS concepts. When no or little prior knowledge exist to measure the distance between codes, the banding step of the mvBSC method can be removed or modified to accommodate such settings although the performance in the absence of banding needs further investigation. Our method can also easily facilitate its adaptivity and conformity to as many human annotations as needed simply by adding penalty terms in the final k-means clustering step. Given its data-driven nature, our method represents a significant step forward for efficient automation on large-scale medical term grouping that advances deep phenotyping in pursuit of precision medicine. One remaining challenge is to automatically label the groups created by such unsupervised algorithms. While this would generally require additional human annotation, a potential starting point is to identify common phrases in the code names for each group as an initial name.