A python based support vector regression model for prediction of COVID19 cases in India

Abstract

The proposed work utilizes support vector regression model to predict the number of total number of deaths, recovered cases, cumulative number of confirmed cases and number of daily cases. The data is collected for the time period of 1^st March,2020 to 30^th April,2020 (61 Days). The total number of cases as on 30^th April is found to be 35043 confirmed cases with 1147 total deaths and 8889 recovered patients. The model has been developed in Python 3.6.3 to obtain the predicted values of aforementioned cases till 30^th June,2020. The proposed methodology is based on prediction of values using support vector regression model with Radial Basis Function as the kernel and 10% confidence interval for the curve fitting. The data has been split into train and test set with test size 40% and training 60%. The model performance parameters are calculated as mean square error, root mean square error, regression score and percentage accuracy. The model has above 97% accuracy in predicting deaths, recovered, cumulative number of confirmed cases and 87% accuracy in predicting daily new cases. The results suggest a Gaussian decrease of the number of cases and could take another 3 to 4 months to come down the minimum level with no new cases being reported. The method is very efficient and has higher accuracy than linear or polynomial regression.

1. Introduction

The spread of coronavirus disease 2019 (COVID-19) has become a global threat and the World Health Organization (WHO) declared COVID-19 a global pandemic on March 11, 2020 [1]. As of April 30, 2020, there were 3,359,055 confirmed cases and 238,999 deaths from COVID-19 worldwide [7] (https://coronavirus.jhu.edu/data/new-cases). The COVID-19 pandemic has been greatly affecting people's lives and the world's economy. Among many infection related questions, governments and people are most concerned with (i) when will the COVID19 infection rate reach the maximum; (ii) how long the pandemic will take to stop spreading and (iii) What could be the total number of individuals that will eventually be infected (iv) what will be the toatl number of deaths [4]. The questions are of primary concern in India also, a country with high population density and economic diversity. The spread of the disease in India is considerably lower than that of China, USA and other European countries. India is under complete lockdown since 21^st March,2020 and experts belief that this could be detrimental in mitigating the COVID19 spread among its citizens. Currently the development of vaccines is still in progress and there are no effective antiviral drugs for treating COVID-19 infections.As on April,30 the total number of COVID19 cases in India is 35043 and 1147 has died due to Severe Actue Respiratory Syndrome(SARS) (https://www.mohfw.gov.in/). The total number of COVID19 recoverd individuals in India is 8889 until date.

The lockdown is severely affecting the poor and migrant labours. Staying at home may not be a feasible option in the near future since a lot of people may die out of hunger and other ailments. Newsmedia reports all over the world is reporting about the crisis and how it is effecting the lives of people. Many research is being carried out at all levels to quickly gather information, develop mitigation tools and methods and implementation of the same. Therefore policy makers and authorities want to have an overall view of the current situation and want to visualize the extent at which it can spread in the near future for informed policy making and deciding the next course of action.

The paper here discusses about the proposed prediction model of COVID19 spread in India using support vector regression implemented in Python.3.6. The steps of the model is discussed in the methodology section wih subsequent analysis. The results are shown and discussed. The autors conclude the overall purpose of the work in Conclusion.

2. Methodology

2.1. Preparation of the dataset

The .csv file of Novel Coronavirus 2019 dataset available at https://www.kaggle.com/sudalairajkumar/novel-corona-virus-2019-dataset is downloaded. A separate .csv file is is created from the global dataset only for India. The columns include Total Deaths, Total Recovered and Total number of confirmed COVID19 patients on day to day basis from 1^st March,2020 to 30^th April,2020 (61 days). All the data is in cumulative form. From the cumulative dataset, we have computed the difference time series to get the values based on daily new case basis.So we have now extended our dataset to have six columns 3 for cumulative cases and 3 for respective daily new cases of deaths, recovery or confirmed COVID19 individuals.

2.2. Data preprocessing

In data preprocessing section, we have set the columns created above as the dependent variable column (y) and number of days starting from 1^st March as the independent variable (X). X column is basically a numpy array of elements 1 to 61. The X and y is then reshaped to be column vector of size 61 (i.e. 61 rows, 1 column)

The dataset is split for Training (60%) and Test (40%) using train_test_split() function imported from class model_selection of sklearn python library.The training and testing variables are saved for further evaluation.

The training and testing variables of both X and y are standardized using StandardScaler() object imported from class preprocessing of sklearn python library. Separate objects have been created for standardization of X and y data. The fit_transform() function is used to fit the object into the data and transform the values of X and y in standard form ranging from -3 to +3. The scaled data is now fit for regression application.

2.3. Support vector regression

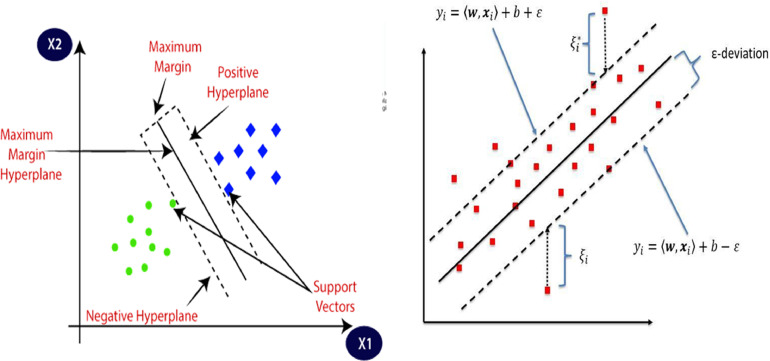
Support vector regression is a popular choice for prediction and curve fiiting for both linear and non linear regression types. SVR is based on the elements of Support vector machine (SVM), where support vectors are basically closer points towards the generated hyperplane in an n-dimensional feature space that distincly seggregates the data ponits about the hyperplane. More discussions on the SVR and SVM can be found on [3,2,6]. The SVR model performs the fitting as shown in Fig. 1 . The generelized equation for hyperplane may be respesented as y = wX + b, where w is weights and b is the intercept at X = 0. The margin of tolerance is represented by epsilon ε. The SVR regression madel is imported from SVM class of sklearn python library.The regressor is fit on the training dataset. The model parameters as chosen here for analysis is shown below.

Fig. 1.

Support vector regression model for linear regression fitting where X1= X and X2 = y are the features and label in our case. [Image credit: https://www.researchgate.net/figure/Schematic-of-the-one-dimensional-support-vector-regression-SVR-model-Only-the-points_fig5_320916953]

SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma='auto', kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

2.4. Visulization

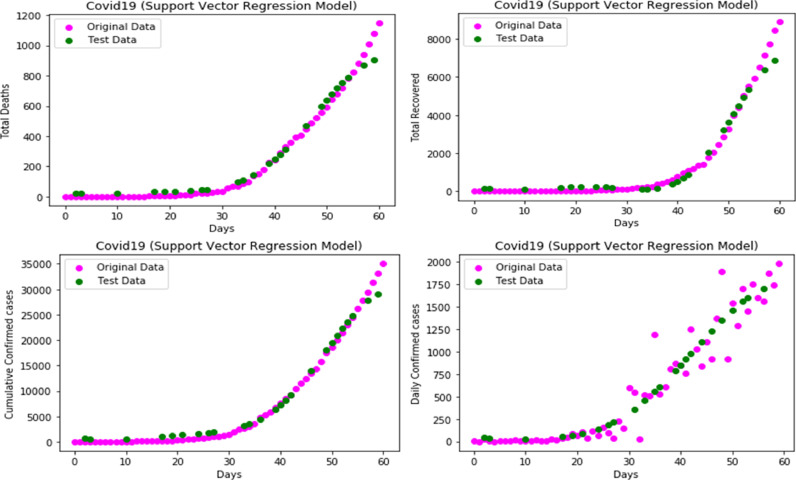
The regression fitting of the data with predicted values of the test data is plotted using scatter plot function imported from matplotlib python library. The actual points and the predicted points are shown in Fig. 2 for all the respective conditions. [5]

Fig. 2.

The figures shown here are the plots of regression fit with the data for total deaths, total recovered, cumulative confirmed cases and daily confirmed cases (in clockwise direction)

2.5. Model performance evaluation

The model performance parameters are then evaluated to check for the reliability in predicting the outcome. The mean square error (MSE), root mean sqaure error (RMSE), R² score and percentage accuracy are calculated and shown in Table 1 .

Table 1.

The support vector regression model performance parameters with RBF kernel and 10 % fitting confidence interval

Data	MSE	RMSE	Reg. score	% Accuracy
Total deaths	0.00849	0.092142	0.986812	99%
Total recovered	0.030289	0.174036	0.973437	97%
Daily confirmed	0.109448	0.330830	0.874900	87%
Cumulative confirmed	0.012856	0.113386	0.988613	99%
Daily deaths	0.130847	0.361727	0.821829	82%

2.6. Prediction

The prediction of the future values of the time series invloves few steps of data manipulation to obtain the cumulative trend so as to match the orignial dataset trend of the past. The past dataset is in cumulative form, but since we have implemented RBF kernel in our model, it is quite evident that the predicted time series would be decreasing gaussian trend. The decresing trend can be preserved by a transformation as discussed below. We have implemented few steps in the algorithm that could help us reach our objective.

Here we have obtained the predicted time series for each case seperately for 60 more days that start just after 30^th April or 61^st day from the starting. Therefore, we wish to merge the 60 days prediction with the past 61 days. The predicted column consits of decreasing values. So, we have computed the difference of the time series and then used absolute values of the difference time series. The difference time series gets inverted and gives us a rising trend, which saturates after certain values. Then we performed cumulative sum of the elements of the time series and added the max value of the the past time series to it. This helps us in preserving the trend and visualizing it in cumulative form. The plots of the past and forecasting values are shown in Fig. 3 and Fig. 4 .

Fig. 3.

The past and forecast of the total deaths, total recovered, cumulative coinfirmed and daily confirmed cases of COVID19 patients in India. [Past: 1st Mar to 30th April; Forecast: 1st May to 30th June]

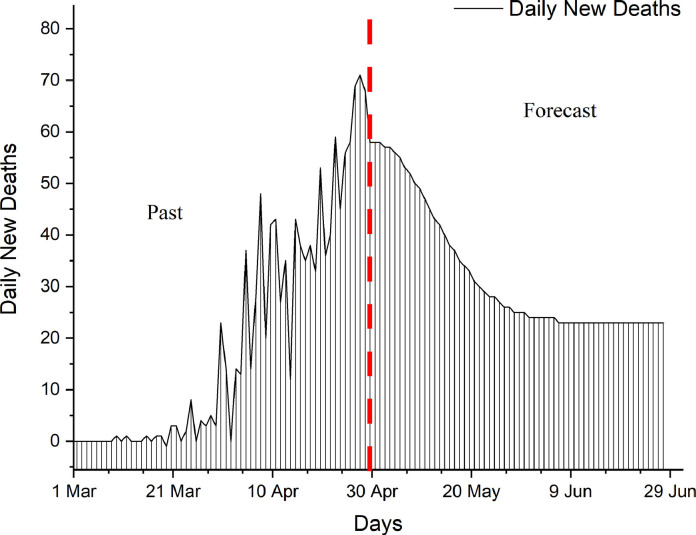
Fig. 4.

The past and forecast of the daily number of deaths

This transformation is not required for prediction of time series of daily new cases analysis.

All the necessary codes used in evaluation of the above mentioned steps is uploaded in GitHub repository for futher use and improvization. The link is https://github.com/DebanjanParbat/Support-Vector-Regression

3. Results and discussion

The results show that the model performed well in fitting the cumulative cases while a poor fiiting is observed in case of daily number of cases. The daily data show that, there are many spikes which reduces the accuracy of predictability of the model. The model predicts that the total numer of infected persons may cross the 55000 mark if the current rate of daily new cases prevail, by the second week of June. The total number of people that can die based on the recent trends predict that it can surpass 1600 mark within second week of June.

Moreover if more spikes are in daily deaths and daily new cases then the total number of infected person may rise and there could be more delay in attaining flatennig of the curve. The spikes induces non-stationarity in the dataset making it difficult for regression models to acccurately predict. But we can say, that if in near future the spikes are controlled with strict physical distancing and containment measures then the flattening of the curve can be achieved by the end of 2^nd week of June.

4. Conclusion

The proposed methodolgy predicts the total number of COVID19 infected cases, total number of daily new cases, total number of deaths and total number of daily new deaths. The total number of recovered individuals is also predicted. Based on the recent trends, the future trends has been predicted using a robust machine learning model, the support vector regression. The SVR has been reported to outperform the consistency in predictabilty with respect to other linear, plynomial and logistic regression models. The variabilty in the dataset is addressed by the proposed methodolgy. The model has above 97% accuracy in predicting deaths, recovered, cumulative number of confirmed cases and 87% accuracy in predicting daily new cases. The disease spread is significantly high and if proper containment measures with physical distancing and hygeinity is maintained then we can reduce the spikes in the dataset and hence lower the rate of progression.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.