Ultrafast Dynamics of Water-Protein Coupled Motions Around the Surface of Eye Crystallin

Abstract

Water dynamics on the protein surface mediate both protein structure and function. However, many questions remain about the role of the protein hydration layers in protein fluctuations and how the dynamics of these layers relate to specific protein properties. The fish eye lens protein γM7-crystallin (γM7) is found in vivo at extremely high concentrations nearing the packing limit, corresponding to only a few water layers between adjacent proteins. In this study, we conducted a site-specific probing of hydration water motions and sidechain dynamics at nine selected sites around the surface of γM7 using a tryptophan scan with femtosecond spectroscopy and NMR nuclear spin relaxation (NSR). We observed correlated fluctuations between hydration water and protein sidechains on the few picoseconds and hundreds of picoseconds timescales, corresponding to local reorientations and network restructuring, respectively. These motions are heterogenous over the protein surface and relate to the various steric and chemical properties of the local protein environment. Overall, we found that γM7 has relatively slower water dynamics within the hydration shell than a similar β-sheet protein, which may contribute to the high packing limit of this unique protein.

Graphical Abstract

INTRODUCTION

Water is the matrix-of-life¹ necessary for protein function.^2–6 Over the past decades considerable strides have been made in understanding water-protein interactions in the so-called hydration layers composed of water near the protein surface and their effect on protein structure and function.^5,7–11 Water in this region experiences slow, distinct dynamics compared to bulk water.⁸ Many techniques, including NMR,^12,13 neutron scattering,^14,15 laser spectroscopies,^9,16 and molecular dynamics simulations (MD)^11,17,18 have studied the hydration layer water molecules at different time and length scales and have sought to clarify the essential nature of the hydration layers and their interactions with protein dynamics.

We developed an ultrafast spectroscopic methodology to probe the hydration layers at specific local environments on the protein surface.¹⁹ Using site-directed tryptophanyl mutagenesis and femtosecond fluorescent spectroscopy, we are able to probe the hydration layers with site-specific spatial and femtosecond temporal resolution. By scanning the tryptophan probe across the surface of the protein, both local and global hydration layer dynamics were obtained on femtosecond to sub-nanosecond timescales. With this method, we have investigated hydration dynamics for a wide range of protein and biomolecular systems, including confined water in lipidic cubic phase,²⁰ water at the activate site of enzymes such as DNA polymerase IV,^21,22 and water around several diverse secondary structures such as α-helical^23–25 and β-barrel proteins.²⁶ Within these studies, we have shown the dynamic heterogeneity of the hydration shell and how local protein environments influence local hydration dynamics which in turn affect sidechain motions.

In this study, we examine the β-sheet protein zebrafish γM7-crystallin (γM7). Crystallins make up a majority of the eye lens cell’s proteome and are responsible for the refractive index and transparency of the lens.^27,28 In particular, γ-crystallins are found in abundance in the nuclear embryonic core of the lens where they are expressed in extremely high concentrations (>1000 mg/mL in some fish lenses) and must remain soluble over the lifespan of the organism.^29–31 γM7 is composed of two domains, connected by a short interdomain linker, each consisting of two intercalated Greek key motifs.³² Unlike other γ-crystallins which have four tryptophan residues, two per domain, γM7 contains only two tryptophan residues in the C-terminal domain, with no tryptophan residues in the N-terminal domain. Lack of N-terminal tryptophan residues makes γM7 a good candidate for our tryptophan fluorescence scan, which requires only one tryptophan residue per molecule for site-specific solvation studies.

Loss of crystallin solubility, resulting in high molecular weight, light scattering aggregates, is the main cause of cataract formation.³³ Hydration water structure and dynamics of γ-crystallins is therefore of great interest to better understand the unique solubility and packing in the lens. Previous studies give conflicted reports to the extent of hydration at the surface of the γ-crystallins,^34–40 yet none have studied the dynamics of such hydration, nor have any experimental methods probed the specific local environments of the hydration waters in a systematic way. As shown in Figure 1, we designed single tryptophan mutants at nine locations on β-strands and coils from both protein domains. Site-specific dynamics of local hydration water and protein sidechains were obtained with ultrafast fluorescent transient and anisotropy measurements. Sidechain motions were also measured with NMR nuclear spin relaxation (NSR) from six of the nine mutants. Here, we present new insights into the coupled water-protein dynamics of this unique protein system, leading to a better understanding of both protein packing and misfolding processes.

Figure 1.

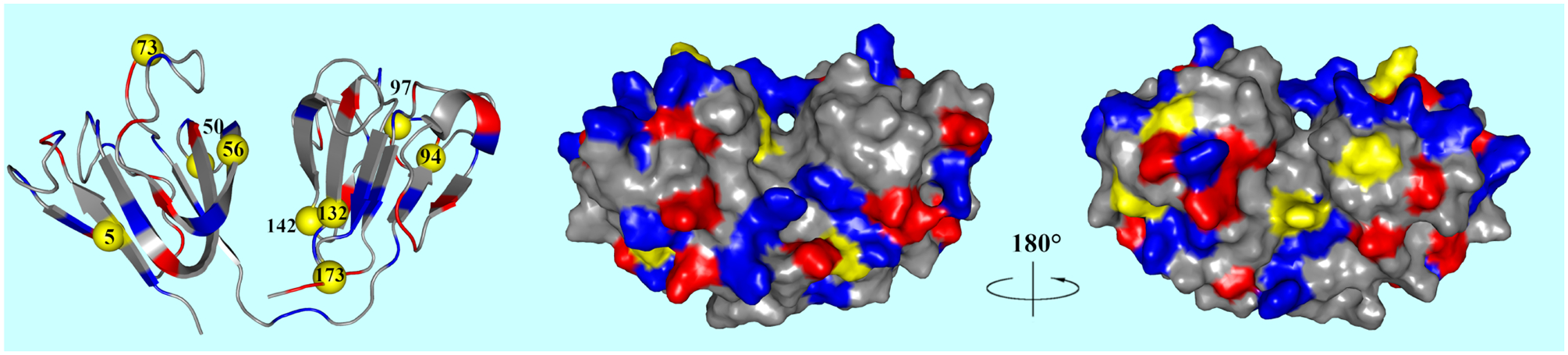
Crystal structure (PDB ID: 2NBR) of zebrafish γm7-crystallin. All mutations except W132 are triple mutants with both native tryptophan mutated to tyrosine (W132F/W158F) and one tryptophan mutated at the site of choice. There is only one tryptophan residue at a time. Yellow patches represent the placement of the tryptophan mutations. Blue patches represent positive residues and red patches negative residues.

MATERIALS AND METHODS

We designed nine γM7 mutants with one tryptophan each. We then measured femtosecond resolved fluorescence transients at multiple wavelengths around the peak of the emission spectra and constructed the femtosecond-resolved emission spectra (FRES) from which we extracted the ultrafast solvation dynamics described by the solvation correlation function, (C(t)). We also measured the fluorescence anisotropy to uncover sidechain motions. This procedure is fully detailed in our previous studies²⁶ and is given again in the Supplemental Information (SI). Finally, we determined the lifetimes and tumbling dynamics of tryptophan mutants with time-correlated photon counting (TCSPC) measurements and ran 30 ns molecular dynamics (MD) simulations, described in the SI.

Sample Preparation.

We subcloned the zebrafish γM7 gene into the pET16b vector (Novagen) between NdeI and HindIII sites. Wild type γM7 contains two native tryptophan residues (W132 and W158) which we mutated to W132F and W158F for the mutant template. We designed eight triple mutants, each with a single tryptophan at the site of interest, as well as one single mutant (W158F) with one tryptophan (W132) at its native site. The mutants were expressed in Escherichia coli cells and then purified as described in Mahler et. al.³² We measured the steady-state emission spectra using a Horiba FluoroMax-3 spectrometer at a concentration of 20 μM. We preformed laser experiments at a concentration between 700–800 μM in 50 mM Tris pH 7.5, 400 mM NaCl, 1 mM EDTA, and 2 mM DTT.

Femtosecond-Resolved Upconversion Spectroscopy.

We investigated the dynamics of ultrafast solvation motions using femtosecond-resolved fluorescence upconversion spectroscopy. Briefly, a 295 nm pump pulse of ~120 nJ was focused onto a rotating sample cell. Parabolic mirrors collected and focused the fluorescence emission onto a 0.2 mm β-barium borate (BBO) crystal, generating the upconverted signal. The response time of the system was between 400 and 450 fs, as determined by measuring the Raman signal at 320 nm. The polarization of the pump pulse was at the magic angle (54.7°) with respect to the acceptance axis of the upconversion BBO crystal for each transient. To determine the fluorescence anisotropy, we set the pump beam polarization either parallel or perpendicular to the acceptance angle. The probe beam remained parallel to the BBO acceptance axis for all measurements. Full detail of this procedure has been fully described previously.¹⁹

Data Analysis.

The C(t) can be fit by a triple exponential function

$$C\left(t\right)=a_1{e}^{\frac{-t}{{\tau }_{1s}}}+a_2{e}^{\frac{-t}{{\tau }_{2s}}}+a_3{e}^{\frac{-t}{{\tau }_{3s}}},{\sum }_{i=1}^3{a}_i=1$$ (1)

We derive the energy dissipated by each of these processes from the total Stokes shift (ΔE_TOT). The speeds at which the total Stokes shift energy dissipates by each process is

$$\Delta E_i=a_i\Delta E_{TOT}, S_i=\frac{\Delta E_i}{{\tau }_{iS}}, i=1,2,3$$ (2)

where each speed represents how quickly the probed environment responds to the sudden laser excitation induced perturbation of the tryptophan dipole moment⁴¹ and indicates the flexibility of the hydration water network near the tryptophan probe.

We calculated the fluorescent anisotropy by measuring the perpendicular (I_⊥) and parallel (I_‖) signals with r(t) = (I_‖ − I_⊥)/(I_‖ + 2I_⊥). The anisotropy dynamics can be described by multiple exponentials

$$r\left(t\right)=r_{IC}^{}{e}^{\frac{-t}{{\tau }_{IC}}}+r_{2W}^{}{e}^{\frac{-t}{{\tau }_{2W}}}+r_{3W}^{}{e}^{\frac{-t}{{\tau }_{3W}}}+r_T^{}{e}^{\frac{-t}{{\tau }_T}}$$ (3)

The first decay is generally less than 100 fs after deconvolution from the instrument response and is due to the internal conversion between the coexistent tryptophan excited states ¹L_b and ¹L_a.⁴² The next two terms describe the local wobbling motions of the tryptophan probe, and the last occurs due to the overall protein tumbling motion in nanoseconds. The wobbling semi-angle is estimated as followed:⁴³

$$1- \frac{r_{iW}^{}}{{\sum }_j{r}_{jW}^{}+r_T^{}}={\left(\frac{3{\text{cos}}^2{\theta }_i-1}{2}\right)}^2; i,j=2,3; j\le i$$ (4)

From this semi-angle, we define the average wobbling angular speed, which reflects the mobility of the probe:

$${\omega }_i=\frac{{\theta }_i}{{\tau }_{iW}}; i=2,3$$ (5)

NMR Spin Relaxation Analysis.

For six single tryptophan-containing mutants (I5W, Y56W, N50W, N73W, S97W, and W132), ¹⁵N spin relaxation measurements, T_1,⁴⁴ T_1ρ,⁴⁵ and heteronuclear NOE,⁴⁴ were performed at 298K on Bruker Avanced 800 MHz, 700 MHz and 600 MHz spectrometers equipped with a cryogenic probe using uniformly ¹⁵N-labeled samples with protein concentration being 800 μM. T₁ relaxation delay were set to 40, 360, 720, 1080, 1440, and 1800 ms including two duplicate points for error calculation and T_1ρ was measured with a spin lock field strength of 2.0 KHz for a variable relaxation duration of 20, 40, 60, 80, and 100 ms.⁴⁵ R₂ was derived from the measured T_1ρ and T₁ experiments using the following equation;

$$R_2=\frac{R_{1\rho }}{{\text{sin}}^2\theta }-\frac{R_1}{{\text{tan}}^2\theta }$$ (6)

where $\text{tan\hspace{0.17em}}\theta =\frac{{\omega }_1}{\Omega }$, and ω₁ is the spin lock frequency and Ω is the offset frequency which equals the difference between the measured frequency of each resonance and the carrier frequency.^{45 15}N-heteronuclear NOE was measured with and without 1.5 sec ¹H saturation period at the beginning of the pulse sequence. All data were processed using NMRPipe.⁴⁶ For model free analysis, both DYNAMICS and ROTDIF programs were used,^47,48 yielding site-specific dynamic parameters such as S², τ_c, τ_loc, and R_ex from all NMR relaxation data collected from three different external magnetic field strength.

RESULTS AND DISCUSSION

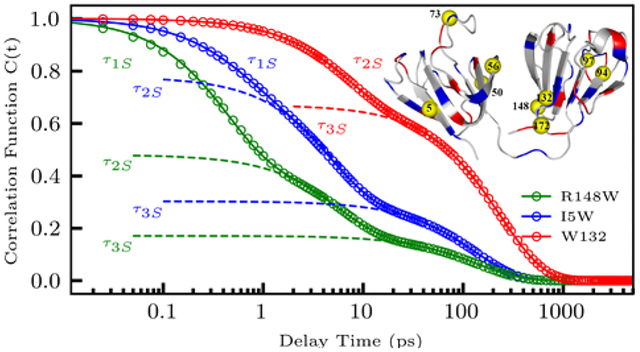
Figure 2 shows femtosecond-resolved fluorescence transients for R148W and W132 mutants, gated at wavelengths from blue to red sides of the emission spectra, measured within 3 ns of sample excitation. Both mutants show clear solvation features with decays on the blue side of the emission spectra and rises on the red side. R148W has a sub-picosecond decay on the blue side which W132 lacks. As we have shown in previous studies,^20,21,49 this decay is characteristic of surface exposed probs which buried probes lack. R148W and W132 have steady-state emission peaks of 346.0 nm and 323.0 nm, respectively, implying that the indole ring of the R148W tryptophan probe is exposed to surface water whereas the W132 probe is buried inside the protein surface (Fig. 1). Besides two lifetime decays of 2.9 and 5.7 ns, we observed three decays for R148W, one between 0.18 – 0.52 ps, a second between 2.3 – 6.5 ps, and the third between 85 – 141 ps. We also observed two rises on the red side between 0.51 – 0.85 ps and 6.5 – 7.0 ps. Conversely, we detected only two decays for the W132 mutant, the shorter between 5.0 – 8.2 ps and the longer between 172 – 282 ps, as well as two lifetime components of 1.4 and 2.3 ns. Interestingly, while recent studies suggest a fast tryptophan deactivation channel of less than 100 ps at the red side of the emission spectra for human γS and γD crystallins, we did not observe any sub-nanosecond decays from 350 to 370 nm in either intrinsic tryptophan (Figure 2, S1).^50,51

Figure 2.

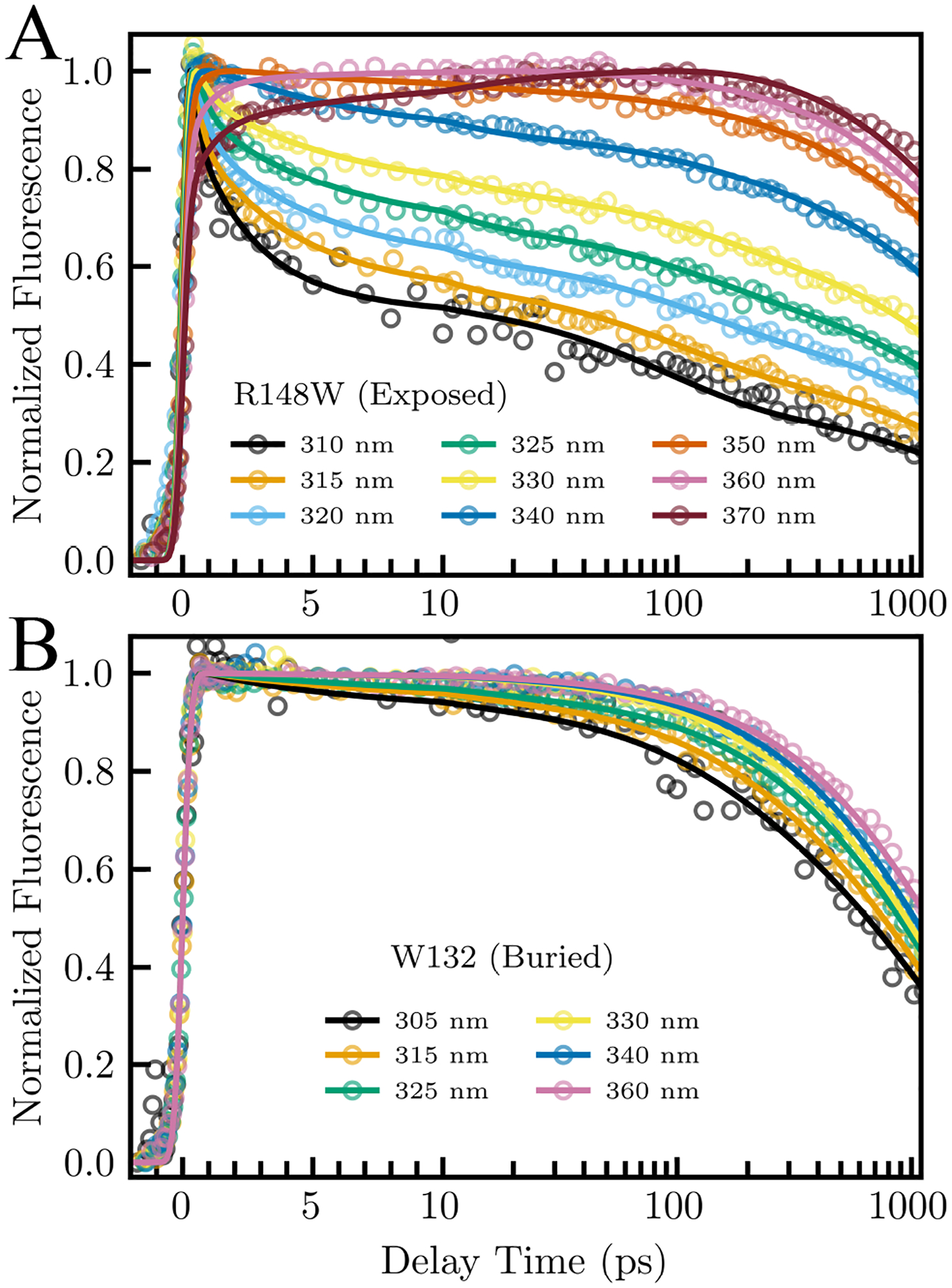
Normalized fluorescent transients gated from blue to red side of the emission spectrum of an (A) exposed (R148W) and (B) buried (W132) mutant.

Using results from our multi-exponential transient fitting, we constructed femtosecond-resolved emission spectra (FRES) and femtosecond-resolved lifetime associated spectra for all mutants, then extracted the time dependent maxima of each FRES and lifetime associated spectra to calculate the solvation correlation function (C(t)). Figure 3 plots the derived C(t) and multi-exponential fit for an exposed R148W, partially buried I5W, and fully buried W132 mutation as determined by each mutant’s steady-state emission peak of 346.0, 337.0, and 323.0 nm, respectively. R148W displays three solvation decays of 0.41 ps (52 % of total Stokes shift), 5.6 ps (31%), and 141 ps (17%). I5W shows solvation decays of 0.54 ps (22%), 4.8 ps (48%), and 130 ps (30%). Finally, we observed two solvation decays of 6.8 ps (32%) and 237 ps (68%) for the buried mutant W132. As evidenced by our studies of nanochannels in the cubic lipid phase²⁰, the steady-state emission peak shifts more blue with the increase of hydrophobicity of the indole ring environment and thus as the probe become increasingly buried. Along with this shift of steady-state emission peak, this study and multiple studies of other systems^49,52 have shown that as the indole ring becomes more buried as measured by the steady-state emission peak, the sub-picosecond decay accounts for significantly less of the total Stokes shift, while the amount of the Stokes shift from other decays remain fairly constant. The gradual decrease of the sub-picosecond solvation decay percentage as the indole ring moves into the surface of the protein implies that this decay probes ultrafast bulk-type water motions beyond 7 Å from the protein surface in the outer hydration layers.

Figure 3.

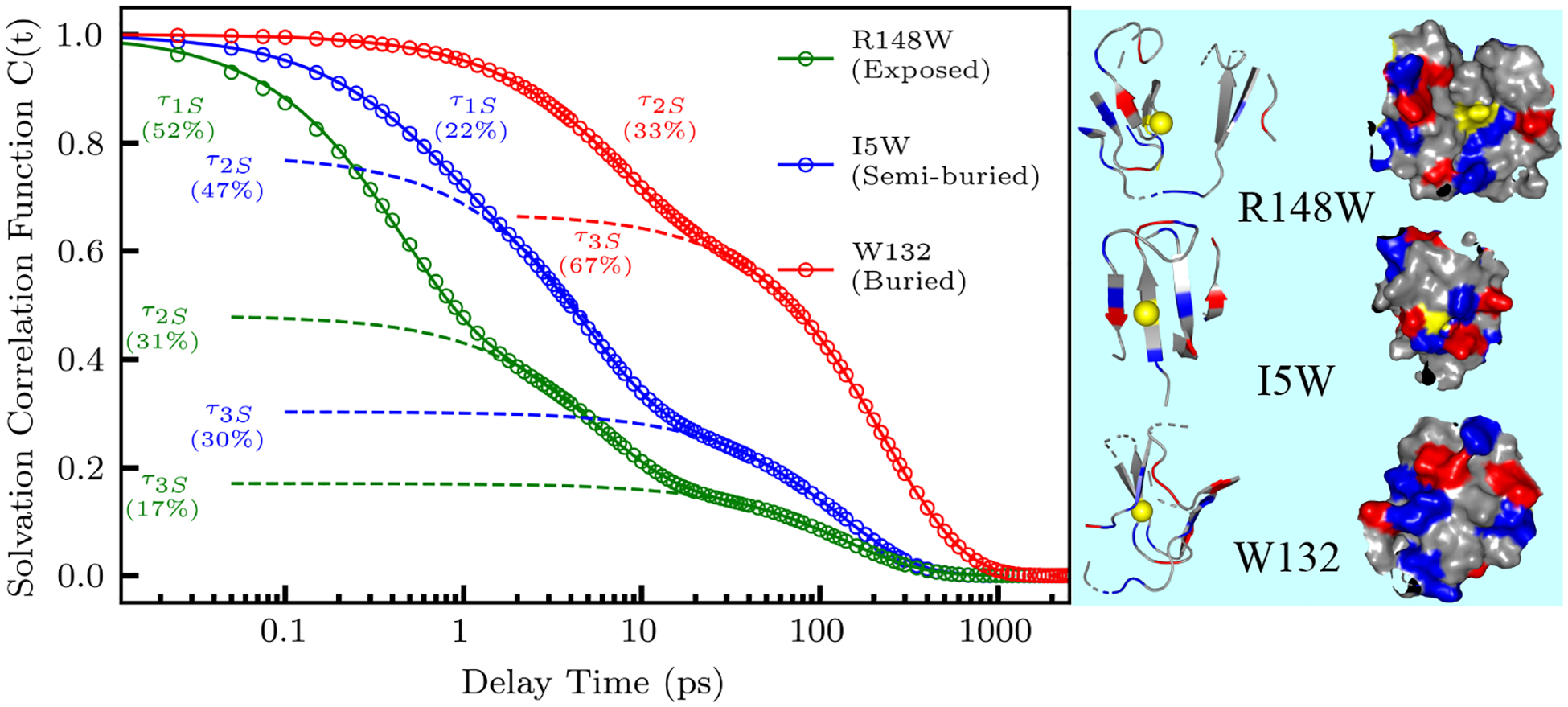
Constructed solvation correlation function and fit (dotted lines) for an exposed (R148W), semi-buried (I5W), and buried (W132) mutant. The exposed and semi-buried mutants were fit with three well separated exponentials, while the buried mutant was fit with two exponentials. The structures of each mutation show the location of each mutation (yellow) and the surrounding protein 10 Å from the mutated site. Positively charged residues are shown in blue, and negatively charged residues in red.

The second solvation component, occurring in a few picoseconds, mainly arises from dynamically slowed reorientation of water molecules within 7 Å of the protein surface. These dynamics are slowed by an order of magnitude compared with bulk water and reveal a perturbation of solvent motions caused by the unique local environment of the protein surface.^{23–26,49,52–54} The third solvation component, occurring in hundreds of picoseconds, reflects restructuring of the local water network and the corresponding coupled sidechain fluctuations, in agreement with timescales reported in simulation and NMR dynamic studies.^13,18,55 Both types of motions are heterogeneous around the protein surface, reflecting the local environment and water network around the probe.

Using (2), we calculated the solvation energy for each decay component. Figure 4 shows these solvation energies plotted against the degree of exposure to surface water as measured by the steady-state emission peak (λ_peak). All energies increase monotonically with λ_peak and the increasing trends are fit with sigmoidal functions for the increasing trend. The total Stokes shift increases gradually from 283 cm⁻¹ to 1736 cm⁻¹ with an inflection point around 338 nm. Because tryptophan is mostly sensitive to the dipoles of water molecules within 10 Å of the indole ring,^8,54 the increase in total Stokes shift reflects increasing numbers of water molecules probed by the tryptophan as the indole ring moves toward the protein surface. The energy of the first solvation component decreases around 340 nm and dies off around 338 nm. The tryptophan clearly probes the maximum possible amount of bulk water at longer steady-state emission peaks and then quickly loses sensitivity to bulk water as it moves towards the surface of the protein. Our 30-ns MD simulations confirm that proteins with redder emission peaks probe more water molecules further than 7 Å from the protein surface (Figure 5, Table S3). At wavelengths shorter than ~338 nm, transients lack a sub-picosecond component because the probe is buried within the protein surface. The second and third solvation energies increase steadily with solvent exposure becoming flatter after ~340 nm. The insensitivity of the solvation energies after this point imply that almost all the interfacial water molecules within 10 Å of the indole ring are probed once λ_peak is around 340 nm. Interestingly, the solvation energy of the third component increases very little with increasing solvent exposure. Figure 5 shows all water molecules within 10 Å of the indole ring. For the buried W132 mutant, all water molecules are located on the water-protein interface and are the first layer hydration water, implying the majority of the third component dynamics arise from direct coupled water-protein motions at the surface of the protein.

Figure 4.

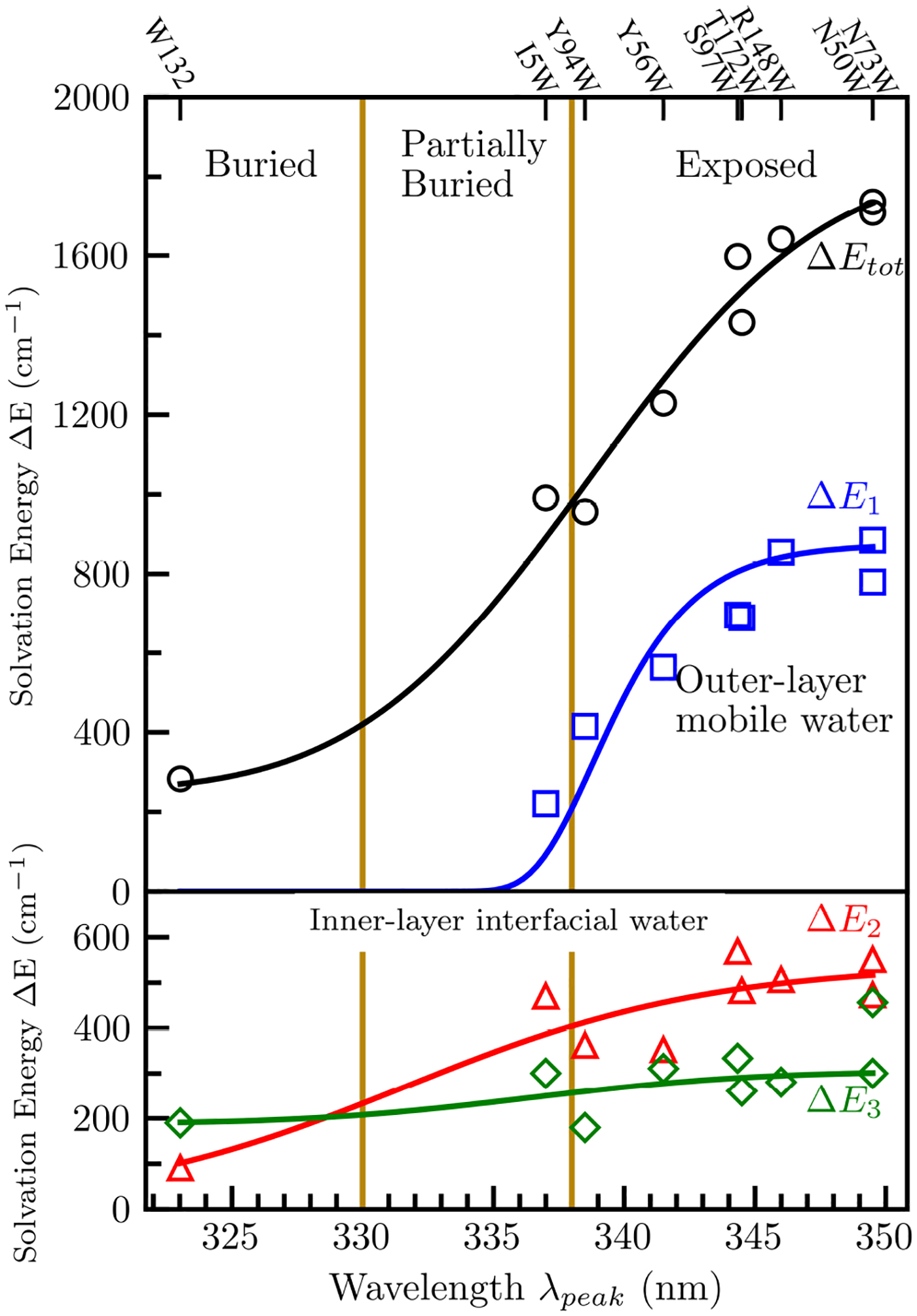
Total Stokes shift (ΔE_tot) and solvation energy of each solvation decay (ΔE₁, ΔE₂, ΔE₃) of all nine mutants with respect to steady-state emission peak λ_peak. The solid lines show the increasing trends by fitting with sigmoid functions.

Figure 5.

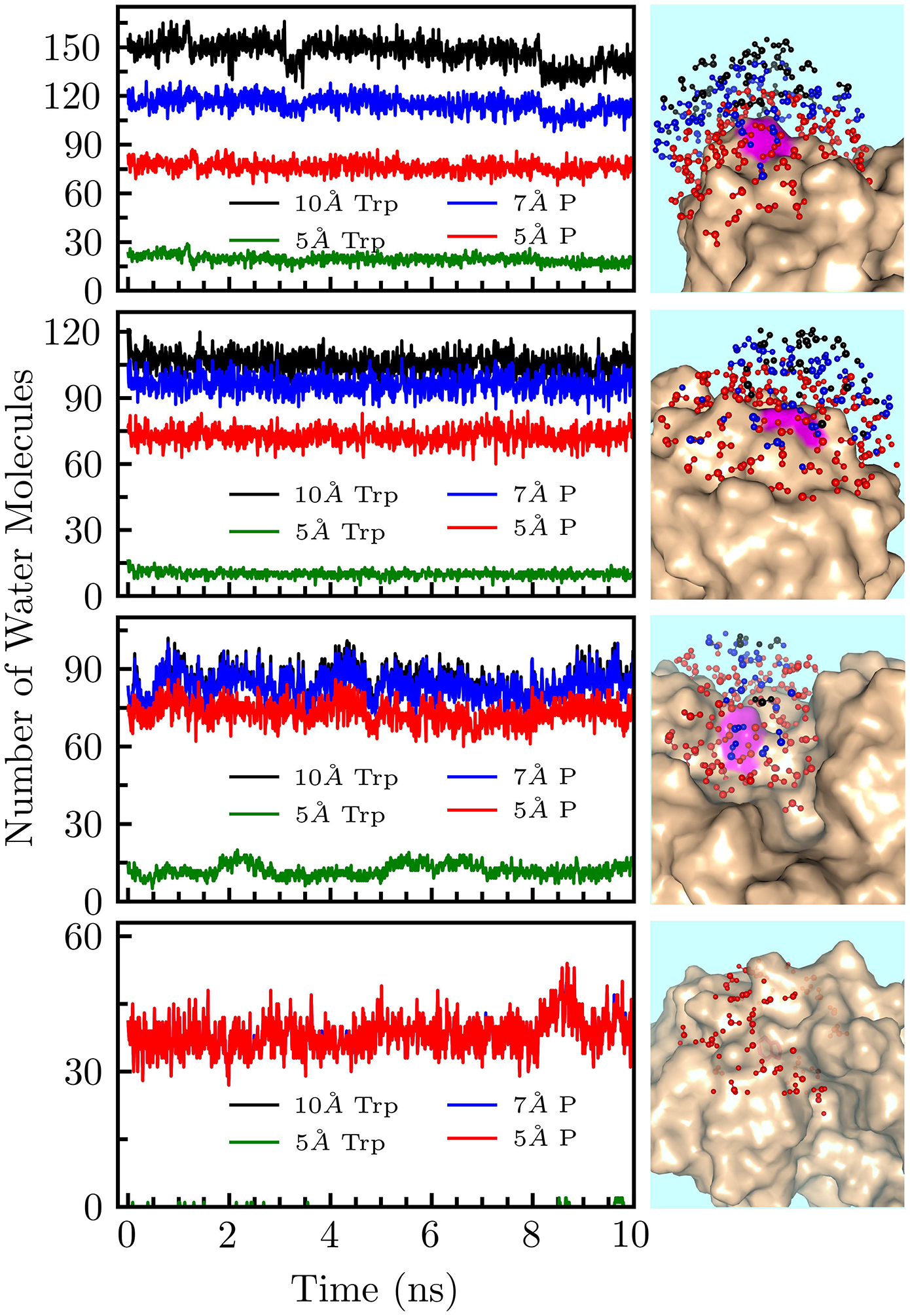
10 ns Snapshots of 30 ns MD-simulation trajectories. The top figure (S97W) represents a fully exposed mutant, I5W is a partially exposed mutant, Y56W is a mutant within a nanospace, and W132 is a fully buried mutant. Left: Lines represent numbers of water molecules at each time. All water molecules ≤10 Å from the indole ring are plotted in black. Water molecules ≤5 Å from the indole ring are plotted in green. Water molecules within 10 Å of the indole ring and ≤7 Å of the protein surface are plotted in blue. Water molecules within 10 Å of the indole ring and ≤5 Å of the protein surface are plotted in red. Right: All water molecules within 10 Å of tryptophan were plotted with the protein shown as beige surface structures. Water molecules within 10 Å of the indole ring and greater than 7 Å from the protein surface are plotted in black. Molecules between 5 and 7 Å of the surface are plotted in blue. Molecules closer than 5 Å to the surface are plotted in red.

The time constants of the solvation correlation function decays (Figure 6) report on the site-specific dynamics of each solvation process. The ultrafast bulk-type solvation process (τ_1S) occurs between 0.36 ps and 0.54 ps and is absent from the buried probe W132 (Figure 3). This is because the buried tryptophan detects only water near the protein surface, and cannot sense the nearly free, bulk-like water motions further from the protein surface.⁵⁶ Intriguingly, the nanospace confined Y56W mutant contains a significant sub-picosecond solvation process and has a steady-state emission peak over 338 nm yet, according to our MD simulations, probes very few bulk water molecules. We have seen this behavior previously in another nanospace mutation at the active site of the enzyme DNA polymerase IV (Dpo4).⁵² These mutants suggest the presence of frustrated water in nanospaces which, even though within 7 Å of the protein surface, still have initial bulk-type motions as a result of a weak H-bond network with nearby water molecules due to the surrounding electrostatics.⁵⁷ The second solvation component (τ_2S) occurs between 3.4 ps and 7.5 ps. Figure 6B shows that this relaxation displays a clear correlation with both the charge and steric environment of the tryptophan⁵⁸. The slowest relaxations occur when the probe is in concave or nanospace environments (R148W, Y94W, Y56W), or when the probe is completely buried (W132), indicating the restricted motions of water molecules near the protein surface. Notably, Y56W, located in a small channel between the two domains, is particularly slow due to the hindered motions of the water molecules within the nanospace.^52,57 The fastest decays occur when mutants are fully exposed to solvent as in S97W, N50W, and N73W where the local water network is relatively flexible and unconstrained. Mutations in densely charged environments (T172W, I5W, and N73W) experience some slowdown, but not as much as those in concave environments, indicating slightly slowed solvation motions caused by nearby charged residues. We can thus assign τ_2S motions as inner layers water reorientations, as in previous systems.^25,26,49 The third decay component (τ_3S) occurs between 110 ps and 237 ps. As shown in Figure 6C, these dynamics are roughly related with the secondary structure of the protein, with β-sheets mutations relatively slower than coil mutations. We also see that the fastest τ_3S occurs on the C-terminal of the protein (T172W), while the slowest decays come from interfacial waters probed by the buried β-sheet mutation W132. Comparing mutations in similar environments (T172W vs. I5W, Y94W vs. R148W, see Fig. 1), we find that water near β-sheet mutations is slower that near coils. We also see that water near β-hairpins experience noticeable retardation, consistent with the stability of crystallin β-hairpins in the Greek-key folds.⁵⁹ Thus, τ_3S dynamics can be assigned to the coupled water-protein restructuring that occurs after the initial fast reorientations.^19,60

Figure 6.

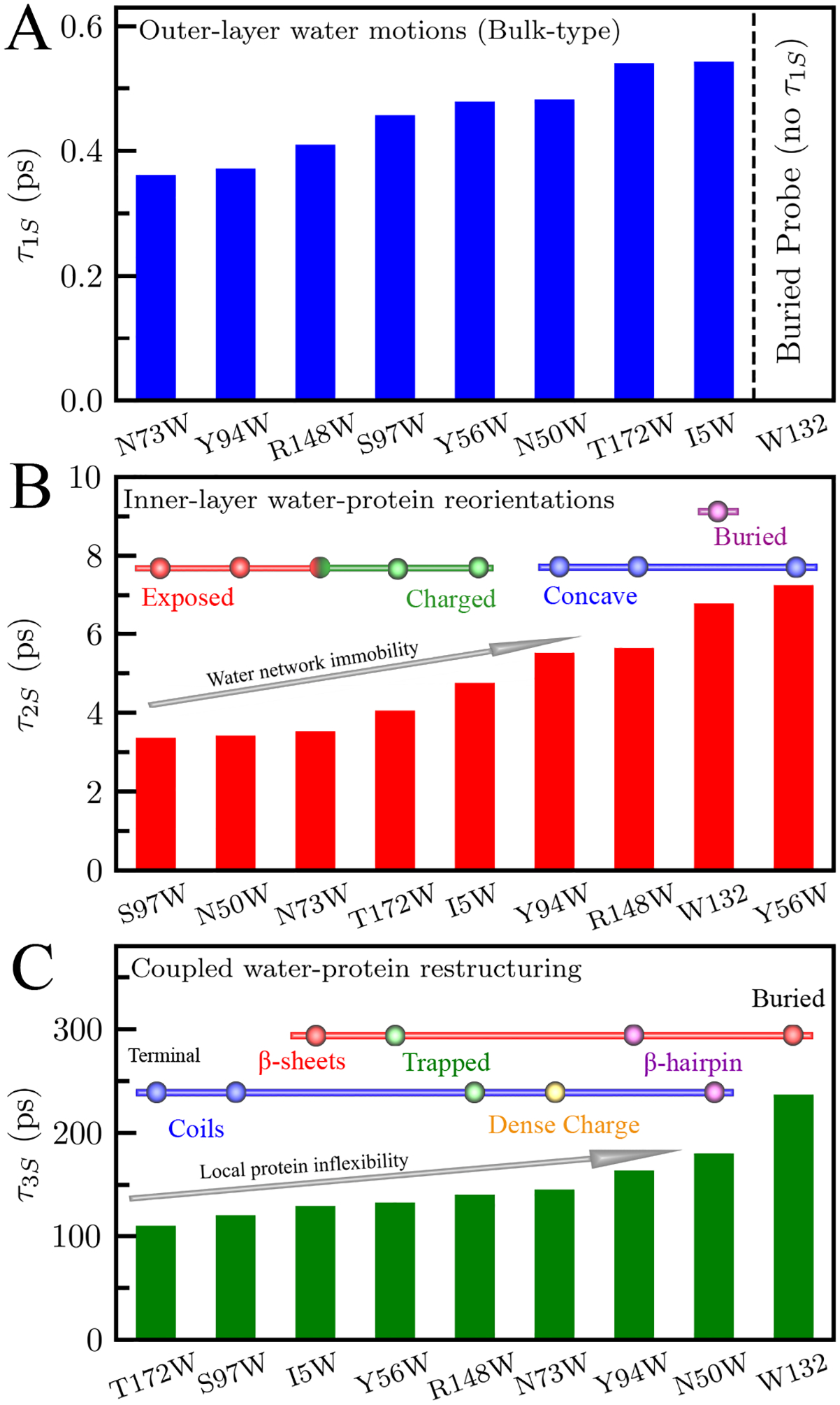
Time scales of water relaxations τ_1S (A), τ_2S (B), and τ_3S (C). τ_1S is from outer-layers water motions and not detected by the buried mutant W132. In (B) the mutants are classified based on their local steric and chemical identities (solid red, exposed; green, charged; blue, concave; purple, buried). In (C) mutants are classified by secondary structures (blue bar, coils including loops and end terminal regions; red bar, β-sheet; purple, β-sheet), and local environment (yellow; dense charge, green; trapped).

To determine the tryptophan sidechain motions, we measured the femtosecond resolved fluorescence anisotropy of the indole probe (Figure 7) and the NSR. We constructed the fluorescent anisotropy, r(t), with parallel and perpendicularly polarized fluorescent transient intensities for all mutants, shown in Figure 7A for R148W. We fit this anisotropic function with a multi-exponential decay as in (3). Figure 7B shows the r(t) and multi-exponential fit for R148W. We fit all mutants with four exponential decays. The first sub-picosecond decay constant, τ_IC, is the initial electronic relaxation time.⁴² The next two decays, τ_2W and τ_3W, represent wobbling motions of the tryptophan sidechain which occur in tens and hundreds of picoseconds, respectively. The last decay, τ_T, is the overall protein tumbling motion and was determined to be 13 ns by time-correlated single photon counting experiments. The two wobbling motions, τ_2W and τ_3W, are especially of interest concerning the relationship between solvation and sidechain dynamics. The first wobbling motion, τ_2W, occurs between 7.1 ps and 19.3 ps and is usually of small amplitude, corresponding to the indole ring reorientation with surrounding water molecules. The longer motion, occurring between 220 ps and 900 ps, may correspond to the overall tryptophan wobbling motion, including the indole ring and possibly the backbone, coupled with the water-network reorganization. The wobbling of the tryptophan probe is much slower than the corresponding solvation motions (τ_2S, τ_3S) as seen in Figure 8. Recent studies have shown that the wobbling of the tryptophan probe is coupled with the local solvent motions within the hydration shell.^49,52 As we have seen in many previous systems,^25,49,52,60 the solvent motions always occur faster than the sidechain fluctuations. Our recent studies in many protein systems have shown that the motions of the sidechain and solvent are from the same origin and are governed by similar energy barriers,^25,49,52 indicating that the local solvation fluctuations drive the wobbling of the tryptophan probe. In Figure 8A, we define a ratio between the sidechain and solvation decay times $\left(n_i=\frac{{\tau }_{iW}}{{\tau }_{iS}},i=2,3\right)$ as the slowing factor, representing the number of hydration water fluctuations needed to change the protein conformational substate.¹⁷ In our experiments, this number is always greater than one, reflecting the primacy of hydration fluctuations in the hydration layers. The slowing factors n₂ and n₃ represent different kinds of protein motions and so are not necessarily equal within the same mutation. Mutations on coils tend to have stronger water-protein coupling on the hundreds of picosecond timescale than on the picosecond timescale. Conversely, mutations on β-sheets tend to have stronger coupling on the picosecond timescale than on the hundreds of picosecond timescale. This reflects the relative stiffness of the β-sheets as compared to coiled regions which are much more flexible and therefore responsive to water-network restructuring. Fascinatingly, we observe both wobbling motions for the buried W132 mutation (28.13 and 745.98 ps), even though the probe is 7 Å from the protein surface within the core; a phenomenon seen previously in other deeply buried mutations⁵². This suggests that surface water fluctuations can penetrate inside the protein and thus the buried tryptophan mutant can still respond to surface motions with slowing factors for both processes comparable to other mutants (Figure 8C).

Figure 7.

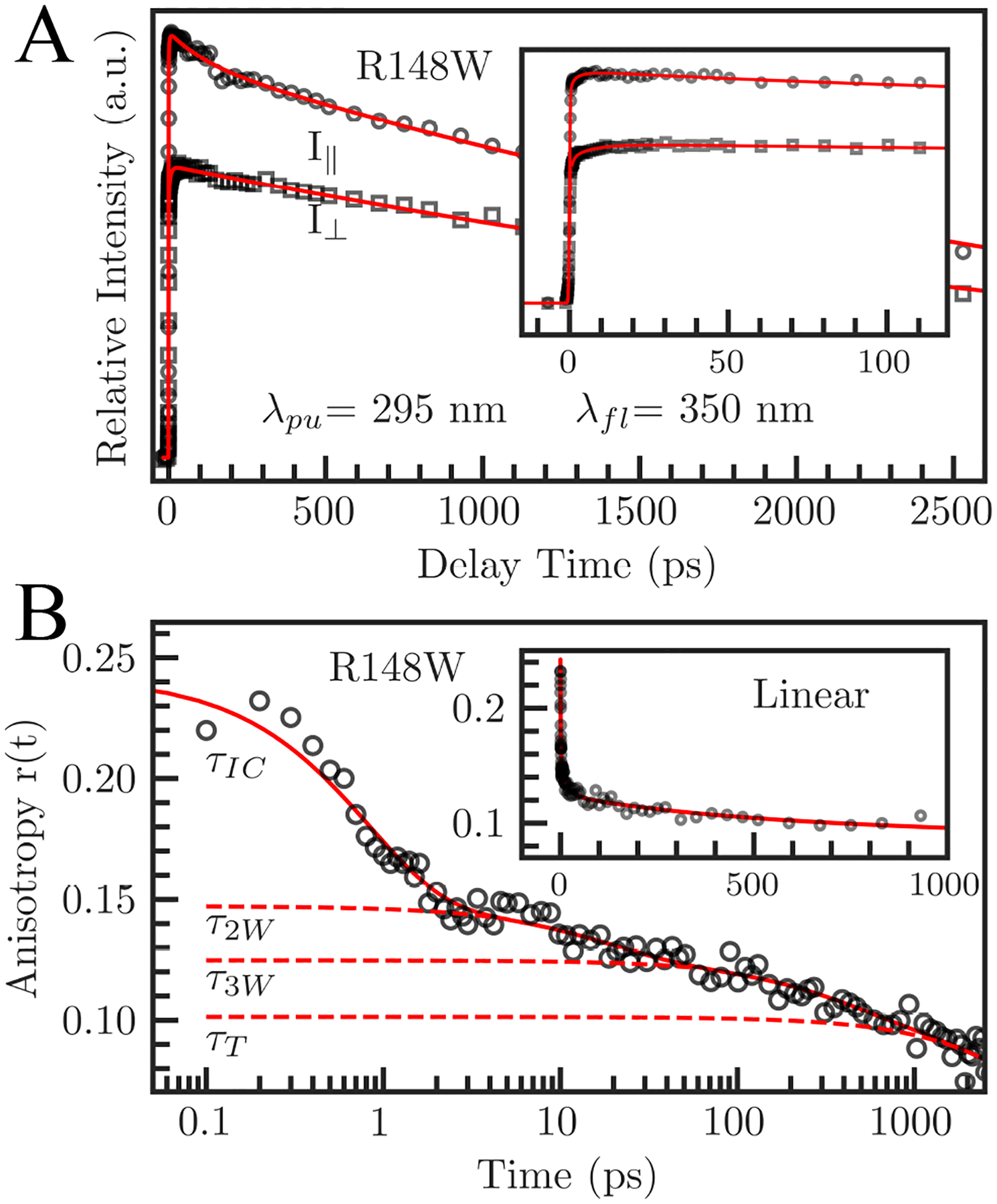
Fluorescent transients of parallel and perpendicularly polarized excitation pulses for a fully exposed mutant (R148W), gated at 350 nm (A) and the constructed anisotropy dynamics r(t) (B). The symbols are the experimental data, and the solid lines are the best fits. Decomposition of r(t) into four decays is shown with dashed lines. The inset in (A) shows I_|| and I_⊥ in a short time range. The inset in (B) shows r(t) on a linear time scale.

Figure 8.

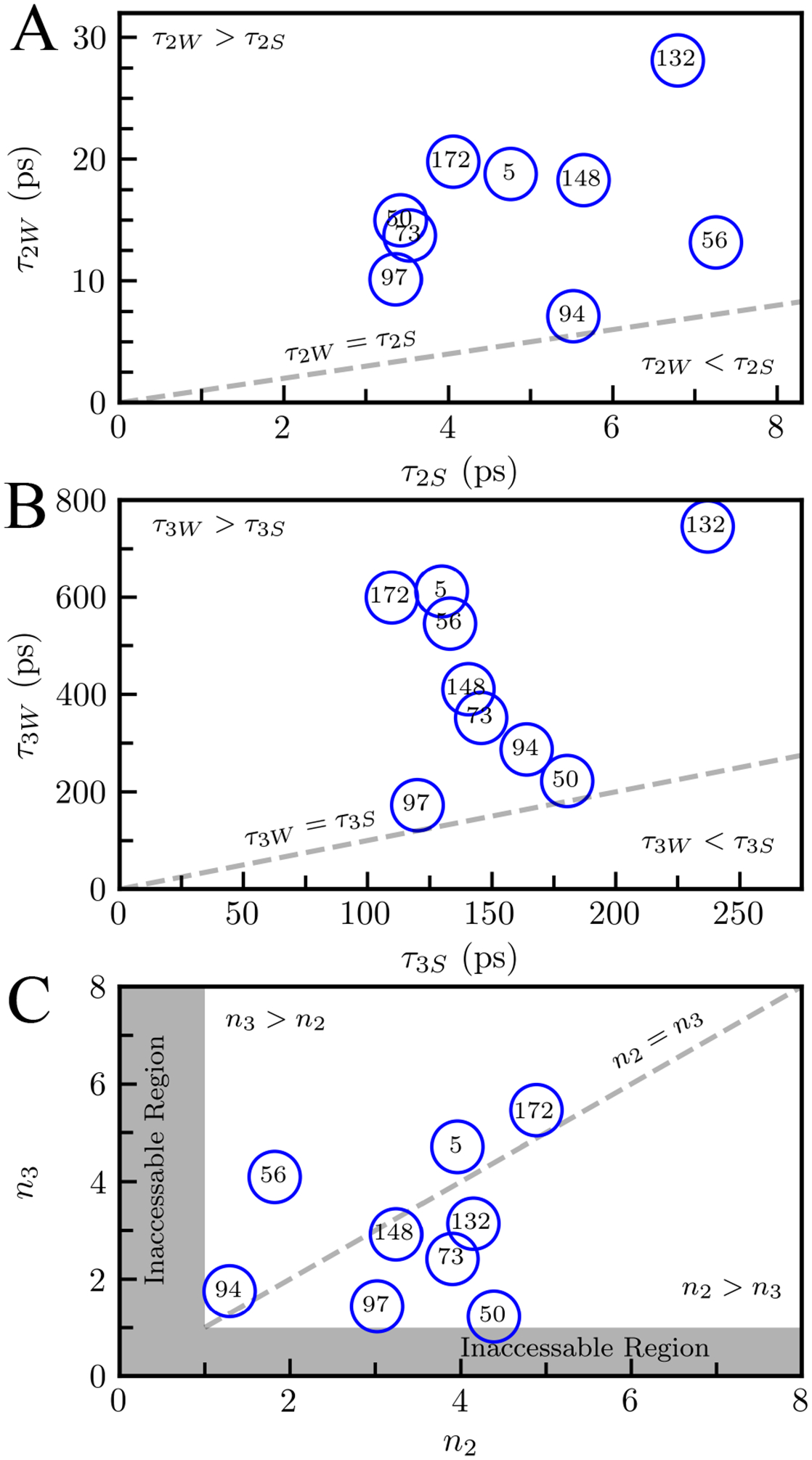
Correlations between τ_2W and τ_2S (A), τ3W and τ3S (B). (C) Slowing factors n₂ and n₃ defined by $n_i=\frac{{\tau }_{iW}}{{\tau }_{iS}},i=2,3$. A relationship of τ_iW ≥ τ_iS (i = 2, 3) was observed for all mutants. Both n₂ and n₃ are always larger than 1 in (C).

Using (2), we calculated the solvation speed for each mutant’s solvation decays. Figures 9A and B display solvation speeds in cm⁻¹/ps for the second and third decays, showing the increasing mobility of the water network. In Figure 9A, S₂ reflects the speed of the reorientation of hydration water relaxation. Overall, we see that fully exposed mutants have the fastest solvation speeds while mutants found in concave geometries generally have the slowest. Mutants in densely charged environments show a modest slowdown compared to exposed mutants. The buried mutant W132 has the slowest S₂ solvation speed because this mutant probes only water from the first, and most inflexible, hydration layer. Water molecules in confined geometries or charged environments are slower to relax than unhindered waters in exposed geometries. S₂ thus reports on the mobility of the water network and is correlated with both the steric and chemical properties of the probe’s local environment. Figure 9B shows solvation speeds for decays in hundreds of picoseconds (S₃). S₃ is correlated with the secondary structure of the mutation, with water near β-sheets typically relaxing slower than water near coils. This is especially apparent when comparing mutants in similar environments such as Y94 and N50W which are both in concave geometries. Again we see that water near β-hairpins are especially slowed reflecting the stability of water near this structure. The buried mutation W132 has the slowest solvation speed because it probes water molecules that are in the first solvation layer and therefore are slowed significantly. S₃ therefore reports on the feasibility of water network restructuring from the initial, non-equilibrium state to the final equilibrated state.

Figure 9.

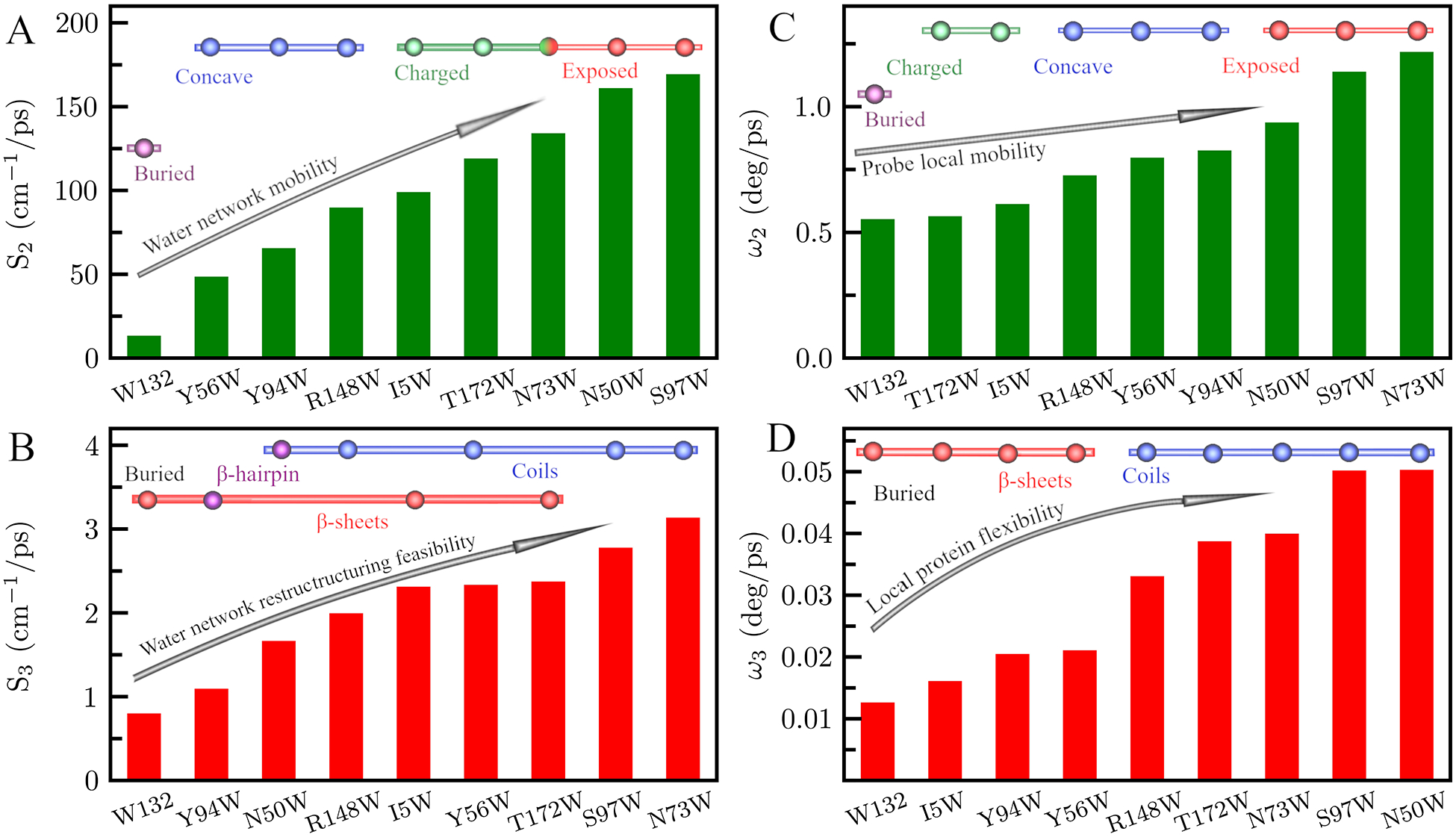
(A,B) Solvation speeds for γm7-crystallin, defined by S_i = ΔE/τ_i, i = 2,3 corresponding to the two relaxation decays of the hydration layers. (C,D) Angular speed of the tryptophan probe as defined by the two wobbling motions of the anisotropy decay.

Next, we characterized the motions of the tryptophan sidechains using the constructed fluorescent anisotropy and NSR analysis. Using (4) we estimated the wobbling semi-angle of indole ring, which represents the range of motion for the tryptophan sidechain, then with (5) we calculated the wobbling angular speed representing the flexibility of the tryptophan sidechain. On the tens of picoseconds timescale, the probe motion is restricted to a small semi-angle between 6° and 17°. The wobbling angular speed (ω₂), plotted in Figure 9C, is slowest in buried and densely charged environments, ranging from 0.55 to 0.61 deg/ps. We observe the fastest angular speed in fully exposed local environments, spanning 0.78 to 1.22 deg/ps. Probes in concave environments experience moderate retardation with angular speeds ranging from 0.73 deg/ps to 0.83 deg/ps. ω₂ consequently indicates the local mobility of the probe within the water-network depending on both the steric environment of the probe and local charges around the probe. On the hundreds of picoseconds timescale, wobbling is contained within a semi-angle between 5.9° and 23.2°. The angular speed ω₃, as shown in Figure 9D, is highly correlated with protein secondary structure. The least flexible probes are located on β-sheets, with angular speeds between 0.013 and 0.021 deg/ps. The most flexible sidechains are on coils with angular speeds between 0.033 to 0.050 deg/ps. Therefore, ω₃ reflects the local protein flexibility, depending primarily on the flexibility of the secondary structure.

To delineate the site-specific protein dynamics, we performed NSR experiments on six of the nine mutants (I5W, Y56W, N50W, N73W, S97W, and W132) under three different external magnetic fields (600, 700, and 800 MHz ¹H). Using model free analysis, we determined the order parameter (S²) and the internal motions of the protein backbone and the sidechain of the tryptophan for each mutant. All mutants were best-fitted with an axial symmetric diffusion model yielding an overall molecular tumbling correlation time of ~13.2 ns, consistent with that of the WT protein and the tryptophan fluorescence anisotropy results. For six Trp sidechain N-H vectors, S² ranges from 0.52 to 0.90 and the chemical shift anisotropy value derived from NSR measurements under three different magnetic field strengths is ~120 ppm, in good agreement with the previously reported value.⁵⁴ To further compare the tryptophan sidechain motion revealed by these two methods, we assume that the ¹H-¹⁵N bond vector rotates within a cone with semi-angle θ defined by $S=\frac{1}{2}\text{cos\hspace{0.17em}}\theta \left(1+\text{cos\hspace{0.17em}}\theta \right)$ which represents the amplitude of the N-H vector motion. From this semi-angle and the value of the correlation time of the local motion, τ_loc, we derived the angular speed of the bond vector as ${\omega }_{NSR}=\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{${\tau }_{loc}$}\right.$. When compared to the anisotropy angular speed ω_3W, as shown in Figure 10, there is a strong linear correlation between ω_3W and ω_NSR, though not through the origin, consistent with both angular speeds detection of the sidechain motion which is in turn affected by the flexibility of the nearby protein secondary structure. It is noteworthy that the cone-model is an over-simplified treatment of the order parameter, and therefore can arguably provide a reasonable estimate of the amplitude of the internal motion. However, since the tryptophan transition dipole moment measured by the fluorescence anisotropy is also treated using a similar cone-model, we think it is a fair comparison between these two results. Nevertheless, both measurements report on the local flexibility of the protein sidechain that is mainly influenced by the protein secondary structure.

Figure 10.

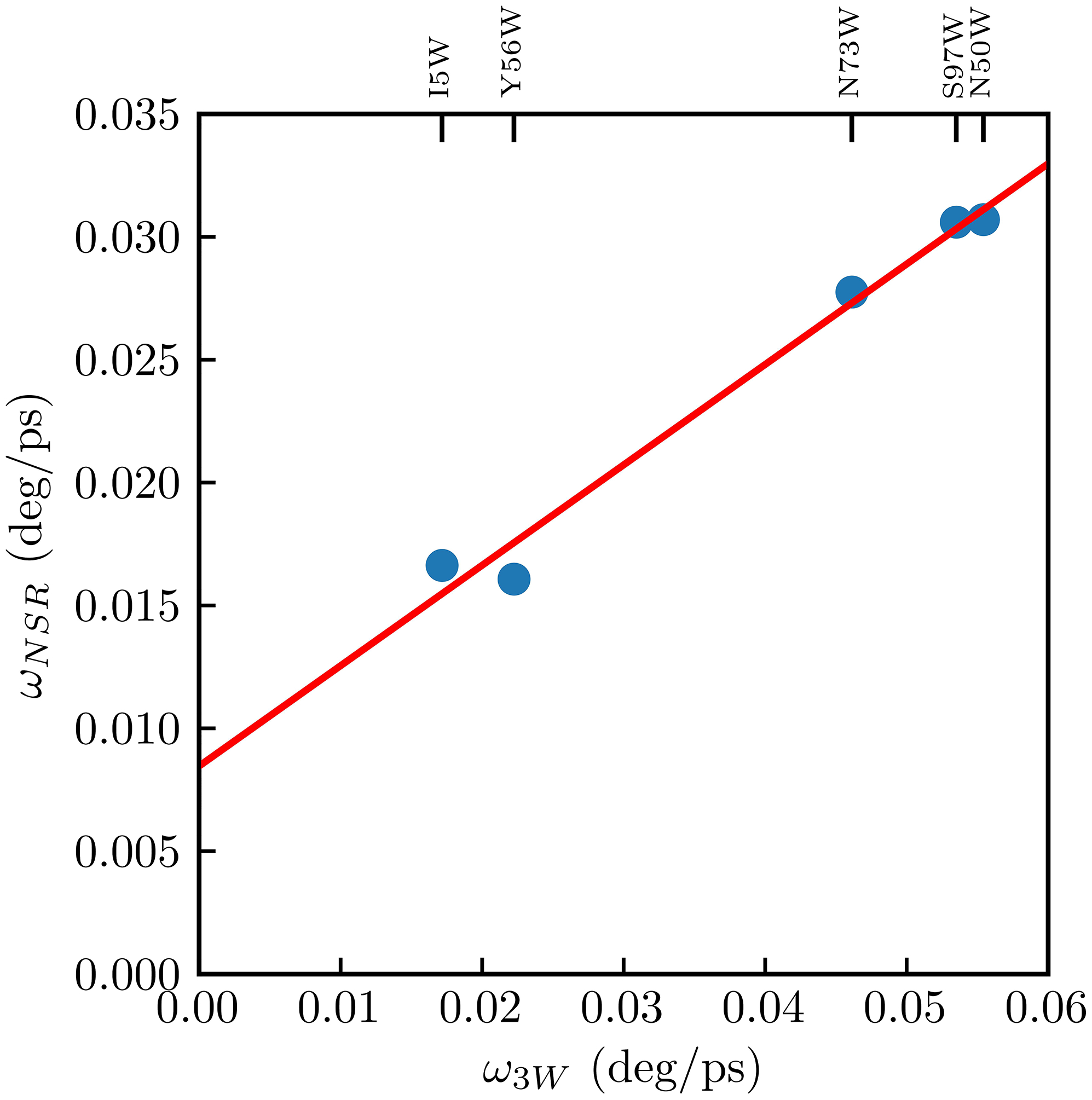
Linear correlation of angular speed as derived from by NMR (ω_NSR) and ultrafast fluorescent anisotropy (ω_3W). The data are fit by the linear equation ω_NSR = 0.408(ω_3W) + 0.008.

We finally compare solvation and anisotropy dynamics of γM7 with another β-sheet protein we have previously studied,²⁶ rat liver fatty acid-binding protein (rLFABP). Figure 11A shows that S₂ of both proteins increases with surface exposure as measured by the steady-state emission peak with no considerable difference between the proteins. The increase in S₂ is a signature of the gradual retardation of hydration waters as they move near to the surface of the protein. ω₂, shown in Figure 11B, is similarly dependent on solvent exposure like S₂ and displays little difference between the proteins.

Figure 11.

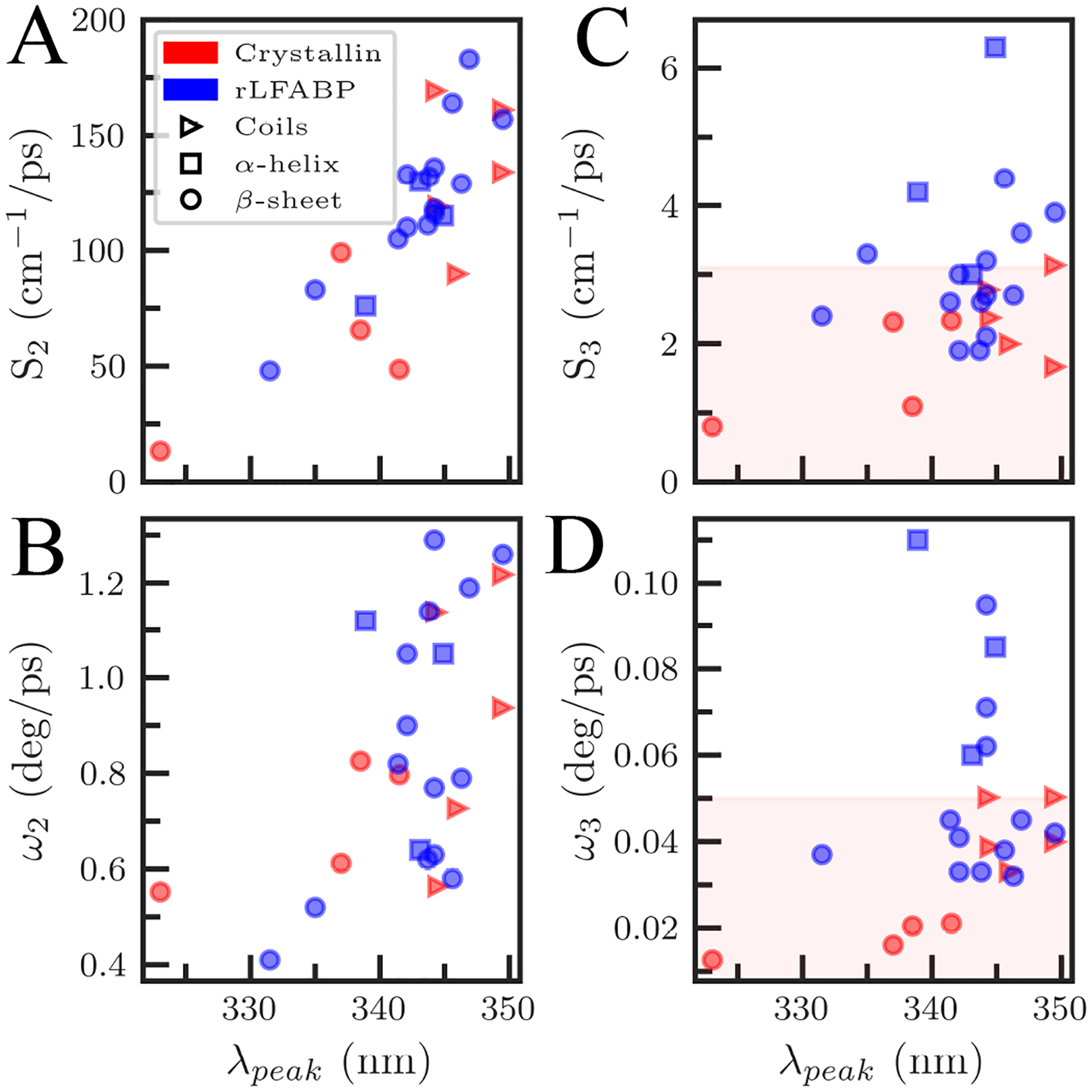
Comparison between γM7-crystallin (red) and rLFABP (blue) (A) solvation speeds and (B) angular speed for the faster τ_2i hydration shell dynamics for all mutants. Results are plotted with respect to probe exposure as measured by the tryptophan steady-state emission peak. Comparisons for the slower τ_3i hydration shell dynamics solvation speeds (C) and angular speeds (D). Note that secondary structure is given by the shape of the marker (triangles, coils; squares, α-helices; circles, β-sheets).

We have previously shown that S₃ is related to secondary structure.²⁶ γM7 and rLFABP contain mostly β-sheets, although in different tertiary structures. The β-strands of γM7 are folded into two domains, each consisting of a β-sheet sandwich made of two Greek key motifs. Conversely, rLFABP is a β-barrel protein with 10 anti-parallel β-strands and two short α-helices.^61,62 The β-barrel forms a cavity which can bind various fatty acids while the helix-turn-helix regions form a cap to the cavity.^63,64 Figure 11C shows S₃ is significantly slower in γM7 than in rLFABP with γM7 coils, normally the most flexible and fastest secondary structure, at about the same speed as rLFABP β-sheets and γM7 β-sheets slower than rLFABP β-sheets at the same levels of solvent exposure. Figure 11D shows that ω₃ in γM7 coils are about the same speed as rLFABP β-sheets while the speed of γM7 β-sheet mutants are slower than any rLFABP secondary structure. We observe a global slowing of the coupled solvation component in γM7 relative to rLFABP, while the faster reorientation in picoseconds to tens of picoseconds remains similar between the systems. This implies an overall stiffening of the protein-hydration water system in γM7 relative to other β-sheet proteins such as rLFABP, indicative of a relatively thick, slow hydration shell.

CONCLUSIONS

Here we report on the global hydration and sidechain dynamics in γM7 using ultrafast fluorescence spectroscopy and nuclear spin relaxation. Using site-directed mutagenesis to engineer total of nine mutants over all major structures in the protein, we observed two relaxations occurring in picoseconds and hundreds of picoseconds (τ₂ and τ₃, respectively) for all mutations, corresponding to the collective motions of water molecules within the hydration layers. τ_2, occurring in picoseconds, arises from reorientations within the hydration layers and is slowed significantly in confined spaces and near charged residues. This motion is especially slowed in protein nanospaces, where waters are confined on three sides by the protein surface. τ₃ relaxations, occurring in hundreds of picoseconds, arise from water-network restructuring coupled to protein sidechain fluctuations and are correlated primarily with the secondary structures of the protein. For relaxations in hundreds of ps, the sidechain dynamics reported by our anisotropy and NSR studies agree very well and have correlation times longer than that of solvent motions. We also observed sub-picosecond dynamics (τ₁) that occur only in solvent exposed tryptophan mutants, generally arising from bulk-type motions of water molecules beyond 7 Å from the protein surface. In addition, we observed sub-picosecond motions in a confined nanospace within 7 Å of the protein surface that likely originates from frustrated waters in the center of the nanospace. These water molecules not only show slow motions characteristic of confined spaces, but also exhibit bulk-type behaviors caused by the difficulty of H-bond networking in the center of the nanospace.⁵⁷

By comparison of γM7 with another β-sheet protein rLFABP, we determined that the γM7 dynamic hydration layers are likely less flexible and thicker than other β-sheet proteins. This observation is further evidenced by recent studies which found γS crystallin to have a stable hydration shell at a broad range of concentrations.⁴⁰ However, other studies using sedimentation equilibrium ultracentrifugation to determine the hydration of various crystallin species have suggested that the hydration shell of γM7 is thinner than in other proteins.³⁸ Notably, these studies probe tightly bound water, ostensibly at the protein-water interface, in the determination of the Stokes radius whereas our method probes all water within 10 Å of the indole ring and classifies the dynamic hydration shell as water that are dynamically perturbed by the protein surface. It is entirely plausible that a protein with a thick dynamic shell would have a smaller than normal Stokes radius containing tightly bound water depending on the overall structure and chemical composition of the protein surface. Thus, our study provides a broader overall picture of the surface hydration dynamics which extend beyond tightly bound water. A thick, slow dynamic hydration shell for all crystallins makes good sense in a highly concentrated lens environment since a stable hydration shell may shield the crystallins from harmful protein-protein interactions known to trigger cataract.^{33,40,65–67}