Abstract
Advanced technology in whole-genome sequencing has offered the opportunity to comprehensively investigate the genetic contribution, particularly rare variants, to complex traits. Several region-based tests have been developed to jointly model the marginal effect of rare variants but methods to detect gene-environment (GE) interactions are underdeveloped. Identifying the modification effects of environmental factors on genetic risk poses a considerable challenge. To tackle this challenge, we develop a method to detect GE interactions for rare variants using generalized linear mixed effect model. The proposed method can accommodate either binary or continuous traits in related or unrelated samples. Under this model, genetic main effects, GE interactions, and sample relatedness are modeled as random effects. We adopt a kernel-based method to leverage the joint information across rare variants and implement variance component score tests to reduce the computational burden. Our simulation studies of continuous and binary traits show that the proposed method maintains correct type I error rates and appropriate power under various scenarios, such as genotype main effects and GE interaction effects in opposite directions and varying the proportion of causal variants in the model. We apply our method in the Framingham Heart Study to test GE interaction of smoking on body mass index or overweight status and replicate the CHRNB4 gene association reported in previous large consortium meta-analysis of single nucleotide polymorphism (SNP)-smoking interaction. Our proposed set-based GE test is computationally efficient and is applicable to both binary and continuous phenotypes, while appropriately accounting for familial or cryptic relatedness.
Keywords: rare variant analysis, gene × environment interaction, generalized linear mixed model, variance components score test, sequence kernel association test, family data
1. Introduction
Although genome-wide association studies (GWAS) have been successful in identifying genetic variants with strong association with disease, the variants evaluated in GWAS have been mostly restricted to common variants, typically defined as those with minor allele frequency (MAF) greater than 1 or 5%. Additionally, these identified variants explain only a small portion of disease heritability, which could be due to limited sample size and power in GWAS, and thus calls for performing meta-analysis.1 Nevertheless, even in large scale GWAS meta-analyses, much of the heritability remains unexplained. For example, in GWAS meta-analysis of adult height in > 93,000 East Asians, the investigators identified 98 loci at genome-wide significance that explain only about 9% of height heritability, which is a small proportion considering that human height heritability is approximately 80%.2
One plausible explanation for missing heritability is the presence of rare variants, which are not analyzed in GWAS due to their low MAF. It is well known that rare variants are responsible for many Mendelian disorders, but they have not been fully investigated in complex diseases.3,4 With rapid advances and decreasing cost of whole-genome sequencing, attention has been shifted to investigating the potential role of low frequency variants in complex human disease etiology. There is now an abundance of growing empirical evidence that rare variants may be responsible for complex diseases, which might account for missing heritability.4,5,6 For example, Igartua et al.7 identified two novel rare variants associated with low-density lipoprotein cholesterol and high-density lipoprotein cholesterol with larger effects than the previously discovered variants within the known blood lipid associated loci. In another study by He et al.,8 multiple rare variants were found to be associated with lower systolic blood pressure. Successes from rare variant association studies highlight the importance of rare variants to complex disease susceptibility.
When single variant tests are applied to rare genetic variants, they are severely underpowered, and hence several statistical methods have been developed to increase power. These methods are usually region-based tests that study the joint effects of rare variants in a specified region and can be broadly categorized into burden tests and non-burden tests. For burden tests, the cumulative effects of variants in a region are summarized into a single variable which is then tested for association with the trait of interest. Variants can be collapsed by summing up the number of rare alleles in a region or by using a binary variable to indicate whether an individual has any rare alleles in that region. Other extensions of burden tests have been developed.8,9,10 Burden tests are most powerful when variants in consideration are causal and the direction of the effect on risk of the alternate/minor allele is the same. When the alternate/minor alleles of causal variants have effects on the phenotype in different direction, and/or the proportion of causal variants is small, burden tests suffer from low power.4,12,13 To address this issue, non-burden tests have been proposed that focus on aggregating individual test statistics. Among non-burden tests, the sequence kernel association test (SKAT) is a popular method that summarizes variant information using a kernel function and applies variance component score test to evaluate the significance.14 SKAT is powerful when there are variants in mixed directions or when the proportion of causal variant is small, but it is less powerful than the burden tests when the majority of variants in a region are causal with effects in the same direction.14,15
Another plausible explanation for missing heritability is due to gene-environment (GE) interactions. Complex diseases are multifactorial and involve both genetics and environmental factors. Therefore, studying just the main effects, either genetic or environmental, cannot provide full insights into the biological mechanisms. Studying GE interactions can provide better insights into the biological mechanisms of complex diseases, which help to identify subgroups that are at high risk and eventually lead to better diagnostics and personalized treatments.16,17 Typically, GE tests require larger sample sizes than a main effects test to achieve appropriate power, and rare variant analysis also needs bigger sample compared to common variant analysis to maintain power.17,18,19
Several GE interaction of rare variant methods are available but they are only applicable to unrelated individuals and cannot correctly account for familial correlation in their models.12,20 Tzeng et al.19 developed similarity-based regression method (SimReg) to test GE interaction effects of rare variants for continuous traits. SimReg allows for covariate adjustments, models both main and interaction effects, and is computationally efficient. Zhao et al.17 extended SimReg to allow for binary traits for common or rare variants. Lin et al.21 introduced rare variant by environment interaction method using a variance component test under the generalized linear model framework. Chen et al.18 proposed two GE interaction tests (rareGE) and a joint test of main effect and interaction effect for rare variants using variance component score tests. In rareGE, genetic variants can be included as fixed or random effects for the interaction test and rareGE works for both binary and continuous traits. Recently, Mazo Lopera et al.22 developed SNP-set GE interaction method for family data but it was proposed in the context of common variants. Coombes et al.23 extended gene-based GE interaction methods to account for multiple interactions in family data but they are applicable to continuous outcomes only.
In this article, we introduce a unified approach for GE interaction tests for rare variants (famGE) to correctly incorporate sample relatedness. Our approach can accommodate both binary and continuous traits in family data, eliminating the need to restrict samples to just unrelated individuals. We adopt a kernel-based method to leverage the joint information across rare variants. We assume main genetic variants, GE interaction term, and family correlation to be random effects and implemented a variance component score test in the generalized linear mixed model (GLMM) framework to reduce the computational burden.
The paper is organized as follows. In section 2, we introduce our notation, the GE interaction model, and the test statistic. In section 3, we conduct extensive simulations under various settings to assess type 1 error rates and power of our approach, comparing it to rareGE and the burden test. We apply our method in testing gene by smoking interaction on body mass index (BMI), using family data from the Framingham Heart Study (FHS) in section 4. We discuss our findings of our approach in section 5.
2. Methods
Notations and model settings for interaction test for family data
Assuming a sample of size n, let Y be n × 1 vector of phenotype (binary or continuous) with E(Y) = μ and var(Y) = ϕv(μ), where μ = [μ1…μn]T is the mean vector, ϕ is the dispersion parameter (1 for binary), and v(·) is the variance function. We consider the following GLMM for testing GE interactions:
| (1) |
where g(·) is the link function, X is an n × p covariate matrix including the intercept and the environmental variable E, α is a p × 1 vector associated with the fixed covariate effects, G is an n × q genotype matrix, θ is a q × 1 vector of random effects for the genetic variants, EG is an n × q GE interaction matrix, γ is a q × 1 vector of random effects for GE interaction, and d is an n × 1 vector for the random effects of familial correlation. W1 and W2 are q × q diagonal matrices with pre-specified weights for genetic main effects and GE interaction effects, respectively. In famGE framework, user-defined weights can be flexibly included, such as weighs calculated based on MAF or functional annotation scores. Good choices of weights can boost power. For the three random effects (genetic variants, GE interactions, and relatedness in families respectively), we assume that
where ψ is twice the n × n kinship matrix from family relationships obtained from a pedigree or an empirical kinship calculated from genotype data to account for cryptic relatedness. Kinship coefficient summarizes genetic similarity between two individuals. The random effects θ, γ, and d are assumed to be independent from each other. If γ is treated as a fixed effect, we would perform a q degrees of freedom score test, but this test can lead to power loss when q is large.12 By assuming that γ follows a normal distribution with mean 0 and variance , the null hypothesis for the interaction test: H0: γ = 0 is equivalent to testing H0: with a variance component score test.12,14 Score tests only require fitting the model under the null hypothesis, so they are more computationally efficient.
Estimation and hypothesis testing
To fit the null model for binary traits, we use the penalized quasi-likelihood method. (See Appendix 1 for complete derivation). Because the integrated quasi-likelihood function for binary traits contains a high dimensional integral that is intractable, we use the Laplacian method to approximate the integral. To estimate the parameters, we define the linear working vector under the null hypothesis Y0 = Xα + GW1θ + d + Δ(Y−μ), where Δ = diag{g′(μi)}, and let . We iteratively fit the working vector to estimate the parameters until convergence to obtain our restricted maximum likelihood (or maximum likelihood) estimates.24
Let , , and be the restricted maximum likelihood (or maximum likelihood) estimates under the null hypothesis. We can then calculate , and using the aforementioned restricted maximum likelihood (or maximum likelihood) estimates. Restricted maximum likelihood estimates the variance components independent of the fixed effects. Maximum likelihood produces unbiased estimation for the fixed effects but biased estimation of variance components. In large samples, their results are usually close to each other. The restricted maximum quasi-likelihood function is defined as:
| (2) |
where .
To derive the score test for H0: , we take the first derivative of the quasi-likelihood with respect to ,
| (3) |
The first term in equation 3 is fixed and independent of the phenotype. We follow the same rationale in the derivation of the SKAT score statistic and take twice the second term to be our test statistic14,25
| (4) |
where .
Under the null hypothesis, , where λj’s are eigenvalues of the matrix .14,26
3. Simulation studies
Simulation settings for type I error evaluation
We performed simulation studies to evaluate type I error rates for our proposed approach. For the null simulation study, we first considered the scenario where there are main genotype effects but no GE interaction effects. To simulate the genotypes, we used SeqSIMLA software, which can simulate sequence data in families with user-specified pedigree structures and different disease models. We used reference sequence based on 1000 Genomes Project for European populations.27 We picked 7 pedigrees from FHS with family membership ranging from 120 to 640 (2030 individuals in total). In the simulated genotypes, we chose a region that spans from 1,100 base pairs to 1,140 base pairs in chromosome 1. To simulate our phenotype, we varied the proportion of low frequency (MAF <5%) causal SNPs included in our model to 20% to 40% to 60% and 80% for each of 20,000 replicates. We considered both continuous and binary phenotypes. For each of 20,000 replicates, we simulated phenotype datasets from
where age was generated from a normal distribution with mean of 50 and standard deviation equal to 5, sex was generated from a Bernoulli distribution with probability 0.5, smoke was generated from a Bernoulli distribution with probability 0.5, and ϵ was generated from a standard normal distribution. W1 are the weights from beta density function with parameters 1 and 25 that are applied to the main genotype effects.14 Family correlation, d, is from a multivariate normal distribution with means 0 and covariance , where is set to 1 and ψ is twice the kinship matrix. γ consist of effect sizes for the causal SNPs. For binary traits, we simulated the continuous traits and set the lower 80% as controls (0’s) and the upper 20% as cases (1’s). We simulated variants where the directions of the main effect (represented by γ) on risk of the minor allele are either all positive or mixed with 50% positive and 50% negative and the effect sizes were determined by
where MAF is the minor allele frequency of SNP i. The constant h is calculated as
where R2, the proportion of variance explained by the causal SNPs, was fixed at 1% for causal SNPs with effect sizes in same direction and 5% for causal SNPs with effect sizes in opposite directions. The correlations between the SNPs are in matrix L, and v is a vector that indicates the direction of the SNP effects. We performed three tests for the type I error comparison: our proposed method that correctly accounts for familial correlation (famGE), rareGE where the main genetic effects are treated as random and family correlation is ignored (rareGE), and the burden test using GLMMs to account for familial correlation (BT). For the burden test, we used an indicator of whether or not the rare allele was present in the testing region. We simulated 20,000 replicates and used Wu weights, which are the beta density function with parameters 1 and 25 evaluated at the MAF of the variants, for famGE and rareGE tests.14
Simulation settings for power analysis
To assess power, we simulated data under the alternative hypothesis, where we include a gene by smoking interaction effect in addition to the main genotype effects. Similar to the type I error simulation, genotypes were simulated using the SeqSIMLA software and we varied the direction of genetic main effect and the proportion of causal SNPs with MAF less than 5%. We simulated 10,000 phenotype datasets from
where age, sex, and smoke, family correlation, and error terms were generated from the same distribution described in the type I error simulation study and the genotype effects γ were determined the same way as in our null simulation study. Interaction effects δ were generated independently from the genotypes from a normal distribution with mean 2 and standard deviation of 0.3. W1 and W2 are the weights from beta density function with parameters 1 and 25 that are applied to the main genotype and interaction effects respectively.14 We considered the scenarios where the directions of the interaction of a causal variant (represented by δ) is either the same or opposite to the directions of the corresponding main effect (represented by γ). Negative interaction effects were simulated the same way as above except we multiplied the effects by −1. To test binary outcomes, we set the lower 80% of the simulated continuous outcome to be the controls and the upper 20% to be the cases. For power comparison, we also performed a burden test, where the summary variable for each individual was created using an indicator of whether or not the rare allele was present in the testing region.
Results for type 1 error simulations
Table 1 includes the partial results for type 1 error for famGE, rareGE, and BT at significance levels, α, of 0.05, 0.01, and 0.001 from 20,000 simulation replicates (refer to Appendix 2 for full results). Both famGE and BT have correct type 1 error rates at all three α levels for both continuous and binary traits. When familial correlation is not appropriately taken into account in the model, rareGE test suffers from type 1 error inflation, which is more pronounced in binary traits. FamGE has valid type 1 error rates under various scenarios, such as differing the direction of main genotype effects and increasing the proportion of causal variants in the model for both continuous and binary traits. Because rareGE does not have correct type 1 error rate when familial correlation is not taken into account, we did not include rareGE in the power comparison in the next section.
Table 1.
Comparison of type 1 errors based on 20,000 replications (in %)
| Continuous | Binary | ||||||
|---|---|---|---|---|---|---|---|
| Scenarios (+/−/0) | α level | famGEa | rareGEb | BTc | famGEa | rareGEb | BTc |
| 4/0/16 | 5 | 4.96 | 5.30 | 5.01 | 5.03 | 5.51 | 5.07 |
| 1 | 1.00 | 1.10 | 1.02 | 1.02 | 1.25 | 1.05 | |
| 0.1 | 0.10 | 0.17 | 0.10 | 0.12 | 0.18 | 0.11 | |
| 16/0/4 | 5 | 5.04 | 5.38 | 5.00 | 4.84 | 5.70 | 5.00 |
| 1 | 0.91 | 1.16 | 0.99 | 0.97 | 1.41 | 0.94 | |
| 0.1 | 0.10 | 0.16 | 0.10 | 0.10 | 0.20 | 0.10 | |
| 2/2/16 | 5 | 4.80 | 5.25 | 5.00 | 4.97 | 5.56 | 5.06 |
| 1 | 0.95 | 1.20 | 1.01 | 0.94 | 1.16 | 0.97 | |
| 0.1 | 0.10 | 0.14 | 0.11 | 0.11 | 0.16 | 0.11 | |
| 8/8/4 | 5 | 5.02 | 5.31 | 4.93 | 4.89 | 5.55 | 4.79 |
| 1 | 0.90 | 1.11 | 0.99 | 0.97 | 1.27 | 0.94 | |
| 0.1 | 0.10 | 0.17 | 0.12 | 0.10 | 0.16 | 0.10 | |
+/−/0: number of variants with main genotype effect sizes that are positive, negative, and neutral
famGE: our proposed method accounting for family correlation
rareGE: interaction test ignoring family correlation
BT: burden test
Results for power simulations
Figure 1 shows the power comparison for famGE and BT for continuous traits at α = 0.001 from 10,000 replicates. When the proportion of causal variants is low, BT has lower power than famGE (1A). This is expected because burden tests are powerful when a large proportion of causal variants are included in the region. When the proportion of causal variants increases, we see that powers for both BT and famGE increase but we see a larger power increase in BT compared to famGE. However, when variants have interaction effects in different direction, we observe a power drop, with power close to 0 for BT, whereas famGE shows increasing power as proportion of causal variants increases (1B). FamGE maintains fairly consistent power across different scenarios, regardless of the direction of the main effects.
Figure 1. Power comparison of famGE and BT for continuous trait.
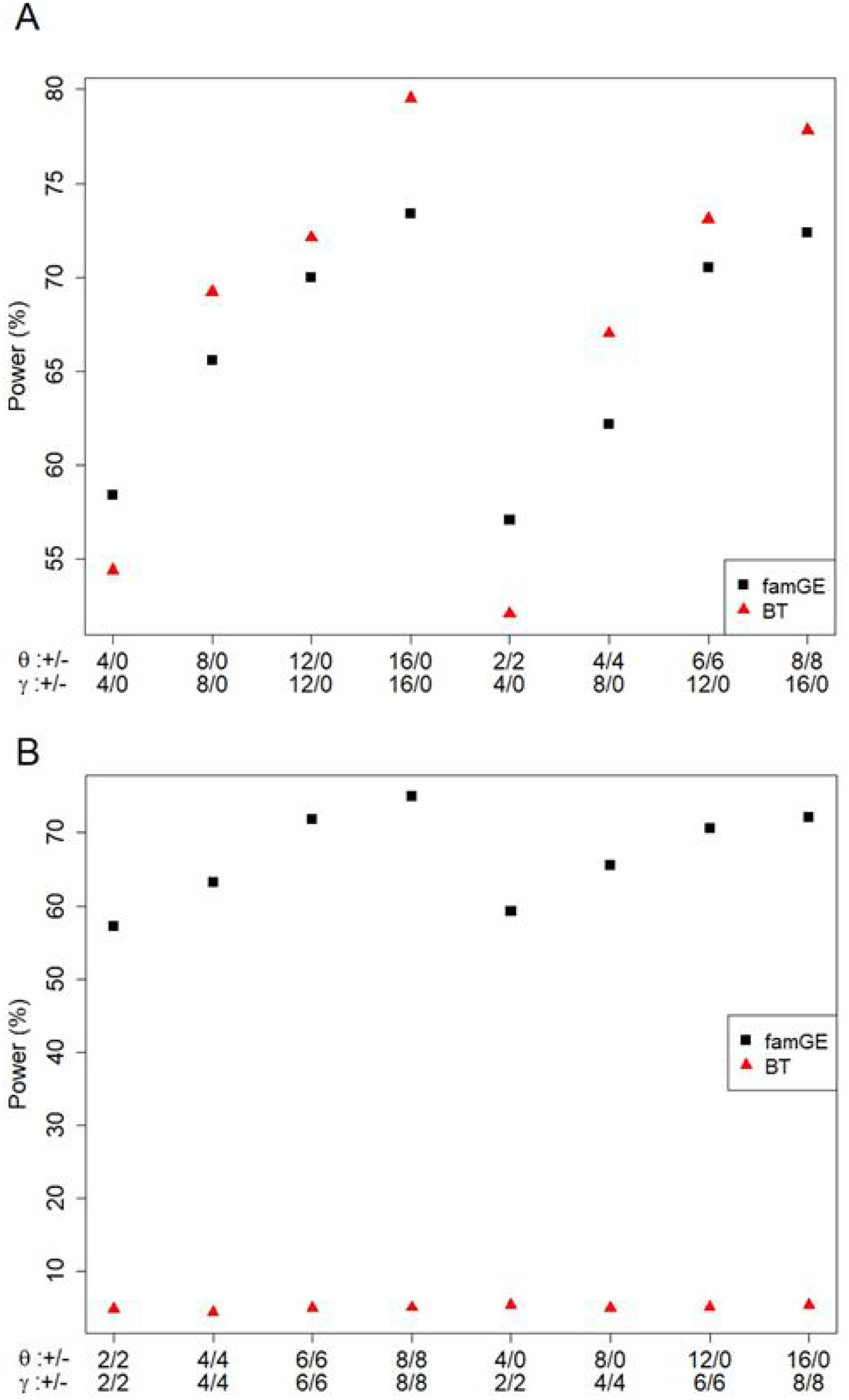
The X-axis indicates different SNP scenarios and the y-axis presents power (%). For example, in the first scenario, there are 4 variants where the minor alleles have positive main effects (16 variants with no main effect), and 4 variants where the minor alleles have positive GE interaction effect (16 variants with no GE interaction effect).
(A) All positive interaction effects
(B) Minor alleles with both positive and negative interaction effects
+/− indicates the number of SNPs with positive and negative effects. θ denotes SNP main effects and γ denotes GE interaction effects
Figure 2 shows power comparisons of famGE and BT for binary traits at α = 0.001 from 10,000 replicates. We come to the same conclusion as the results seen from continuous traits. Even though burden tests have higher power than famGE in the case where interaction effects are in the same direction, with the exception where there are 4 causal variants and 16 neutral variants in the model, famGE is able to maintain high power regardless of the direction or the proportion of variants (2A). The burden test significantly loses power in the presence of both trait-increasing and decreasing alleles, whereas performance of famGE is robust across different scenarios (2B).
Figure 2. Power comparison of famGE and BT for binary trait.
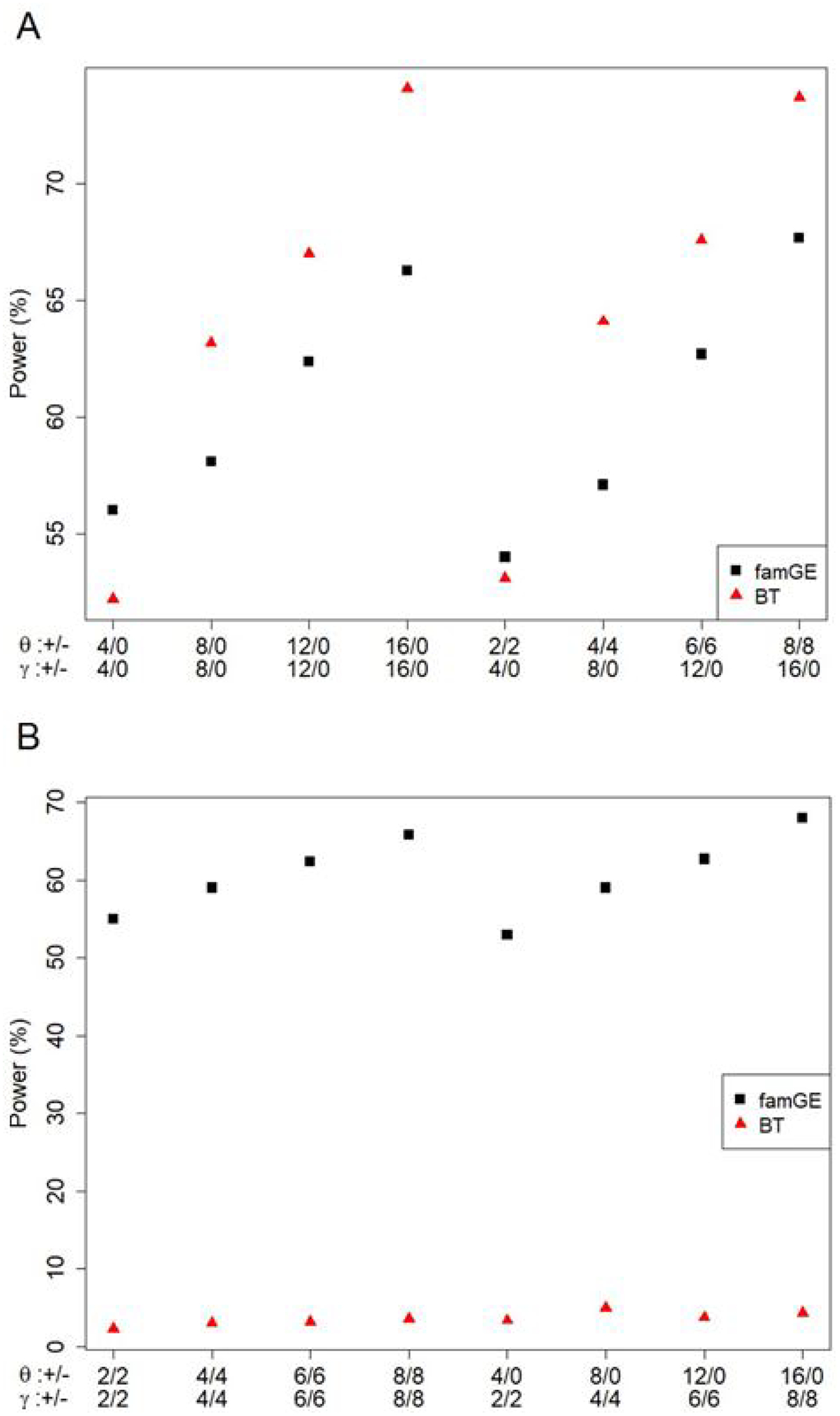
The X-axis indicates different SNP scenarios and the y-axis presents power (%). For example, in the first scenario, there are 4 variants where the minor alleles have positive main effects (16 variants with no main effect), and 4 variants where the minor alleles have positive GE interaction effect (16 variants with no GE interaction effect).
(A) All positive interaction effects
(B) Minor alleles with both positive and negative interaction effects
+/− indicates the number of SNPs with positive and negative effects. θ denotes SNP main effects and γ denotes GE interaction effects
4. Application to the Framingham Heart Study
In the real data application, we illustrate our method to test gene-based interaction with smoking on a quantitative trait, BMI, and a dichotomous trait, overweight status (BMI ≥ 25), using participants from the Framingham Heart Study (FHS). FHS is a longitudinal cardiovascular cohort study that was initiated in 1948 in Framingham, Massachusetts. The study began with 5209 participants (Original Cohort) in 1948 and in 1971, 5124 children of the original cohort and their spouses (Offspring Cohort) were enrolled. A total of 4095 additional participants, who were the grandchildren of the original cohort, were recruited in the third generation cohort (Gen 3 Cohort) in 2002.28 To reflect ethnic diversity in Framingham, 917 additional non-white participants were recruited to form the Omni Cohort.29
Obesity is a world-wide problem that can lead to serious health problems, such as high blood pressure, type 2 diabetes, heart disease. Conventionally, BMI has been used to measure obesity. GWAS have identified numerous loci associated with BMI, but whether these genetic effects are modulated by environmental factors has not been extensively investigated.30,31 Recently, Justice et al.32 investigated the effect of smoking on genetic susceptibility to obesity in a large consortium meta-analysis of 241,258 individuals and reported two common variants reaching genome-wide significance, rs12902602 and rs336396 near the CHRNB4 and INPP4B genes respectively. Here we evaluated whether there are modification effects of smoking status on genetic risk from these two loci for obesity with rare or less frequency variants.
We analyze genotype data from the Illumina V1.0 Exome Chip and select variants with MAF less than 5%. We adjust for age, sex, cohort (four category variable), first two principal components, and smoking main effect in our model and pedigree-based kinship matrix to account for familial correlation. Our data consists of 596 individuals from the Original Cohort (Exam 21), 2547 from the Offspring Cohort (Exam 8), 3868 from the Gen 3 Cohort (Exam 1), and 177 from the Omni Cohort (Exam 1). There are 3264 males (45.4% males), 6063 non-smokers (84.4% non-smokers), and their age ranges from 19 to 85 (median = 49). We test for gene × smoking interaction by treating BMI as continuous trait or dichotomizing BMI at 25 into a binary trait, which classified 4502 individuals as overweight and 2686 individuals in the normal range. A total of 7188 individuals are included in the gene × smoking interaction analysis.
We consider two genes, Cholinergic Receptor Nicotinic Beta 4 (CHRNB4) and Inositol Polyphosphate-4-Phosphatase (INPP4B). Table 2 summarizes the analysis results for the two aforementioned genes using our proposed method and the burden test. In order to minimize the inclusion of potential noise in our testing region, we consider variants that are annotated as either stop-gain/loss, splice, or missense. We can achieve higher statistical power by utilizing functional annotation to prioritize variants predicted to have potential biological significance. With the burden test, we find a significant CHRNB4 × smoking interaction for overweight status (p-value = 0.0184) at α = 0.025. Using famGE, we find CHRNB4 to be statistically significant at α = 0.025 for both continuous (p-value = 0.0063) and dichotomized (p-value = 0.0023) BMI, but no gene × smoking interaction were identified for gene INPP4B. (See Appendix 3 for quantile-quantile plot of famGE applied genome-wide.) For CHRNB4, we noticed that the signal is stronger in the binary model, which could potentially indicate a non-linear interaction between smoking and CHRNB4.
Table 2.
Association results of gene by smoking interaction on continuous trait: BMI and binary trait: overweight status (BMI ≥ 25) for two previously identified loci using the Framingham Heart Study
| Gene | Chromosome | # of variants used | famGE p-value | Burden test p-value |
|---|---|---|---|---|
| Continuous: BMI | ||||
| CHRNB4 | 15 | 8 | 0.0063 | 0.3787 |
| INPP4B | 4 | 5 | 0.5504 | 0.7797 |
| Binary: BMI ≥ 25 | ||||
| CHRNB4 | 15 | 8 | 0.0023 | 0.0184 |
| INPP4B | 4 | 5 | 0.9166 | 0.9952 |
# of variants used refer to functionally relevant variants (stop-gain/loss, splice, or missense) that were included in famGE test
From the two genes we test in the real data application, CHRNB4 shows statistical significance in interacting with smoking on BMI. The CHRNB4 gene has been reported to be associated with higher BMI in never smokers and lower BMI in current smokers, implying that genetics variants may influence BMI via the weight-reducing effects of smoking in opposite directions.33 INPP4B gene is a novel locus identified in the meta-analysis by Justice et al.32 but to our knowledge, this finding has not yet been replicated in other studies. We cannot exclude the possibility that there are no rare variants interacting with smoking in INPP4B gene.32 However, it is also possible that reduced power due to limited sample size in our study compared to that of in the meta-analysis restrict us from finding a significant association.
5. Discussion
In this article, we develop a unified method called famGE to detect GE interactions of a set of rare variants under the GLMM framework. This proposed approach can accommodate both binary and continuous traits in family data or samples with cryptic relatedness. Additionally, famGE allows weighting variants differently based on prior information such as allele frequency. Under this model, we treat the genetic variants, familial correlation, and GE interaction effects as random effects and implement a variance component score test, which only requires fitting the null model, and thus, reduces computational burden. Our simulation studies show that famGE maintains correct type 1 error and high power under various scenarios.
Ignoring familial correlation when using linear or logistic regression to analyze family data lead to inflated type I error.25 One way to resolve this issue is to select a subset of unrelated individuals, but this may substantially reduce the sample size and lead to power loss. In the case of rare variants, especially for GE interaction test, it is important to retain as many samples as possible to have appropriate power. A preferable method is to use GLMMs that account for familial correlation as a random effect and thus, eliminates the need to restrict to unrelated individuals. In famGE, kinship coefficients can be obtained either from a pedigree or an empirical kinship matrix. Because the empirical kinship matrix can account for cryptic relatedness, it is advantageous to use the empirical kinship to estimate the level of relatedness among individuals.14
The proposed famGE method models the main genotypes as random effects in order to reduce the number of parameters that need to be estimated. If one wishes to model the main effect as fixed effects, the derivations of the new test statistic follows the same framework as the statistic for famGE with random genotype main effects. When the number of variants included in the model is large, however, there is a potential for multicollinearity with the covariates and/or among the variants when fitting the model. It is also shown that modeling the genetic main effects as fixed leads to slightly inflated type 1 error rate at less stringent α levels when the number of variants included in the testing region is large.18 Therefore, modelling genetic main effects as random effects is preferable.
Further efforts are warranted along the lines of this work. For example, developing a joint test of both genetic main effects and GE interaction effects in the presence of related individuals may enhance the statistical power for identifying genetic associations. Considering both the main effect and interaction effect can potentially identify important genes that were originally missed.
Advanced development and decreasing cost of sequencing technology have facilitated the discovery and accessibility to low frequency variants and there is growing evidence that they are implicated in complex diseases. Therefore, more attention has been brought to analyzing and developing rare variants methods. GE interaction may contribute to the unexplained heritability, provide insight into etiology of disease, identify subgroups in the population that are at high risk, and help develop personalized treatments. Our proposed approach provides a powerful, robust and efficient test to identify GE interaction of rare variants for both continuous and binary traits in the sample with related or independent participants.
Acknowledgements
This work was in part supported by NIH grants: T32 GM 074905 (EL), R00 HL 130593 (HC) and U01 HL 120393 (HC), U01 DK078616 (JD and CTL), R01 AR072199 (CTL), R01 DK089256 (EL and CTL), and R01 HL118305 (EL and CTL).
Appendix 1: Derivation of famGE
We used a generalized linear mixed model (GLMM) framework to derive the famGE statistic. We consider the following gene-environment (GE) model:
where b1 = GW1θ, b2 = EGW2γ, and b3 = d and Z = [In, In, In], , where depends on an unknown vector of variance components σ2.
For subject i, the quasi-likelihood given random effects b is defined by:
The integrated quasi-likelihood function used to estimate (α, σ2) is written as
| (A1) |
After applying the Laplacian transformation for integral approximation, the log of A1 becomes
| (A2) |
where is the solution to
| (A3) |
For canonical link functions, the second partial derivative with respect to b is equal to
| (A4) |
where .
Combining equations (A3) – (A4), equation (A2) becomes
| (A5) |
where is the solution to
Defining Δ = diag{g′(μi)} and assuming that the weight matrix D vary slowly as a function of the mean24, we maximize by differentiating with respect to α and b:
| (A6) |
| (A7) |
Defining the working vector Y0 = Xα + Zb + Δ(y−μ), solutions to A6 and A7 can be expressed as an iterative solution to the system
The test statistic for H0: is
where .
Appendix 2:
Full table for type 1 errors results based on 20,000 replications (in %)
| Continuous | Binary | ||||||
|---|---|---|---|---|---|---|---|
| Scenarios (+/−/0) | α level | famGEa | rareGEb | BTc | famGEa | rareGEb | BTc |
| 4/0/16 | 5 | 4.96 | 5.30 | 5.01 | 5.03 | 5.51 | 5.07 |
| 1 | 1.00 | 1.10 | 1.02 | 1.02 | 1.25 | 1.05 | |
| 0.1 | 0.10 | 1.70 | 0.10 | 0.12 | 0.18 | 0.10 | |
| 8/0/12 | 5 | 4.88 | 5.21 | 4.99 | 4.84 | 5.57 | 4.92 |
| 1 | 1.00 | 1.03 | 1.00 | 0.97 | 1.34 | 0.95 | |
| 0.1 | 0.10 | 0.11 | 0.10 | 0.11 | 0.19 | 0.09 | |
| 12/0/8 | 5 | 4.95 | 5.20 | 4.99 | 4.82 | 5.54 | 4.98 |
| 1 | 0.94 | 1.20 | 0.96 | 1.06 | 1.22 | 0.90 | |
| 0.1 | 0.10 | 0.15 | 0.10 | 0.08 | 0.15 | 0.10 | |
| 16/0/4 | 5 | 5.04 | 5.38 | 5.00 | 4.84 | 5.70 | 5.00 |
| 1 | 0.91 | 1.16 | 0.99 | 0.97 | 1.41 | 0.94 | |
| 0.1 | 0.11 | 0.16 | 0.10 | 0.12 | 0.20 | 0.10 | |
| 2/2/16 | 5 | 4.80 | 5.25 | 5.00 | 4.97 | 5.56 | 5.06 |
| 1 | 0.95 | 1.20 | 1.01 | 0.94 | 1.16 | 0.97 | |
| 0.1 | 0.10 | 0.14 | 0.11 | 0.11 | 0.16 | 0.11 | |
| 4/4/12 | 5 | 4.99 | 5.33 | 5.02 | 4.84 | 5.52 | 4.89 |
| 1 | 0.93 | 1.05 | 1.00 | 0.97 | 1.16 | 0.96 | |
| 0.1 | 0.10 | 0.19 | 0.10 | 0.10 | 0.14 | 0.09 | |
| 6/6/8 | 5 | 4.93 | 5.41 | 4.94 | 4.88 | 5.61 | 4.88 |
| 1 | 1.03 | 1.10 | 1.04 | 0.92 | 1.37 | 1.00 | |
| 0.1 | 0.10 | 0.14 | 0.10 | 0.11 | 0.17 | 0.11 | |
| 8/8/4 | 5 | 5.02 | 5.31 | 4.93 | 4.89 | 5.55 | 4.79 |
| 1 | 0.90 | 1.11 | 0.99 | 0.97 | 1.27 | 0.94 | |
| 0.1 | 0.10 | 0.17 | 0.12 | 0.10 | 0.16 | 0.10 | |
+/−/0: number of variants with main genotype effect sizes that are positive, negative, and neutral
famGE: our proposed method accounting for family correlation
rareGE: interaction test ignoring family correlation
BT: burden test
Appendix 3:

QQ plot of famGE applied genome-wide to detect gene × smoking interaction on BMI in the Framingham Heart Study data
Footnotes
Availability of Data
Data sharing is not applicable to this article as no new data were created or analyzed in this study
Conflict of Interest
The authors declare no conflict of interest.
References
- 1.Riancho JA. Genome-wide association studies (GWAS) in complex diseases: advantages and limitations. Reumatol Clin. 2012;8(2):56–57. doi: 10.1016/j.reuma.2011.07.005. [DOI] [PubMed] [Google Scholar]
- 2.He M, Xu M, Zhang B, et al. Meta-analysis of genome-wide association studies of adult height in East Asians identifies 17 novel loci. Hum Mol Genet. 2015;24(6):1791–1800. doi: 10.1093/hmg/ddu583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ionita-Laza I, Makarov V, Yoon S, et al. Finding disease variants in mendelian disorders by using sequence data: Methods and applications. Am J Hum Genet. 2011;89(6):701–712. doi: 10.1016/j.ajhg.2011.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lee S, Abecasis GR, Boehnke M, Lin X. Rare-variant association analysis: Study designs and statistical tests. Am J Hum Genet. 2014;95(1):5–23. doi: 10.1016/j.ajhg.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kao PYP, Leung KH, Chan LWC, Yip SP, Yap MKH. Pathway analysis of complex diseases for GWAS, extending to consider rare variants, multi-omics and interactions. Biochim Biophys Acta - Gen Subj. 2017;1861(2):335–353. doi: 10.1016/j.bbagen.2016.11.030. [DOI] [PubMed] [Google Scholar]
- 6.Yu C, Arcos-Burgos M, Baune BT, et al. Low-frequency and rare variants may contribute to elucidate the genetics of major depressive disorder. Transl Psychiatry. 2018;8(1). doi: 10.1038/s41398-018-0117-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Igartua C, Mozaffari SV, Nicolae DL, Ober C. Rare non-coding variants are associated with plasma lipid traits in a founder population. Sci Rep. 2017;7(1):1–13. doi: 10.1038/s41598-017-16550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.He KY, Wang H, Cade BE, et al. Rare variants in fox-1 homolog A (RBFOX1) are associated with lower blood pressure. PLoS Genet. 2017;13(3):1–15. doi: 10.1371/journal.pgen.1006678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li B, Leal S. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5(2). doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Price AL, Kryukov GV, de Bakker PIW, et al. Pooled Association Tests for Rare Variants in Exon-Resequencing Studies. Am J Hum Genet. 2010;86(6):832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lin X, Lin X, Lee S, Christiani DC. Test for interactions between a genetic marker set and environment in generalized linear models. Biostatistics. 2013;14(4):667–681. doi: 10.1093/biostatistics/kxt006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lin W, Lou X, Gao G, Liu N. Rare Variant Association Testing by Adaptive Combination of P-values. 2014;9(1):1–7. doi: 10.1371/journal.pone.0085728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89(1):82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee S, Emond MJ, Bamshad MJ, et al. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am J Hum Genet. 2012;91(2):224–237. doi: 10.1016/j.ajhg.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang Y, Lin S, Biswas S. Detecting rare and common haplotype–environment interaction under uncertainty of gene–environment independence assumption. Biometrics. 2017;73(1):344–355. doi: 10.1111/biom.12567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhao G, Marceau R, Zhang D, Tzeng JY. Assessing gene-environment interactions for common and rare variants with binary traits using gene-trait similarity regression. Genetics. 2015;199(3):695–710. doi: 10.1534/genetics.114.171686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen H, Meigs JB, Dupuis J. Incorporating gene-environment interaction in testing for association with rare genetic variants. Hum Hered. 2014;78(2):81–90. doi: 10.1159/000363347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tzeng JY, Zhang D, Pongpanich M, et al. Studying gene and gene-environment effects of uncommon and common variants on continuous traits: A marker-set approach using gene-trait similarity regression. Am J Hum Genet. 2011;89(2):277–288. doi: 10.1016/j.ajhg.2011.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Su Y, Di C, Hsu LI. A unified powerful set-based test for sequencing data analysis of GxE interactions. 2017:119–131. doi: 10.1093/biostatistics/kxw034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lin X, Lee S, Wu MC, et al. Test for Rare Variants by Environment Interactions in Sequencing Association Studies. 2016;(March):156–164. doi: 10.1111/biom.12368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mazo Lopera M, Coombes B, de Andrade M. An Efficient Test for Gene-Environment Interaction in Generalized Linear Mixed Models with Family Data. Int J Environ Res Public Health. 2017;14(10):1134. doi: 10.3390/ijerph14101134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Coombes BJ. A linear mixed model framework for gene ‐ based gene – environment interaction tests in twin studies. 2018;(December 2017):648–663. doi: 10.1002/gepi.22150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Breslow NE, Clayton DG. Approximate Inference in Generalized Linear Mixed Models. J Am Stat Assoc. 1993;88(421):9–25. doi: 10.1080/01621459.1993.10594284. [DOI] [Google Scholar]
- 25.Chen H, Meigs JB, Dupuis J. Sequence Kernel Association Test for Quantitative Traits in Family Samples. Genet Epidemiol. 2013;37(2):196–204. doi: 10.1002/gepi.21703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang D, Lin X. Hypothesis testing in semiparametric additive mixed models. Biostatistics. 2003;4(1):57–74. doi: 10.1093/biostatistics/4.1.57. [DOI] [PubMed] [Google Scholar]
- 27.Chung R, Shih C. SeqSIMLA : a sequence and phenotype simulation tool for complex disease studies. 2013. [DOI] [PMC free article] [PubMed]
- 28.Mahmooda SS, Levy D, Vasan RS, Wang TJ. The Framingham Heart Study and the epidemiology of cardiovascular diseases: A historical perspective. Lancet. 2014;383(9921):1933–1945. doi: 10.1016/S0140-6736(13)61752-3.The. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tsao CW, Vasan RS. Cohort Profile: The Framingham Heart Study (FHS): Overview of milestones in cardiovascular epidemiology. Int J Epidemiol. 2015;44(6):1800–1813. doi: 10.1093/ije/dyv337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liao C, Gao W, Cao W, et al. The association of cigarette smoking and alcohol drinking with body mass index: A cross-sectional, population-based study among Chinese adult male twins. BMC Public Health. 2016;16(1):1–9. doi: 10.1186/s12889-016-2967-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rask-Andersen M, Karlsson T, Ek WE, Johansson Å. Gene-environment interaction study for BMI reveals interactions between genetic factors and physical activity, alcohol consumption and socioeconomic status. PLoS Genet. 2017;13(9):1–20. doi: 10.1371/journal.pgen.1006977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Justice AE, Winkler TW, Feitosa MF, et al. Genome-wide meta-analysis of 241,258 adults accounting for smoking behaviour identifies novel loci for obesity traits. Nat Commun. 2017;8:1–19. doi: 10.1038/ncomms14977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Taylor AE, Morris RW, Fluharty ME, et al. Stratification by Smoking Status Reveals an Association of CHRNA5-A3-B4 Genotype with Body Mass Index in Never Smokers. PLoS Genet. 2014;10(12):1–6. doi: 10.1371/journal.pgen.1004799. [DOI] [PMC free article] [PubMed] [Google Scholar]


