Incorporating minimal user input into deep learning based image segmentation

Abstract

Computer-assisted image segmentation techniques could help clinicians to perform the border delineation task faster with lower inter-observer variability. Recently, convolutional neural networks (CNNs) are widely used for automatic image segmentation. In this study, we used a technique to involve observer inputs for supervising CNNs to improve the accuracy of the segmentation performance. We added a set of sparse surface points as an additional input to supervise the CNNs for more accurate image segmentation. We tested our technique by applying minimal interactions to supervise the networks for segmentation of the prostate on magnetic resonance images. We used U-Net and a new network architecture that was based on U-Net (dual-input path [DIP] U-Net), and showed that our supervising technique could significantly increase the segmentation accuracy of both networks as compared to fully automatic segmentation using U-Net. We also showed DIP U-Net outperformed U-Net for supervised image segmentation. We compared our results to the measured inter-expert observer difference in manual segmentation. This comparison suggests that applying about 15 to 20 selected surface points can achieve a performance comparable to manual segmentation.

1. INTRODUCTION

Recently, fully-automatic deep learning approaches are widely used for medical image analysis such as image segmentation^1–5. Although deep learning demonstrated a very high capability in fast and accurate segmentation of medical images, there are still segmentation challenges that have not been well addressed yet. One of the main challenges in using convolutional neural networks (CNNs) in medical imaging is the lack of a sufficiently large dataset to train the network^1,2. The small sample size of the training data could have a negative impact on the network accuracy and reliability. Data augmentation is an approach for addressing the data size issue by increasing the size of the training dataset. However, data augmentation is not always helpful to reach a clinically accepted accuracy⁶. More specifically, in medical imaging, some simple augmentation techniques such as, rotation, translation, and reflections are not always valid. Therefore, in some studies more complicated data augmentation approaches such as using generative adversarial networks (GANs) to generate synthetic data have been used^7,8.

Another way to address the accuracy issue is to supervise the CNN by incorporating an expert operator interaction. However, it is not straightforward to supervise a deep learning algorithm with user inputs during evaluation and testing, and to the best of our knowledge, there are no studies in the literature on semiautomatic CNN-based techniques. In this paper, our goal is to direct a fully convolutional neural network with minimal manual initialization to improve the three-dimensional (3D) image segmentation accuracy and reliability. We tested our method for segmentation of the prostate in magnetic resonance imaging (MRI) and compared the results to fully automatic deep learning-based segmentation results. We used manual segmentation performance as the reference for evaluation of the algorithm.

2. METHODS

2.1. Data

In this work, we used a set of 43 T2-weighted pelvic MRI from 43 prostate cancer patients. The MRI dataset contains 1.5 T and 3.0 T T2-weighted magnetic resonance (MR) images with the original size of 256 × 256 to 320 × 320 voxels. The slice thickness ranged from 0.625 mm to 1.0 mm, and the slice spacing ranged from 1.0 mm to 6.0 mm. All the MR images were resampled to make the voxel size isotropic to the in-plane image resolution. For each MR image, two manual segmentation labels were provided by two expert radiologists.

In this work, we used one set of manual labels as the segmentation reference for training, validation, and testing purposes, and the second set is used for inter-observer difference measurements. From the first observer, we randomly selected 75% of the images (32 images) for training purposes (i.e., 60% for training [26 images] and 15% for validation [6 images]). The remaining 25% of the images (11 images) were reserved for final testing of the method.

2.2. Preprocessing

To minimize the data load on the graphics processing unit (GPU) and speed up the training process, we cropped the MR images to a bounding box of 128×128×70 voxels. We scaled the image intensity dynamic range to the range of zero to one. We doubled the number of training samples by using horizontal reflection of the images to exploit the left-right symmetry of the images.

2.3. Operator manual interaction:

To supervise the network for more accurate segmentation of the prostate we involved a set of sparse boundary landmarks as one input of the CNN along with the input image. In this study, we select a set of N randomly distributed points on the shape surface:

$$\left\{p_1,p_2,\dots ,p_N\right\},$$

where p_n = (x_n, y_n, z_n) is the n^th selected surface point. We restricted the distance between each point pair based on the size of the 3D shape to have the points uniformly distributed on the surface. We repeat the randomized point selection process five times per image for data augmentation purposes. For each set of selected points, we made a binary image the same size as the actual MR image with all voxels equal to zero except at the point locations (P(x,y, z)):

$$P(x,y,z)=\{\begin{array}{cc}1,& (x,y,z)\in \left\{p_1,p_2,\dots ,p_N\right\}\\ 0,& \mathit{\text{otherwise}}\end{array}$$

We used this binary mask as the basis for one input of our algorithm. To allow the CNN to extract useful features from the binary point mask, we made an intensity gradient around the points by measuring the Euclidean distance function of the point mask:

$$D_P(x,y,z)=min\left\{d_1,d_2,\dots ,d_N\right\},$$

where d_n is the Euclidean distance between (x,y, z) and p_n. We then scale the distance values to range between zero and one by dividing the distance values by half of the 3D image diagonal length:

$${\widehat{D}}_P(x,y,z)=\frac{D_P(x,y,z)}{\frac{1}{4}\sqrt{\left(D_x{}^2+D_y{}^2+D_z{}^2\right)}},$$

where D_x, D_y, and D_z are the dimensions of the image along x, y, and z axes.

To provide the points’ information to the network we used two different schemes:

Two input channels:

We used the distance function of the points mask $\left({\widehat{D}}_P\right)$ along with the MR image (I) as the two channels of the CNN input (Figure 1a).

Figure 1.

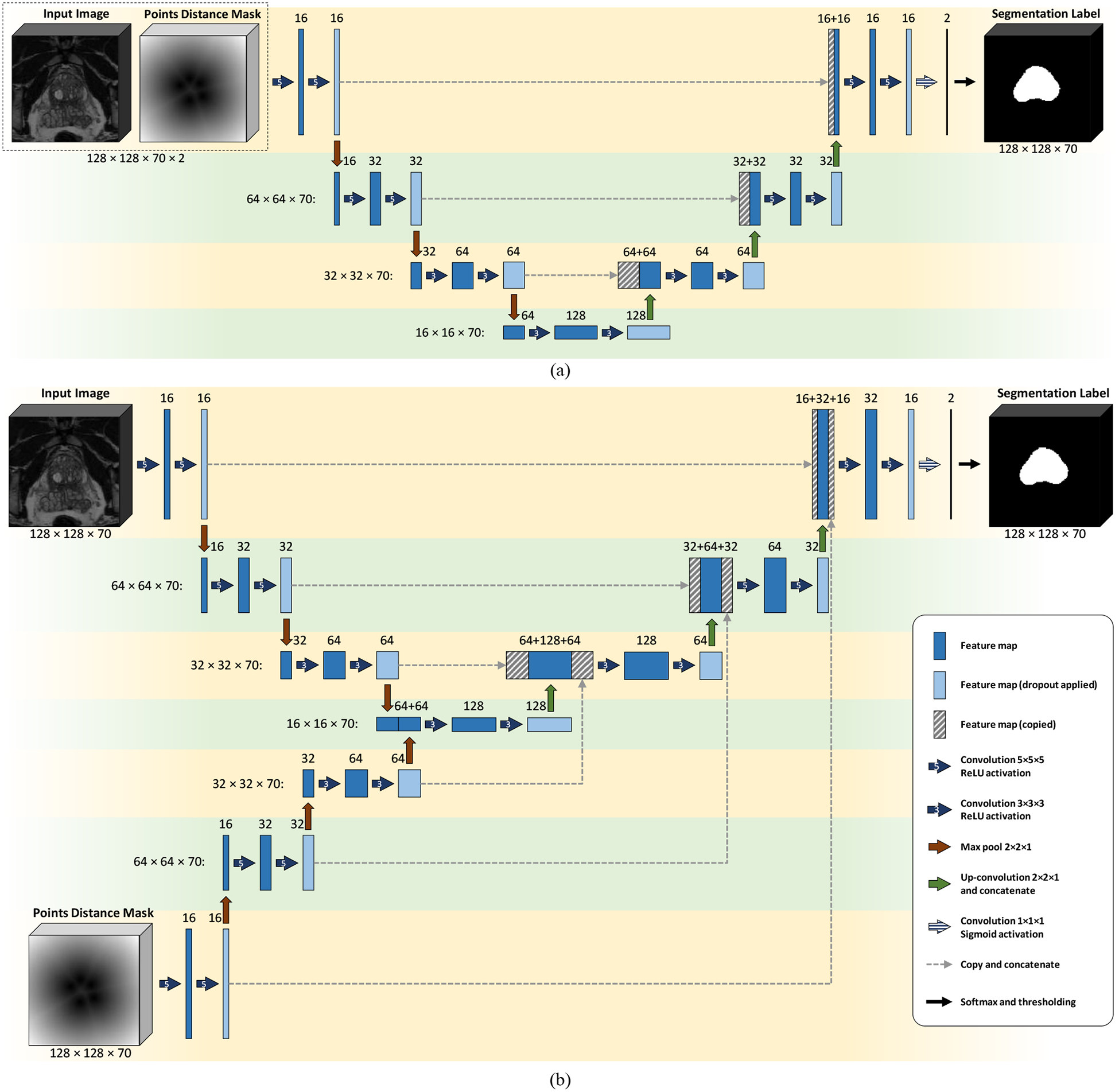
CNN architectures. (a) Model I: four-level U-Net with two input channels, and (b) Model II: four-level DIP U-Net with two contraction paths. The number of feature maps in each layer is mentioned on the top of that layer. For each level, the size of each feature map is mentioned at the left side of the level.

Two input paths:

We used a CNN architecture with two input paths (as seen in Figure 1b), one for I and the other for ${\widehat{D}}_P$.

2.4. Fully convolutional neural network architectures

In this work, we used two different network architectures based on a U-Net architecture² customized for 3D images. Figure 1 shows these architectures. We trained two CNN models using these two architectures:

Model I (U-Net with two input channels):

For training this model, we used U-Net architecture shown in Figure 1a with / and ${\widehat{D}}_P$ as the two input channels of the network.

Model II (U-Net with two contraction paths):

In this model, we used the dual-contraction path U-Net shown in Figure 1b. Hereafter, we call this model dual-input path (DIP) U-Net.

For both networks, we used the Adadelta optimizer with “soft Dice” similarity coefficient-based loss function defined as follows:

$$L=1-\frac{2{\sum }_{x,y,z}\left[h\left(I(x,y,z),{\widehat{D}}_P(x,y,z)\right).G(x,y,z)\right]}{{\sum }_{x,y,z}h\left(I(x,y,z),{\widehat{D}}_P(x,y,z)\right)+\sum _{x,y,z}G(x,y,z)}$$

where $h\left(I(x,y,z),{\widehat{D}}_P(x,y,z)\right)$ is the probability value of the output probability map at (x,y,z) and G(x,y,z) is the value of the reference binary mask at (x, y, z).

2.5. Post-processing

To reduce the output noise and smoothen the segmentation label, we used a morphological filtering technique composed of a closing filter followed by an opening filter. We applied the morphological filtering to each axial slice using a two-dimensional (2D) structural element of size 3×3. We kept the largest 3D objects in the segmentation label and removed all the other objects, considering them as false positive regions.

2.6. Implementation details

We used TensorFlow⁹ to implement the CNN models in a Python platform. We used a computer with Intel Xeon Processor E5–2623 v4 (2.60 GHz), 512 GB DDR4 2400 MHz RAM, and NVIDIA TITAN Xp GPU.

2.7. Evaluation

To quantify the impact of our method on segmentation performance, we trained the U-Net architecture with image-only input and optimized it separately. We compare the results based on image and points to the results based on image-only input.

We compared the algorithm segmentation results against manual segmentation using Dice similarity coefficient¹⁰ (DSC), sensitivity (or recall) rate¹¹ (SR), and precision rate¹¹ (PR). DSC is the volume of the overlap between reference shape and segmentation shape divided by the average volume of the shapes. SR is the volume of the overlap divided by the reference volume, and PR is the volume of the overlap divided by the segmentation volume.

3. RESULTS

3.1. Training

We train each CNN model in five different conditions based on the number of boundary points used for guiding the segmentation algorithm. In this study, we used 5, 10, 15, 20, and 30 boundary landmark points yielding five trained models for each architecture. We trained each model for up to 1000 epochs and used the highest validation DSC to choose the best trained model. Table I shows the highest validation DSC for each model.

Table I.

Segmentation accuracy of the different models in comparison with automatic segmentation and inter-observer variability in manual segmentation. First observer’s manual segmentation labels were used as the reference labels.

Model	# Boundary Points	Validation			Test			Exec. Time (s.)
		DSC (%)	SR (%)	PR (%)	DSC (%)	SR (%)	PR (%)
2nd Observer	-	83.0 ± 5.8	75.5 ± 7.1	92.8 ± 8.9	87.0 ± 7.4	80.0 ± 11.2	96.4 ± 2.5	-
Automatic	-	83.5 ± 7.0	88.8 ± 5.3	80.0 ± 12.8	84.4 ± 10.8	91.7 ± 7.6	80.9 ± 17.1	0.8
Model I (U-Net)	5	83.0 ± 7.3	87.6 ± 5.4	80.4 ± 12.6	86.2 ± 8.9	92.2 ± 5.5	82.9 ± 14.3	0.8
	10	83.2 ± 7.5	90.0 ± 5.1	78.8 ± 12.4	85.3 ± 10.8	93.4 ± 5.2	80.9 ± 16.7
	15	83.3 ± 7.2	90.4 ± 4.8	78.4 ± 12.0	86.5 ± 8.6	92.5 ± 4.8	82.7 ± 13.7
	20	85.7 ± 5.8	90.8 ± 4.5	82.1 ± 10.2	86.6 ± 8.8	91.9 ± 4.6	83.2 ± 13.5
	30	86.8 ± 3.6	93.9 ± 2.7	81.2 ± 6.9	89.9 ± 2.9	92.8 ± 4.2	87.5 ± 5.1
Model II (DIP U-Net)	5	83.9 ± 6.0	88.4 ± 6.9	81.0 ± 10.0	87.5 ± 8.1	92.6 ± 5.0	84.4 ± 13.3	0.9
	10	84.7 ± 6.1	90.3 ± 4.9	80.7 ± 10.5	85.3 ± 10.1	92.7 ± 4.9	81.0 ± 15.5
	15	84.5 ± 5.7	89.9 ± 3.7	80.6 ± 10.3	88.1 ± 6.2	92.0 ± 5.3	85.4 ± 10.0
	20	84.2 ± 5.3	93.1 ± 3.8	77.5 ± 9.4	88.8 ± 4.6	93.7 ± 3.8	85.0 ± 8.3
	30	85.4 ± 5.0	92.1 ± 3.5	80.2 ± 9.1	88.8 ± 6.1	93.2 ± 4.4	85.8 ± 10.6

3.2. Testing results

Table I shows the results of testing each trained model on our test set based on the three error metrics. The results illustrate a higher segmentation accuracy for points involved segmentations compare to image-only approach. Including more selected surface points yielded better segmentation performance from both models. Using two-tailed, heteroscedastic student’s t-test¹² for inter-model comparison in each of the five test groups indicates no statistically significant difference between the results of the two models (α = 0.05). The one-tailed t-test was used to compare the results of each model in each of the five groups to automatic segmentation. The null hypothesis was that the mean DSC value for automatic segmentation (DSC_a) is equal to the mean DSC value for the tested model (DSC_t), and the alternative hypothesis is that DSC_t is greater than DSC_a. The asterisk symbols on Figure 2 indicate where the null hypothesis was rejected (α = 0.05). For our proposed model (DIP U-Net), using 15 or more points improved the segmentation accuracy significantly compared to fully automatic segmentation. For U-Net we detected significant improvement over automatic segmentation when we involved 30 selected surface points.

Figure 2.

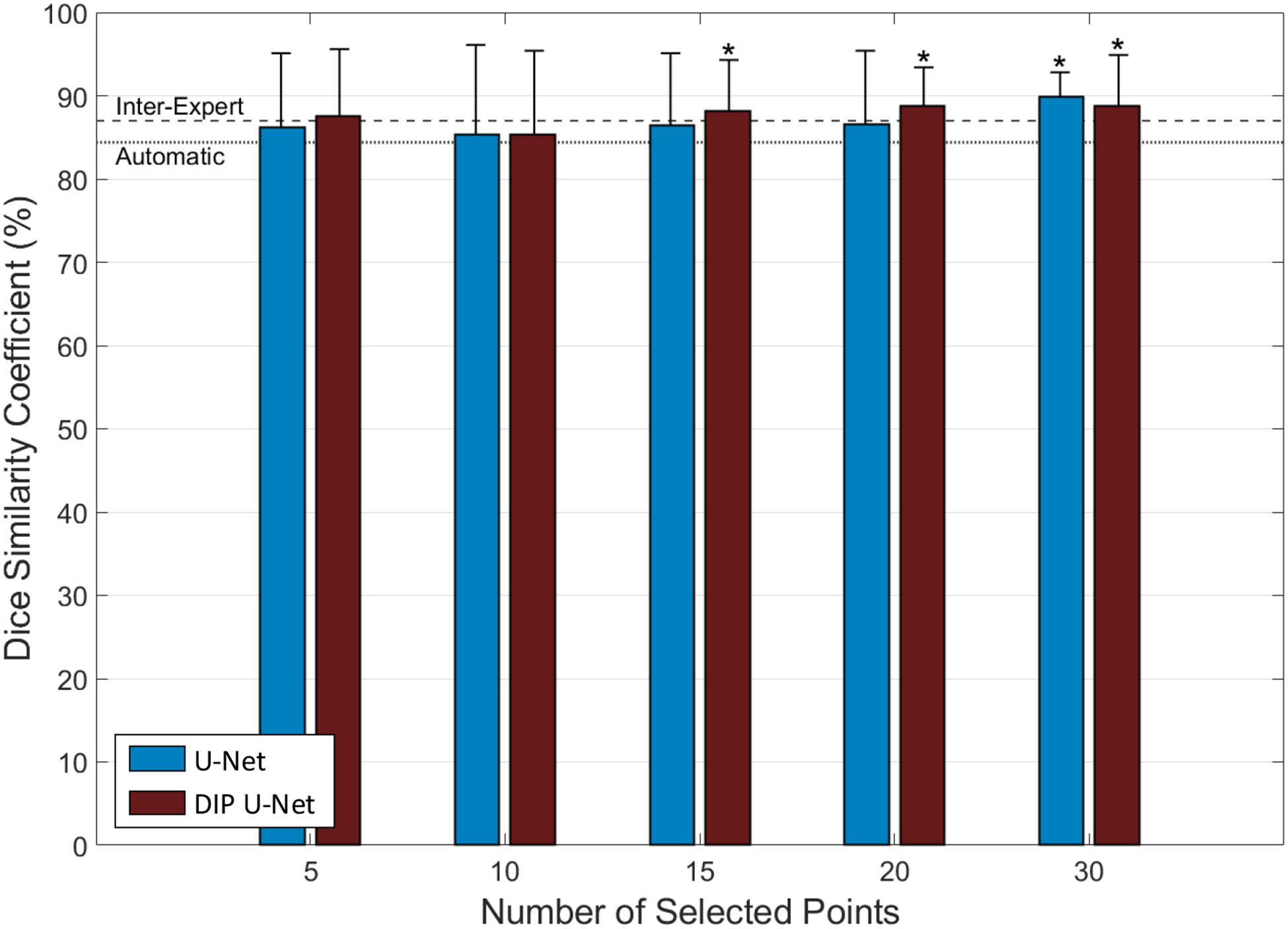
Supervised segmentation accuracy in terms of DSC in comparison with inter-expert observer difference (dashed line) and automatic segmentation (dotted line). The asterisk symbols indicate the significant improvement of segmentation performance compared to automatic segmentation (p < 0.05).

On the test images, both models approach the inter-expert observer difference level when at least 15 surface points has been involved. These results suggest that the use of 15–20 sparse manually selected surface points achieves a segmentation performance close to manual segmentation. According to our previous studies^{13, 14}, manual selection of 12 prostate surface points on both MRI and CT images could be done within 20 seconds, which is considerably shorter than the average time of manual prostate MRI segmentation, as reported in the literature^{15, 16}. Therefore, we think minimal user interaction could be helpful to improve the segmentation accuracy significantly.

Figure 3 shows the qualitative results of the automatic approach, Model I, and Model II for three sample test cases and compares them to the manual segmentation.

Figure 3.

Qualitative segmentation results for two test patients (semi-transparent, purple shapes) compared to manual segmentation reference #1 (green solid shapes). First column shows the automatic segmentation results using U-Net, the second and third column shows the supervised segmentation results using 20 selected surface points (shown with yellow dots) based on U-Net and DIP U-Net, respectively, and the last column compares the two manual segmentation labels.

4. DISCUSSION AND CONCLUSIONS

We developed a new CNN architecture by adding a new contraction path to the conventional U-Net structure. We used this model to propose a new technique for incorporating the user selected point information into a convolutional neural network for image segmentation to improve the performance. The proposed 3D fully convolutional deep learning segmentation technique is able to segment the prostate in 3D MR image volumes under minimal observer supervision. The results of Figure 2 show using our approach could significantly improve the segmentation accuracy compared to automatic segmentation when 15 or more surface landmark points were used.

The results of this study show that our approach for combining the deep learning-based automatic segmentation with the user interaction could improve the accuracy and robustness of the prostate MRI segmentation. Using DSC as the accuracy measurement metric, the results in Table I and Figure 2 show that by incorporating the input points, the accuracy increased and reached the inter-expert observer difference, and the standard deviation decreased. Lower standard deviation values indicate the increased robustness and reliability of the system.

Both CNN models (Model I and Model II) could segment the prostate in less than a second, excluding the user interaction time. The measured execution times for U-Net and DIP U-Net (Table I) were 0.8 and 0.9 seconds, respectively. The slightly higher execution time of DIP U-Net is because of the higher number of layers in the network architecture compared to the U-Net architecture. The execution time did not depend on the number of the selected landmark points because regardless of the number of points, the points were provided to both networks as an input channel with the same size as the input MR image.

4.1. Limitations

The limitations of this study must be considered for interpretation of the achieved results. The proposed approach has been tested only on prostate MRI dataset. To confirm the hypothesis of this work, it is required to test the proposed network on different datasets. Moreover, in this study we assumed that the number of the selected points were constant and they were uniformly distributed on the prostate surface. However, in a real situation, the physician may select a different number of points for each patient, which are not necessarily well distributed on the prostate surface. Therefore, an observer study is required to confirm the effectiveness of this approach for prostate segmentation in a real clinical situation. In addition, although our previous studies^{13, 14, 17} showed that using minimal user interaction for prostate segmentation could substantially speed up the process when compared to manual segmentation time, the observer study must confirm that for this study.

4.2. Conclusions

We presented a new approach to include user input into deep learning segmentation algorithms. We guided the CNN by involving a set of sparse surface points as an input of the network. We also developed a new CNN architecture by adding a new contraction path to the conventional U-Net structure and compared the performance of the presented model to U-Net. The results show statistically significant improvement in segmentation accuracy for the proposed CNN when compared to the automatic segmentation method of U-Net. The results also suggest that the presented architecture outperformed U-Net when there were fewer surface points involved. The proposed approach can be easily applied to different imaging methods and medical image segmentation applications to improve their performance and facilitate the adoption of the algorithms by clinical end users.