Segmentation of uterus and placenta in MR images using a fully convolutional neural network

Abstract

Segmentation of the uterine cavity and placenta in fetal magnetic resonance (MR) imaging is useful for the detection of abnormalities that affect maternal and fetal health. In this study, we used a fully convolutional neural network for 3D segmentation of the uterine cavity and placenta while a minimal operator interaction was incorporated for training and testing the network. The user interaction guided the network to localize the placenta more accurately. We trained the network with 70 training and 10 validation MRI cases and evaluated the algorithm segmentation performance using 20 cases. The average Dice similarity coefficient was 92% and 82% for the uterine cavity and placenta, respectively. The algorithm could estimate the volume of the uterine cavity and placenta with average errors of 2% and 9%, respectively. The results demonstrate that the deep learning-based segmentation and volume estimation is possible and can potentially be useful for clinical applications of human placental imaging.

1. INTRODUCTION

The placenta is a critical and complex organ that provides oxygen and nutrition to the growing fetus and removes waste from its blood. Three-dimensional (3D) segmentation of placenta in magnetic resonance (MR) images is useful in studying conditions that result in pregnancy and birth complications such as placenta accreta spectrum (PAS), fetal growth restriction, and intrauterine fetal death^{1, 2}. However, manual segmentation of the placenta is time-consuming with high inter- and intra-observer variability³.

This is the first time that a multi-class segmentation has been presented for uterine cavity and placenta segmentation in pregnant women. Although there were efforts to develop computerized algorithms to segment the placenta in MRI,^{4, 5} either the accuracy of the presented methods was low (Dice coefficient⁶ is about 72%⁵) or the computational time is high (one to two minutes/volume in average) and required multiple image volumes (sagittal and axial acquisitions)⁴. The size of the dataset (16 images) was another limitation of a previous study⁴. There are also a few algorithms presented in the literature for uterine segmentation in MRI^{7, 8} in non-pregnant women. Namias et al.⁷ used a local binary pattern-based texture feature extraction to segment the uterus. They tested their algorithm on nine patients and reported a Dice coefficient of 81%. Kurata et al.⁸ used a deep learning algorithm for uterine segmentation in MRI using U-Net architecture. They tested their method on 122 MR images acquired from 72 patients with benign or malignant tumors and 50 healthy cases. They reported Dice coefficients of 84% and 78% for patients and healthy cases, respectively. They also reported the average mean absolute distance but in pixel units while their voxel size was not consistent across the image dataset.

Deep learning-based approaches demonstrated a strong capability for fast segmentation of medical images with high accuracy. We present an automatic 3D deep learning-based multi-label segmentation algorithm for fast, accurate, and repeatable 3D segmentation of the uterine cavity and placenta in MRI. We modified U-Net architecture to present a 3D end-to-end fully convolutional neural network for 3D image segmentation. We used minimal operator inputs to improve the segmentation performance.

2. METHODS

2.1. Data

Our dataset contained 100 3D uterus MRIs from 100 pregnant women. Each image volume had 28 to 52 two-dimensional (2D) transverse slices. For 99 cases, each slice was originally 256 × 256 pixels in size. For one case, the slice size was 212 × 256 pixels. We resized that image to 256 × 256 by zero-padding to make the slice size consistent across the dataset. The axial image slice spacing for all the images were 7.0 mm and the pixels were isotropic for all the slices with resolutions ranging from 1.0547 × 1.0547 mm² to 1.7188 × 1.7188 mm². For each image, the uterine cavity and placenta were manually segmented by an expert radiologist.

2.2. User interaction

For each test image, the operator selected the first (superior-most) and last (inferior-most) slices of the uterine cavity. This information was used for image block extraction explained in the preprocessing subsection. In addition, the first (superior-most) and last (inferior-most) slices of the placenta were selected for each patient, and the center of the placenta tissue was estimated on both slices. Then three image slices, evenly spaced between the two selected slices, were automatically selected and the operator was asked to define the approximate center of the placenta tissue on each of the three slices. Therefore, the operator needed to browse through the image slices and click seven times in total; twice for the uterus bounding box, and five times for the placenta bounding box and center points. In this study, we simulated the operator interaction by selecting a point defined for each slice randomly from the 5% of the placenta tissue pixels around the tissue center on the slice (see Figure 1A). Therefore, there are 5 points selected on placenta tissue. We use linear interpolation to define one point per placenta slice. To provide this information as an input, we made a binary image volume with the same size of the MR image and assigned ones to the voxels that are selected as center points on each slice and zeros to all the other voxels. We applied the Euclidean distance transform to this binary image and used the result as the second channel of input.

Figure1.

(A) Simulating user manual interaction. The yellow solid contour show the placenta, the green, hashed area is the 5% placenta’s central pixels, and the purple cross is the randomly selected point within that area. (B) Image blocks extraction.

2.3. Preprocessing

We applied a median filter to all the 2D image slices under a 3 × 3 window to reduce the noise while preserving the edges. Then, we truncated and normalized the voxel intensity distribution of each image as shown in equation (1), whichhelps to reduce the effect of background voxels and makes the intensity distribution more consistent across the image dataset:

$${\widehat{I}}_i(x,y,z)=\{\begin{array}{cc}0,& I_i(x,y,z)<p_5(I_i)\\ 1,& I_i(x,y,z)>p_{99.9}(I_i)\\ \frac{I_i(x,y,z)-p_5(I_i)}{p_{99.9}(I_i)-p_5(I_i)},& \mathit{\text{otherwise}}\end{array}.$$ (1)

Here. I_i(x,y,z) represents the i^th image in the image dataset, and p₅(I_i) and p_99.9(I_i) are the 5^th and 99.9^th percentiles of the pixel intensities in the image, respectively. ${\widehat{I}}_i(x,y,z)$ is the normalized image.

To reduce the inter-subject variability in placenta intensity, we linearly scaled the intensities of the voxels to make the average intensity of the selected center points and a set of voxels around them with in-plane distances of less than three pixels a constant value ($\overline{\iota }$) across the image set. We change them to the average placenta intensity of one sample image (here $\overline{\iota }$ = 0.154).

There is a full-overlap between the placenta and uterine cavity. To make the segmentation labels independent from each other with no overlap (one-hot encoding), we used the portion of the uterus that was not covered by the placenta as the uterine cavity channel and we made a three-channel label which included background, uterine cavity (with no overlap with placenta), and placenta labels.

We randomly divided the image dataset to 70 training, 10 validation, and 20 test images. We used data augmentation to double the number of data using left-to-right flipping of the images, yielding 140 training, 20 validation, and 40 test images.

We used a block-based segmentation approach by extracting a set of 3D five-slice blocks from the images. Each block $B_i^k$ contained five sequential 2D axial slices and the uterus has been seen in at least one of the slices. For each image, the adjacent blocks defined with four-slice overlaps (Figure 1B). We applied the same process for extracting blocks from the second input channel.

2.4. Fully convolutional neural network architecture

In this study, we used a customized version of U-Net⁹ which is a fully convolutional neural network (FCNN). We modified the architecture to make it 3D and used that for multi-label image segmentation. Figure 2 shows the architecture of the proposed network. The network is a four-level U-Net model with 21 layers including 18 convolutional and three max pool layers. We kept the size of the output channels for all the convolutional layers the same as the input channels by zero-padding the input channel before convolution. For the two upper levels, we used a convolution kernel size of 5×5×3, and for the two lower levels we used kernel size of 3×3×3. We applied a dropout rate to the neurons of 10 layers shown in Figure 2. The input has two channels, the 3D image blocks of the MRI and the points’ distance mask. The output has three channels, one for background, one for uterine cavity and one for the placenta.

Figure 2.

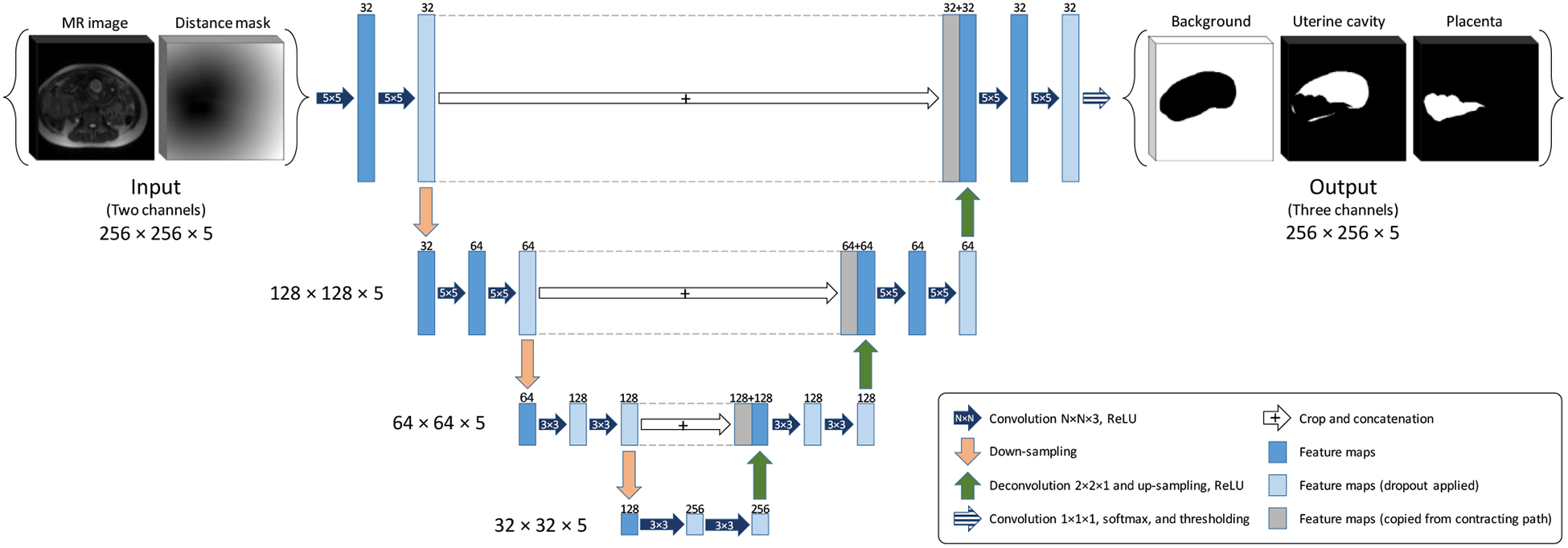
The FCNN architecture (3D U-Net).

Due to an imbalance between the number of background and foreground (placenta and uterus) voxels, we used a loss function based on Dice similarity coefficient⁶ (DSC):

$$L=1-\frac{2{\sum }_x{\sum }_y{\sum }_z\left[p(I_{x,y,z})\cdot G_{x,y,z}\right]}{{\sum }_x{\sum }_y{\sum }_z\left[p(I_{x,y,z})\right]+{\sum }_x{\sum }_y{\sum }_z\left[G_{x,y,z}\right]},$$ (2)

where p(I_x,y,z) is the probability value of the output probability map corresponds to the input image (I_x,y,z) at (x,y,z) and G_x,y,z is the value of the reference binary mask at (x,y,z). To avoid bias toward placenta or uterine cavity segmentation, we calculated two loss values, L_uterus for uterine cavity and L_placenta for placenta. We used the average of the losses as the total loss. The loss was calculated at block-level during training. For optimization, during training, we used the Adadelta¹⁰gradient-based optimizer.

2.5. Implementation details

We used TensorFlow¹¹ machine learning system to implement the 3D U-Net model in Python platform on a high-performance computer with 512 GB of memory and NVIDIA TITAN Xp GPU. We used a batch size of five and an initial learning rate of 1.0, with a dropout rate of 40%, and the decay rate and epsilon conditioning parameters for Adadelta optimizer of 0.9 and 1×10⁻¹⁰, respectively.

2.6. Post-processing and evaluation

After testing the network on the 3D image blocks of an MR image, we integrated the results by averaging the probabilities over the overlapped slices results to a probability map for the whole image. We applied a similar process to the flipped version of the image and to improve the segmentation result we used the average of the output probabilities corresponded to that image and the flipped image as the final probability map. Thresholding was applied to build output binary masks out of the probability maps which were then compared against manual segmentation labels. Our segmentation error metrics included the DSC and signed volume difference (ΔV):

$$\Delta V=V_{seg}-V_{ref},$$ (3)

where V_seg is the volume of the object on the output segmentation label and V_ref is the volume of the object on the manual segmentation label. We reported DSC in percent and ΔV in cm³ and percent.

3. RESULTS

3.1. Training and testing results

We trained the network until we reached the highest validation accuracy at epoch 530. The image block-level training and validation DSCs were 93.2% and 86.7%, respectively.

We segmented all the validation and test images using the saved model. Table I shows the results. The metric values in the table are all at image-level. The total computational time for segmenting a 3D image was 25 seconds on average. The volume of the uterine cavity ranged from 818 cm³ to 3993 cm³ and the volume of placenta ranged from 161 cm³ to 1149 cm³ for the test dataset based on the manual segmentation labels. Figure 3 and Figure 4 show the qualitative results for four sample cases in 3D and on 2D axial slices, respectively.

Table I.

Validation and test results for the uterine cavity and placenta with standard deviations.

Data set	N	Uterine cavity			Placenta
		DSC (%)	ΔV (cm3)	ΔV (%)	DSC (%)	ΔV (cm3)	ΔV (%)
Validation	10	92.2 ± 5.1	40 ± 141	3 ± 9	81.6 ± 8.3	0 ± 106	1 ± 24
Test	20	92.0 ± 4.3	6 ± 254	2 ± 12	81.9 ± 6.1	−53 ± 100	−9 ± 16

Figure 3.

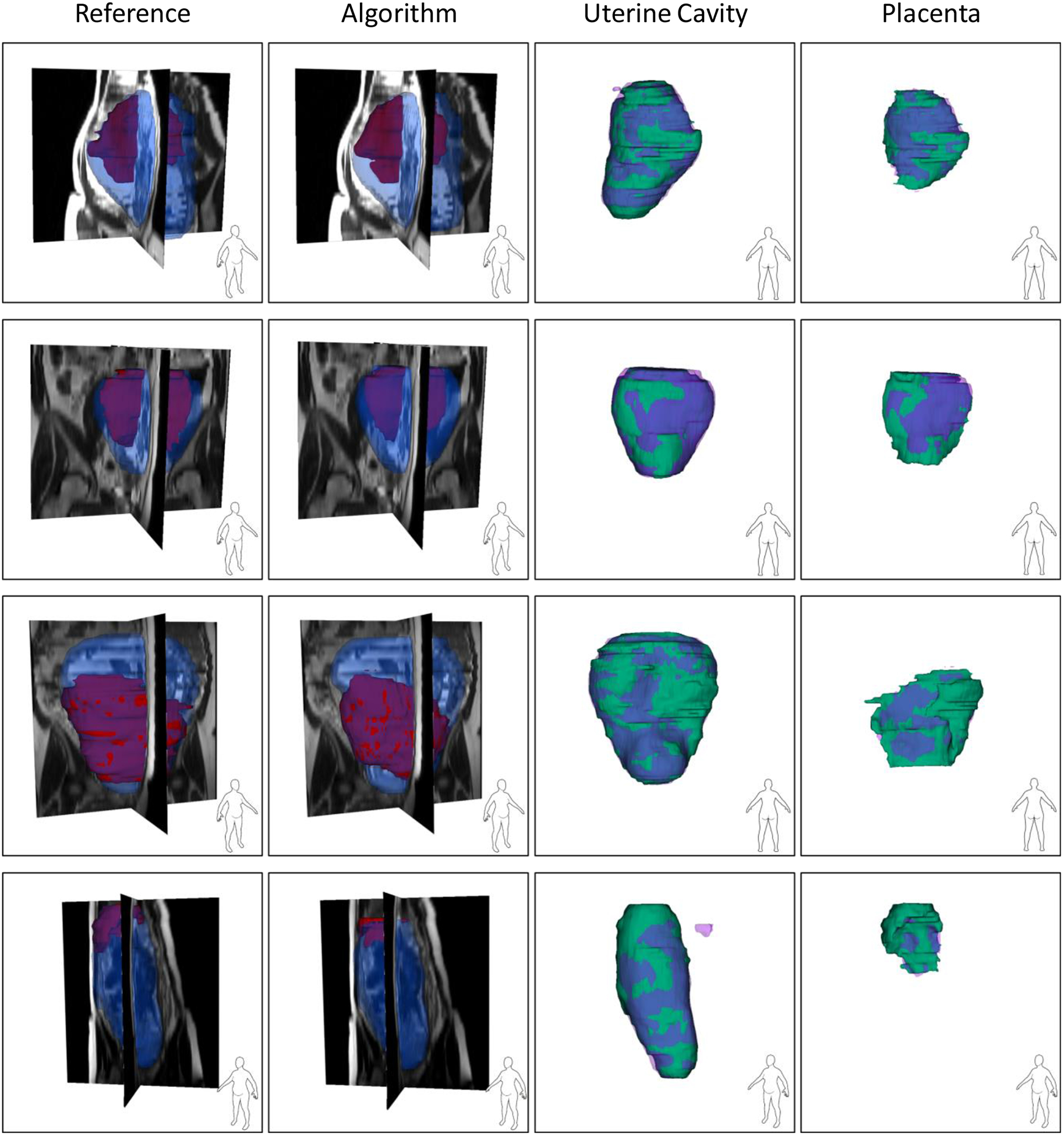
Qualitative results of the uterus and placenta segmentation in 3D. Each row shows the results for one patient. For the first two columns, the blue, semi-transparent shapes show the uterine cavity and the solid, red shapes show the placenta. For the last two columns, the green, solid shapes show the manual segmentations and the semi-transparent, purple shapes show the algorithm segmentation results.

Figure 4.

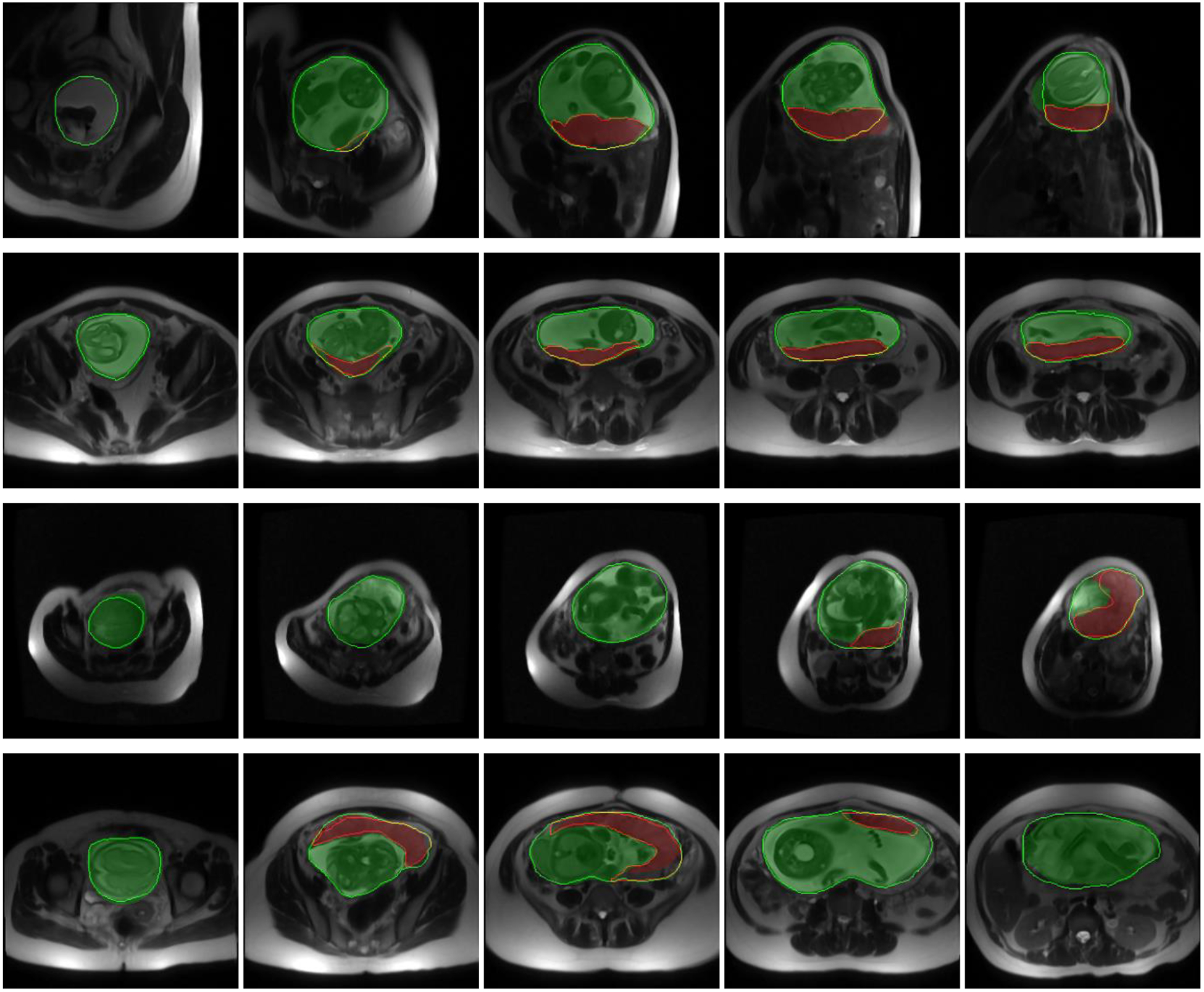
Qualitative results of the uterus and placenta segmentation in 2D. Each row shows the results for one patient on five sample axial slices from inferior (left) to superior (right). The semi-transparent green (bright) and red (dark) regions show the algorithm segmentation results for uterine cavity and placenta, respectively. The solid green (bright) and red (dark) contours show the manual segmentation provided by the expert observer for uterine cavity and placenta, respectively.

Although the DSC value for placenta segmentation is about 10% lower than that of uterine cavity segmentation, the qualitative results show that the algorithm could localize the placenta correctly and ΔV values show an accurate estimation of placenta size (|ΔV|<10%).

4. DISCUSSION

The proposed, full 3D fully convolutional deep learning multi-class segmentation technique is able to segment the uterine cavity and placenta in 3D MR image volumes with high segmentation accuracy using a single CNN model. We incorporate observer interaction for initializing the CNN to improve the results and make the algorithm more reliable for clinical assessments. We included the user interaction as the second channel of the CNN input. We could achieve test DSC of 92% and 82% for uterine cavity and placenta, respectively, with the absolute volume difference (|ΔV|) of less than 10%. The accuracy of the algorithm was substantially higher than the reported results in the literature. The qualitative results in Figure 3 show that the method could segment both the uterine cavity and placenta with acceptable quality. The algorithm detected the shape and position of the uterus and placenta correctly. Therefore, the algorithm could also be helpful for detecting those abnormalities that are diagnosed based on the relative position of the placenta within the uterine cavity. In some of the results shown in Figure 3 (e.g., the uterine cavity in the last row) there are some small, incorrectly segmented objects seen close to the region of interest that increased the false-positive rate and decreased the measured segmentation accuracy. An extra post-processing step could remove them and increase the accuracy.

We used a 3D block-based segmentation approach for better adaptability of the method for image volumes with different numbers of slices. The block-based approach also improved the segmentation accuracy by averaging the output probabilities for the overlapped regions of the blocks.

The average computation time per patient was about 25 seconds which is substantially lower than manual segmentation time. However, it is required to measure user interaction time to confirm using this segmentation method could decrease the segmentation time substantially.

4.1. Limitations

The small size of the training set is the main limitation of this study. Since there is high inter-subject variability in placenta shape and position, the training set must be large enough to represent all the shape and location variations of the placenta within the uterine cavity. Moreover, the pregnancy stages affect the fetus’s size, appearance, and orientation. This could directly impact the segmentation performance of the algorithm. Using separate CNN models for each pregnancy trimester, when a large training dataset is available, could be helpful for more accurate segmentation performance. The other limitation of this work is the block-based segmentation approach. Although it helped with algorithm implementation and improved the accuracy, it increased the segmentation time and added more computations for integrating the block-level results. We also need to design a user study to test the hypothesis in a more realistic situation. The current results were achieved based on a simulation of the user interaction.

5. CONCLUSIONS

We proposed a modified U-Net based deep learning approach for simultaneous 3D segmentation of the uterine cavity and placenta in MRI. We guided the FCNN training and test by incorporating minimal user inputs (seven clicks) for more robust and reliable segmentation performance. The results showed accurate segmentation performance of the algorithm with average DSC values of 92% and 82% for uterine cavity and placenta, respectively. The segmentation method is able to measure placenta size and assess its location, which is a first step in the application of textural analysis radiomics within the segmentation to aid in the diagnosis of placenta abnormalities. The future work will be focused on testing the algorithm on a larger dataset and measuring user interaction time.