Influence of a shape of gold nanoparticles on the dose enhancement in the wide range of gold mass concentration for high-energy X-ray beams from a medical linac

Abstract

Aim

This work is focused on the Monte Carlo microdosimetric calculations taking into account the influence of the AuNPs’ shape, size and mass concentration on the radiation dose enhancement for the high-energy 6 MV and 18 MV X-ray therapeutic beams from a medical linac.

Background

Due to a high atomic number and the photoelectric effect, gold nanoparticles can significantly enhance doses of ionizing radiation. However, this enhancement depends upon several parameters, such as, inter alia, nanoparticles’ shape etc.

Method

The simulated system was composed of the therapeutic beam, a water phantom with the target volume (with and without AuNPs) located at the depth of the maximum dose, i.e. at 1.5 cm for the 6 MV beam and at 3.5 cm for the 18 MV one. In the study the GEANT4 code was used because it makes it possible to get a very short step of simulation which is required in case of simulating the radiation interactions with nanostructures.

Results

The dependence between the dose increase and the mass concentration of gold was determined and described by a simple mathematical formula for three different shapes of gold nanoparticles — two nanorods of different sizes and a flat 2D structure. The dose increase with the saturation occurring with the increasing mass concentration of gold was observed.

Conclusions

It was found that relatively large cylindrical gold nanoparticles can limit the increase of the dose absorbed in the target volume much more than the large 2D gold nanostructure.

1. Background

The effectiveness of nanoparticles as radiosensitizers, dose enhancers and contrast agents is becoming increasingly recognized. Gold nanoparticles (AuNPs) are a dominant choice among other nanoparticles for medical applications¹ because of their relatively easy synthesis in a range of various sizes2, 3, 4, 5 and shapes,⁶ straightforward attachment of ligands and good biocompatibility.7, 8, 9, 10, 11, 12, 13 They can be used as agents preferentially sensitizing tumors to ionizing radiation, termed radiosensitizers, and as such attract a great interest in radiation oncology.14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 Moreover, they are of interest as non-toxic carriers for drug delivery to tumor sites. Gold has a high atomic number, which is approximately 10 times higher than that of soft tissue. Due to a large number of electrons, electron density is increased in the vicinity of a gold nanoparticle which induces a local dose enhancement caused mainly by an increase of the photoelectric effect yield in the irradiated medium. The photoelectric effect is the most effective way of energy transfer from radiation to the irradiated medium. In case of high-energy photons, Compton scattering plays a significant role in the energy transfer. The details of the dose enhancement mechanism were described by Kuncic and Lacombem¹⁶ and by Morales-Orue et al.¹⁷ The latest studies indicate that the dose enhancement depends strongly on the type of radiation and, in the case of photons, it depends also on the energy spectrum of the radiotherapeutic beam.^15,19, 20, 21, 22, 23, 24, 25, 26, 27, 28 The effect of dose enhancement was comprehensively investigated mainly for low-energy photons, i.e. for X-rays of several hundred keV and for gamma-rays used in brachytherapy. This effect was also studied for the 6 MV X-ray beam,29, 30, 31, 32 but there is still a lack of extensive data for high-energy photons used in teleradiotherapy. From the medical point of view the local dose enhancement – meaning a possibility to deliver ablative therapeutic doses to the tumor microstructures while maintaining established dose constraints for the organs at risk – may contribute significantly to tumor eradication and treatment efficacy during radiation therapy.

2. Aim

In this work a numerical Monte Carlo microdosimetric study of the influence of gold nanoparticle sizes and shapes on dose enhancement in high-energy X-ray teleradiotherapy was performed, for the gold mass concentration changing continuously in a target volume. The dependence between the dose enhancement and the gold mass concentration was mathematically described. The calculations were done for the therapeutic flattened (FF) X-ray beams with nominal potentials of 6 MV and 18 MV generated by the Varian Clinac 2300 medical linear accelerator.

3. Method

3.1. Simulated system

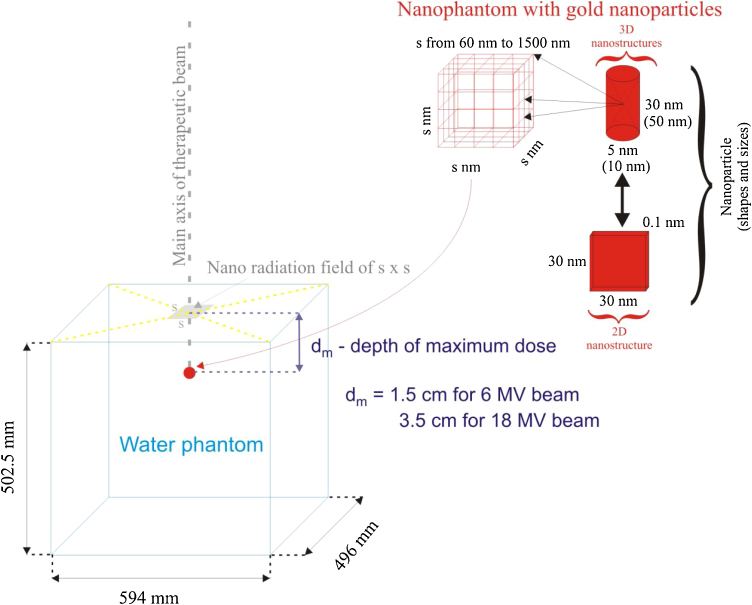
The simulated system was composed of a therapeutic beam, a water phantom with the target volume located at the depth of the maximum dose, i.e. at 1.5 cm for the 6 MV beam and at 3.5 cm for the 18 MV one. The dimensions of the water phantom were equal to those of a clinical dosimetric phantom (Fig. 1). The target volume was represented by a water nanophantom of a box shape with dimensions from 60 nm × 60 nm × 60 nm to 1500 nm × 1500 nm × 1500 nm. The nanophantom (Fig. 1) contained 125 nanoparticles located in 5 planes (25 nanoparticles in each plane). Three different shapes of the nanoparticles were considered: a 50 nm high nanorod with a base diameter of 10 nm, a 30 nm high nanorod with a base diameter of 5 nm and the 2D structure of 30 nm × 30 nm × 0.1 nm. The spectrum of the therapeutic 6 MV X-ray FF beam was taken from the studies by Konefał and Pietrzak et al.,37, 38, 39 whereas the one for the FF 18 MV-rays was copied from the study by Sheikh-Bagheri and Rogers.⁴⁰ These spectra were pure photon ones with no electron contamination. The 6 MV beam spectrum was determined at the centre of the 3 cm × 3 cm radiation field whereas the 18 MV beam spectrum was related to the centre of the circular field with a radius of 2.25 cm, both for SSD = 100 cm. In this work much less radiation fields with the sizes of the nanophantoms were simulated, as presented in Fig. 1. Such approach permitted to limit the time of simulations as well as to obtain relatively good statistics. The primary photons were distributed uniformly on the phantom surface. They started from the plane located at 1 mm over the phantom. The tracks of primary photons were perpendicular to the phantom surface. Basing on the simulations with the nano radiation fields, the phase space files with parameters describing the fluence of photons and electrons coming into a sphere with the radius of 1000 nm were prepared. A separate phase space file was created for each simulated nano radiation field. These files were a set of input parameters used in the dose enhancement calculations, which additionally speeded up the study. The thickness of the 2D structure corresponded to a single atom layer, i.e. about 0.1 nm, whereas the cylindrical nanoparticles were filled with gold atoms. The density of all considered nanoparticles was equal to that of the metallic gold i.e. 19.3 g/cm³. The gold nanoparticle spatial distribution was uniform in the whole target volume, i.e. the distances between the centers of all AuNPs were the same. In the subsequent simulations the nanophantom sizes were chosen in such a way as to get a required mass concentration of gold. In this work the mass concentration of gold varied from 3 mg/cm³ to 100 mg/cm³. In the case of the smaller nanocylinder, the nanophantom with dimensions of 200 nm × 200 nm × 200 nm corresponded to the mass concentration of gold 3 mg/cm³, whereas 100 mg/cm³ was obtained for the 60 nm × 60 nm × 60 nm nanophantom. The 1500 nm × 1500 nm × 1500 nm nanophantom was related to 3 mg/cm³ and the 450 nm × 450 nm × 450 nm nanophantom corresponded to 100 mg/cm³ for the larger nanocylinder. In the case of the 2D nanostructure the mass concentration of gold was 3 mg/cm³ and 100 mg/cm³ for the nanophantom with dimensions of 600 nm × 600 nm × 600 nm and 190 nm × 190 nm × 190 nm, respectively. The spatial arrangement of the axes of each nanoparticle was determined randomly for each simulated primary photon. In this study, water – a close soft-tissue equivalent material and a standard choice for radiotherapy dosimetry – was declared as an irradiated medium, because it is recommended by the dosimetry protocols for any dosimetric calculations or measurements.⁴¹ The doses to water in the target volume were calculated in the nanophantom with and without the nanoparticles. The deposited dose was collected in water (not in nanoparticles) in the entire volume of the nanophantom. The considered doses were averaged for water in the nanophantom.

Fig. 1.

The scheme of the simulated system.

3.2. Simulated physics

Monte Carlo simulations were performed using the GEANT4 code because of its good validation in the range of electromagnetic interactions when applying the Low Energy model of physical processes.33, 34, 35, 36 Although many professional Monte Carlo codes provide possibilities calculating very small distances, the GEANT4 code makes it possible to get a very short step of simulation which is required when simulating radiation interactions with nanostructures. The 4.10.1 version (patch-03) of GEANT4 with the low energy electromagnetic processes’ libraries in version 6.41 was applied in the simulations.⁴² The following physical processes were implemented in the simulation code:- photoelectric effect, Compton scattering, electron-positron pair production and Rayleigh scattering for photons – ionization, multiple scattering, bremsstrahlung production for electrons and positrons and, additionally, positron annihilation – some other processes, e.g. atomic relaxation, the Auger effect, etc.

The low energy limit for primary photons within the applied models of physical processes is 250 eV. It is much below the energies of the K and L emission lines for gold (68.79 keV (K_α1), 77.97 keV (K_β1), 9.71 keV (L_α1), 11.44 keV (L_β1)) and oxygen (526 eV (K)). Thus, there is no limitation to simulate ionization of Au and O atoms in the photoelectric effect. The results presented in this work were obtained using a CutValue parameter of 1.0 nm. This small value means that no secondary photons, electrons or positrons will be produced if the current range of the secondary radiation in water or in gold is less than 1.0 nm. It gives 1 eV and 0.1 eV as the cut-off energy of secondary electrons produced in electromagnetic interactions for water and for gold, respectively. Such cut-off energies make it possible to get accurate values of the absorbed dose, because even ionization of slightly bonded electrons is simulated. In the simulations the computer cluster of the Department of Nuclear Physics and Its Applications of Institute of Physics at the University of Silesia in Katowice (Poland) was used. Three 3 GHz Pentium computers with four core processors were used. It permits to get approximately 5 × 10² ÷ 10³ events per hour in a result file in the calculations producing the phase space files. However, in the dose enhancement calculations the efficiency of the data collection was higher, i.e. approximately 10⁵ events per hour in a result file because of the use of the phase space files. All presented characteristics and spectra were obtained for 10⁹ primary photons.

4. Results

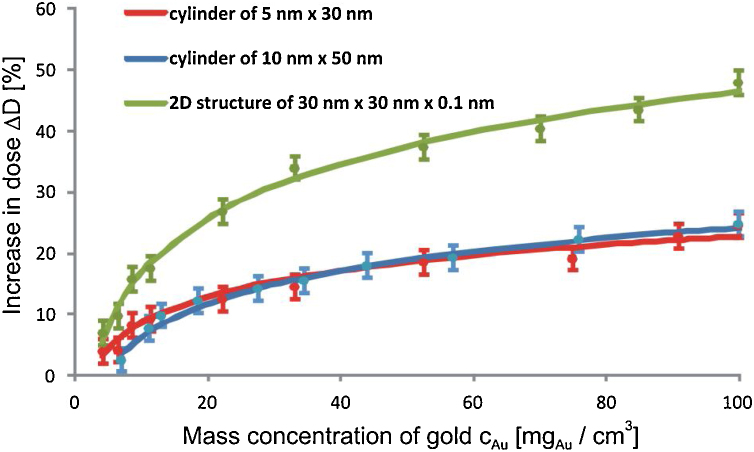
The dose increase caused by gold nanoparticles (in percent) was determined in relation to the dose absorbed in water in the target volume with no gold nanoparticles. The dose enhancement with the increasing Au mass concentration is visible and as is the saturation of the enhancement. The increase of the dose absorbed in water in the nanophantom as a function of the Au mass concentration for various shapes and sizes of the nanoparticles for 6 MV X-rays is presented in Fig. 2. The analogous dependence for 18 MV X-rays is shown in Fig. 3.

Fig. 2.

The increase of the dose absorbed in water in the target volume irradiated by 6 MV X-rays versus the mass concentration of gold for AuNPs with the considered shapes and sizes. The logarithmic function (solid lines) was fitted to the points from the simulations (the details in the text).

Fig. 3.

The increase of the dose absorbed in water in the target volume irradiated by 18 MV X-rays versus the mass concentration of gold for AuNPs with the considered shapes and sizes. Otherwise as in Fig. 2.

The simple two-parameter logarithmic function fitted to the points from the simulations using the least-squares method describes well the dependence between the dose increase in the irradiated target volume due to the presence of gold nanoparticles and the Au mass concentration. The function can be expressed as follows:

ΔD = a ∙ log(c_Au) – b, (1)

where ΔD is the dose increase in the target volume, caused by the presence of Au nanoparticles with a mass concentration c_Au, a and b are the fitted parameters. The Pearson coefficient is close to 1 for all performed fits. The uncertainties of a single simulation from statistical fluctuations do not exceed 2% for most cases which is denoted by the error bars in Fig. 2, Fig. 3. In each individual simulation, the fractional dose uncertainty was calculated as $\frac{\sqrt{N}}{N}\bullet 100\%$, where N is a number of events registered in the nanophantom as the absorbed dose. The values of the parameters a and b are included in Table 1.

Table 1.

The values of the parameters a and b for the gold nanoparticles of the studied sizes and shapes, for the 6 MV and 18 MV beams.

	Smaller cylinder 5 nm × 30 nm		Larger cylinder 10 nm × 50 nm		2D structure 30 nm × 30 nm × 0.1 nm
Beam	a	b	a	b	a	b
6 MV	6.184	5.763	7.678	11.268	12.851	12.834
18 MV	8.058	25.991	12.138	41.464	14.178	14.618

The a and b values are higher for the ΔD(c_Au) curves with the larger gradient of the dose increase. The dose enhancement increases with the increasing Au mass concentration for all considered nanoparticles, but the dose increase and the dose increase gradient are strongly affected by the shape of AuNPs. The characteristics of the dose increase are similar for both nanorods. The difference between these characteristics do not exceed the statistical uncertainty of 2% across the whole considered range of the gold mass concentration. In case of the rod-like nanoparticles the maximum dose increase reaches 20% for the 6 MV X-rays and about 13% for the 18 MV X-rays. The largest dose increase was observed for the 2D gold nanoparticles amounting to about 46% and 50.5% for the 6 MV X-rays and 18 MV X-rays, respectively.

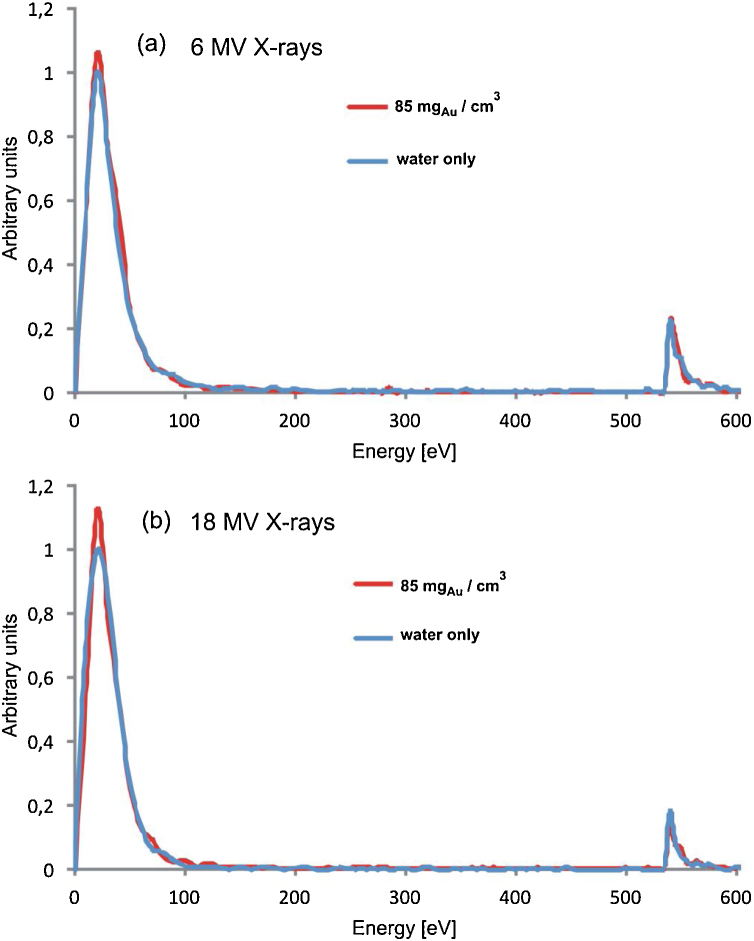
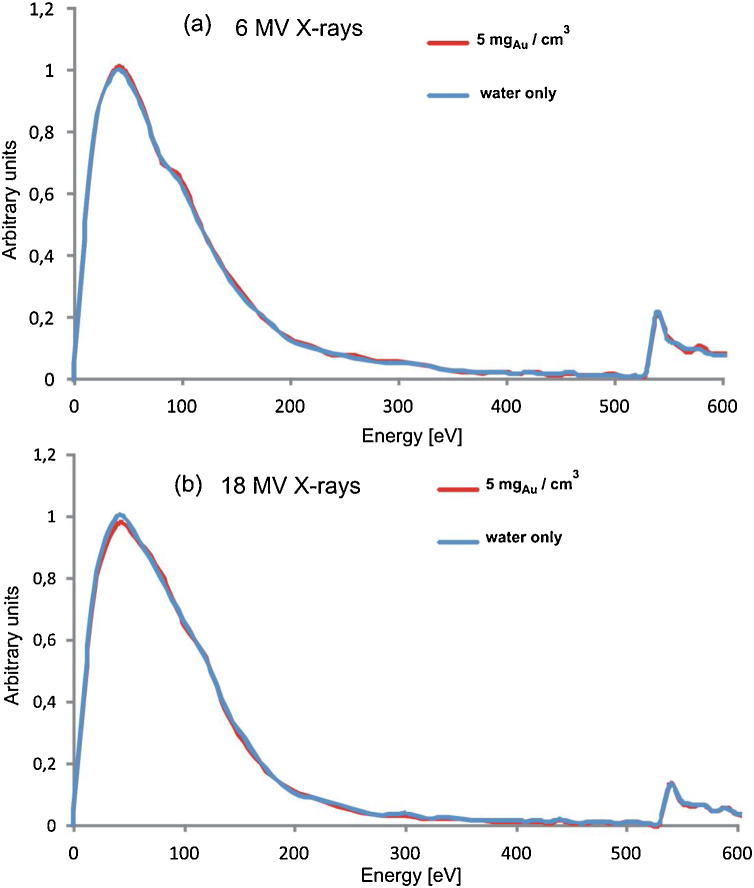
Fig. 4, Fig. 5 present the spectra of energy absorbed in water in the nanophantom with and without AuNPs to visualize the dependencies between the dose enhancement and the Au mass concentration. The low–energy regions of the spectra, originating mainly from the absorption of energy of secondary electrons produced via Compton scattering differ, whereas the resonance regions corresponding to 526 eV overlap. The predominance of energy absorption in the low-energy part for the nanophantom containing the 2D AuNPs structures (30 nm × 30 nm × 0.1 nm) of a high gold concentration of 85 mg_Au/cm³ is visible in Fig. 4. This absorption effect is responsible for the dose increase. For 6 MV X-rays the spectra obtained with and without the Au nanorods of 10 nm × 50 nm are identical (Fig. 5(a)) for a relatively small Au mass concentration of 5 mg_Au/cm³. It may be explained by the balance between the amount of energy of secondary electrons originating from the interactions with AuNPs, absorbed by water and the amount of energy of secondary electrons produced in the interactions with the water molecules, absorbed by AuNPs. This balance defines the Au mass concentration threshold over which the dose to water increases. In case of irradiation with 18 MV X-rays the visible predominance of energy absorption in the low-energy part of the spectrum for the nanophantom without AuNPs is responsible for the decrease of the dose to water (Fig. 5(b)). This effect disappears when the gold concentration increases, which is due to the increase in the number of interactions of photons with gold atoms.

Fig. 4.

The spectra of energy absorbed in water in the nanophantom with and without 2D AuNPs for the gold mass concentration of 85 mg_Au/cm³ for 6 MV X-rays (a) and for 18 MV X-rays (b). The events were counted in the 10 eV bins up to 250 eV and in the 5 eV ones for the higher energies. The counts in the bins were normalized to the maximum of the spectra without AuNPs.

Fig. 5.

The spectra of energy absorbed in water in the nanophantom with and without the cylindrical AuNPs with dimensions of 10 nm × 50 nm and for the gold mass concentration of 5 mg_Au/cm³ for 6 MV X-rays (a) and for 18 MV X-rays (b). Otherwise as in Fig. 4.

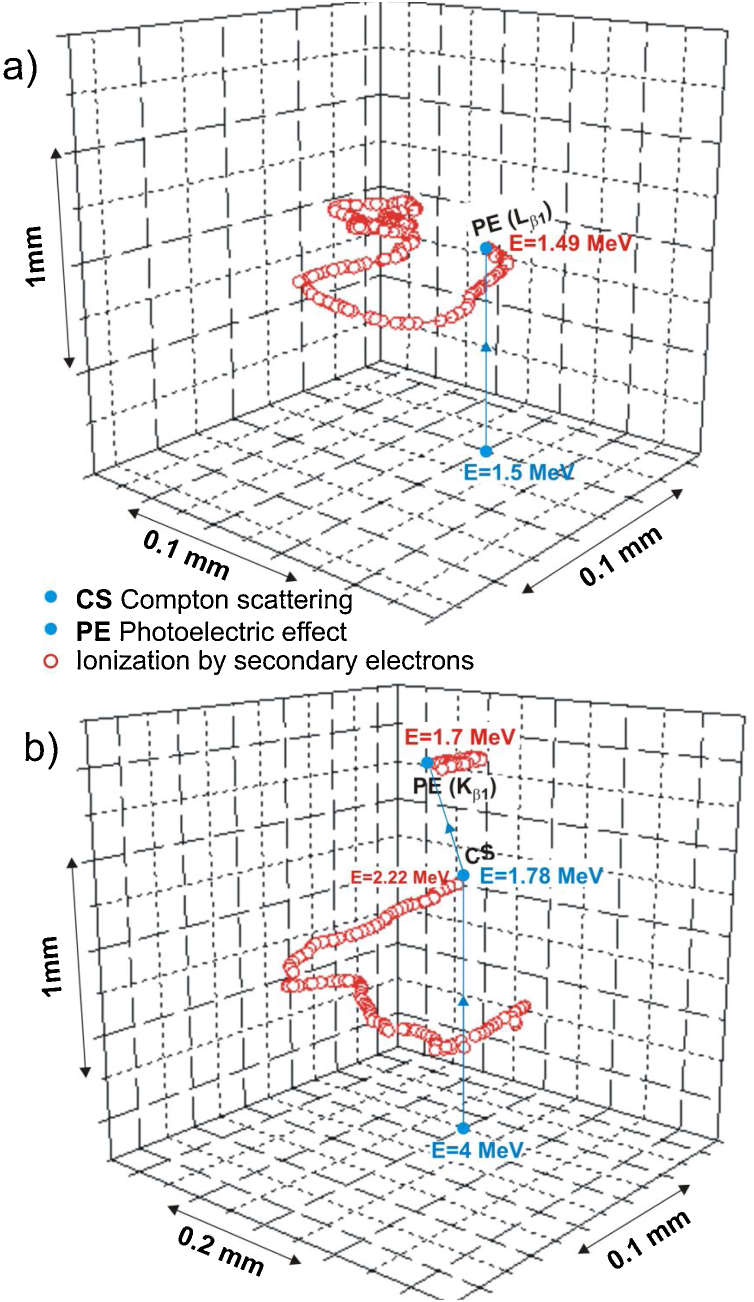
The randomly generated tracks of primary photons with the energies representative of the considered therapeutic X-ray beams and the analogous tracks of secondary radiation produced in gold are presented in Fig. 6. The primary photons have the energies of 1.5 MeV and 4 MeV, being close to the most probable energies for the 6 MV and 18 MV FF X-ray beams from Clinac-2300, respectively.

Fig. 6.

The view of the exemplary tracks of photons with most probable energy of (a) 1.5 MeV and (b) 4 MeV in gold for the 6 MV X-ray beam from the Clinac 2300 and for the 18 MV one, respectively, generated by the simulation program used in this work. The circles denote the locations of the interactions.

Generally, the higher-energy photons undergo mostly Compton scattering or produce a pair of electron–positron followed by the photoelectric effect, whereas the lower-energy ones interact mainly by the photoelectric effect. This is shown in Fig. 6. The tracks of the secondary electrons are long enough for the energy of the produced electrons to be deposited outside the target volume, even in the case of relatively large irradiated volumes. Particularly, the electrons originating from close to the edges of the target volume may escape to the adjoining tissues.

The chosen parameters describing the secondary electrons and positrons are collected in Table 2. In case of the 6 MV beam, the number of secondary electrons produced in the interactions between photons and Au atoms is approximately four times greater than for the 18 MV one. However, the total energy of secondary electrons induced by the 18 MV beam is about two times greater than for the 6 MV one. The contribution of positrons for the 18 MV beam is greater than for the 6 MV one. It cannot be neglected, because positrons undergo annihilation when they reach thermal energy by ionization of atoms, i.e. by energy transfer to the irradiated medium.

Table 2.

The mean number of electrons\positrons originated from the interactions with AuNPs and the total energy of the produced electrons\positrons per a million photons getting to a nanoparticle for the therapeutic beams from Clinac 2300.

	6 MV beam	18 MV beam
Mean number of electrons per 106 photons	3.8	0.9
Total energy of secondary electrons per 106 photons	9.7 × 10−14 J	19.1 × 10−14 J
Mean number of positrons per 106 photons	0.05	0.12
Total energy of positrons per 106 photons	0.6 × 10−14 J	8.0 × 10−14 J

5. Discussion

5.1. The influence of the gold nanoparticles sizes and shapes — the review of literature Monte Carlo results

As reveals from the literature review, the experimentation with a variety of nanoparticles shapes and sizes has shown that these parameters may strongly affect the AuNPs uptake by the cells. The particle size is particularly important for a successful AuNPs deposition within tissue: with small molecular sizes, therapeutic and imaging agents are able to penetrate into the tumor tissues but are also cleared out quickly; moreover, the smaller are the nano-objects the more widespread are they distributed within normal tissues.⁴³ Chithrani et al.⁴⁴ found that the cellular uptake of spherical gold nanoparticles is size-dependent. Particles larger than 300 nm are potentially eliminated by macrophages, while those smaller than 100 nm in diameter can enter the tumor tissue. In biological applications, the overall optimum particle size is often reported as being ca. 30 nm or less.⁴³

Although much less studied, the shape of a nanoparticle can have a strong impact on its biophysical properties. The shapes that can be achieved with gold nanoparticle syntheses cover a wide variety of unique and geometrical morphologies including spheres, rods, cubes, stars, discs, cages, etc.⁴³ The rod-shaped nanoparticles are claimed to exhibit smaller uptake by cells as compared to the spherical structures, but their intratumoral transport and distribution are better than those of the nanospheres.44, 45, 46

Importantly, the physical and geometrical parameters of AuNPs, such as the particle size, shape, concentration and distribution significantly affect the dose enhancement.⁴⁷ Monte Carlo simulation can be used to investigate such effects in radiotherapy, which can further help to predict the biological consequences related to cancer cell killing, such as DNA damage. In our study, based on a simulation Monte Carlo model containing a radiation source and a target composed of AuNPs in a water medium, the energy produced by the secondary electrons from the AuNPs and the irradiated volume was estimated and the role of the parameters such as the nanoparticles size, shape or concentration was determined. The AuNPs simulated by us in the Monte Carlo models are the 50 nm long rod-like particles with a diameter of 10 nm, the 30 nm long nanorods with 5 nm diameter and the 2D structure of 30 nm × 30 nm × 0.1 nm; thus, all being within the optimum particle sizes range; similarly, the shapes have been selected for their possible use in radiotherapy.

Because of the differences in the irradiation conditions as well as in the shapes and sizes of the nanoparticles used in various studies, it is difficult to perform a direct comparison of our results with the results by others. Berbeco et al.²⁹ used cellular microdosimetry to calculate anticipated local radiation dose enhancements by vasculature-confined AuNPs during irradiation by a conventional 6-MV linac beam. In their work a spherical nanoparticle was simulated attached to the vascular-side surface of the endothelial cell. The endothelial cells were modeled as thin slabs with 100-nm-diameter AuNPs attached within the blood vessel. The nanoparticle size was small relative to the endothelial cells but large enough not to be transmitted intracellularly or through the leaky vasculature. They report the dose increase of 20% and 70% for the gold concentration of 7 mg_Au/g and 30 mg_Au/g, respectively. In our study, for these gold concentrations the dose increases were 12% and 31% for the 2D Au structure, and 3.5–6% and 15% for the larger and smaller nanorods, for the 6 MV FF X-ray beam.

Detappe et al.³⁰ studied the dose enhancement to tumor endothelial cells by spherical gold nanoparticles. Their Monte Carlo calculations were performed for the spheres with the radius of 50 nm and the endothelial cells irradiated with 6 MV X-ray FFF beam. The observed dose increase of about 20% for the gold concentration of 30 mg/mL was reported. This value falls between the values calculated by us for the nanorods and 2D nanoparticles.

Cho³¹ observed the dose enhancement effect to be negligible for a 6 MV photon beam, when the gold concentration was low (2 mg_Au/g), which is in accordance with our results.

In turn, Pakravan et al.³² using the 6 MV X-ray FF beam detected almost negligible dependence between the nanoparticles sizes and dose enhancement for the nanospheres with diameters from 50 nm to 200 nm. They report a relatively low dose increase (up to 5%) induced by the gold concentration in the range from 12 mg/g to 36 mg/g for these massive nanostructures. This dose increase is somewhat below the values obtained by us for the Au nanorods.

To the best of our knowledge, there are no studies dealing with the Monte Carlo simulation of asimilar dose enhancement for the 18 MV FF beam.

5.2. Physical interpretation of the results

Dose enhancement was observed for all shapes of the Au nanoparticles we studied, and was clearly shape-dependent. Because the mean number of electrons in the irradiated medium with AuNPs increases, thus, both the cross sections: for the photoelectric effect and for Compton scattering, increase as well. Obviously, the number of electrons emitted from gold atoms (i.e. secondary electrons) is greater when the Au mass concentration in the nanophantom (target volume) is higher. However, the dose enhancement caused by the presence of gold nanoparticles in the nanophantom results mainly from two competitive processes: the production of secondary electrons and positrons in the interactions of photons of the megavoltage X-ray beam with gold atoms, and the process of AuNPs absorbing the energy of these electrons\positrons as well as the energy of the electrons produced in the interactions of the photons with atoms of water molecules. This absorption is the way in which energy is not deposited in the irradiated medium, but rather lost. Massive 3D nanostructures absorb energy of the produced electrons and positrons more effectively than the 2D ones. The absorption is a main factor inducing saturation of the dose increase occurring with the Au mass concentration increase. Therefore, in case of the 2D nanostructure the dose increase and the increase gradient are significantly greater than for the nanorods. Generally, from a physical point of view, the increase of the dose to water is mainly due to the ionization of water molecules by electrons and positrons produced in the interactions between photons of the beam and Au atoms. The confirmation of this statement comes from the comparison of the spectra of energy absorbed in water in the nanophantom with and without AuNPs.

The intensities of the photopeaks at 526 eV are not affected by the AuNPs presence in the nanophantom. It indicates that because of the energy mismatching the low-energy photons emitted by Au atoms in the de-excitation processes escape from the nanophantom before the photoelectric effect in oxygen atoms could be induced.

As shown in this work, the Au mass concentration threshold of the dose increase depends on the nominal potential of the X-ray beam (i.e. photons energy) used for irradiation as well as on the nanoparticles shape. In case of the nanorods the dose absorbed in water starts to increase at a higher Au mass concentrations for the higher beam energy (18 MeV). This is caused by the predominance of the secondary electron\positron energy loss due to the AuNPs absorption over the water absorption of energy of electrons\positrons produced in the interactions with Au atoms for the low Au concentration. Generally, the yield of secondary electron production is smaller for higher energy of photons and a greater Au mass concentration is needed to balance the absorption by nanoparticles. This absorption is of less significance in the case of the 2D structures for the low Au concentration, as shown by the Monte Carlo modeling, i.e. the clear shift of the thresholds related to the beam with the different nominal potentials was not observed for the 2D structure with the thickness of a single atom. It should be stressed that in the case of massive nanoparticles, like the studied rod-like ones, secondary electrons and positrons may be absorbed by the nanoparticle participating in their production. Because of the isotropic spatial distribution of photoelectrons and positrons, it is more likely for the electron\positron to be emitted towards a nanoparticle and the for its energy to be absorbed.

5.3. General considerations

The mathematical description of the ΔD(c_Au) dependence based on the simple logarithmic function can be very useful for the future use of AuNPs because it permits to determine precisely the dose increase caused by gold nanoparticles with given shape and sizes for the current Au mass concentration. The suggested function can also be useful for the future search of optimal sizes and shapes of AuNPs applied for dose enhancement. It is worth noting that the proposed mathematical model is quite innovative. To our knowledge, no mathematical description has as yet been given in the literature of the dependence between the dose increase in the irradiated target volume containing Au nanoparticles and the Au mass concentration. The obtained results are representative of low radiation fields with no significant scattered therapeutic photon component, because in this study the radiation field size was related to the sizes of the nanophantom.

6. Conclusions

The Monte Carlo simulation results indicate that in the case of massive 3D Au nanorods the increase of the dose absorbed in the medium irradiated with the megavoltage X-rays is strongly limited. The 2D gold nanoparticles seem to be more promising for dose enhancement in teleradiotherapy with the use of 6 MeV beams. Although for 18 MV X-rays the dose enhancement is also observed when AuNPs are used, however, in such a case the dose increase results also from the energy deposition by electrons originating from Compton scattering, whereas for the 6 MV beam the photoelectric effect dominates. This study is our first approach to systematize the Monte Carlo results on the dose enhancement by means of gold nanoparticles in teleradiotherapy.

Conflict of interest

None declared.

Financial disclosure

None declared.