Adaptive Learning Recommendation Strategy Based on Deep Q-learning

Abstract

Personalized recommendation system has been widely adopted in E-learning field that is adaptive to each learner’s own learning pace. With full utilization of learning behavior data, psychometric assessment models keep track of the learner’s proficiency on knowledge points, and then, the well-designed recommendation strategy selects a sequence of actions to meet the objective of maximizing learner’s learning efficiency. This article proposes a novel adaptive recommendation strategy under the framework of reinforcement learning. The proposed strategy is realized by the deep Q-learning algorithms, which are the techniques that contributed to the success of AlphaGo Zero to achieve the super-human level in playing the game of go. The proposed algorithm incorporates an early stopping to account for the possibility that learners may choose to stop learning. It can properly deal with missing data and can handle more individual-specific features for better recommendations. The recommendation strategy guides individual learners with efficient learning paths that vary from person to person. The authors showcase concrete examples with numeric analysis of substantive learning scenarios to further demonstrate the power of the proposed method.

Introduction

Adaptive learning refers to an educational method that delivers personalized educational interventions, typically implemented through computerized algorithms that output personalized action recommendations based on analysis of the learning histories of the learners. The popularization of the Internet access has facilitated the application of adaptive learning in practice, which in turn prompted further research interests (Sleeman & Brown, 1982; Wenger, 1987). However, the past few years have seen great advances in big data technology. In particular, a sensational success was achieved by AlphaGo, which employed the cutting-edge techniques on deep reinforcement learning. The aim of this article is to bridge adaptive learning with the recent developments in deep reinforcement learning and consequently propose novel recommendation strategies for the adaptive learning system.

Emanated from behaviorist psychology (Skinner, 1938), reinforcement learning is concerned about how an agent interacts with the environment and learns to take actions to maximize total rewards. Reinforcement learning is one of the central topics in artificial intelligence (Kaelbling, Littman, & Moore, 1996) and has broad applications to areas such as robotics and industrial automation (Kober & Peters, 2012), health and medicine (Frank, Seeberger, & O’reilly, 2004), and finance (Choi, Laibson, Madrian, & Metrick, 2009), among many others. As a significant progress in recent years, deep reinforcement learning was proposed by Google Deepmind in 2013. In applications to play Atari 2600 games, it achieved the expert human proficiency (Mnih et al., 2013). In applications to playing the game go, it surpassed human level of play, starting from tabula rasa, within a training period as short as a few days (Silver et al., 2016).

To apply reinforcement learning techniques to adaptive learning, a proper formulation of adaptive learning process in terms of the setup is commonly used in reinforcement learning (Chen, Li, Liu, & Ying, 2018). Each time the learner takes an action following the recommendation strategy, the system enters a new knowledge state and then receives a reward. The authors’ goal is to maximize students’ learning efficiency, that is, helping learners master knowledge points in the most effective path. This is equivalent to balancing the trade-off between the expected total gain of knowledge points being mastered by the learner and total learning steps during the process. In a substantive learning scenario with the presence of assessment errors, unknown learning model, and complex reward forms, a good recommendation strategy is supposed to make full use of current information to maximize the learning gain and is feasible in various learning designs. Such an optimal strategy design problem is cast into a Markov decision problem and will be solved under a reinforcement learning framework.

In this article, an approach based on deep reinforcement learning, providing personalized recommendations and addressing the cost-effective learning need of learners, was presented. Specifically, a variant of deep Q-learning algorithm (Hasselt, Guez, & Silver, 2016) was adopted and tailored modifications for adaptive learning recommendations were made. The objective function is approximated by a neural network which is used to determine the optimal strategy. The authors made several novel contributions. First, the parameter space is enlarged and early stopping is incorporated into the learning process. As a result, the deep Q-learning approach maximizes the overall gain within the shortest time, serving the purpose of maximizing the learner’s learning efficiency. Second, the model is designed with the ability to handle missing data. In existing work (e.g., Chen et al., 2018), it is assumed that the learning process has fixed procedures, where the assessment model is considered to be indispensable at each step, and the recommendations cannot appropriately deal with missing knowledge status. In this article, a missing index is introduced and modeled, which helps to analyze incomplete data in a flexible fashion. Third, the effect of learning interest is considered. As the learning model differs among learners, a real-time recommendation system that is sensitive to the characteristics of each learner can be further obtained by introducing more personal features, such as learning interest. Thanks to the nature of the deep neural network, the proposed method can scale up comparatively easily in handling big data. It is expected that, by combining domain knowledge and more individual information, the proposed method may be further improved to a more efficient and competitive adaptive learning system.

The rest of this article is organized as follows. In section “Background,” a mathematical framework for adaptive learning is reviewed, where a general cost-efficient reward for the recommendation strategy was defined. Then, a variant of deep Q-learning tailored to adaptive learning is presented in section “Deep Q-learning recommendation strategy.” In section “Learning scenarios and experiments,” concrete simulated examples are given to support the methods in the more realistic learning scenarios, followed by discussion in section “Discussion.”

Background

The objective of recommendation is to help individual learners achieve their learning goals in the shortest time by utilizing all the currently available information. Consider $K$ knowledge points in total with the learning time $t\in [0,T]$. Let $\mathit{s}(t)=(s_1(t),s_2(t),\dots ,s_K(t))$ be a latent dynamic $K$-dimensional random vector, denoting the learner’s latent knowledge state at time $t$, where $s_i(t)$ is the student’s mastery level on the ith knowledge point. Based on the assessment result of a learner’s knowledge state $\mathit{s}(t)$, an appropriate action $a(t)$ is recommended from action space $A$. In this section, the authors elaborate the learning procedure in three parts.

Assessment Model

The study on the diagnosis of one’s latent abilities has been developed in modern psychometrics. Online learning systems can track the entire online learning behaviors, including frequency of login, clips on the lecture video, and item responses which can be dichotomous or polytomous. Such information can be incorporated to model one’s learning styles and preferences so as to make learning designs more accurate and enjoyable for learners (Coffield, Moseley, Hall, & Ecclestone, 2004).

Consider the assessment on the proficiency level of knowledge points with the test item pool $\chi$. The knowledge state $\mathit{s}(t)$ can be partially observed from responses to the test items (i.e., questions). Let $Y_j$ be the response to the jth item with a given mastery for knowledge points $\mathit{s}(t)$ following a distribution, that is,

$$Y_j~h_{j,\mathit{s}(t)}\left(y\right),$$

which implies that $h_{j,\mathit{s}(t)}(y)$ depends, in addition to $\mathit{s}(t)$, on a set of item parameters of the jth item. Specifically, $h_{j,\mathit{s}(t)}(y)$ varies based on discrete and continuous latent traits $\mathit{s}(t)$ and different test designs. In this article, the authors use the multidimensional three-parameter logistic (M3PL) item response theory (IRT) model (Reckase, 2009) as the assessment model to estimate the knowledge state and assume the parameters well calibrated by historical data in all experiments.

Through the learner’s item responses, how knowledge points have been mastered so far can be observed partially. The assessment result $\hat{\mathit{s}}$ can be further obtained from either the maximum likelihood estimate or the posterior mean. In practice, it is not a general case that there always exist interactive learning histories to diagnose $\mathit{s}(t)$ at each $t$. For example, the learner may skip the questions after learning a material, and the knowledge state $\mathit{s}(t)$ is called missing data at time $t$. How to recommend given such incomplete learning data has not been discussed yet. In this article, a missing index was defined as the number of missing items, which can partially reflect one’s learning history and help the agent recommend proper actions even when the learner’s knowledge state is missing. The detailed method and numerical results are presented in section “Experiment on missing data.”

Learning Model

In a learning system, the learning model responses to action at each time. Given action $a(t)$, the knowledge state may have a corresponding change at next time point. It is assumed as a Markov process for the transition from $\mathit{s}(t)$ to $\mathit{s}(t+1)$, with probability

$$P(\mathit{s}(t+1)=\tilde{\mathit{s}}|\mathit{s}\left(t\right)=\mathit{s},a\left(t\right)=a).$$

In the context of adaptive learning, more factors beyond the learners’ knowledge states should be taken into considerations to train the learning model comprehensively while learning the recommendation strategy at the same time. These factors including cognitive abilities, learning styles, and other learning behaviors enable to distinguish various learning models for learners. Intuitively, interest in this subject could be a useful feature in the personalized recommendation system. Imagine two learners with different, strong and weak, interest in a course. They are likely to have very different learning processes and outcomes as a result of different interest. In mathematical modeling, different transition probabilities should be assumed for these two learners and different actions may be recommended even if they are at the same knowledge state. The detailed simulation study is presented in section “Experiment on the effect of learning interest” to illuminate how to combine interest as a feature into recommendation.

Recommendation Strategy

With learners’ information up to time $t$, the recommendation strategy determining actions in the Markov decision process is called policy, denoted as $\pi$. Every time the learner takes action, the agent will receive a scalar reward $R(t)$ as feedback. The best sequence of actions can be quantified by rewards provided by the environment and the goal is to find a policy $\pi$ that achieves the maximum expected total rewards. For $t=0,1,\dots ,T$, the authors define the oracle policy ${\pi }^{*}=\arg \underset{\pi }{\max }{E}_{\pi }[\sum _{t=0}^{T}R(t)]$ when there exists the perfect assessment and the learning model is known. The expectation takes the randomness in future actions and the learning model into account.

Given policy $\pi$, the Q-value function can be defined, measuring the expected return of being a given state $\mathit{s}(t)$ and taking action $a(t)$, that is

$$Q_{\pi }^t(\mathit{s}\left(t\right),a\left(t\right))=E_{\pi }[\sum _{t\prime =t}^{T}R(t\prime )|\mathit{s}\left(t\right)=\mathit{s},a\left(t\right)=a].$$

According to $Q_{{\pi }^{*}}^t(\mathit{s},a)$ at each time, the agent takes action greedily at every state, that is, $a^{*}=\arg \underset{a}{\max }{Q}_{{\pi }^{*}}^t(\mathit{s},a)$. That is to say, if $Q_{{\pi }^{*}}^t(\mathit{s},a)$ is known at every step, the optimal policy is determined ideally.

To find an efficient learning path to balance total gains on knowledge and learning steps, the action space $A$ includes three categories of actions, that is, $A=\{d_1,d_2,\dots ,d_n,a_s,"\mathrm{null}"\}$, where $d$ stands for learning materials and $a_s$ suggests stopping learning. After taking $a_s$, learners will take “null” action until terminal time. Given the reward at the terminal time (i.e., terminal reward $R(T)$), the reward form is defined as

$$R(t)=\{\begin{array}{cc}-1,\hfill & \mathrm{if}\mathrm{taking}\mathrm{learning}\mathrm{actions}{d}_1,d_2,\dots ,d_n\mathrm{at}\mathrm{time}t\hfill \\ \multicolumn{1}{c}{0,}& \mathrm{if}\mathrm{taking}"\mathrm{null}"\mathrm{or}{a}_s\hfill \\ \multicolumn{1}{c}{R(T),}& \mathrm{if}\mathrm{at}\mathrm{the}\mathrm{terminal}\mathrm{time}t=T.\hfill \end{array}$$

The reward setting imposes the penalty on total rewards by $-1$ for every step, thus the policy may lead the learning to stop. Consider $R(T)=\varphi \sum _{k=1}^K{w}_k{s}_k(T)$, where $\varphi$ is a scale parameter and $w_k$ is the weight of the kth knowledge point $s_k$ from domain knowledge. The idea behind $R(T)$ and $\varphi$ will be further discussed in section “Learning scenarios and experiments.” Specifically, reward function can take varied forms, for instance, Chen et al. (2018) and Tang, Chen, Li, Liu, and Ying (2019) raised $R(t)=\sum _{k=1}^K{w}_k(s_k(t+1)-s_k(t))$, which intuitively visualizes the improvement on knowledge states after learning at each step.

Following the reward setting above, the Q-value function of policy $\pi$ specifies that $Q_{\pi }^t(\mathit{s}(t),a(t))=E_{\pi }[R(T)-\mathrm{learning}\mathrm{steps}|\mathit{s}(t)=\mathit{s},a(t)=a]$, where “learning steps” is the number of total steps from time $t$ in a trajectory. A sequence of actions will be chosen by consulting $Q_{\pi }^t(\mathit{s},a)$. In the next section, the authors start from learning Q-value function to approximate ${\pi }^{*}$ under the framework of adaptive learning system.

Deep Q-learning Recommendation Strategy

Finding the Q-value function with respect to uncertainties in the system is challenging. For traditional methods, dynamic programming (Bellman, 2003) fails due to the curse of dimensionality (Niño-Mora, 2009) inherent in relatively large state spaces. Then, approximate dynamic programming methods (Powell, 2007) have constraints on forms of parameterization and may have convergence problems when the form of Q-value function is complicated. In this section, a method based on deep Q-learning (Mnih et al., 2015) to optimize the policy was employed, which is called the DQN method in the rest of this article.

Q-learning

Q-learning (Watkins & Dayan, 1992) is the basic idea behind the proposed method. In a learning system, a sequence of state transitions $(\hat{\mathit{s}}(t),a(t),R(t),\hat{\mathit{s}}(t+1))$ at each time $t$ is formulated in the Markov decision problem. At each time, the agent selects an action and the learner receives a reward, transits to next knowledge state, and then Q-value function is updated. Consider $t=0,1,2,\dots ,T-1$. Starting from a random initialized Q-value function, the Q-value is updated in the ith iteration

$$Q_i^t(\hat{\mathit{s}}(t),a(t))=E[R(t)+\underset{a}{\max }{Q}_{i-1}^{t+1}(\hat{\mathit{s}}(t+1),a)|\mathit{s}(t),a(t)].$$

The above equation derived from the Bellman equation (Sutton & Barto, 1998) is based on the following intuition: if the optimal Q-value is known at the next time point, the optimal strategy is to select the action maximizing the expected value of $R(t)+\underset{a}{\max }{Q}_{i-1}^{t+1}(\hat{\mathit{s}}(t+1),a)$. The authors aim to use it as an iterative update to optimize the Q-value function in the training.

Deep Q-network

For large state space, it is often impractical to maintain the Q-values for all state-action pairs. The authors consider to approximate $Q^t(\hat{\mathit{s}}(t),a)$ using a parameterized nonlinear function $Q(\hat{\mathit{s}}(t),a,t;\mathrm{\theta })$. According to current time $t$ and state estimator $\hat{\mathit{s}}(t)$, the DQN method approximates $Q^t(\hat{\mathit{s}}(t),a)$ by a feed-forward neural network with weight parameter $\mathrm{\theta }$, which outputs Q-values for all possible actions $a\in A$ simultaneously. The network approximation avoids the risk that optimization methods used for training may not able to find the parameters for the desired Q-value function or choose an unsuitable approximation function due to over-fitting. As universal approximators (Barron, 1993), networks organized by layers have a chain-based structure which makes them be well adapted to learn the hierarchies of information, especially such dynamic problems. Furthermore, the architecture of the networks is flexible, which can be scaled up and aligned to more complex learning circumstances. For example, the structure of the network in the experiments is shown in Figure 1, which has two hidden layers, and the rectified linear unit (ReLU) serves as the activation function, that is, $\mathrm{ReLU}(x)=\max (0,x)$. The readers are referred to Chapter 6 in Goodfellow, Bengio, Courville, and Bengio (2016) for a comprehensive review about neural networks.

Figure 1.

The architecture of the neural network with two layers in the experiments.

Algorithm

In this part, deep Q-learning algorithm is elaborated. The learner’s learning experiences at each time, ${\mathit{e}}_t=(\hat{\mathit{s}}(t),a(t),R(t),\hat{\mathit{s}}(t+1))$, are stored in the memory $D$ with size $N$, $D=\{{\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_N\}$. The authors apply mini-batch updates, a batch of samples drawn at random from $D$ and used to optimize the parameterization. In the iteration $i$, $\mathrm{\theta }$ can be updated by reducing error between the predicted value $Q_i(\hat{\mathit{s}}(t),a,t;{\mathrm{\theta }}_i)$ of current state and the target Q-value given by the sum of $R(t)$ and the maximized Q-value of the next state, $\underset{a}{\max }{Q}_{i-1}(\hat{\mathit{s}}(t+1),a,t+1;{\mathrm{\theta }}_i^{-})$, where ${\mathrm{\theta }}_i^{-}$ is from the previous iteration. Thus, the loss function is defined as

$$L({\mathrm{\theta }}_i)=E_{\hat{\mathit{s}},a}[(y_i-Q_i(\hat{\mathit{s}}(t),a(t),t;{\mathrm{\theta }}_i){)}^2],$$

where $y_i=R(t)+\underset{a}{\max }{Q}_{i-1}(\hat{\mathit{s}}(t+1),a,t+1;{\mathrm{\theta }}_i^{-})$. The complete training algorithm including more training tricks are presented in the online supplementary material, and the training procedure is briefly summarized as follows:

1. Initialize Q-value function $Q$ with parameter $\mathrm{\theta }$ and ${\mathrm{\theta }}^{-}=\mathrm{\theta }$;

2. Take action $a(t)$ according to the $ϵ$-greedy policy;

3. Store transition $(\hat{\mathit{s}}(t),a(t),R(t),\hat{\mathit{s}}(t+1))$ of time $t$ in the memory $D$;

4. Sample a mini-batch of transitions from $D$;

5. Compute the predicted Q-value with $\mathrm{\theta }$ and the target Q-value with ${\mathrm{\theta }}^{-}$;

6. Update parameter $\mathrm{\theta }$ by optimizing the loss function given the target and prediction;

7. Every C steps, reset ${\mathrm{\theta }}^{-}=\mathrm{\theta }$;

8. Repeat steps 2 to 7.

Some intuitions about training tricks in the algorithm are presented as follows:

1. Each transition of experiences is potentially used in many parameter updates, which allows for greater data efficiency. Besides, drawing transitions randomly from $D$ not only breaks correlations between samples but also smooths out the learning and avoids oscillations during training (Mnih et al., 2013).

2. The dynamic $ϵ$-greedy policy (Sutton & Barto, 1998) in Step 2 guarantees an adequate exploration of the state space. The agent takes the optimal action, that is, $a(t)=\arg \underset{a}{\max }Q(\hat{\mathit{s}}(t),a,t;\mathrm{\theta })$, with probability $1-ϵ$ and selects a random action with probability $ϵ$. Starting from a large initialized value, the exploration rate $ϵ$ will gradually decrease as the number of episodes increases and finally guarantees the full utilization of high-payoff actions.

3. Periodically updating ${\mathrm{\theta }}^{-}$ in Step 7 avoids the constant shift of the target Q-value and further mitigates the risk that the network falls into feedback loops between the target and estimated Q-values in the training (Mnih et al., 2015).

Reinforcement learning refers to goal-oriented algorithms and Figure 2 visualizes how it works in a flow chart. The DQN method starts from an initialized Q-value function and improves the policy design according to interactions with the environment, which can handle a relatively large state space.

Figure 2.

The interactions between the agent and environment with the DQN method.

Note. DQN = deep Q-learning; IRT = item response theory.

Learning Scenarios and Experiments

In this section, the authors present a concrete learning system, conduct simulations in different learning scenarios, and explore the effect of learning interest by combining the classification problem in the DQN method. Two recommendation strategies are considered as baselines: one is the random policy that chooses actions uniformly at random from all available actions; another one is the oracle policy ${\pi }^{*}$, where knowledge states can be observed without assessment error and the true learning model is known. Recall that a special terminal reward takes the form as

$$R(T)=\varphi \mathit{w}\prime \mathit{s}(T),$$

where $\varphi$ is the scale parameter and $\mathit{w}\prime \mathit{s}(T)$ is the weighted achievement on all knowledge points, that is, $\sum _{k=1}^K{w}_k{s}_k(T)$, $w_k$ is the weight of the kth knowledge point $s_k$. Therefore, the authors rewrite the reward as

$$R(t)=\{\begin{array}{cc}-1,\hfill & \mathrm{if}\mathrm{taking}\mathrm{learning}\mathrm{actions}{d}_1,d_2,\dots ,d_n\mathrm{at}\mathrm{time}t\hfill \\ \multicolumn{1}{c}{0,}& \mathrm{if}\mathrm{taking}\prime \mathrm{null}\prime \mathrm{or}{a}_s\hfill \\ \multicolumn{1}{c}{\varphi \mathit{w}\prime \mathit{s}(T),}& \mathrm{if}\mathrm{at}\mathrm{the}\mathrm{terminal}\mathrm{time}t=T.\hfill \end{array}$$

Some intuitions about the reward setting are provided in the following:

1. Suppose there indeed exists a final exam at the terminal time and the final grade is a value measuring learners’ proficiency. If the $K$-dimensional weight $\mathit{w}$ represents the importance of knowledge points, then final grade can be expressed by $\mathit{w}\prime \mathit{s}(T)$, which refers to the weighted achievement after the whole learning process.

2. Let $\varphi$ be a scale parameter of the final grade, regarded as a character index, showing the degree of the learner’s desire to achieve better. Imagine a course is very important and the learner views the final grade heavily. It is worth the efforts and thus a large $\varphi$ makes sure that the learner will take enough learning steps to master almost all the knowledge points for a good final grade. In this case, terminal reward $R(T)$ compensated for the cost from learning steps. The scale factor phi can be determined by the learner’s self-evaluation and even set by the instructor in some learning scenarios.

Toy Experiment

The authors first go through a toy example, where the oracle policy is known. Assume that a course consists of three knowledge points $(K=3)$, corresponding to two proficiency levels in the Markov learning model, that is, $\mathit{s}\in \{0,1{\}}^3$, where 0 means nonmastery and otherwise, 1. In addition, the learning of knowledge points is hierarchical as shown in Figure 3. For example, mastering point 1, that is, $s_1=1$, is the prerequisite to learn point 2. So, there are only four possible knowledge states $(0,0,0),(1,0,0),(1,1,0),(1,1,1)$, denoted as ${\mathit{s}}_1,{\mathit{s}}_2,{\mathit{s}}_3$, and ${\mathit{s}}_4$, respectively.

Figure 3.

The hierarchy of knowledge points in the toy example.

Consider three lecture materials $\{d_1,d_2,d_3\}$ related to three points. Then, the transition matrices given learning actions, $d_1,d_2,d_3$, can be represented as

$${\mathit{P}}^{{\mathit{d}}_1}=\left[\begin{array}{cccc}0.3\hfill & 0.7\hfill & 0.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 1.0\hfill & 0.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 1.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 0.0\hfill & 1.0\hfill \end{array}\right],{\mathit{P}}^{{\mathit{d}}_2}=\left[\begin{array}{cccc}1.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.5\hfill & 0.5\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 1.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 0.0\hfill & 1.0\hfill \end{array}\right],{\mathit{P}}^{{\mathit{d}}_3}=\left[\begin{array}{cccc}1.0\hfill & 0.0\hfill & 0.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 1.0\hfill & 0.0\hfill & 0.0\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 0.7\hfill & 0.3\hfill \\ \multicolumn{1}{c}{0.0}& 0.0\hfill & 0.0\hfill & 1.0\hfill \end{array}\right],$$

which are the $4\times 4$ matrices corresponding to four possible knowledge states. The transition matrices indicate transition probabilities by taking actions. For example, if a learner is at ${\mathit{s}}_1=(0,0,0)$ and takes the action $d_1$, he or she has 0.7 chance to master knowledge 1 and transits to next state ${\mathit{s}}_2=(1,0,0)$, that is, ${{\mathit{P}}^{{\mathit{d}}_1}}_{12}=P(\mathit{s}(t+1)={\mathit{s}}_2|\mathit{s}(t)={\mathit{s}}_{\mathit{1}},a(t)=d_1)=0.7$. In addition, there exists an underlying assumption in the transition matrices that once a knowledge point is mastered, there is no retrograde anymore. The weight of knowledge points $\mathit{w}$ in the final exam is set to be $(0.6,0.25,0.15)\prime$; $(0,0,0)$ is set as the initial state and $T=10$ as the terminal time to ensure that the early stopping phenomena can be observed.

Notice that the assessment model is employed to obtain estimator $\hat{s}$ at each step and the estimators were roughly divided into 0 and 1. The items measure the knowledge points that relate to the corresponding learning action. As the learner answers more items (i.e., questions) students do, the assessment model can get more accurate estimates of current states. For the strategies with the IRT model, three experiments denoted as IRT_2, IRT_8, and IRT_64 were conducted, where a total of 2, 8, and 64 items at each step are used to estimate knowledge states. An additional experiment where knowledge states can be observed without assessment error is conducted as well, denoted as NOIRT. The policies in the above four experiments are designed by the DQN method, and a total of six strategies were conducted, where the random policy and oracle policy as baselines are included.

Criteria

To show the power of the DQN method, the random policy serves as a lower benchmark, while the oracle policy is the upper benchmark. The performances of the recommendation strategies are evaluated by total rewards received in the learning processes. Given a scale parameter $\varphi$, the higher total rewards are obtained and the better the strategy is.

Simulation results

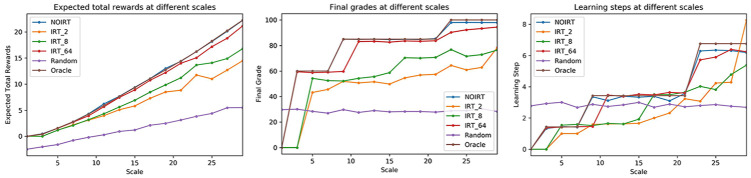
Figure 4 shows the results of the toy example. Considering total rewards, the NOIRT curve with the DQN strategy and the oracle curve almost coincide. The other DQN methods with IRT can still work well with relatively high rewards in the end. Furthermore, the authors have an intuitive conclusion that the model including more items can lead to a better result from comparisons among IRT_2, IRT_8, and IRT_64. For clarity of expression, the final grade $\mathit{w}\prime \mathit{s}(T)$ was rescaled to 100. It shows that the final grade increases along with the increase in scale parameter $\varphi$. When the scale is set to be around 23, the final grade in the oracle, NOIRT, and IRT_64 can all rise up to 90. The right figure presents the number of learning steps at different scales in the experiments, where the scale $\varphi$ explores how early stopping occurs in the learning process. When the scale is relatively small, the learner is suggested to stop in the early stages. Due to the randomness and imprecise assessments in the simulation, the IRT_2 curve takes more steps than expectation and fails to stop early.

Figure 4.

The results of the experiments in the toy example.

Note. IRT = item response theory.

Continuous Case

A more practical learning environment was provided, where the continuous state space is considered. In this case, the proficiency level of each knowledge point is rescaled to be a continuous value in the interval $[0,1]$ by the logistic function.

The learning system consists of 10 knowledge points $(K=10)$ marked by $1,2,\dots ,10$, and the knowledge graph in Figure 5 describes the hierarchical relationships and constraints on learning certain points. The number on each arrow indicates the prerequisite of the proficiency for certain knowledge points. For instance, the number 0.2 on the arrow from 1 to 4 means that the point 4 is assumed to be learned unless the knowledge state of point 1 is less than 0.2. These constraints imposed on the knowledge structure make the learning model close to reality and more complicated. For ease of training, the prerequisites into a function $P(·)$ were summarized and include $P(·)$ in the environment. $P(·)$ maps a knowledge state to a 10-dimensional zero-one vector where one means the learner is qualified to learn that corresponding knowledge point. For example, input the state $\mathit{s}=(0.4,0,0,0,0,0,0,0,0,0)$ and a vector is obtained through $P(\mathbf{s})=(1,0,0,1,0,0,0,0,0,0)$, indicating the proficiency of knowledge point 1 is 0.4 and the learner is able to learn point 4.

Figure 5.

The knowledge graph in the continuous case: the numbers in the circle indicate corresponding knowledge points, while the numbers on the arrow indicate learning prerequisites.

For learning actions, a total of 30 materials, that is, $\{d_1,d_2,\dots ,d_{30}\}$, are generated, of which three materials are associated with one related knowledge point, seven materials with two points, 10 materials with three points, and the rest of materials with all points. As designed in the toy example, items given in the assessment at each step measure the knowledge points related to the corresponding learning action. ${\mathit{W}}_a$ was denoted as the $K$-dimensional weight of all knowledge points for the learning action $a\in \{d_1,d_2,\dots ,d_{30}\}$.

The transition kernel was taken as a density function to reduce the storage space. Assume the learner takes action $a(t)$ at time $t$ and the transition function takes the form

$$\mathit{s}(t+1)=1-(1-\mathit{s}(t))\odot \exp \{-2\xi ·{\mathit{W}}_{a(t)}\odot P(\mathit{s}(t))\},$$ (1)

where ⊙ stands for element-wise multiplication of vectors and $\xi ~{\chi }_m^2$, $m$ is the degree of freedom meaning the extent of learning efficiency. The randomness in the learning model is reflected in $\xi$ and a large $m$ stands for a quick and effective learner. The authors set $m=2$ here, and in the last experiment, they use different $m$ in the transition function to represent different types of learners.

The transition function shows some properties of the learning model. On one hand, the exponential term is always smaller than one, which implies no retrograde in the learning. On the other hand, Equation 1 can be rewritten as

$$\frac{1-\mathit{s}(t+1)}{1-\mathit{s}(t)}=\exp \{-2\xi ·{\mathit{W}}_{a(t)}\odot P(\mathit{s}(t))\}.$$

The above equation shows that at the initial stage, learners always acquire knowledge quickly and knowledge states have a fast increase. On the contrary, it is hard to have a big improvement when the state approaches 1. This phenomenon is a common occurrence in the learning process. It is easy to have a basic understanding for beginners, while doing some in-depth work on that basis is rather hard and effortful. Finally, let the initial knowledge state be $\mathit{s}(0)=(0,0,0,0,0,0,0,0,0,0)\prime$, $\mathit{w}=(0.05,0.1,0.05,0.1,0.1,0.2,0.15,0.1,0.1,0.05)\prime$, and $T=20$.

Criteria

Five simulations in total are conducted to compare with the random policy when the knowledge state space is continuous. Due to the complicated learning model, it is hard to determine the oracle policy at every scale $\varphi$ and the oracle policy is not presented in this part. Instead, the DQN method is compared with the linear approximation marked as Linear, where the Q-value function is approximated by a weighted linear sum of knowledge states (Melo & Ribeiro, 2007). In the linear approximation method, eight items in the IRT model are used to estimate the state at each step. The same three indicators including expected total rewards, the final grade, and learning steps will be given to evaluate the efficiency of strategies.

Simulation results

The results are shown in Figure 6. Clearly, the NOIRT curve without assessment error receives the highest final grade and the smallest number of learning steps. The left graph presents an intuitive performance, showing the more accurate measurement lays a foundation for a better recommendation. In terms of the Linear curve, although it can beat random policy, compared with DQN method, the linear approximation cannot fit Q-value function well when the form of Q-value function is complicated and thus does not have a solid performance. In summary, the DQN method outperforms the random policy and linear approximation method under the above settings, even in the case of IRT_2.

Figure 6.

The results of the experiments in the continuous case.

Note. IRT = item response theory.

Experiment on Missing Data

Generally, the diagnosis and recommendation for a learner in an adaptive learning system have fixed procedures as shown in Figure 7. However, students are likely to skip exercises, thus it cannot be always observed whether their knowledge states have an increment or not. In the case when $\hat{\mathit{s}}(t)$ is missing, an appropriate action should be still recommended. In this part, a simulation study on dealing with incomplete learning data was provided. Here, the continuous state space was considered and the same background setting was used as in the previous experiment.

Figure 7.

The flow chart of general procedures in the adaptive learning system: (1) the knowledge state $\mathit{s}(t)$ is partially observed by responses, estimated as $\hat{\mathit{s}}(t)$ in the assessment model; (2) given $\hat{\mathit{s}}(t)$, action $a(t)$ is recommended following the policy $\pi$; and (3) according to the learning action $a(t)$, the learning model determines the next knowledge state $\mathit{s}(t+1)$.

Note. IRT = item response theory.

With full utilization of current information, the number of missing items was taken as a missing index. Note that the missing index can partially reflect efforts the learner has paid during the unobserved state period. Thus, it can be combined as a personal feature to track the learning model. When the learner skips the questions at time $t$ after taking a learning action, the missing index at $t$ counts 1. If the learner skips the assessment part again at $t+1$, the missing index is added up to 2 and so on. Once the knowledge state can be observed, the missing index will be reset to be 0.

Following above setting, the dimension of input of the network was expanded from $(K+1)$-dimensional to $(K+2)$-dimensional, and then, the input is 12-dimensional. The architecture of the neural network is the same as previous simulations.

Criteria

The expected total rewards of DQN strategies based on varying percents of the missing data against the random policy were compared. Specifically, randomly take $0\%$, $20\%$, $40\%$, $60\%$, and $80\%$ of knowledge states of one learning trajectory to be missing, and the assessment model with 16 items is given in all recommendation strategies.

Simulation results

The results are presented in Figure 8. The left figure shows that compared with the $0\%$ curve (i.e., $\hat{\mathit{s}}$ is known at each step), other missing cases can achieve almost same total rewards at $T$. With increasing missing levels, more learning steps are taken and fewer total rewards are obtained. It reveals that the DQN method properly handles the missing data and extracts efficient learning information from the missing index, although the knowledge state is unobserved.

Figure 8.

The results of the experiments on the missing data.

It is worthy pointing out several exceptions, for example, when scale parameter $\varphi =26$, the expected total rewards of 40% missing case are higher than 20%. This is due to randomness in the simulation. When applying in practice, the authors need enough interactions with environment and train several independent neural networks to get a stable policy.

Experiment on the Effect of Learning Interest

The learning model differs among learners. To make a good recommendation, more individual-specific features added to distinguish types of learners can further improve the policy design. Intuitively, the interest in the subject can be an obvious personal feature of the learner. Therefore, the reinforcement learning and classification problem were combined by adding the interest into the approximation of Q-value function to thoroughly learn the learning model.

Two types of learners were simulated, type 1 and type 2, and they have different transition probabilities for different learning efficiency. For learners of type 1 with low learning efficiency, $\xi$ in Equation 1 follows ${\chi }_1^2$, but ${\chi }_8^2$ for efficient learners of type 2. Notice that the learning model is unknown in applications. The learners’ interest in the subject can be easily tracked by a questionnaire in the learning system. In the simulation, two choices are considered to be given in the questionnaire: “interested” and “uninterested.” Learners interested in the subject are assumed to be from type 1 with probability 0.1, while uninterested learners are from type 1 with probability 0.9. That means the learning interest reflects the learning efficiency of learners, and then, the effect of learning interest to classify the learning model and assist the decision-making simultaneously was introduced.

Similar to the missing data experiment, the authors consider the learner’s interest as an additional dimension in the input which is $12$-dimensional. The architecture of the neural network is the same as previous simulations. Although more specific information is included into training, the approximation of the optimal strategy is computationally feasible and easy to implement with the DQN method.

Criteria

Three recommendation strategies are conducted. For better comparison, the authors apply the DQN method in the model involving the interest feature, denoted as interest, and also in the non-interest model. In addition, the experiment where types of learners are already known is also presented as the upper benchmark, denoted as type_classified. To validate the interest effect, the authors assume that the knowledge states are measured without error in these three simulations.

Simulation results

As shown in Figure 9, the authors’ model involving high learner interest is better than the non-interest case. It demonstrates that the DQN method learns from the interest feature and successfully distinguishes these two types of students to some extent. Because of the flexibility of the network, the DQN method avoids adding high-level terms in the parameterization compared with function approximation methods.

Figure 9.

The results of the experiments with the effect of learning interest.

The effect of learning interest as an example to show the efficiency and feasibility of the DQN method in learning features was elaborated. Of course, one feature is not enough to learn the learning model comprehensively and more personal features can be further considered to make a more precise recommendation.

Discussion

In this article, a DQN recommendation strategy that makes full use of available information under the framework of the adaptive learning system was proposed. The authors introduce three components of the learning system and formulate their problem into a Markov decision problem. Based on the set cost-efficient reward, a feed-forward neural network is used to approximate the Q-value function and a deep Q-learning algorithm is developed to train the optimal policy. The proposed method takes into account several needs in substantive learning scenarios, allowing for early stopping, handling missing data, and learning interest. Four concrete examples were provided in the simulation to show the power of the DQN method.

In the future work, more practical issues need to be considered. As illuminated in the first two simulations, the accuracy in the estimation of knowledge state can affect the quality of the recommendation strategy. Even though the assessment model is not paid much attention here, more individual-specific information can further improve the estimation accuracy. For example, cognitive skills can also be modeled by psychological tests (Brown & Burton, 1978). Combining good designs of learning materials, the recommendation can not only help master knowledge but also strengthen cognitive abilities. Moreover, the proposed method may be further improved by taking a reward setting that better reflects the real learning scenario. For example, the terminal reward may be defined in a different form to measure the feedback of a sequence of actions: for instance, it may directly relates to the learning duration.

The deep Q-learning method in practice needs to collect data and train the optimal strategy simultaneously in the initial stage, where the initial policy may be uncomfortable for learners. Some prior information to build the initial policy can improve the user experience. Moreover, a virtual but reasonable learning model serving as the environment can generate data for further training. As a data-driven approach, it is of interest to explore a more effective structure for the networks to better extract behavior information. For example, the number of layers in the neural network can be scaled up to meet more complicated situations. Besides, the method of policy gradient (Sutton, McAllester, Singh, & Mansour, 1999) may be borrowed, by which a more flexible stochastic policy can be obtained. Finally, theoretical interpretations remain to be studied to prove the feasibility of the deep Q-learning method in the practical large-scale learning environment.