Identification of topological features in renal tumor microenvironment associated with patient survival

Abstract

Motivation

As a highly heterogeneous disease, the progression of tumor is not only achieved by unlimited growth of the tumor cells, but also supported, stimulated, and nurtured by the microenvironment around it. However, traditional qualitative and/or semi-quantitative parameters obtained by pathologist’s visual examination have very limited capability to capture this interaction between tumor and its microenvironment. With the advent of digital pathology, computerized image analysis may provide a better tumor characterization and give new insights into this problem.

Results

We propose a novel bioimage informatics pipeline for automatically characterizing the topological organization of different cell patterns in the tumor microenvironment. We apply this pipeline to the only publicly available large histopathology image dataset for a cohort of 190 patients with papillary renal cell carcinoma obtained from The Cancer Genome Atlas project. Experimental results show that the proposed topological features can successfully stratify early- and middle-stage patients with distinct survival, and show superior performance to traditional clinical features and cellular morphological and intensity features. The proposed features not only provide new insights into the topological organizations of cancers, but also can be integrated with genomic data in future studies to develop new integrative biomarkers.

Availability and implementation

https://github.com/chengjun583/KIRP-topological-features

Supplementary information

Supplementary data are available atBioinformatics online.

1 Introduction

Cancers are highly heterogeneous diseases. Even for a specific type of cancer, there are often different subtypes conferring different clinical outcomes including different prognoses (i.e. survival times) and responses to treatments. For instance, according to the International Union Against Cancer and the American Joint Committee on Cancer, renal cell carcinoma (RCC, also called kidney cancer) histologic subtypes are categorized as clear cell, papillary, chromophobe, collecting duct and unclassified RCC types based on the Heidelberg classification system (Kovacset al., 1997), and some types of RCC also have its own subtypes. Previous studies on many cancers have suggested that stratification by histologic subtype could provide prognostic value (Patardet al., 2005). Stratifying cancer patients into different subtypes with more accurate prediction of the clinical outcome will greatly enhance precision medicine practices. For example, patients with worse prognosis may benefit from closer follow-up, more aggressive treatment, and advance care planning.

Currently, despite fast advances in genome medicine, patient stratification is still often carried out by pathologists by reviewing histopathology slides under a light microscopy. However, such review is often subjective, and both intra- and inter-operator variations are large, frequently leading to discrepancies in diagnosis and subtyping results and sometimes even misdiagnosis. Thus there is an urgent need for developing effective computer vision based algorithms and workflows to extract quantitative features that can effectively stratify patients with distinct prognosis.

1.1 Scope of study

In this study, we focus on the second most common subtype of kidney cancer called papillary renal cell carcinoma (pRCC), accounting for 11% to 15% of all cases (Hansel, 2010). pRCC is a less well understood cancer, and currently there are no effective morphological markers for pRCC that pathologists can use to effectively predict prognosis. We aim to improve the prognostic prediction of pRCC through objective features derived from histopathology images. Despite the specific application, our workflow is a general one focusing on an important aspect of the development of all solid tumors—the interaction between tumor and its surrounding stroma.

With the development of cancer biology, scientists and clinicians have gained deep insights into the importance of the tumor microenvironment. As a highly heterogeneous organ-like structure, the development of tumor is not only achieved by unlimited growth of the tumor cells, but also supported, stimulated, and nurtured by the microenvironment around it (Pietras and Östman, 2010;Trimboliet al., 2009). The tumor microenvironment includes fibroblasts with large amount of extracellular matrices, blood vessels with endothelial cells, and various immune cells such as macrophages, T-cells, and B-cells, which form the stroma. In fact, the amount of stroma, its organization, gene expression profiles, and interaction with the tumor cells are sometimes more effective predictors for clinical outcomes than the tumor cells alone. For instance,Yuanet al. (2012) found that spatial distribution of stromal cells is critical for predicting patient survival in ER-breast cancers whileBecket al. (2011) found that most of the quantitative histopathological features predicting general breast cancer survival are stromal features.

1.2 Related work

Commonly used clinical and pathological factors include patient age, gender, tumor multifocality, stage, grade, cancer specific subtyping and so on.Patardet al. (2005) conducted a retrospective study in a large cohort which contains 4063 patients from eight international centers. They concluded that the stratification in three main renal cell carcinoma histologic subtypes (clear cell, papillary, and chromophobe carcinoma) should not be considered as a major prognostic variable comparable to TNM stage, Furman grade, and eastern cooperative oncology group performance status. pRCC is usually classified into two subtypes based on specific histologic features, consisting of type 1 (or basophilic) and type 2 (or eosinophilic) (Sukovet al., 2012). Although some pRCCs can be easily split into two subtypes, pRCC is usually heterogeneous and can show both type 1 and type 2 features. For this reason, the prognostic value of pRCC type varies between studies. For example, several studies show type 2 pRCC has a significantly worse prognosis than type 1(Mochet al., 2000;Pignotet al., 2007). However, the prognostic utility of subtyping pRCC remains controversial.Kuet al. (2009) compared pRCC type 1 and type 2 in a small group of 70 patients, and did not observe a statistically significant difference in survival times. Gonteroet al. (2008) confirmed that finding.

With the recent availability of digital whole-slide images, we can perform systematic analysis of the diverse structures present in histopathology images and may find previously unrecognized image features that correlate with patient prognosis, while reducing the inconsistence arising from subjective interpretation. Quantitative analysis of biomedical images has been an area gaining increasing interest. Plenty of methods have been proposed for tasks like object detection and segmentation (nuclei, mitosis, and glands) (Albarqouniet al., 2016;Xuet al., 2014), benign/malignant image classification (Zhanget al., 2015a), and discovery of prognostic factors (Becket al., 2011;Chenet al., 2015;Vetaet al., 2012;Yuanet al., 2012). For prognostic factor discovery, most studies focus on tumor morphology; however, we provide an effective workflow taking into account not only cell morphology but also the spatial arrangement of different cell patterns, with demonstrated advantages over existing subtyping or cell-based features in pRCC.

1.3 Technical challenges and overview of our contribution

One big challenge for computerized histopathological image analysis is that each type of cancer, given the specific anatomical origin, will often have specific structures, calling for specific features. This is also reflected in the fact that pathologists are highly diversified in their expertise usually with focus on one or a couple of types of cancers instead of all cancers. From the computing point of view, it means that researchers need to strike a balance between general workflows and specific quantitative features tailored for specific cancers.

In this paper, we aim at developing a bioimage informatics workflow to quantitatively characterize the interaction between different types of cells in the cancer tissue and examine if such interactions are associated with the outcomes of patients. The tumor microenvironment is a complex milieu, which includes not only the tumor cells but also the stromal cells, immune cells, and even normal, healthy cells. Biopsy tissue staining by such as hematoxylin and eosin (H&E), can provide a spatial layout of heterogeneous tumor cellularity. Our contributions include: (i) an integrative pipeline to automatically learn different cell types and (ii) novel topological features characterizing the topological organization of different cell types including both tumor and stroma. This pipeline is universal for other solid tumors, and our application on pRCC will have a high impact on clinical practice.

2 Materials and methods

2.1 Dataset

The dataset used in the experiments was downloaded (at May 4, 2016) from The Cancer Genome Atlas (TCGA) portal (project TCGA-KIRP). It consists of 190 patients with H&E stained whole slide images (WSI) as well as corresponding clinical information (patients with survival times <1 month have been excluded from the study). The typical resolution of a WSI is about 100 K by 90 K pixels. Due to the limited computational resource and the artifacts present in the image, in each WSI, 2–8 regions of interest (ROI) of size 3 K by 3 K are extracted, resulting in 856 ROIs in total. Regions having too much blood or artifacts are avoided. The patient demographics and tumor characteristics of our dataset are summarized inTable 1. Note that the stage and subtype information of some patients is not available. In addition, since the prognosis prediction is more important for relatively early-stage patients, we focus our study on the patients with stages I, II and III and exclude the patients with stage IV (the latest stage).

Table 1.

Patient demographics and tumor characteristics

Characteristics	Summary
Patient no.	190
Age (year)
Median	60.5
Range	28–85
Gender
Female	51
Male	139
Follow-up (month)
Median	16.3
Range	1–185.3
Number of Death	27
Subtype
Type 1	46
Type 2	60
Not available	84
TNM stage
I	110
II	10
III	39
IV	12
Not available	19

2.2 Overview of the workflow

Figure 1 shows the overview of our workflow to extract topological features, which consists of two modules. The first module (Fig. 1A) shows the process for learning nucleus patterns from the imaging dataset. The second one (Fig. 1B) demonstrates how to generate topological features (bag of edge histogram features) for an image using the learned nucleus patterns and Delaunay triangulation. In the following subsections we provide details of our workflow.

Fig. 1.

Overview of our workflow. (A) Learning nucleus patterns in an unsupervised manner. (B) Generating bag of edge histogram features and identifying survival-related edge patterns (Color version of this figure is available atBioinformatics online.)

2.3 Nucleus segmentation and patch extraction

For nucleus segmentation, we employ a recently proposed approach by Phouladyet al. (Phouladyet al., 2016), which is an unsupervised segmentation method for cell nuclei in histopathology images. More specifically, following an initial preprocessing step involving color deconvolution and image reconstruction, the segmentation step consists of multilevel thresholding and a series of morphological operations. Unlike the methods in (Al-Kofahiet al., 2010;Wienertet al., 2012), which require many parameters, this method requires no parameter learning or training data because the parameters are set adaptively, making the approach insensitive to variations in staining intensity and appealing to our applications.

After nucleus segmentation, we need to extract nucleus patches centered at the centroids of nuclei to train anautoencoder. In order to choose an appropriate patch size that can frame most nuclei and is not too large, for each nucleus we compute the size of the smallest square bounding box that exactly covers it. The patch size in our experiments is set to the 90th percentile of all the sizes, which is 41 by 41 pixels.

2.4 Nucleus subtyping using stacked sparse autoencoder

Since there are a large number of cell types in the tumor microenvironment each calling for a different set of features for its recognition, it is difficult to design a repertoire of algorithms for this classification. Instead we take an unsupervised approach to categorize the cells based on their morphology without explicitly labeling their histological types using a stacked sparse autoencoder (SSAE) (Fig. 1A). A SSAE is a neural network that consists of multiple layers of sparse autoencoder (SAE) in which the outputs of each layer are wired to the inputs of each successive layer. In a recent work on cell nucleus detection (Xuet al., 2016), SSAE is utilized to learn high-level features from just pixel intensities of small patches. A slide window is applied to each image in order to represent image patches via high-level features obtained from SSAE. The features are subsequently fed into a classifier to determine whether an image patch contains nucleus. However in this paper, instead of putting the learned features into a classifier, we put them into the K-means clustering algorithm to learn K distinct nucleus patterns.

Similar to Xu’s work (Xuet al., 2014), we also employ two SAE layers to form the SSAE whose architecture is shown inFigure 1A. The SSAE is trained by a greedy layer-wise approach, i.e. training each layer in turn. First, we train a SAE on the training nucleus patches$x_k$. Next, we feed all the training nucleus patches into the first trained SAE, obtaining the primary features$h_k^1$ for each$x_k$. We then use$h_k^1$ as input to another SAE to learn secondary features$h_k^2$. After that, we perform K-means algorithm on$h_k^2$ to generateK nucleus patterns.

We randomly choose 50 000 nucleus patches to train the SSAE. The input to the first SAE layer is the vector of pixel intensities corresponding to the nucleus patch, which is 41 × 41 × 3 dimensional. The number of units of the first and second SAE is set to 400 and 200, respectively.

2.5 Topological features based on Delaunay triangulation

For each image, we obtain the label of every nucleus therein by the following steps: nucleus segmentation, nucleus patch extraction, feeding them into the learned SSAE to generate high-level features, and quantizing these features to one of theK clusters. Given an imageI consisting of its nuclei$O(I)=\left\{o_i\right\}$, we construct a graph$G=\{V,E\}$ on the nuclei's centroids using Delaunay triangulation, where vertex setV includes every nucleus$o_i\in O(I)$, and edge setE contains triangle edges$edge(o_m,o_n)$. Edges are labeled with regard to their end nodes, regardless of their order.

Then, we characterize the image by the histogram of edge types, which we callbag of edge histogram (BOEH for short) (Fig. 1B). If there areK nucleus patterns, the dimensionality of BOEH would be$K\times (K-1)/2+K$. The first term is the number of combinations when two nuclei come from different types, and the second term is the number of combinations when two nuclei are of the same type. Note that each patient has multiple images and the BOEH representations of these images for each patient are summed and then L1-nomalized.

The BOEH representations encode the neighborhood information between adjacent nuclei.Figure 1B shows a schematic diagram of constructing a Delaunay graph on eight nuclei. For the sake of simplicity, there are only three types of nuclei and therefore six edge types. Triangle edge types are indicated with different colors.

2.6 Morphological and intensity features

In addition to the proposed BOEH representations, we also implement some morphological and intensity features (Yanget al., 2011) for comparison. Ten cell-level features are computed for each segmented nucleus: nuclear area, lengths of major and minor axes of cell nucleus and their ratio, mean pixel values of nucleus in RGB three channels, respectively, as well as mean, maximum and minimum neighbor distances of cell nuclei in Delaunay triangulation graph. Afterwards, for each type of cell-level features extracted from a patient, five statistical distribution parameters, including mean value, standard deviation, skewness, kurtosis and entropy, are calculated to characterize the distribution of cell-level features. Consequently, a total of 50 patient-level features are extracted to describe each patient. Skewness is a measure of the asymmetry of the data around the sample mean. Kurtosis is a measure of how outlier-prone a distribution is. And entropy is a statistical measure of randomness.

2.7 Machine-learning methods for prognosis prediction

A lasso-regularized Cox regression model (lasso-Cox model) is built on image features to predict the risk indices of patients and divide them into a low-risk or high-risk group (R package ‘glmnet’). To validate our method, Leave-one-out cross validation (CV) strategy is used due to relatively small sample size and low death rate (Table 1). More specifically, in each round of the leave-one-out CV process, a single patient is left out as test set with the rest as training set. In the training set, to reduce high dimensionality of BOEH features, we first perform univariate Cox regression to select features strongly related to survival by dichotomizing patients using median feature value and calculating the hazard ratio between the two groups. Features with hazard ratios >4 or <0.25 are selected. Next, principle component analysis (PCA) is used to reduce noise and decorrelate these features, and Cox regression model is trained using the top two principle components. To predict the risk index of the held-out patient, we select survival-related features based on the feature selection results in the training set, apply the PCA projection matrix learned from training set to the test data, and put the reduced features to the learned Cox regression model. Note that only the training set is used for feature selection and PCA while the test sample is excluded from training. After n rounds, each patient is assigned a predicted risk index. Finally, patients are divided into two groups (low-risk versus high risk) using the median risk index as cut-off point, and log-rank test is used to test if there are distinct survival outcomes between the two groups.

In addition, we conduct receiver-operator characteristics (ROC) curve analysis for binary outcome of 5-year survival to determine the prognosis prediction capability for tumor stage, tumor subtype and the predicted risk index of Cox regression model by using nearest neighbor estimation method (Heagerty and Zheng, 2005;Heagertyet al., 2000).

3 Results

3.1 Nucleus segmentation, subtyping and BOEH representations

For evaluating nucleus segmentation algorithm, we manually count the true number of nuclei, the number of nuclei identified by the segmentation algorithm, and the number of false positives in eight image patches of size 1500 × 1500 pixels; the three numbers are 4082, 4159 and 168, respectively. The recall is (4159 − 168)/4082 = 97.77%, and precision is (4159 − 168)/4159 = 95.96%. Thus this nucleus segmentation algorithm performs well enough for the subsequent steps in our pipeline. Examples of segmentation results are shown inSupplementary Figure S1.

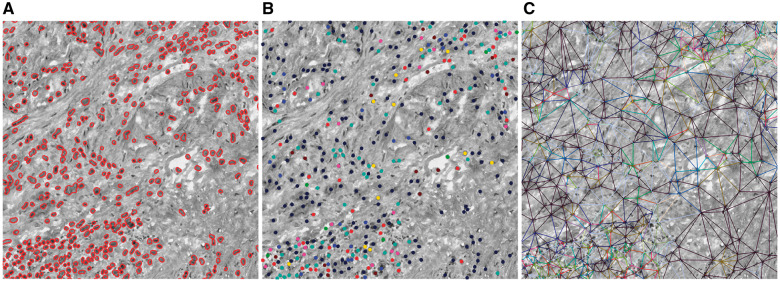
Using a ROI as an example,Figure 2 shows the results of several steps involved in our computer-aided image analysis pipeline, including nucleus segmentation, nucleus subtyping by K-means clustering algorithm on the high-level features learned by SSAE, Delaunay triangulation on nucleus centroids, and construction of bag of edge histogram features. In this figure, we set the number of clusters to 8 in K-means algorithm, so we will have 8 distinct nucleus patterns and therefore 8 × (8 − 1)/2 + 8 = 36 edge types. We can see clearly that the proposed feature representations can capture the interaction between nuclei and their neighbors, which may provide useful information about patient prognosis.

Fig. 2.

Illustration of the three main steps involved in our feature extraction workflow. (A) Nucleus segmentation. (B) Nucleus pattern learning using stacked sparse autoencoder to learn high-level features followed by clustering. Nucleus patterns are indicated by different colors. There are eight nucleus patterns. (C) Delaunay triangle edge patterns showed in different colors. Edge patterns are defined in terms of their end nodes. There are 36 edge patterns since we have eight nucleus patterns. The H&E image is converted to a grayscale image to highlight colors (Color version of this figure is available atBioinformatics online.)

3.2 Prognostic values of BOEH representations

Since prognosis prediction for patients with terminal cancer is not crucial, instead we focus on survival analysis for relatively early to middle-stage (I, II, and III) patients, and patients with stage IV are excluded. By setting a large number of nucleus patterns, we can characterize nuclei more distinctively and discover the potential topological arrangements of nuclei that are related to patient prognosis. Several values of the number of nucleus patterns are tried, 8, 16, 32 and 64, which corresponds to 36, 136, 528 and 2080 dimensional BOEH representations (see Section 2.5). To conduct univariate survival analysis, patients are divided into two groups using the median of each feature. Results from log-rank test on each feature reveal that 1 out of 36, 1 out of 136, 16 out of 528 and 51 out of 2080 are significantly associated with patient survival. Besides, we also conduct univariate survival analysis on the 50 morphological features and two pathological variables, i.e. TNM stage and pRCC subtypes. We merge stage II and III into one group and compare it with stage I. Among the 50 morphological features, two features are identified to be related to survival.Table 2 shows theP values of log-rank test for the pathological and image features. Due to limited space, only the two significant morphological features are listed, and only the top five significant BOEH features with the smallestP values are listed. For extracting the BOEH features inTable 2, the number of nucleus patterns is set to 64.

Table 2.

Univariate survival analysis results using log-rank test

Feature	P value
TNM stage (I versus II, III)	0.073
Subtype (type 1 versus type 2)	0.009
Skewness of length of major axis	0.044
Kurtosis of length of minor axis	0.034
Edge(14, 58)	0.005
Edge(58, 62)	0.007
Edge(16, 56)	0.008
Edge(21, 58)	0.009
Edge(15, 23)	0.010

Note: For morphological and intensity features only the significant features are listed, and for the proposed BOEH features only the top five features with smallestP values are listed. The number of nucleus patterns is set to 64. Edge (14, 58) means the edge type with the 14th and 58th nucleus patterns as its end nodes, and the other pairs are listed in the same fashion.

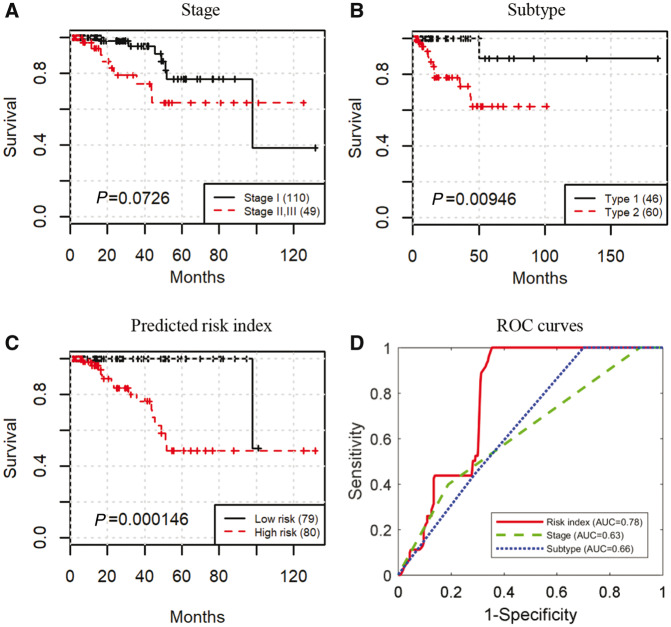
Figure 3A–C shows the Kaplan–Meier survival curves stratified by stage, subtype, and lasso-Cox on BOEH features, respectively. Early stage trends with better survival (log-rank testP = 0.0726,Fig. 3A). Patients with pRCC type 2 have worse prognosis than those with pRCC type 1 (log-rank testP = 0.00946,Fig. 3B), which is consistent with the conclusion by Pignot (Pignotet al., 2007). Patient stratification by the predicted risk inedx provides the best prognosis prediction (log-rank testP = 1.46e-4,Fig. 3C; see Section 2.7 for details of model training and classification). In addition, area under the curve (AUC) of ROC that predicts the binary outcome of 5-year survival for the stage and subtype is 0.63 and 0.66, respectively. The predicted risk index achieves an AUC of 0.78 (Fig. 3D; see Section 2.7 for the methods used to plot ROC curves). Therefore, the proposed BOEH features have a better predictive capability than stage or subtype.

Fig. 3.

The proposed BOEH features provide better prognosis prediction than clinical variables. (A–C) Kaplan–Meier curves stratified by tumor stage, tumor subtype, and predicted risk index of lasso-Cox model built on BOEH features, respectively. (D) ROC curves that predict the binary outcome of 5-year survival using predicted risk index of lasso-Cox model built on BOEH features, tumor stage, and tumor subtype, respectively. For extracting BOEH features, the number of nucleus patterns is set to 64 (Color version of this figure is available atBioinformatics online.)

Figure 4 shows some nucleus patch patterns that form the edge types that are strongly associated with survival, identified by univariate survival analysis (Table 2). Although these nucleus clusters contain mostly tumor cells with diverse texture, there exist different levels of stromal deposition around the nucleus clusters (e.g. 1, 58, and 56). The clusters 16 and 14 also show strong interactions between tumor cells and lymphocytes (as shown inSupplementary Fig. S2). Therefore these four pairs of clusters with most significant difference between patient survival times are involved in tumor heterogeneity, implying the importance of stroma-tumor-lymphocyte interaction which is consistent with previous findings (Becket al., 2011;Loiet al., 2013;Yuanet al., 2012) that stromal tissue and tumor-infiltrating lymphocytes also play an important role in predicting survival times.

Fig. 4.

Examples of the learned nucleus patterns forming edge types that are strongly associated with survival. The number of nucleus clusters is set to 64. The number in the upper-left corner of each image is the cluster index. Each image consists of 10 × 10 nucleus patches from the same cluster (Color version of this figure is available atBioinformatics online.)

4 Discussion

Nuclei in histopathology images play a very important role in cancer diagnosis and prognosis prediction. Many studies have been focusing on nuclear morphological features. However, in this study we present a workflow to automatically extract image features which considers both nucleus morphology and topology of the distribution of different types of nuclei. Based on these features, we find that the co-occurrences of some nucleus patterns are potential biomarkers for pRCC with stronger prognostic power than clinical staging or existing subtyping in the TCGA-KIRP dataset. The interaction among different tumor cells, stromal cells and lymphocytes is known to play a major role in cancer growth and progression. Our method provides a way of quantitatively characterizing this interaction, and our results suggest that some connecting edges between tumor cells and stromal cells are related to patient survival.

Many previous studies for discovering prognostic image features require laborious labeling by skilled pathologist, such as labeling various cell types (Yuanet al., 2012) and classifying tissues into epithelium or stoma (Becket al., 2011;Wanget al., 2013). In contrast, our approach is fully automated, which can learn potential nucleus patterns via an unsupervised feature learning algorithm (i.e. stacked sparse autoencoder) followed by clustering. Although the learnt nucleus patterns may not explicitly correspond to known cell types such as cancer cells, stromal cells or lymphocytes, due to this flexibility it enables us to thoroughly investigate nucleus morphology and their spatial arrangement which are proved by our experiments to be related to clinical outcomes.

Our study has several limitations. First, although cross validation is used to validate our method, the proposed topological features need to be tested on other validation cohorts to fully validate its generalizability. This is an ongoing effort as we are collecting pRCC samples from multiple sites. Secondly, a common practice in survival analysis is to first conduct univariate survival analysis to identify significant variables and then to carry out multivariate survival analysis on these variables using Cox regression to determine independently significant variables. However, in order for results of the multivariate Cox regression to be reliable, there must be at least 10 events (deaths) for each investigated variable (Peduzziet al., 1995). Due to the relatively few events in our dataset (16 in 159), we do not do testing for independence of features. Lastly, since the nucleus patterns are learnt directly from the images by the SSAE, they need to be further interpreted by pathologists.

Future work of research includes automated detection of artifacts in histopathological images and application of our method to other cancers and tasks. Currently regions of interest are manually selected in our study, which is infeasible for very large dataset. Automated detection of artifacts can make our pipeline fully automated and therefore applicable to large clinical trials. The proposed features are the histogram of co-occurrence of nucleus patterns, so in order for the features to be robust it is important that the features are summarized over a much larger area of the tumor. Although our study focuses on predicting prognosis in patients with pRCC, our flexible workflow is not specific to this application and can be applied to other cancer types or even diseases other than cancers. In addition, we plan to investigate how the proposed bag of edge histogram representations perform in other applications in digital pathology and bioimage informatics such as the problem of histopathology image classification and retrieval (Zhanget al., 2015a,2015b). Furthermore, these features not only provide new insights into the topological organization of cancers, but also can be integrated with genomic data in future studies to develop new integrative biomarkers and to generate new insights regarding the genomic basis for tissue morphology and organization.