Inferring leading interactions in the p53/Mdm2/Mdmx circuit through live-cell imaging and modeling

Summary

The tumor suppressive transcription factor p53 is a master regulator of stress responses. In non-stressed conditions, p53 is maintained at low levels by the ubiquitin ligase Mdm2 and its binding partner Mdmx. Mdmx depletion leads to a biphasic p53 response, with an initial post-mitotic pulse followed by oscillations. The mechanism underlying this dynamical behavior is unknown. Two different roles for Mdmx have been proposed: enhancing p53 ubiquitination by Mdm2, and inhibiting p53 activity. Here, we developed a mathematical model of the p53/Mdm2/Mdmx network to investigate which Mdmx functions quantitatively affect specific features of p53 dynamics under various conditions. We found that enhancement of Mdm2 activity was the most critical role of Mdmx under unstressed condition. The model also accurately predicted p53 dynamics in Mdmx-depleted cells following DNA damage. This work outlines a strategy for rapidly testing possible network interactions to reveal those most impactful in regulating the dynamics of key proteins.

Introduction

Decades of research in molecular biology and biochemistry has led to the identification of the key molecular players that sense and transfer cellular information, and to the assembly of complicated networks describ-ing the interactions between them. Such biological maps often include interactions collected from a large number of studies performed across different conditions, cell lines, or organisms. In addition, these maps are often built based on information collected at a single or small number of time points, providing only static descriptions of network behavior. It is now becoming clear that the dynamical properties of a system—i. e. changes in the levels of components or their interactions with each other over time—are also critical for directing biological outcomes. The specific interactions that are functional and dominate the response in each situation, as well as the role of these interactions in triggering the appropriate outcome, often remain elusive. Mathematical modeling of network behavior is an effective approach for identifying and quantifying functional interactions in a network based on the dynamics of key network proteins (Cirit et al., 2010; Geva-Zatorsky et al., 2006; Hao and O’Shea, 2012; John J Tyson and Novak, 2003; Ronen et al., 2002; Tay et al., 2010). Such insights are crucial for better understanding the underlying causes of disease and for developing therapeutics that quantitatively target protein dynamics (Behar et al., 2013).

The tumor suppressor p53 is highly regulated by a complex network of interactions whose dominant features vary according to cellular stresses, cell types, and species (Stewart-Ornstein and Lahav, 2017). The core of the p53 circuit includes a negative feedback loop between p53 and Mdm2 (Wu et al., 1993) (Figure 1A), an E3 ubiquitin ligase that leads to p53 degradation and is itself transcriptionally activated by p53 (Fuchs et al., 1998; Haupt et al., 1997; Honda et al., 1997; Kubbutat et al., 1997). The oncogene Mdmx modulates this loop (Barboza et al., 2008; ElSawy et al., 2013; Karni-Schmidt et al., 2016) by both stimulating Mdm2-mediated degradation of p53 (Gu et al., 2002; Wang et al., 2011) (Figure 1A, blue arm) and by directly inhibiting p53 function by binding to the transactivation domain (Pei et al., 2012) (Figure 1A, orange arm).

Figure 1: Quantitative features of p53 dynamics after Mdmx depletion.

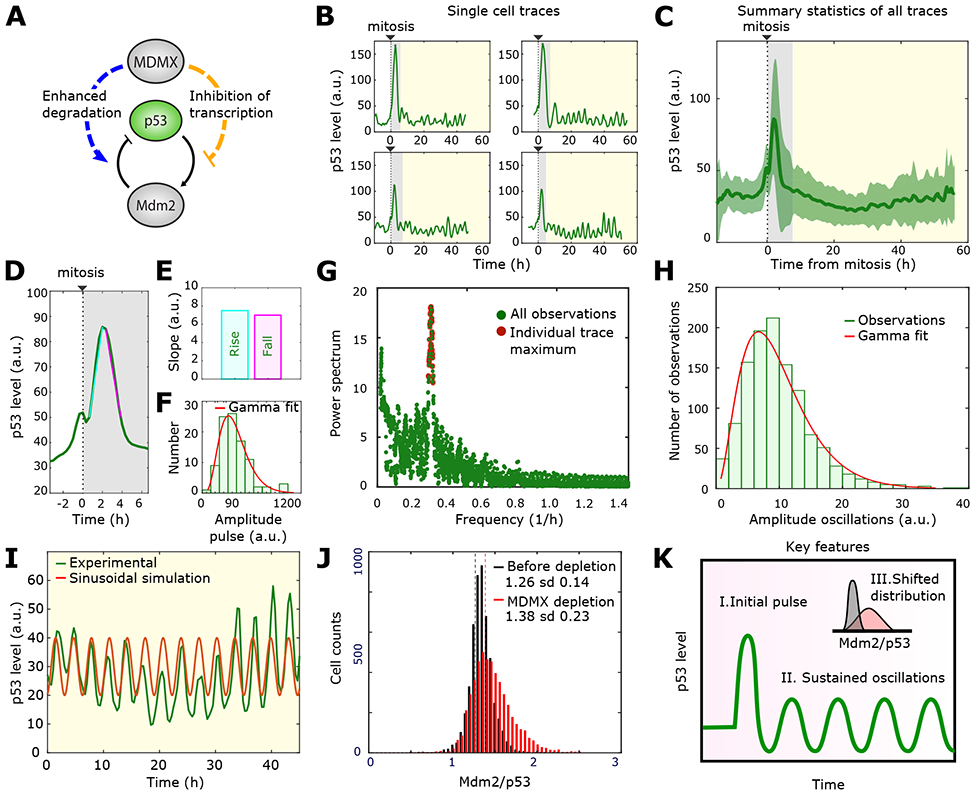
A) Schematic diagram of the Mdm2-Mdmx -p53 network. Mdmx inhibits the p53-Mdm2 oscillator through two arms: degradation of p53 through catalyzing Mdm2-mediated ubiquitination (blue left arm) and inhibition of p53 transcriptional activity (orange right arm).

B) Four representative single-cell time series of p53 dynamics following Mdmx depletion. The grey region indicates the initial pulse and the yellow region highlights the sustained oscillations.

C) p53 population dynamics obtained by averaging individual cell traces over time. Green bold line and green shaded areas correspond to mean and standard deviation respectively. Individual p53 traces were aligned based on the time of cell division (n= 96 traces).

D) Mean value of the initial peak of p53 expression following Mdmx depletion. Cyan and pink lines were used to calculate the rise and fall slopes of panel E.

E) Increasing (Rise) and decreasing (Fall) slopes of the initial p53 pulse shownn in D.

F) Histogram showing the distribution of amplitudes of the initial p53 pulse. Fitted gamma distribution in red.

G) Fourier spectrum of the sustained oscillations. The red dots mark the highest Fourier signal for each individual cell.

H) Histogram showing the distribution of amplitudes of the oscillatory phase.

I) Comparison of a single cell oscillatory expression (green) to a modelled sinusoidal oscillation (red) with amplitude and frequency corresponding to the most probable values of the Fourier spectrum in Figure 1G.

J) Distribution of the Mdm2/p53 ratio before (black) and after (red) Mdmx depletion based on the immunofluorescent staining of Mdm2 and p53 in single cells. Vertical lines show the corresponding mean values. Sd: standard deviation.

K) Characteristic features of p53 dynamics following Mdmx depletion. A large initial pulse (I) is followed by sustained oscillations (II). Mdmx depletion also causes a shift in the Mdm2/p53 ratio (III).

Many cancers overexpress Mdmx, resulting in downregulation of p53 and an inability to trigger cell cycle arrest or cell death programs in response to DNA-damaging chemotherapeutics. A promising therapeutic approach for these cancers is to elevate p53 levels by inhibiting Mdmx. We have previously shown that suppression of Mdmx alters p53 dynamics and alters cellular outcomes when combined with DNA damage. In unstressed cells, depletion of Mdmx triggers complicated two-phase dynamics of p53 in single cells (Chen et al., 2016): in the first phase, p53 undergoes a pulse of expression following cell division. In the second phase, p53 shows a series of undamped oscillations. When combined with DNA damage, Mdmx suppression led to unique cellular outcomes depending on when the damage occurred: DNA damage during the first phase promoted apoptotic gene expression programs, whereas DNA damage during the second phase promoted cell cycle arrest and suppressed apoptosis (Chen et al., 2016).The molecular mechanisms leading to the biphasic response in unstressed cells, and specifically which functions of Mdmx dominate the response in unstressed conditions or after DNA damage, are unknown.

Previous molecular mechanisms and mathematical models have been suggested for p53 oscillations following DNA damage (Batchelor et al., 2008, 2011; Geva-Zatorsky et al., 2006; Lahav et al., 2004; Mönke et al., 2017; Purvis et al., 2012). However, they did not incorporate Mdmx-mediated regulation of p53 and Mdm2. Therefore the relative quantitative contributions of the interactions between p53/ Mdm2 and Mdmx (Figure 1A) in controlling p53 dynamics in non-stressed and after DNA damage remain unknown. Classical genetic and chemical perturbation studies are unsuitable for deconvolving the functions of Mdmx, since they often affect multiple interactions within the network. Here, to circumvent the limitations of genetic and pharmacological perturbations, we dissected two independent contributions of Mdmx to p53 behavior mathemati-cally, then tested specific predictions of our mathematical models in cells and identified the regulatory mechanisms that shape specific features of p53 dynamics under various conditions.

Results

I. Identifying quantitative features of p53 dynamics and activity following Mdmx depletion

To elucidate the molecular functions of Mdmx in the p53 network and mimic therapy protocols aiming to inhibit Mdmx, we compared the dynamics of p53 in unstressed control cells and cells depleted of Mdmx, which was efficiently reduced by siRNA (Chen et al., 2016). The dynamics of p53 in response to Mdmx depletion in single cells occurs in two phases, with a high-amplitude pulse after mitosis (Figure 1B, grey region) followed by a series of low amplitude oscillations (Figure 1B, yellow region) (Chen et al., 2016). Note that these dynamics were observed in both cancerous (MCF7) and non-cancerous (RPE1) human cell lines (Chen et al., 2016). Our first goal was to identify specific quantitative features of these dynamics in order to guide the mathematical analysis.

We first characterized p53 dynamics during the initial response of the system (Figure 1B, grey region). Because this first phase is triggered after mitosis (Chen et al., 2016), we performed an in silico alignment of all individual single-cell p53 traces to the time of cell division. The average population trace (Figure 1C, green trace) showed a strong post-mitotic pulse, while the low-amplitude oscillations were masked by the mean value. Note that the small peak preceding mitosis is due to an increase in auto-fluorescence seen in all chan-nels. From this in silico alignment we found the average initial pulse (Figure 1D) to be symmetric, i.e. showing identical increasing and decreasing slopes (Figure 1E) and with a maximal amplitude approximately three times larger than the basal level prior to Mdmx depletion (Figure 1D). Further, we found that the distribution of amplitudes across individual cell traces could be well described by fitting it to a gamma distribution (Figure 1F).

We next characterized p53 dynamics during the second phase of the response, when it exhibits oscillations (Figure 1B, yellow region). Using Fourier analysis, we decomposed each individual cell trace into a sum of sine waves of different frequencies. For every cell, we obtained a Fourier spectrum in which the absolute value of the power spectrum (y-axis Figure 1G) represents the contribution of a given frequency present in the original p53 oscillatory signal (x-axis Figure 1G). A sharp maximum of all power spectrums confirmed that p53 oscillations are well defined and regular, having a frequency of approximately 0.3/hour (Figure 1G).

In order to measure the amplitude of oscillations, we used an independent algorithm that estimated the oscillatory amplitude as the distance from each peak to the two neighboring valleys. From these single-cell measurements, we plotted the distribution of amplitudes during the oscillatory phase, which was also well described by a gamma distribution (Figure 1H). Using the most probable amplitude and frequency defined from these algorithms, we showed that a sinusoidal function with these parameters agreed well with the experimentally observed oscillations in single-cells (Figure 1I), showing the regularity of p53 oscillations. Note that the amplitude of the experimentally-observed oscillations showed a greater variation than did the frequency, which was relatively stable, as was previously reported for p53 oscillations following DNA damage (Geva-Zatorsky et al., 2006; Reyes et al., 2018).

In order to quantitatively determine the effect of Mdmx on P53’s transcriptional activity (Figure 1A, orange arm), we compared the ratio of Mdm2 to p53 in individual cells before and after Mdmx depletion using immunofluorescence (Figure 1J). We found that depletion of Mdmx shifts the mean of the distribution to a higher value, meaning that more Mdm2 proteins are produced per p53 protein when Mdmx is depleted. This finding agrees with previous studies suggesting that Mdmx suppresses p53 transcriptional activity (Figure 1A, orange arm) (ElSawy et al., 2013; Pei et al., 2012). Based on these sets of observations and measurements, we identified three key quantitative features of p53 dynamics and activity following Mdmx depletion: (I) an initial high amplitude symmetric pulse; (II) sustained low-amplitude oscillations; (III) a shift in the distribution of the Mdm2/p53 ratio (Figure 1K). Next, we used these quantitative features to guide us in developing a mathematical model for capturing p53 and Mdm2 regulation by Mdmx.

II. Mathematical model points to the specific functional interactions regulating p53 dynamics by Mdmx in non-stressed conditions.

In order to asses the effect of Mdmx on the core p53-Mdm2 network, we developed a minimal model of the P53-Mdm2 feedback-loop using two ordinary differential equations, which represent a negative feedback loop determined in previous studies (Geva-Zatorsky et al., 2006; Tiana et al., 2002) where one transcription factor (p53) enhances the productions of its own negative regulator (Mdm2):

$$\begin{gathered} \frac{d}{dt}[p53]=\alpha -\beta [Mdm2]\frac{[p53]}{\gamma +[p53]} \\ \frac{d}{dt}[Mdm2]=\psi [p53(t-T_{Del})]-\delta [Mdm2] \end{gathered}$$

In this model, p53 is produced at a constant rate (α) and degraded upon binding to Mdm2 through a saturated degradation process (β, γ), where β and γ represent the maximum rate of p53 degradation by Mdm2 and the Michaelis constant for p53 degradation, respectively (Goldbeter, 1991). Mdm2 is produced propor-tionally to the p53 level (Ψ) and degraded through a first-order decay process (δ) (Figure 2A). We restricted the model to include a minimal number of parameters, as no cooperativity is assumed (i.e. no use of Hill coefficients). We used numerical analysis to choose appropriate values for each biological parameter (SI, sections I and II), based on results from Batchelor et al. (Batchelor et al., 2011). Particularly, in order to recapitulate p53 oscillatory behavior, we found that introducing a time delay (TDel) (Novák and Tyson, 2008; Tiana et al., 2002) representing the transcription and translation of Mdm2 led to oscillations (Figure S1). The set of chosen parameters for the core p53-Mdm2 network (Supplementary Table 1) agreed with the biological estimates of time delay (~30min) (Hirata et al., 2008) and frequency (~5.5hours) of p53 oscillations (Lahav et al., 2004). Thus, these two equations serve as a minimal model for p53 oscillatory behavior.

Figure 2: Impact factors identify modulation of β as primary function of Mdmx.

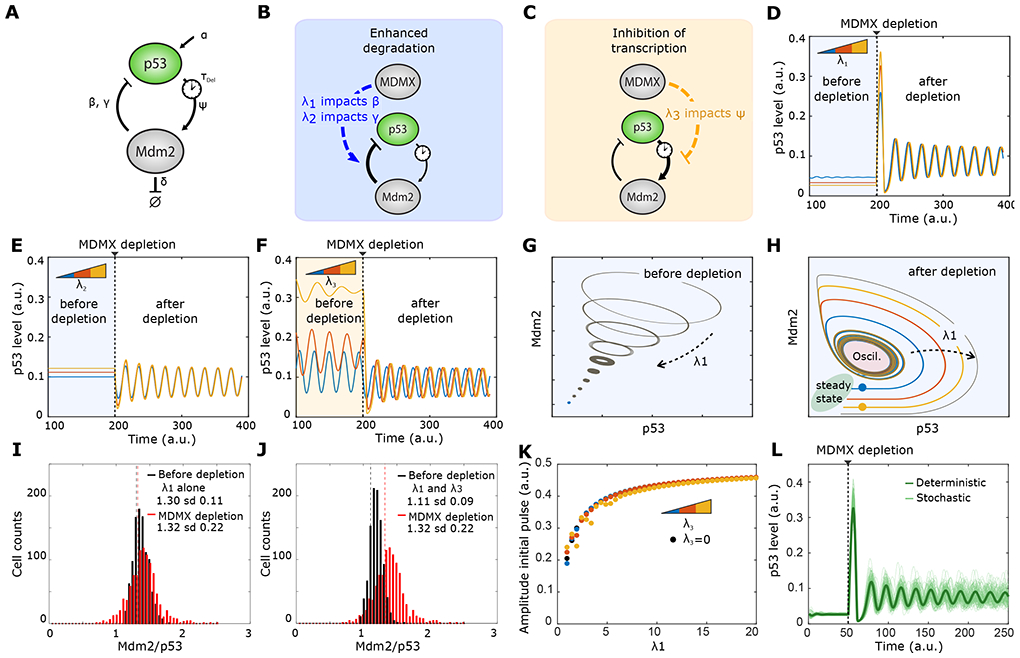
A) Schematics of the p53-Mdm2 negative feedback loop with the parameters (β, γ, Ψ, T_Del) in our mathematical model.

B) Possible mechanisms for Mdmx-enhanced p53 degradation through enhancing Mdm2-mediated p53 poly-ubiquitination.

C) Possible mechanism of Mdmx-mediated inhibition of p53 transcriptional activity through competitive binding.

D) Predicted p53 dynamics before and after Mdmx depletion at three different values of impact factor λ_1., affecting parameter β. λ₁ values for blue, red and yellow curves are, respectively,1, 2, 3.

E) Predicted p53 dynamics before and after Mdmx depletion at three different values of impact factor λ₂ on parameter Ψ. λ₂ values for blue, red and yellow curves are, respectively, 2, 4, 6.

F) Predicted p53 dynamics before and after Mdmx depletion at three different values of impact factor λ₃ affecting parameter γ. λ₃ values for blue, red and yellow curves are, respectively, 0.25, 0.5, 0.75.

G) Evolution of p53-Mdm2 behavior prior to Mdmx depletion in phase space with increasing λ₁. Increase in λ₁ drives the limit cycle towards a fixed point.

H) Evolution of p53-Mdm2 behavior following Mdmx depletion in phase space when λ₁ increases. Increase in λ₁ enhances the amplitude of the initial pulse.

I) Simulations of the distribution of Mdm2/p53 before (black) and after (red) Mdmx depletion, taking into account λ₁ alone (λ₁ =3; λ₃ =0). Sd: standard deviation.

J) Simulations of the distribution of Mdm2/p53 before (black) and after (red) Mdmx depletion, taking into account both λ₁ and λ₃ (λ₁ =3; λ₃=0.15).

K) Predicted amplitude of the initial pulse for distinct combinations of λ₁ and λ₃. λ₃ values for black, blue, red and yellow dots respectively: (0; 0.25; 0.5; 0.75).

L) 100 simulations of p53 dynamics with Langevin noise before and after Mdmx depletion. λ₁ = 3, λ₂ = 0, λ₃ = 0.15. The green line represents the deterministic trajectory.

We used this minimal model to investigate the potential interactions between Mdmx and the p53-Mdm2 loop. Mdmx can potentially affect the core p53 system by either increasing p53 degradation or interfering with p53 transcriptional activity (Figure 1A). To model these potential effects, we introduced a series of parameters λ_i that we refer to here as “impact factors.” This approach is a simplified version of sensitivity analysis that has been used in previous studies of biological networks (e.g. Pfeuty et al., 2012). The use of impact factors in simple models enabled us to develop an intuitive understanding of the functions of Mdmx in silico and to explore the effects of each arm independently, which is difficult to assess experimentally. Specifically, impact factors enable us to reject hypotheses that contradict the observed behavior of the system. The magnitudes of the impact factors correspond to the strength/intensity of Mdmx’s impact on the specific parameter. For instance, an impact factor of zero means Mdmx has no effect on a parameter, whereas a high value indicates that the parameter is highly sensitive to Mdmx levels. In this model, Mdmx levels are kept constant before ([Mdmx]=1) and after ([Mdmx]=0) depletion, and the biological parameters of the core p53 network (β, γ, Ψ) now incorporate the effects of Mdmx and become (β′, γ′, Ψ′) as follows:

$$\begin{gathered} {\beta }^{\prime }=\beta (1+{\lambda }_1[Mdmx]) \\ {\gamma }^{\prime }=\gamma (1+{\lambda }_2[Mdmx]) \\ {\psi }^{\prime }=\psi (1-{\lambda }_3[Mdmx]) \end{gathered}$$

Impact factors λ₁ and λ₂ account for the effect of Mdmx on p53 degradation, affecting biological parameters (β) and (γ), respectively, (Figure 2B) and impact factor λ₃ accounts for the effects of Mdmx on p53 transcriptional activity (Ψ) (Figure 2C). Our goal was to investigate which potential interaction of Mdmx best recapit-ulates the quantitative features of p53 dynamics following Mdmx depletion. Therefore, we tested the effect of each impact factor separately. We simulated p53 dynamics using a range of values for each factor (Figure 2D-F) and assesed whether the simulations reproduced the experimentally-observed p53 dynamics. Different values of the impact factors model different strengths of interaction of Mdmx with the p53-Mdm2 network.

We found that incorporating impact factor λ₁ best fit to p53 dynamics following Mdmx depletion. Before Mdmx depletion, all tested values of λ₁ led to a steady state level of p53, with higher λ₁ leading to lower basal levels of p53 (Figure 2D). After Mdmx depletion, a large p53 pulse was observed followed by oscillations (Figure 2D). It is noted that as λ₁ increased, so did the height of the initial pulse. However the amplitude of oscillations did not vary with λ₁. Notably, incorporating impact factor λ₂ led to p53 oscillations after depletion but did not reproduce the initial high-amplitude pulse of p53 (Figure 2E). Last, introducing impact factor λ₃ resulted in oscillatory p53 behavior before Mdmx depletion, which did not fit our experimental observations (Figure 2F). Based on these simulations, we concluded impact factor λ₁, which accounts for the role of Mdmx in enhancing p53 degradation by Mdm2, is critical for generating p53 biphasic dynamics and can re-capitulate the first two key features of p53 dynamics following Mdmx depletion (i.e. an initial pulse followed by sustained low-amplitude oscillations).

In order to better understand the role of impact factor λ₁ on p53 dynamics we used tools of dynamical systems theory. We first visualized the phase portrait of p53-Mdm2 before depletion and explored how varying the value of λ₁ affected the system’s behavior. As λ₁ increased, the size of limit cycles (closed loops) progres-sively narrowed (Figure 2G). That is, small values of impact factor λ₁ can lead to oscillations before Mdmx depletion, with smaller values causing higher-amplitude oscillations. This observation further strengthens our previous choice of λ₁ values for p53 simulations, with values high enough to reproduce the observed p53 steady-state levels before Mdmx depletion (Figure 2D). A second phase portrait of the p53-Mdm2 system drawn after Mdmx depletion showed how p53 levels transition from a steady state (green zone) to an oscillatory regime (red zone) (Figure 2H). Given an initial point in the phase space, the trajectory determines all future positions. We compared the trajectories starting at two distinct initial states (blue and yellow dots Figure 2H) that corresponded to two distinct constant values of p53 before depletion. Both trajectories follow an increase then decrease of p53 (corresponding to the initial p53 pulse) then converged towards a single limit cycle (corresponding to the sustained low-amplitude oscillations). For increasing values of λ₁, the trajectory took a longer path to reach the oscillatory regime. Because the length of the trajectory corresponds to the height of the initial pulse, the graph helps explain how increasing values of λ₁ led to higher amplitudes of the initial pulse (Figure 2D). Although Mdmx values were modeled as 1 (control) or 0 (depleted), we note that due to the architecture of the impact factors, a potential incomplete knockdown of Mdmx would not yield qualitatively different conclusions from our simulations: a transition from a steady state to an oscillatory regime would still be detected.

We next investigated whether the effect of Mdmx on p53 degradation through impact factor λ₁ can also capture the third quantitative feature of p53 dynamics: the shift in the ratio between Mdm2/p53 (Figure 1J and 1K). We found that incorporating λ₁ alone is insufficient for accounting for this experimentally-observed shift (compare Figure 1J to Figure 2I). In order to capture the shift, we chose to test the effect of impact factor λ₃, which accounts for the direct effect of Mdmx on Mdm2 transcription by p53 (parameter Ψ) and therefore is a good candidate to affect the ratio of Mdm2/p53. Although λ₃ alone resulted in aberrant oscillatory p53 behavior before Mdmx depletion (Figure 2F), we chose to explore whether a low value of λ₃ in combination with λ₁ could reproduce all experimentally observed features (correct p53 dynamics and shift in the Mdm2/p53 distribution). From the immunofluorescence data, we extracted the average ratio of Mdm2/p53 both in the control and Mdmx-depleted cells. These values can be used to set the bounds for the value of λ₃ (see SI). We inferred that values of λ₁ equal to 3 and λ₃ equal to 0.15 could capture the experimen-tally-observed shift in the Mdm2/p53 distribution (see detailed analysis in SI, and compare Figure 1J to Figure 2J). In order to test whether including λ₃ affected any of the quantitative features λ₁ could recapitulate, we further tested the amplitude of the initial p53 pulse as a function of λ₁ for different values of λ₃. We found that the amplitude of the pulse was almost solely defined by the value of λ₁ (Figure 2K). Therefore, a high value of λ₁ (λ₁ = 3.0) was chosen to maintain p53 at steady state before Mdmx depletion and a small value of λ₃ (λ₃ = 0.15) ^was chosen to capture the shift in the Mdmx/p53 distribution.

Combining both impact factors (λ₁ and λ₃) at the fixed values mentioned above, we simulated the system with internal and external noise (applying Chemical Langevin equation) to examine its robustness. We confirmed robust biphasic dynamics of p53 after Mdmx depletion in the presence of noise that accurately captured the experimental behavior in single cells (Figure 2L). Taken together our mathematical analysis showed that Mdmx-mediated p53 degradation (through impact factor λ₁) and Mdmx-mediated regulation of p53 activity (through impact factor λ₃) were sufficient for capturing the three quantitative features of p53 biphasic dynamics following Mdmx depletion: the initial high amplitude pulse, the low amplitude oscillations, and the shifted distribution of Mdm2/p53 with increased variance. These results were robust to variations in the initial parameters (α, β , γ , ψ , δ , T_Del) with λ₁ governing the initial peak and subsequent oscillations after Mdmx depletion, and λ₃ governing the Mdm2/p53 ratio (Figure S2).

III. Simulation of the model predicts the effect of Mdmx on p53 dynamics after DNA damage

Having optimized λ₁ and λ₃ to mimic the observed p53 dynamics before and after Mdmx depletion, we proposed a unified model of the core p53-Mdm2-Mdmx feedback. We next aimed to further develop this model to predict the combined effects of Mdmx depletion and DNA damage on p53 dynamics. In the presence of Mdmx, DNA damage caused by UV irradiation has been shown to cause a single pulse of p53 that decays exponentially as damage is repaired (Batchelor et al., 2011). The increase in p53 is, in part, achieved by UV dose-dependent activation of the ATR kinase, which stabilizes p53 through inhibitory phosphorylation of Mdm2 (Shieh et al., 1997). In our revised model, increasing UV dose was reflected as increasing ATR activity, since UV exerts most of its effects through ATR (Batchelor et al., 2011; Tibbetts et al., 1999) (Figures S3-S4). We expected that ATR-mediated phosphorylation of Mdm2 would affect its ability to bind p53 (reflected in the constant γ) and/ or its efficiency at causing p53 degradation (reflected in the constant β). Therefore, we introduced the two non-zero impact factors κ₁ and κ₂ to modify these terms to account for the effects of active ATR (denoted as ATR*) on these two processes (Fig. 3A).

Figure 3: UV irradiation combined with Mdmx depletion is predicted to increase the amplitude of both the initial p53 pulse and subsequent oscillations.

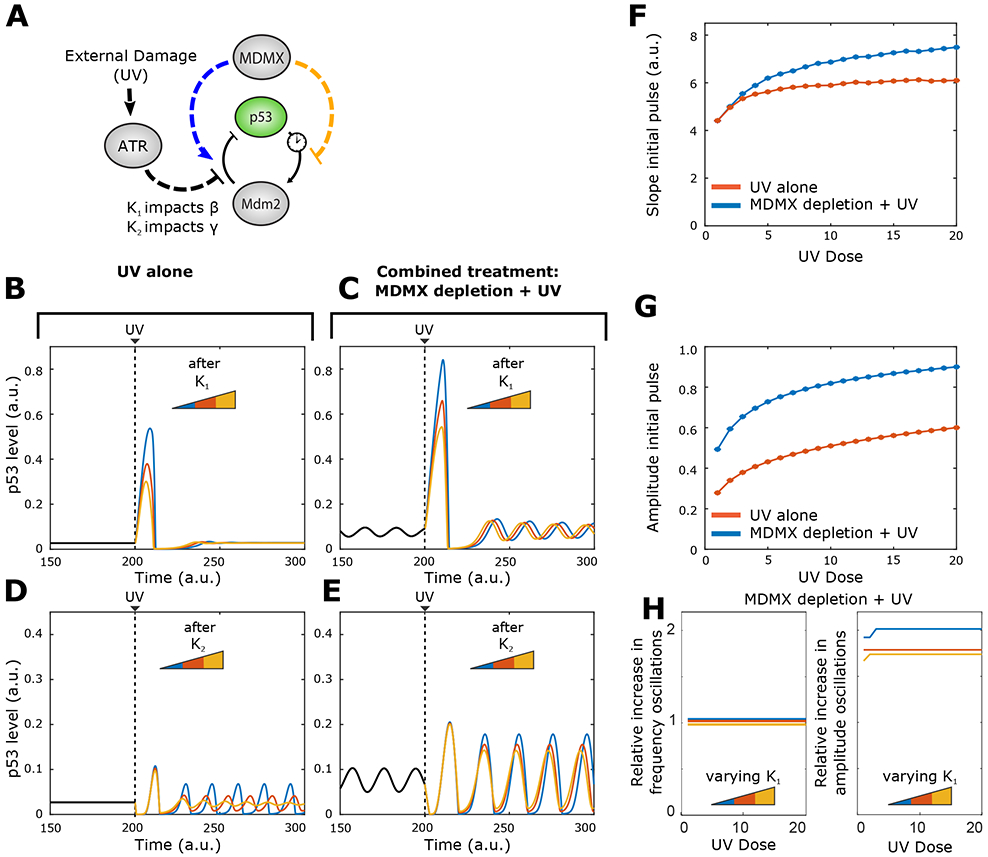
A) Schematic of the p53-Mdm2 system with regulation by Mdmx and ATR. ATR can inhibit Mdm2-mediated p53 degradation through two impact factors (κ₂ or κ₂)

B, C) p53 dynamics in (B) control and (C) Mdmx-depleted cells before and after UV-irradiation at three different values of κ₁. κ₁ values for blue, red and yellow curves are, respectively, 1, 2, 3.

D, E) p53 dynamics in (D) control and (E) Mdmx-depleted cells before and after UV-irradiation at three different values of κ₂. κ₂ values for blue, red and yellow curves are, respectively, 0.01; 0.04; 0.09.

F) Predicted slope of the increasing phase of the p53 initial pulse with increasing UV dose in control or Mdmx-depleted cells subjected to UV irradiation. κ₁ fixed at 1.

G) Predicted amplitude of the p53 initial pulse with increasing UV dose in control or Mdmx-depleted cells subjected to UV irradiation. κ₁ fixed at 1.

H) Predicted amplitude of the p53 sustained oscillations after the initial pulse for different levels of of κ₁. κ₁ values for blue, red and yellow curves are, respectively, 1, 2, 3.

$$\begin{gathered} {\beta }^{″}={\beta }^{\prime }(1-\frac{[AT{R}^{\ast }]}{[AT{R}^{\ast }]+{\kappa }_1}) \\ {\gamma }^{″}=\gamma (1-\frac{[AT{R}^{\ast }]}{[AT{R}^{\ast }]+{\kappa }_2}) \end{gathered}$$

We used this extended model to compare the effects of UV-radiation alone (Figure 3B, D) to that of Mdmx depletion followed by UV-radiation (Figure 3C, E). We modeled three different values of κ₁ and κ₂ under each condition (see STAR Methods).

We analyzed the effects of κ₁ and κ₂ on the initial p53 pulse and on any subsequent oscillations in control or Mdmx-depleted cells subjected to UV irradiation. In Figures 3B to 3E, we observed that only impact factor κ₁ had a strong effect on the amplitude of the UV-triggered p53 pulse in both control and Mdmx-depleted cells. Specifically, ATR activation (through its effect on p53 degradation (β)) led to a single p53 pulse with an amplitude that scaled with κ₁ (Figure 3B-C). In Mdmx-depleted cells, the initial UV-induced pulse of p53 reached a higher amplitude for a given value of κ₁ compared to that in control cells (Fig. 3B). Furthermore, the post-UV p53 oscillations also showed a higher amplitude than the pre-UV oscillations in Mdmx-depleted cells. In contrast, κ₂ led to oscillations with no initial p53 pulse across all tested values in both control and Mdmx-depleted cells (Figure 3D, E) and we therefore omitted further study of parameter κ₂. Together, these results suggested that ATR inhibition of Mdm2-mediated p53 degradation occurred through the effects of impact factor κ₁ on β (degradation of p53 by Mdm2). We next analyzed how different UV doses affected the slope (Figure 3F) and amplitude (Figure 3G) of the UV-triggered initial p53 pulse in control and Mdmx-depleted cells. Simulation of the model (with κ₁ fixed at 1) suggested that both cell types exhibited increased slope (Fig. 3F) and amplitude (Fig. 3G) of the initial pulse with increasing UV doses, with Mdmx-depleted cells consistently showing higher values for both compared to control cells.

Lastly, we tested how different UV doses might affect the amplitude of p53 oscillations in Mdmx-depleted cells following the initial p53 pulse in response to UV. The model simulations measure the relative increase in the oscillatory amplitude after UV with κ₁ varying independently (Figure 3H). For all values of impact factor κ₁, the amplitude of p53 oscillations following UV was independent of the UV dose. Taken together our model suggests that a combined treatment of Mdmx depletion followed by UV radiation will lead to a large p53 pulse followed by oscillations (Figures 3C). In addition, our model predicts that the UV-triggered p53 oscillations will maintain the frequency of oscillations while having higher amplitude compared to the oscillations prior to UV irradiation (Figures 3C, 3H).

IV. Experimental data confirming the effect of Mdmx on p53 dynamics in response to UV

We next tested experimentally whether our mathematical model accurately predicted the potential p53 dynamics that result from combining Mdmx depletion and DNA damage. Cells were exposed to UV alone (8 J/m² or 16 J/m²) (right-most single cell p53 traces in Figure 4A and Figure 4B) or to UV after Mdmx depletion (left-most single cell p53 traces in Figure 4A and Figure 4B). The average population behavior is shown in Figures 4C and 4D. Our model accurately predicted the main features of the initial p53 pulse in Mdmx-depleted, UV-irradiated cells. The amplitude and duration of the pulse were increased compared to those in control cells (Figure 4C, D, E, F), and both the amplitude and slope of the pulse depended on the UV dose (Figure 4E, 4F). The lower UV dose of 8 J/m² showed minimal effects on these feature, either because the effects were below the limit of detection of the experimental system, or because the effects were counter-acted by interactions with additional factors at this dose.

Figure 4: Mdm2-dependent degradation of p53 is the primary interaction regulating p53 dynamics following DNA damage.

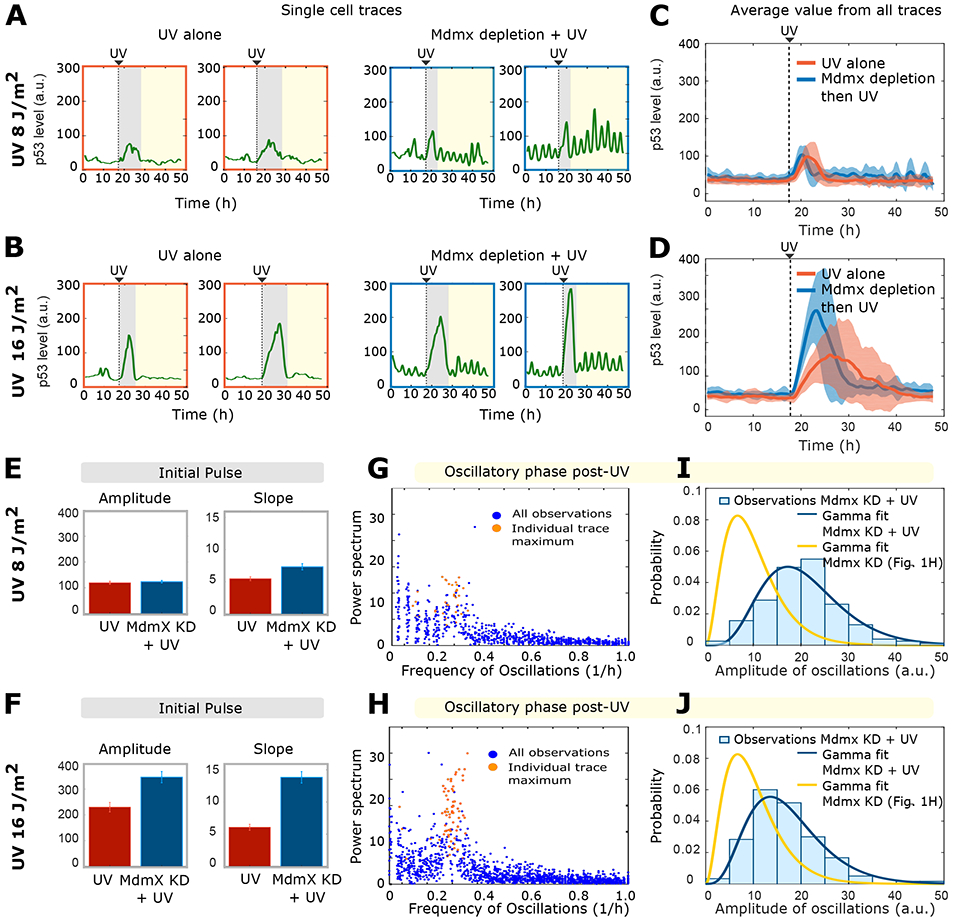
A-B) Four representative single-cell p53 traces are colored according to the different phases of their dynamic behavior: before treatment (white region), initial response (grey region) and long-term response (yellow region). Dynamics were measured following UV-radiation (8 and 16 J/m2 respectively). Right-most panels show prior Mdmx depletion.

C-D) Mean p53 dynamics trajectories (bold lines) ± std deviation (shaded areas) before and after UV irradiation (8 and 16 J/m2 respectively) in scrambled siRNA-treated (control, red) or Mdmx-depleted (blue) cells. n= 30 selected traces per experiment.

E-F) Slope and amplitude of the p53 initial pulse after treatment of scrambled siRNA-treated (control, red) or Mdmx-depleted (blue) cells with 8 J/m² (E) or 16 J/m² (F) UV radiation.

G-H) Fourier spectrum of the sustained oscillatory phase after treatment of scrambled siRNA-treated (control, red) or Mdmx-depleted (blue) cells with 8 J/m² (G) or 16 J/m² (H) UV radiation.

I-J) Distribution of amplitudes of the p53 oscillations in Mdmx-depleted cells subjected (blue) or not (yellow) to 8 J/m² (I) or 16 J/m² (J) UV radiation. Curves for unirradiated cells in yellow are identical to Figure 1H.

We next compared the late p53 response (following the initial pulse) generated by the model to the experimentally observed data. In agreement with our model predictions, in the combined treatment (Mdmx depletion followed by UV irradiation), the initial single pulse was followed by oscillations with higher amplitude compared to before UV treatment (left-most single cell traces Figure 4B). We used Fourier spectrum analysis to compare the oscillatory frequencies of Mdmx-depleted cells subjected to 0, 8, or 16 J/m² irradiation, and found little difference in frequency between the 3 conditions (Figures 4G and 4H, compared with Figure 1G). However, 16 J/m² UV irradiation caused an approximately 2-fold increase in the amplitude of oscillations in Mdmx-depleted cells (compare gamma fits in blue of Figures 4I and 4J to gamma fits in yellow from of Figure 1H). Thus, our model correctly predicted that both the maintenance of the oscillatory frequency and the increase in oscillatory amplitude after irradiation would be independent of the UV-dose (compare Figure 3H with Figures 4 G-J).

Our mathematical model captured the key features of p53 dynamics in response to Mdmx depletion combined with UV-radiation, namely an enhanced UV-triggered initial pulse followed by large-amplitude oscillations. Following the strong agreement between our model and experimental results, we concluded that the effect of ATR on Mdm2-mediated degradation of p53 (through impact factor κ₁) dominated the p53 dynamical response following DNA damage. Indeed, we found that the Mdm2-dependent degradation of p53 (facilitated by Mdmx and hindered by ATR) was the most critical interaction regulating p53 dynamics both in non-stressed conditions and following DNA damage. A final model that captures the dependencies of parameters (β) and (ψ) to Mdmx and ATR can be described as follows:

$$\begin{gathered} \frac{d}{dt}[p53]=\alpha -{\beta }_{Mdmx}^{ATR}[Mdm2]\frac{[p53]}{\gamma +[p53]} \\ \frac{d}{dt}[Mdm2]={\psi }_{Mdmx}[p53(t-T_{Del})]-\delta [Mdm2] \end{gathered}$$

where

$$\begin{gathered} {\beta }_{Mdmx}^{ATR}=\beta (1+{\lambda }_1[Mdmx])(1-\frac{[AT{R}^{\ast }]}{[AT{R}^{\ast }]+{\kappa }_1}) \\ {\psi }_{Mdmx}=\psi (1-{\lambda }_3[Mdmx]) \end{gathered}$$

V. Discussion

How dynamics of signaling molecules emerge through interacting components in space and time remains a fascinating and poorly-understood question. Here we investigated the regulation of p53 dynamics through a combination of single-cell imaging and mathematical modeling. This strategy allowed us to dissect the two roles of Mdmx-- activation of Mdm2-mediated degradation of p53, and direct inhibition of p53 activity-- which is not possible to accomplish by pure experimental approaches. We constructed a minimal mathematical model with minimum free parameters and no nonlinearity to represent the three key features of p53 dynamics following Mdmx depletion, namely, a high-amplitude initial pulse, subsequent lower-amplitude oscillations, and a shift in the Mdm2/p53 ratio. We used impact factors to determine the contribution of each of the two known functions of Mdmx on these features, and revealed that Mdmx primarily enhanced degradation of p53. Furthermore, our model accurately predicted p53 dynamics in Mdmx-depleted cells subjected to UV irradiation. UV radiation has been shown to induce a graded p53 response (Batchelor et al., 2011). However, the molecular mechanism that shapes the UV-induced p53 pulse remained unclear. Our results suggested an inhibitory role for Mdmx in modulating the slope and height of the p53 pulse after UV radiation(Figures 4E, 4G, and 4H).

We present a simplified approach for discriminating between a limited number of possible known interactions within a network. Other approaches for identifying interactions that explain observed dynamics include sensitivity analysis (e.g. Pfeuty et al., 2012) and bifurcation diagrams (e.g. (Mönke et al., 2017). Sensitivity analysis provides information on how small changes to each parameter influence network dynamics. Our approach efficiently discriminated between two possible interactions without requiring detailed information about the quantitative effects of each parameter. Bifurcations diagrams predict the behavior of a system at all possible values of each parameter, in contrast to our approach, which predicts behaviors at a small number of selected values. Although our approach was sufficient to identify dominant interactions from a finite set of possibilities, this method does not provide information on how each parameter affects the precise timing or expression profile of network components, the optimal values of each parameter that best fit the data, or on how noise induces heterogeneity at the single-cell level. The method outlined here is effective for analyzing a protein that is not directly affected by the network it regulates, e.g. Mdmx or ATR.

Given that enhancing Mdm2-mediated degradation of p53 emerged as the main role of Mdmx, it is tempting to speculate that Mdmx’s main function could be to maintain p53 levels at low steady state levels by constantly catalyzing Mdm2-mediated p53 ubiquitination. In non-stressed conditions, p53 undergoes a single pulsatile induction during G1/S cell cycle phase (Loewer et al., 2010). Thus, it is possible that ubiquitination activity of the Mdmx/Mdm2 complex toward p53 is rhythmic and is the lowest during the G1/S cell cycle phase. In support of this hypothesis, Mdm2 has been implicated in regulating cell cycle progression by targeting cell-cycle machineries (Frum et al., 2009; Giono et al., 2017). It remains to be tested if the same mechanism applies to Mdmx.

How signal-specific p53 dynamics emerge and specify transcriptional programs for cellular decision-making remains elusive. It has been shown that p53 oscillations are flexible in amplitude but robust in period (Chen et al., 2016), which our model recapitulated. It remains unclear if different amplitudes of p53 oscillations activate distinct transcriptional programs and therefore encode distinct biological information for cell state determination (Heltberg et al., 2016, 2019; Lee et al., 2014; Mengel et al., 2010; Purvis and Lahav, 2013). The fact that ATR activation leads to a higher amplitude of p53 oscillations provides a plausible approach to further dissect the effects of p53 amplitude. From the dynamics point of view, Mdmx acts as a key suppressor of p53 oscillations in both non-stressed conditions and after gamma-irradiation (Chen et al., 2016). It remains to be tested if other cellular signals modulate p53 dynamics through regulating Mdmx stability or its binding to p53. Clinically, Mdmx overexpression is observed in multiple cancers (Danovi et al., 2004; Gembarska et al., 2012; Wade et al., 2013). Thus, it would be interesting to further investigate the role of Mdmx in regulating p53 dynamics in MDMX overexpressing cancers. Due to the sophisticated and asynchronous p53 dynamics after Mdmx suppression, it is currently impossible to directly examine the link between Mdmx-mediated p53 dynamics and the fate of each individual cells after UV-radiation. The development of an Mdmx small molecule inhibitor that rapidly suppresses Mdmx would enable investigating how the combination of Mdmx suppression with DNA damage changes p53 dynamics and the survival of each cell. In the absence of such an inhibitor, our study provides an avenue to examine mechanisms responsible for signaling dynamics by developing a minimal mathematical model based on quantitative perturbations of signaling dynamics in single cells. Similar approaches can be used to idenfify the dominating intercations controlling the dynamics of other key molecular players in highly connected circuits.

STAR Methods:

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Galit Lahav (galit@hms.harvard.edu). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Human breast cancer MCF7 parental cells were purchased from ATCC. MCF7 p53 reporter cell line (MCF7+p53shRNA+p53-mCerulean) has been previously described (Gaglia et al., 2013). Briefly, TP53 gene was expressed under the EF1α promoter fused with mCerulean. The vector was introduced into MCF7+p53shRNA cells (kindly provided by the Reuven Agami Group) via lentiviral infection followed by clonal selection by serial dilution method.

METHOD DETAILS

Cell Culture and UV radiation

Both parental and MCF7 reporter (MCF7+p53shRNA+p53-mCerulean) cells were grown in RPMI media supplemented with 10% fetal bovine serum (FBS). Cells were kept at constant temperature (37°C) and atmosphere (5% CO₂) with confluency below 80%. For imaging experiments, cells were grown in RPMI without phenol red and riboflavin with 10% FBS in poly-D-lysine coated glass-bottom plates (MatTek Coporation) for two days before imaging. For UV-irradiation, cells were cultured in transparent RPMI without phenol red and riboflavin which can scavenge reactive oxygen species formed during irradiation and reduce the effective dose of UV light. Right before irradiation, the cells were washed twice with DPBS to eliminate FBS which can also absorb UV light. Cells were then subjected to UV lamp (Spectroline™ E-Series Handheld Lamps, Thermo Fisher Scientific) radiation at a rate of 1.5 J/m²/s for a total of 8 or 16J, as indicated in each figure. The dose of UV lamp was pre-calibrated using UV light meters from General.

MDMX knockdown

Small interfering RNAs targeting MDMX (sequences: AGCCCTCTCTATGATATGCTA and GACCACGAGACGGGAACATTA) or a scrambled siRNA control, all from Qiagen, were transfected with DharmaFect I from Dharmacon for MDMX knockdown following the standard protocol. Two siRNAs show qualitatively identical results. For all MDMX knockdowns, different doses of siRNA (0.5nM to 50nM) were tested for their efficiency of MDMX knockdown and 5nM of siRNA was used for achieving the best efficiency (>80%) of MDMX knock-down without off-target effect evaluated by the non-specific siRNA induced p21 using western blot analysis. The validation of siRNA knockdown efficiency was carried out by Western blot (Chen et al., 2016).

Immunofluorescence

Cells were grown on glass-bottom plates (MatTek Coporation) coated with poly-D-lysine and fixed with 4% paraformaldehyde. Cells were permeabilized in PBS+1% Triton for 5 min, blocked with 2% BSA, incubated with primary antibody overnight. Antibodies were anti-Mdm2 (SMP14) or anti-p53 (FL-393) all from Santa Cruz Biotechnology and used at 1:1000 dilution. Secondary antibody (ThermoFisher Scientific, 1:10,000 dilution) was coupled to either Alexa488 or Alexa647 for one hour. After washing, cells were stained with DAPI and embedded in imaging media (20mM Tris-HCl, ph8.0, 2.5% DABCO and 80% Glycerol). Images were acquired with a 20× plan apo objective (NA 0.75) with the appropriate filter sets. Image analysis was done with CellProfiler. At least fifty thousand cells were measured per condition.

Live-Cell Microscopy

All time-lapse microscopic experiments were performed with a Nikon Eclipse TE-2000 inverted microscope equipped with a Nikon Perfect Focus System, and a Hammamatsu Orca ER camera. The microscope was equipped with an environmental chamber controlling temperature (37^oC), atmosphere (5% CO2), and hu-midity. For quantifying p53 levels in single cells, cells were excited with 440 nm (20% intensity, and 150 ms exposure), with a 440/20-nm band-pass filter, a 458-nm beam-splitter, and a 483/32-nm emission filter. Images were acquired every 30 min controlled by MetaMorph Software (Molecular Devices). For all sets of experiment, a 20' Nikon plan apo objective (NA 0.75) was used. For each experiment, at least one hundred randomly chosen cells were analyzed for the quantification of p53 levels. For conditions where only surviving cells were considered, at least one hundred were randomly chosen from the population of surviving cells for further analysis. For each experimental design, three experimental repeats were carried out and showed quantitatively similar results.

Mathematical analysis of the phase space

We consider the two dimensional system:

$$\begin{gathered} \frac{d}{dt}[p53]=\alpha -\beta \cdot [Mdm2]\frac{[p53]}{\gamma +[p53]} \\ \frac{d}{dt}[Mdm2]=\psi \cdot [p53(t-{\tau }_{Del})]-\delta \cdot [Mdm2] \end{gathered}$$

First, we consider the boundaries of the phase space in the first quadrant, where both p53 and Mdm2 concentrations hold positive values. These variables cannot run off to infinity since:

$$\begin{gathered} \frac{d}{dt}[Mdm2]{\mid }_{[Mdm2]=\infty )}<0 \\ \frac{d}{dt}[p53]{\mid }_{[p53]=\infty ,[Mdm2]=\infty }<0and \\ \frac{d}{dt}[p53]{\mid }_{[p53]=\infty ,[Mdm2]=0}>0but \\ \frac{d}{dt}[p53]{\mid }_{[p53]=\infty ,[Mdm2]=0}<<\frac{d}{dt}[Mdm2]{\mid }_{[p53]=\infty ,[Mdm2]=0} \end{gathered}$$

We then consider the fixed points of the system, defined by:

$$\frac{d}{dt}[p53]=\frac{d}{dt}[Mdm2]=0$$

As we search for the fixed points of the system we can neglect the time delay τ_Del in the following derivations and write:

$$Mdm{2}^{\ast }=\frac{\psi }{\delta }p{53}^{\ast }$$

This equation defines the fixed point of the system without time delay. It also represents an essential feature of the system that is the relation between the concentrations of Mdm2 and P53. We note that only the transcriptional activity of p53 (ψ) and the degradation of Mdm2 (δ) have an effect in the ratio between Mdm2 and p53. From experimental data we can extract an approximation of this ratio when Mdmx is depleted (Fig. 1J, red distribution) and use this ratio to put a bound on ψ (keeping δ fixed):

$$\psi =\langle \frac{[Mdm2]}{[p53]}{\rangle }_{obs}^{supp}\cdot 0.1\approx 0.15and\delta =0.1$$

From this we can directly determine the value of the impact parameterλ₃, since we know the mean value of the distribution in the control experiment (Fig. 1J, black distribution):

$$\begin{gathered} \frac{\psi }{\delta }(1-{\lambda }_3)=\langle \frac{[Mdm2]}{[p53]}{\rangle }_{obs}^{WT} \\ \Rightarrow {\lambda }_3=1-\frac{\psi }{\delta }\langle \frac{[Mdm2]}{[p53]}{\rangle }_{obs}^{WT}\approx 0.15 \end{gathered}$$

We can now derive an equation for steady state level of p53:

$$\begin{gathered} 0=\alpha -\frac{\psi \beta }{\delta }\frac{(p{53}^{\ast }{)}^2}{\gamma +p{53}^{\ast }} \\ =(p{53}^{\ast }{)}^2-\frac{\alpha \delta }{\psi \beta }p{53}^{\ast }-\gamma \frac{\alpha \delta }{\psi \beta } \\ =(p{53}^{\ast }{)}^2-\mathcal{K}p{53}^{\ast }-\gamma \mathcal{K} \\ \Rightarrow p{53}^{\ast }=\frac{\mathcal{K}}{2}(1+\sqrt{1+4\gamma {\mathcal{K}}^{-1}}) \end{gathered}$$

With $\mathcal{K}=\frac{\alpha \delta }{\psi \beta }$

This equation gives an analytical result of the p53 steady state concentration as a function of the five parameters in the system, where for simplicity α is fixed to 0.1. We observe that a) decreasing the Mdm2 mediated degradation of p53 (β) increases the steady state level and b) increasing the transcriptional activity of p53 (ψ) decreases the level of P53. We can now consider a linear stability analysis of the system in order to investigate the onset of oscillations in the system. In order to do the analytical calculations, we neglect the time delay and set up the Jacobian that has the form:

$$J={(}^{{}^{-}}\begin{array}{c}\hfill \frac{\gamma \beta Mdm{2}^{\ast }}{(\gamma +p{53}^{\ast }{)}^2}\hfill \\ \hfill \psi \hfill \end{array}{}^{{}^{-\beta }}\begin{array}{c}\hfill \frac{p{53}^{\ast }}{\gamma +p{53}^{\ast })}\hfill \\ \hfill -\delta \hfill \end{array}$$

With trace and determinant:

$$\begin{gathered} \tau =-\gamma \beta \cdot \frac{Mdm{2}^{\ast }}{(\gamma +p{53}^{\ast }{)}^2}-\delta \\ \Delta =\gamma \beta \delta \cdot \frac{Mdm{2}^{\ast }}{(\gamma +p{53}^{\ast }{)}^2}+\beta \psi \frac{p{53}^{\ast }}{\gamma +p{53}^{\ast }} \end{gathered}$$

We can estimate the eigen frequency of the system that describes the frequency of the oscillatory dynamics around the fixed point. This is given by:

$$\omega =\frac{1}{2}\sqrt{4\Delta -{\tau }^2}$$

Thus, for the eigenvalues to be complex we need the value of τ² to be smaller than 4Δ. In order to have oscillations, not only eigenvalues have to be complex but the system needs to be non-decaying. We are thus searching for a so called Hopf bifurcation, which occurs when τ calculated from the Jacobian changes from negative to positive. We reorganize τ, and find that this system can never have a stable limit cycle since τ is strictly negative:

$$\tau =-(\frac{\gamma \beta Mdm{2}^{\ast }}{(\gamma +p{53}^{\ast }{)}^2}+\delta )$$

Therefore, for this system without a time delay, the existence of a limit cycle is impossible. However since there is a well-defined eigen frequency in the system, oscillatory dynamics generated solely by the presence of noise can still occur if we consider the system to be stochastic.

The existence of a limit cycle from a time delay

From the previous section we learned that no limit cycle can exist in the above formulation without a time delay. In this section we want to study the effect of a time delay and its ability to initiate oscillations. We observe that, as we gradually increase the time delay, oscillations are present for a longer time before they decay. We study the effect of the decay by introducing a Poincare section as a line in the p53-Mdm2 phase plane from[(0, Mdm2*); (p53*, Mdm2*)]. In this way, we can estimate the distance the trajectory travels before it reaches the fixed point (Fig. S1A). Theoretically, this decay distance can be approximated by:

$$\begin{gathered} P(n)\approx P(t=\frac{2\pi }{\omega }) \\ =P_{n-1}{e}^{-\frac{\tau 2\pi }{2\omega }} \\ =P_0{e}^{-n\frac{\tau }{\omega }\pi } \end{gathered}$$

We can estimate the decay at each Poincare section as:

$$\begin{gathered} P_{n-1}-P(n)\approx P_0(e^{-(n-1)\frac{\tau }{\omega }\pi }-e^{-n\frac{\tau }{\omega }\pi }) \\ =P_0{e}^{-n\frac{\tau }{\omega }\pi }(-e^{\frac{\tau }{\omega }\pi }-1) \\ =C{e}^{-n\frac{\tau }{\omega }\pi } \end{gathered}$$

Thus the value of τ will be the slope at which the decay is observed in a logarithmic plot, since ω is approximately constant (data not shown). In Fig S1B we observe the decay as a line, with decay constant τ/ω * π. In Fig. S1C the decay is observed when the limit cycle has occurred. By fitting a linear fit to the points in a logarithmic plot we get a relation shown in Fig. S1D, where the decay rate is shown on the y-axis as a function of the increasing time delay. Thus we can use this to predict when the limit cycle sets in due to the time delay.

Parameters in the model

The parameters were chosen to align with those reported by Batchelor et al. (Batchelor et al., 2011). α was set to 0.1, and the remaining parameters were rounded to the nearest 1/20^thunit. A scaling factor, T_u (defined as $T_u=\frac{R_T}{S_T}$hwhere R_T is the real amplitude period and S_Tthe period from the simulation) was applied to relate the a.u. in the simulation to the experimentally derived p53 oscillations period of 5.5h. This method allowed us to directly compare the model with experimental observations (Supplementary Tables 1 and 2, Fig. S2).

Derivation of the saturated degradation

An important element in the model is the description of the negative feedback mechanism modeled as a so called saturated degradation term. The process we are considering is the following:

$$[p53]+[Mdm2]\iff C_{p53-Mdm2}\Rightarrow C[k_3]\varnothing +[Mdm2]$$

If we now assume there is a quasi-steady state, the rate of change in the complexes can be neglected and we can write:

$$k_1\cdot ([p53]-\varnothing )\cdot ([Mdm2]-C_{p53-Mdm2})-k_2{C}_{p53-Mdm2}-k_3{C}_{p53-Mdm2}=0$$

Now isolating C_p53–Mdm2 we obtain:

$$C_{p53-Mdm2}=[Mdm2]\frac{([p53]-\varnothing )}{([p53]-\varnothing )+\frac{k_2+k_3}{k_1}}$$

Since

$$\stackrel{.}{\varnothing }=k_3{C}_{p53-Mdm2}$$

we can express the degradation of p53 through the expression:

$$[p53]\approx -k_3[Mdm2]\frac{[p53]}{[p53]+\frac{k_2+k_3}{k_1}}=-\beta [Mdm2]\frac{[p53]}{[p53]+\gamma }$$

The slope following Mdmx depletion

We consider the fixed point of P53. When Mdmx is suppressed, we have oscillations around the fixed point

$$p{53}^{\ast }=\frac{1}{2}\mathcal{K}(1+\sqrt{1+4\gamma {\mathcal{K}}^{-1}})$$

For the Mdmx depleted cells we can write:

$$\begin{gathered} \mathcal{K}=\frac{\alpha \delta }{\beta \psi }\approx \frac{1}{15} \\ \Rightarrow p{53}^{\ast }=\frac{1}{30}(1+\sqrt{1+4\cdot 0.15})\approx 0.075. \\ \Rightarrow Mdm{2}^{\ast }\approx 0.075\cdot 1.5=0.11 \end{gathered}$$

For the control we can write:

$$\begin{gathered} \mathcal{K}=\frac{\alpha \delta }{{\beta }_{MdmX}\psi }\approx \frac{1}{50} \\ \Rightarrow p{53}^{\ast }=\frac{1}{100}(1+\sqrt{1+4\cdot 0.5})\approx 0.027 \\ \Rightarrow Mdm{2}^{\ast }\approx 0.027\cdot 1.25=0.035 \end{gathered}$$

As we remove Mdmx, we make a transition so $\mathcal{K}=\frac{1}{50}\mapsto \frac{1}{15}$ and therefore the slope will be:

$$\frac{d[p53]}{dt}{\mid }_{t=0}=\alpha -\frac{1}{15}0.034\cdot \frac{0.0268}{0.0268+0.01}\approx 0.075$$

This equation explains how the initial pulse after Mdmx depletion arises due to a parameter change that causes an immediate out of equilibrium state. This state in turn creates a positive value for $\frac{d[p53]}{dt}$.

Inclusion of ATR

Active ATR (ATR*) is described as following:

$$\begin{gathered} \frac{d}{dt}[AT{R}^{\ast }]=\theta -[AT{R}^{\ast }] \\ \theta =\{\begin{array}{c}0ift<T_{UV}\hfill \\ 2\sqrt{D_{UV}}ift<T_{UV}+\Omega \hfill \\ 0.1else\hfill \end{array} \end{gathered}$$

where Θ is a UV-dose dependent parameter, T_uv is the time of UV exposure and Ωa parameter in units of time. ATR* concentration quickly reaches a dose dependent level after UV-radiation and then decays exponentially representing the repair of DNA damage (Fig. S3, Fig. S4) (Batchelor et al., 2011). For simplicity, we fixed the decay parameter to unity.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image analysis and Single-Cell Tracking

An in-house Matlab program (https://qithub.com/balvahal/p53CinemaManual) was used to track individual cells for quantifying p53 levels. This consists on a semi-automated method develop to allow tracking and cell fate annotation of individual moving cells over long time scales. The method relies on (i) automatic identification of single cell centroids using intensity and shape information of a constitutive nuclear marker; (ii) centroid linkage and track propagation using nearest-neighbor criteria; and (iii) real-time user correction of tracking, and annotation of cell fate events.

DATA AND CODE AVAILABILITY

The raw data of p53 quantification in single cells and the code generated during this study are available at: https://qithub.com/Mathiasheltberq/InteractionsP52Network.The movie file is available upon request.

Key Resource Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Mdm2 (SMP14)	Santa Cruz	Cat. No. sc-965
P53 (FL-393)	Santa Cruz	Cat. No. sc-6243
Goat anti-Mouse IgG (H+L) Highly Cross-Adsorbed Secondary Antibody, Alexa Fluor Plus 488	ThermoFisher Scientific	Cat. No. A32723
Donkey anti-Rabbit IgG (H+L) Highly Cross-Ad-sorbed Secondary Antibody, Alexa Fluor Plus 647	ThermoFisher Scientific	Cat. No. A32795
DharmaFect I	Dharmacon	Cat. No. T-2001
Chemicals
DAPI	Sigma	D9542
DABCO 33-LV	Sigma	Cat. No. 290734
Experimental Models: Cell Lines
MCF7+p53shRNA+p53-mCerulean	(Gaglia et al., 2013)	N/A
Oligonucleotides
MDMX siRNA: AGCCCTCTCTATGATATGCTA	Qiagen	Cat. No. 1027417
MDMX siRNA: GACCACGAGACGGGAACATTA	Qiagen	Cat. No. 1027417
AllStars Negative Control siRNA	Qiagen	Cat. No. 1027280
Software and Algorithms
MATLAB 2019b	The MathWorks, Inc.	https://www.math-works.com
P53 Cinema Single Cell Tracking Software	(Reyes et al., 2018)	https://github.com/balvahal/p53Cine-maManual
Custom Matlab script- model	This work	https://github.com/Mathiasheltberg/In-teractionsP53Net-work

Box 1: Impact factors in systems biology - Using models to rule out and validate hypotheses.

Mathematical models are routinely built to represent known biological interactions and recapitulate the behaviors they generate. However, not all interactions operate in each context, and determining which are relevant in a given situation can be challenging. The approach described here allows for rapid interrogation of a model’s structure and identification of the interactions that contribute to biological behavior under a specific situation, provided that the model is an accurate, though purposefully simplified, representation of known biology. It can be implemented in the following steps:

1. Choose a biological system that displays dynamical behaviors of interest. For example, the system studied here contains three main features: maintenance of a steady baseline before perturbation, an initial high-magnitude pulse following perturbaton, and sustained oscillations that follow the pulse.

2. Construct a minimal model of the system. The model shown here used two ordinary differential equations to describe concentrations of p53 and Mdm2 over time, six free biological parameters (α, β, γ, Ψ, δ, TDel), and included no non-linearity. Biological parameters were chosen based on previous knowledge and experimental observation; in this case, they allow for stereotypical p53 oscillations with a period of 5.5 hours.

3. Incorporate impact factors into the model. Allocate an impact factor to each biological parameter susceptible to variation with perturbation to the system, in this case Mdmx depletion. Each potential interaction is mathematically modeled based on experimentally determined parameters, and an impact factor (by definition of value > 0) is introduced into each equation to model the strength of the interaction.

4. Simulate the models. Each potential interaction is simulated at a range of impact factor values, and the outcomes are compared with the experimentally-observed data. If a value of zero best fits the data, the result implies that the associated interaction is not relevant in the given context. Although values of different impact factors cannot be directly compared, the relative contribution of a given interaction in different contexts can be ascertained by the magnitude of the impact factor in each setting.

5. Observe the dynamical behaviors of relevant components of the model, looking for qualitative agreement between the behaviors the model displays and experimental observations. For example, in this work we looked for a steady baseline of p53 before Mdmx depletion, a high-magnitude pulse after, then sustained oscillations.

The chosen models can be further analyzed to reveal other dynamical features that may or may not be possible to extract from experimental data. In this case, our models yielded insights into the size of limit cycles (reflected in the amplitude of p53 oscillations) and the length of trajectories between the initial and final steady state (reflected in the amplitude of the first peak). (Figs. 2G, H, L).