Performance of matching methods in studies of rare diseases: a simulation study

Summary

Matching is a common method of adjusting for confounding in observational studies. Studies in rare diseases usually include small numbers of exposed subjects, but the performance of matching methods in such cases has not been evaluated thoroughly. In this study, we compare the performance of several matching methods when number of exposed subjects is small. We used Monte Carlo simulations to compare the following methods: Propensity score matching (PSM) with greedy or optimal algorithm, Mahalanobis distance matching, and mixture of PSM and exact matching. We performed the comparisons in datasets with six continuous and six binary variables, with varying effect size on group assignment and outcome. In each case, there were 1,500 unexposed subjects and a varying number of exposed: N = 25, 50, 100, 150, 200, 250, or 300. The probability of outcome in unexposed subjects was set to 5% (rare), 20% (common), or 50% (frequent). We compared the methods based on the bias of estimate of risk difference, coverage of 95% confidence intervals for risk difference, and balance of covariates. We observed a difference in performance of matching methods in very small samples (N = 25-50) and in moderately small samples (N = 100-300). Our study showed that PSM performs better than other matching methods when number of exposed subjects is small, but the matching algorithm and the matching ratio should be considered carefully. We recommend using PSM with optimal algorithm and one-to-five matching ratio in very small samples, and PSM matching with any algorithm and one-to-one matching in moderately small samples.

1. Introduction

The generation of an appropriate comparator group is a challenge for many studies related to epidemiology, health care, benefit assessment, and the cost-effectiveness of treatments. The potential exists to establish a comparator group from either secondary data, historical groups or meta analyses. The number of studies using propensity score matching (PSM) for this purpose is increasing, with the number of publications using these methods increasing from 432 in 2010 to 3,335 in 2018 (1).

Studies of rare diseases often include comparisons between two or more groups, at least one of which has a small sample size. Such comparisons are subject to confounding and the consequent biases that are generated. Confounding is present when subjects' characteristics, both observed and unobserved, are not randomly imbalanced between two comparison groups (2). In randomized controlled trials, the balance (or imbalance due only to chance) of characteristics is usually achieved in the study design stage, when the two groups are randomized before treatment assignment. In observational studies, it is impossible to achieve this balance before the group assignment, and accounting for it in the analysis stage is therefore necessary.

Confounding in comparison analyses can be reduced in a number of ways, such as by regression adjustment, stratification, or matching (3) or by a combination of two methods (4). Regression adjustment is a common method, which adjusts for confounding by directly including the confounding covariates in the regression model. Another method of confounding adjustment involves stratifying the observations into groups based on the fixed values of a confounder, so that the values of the confounder do not vary within each group. The analyses are performed separately in each of the stratified groups, and the results are then combined. Lastly, adjusting for confounding in large observational studies can be achieved by matching, where similar exposed and unexposed subjects are matched, and the analysis is performed on the matched exposed and unexposed subjects only. One common method for matching the observations is PSM (2). In this method, exposed and unexposed subjects are matched on a similar propensity score, which is the probability of being exposed given the values of other covariates. As with all the methods for adjusting for confounding, PSM is based only on a subject's observed characteristics. That is, PSM can only adjust for characteristics included in the propensity score model, and it is sensitive to how the propensity score model is specified.

Various aspects of PSM have been studied in the past; however, most of the studies on and using the method have involved datasets with large samples (5,6). Studies have also been conducted to gain more specific details about matching, such as the advantages of one-to-many matching in PSM (7) or the ideal caliper widths in PSM (8). However, to our knowledge, the performance of PSM in small samples has only been scarcely studied (6,9,10). A recent study by Cottone (11) explored the advantages of combining propensity score methods (matching, stratification, and weighting) with regression adjustment. Austin (12) performed one of the most detailed studies on propensity-score-based matching in small samples, in which several propensity-score-based matching methods were compared to one another. None of the previous studies, however, including the studies by Cottone (11) and Austin (12), has compared the performance of PSM methods in small samples to matching methods that are not based on propensity scores, and no study has assessed the performance of matching methods across different outcome rates. In addition, no studies have been carried out with small samples examining the sensitivity of various matching models to unobserved confounding.

Statistical methods have been developed to provide unbiased results under certain assumptions, such as appropriate variable distribution or adequate sample size (13). Those assumptions are especially likely to be violated in studies with small sample sizes, and the methods used in such studies should be carefully considered (14-17). Matching observations from small samples can pose some unique problems that might not exist in matching larger datasets. First, because of the small sample size, building a propensity score model that takes into account all the relevant variables might be difficult. Furthermore, if a propensity score model is not specified correctly or does not include all the variables associated with the outcome, then the bias in the results might not be lessened using PSM. Second, there has recently been a discussion about whether PSM increases or decreases the balance in matching variables (18,19), but the balance in these variables has not been studied in small samples. Since PSM does not balance the sample on individual variables, but on an overall score, it is possible that in small samples, the overall balance of the samples will not be achieved. Finally, in small samples, the outcome rate should possibly influence the analysis method that is used. Outcomes with low rates of occurrence can result in a small number of outcomes observed, thus making the analysis highly sensitive to analysis methods.

In this study, we evaluate the performance of PSM when the number of exposed subjects is small, and we compare it to performance of matching methods that are not based on propensity scores or not based only on propensity scores. We examine the performance of each of the methods in several different scenarios in terms of sample size and outcome rate. Lastly, we examine the effect that unobserved confounding has on the results from each matching method.

2. Materials and Methods

We used a series of Monte Carlo simulations (20) to compare the performance of different matching methods when the number of exposed subjects is small. Each simulated dataset included one binary outcome and 12 covariates, 6 of which were continuous and 6 of which were binary. We evaluated the performance of seven matching methods, which are described in Table 1. Briefly, four of the matching methods were based on propensity score distance, with two of them using greedy and two of them using optimal matching algorithms. Two of the methods were based on the Mahalanobis distance. The last method was based on a mixture of PSM with a greedy algorithm for continuous covariates and exact matching for binary variables. For three of the methods, we assessed both one-to-one matching, where each exposed subject is matched to only one unexposed subject, and one-to-five matching, where each exposed subject is matched to five unexposed subjects. All matching algorithms were assessed without replacement, meaning that each unexposed subject can be matched to only one exposed subject.

Table 1. The list of matching methods evaluated in the study.

Method	Distance Measure	Variables included	Matching Algorithm	Matching Ratio
1	Propensity Score	All	Greedy	one-to-one
2	Propensity Score	All	Greedy	one-to-five
3	Propensity Score	All	Optimal	one-to-one
4	Propensity Score	All	Optimal	one-to-five
5	Mahalanobis	All	N/A	one-to-one
6	Mahalanobis	All	N/A	one-to-five
7	Propensity Score	Continuous	greedy	one-to-one
	Exact	Binary	N/A

2.1. Description of the matching methods

Propensity score matching identifies pairs of exposed and unexposed subjects based on propensity score and not based on any specific variable value. Propensity score is the probability of a subject being exposed based on its characteristics (2). Two algorithms are commonly used to determine how exposed and unexposed subjects should be matched based on propensity score (12):

1). Greedy algorithm. Here, an exposed subject is matched to an unexposed subject with a propensity score closest to that of the exposed subject.

2). Optimal algorithm. Here, all matched pairs are formed by minimizing the average within-pair difference of propensity scores.

Mahalanobis distance matching (3,21) is another matching method that considers the overall distance between subjects, not the values of individual variables. This distance measurement is based on the Euclidean distance between two observations, and it takes into account the variance-covariance matrix (Ʃ). The Mahalanobis distance between two observations i and j with covariate vector x is defined as follows:

$$d^2(i,j)=(x_i-x_j{)}^T\sum {}^{-1}(x_i-x_j)$$

Exact matching (3) is a method that examines the value of each variable, and it matches subjects only when they have the exact same values for matching variables. This method is most commonly used for discrete variables.

2.2. Description of the Monte Carlo simulations

We based the design of our study on previous studies by Peter Austin (8,12); however, we adapted it to our research question. The specific details for covariates and outcome simulations are presented below.

2.2.1. Covariates

For each observation, we generated six continuous variables and six binary variables with values of either 0 or 1. For the unexposed subjects, each continuous variable was drawn from an N(0,1) distribution. For the exposed subjects, variables X₁ - X₃ were drawn from an N(0,1) distribution, and variables X₄ - X₆ were drawn from an N(0.5,1) distribution. Furthermore, all the binary variables for the unexposed subjects were drawn from Bin(1,0.5) distribution, whereas for the exposed subjects, variables X₇ - X₉ were drawn from a Bin(1,0.5) distribution, and variables X₁₀ - X₁₂ were drawn from a Bin(1,0.75) distribution. The reason for choosing different variable distributions between exposed and unexposed subjects was to simulate confounding. If the distribution of a variable is different for exposed versus unexposed subjects, and if the variable is associated with the probability of the outcome, then such a variable is considered to be a confounder.

2.2.2. Outcome

We generated a binary outcome for each observation based on the values of the covariates. Binary outcomes are common outcomes in observational health-care research. Some examples of binary outcomes include mortality, the presence or development of a comorbidity (e.g. cancer or heart disease), the presence or development of a symptom (e.g. pain), and hospital readmission. We assumed the following logistic regression model that relates the probability of outcome (Y) to the covariates (X₁ - X₁₂) and the assignment variable (exposed: T = 1; unexposed: T = 0).

$$\begin{array}{cc}\hfill logit(p_{i,outcome})& ={\alpha }_{0,outcome}+\beta T_i+{\alpha }_N{X}_{1,i}+{\alpha }_M{X}_{2,i}\hfill \\ \hfill & +{\alpha }_H{X}_{3,i}+{\alpha }_N{X}_{4,i}+{\alpha }_M{X}_{5,i}+{\alpha }_H{X}_{6,i}\hfill \\ \hfill & +{\alpha }_N{X}_{7,i}+{\alpha }_M{X}_{8,i}+{\alpha }_H{X}_{9,i}+{\alpha }_N{X}_{10,i}\hfill \\ \hfill & +{\alpha }_M{X}_{11,i}+{\alpha }_H{X}_{12,i}\hfill \end{array}$$

The regression coefficients were set to reflect no effect, a medium effect size, and a high effect size:

$${\alpha }_N=log(1),{\alpha }_M=log(1.25),{\alpha }_H=log(2).$$

Here, α_0,outcome was estimated three times using a Monte Carlo iterative process and bisection method (22), so that the probability of outcome in unexposed subjects was one of the following: 5% (rare outcome), 20% (common outcome), or 50% (frequent outcome). In addition, β was estimated using a separate Monte Carlo iterative process and bisection method (22), so that the risk difference between exposed and unexposed subjects equaled 0.1.

2.2.3. Monte Carlo simulations

We used a complete factorial design in which two factors are allowed to vary: the number of exposed subjects and the probability of outcome among the unexposed subjects. We randomly generated datasets with size 1,500+N. In each case, there were 1,500 unexposed subjects and a varying number (N) of exposed subjects: N = 25, 50, 100, 150, 200, 250, or 300. This led to final datasets (exposed and unexposed subjects combined) with sample sizes varying from 1,525 to 1,800. The results from any method with a one-to-five matching ratio when N = 300 are equivalent to those without matching, since in this case, one-to-five matching will include all exposed and unexposed subjects. This scenario is included in the study to illustrate the general significance of matching. Next, we generated 1,000 samples from each of the 1,500+N observations, with error term ~N(0,1). We calculated the probability of outcome (p_i,outcome) using the logistic regression model above, and we then used the probability to generate the outcome for each observation from binary distribution Bin(1,p_i,outcome).

2.3. Analysis

Once the datasets were generated, we applied the seven matching methods described above in each of the 1,000 samples of each scenario. We used all 12 covariates in the estimation of the propensity score model and the Mahalanobis distance. In each matched sample, we estimated the following characteristics:

Bias of the estimate of risk difference. We estimated the prevalence of the outcome both in exposed and in unexposed subjects in each matched dataset and calculated the difference between them. The overall bias of the estimate was the difference of mean of this measure across the 1,000 samples and 0.1 (the risk difference set by simulations).

Balance. we calculated the mean of absolute values of standardized difference between exposed and unexposed subjects across all the variables. The overall balance was the mean of this measure across the 1,000 samples. This measure of balance was introduced by Austin (23) and is defined as follows:

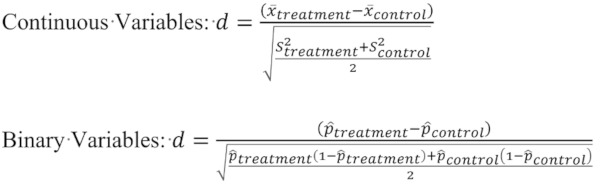Coverage. For each matched dataset, we determined whether the 95% confidence interval for risk difference contained the true risk difference (24) (0.1). The overall coverage was the percentage of 1,000 samples in which the 95% confidence interval included 0.1.

The simulations were conducted using SAS software (25), and the matching was performed using MatchIt (26,27) R package.

3. Results

3.1. Bias

We observed three noteworthy points when examining the bias of estimated risk difference across different outcome rates and sample sizes of the exposed subjects. First, the baseline outcome rate was a factor in how different matching methods performed when estimating the risk difference between exposed and unexposed subjects (Figure 1). When the outcome was rare (5%), the differences in the bias of estimated risk difference were smaller between the methods studied than when the outcome was frequent (20%) or common (50%). The outcome rate also seems to affect whether the methods lead to overestimation or underestimation of the risk difference. When the outcome was rare, all methods led to overestimation of the risk difference, and when the outcome was common or frequent, five of the matching methods (propensity score methods using one-to-five matching, Mahalanobis distance methods, and the mixture of propensity score and exact matching methods) also consistently overestimated the risk difference. While PSM methods with one-to-one matching did not necessarily estimate the risk difference exactly, they did not consistently overestimate or underestimate it.

Figure 1.

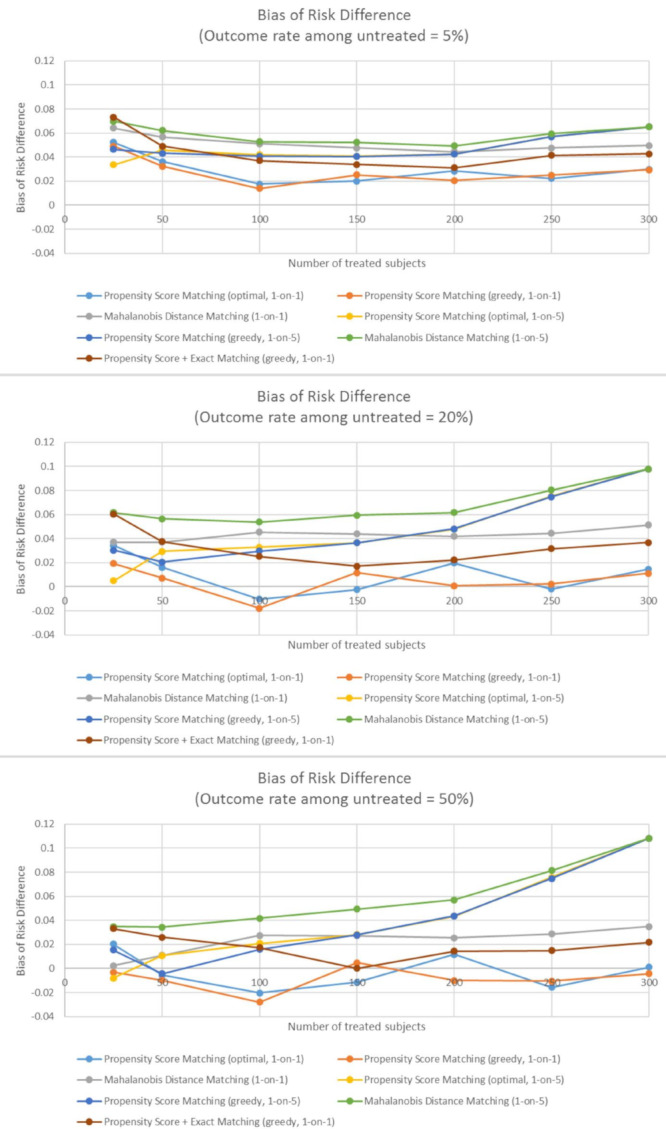
The bias of risk difference across different samples sizes of exposed subjects and different matching methods when outcome is rare (panel A), common (panel B), and frequent (panel C).

Second, the more common the outcome, the largest the bias in risk difference for fully matched samples. That is, in one-to-five matching with 300 exposed subjects, which is equivalent to no matching at all, the bias was largest for the frequent outcomes and smallest for the rare outcomes (Figure 1).

Third, a difference in the performance of methods was found in very small samples (25-50 exposed subjects) and in moderately small samples (100-300 exposed subjects). In very small sample sizes, no method was found that clearly outperforms all others. Mahalanobis distance matching using one-to-five matching led to the largest bias in very small samples, independent of outcome rate. Moreover, all the propensity-score-only methods performed similarly in very small samples, and there is some indication that propensity score one-to-five matching with the optimal algorithm performed especially well in the smallest samples (N = 25) (Figures 1 and Figure 2). The mixture of propensity score and exact matching did not perform as well as propensity-score-only matching methods in very small samples.

Figure 2.

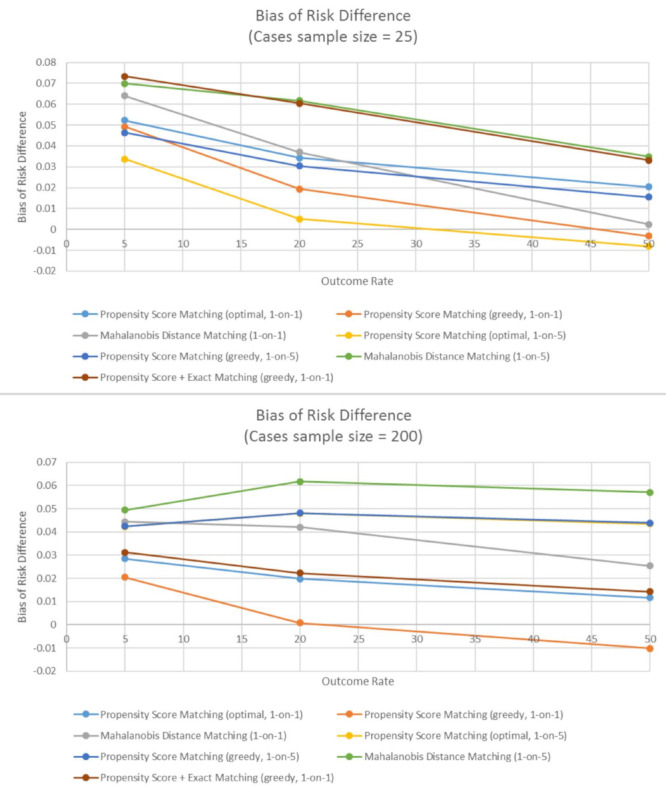
The bias of estimated risk difference when number of exposed subjects is 25 (Panel A), and when number of exposed subjects is 200 (Panel B). The bias is evaluated across different outcome rates and different matching methods.

In the moderately small samples, PSM with a one-to-one ratio, with either an optimal or a greedy matching algorithm, resulted in smaller bias than any other matching method. Furthermore, the mixture of propensity score and exact matching performed better than the Mahalanobis methods or any one-to-five matching methods, but not better than propensity-score-only one-to-one matching methods (Figures 1 and Figure 2). In addition, independent of outcome rate, the performance of propensity-score-only one-to-one matching methods and a mixture of propensity score and exact matching methods were better in moderately small samples than in very small samples, which was not true for other matching methods (Figure 1). Finally, similar to very small samples, the bias was also the largest for one-to-five Mahalanobis distance matching in moderately small samples.

3.2. Balance

As with the bias of estimated risk difference, the method that leads to the best balance differs between very small samples of exposed subjects (N = 25-50) and moderately small samples (N = 100-300). In very small samples, all propensity-score-based matching methods performed similarly well, with the exception of propensity score one-to-one matching with an optimal algorithm. In moderately small samples, similar to bias in most cases, propensity score one-to-one matching, with either optimal or greedy algorithm, lead to the best balance between exposed and unexposed subjects. All the matching methods with one-to-five matching result in worse balance, especially as the sample size increases (Figure 3).

Figure 3.

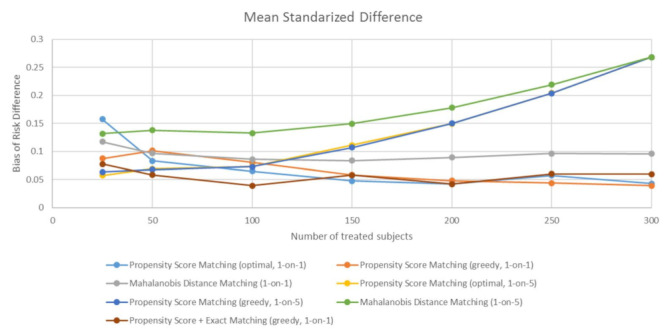
The balance of covariates in matched datasets, defined as mean standardized difference. The balance is evaluated across different sample sizes and different matching methods.

3.3. Coverage

In very small samples, all of the matching methods result in 95% confidence intervals that include the true risk difference between 83.2% and 91.8% of the time. Overall, methods based on propensity score only perform better than other methods, especially as the sample size increases. In very small samples, methods with one-to-five matching ratio outperformed methods with one-to-one matching ratios (Figure 4).

Figure 4.

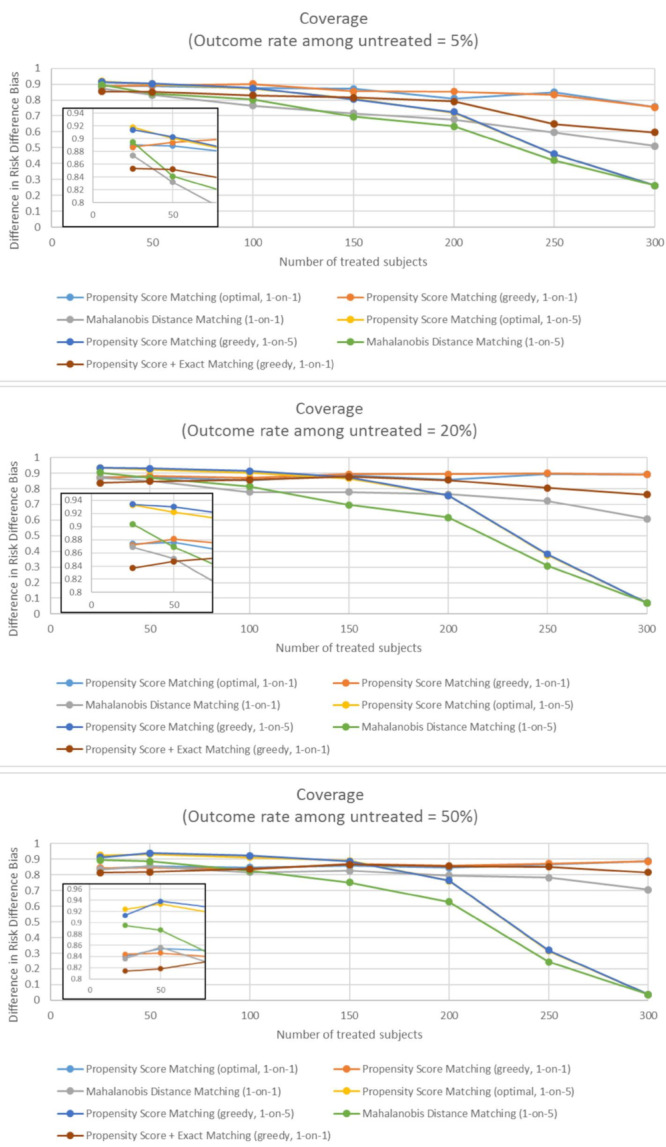
The coverage of matching methods, defined as percent of matched datasets in which the 95% confidence intervals contains the true risk difference, when outcome is rare (panel A), common (panel B), and frequent (panel C). The coverage is evaluated across different sample sizes and different matching methods.

As the number of exposed subjects increased, increasing the matching ratio led to a loss of accuracy. Therefore, for the moderately small samples, the coverage was the best when using one-to-one PSM, in which case the 85% confidence intervals (CIs) included a true risk difference between 85% and 90%. Finally, across all sample sizes of exposed subjects, the mixture of propensity score and exact matching resulted in worse coverage than propensity-score-only matching methods (Figure 4).

4. Discussion

In this study, we used Monte Carlo simulations to evaluate and compare the performance of several matching methods for a small sample of exposed subjects. The methods we considered were based on propensity scores, the Mahalanobis distance, and a mixture of propensity score and exact matching. We considered a combination of continuous and binary variables, various baseline outcomes rates, and various numbers of exposed subjects in a dataset.

Our study demonstrates that differences exist in the performance of matching methods between very small samples (N = 25-50) and moderately small samples (N = 100-300). Based on the results of our study, we conclude that in very small samples, PSM still performs better than matching based on the Mahalanobis distance; however, there are still differences between PSM algorithms and ratios. Depending on the goal of the matching analysis, different methods might be considered. Both algorithms in one-to-one matching lead to a relatively small bias, and some evidence was found that in very small sample sizes, one-to-five matching with an optimal algorithm results in the smallest bias. The mixture of propensity score and exact matching does not perform as well as methods that include both continuous and binary variables in the estimation of propensity scores, and it should therefore not be used in studies with very small samples. Furthermore, propensity score one-to-one matching with an optimal algorithm results in a relatively high imbalance in the distribution of covariates, but the greedy algorithm in one-to-one matching performs better. Propensity score one-to-five matching results in the highest coverage when the number of exposed subjects is very small. Therefore, if the goals of the matching are to decrease the bias of estimated risk difference, increase the balance in covariates, and increase the coverage of 95% confidence intervals in very small samples, then propensity score one-to-five matching with an optimal algorithm should be used.

In moderately small samples, PSM with an optimal algorithm performs similarly to PSM with a greedy algorithm, and they both perform better than matching on the Mahalanobis distance. In addition, one-to-one matching leads to a smaller bias of estimated risk difference, better balance, and better coverage than one-to-five matching. The poor performance of one-to-five matching in moderately small samples is likely a result of the lack of high-quality matches once the sample size of exposed subjects increases. Nonetheless, propensity score one-to-one matching is the better method in moderately small samples.

Our study also demonstrates that the baseline outcome rate affects the size of the bias in estimated risk difference, but it does not necessarily influence which method performs best compared to others. The more important factor in distinguishing between the methods is the number of exposed subjects.

Our results are similar to other studies that have suggested that there is no clear best-matching method. Fullerton et al. assessed the performance of propensity-score-based methods and exact matching methods in terms of balance (28). While their study was not performed using small samples, it concluded that the best method is sensitive to the definition of balance, and they recommended that best practice would be to include the application of several matching methods. Moreover, a study by Baser examined the performance of different PSM methods (29) in a large sample; it also concluded that no superior method exists and that sensitivity analysis should be used. In one of the rare studies with small samples, Pirracchio found that PSM matching methods lead to unbiased results for estimating marginal odds ratios (9). Our study builds on these conclusions and demonstrates that there is no one superior propensity-score-based matching method in small samples, but that any such method is better than the Mahalanobis-distance-based method or a mixture of propensity score and exact matching methods.

One other important point in analyzing matching samples is the statistical significance. Our study suggests that, as expected, one-to-five matching can lead to a higher bias than one-to-one matching. However, the higher number of subjects in a comparison sample increases the accuracy of statistical comparisons, as revealed by the increased coverage of one-to-five matching in very small samples. This increase in coverage might be more important in studies with a small number of exposed subjects than in larger studies. In small samples, variability is a more significant problem; therefore, adding more observations to the analysis might have an important impact. Prior studies have found possible benefits of one-to-many matching (7,30) and the optimal matching ratio for decreasing bias but increasing power. Those studies, however, did not focus on scenarios when samples are very small, and our finding is thus significant.

While our study explored different scenarios in terms of sample size and outcome rates, it has several limitations, and other topics should be studied further. For example, the optimal caliper width was not studied in small samples. In such samples, the trade-off between the percentage of observations matched and the quality of matches might be different than in large samples. In addition, in our study, we did not examine the effects of including in the propensity score model matching variables that are not associated with the exposure and/ or outcome. The effect of including variables with little or no associations should be studied more closely, since inclusion of variables might have a major impact in small samples.

Our study has significance in several applications, such as health-care research; pharmacoepidemiology; clinical effectiveness studies; and health economics studies in rare diseases based on nonexperimental observational studies, secondary data, or registries. Studies in health-care research can be time and resource consuming, and often only samples of limited sizes can consequently be collected. It is important to ensure that the results and conclusions of those studies are accurate, as they might lead to significant policy changes. Similarly, pharmacoepidemiological studies and research in clinical effectiveness are also often performed using small groups of patients; therefore, appropriate methods are imperative to ensure drug safety. For example, the number of innovative treatments developed for rare diseases is growing each year, and an increasing number of them are licensed on the fast track (31,32). Studies that do not undergo a regular approval process require subsequent additional pharmacovigilance, relative effectiveness, and health economics studies (33). The validity of methods used in these studies is of high importance.

In conclusion, our study demonstrates that PSM performs better than other matching methods in terms of bias in estimating risk difference, coverage, and balance of covariates, when matching a small number of exposed subjects to a larger dataset of unexposed subjects. Based on the results of the study, we recommend that a higher matching ratio (e.g. one-to-five) be used in very small samples, and a lower matching ratio (e.g. one-to-one) be used as the sample size of exposed subjects increases. It is unclear whether a greedy or an optimal algorithm performs better in PSM, and our recommendation is that both algorithms be performed as sensitivity analyses.