Abstract
The spatial resolution achievable in photoacoustic imaging decreases with the imaging depth, resulting in blurred images for deeper structures. Apart from technical limitations, the ultimate resolution limit results from the second law of thermodynamics. The attenuation of the optically generated acoustic waves on their way from the imaged structure to the sample surface by scattering and dissipation leads to an increase of entropy. The resulting loss of spatial resolution for structures embedded in attenuating media can be compensated by numerical methods that make use of additional available information. In this article, we demonstrate this using experimental data from plane one-dimensional (1D) acoustic waves propagating in fat tissue. The acoustic waves are optically induced by nanosecond laser pulses and measured with piezoelectric transducers. The experimental results of 1D compensation are also relevant for photoacoustic imaging in 2D or 3D in an acoustically attenuating medium by dividing the reconstruction problem into two steps: First, the ideal signal, which is the solution of the un-attenuated wave equation, is determined by the proposed 1D attenuation compensation for each detector signal. In a second step, any ultrasound reconstruction method for un-attenuated data can be used for image reconstruction. For the reconstruction of a small step milled into a silicon wafer surface, which allows the generation of two photoacoustic pulses with a small time offset, we take advantage of non-negativity and sparsity and inverted the measured, frequency dependent acoustic attenuation of the fat tissue. We were able to improve the spatial resolution for imaging through 20 mm of porcine fat tissue compared to the diffraction limit at the cut-off frequency by at least a factor of two.
Keywords: Photoacoustic imaging, Acoustic attenuation, Diffraction limited resolution, Super resolution, Non-linear reconstruction, Sparsity
1. Introduction
1.1. Resolution limit in photoacoustic imaging
Photoacoustic (or optoacoustic) imaging uses the thermo-elastic expansion following a rapid temperature rise after illumination of light absorbing structures within a semitransparent and turbid material, such as a biological tissue. It allows acoustic resolution with simultaneous optical absorption contrast and enables to detect hemoglobin, lipids, water and other light-absorbing chromophores, with greater penetration depth than with purely optical imaging modalities that rely on ballistic photons [[1], [2], [3]]. In photoacoustic tomography, the temporal evolution of the acoustic pressure field is sampled using an array of ultrasound detectors placed on the sample surface or by moving a single detector across the sample surface. From the measured pressure signals, images of the optical absorption within the tissue are reconstructed by solving an inverse source problem [[3], [4], [5]].
In this work, the achievable spatial resolution for photoacoustic imaging in porcine fat tissue is investigated. At depths larger than the range of the ballistic photons, i.e. more than a few hundreds of microns in tissue, light is scattered several times and the spatial resolution in photoacoustic imaging is limited by acoustic attenuation, which is caused by acoustic absorption, dispersion, and scattering. The spatial resolution degrades with increasing depth because higher acoustic frequencies, which have smaller wavelengths and allow a better resolution, are stronger attenuated than lower frequencies. As a rule of thumb, the ratio of the imaging depth to the best spatial resolution is roughly constant and has a value of 200 [3]. Although acoustic attenuation defines the ultimate spatial resolution limit, other factors such as detector bandwidth, element size and the area over which the acoustic signals are recorded at the sample surface – the detection aperture – can be limiting factors in practice [2]. These technical limitations can be avoided in principle – or at least can be reduced.
There have been several attempts for mathematically compensating the acoustic attenuation to get images with a higher spatial resolution. Already in 2005, La Riviere et al. proposed an integral equation that relates the measured acoustic signal at a given transducer location in the presence of attenuation to the ideal signal in the absence of attenuation [6,7]. The frequency dependent attenuation was mathematically described by the imaginary part of a complex wave-vector, and shows a power-law behavior in frequency [8]. Ammari et al. later gave a compact derivation of this integral equation directly by using wave equations, which is equally valid for all dimensions [9]. Moreover, compensation of acoustic attenuation and dispersion in two or three dimensions can always be reduced to a one-dimensional problem in a two-stage process: first, for each detector location the ideal signal in the absence of attenuation is calculated from the measured signal. This is a one-dimensional (1D) reconstruction problem. In a second step, any reconstruction method for photoacoustic tomography without acoustic attenuation, such as time-reversal or backprojection, can be used for reconstructions in higher dimensions [4,6,7]. Therefore it is sufficient to examine the acoustic attenuation of 1D acoustic waves and the reconstruction in 1D. Compensation of acoustic attenuation in higher dimensions can always be reduced to 1D, which was also shown explicitly for signals from a layer (1D), cylinder (2D), and a sphere (3D) [10].
Dean-Ben et al. compared the signal amplitude reduction and the broadening due to acoustic attenuation to the influence of the transducer bandwidth and space-dependent speed of sound and established a correction term for space-dependent attenuation [11]. Kowar and Scherzer presented compensation for acoustic attenuation for different wave equations [12]. Burgholzer et al. have compensated directly the attenuation in photoacoustic tomography by using a time reversal finite differences method [4,13,14]. This approach was later extended by Treeby et al. to account for general power law absorption behavior [15,16]. Inspired by attenuation compensation in seismology, Treeby proposed a new method for attenuation compensation in photoacoustic tomography using time-variant filtering [17].
Mathematically, the compensation of frequency-dependent acoustic attenuation is an ill-posed inverse problem, where the cut-off frequency is an adequate regularization parameter. The physical reason for the ill-posedness is the second law of thermodynamics: acoustic attenuation is an irreversible process and the entropy production, which is the energy decay during wave propagation due to attenuation divided by the temperature, is equal to the information loss for the reconstructed image [14]. This information loss due to entropy production cannot be compensated mathematically. As the information content of the reconstructed image strongly correlates with the spatial resolution, this results in a fundamental resolution limit due to thermodynamic principles. Non-equilibrium thermodynamics describes the connection between entropy production and information loss, e.g. [18], and as we have already elaborated for heat diffusion [19,20], we could determine a cut-off frequency also for damped acoustic waves in water [21]. Here, this approach is generalized for a frequency dependent acoustic attenuation described by a power-law using a general exponent which might be different from two in water.
In frequency space, the information content of wave components with frequencies above that cut-off frequency is so low that they cannot be statistically distinguished from the equilibrium distribution. This is equivalent that the acoustic wave amplitude on the sample surface is damped just below the noise level [21]. Consequently, the spatial resolution limit becomes diffraction limited and according to Nyquist it is half of the wavelength at this cut-off frequency [21]. It is not just a fortunate coincidence that the same cut-off frequency can be determined from entropy production and from noise-fluctuations, but results from the fluctuation-dissipation-relation described in statistical physics [14,19,20]. The spatial resolution is diffraction limited and corresponds to the wavelength at the cut-off frequency. To reach this thermodynamic resolution limit for compensation of acoustic attenuation experimentally, it is necessary to measure the broadband ultrasonic attenuation parameters of tissues or liquids very accurately [22] and to evaluate the existing mathematical models to get an adequate description of attenuation [23]. For the used porcine fat tissue in the measured frequency range, a power law very well describes the dependence of the attenuation on frequency. We emphasize, however, that the proposed method for evaluating the principle resolution limit is applicable to any acoustic attenuation model described by a complex wave number.
1.2. Breaking the resolution limit
If additional information is used, the fundamental resolution limit can be overcome. In optical imaging, the diffraction limit could be overcome for the first time by Stimulated Emission Depletion (STED) microscopy [24,25]. Later, other super-resolution methods like stochastic optical reconstruction microscopy (STORM) [26], photo-activated localization microscopy (PALM) [27], or super-resolution optical fluctuation imaging (SOFI) [28] emerged. Although resolution in optical imaging has been significantly improved, there is still rapid progress in the development of high resolution imaging for many other imaging modalities. Localization microscopy has been used to achieve super-resolution in ultrasound imaging by employing scattering microbubbles instead of fluorescent molecules as point sources [29,30]. Ultrafast localization microscopy allows for super-resolution ultrasound imaging of vasculature in whole organs [31]. For photoacoustic imaging in a (quasi) diffusive regime a comprehensive overview about the advances in super-resolution imaging was recently given by Junhui Shi et al. [32].
How is it possible for these methods to gain additional information about the structures to be imaged and to use this information for image reconstruction? In these methods, information gaining is based on the localization of point sources, which can be achieved to a much higher precision than the diffraction limit. Point sources can be activated fluorescent molecules [[26], [27], [28]], particles or droplets [33,34], or optical absorbers illuminated by structured illumination such as laser speckles [[35], [36], [37]]. Multiple such images are combined for the reconstruction of one “super-resolution” image. This can be demonstrated on our iterative joint sparsity (IJOSP) algorithm [36], which favors small sources (“sparsity”) having the same location on each of the multiple images (“joint”). All these methods need additional experimental effort to obtain such point sources in multiple images, either by moving particles or droplets, or by changing the structured illumination pattern.
In this work, it is demonstrated, that even for conventional photoacoustic data acquisition using one image with homogeneous illumination and without moving particles or droplets, this resolution limit can be significantly exceeded by taking non-negativity and sparsity information as an additional knowledge into account. Therefore, resolution enhancement can be achieved for all existing conventional photoacoustic tomography or acoustic resolution microscopy set-ups without additional time required for multiple measurements. This was inspired by works from geophysics, where the attenuation of seismic signals was compensated [38,39]. Sparsity as additional information has been used in compressive sensing, see e.g. Donoho [40]. In 2016 we have introduced sparsifying temporal transforms for compressed sensing in photoacoustic tomography [41], and sparsity / non-negativity constraints have been used for 2D and 3D photoacoustic image reconstruction, but not for the compensation of acoustic attenuation [[42], [43], [44]]. The two-stage process described in section 1.1 allows the parallel computation of attenuation compensation in 1D, where sophisticated iterative algorithms can efficiently implement these constraints. For one-dimensional (1D) photoacoustic pressure pulses, non-negativity is evident, because the initial pressure generated by optical heating is always non-negative and 1D pressure propagation preserves non-negativity. Propagation in 3D gives negative pressure components, but the conversion into spherical projections, which is the time integral of the measured acoustic pressure, again results in positivity for all measured signals [45].
For regularization two different methods are compared: the truncated singular value decomposition (T-SVD) method [46], which allows negative values and does not enforce sparsity, and the “Douglas Rachford splitting algorithm” (DR algorithm), which uses positivity and sparsity [47,48]. We show, that the resolution from T-SVD corresponds to the principle diffraction limit given by the information loss from entropy production. The better resolution by using the DR algorithm is enabled by taking positivity and sparsity into account. Experimentally, this is demonstrated in 1D, but as mentioned in section 1.1, the same resolution enhancement is expected in axial direction in 3D by using spherical projections. In lateral direction, due to limited angle effects, the resolution enhancement might be less, but can be further enhanced by using weight factors [49].
Here, the resolution limit is defined as half of the wavelength of the cut-off frequency, at which the acoustic signal at the surface is damped just below the noise level. For linear reconstruction methods, this is equivalent to the width of the reconstruction of a point-source signal, which is the point-spread function. For non-linear methods, such as the used DR algorithm, the blurring depends on the number of iterations and the acoustic signal itself, and therefore resolution cannot be defined as the width of the point-spread function any more, but how well distinct sources can be distinguished from each other in the reconstructed image. Therefore, resolution has to be defined as a measure of localization.
2. Methods
2.1. Experimental setup
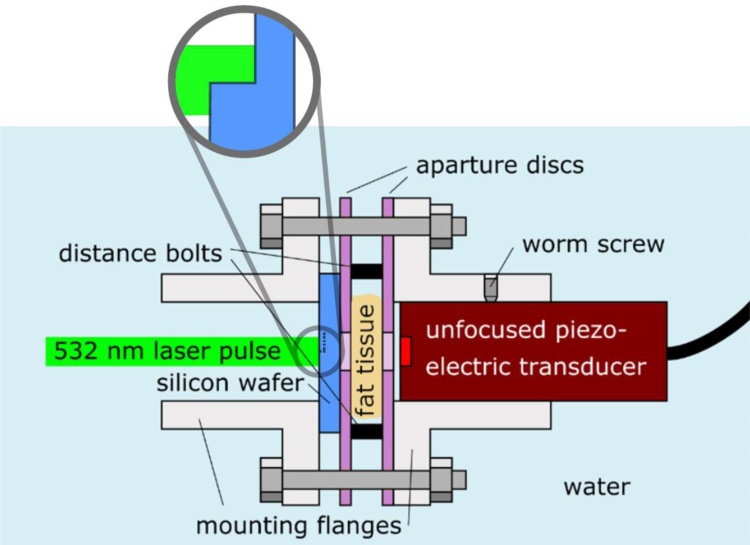
Ultrasonic waves were generated, attenuated, and detected experimentally in a setup sketched in Fig. 1. To excite strong and broadband ultrasonic signals, a laser ultrasound method is employed [50,51]. Short nanosecond laser pulses are directed on a silicon wafer. A cylindrical region of the wafer, ranging from the surface to a depth of a few microns and with a diameter determined by the laser beam, abruptly heats up by optical absorption. The subsequent thermoelastic expansion of the heated volume leads to the emission of ultrasonic waves mainly directed perpendicular to the surface of the wafer. Porcine subcutaneous fat tissue in the propagation path of the sound waves leads to acoustic attenuation due to absorption and scattering. After exiting the tissue the sound waves propagate through water and are detected by a piezoelectric transducer. The resulting electrical signals are amplified (5073PR-40-E, Olympus NDT Inc., Waltham, MA) and sampled by an oscilloscope (DSO 5043, 300 MHz; Agilent Technologies Inc., Santa Clara, CA).
Fig. 1.
Setup for the generation and detection of acoustic plane waves. Abrupt local heating of a silicon wafer by nanosecond laser pulses leads to the emission of strong broadband ultrasonic plane waves. Porcine subcutaneous fat tissue in the propagation path induces frequency dependent attenuation of the acoustic signals. The fat tissue is fastened between two aperture disks applying a small axial force on the tissue. Distance bolts with 6 mm or 20 mm ensure two precise lengths of the attenuation path. For these two lengths, attenuated acoustic plane waves were detected by an unfocused piezoelectric transducer, which was aligned by worm screws to ensure a one-dimensional signal propagation and detection. Image from https://doi.org/10.3390/jimaging5010013 by Burgholzer et al. was edited and is used under CC BY 4.0.
Two mounting flanges hold the parts by a small axial force applied by two screws to keep a well-defined distance to the piezoelectric transducer of 6 mm and 20 mm. To get simultaneously two signals slightly shifted in time through the fatty tissue, a small step is fabricated by ion milling near the beam center of the silicon wafer. By using an unfocused piezoelectric transducer (V358-SU, Panametrics, Waltham, MA) the influence of possibly occurring local variation of the attenuation is decreased. If the silicon wafer shows a small step near the beam center the two slightly shifted signals in time through the fatty tissue overlap. The transducer has a center frequency of 50.6 MHz, a diameter of the sensing element of 6.35 mm and a -6 dB bandwidth of 81.2 %. Within the observed bandwidth, the acoustic attenuation occurring in the short paths of water in the setup can be safely neglected compared to the strong attenuation caused by the relative thick layers of fat [11,21]. Therefore, different water path lengths do not change the measured signals. The mechanical set-up is designed in a way to ensure parallel alignment of the silicon wafer, the fat tissue and the piezoelectric transducer. Inclination of these components would lead to unwanted signal losses due to refraction and reflection. Also, since the waves show plane wave behavior, an inclination of the wavefront relative to the sensing element of the transducer will lead to a misleading low-pass-filtering of the signals. A detailed description of the setup can be found in [22]. The ultrasound-generating optical pulses have a diameter of 6 mm and are emitted by a frequency-doubled Nd:YAG laser (Continuum Surelite, 20 Hz repetition rate, 6 ns pulse duration, 532 nm center wavelength). The used pulse energies ranged from 12 mJ to 65 mJ.
2.2. Compensation of acoustic attenuation and resolution limits
As mentioned in section 1.1, the compensation of acoustic attenuation in photoacoustic imaging can be reduced to 1D. The relation between the ideal acoustic wave pressure without attenuation and the attenuated wave pressure at the same 1D, 2D, or 3D location is identical for all dimensions, as shown by Ammari et al. in a compact way [9], which reads in frequency domain:
| (1) |
where is the angular frequency, and the tilde indicates the Fourier transformation in time of the signals and , respectively. The complex wave number describes the frequency dependent dispersion and attenuation with the phase velocity and the attenuation coefficient . For the ideal wave without attenuation, the wavenumber is real and is the sound velocity for the ideal wave, which shows no dispersion and frequency dependency. Phase velocity and attenuation coefficient are connected by a Kramers-Kronig relationship to guarantee causality [52].
For an acoustic signal, which propagates through an attenuating sample of a defined thickness, the effect of acoustic attenuation in 3D and its compensation was modeled in frequency domain by Dean-Ben et al. [11]. Here, this derivation will be performed in 1D, as we get plane waves according to our experimental setup described in section 2.1. As the acoustic attenuation in water compared to fat tissue for the bandwidth covered by our detector can be neglected [11,12], the signal measured in water without any fat tissue is taken as the ideal one. With the Helmholtz equation for a uniform attenuating medium and a point source located at the origin [11], one gets by using the 1D Greens function the relation between the attenuated and the ideal signal:
| (2) |
where is the difference of the complex wavenumber for the attenuated wave and the real wave number for the ideal wave:
| (3) |
Eq. (2) is derived from Greens functions, but as the Helmholtz equation is a linear differential equation, it can be used for any solution. Compared to the 3D equation from Dean-Ben et al. [11], the additional factor in Eq. (2) turns out to be approximately one for relevant frequencies and attenuation coefficients.
The attenuated wave in contrast to the ideal wave shows a decay in amplitude according to Eq. (2) of a factor of . As the attenuation coefficient increases with frequency, we can determine a cut-off frequency , for which the amplitude of the attenuated wave gets below the noise level:
| (4) |
where the signal-to-noise-ratio is the amplitude of the wave without attenuation divided by the noise level and denotes the natural logarithm. For analyzing spatial resolution in photoacoustic imaging, the width of the acoustic signal in the time domain is essential. A small width enables high spatial resolution, which corresponds to a high frequency bandwidth. If the frequency bandwidth is limited by thermodynamic fluctuations according to Eq. (4), the spatial resolution limit according to Nyquist is half the wavelength at this frequency:
| (5) |
In time domain, is the inverse Fourier transform of :
| (6) |
where denotes the convolution in time. It can be calculated analytically only in a few special cases, for example when is a power-law with exponent two which models liquids [21]. For discretized signals in time, this can be written in matrix notation:
| (7) |
where and are vectors and the matrix describes the influence of acoustic attenuation for a propagation distance of in fat tissue. Later on, this matrix comprises also the impulse response of the piezoelectric transducer and the amplifier to enable an ideal - like signal for . Multiplication by denotes the (discrete) Fourier transform, multiplication by its conjugate transpose is the inverse Fourier transform, and forms a diagonal matrix. Eq. (7) shows immediately the singular value decomposition (SVD). As discussed above the singular values decrease exponentially as . Therefore, cannot be inverted exactly, but the pseudo-inverse matrix can be approximated using the truncated SVD (T-SVD) method (see e.g. [21]). The truncation criterion for the T-SVD method comes from the discrepancy principle and states that the inverse singular values are set to zero if they get larger than the SNR [46]. This gives the same truncation frequency as the cut-off frequency in Eq. (4), and therefore the resolution from T-SVD is the same as derived in Eq. (5).
2.3. Taking non-negativity and sparsity as additional information into account
Here, an iterative algorithm, the “Douglas Rachford splitting method” (DR method) is used [53,54], to invert Eq. (7) where non-negativity and sparsity as additional information is implemented by minimizing the objective function
| (8) |
over all where is the l2-norm, is the l1-norm, and is a regularization parameter. Using the l1-norm as regularizer favors sparse solutions, which is also used in compressive sensing [40].
For each iteration of the DR algorithm the threshold operator applies soft thresholding only to the positive entries and sets the negative entries to zero. This enables to get only non-negative solutions:
| (9) |
with the iteration index , indicates the transpose matrix, is the unity matrix and is a penalty term to make the matrix inversion more robust. We kept at a fixed value, but to speed up convergence it could be adapted after each iteration step, e.g. as suggested by Boyd [55]. A good estimate for the regularization parameter is found at the edge of the L-curve that yields the best trade-off between residual norm and solution norm. For the estimation, the toolbox from Hansen was used [56].
In 3D, the wave propagation causes also negative pressure signals. Therefore, the positivity assumption cannot be applied directly. However, by using the spherical projection, which is the time integral of the measured acoustic pressure [45], positivity can be obtained. The matrix is the time integral operator in discretized form, where in the lower triangular part and in the diagonal are only ones and above the diagonal are zeros. The spherical projection is positive and Eq. (7) reads now as , where as the inverse integral operator is the differential operator. To enhance the spatial resolution for any 3D photoacoustic image reconstruction, the measured signal for each detection point can be “sharpened” by calculating using the DR method. The ideal signals are then used as the input for any 3D photoacoustic computed tomography reconstruction [4].
3. Results
3.1. Measured pressure signals
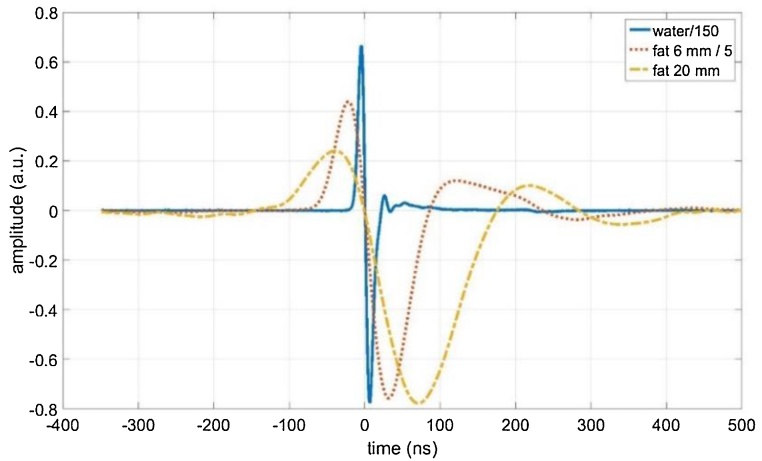
Fig. 2 shows the measured acoustic pressure as a function of time without fat tissue, with a 6 mm thick piece of porcine fat tissue, and with 20 mm thick fat tissue. The arrival time of the acoustic wave is defined as the time, when the signal gets zero between its maximum and its minimum. This time changes slightly when putting the two fat tissue samples into the measurement chamber. The sound velocity in water was 1498 m/s at a water temperature of 25.5 °C, and 1512 m/s in fat tissue at 1 MHz. The arrival time was subtracted, which allows plotting all of the signals with the same time scale. The amplitude was also scaled: the water signal was reduced by a factor of 150, and the 6 mm fat signal by a factor of five. The noise level in Fig. 2 for a single measurement is 0.45 a. u., which is in the range of the signal amplitude after 20 mm propagating in fat, and the signal would appear very noisy. Therefore, 32, 257, and 512 measurements were averaged to reduce the noise level to approximately 0.08, 0.03, and 0.02 for the water-, the 6 mm fat-, and the 20 mm fat – measurement, respectively. Together with the scaling this avoids to show the noise in Fig. 2.
Fig. 2.
Measured acoustic pressure as a function of time without fat tissue (“water”, blue solid line), with 6 mm thick porcine fat tissue (red dotted line) and with 20 mm porcine fat tissue (yellow dashed line), where a total of 32, 256, and 512 measurements were averaged, respectively. To make comparison easier, the signals were time-shifted and scaled.
By Fourier transformation in time the amplitude in frequency domain for the three signals in Fig. 2 was calculated. The acoustic attenuation coefficient in dB was determined by
| (10) |
where log is the logarithm to base 10 (Fig. 3). It turns out that a power law
| (11) |
with an exponent and fits the attenuation in a wide frequency range very well.
Fig. 3.
Measured attenuation as a function of frequency and fits of a power law (Eq. (11)). At frequencies above the truncation frequency determined by Eq. (4), attenuation cannot be evaluated due to the noise (see text).
Above the truncation frequency given by Eq. (4), which is approximately 11 MHz after 20 mm in fat tissue, and 24 MHz after 6 mm, the signal amplitude gets less than the noise level and the attenuation cannot be determined any more. According to Eq. (7), the matrix describing the acoustic attenuation problem is the Fourier transform of a diagonal matrix, where the singular values decay with , with from Eq. (11). The condition number of the matrix is the highest singular value divided by the lowest singular value, which is and therefore depends on the used maximum frequency . This was chosen as 500 MHz in our calculations, with the 2000 × 2000 matrix and results in a condition number of for 6 mm fat and for 20 mm fat it was infinity up to our numerical precision.
For the 20 mm fat signal the , after 512 times averaging the , which gives a maximal attenuation of (see noise level above 11 MHz indicated as red circles in Fig. 3).
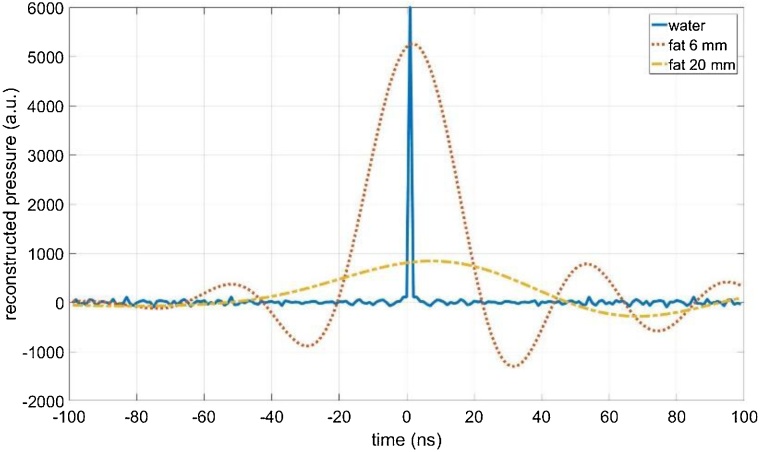
The ideal pressure signal in water without fat (blue solid line in Fig. 2) is no single positive -like pulse, but gets negative and shows additional “ringing”, because of the laser-ultrasound excitation within the silicon wafer and the characteristic of the piezoelectric transducer and the amplifier. However, to be able to use positivity and sparsity, we need a -like ideal signal for in Eq. (7). Therefore, the matrix was multiplied by a convolution matrix using the water signal as convolution kernel, which gives the water signal if a -like pulse (blue solid line in Fig. 4) is multiplied by (). Because of the linearity of Eq. (7), this results in the same signal for for a - like ideal signal as input signal (). The inverted signals using the T-SVD method are shown in Fig. 4. The width of the reconstructed pulse is the reciprocal value of the cut-off-frequency of 24 MHz for 6 mm fat tissue and 11 MHz for 20 mm fat tissue. The spatial resolution according to Eq. (5) is half the width of this reconstructed pulse multiplied by the sound velocity at that frequency: 21 ns or 32 μm for 6 mm fat, and 46 ns or 70 μm for 20 mm fat, respectively. Only by deconvolution with the water pulse from the signals shown in Fig. 2 one gets a FWHM of 75 ns or 113 μm for 6 mm fat, and 170 ns or 257 μm for 20 mm fat, respectively. This clearly demonstrates that the T-SVD method already allows a significant compensation of the acoustic attenuation (Fig. 4).
Fig. 4.
Reconstruction results using T-SVD for regularization to compensate attenuation in fatty tissue of 6 mm thickness (red dotted line) and 20 mm thickness (yellow dashed line). This corresponds to a spatial resolution limit of 32 μm for 6 mm fat and 70 μm for 20 mm fat, resulting from entropy production. The matrix was multiplied by the convolution matrix of the water signal to get a positive - like pulse for the pure water-signal without fatty tissue in the measurement chamber (blue solid line).
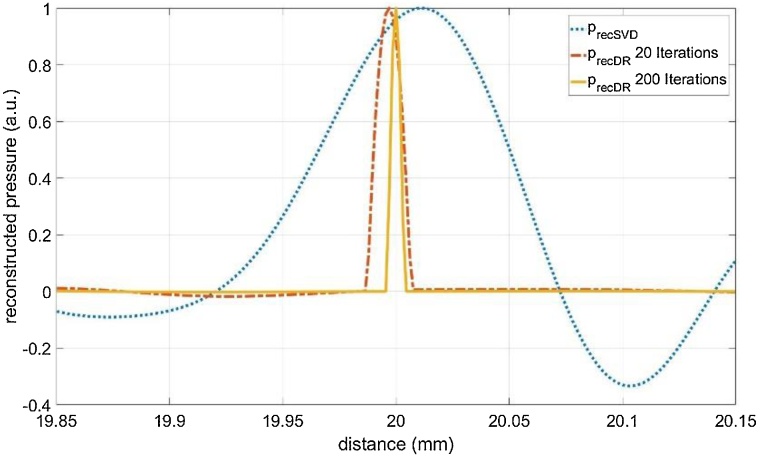
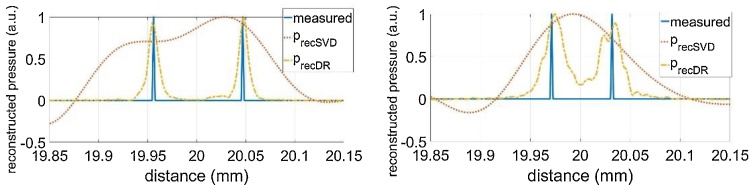
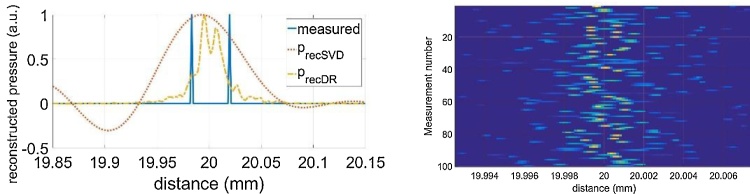
The T-SVD method is a linear reconstruction method. If the measurement is repeated several times, it gives the same result if the measurement data is averaged and then the reconstruction is calculated, or if every measurement is reconstructed and then the average of the reconstructions is calculated. This is different for the non-linear iterative DR method. Another important difference is that for the linear method the spatial resolution of the reconstruction is given by the width of the peak, as shown in Fig. 4. This is not necessarily the case for the DR method, because the width of the peak changes with the number of iterations, as shown in Fig. 5 for 20 and 200 iterations, which took only 8 s for 200 iterations on a Microsoft surface computer. Between 200 and 1000 iterations the DR solution showed only a minor change – thus we stopped at 200 iterations. Therefore, we use two overlapping point-sources at a certain distance, which is experimentally realized by flange silicon absorber having a small step in the beam-center, as described in section 2.1. Due to the unfocused piezoelectric transducer, the slightly time shifted signals propagate through the fatty tissue and overlap. Resolution is now the smallest distance, when these steps can be resolved as two individual peaks. Another difficulty in defining the resolution is, that for repeated identical measurements it can happen that sometimes the peaks can be resolved and sometimes they are not resolved, which is a SNR issue. Here, we have defined resolution as the distance, when at least 50 % of the 1D signals can be resolved as individual peaks, performing 100 identical measurements in total. Fig. 6 shows the sum of the 100 reconstructions, for a 90 μm step and a 45 μm step. The DR can clearly resolve both. In Fig. 7 it is shown that the 35 μm step can be resolved only in approximately half of the 100 measurements and the step-size is reconstructed smaller than it is in reality.
Fig. 5.
Compensation of acoustic attenuation of a 20 mm thick fatty tissue: T-SVD (blue dotted line. FWHM of 76 μm), and DR method (red dashed dotted and yellow solid line) with 20 (FWHM of 13 μm) and 200 iterations (FWHM of 5 μm), respectively. For the linear SVD reconstruction the width of the peak gives the spatial resolution, for the DR method this is not necessarily the case. The signals are normalized to have a maximum of one.
Fig. 6.
Compensation of acoustic attenuation of a 20 mm thick fatty tissue, T-SVD (red dotted line), and DR method (yellow dashed dotted) with 200 iterations, 100 identical measurements are summed after reconstruction: Left: 90 μm step. The SVD resolution is 70 μm (see Fig. 4), therefore also in SVD the two peaks can be resolved. Right: 45 μm step. SVD cannot resolve the two signals, but DR clearly shows two peaks.
Fig. 7.
Compensation of acoustic attenuation of a 20 mm thick fatty tissue, T-SVD (red dotted line), and DR method (yellow dashed dotted) with 200 iterations, 35 μm step. Left: 100 identical measurements are summed after reconstruction. Right: Reconstruction results for the individual measurements.
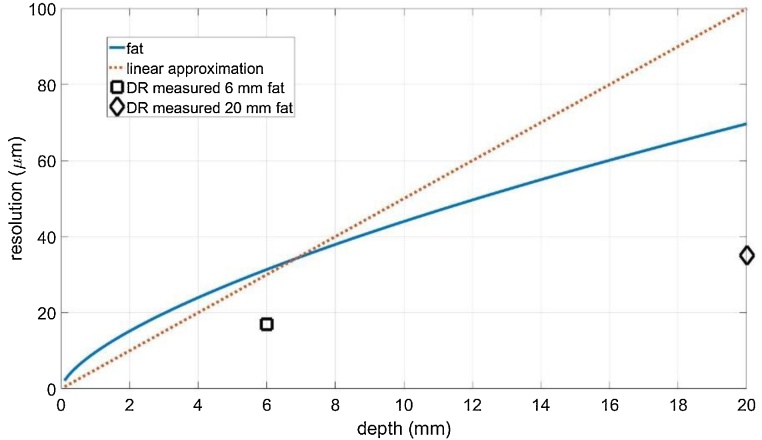
Fig. 8 shows a comparison of the resolution as a function of imaging depth for the “rule of thumb” factor 200 [3], which is called linear approximation. Further it shows the result from Eq. (5), which has been shown to be equal to the T-SVD method and what is the best one can do to compensate acoustic attenuation without using additional assumptions. The markers give the resolutions for the DR method used for inversion at a depth of 6 mm and 20 mm in fatty tissue.
Fig. 8.
Comparison of the spatial resolution as a function of imaging depth: the resolution from Eq. (5), which has been shown to be equal to the T-SVD method and what is the best possible compensation of acoustic attenuation without using additional assumptions (blue solid line), the “rule of thumb” factor 200 [3], which is called linear approximation (red dotted line). The markers give the resolutions using the Douglas Rachford (DR) method at a depth of 6 mm and 20 mm in fatty tissue.
4. Discussion, conclusions, and outlook
For fatty porcine tissue the frequency acoustic attenuation was measured and could be described by a power-law with an exponent and (Fig. 3). Using this law (Eq. (11)) and the corresponding dispersive sound velocity [11], the matrix in Eq. (7) was calculated for a propagation distance of 6 mm and 20 mm in fat. It describes the relation between the attenuated measured signal and the ideal signal (Fig. 2) in time domain. To allow for the assumption of positivity and sparsity for , the matrix was additionally multiplied by a convolution matrix using the water signal as convolution kernel. Then the perfect inverted signal from Eq. (7) would be a - like ideal signal as input signal (Fig. 4).
Two different inversion methods for Eq. (7) are compared: the T-SVD method uses no additional assumptions and it could be shown that the gained spatial resolution fits perfect to the theoretical resolution given in Eq. (5) (blue solid line in Fig. 8). This spatial resolution is also in accordance with the factor 200 given in literature [3], shown in Fig. 8 as the “linear approximation”. The DR method using positivity and sparsity allows for a resolution enhancement of a factor of two for that sample (from 70 μm to 35 μm). For the 6 mm fat tissue, the resolution was enhanced from 32 μm to 17 μm.
Resolution is defined as the step depth, at which a step can be resolved as two individual peaks. For non-linear reconstruction methods this turns out to be larger than the width of the reconstructed peaks, but still smaller than the resolution limit without taking sparsity and non-negativity into account.
Experimentally this resolution enhancement is demonstrated here in 1D, but at least in axial direction the same enhancement is expected in 3D by using the spherical projection. In comparison to other super-resolution photoacoustic imaging methods which overcome the acoustic diffraction limit by structured illumination patterns or localization of small particles or droplets, the proposed method has a big advantage: it is much faster as it uses only one measured image as input and can therefore be used for any existing photoacoustic tomographic set-up. Sophisticated 1D attenuation compensation is not only fast and allows parallelization of the numerical iterative reconstruction algorithm, but is also applicable for attenuation compensation in 2D and 3D imaging, which can always be reduced to 1D [10].
Funding
Measurements were funded by the project “multimodal and in-situ characterization of inhomogeneous materials” (MiCi) by the federal government of Upper Austria and the European Regional Development Fund (EFRE) in the framework of the EU-program IWB2020. Signal and data processing was also funded within the strategic economic-research program “Innovative Upper Austria 2020” of the province of Upper Austria. Parts of this work have been supported by the Austrian Science Fund (FWF), projects P 30747-N32 and P 33019-N.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Declaration of Competing Interest
The authors declare that there are no conflicts of interest related to this article.
Acknowledgement
The authors thank Gregor Thummerer from the University of Applied Sciences Upper Austria for inspiring discussions on iterative regularization methods, especially used in seismology.
Biographies
Peter Burgholzer received his pH.D. in technical science from the Johannes-Kepler-University of Linz, Austria in 1993 with a thesis on X-ray texture measurements and anisotropy of aluminum. Since 1998 he has been lecturer at the University of Applied Sciences Upper Austria. From 2000 to 2010 he was head of the Sensor Technology Department of the Upper Austrian Research. His main working area is non-destructive testing with optical methods, especially laser ultrasound, photoacoustic imaging, and optical coherence tomography. In 2008 he could habilitate on the Technical University of Vienna in Non-Destructive Testing. Since January 2010 he is scientific director of the Christian Doppler Laboratory for Photoacoustic Imaging and Laser Ultrasonics and CEO of the Research Center for Non-Destructive Testing (RECENDT).
Johannes Bauer-Marschallinger studied mechatronics at the Johannes Kepler University of Linz, Austria. After finishing his diploma theses for the soft matter Physics department, he received his M.Sc. degree in 2007. He then joined the sensor Technology department of the Upper Austrian Research GmbH, which became the RECENDT GmbH in 2009. His main research interests are photoacoustic imaging and laser ultrasound. Since 2008, he has been studying time-based media and interactive media at the art University of Linz. From 2014 till 2019 he was PhD student at RECENDT, where he finished 2019 his doctoral thesis on “All-Optical Photoacoustic Imaging with Fiber-Optic MachZehnder Interferometers”.
Markus Haltmeier received his pH.D. degree in mathematics from the University of Innsbruck, Tyrol, Austria, in 2007, for research on computed tomography. He was then involved in various aspects of inverse problems as a research scientist with the University of Innsbruck, the University of Vienna, Austria, and the Max Planck Institute for Biophysical Chemistry, Göttingen, Germany. Since 2012, he is full professor with the Department of Mathematics, University of Innsbruck. His current research interests include inverse problems, signal and image processing, computerized tomography, and machine learning.
References
- 1.Kruger R.A., Kiser W.L., Reinecke D.R., Kruger G.A., Miller K.D. Thermoacoustic molecular imaging of small animals. Mol. Imaging. 2003;2:113–123. doi: 10.1162/15353500200303109. [DOI] [PubMed] [Google Scholar]
- 2.Beard P. Biomedical photoacoustic imaging. Interface Focus. 2011;1:602–631. doi: 10.1098/rsfs.2011.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang L.V., Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science. 2012;335:1458–1462. doi: 10.1126/science.1216210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Burgholzer P., Matt G.J., Haltmeier M., Paltauf G. Exact and approximative imaging methods for photoacoustic tomography using an arbitrary detection surface. Phys. Rev. E. 2007;75 doi: 10.1103/PhysRevE.75.046706. [DOI] [PubMed] [Google Scholar]
- 5.Kuchment P., Kunyansky L. Mathematics of thermoacoustic tomography. Eur. J. Appl. Math. 2008;19:191–224. [Google Scholar]
- 6.La Riviere P.J., Zhang J., Anastasio M.A. Image reconstruction in optoacoustic tomography accounting for frequency-dependent attenuation. Proc. IEEE Nuclear Science Symposium Conference; Las Croabas, Puerto Rico; 2005. pp. 1841–1845. [Google Scholar]
- 7.La Riviere P.J., Zhang J., Anastasio M.A. Image reconstruction in optoacoustic tomography for dispersive acoustic media. Opt. Lett. 2006;31:781–783. doi: 10.1364/ol.31.000781. [DOI] [PubMed] [Google Scholar]
- 8.Szabo T.L. Elsevier; San Diego, USA: 2004. Diagnostic Ultrasound Imaging: Inside Out. [Google Scholar]
- 9.Ammari H., Bretin E., Jugnon V., Wahab A. Photoacoustic imaging for attenuating acoustic media. In: Ammari H., editor. Mathematical Modeling in Biomedical Imaging II: Optical, Ultrasound, and Opto-Acoustic Tomographies, Lecture Notes in Mathematics 2035. Springer- Verlag; Berlin: 2012. pp. 57–84. [Google Scholar]
- 10.Burgholzer P., Berer T., Grün H., Roitner H., Bauer-Marschallinger J., Nuster R., Paltauf G. Photoacoustic tomography using integrating line detectors. J. Phys. Conf. Ser. 2010;214 [Google Scholar]
- 11.Deán-Ben X.L., Razansky D., Ntziachristos V. The effects of acoustic attenuation in optoacoustic signals. Phys. Med. Biol. 2011;56:6129–6148. doi: 10.1088/0031-9155/56/18/021. [DOI] [PubMed] [Google Scholar]
- 12.Kowar R., Scherzer O. Attenuation models in photoacoustics, in mathematical modeling in. In: Ammari H., editor. Mathematical Modeling in Biomedical Imaging II: Optical, Ultrasound, and Opto-Acoustic Tomographies,, Lecture Notes in Mathematics 2035. Springer-Verlag; Berlin: 2012. pp. 85–129. [Google Scholar]
- 13.Burgholzer P., Gruen H., Haltmeier M., Nuster R., Paltauf G. Compensation of acoustic attenuation for high resolution photoacoustic imaging with line detectors. Proc. SPIE. Int. Soc. Opt. Eng. 2007;6437 [Google Scholar]
- 14.Burgholzer P., Roitner H., Bauer-Marschallinger J., Gruen H., Berer T., Paltauf G. Compensation of ultrasound attenuation in photoacoustic imaging. In: Beghi Marco G., editor. Acoustic Waves - From Microdevices to Helioseismology. InTech; 2011. http://www.intechopen.com/books/acoustic-waves-from-microdevices-to-helioseismology/compensation-of-ultrasound-attenuation-in-photoacoustic-imaging ISBN: 978-953-307-572-3 Available from: [Google Scholar]
- 15.Treeby B.E., Zhang E.Z., Cox B.T. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Probl. 2010;26 [Google Scholar]
- 16.Treeby B.E., Cox B.T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J. Acoust. Soc. Am. 2010;127:2741–2748. doi: 10.1121/1.3377056. [DOI] [PubMed] [Google Scholar]
- 17.Treeby B.E. Acoustic attenuation compensation in photoacoustic tomography using time-variant filtering. J. Biomed. Opt. 2013;18 doi: 10.1117/1.JBO.18.3.036008. [DOI] [PubMed] [Google Scholar]
- 18.Esposito M., Van den Broeck C. Second law and Landauer principle far from equilibrium. Europhys. Lett. 2011;95 [Google Scholar]
- 19.Burgholzer P. Thermodynamic limits of spatial resolution in active thermography. Int. J. Thermophys. 2015;36:2328–2341. doi: 10.1007/s10765-015-1890-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Burgholzer P., Stockner G., Mayr G. Acoustic reconstruction for photothermal imaging. Bioengineering. 2018;5(70):1–9. doi: 10.3390/bioengineering5030070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burgholzer P., Bauer-Marschallinger J., Reitinger B., Berer T. Resolution limits in photoacoustic imaging caused by acoustic attenuation. J. Imaging. 2019;5(13):1–11. doi: 10.3390/jimaging5010013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bauer-Marschallinger J., Berer T., Gruen H., Roitner H., Reitinger B., Burgholzer P. Broadband high-frequency measurement of ultrasonic attenuation of tissues and liquids, IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012;59:2631–2645. doi: 10.1109/TUFFC.2012.2504. [DOI] [PubMed] [Google Scholar]
- 23.Roitner H., Bauer-Marschallinger J., Berer T., Burgholzer P. Experimental evaluation of time domain models for ultrasound attenuation losses in photoacoustic imaging. J. Acoust. Soc. Am. 2012;131:3763–3774. doi: 10.1121/1.3699194. [DOI] [PubMed] [Google Scholar]
- 24.Hell S.W., Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994;19:780. doi: 10.1364/ol.19.000780. [DOI] [PubMed] [Google Scholar]
- 25.Klar T.A., Hell S.W. Subdiffraction resolution in far-field fluorescence microscopy. Opt. Lett. 1999;24:954. doi: 10.1364/ol.24.000954. [DOI] [PubMed] [Google Scholar]
- 26.Rust M.J., Bates M., Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat. Methods. 2006;3:793. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Betzig E., Patterson G.H., Sougrat R., Lindwasser O.W., Olenych S., Bonifacino J.S., Davidson M.W., Lippincott-Schwartz J., Hess H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 28.Dertinger T., Colyer R., Iyer G., Weiss S., Enderlein J. Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI) Proc. Natl Acad. Sci. U. S. A. 2009;106:22287. doi: 10.1073/pnas.0907866106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Viessmann O.M., Eckersley R.J., Christensen-Jeffries K., Tang M.X., Dunsby C. Acoustic super-resolution with ultrasound and microbubbles. Phys. Med. Biol. 2013;58:6447. doi: 10.1088/0031-9155/58/18/6447. [DOI] [PubMed] [Google Scholar]
- 30.Christensen-Jeffries K., Browning R.J., Tang M.X., Dunsby C., Eckersley R.J. In vivo acoustic super-resolution and super-resolved velocity mapping using microbubbles, IEEE Trans. Med. Imag. 2015;34:433. doi: 10.1109/TMI.2014.2359650. [DOI] [PubMed] [Google Scholar]
- 31.Errico C., Pierre J., Pezet S., Desailly Y., Lenkei Z., Couture O., Tanter M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature. 2015;527:499. doi: 10.1038/nature16066. [DOI] [PubMed] [Google Scholar]
- 32.Shi J., Tang Y., Yao J. Advances in super-resolution photoacoustic imaging. Quant. Imaging Med. Surg. 2018;8:724–732. doi: 10.21037/qims.2018.09.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chaigne T., Arnal B., Vilov S., Bossy E., Katz O. Super-resolution photoacoustic imaging via flow-induced absorption fluctuations. Optica. 2017;4:1397–1404. [Google Scholar]
- 34.Zhang P., Li L., Lin L., Shi J., Wang L.V. In vivo superresolution photoacoustic computed tomography by localization of single dyed droplets. Light Sci. Appl. 2019;8 doi: 10.1038/s41377-019-0147-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chaigne T., Gateau J., Allain M., Katz O., Gigan S., Sentenac A., Bossy E. Super-resolution photoacoustic fluctuation imaging with multiple speckle illumination. Optica. 2016;3:54–57. [Google Scholar]
- 36.Murray T.W., Haltmeier M., Berer T., Leiss-Holzinger E., Burgholzer P. Super-resolution photoacoustic microscopy using blind structured illumination. Optica. 2017;4:17–22. [Google Scholar]
- 37.Hojman E., Chaigne T., Solomon O., Gigan S., Bossy E., Eldar Y.C., Katz O. Photoacoustic imaging beyond the acoustic diffraction limit with dynamic speckle illumination and sparse joint support recovery. Opt. Express. 2017;25:4875–4886. doi: 10.1364/OE.25.004875. [DOI] [PubMed] [Google Scholar]
- 38.Aster R.C., Borchers B., Thurber C.H. third ed. Elsevier; Amsterdam: 2018. Parameter Estimation and Inverse Problems. [Google Scholar]
- 39.Wang Y., Ma X., Zhou H., Chen Y. L1-2 minimization for exact and stable seismic attenuation compensation. Geophys. J. Int. 2018;213:1629–1646. [Google Scholar]
- 40.Donoho D.L. Compressed sensing. IEEE Trans. Inf. Theory. 2006;52:1289–1306. [Google Scholar]
- 41.Haltmeier M., Berer T., Moon S., Burgholzer P. Compressed sensing and sparsity in photoacoustic tomography. J. Opt. 2016;18 [Google Scholar]
- 42.Betcke M.M., Cox B.T., Huynh N., Zhang E.Z., Beard P.C., Arridge S.R. Acoustic wave field reconstruction from compressed measurements with application in photoacoustic tomography. IEEE Trans. Comput. Imaging. 2017;3:710–721. [Google Scholar]
- 43.Han Y., Ding Lu, Deán Ben X.L., Razansky D., Prakash J., Ntziachristos V. Three-dimensional optoacoustic reconstruction using fast sparse representation. Opt. Lett. 2017;42:979–982. doi: 10.1364/OL.42.000979. [DOI] [PubMed] [Google Scholar]
- 44.Ding L., Deán-Ben X.L., Burton N.C., Sobol R.W., Ntziachristos V., Razansky D. Constrained inversion and spectral unmixing in multispectral optoacoustic tomography. IEEE Trans. Med. Imaging. 2017;36:1676–1685. doi: 10.1109/TMI.2017.2686006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Burgholzer P., Bauer-Marschallinger J., Grün H., Haltmeier M., Paltauf G. Temporal back-projection algorithms for photoacoustic tomography with integrating line detectors. Inverse Probl. 2007;23:S65–S80. [Google Scholar]
- 46.Burgholzer P., Thor M., Gruber J., Mayr G. Three-dimensional thermographic imaging using a virtual wave concept. J. Appl. Phys. 2017;121 [Google Scholar]
- 47.Eckstein J., Bertsekas D.P. On the Douglas—rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992;55:293–318. [Google Scholar]
- 48.Eckstein J., Yao W. Relative-error approximate versions of douglas– rachford splitting and special cases of the admm. Math. Program. 2018;170:417–444. [Google Scholar]
- 49.Paltauf G., Nuster R., Burgholzer P. Weight factors for limited angle photoacoustic tomography. Phys. Med. Biol. 2009;54:3303–3314. doi: 10.1088/0031-9155/54/11/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Scruby C.B., Drain L.E. CRC Press; 1990. Laser Ultrasonics Techniques and Applications. ISBN 0-7503-0050-0057. [Google Scholar]
- 51.Hutchins D.A. Vol. 18. Elsevier; 1988. Ultrasonic generation by pulsed lasers; pp. 21–123. (Physical Acoustics). ISBN 0893-388X. [Google Scholar]
- 52.Nussenzveig H.B. Academic; New York: 1972. Causality and Dispersion Relations. [Google Scholar]
- 53.Parikh N., Boyd S. Proximal algorithms, found. Trends Optim. 2014;1:127–239. [Google Scholar]
- 54.Artacho F.J.A., Borwein J.M., Tam M.K. Recent results on Douglas–Rachford methods for combinatorial optimization problems. J. Of optim. Complex Var. 2014;163:1–30. [Google Scholar]
- 55.Boyd S. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trendsâ® Mach. Learn. 2010;3:1–122. [Google Scholar]
- 56.Hansen P.C. Regularization tools: a matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms. 1994;6:1–35. [Google Scholar]