Abstract
Polarization converters play an important role in modern communication systems, but their wide and multiple band operation to facilitate volume and size reduction is quite challenging. In this paper, a triple-band Linear Polarization to Circular Polarization (LP-to-CP) converter is presented using a novel design procedure based on geometric parameters optimization of a metasheet. The proposed converter is ultrathin, wideband, stable over a wide range of incident angles, and polarization diverse. The conductor layer of metasheet is patterned with a square ring and five square-patches diagonally intersecting each other. To validate the proposed method, an LP-to-CP convertor in X-band (7.3~9.6 GHz) and dual Ka-bands (25.4~31.4 GHz, 35.4~42.2 GHz) is presented. The performance is quite stable in wide range of frequencies and against the variation of incident angles from −25° to 25°. After performing model-based theoretical paradigm analysis, and full-wave simulation and optimization, the converter is fabricated and the measurements are performed inside the anechoic chamber. The measured results, close to simulation results, depict the validity and reliability of the proposed design.
Subject terms: Electrical and electronic engineering, Electronic devices
Introduction
The ever increasing demand for high-speed and high-capacity communication prompts advancements in 5th generation (5 G) and 6th Generation (6 G) wireless communication. Polarization is an important property of the electromagnetic field which describes the direction in which electric field oscillates while the wave passes through the media. In order to control the electromagnetic waves, manipulation of this polarization state has gained much attention in the last decade due to its potential applications in stealth, satellite communication, cloaking and applications requiring asymmetric transmission characteristics1–3. In the microwave and mmWave range, polarization mismatch, atmospheric absorption and multi-path fading degrade the performance of the channel. In such a scenario, CP waves are preferred over LP waves because of their lower sensitivity towards the multi-path fading. In order to obtain CP waves, there can be two ways: one way is to generate them using CP antenna or use LP wave generated by an antenna and convert it into CP wave using LP-to-CP converter.
Multiband CP waves can be obtained from the CP antenna elements using regular methods such as multi-feed antennas, helical antennas and spiral antennas4. Multiband CP waves can also be obtained using shared aperture antennas5,6. However, they are difficult to design at high frequencies because of their complex feeding structures. An efficient solution is to use multi-band LP-to-CP conversion in cascade with LP antenna. There has been an increasing trend towards multiband and multifunctional polarization conversion devices7–9 so that multiple systems may be merged and subsequently efficient miniaturization may be achieved. An LP-to-CP converter can broadly be categorized into a reflection-based and a transmission-based converter. Reflection based converter tends to block the feeding signals. So, transmission-based converters are being investigated for the potential applications requiring incident and outgoing waves to be aligned.
Periodic structures such as metamaterials and chiral metamaterials have been used due to their well-known properties such as polarization conversion and asymmetric transmission10–12. Metasurfaces as 2D equivalent of metamaterials, have been explored for a variety of applications including polarization manipulation13 and LP-to-CP conversion14–29. Multi-band polarization conversion is relatively a new concept. Recent research works have been reported for dual-band polarization control including cross-polarization conversion30,31 and LP-to-CP conversion devices32–40. Liu et al.30 and Huang et al.31 reported dual-band cross polarization converters using metasurfaces. Dual-band LP-to-CP conversion operation has been reported in reflection mode32 and transmission modes using multi-layered33,34,36,37 and single-layered metasurfaces38–40. Zhu et al.40 proposed all-dielectric metamaterial based dual-band LP-to-CP conversion at 6.24 GHz and 6.38 GHz. But, rare work has been reported for triple-band polarization conversion operation41–45. Liu et al.41 presented the design of reflection-based multiband polarization converter having dual-band LP-to-CP conversion and single-band cross-polarization conversion using tri-layered metasurface based structure. They proposed ‘L’ patterned structure, which converts incident linear polarization into circular polarization in 9.1~16.5 GHz and 20.0~25.4 GHz. Moreover, it acts as a cross-polarization converter from 17.4~18.9 GHz band. Yao et al.42 proposed ultra-thin reflection-based triple-band cross polarization converter in THz regime using metasurfaces. The proposed structure consists of double ‘L’ based graphene patches and converts incident linear polarization at 36.15 THz, 48.95 THz and 52.20 THz to cross-polarization. Huang et al.43 reported E-shaped metamaterial based LP-to-CP converter at 10.1 GHz, 11.7 GHz, and 14.2 GHz. M. Fartookzadeh et al.44 reported a tri-band LP-to-CP converter based on dual-layer patch arrays working in reflection modes. It converts LP wave into reflected CP wave at 2 GHz, 8 GHz and 12 GHz. All these proposed tri-band polarization converters41–45 were based on reflection modes. Such converters tend to block the feeding signals and increase the overall profile for the antenna systems. Although, significant advancement has been made in dual-band transmission-based polarization converters33–39, triple-band transmission-based polarization converter is still a challenging problem. In our previous work45, we numerically proposed a triple-band LP-to-CP converter in THz regime, but operating bandwidths were narrow.
In this paper, the realization of a triple-wide-band LP-to-CP converter using a new design procedure based on geometric parameters optimization is presented. The proposed converter has five unusual properties. First, it performs LP-to-CP transmission conversion in three bands, which is practically reported the first time to the best of our knowledge. Secondly, since the structure is based on a single dielectric layer, it makes it an ultrathin device. Thirdly, it works over 19% to 20% bandwidth for all the tree bands of operation which is the widest among other reported multiband transmission based polarization conversion devices. Fourthly, the structure is low-cost and maintains performance over ±25° change in incidence angles. Lastly, the outgoing circular polarizations in second and third bands are orthogonal to the first band which makes it a good candidate for applications requiring polarization diversity.
Results
Unit cell design
Generally, any electromagnetic wave transmitted from a metasurface has two electric field components. One has the same polarization as that of the incident wave while the other has opposite polarization. They are called co-polarized and cross-polarized components respectively. For polarization manipulating devices, cross-coupling between transmitted electric and magnetic fields interacts with each other to produce co and cross-polarized components. For multi-band polarization conversion, coupling between electric and magnetic fields should be deliberately controlled to have multiple Eigen modes. Single-band LP-to-CP conversion has been achieved using many diagonal symmetric/semi-symmetric anisotropic structures21–24. Dual-band LP-to-CP operation has been achieved using center-connected35 and diagonal symmetric30 structures. Here, we selected a diagonal symmetric structure, with multiple square patches to have different resonance characteristics so that multiband operation may be realized.
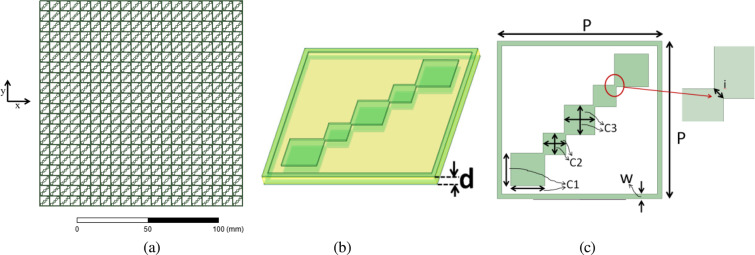
The proposed structure is shown in Fig. 1(a) whose unit cell is constructed by periodic unit cells shown in Fig. 1(b),(c). It consists of two identical layers of conductor patterns based on penta-squares arranged diagonally inside a square ring. Metallic layers are separated by one substrate layer. For the design parameters, center frequencies of three bands of interest are defined as: ‘’, ‘’ and ‘’. As an example, converter’s design is presented for LP-to-CP operation at 8.5 GHz, 28.5 GHz and 38.8 GHz for a geostationary satellite. So, f1 = 8.5 GHz, f2 = 28.5 GHz, f3 = 38.8 GHz. Arithmetic mean of three frequency points denoted as ‘’, can be calculated as ( which equals 25.26 GHz. Thickness for the substrate was chosen to be d , being the free-space wavelength at . Design steps were performed in standard electromagnetic software package High Frequency Structure Simulator (HFSS) using master-slave boundary conditions. Floquet ports at the input and output of the unit cell were applied to realize periodic array structure. FR4 having a thickness as 0.3 mm and relative permittivity as 4.3 and loss tangent as 0.03 was used as a substrate.
Figure 1.
Schematic of the design: (a) Two-dimensional (2D) periodic array structure (b) 3D perspective view (c) Top view (x-y).
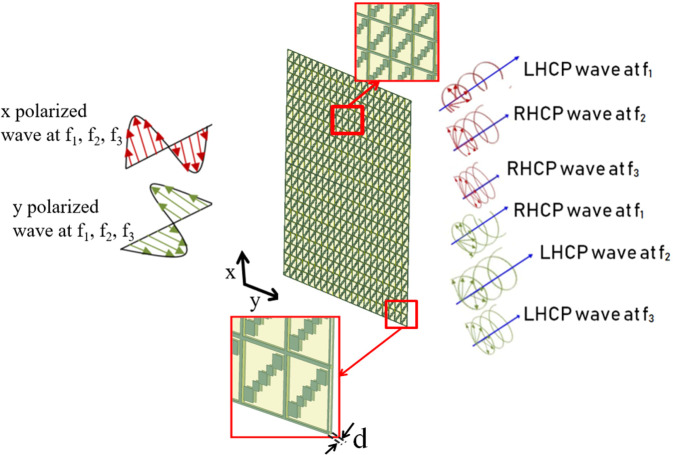
Triple band LP-to-CP conversion scheme using metasheet scheme with orthogonal outgoing polarizations is shown in Fig. 2. For incident x-polarized waves, transmitted waves behave as LHCP at f1 and RHCP at f2 and f3. Whereas for incident y-polarized waves, transmitted waves behave as RHCP at f1 and LHCP at f2 and f3. Following are the detailed design steps for metasheet:
Figure 2.
Scheme of metasheet for triple-wide-band centered at f1, f2, and f3.
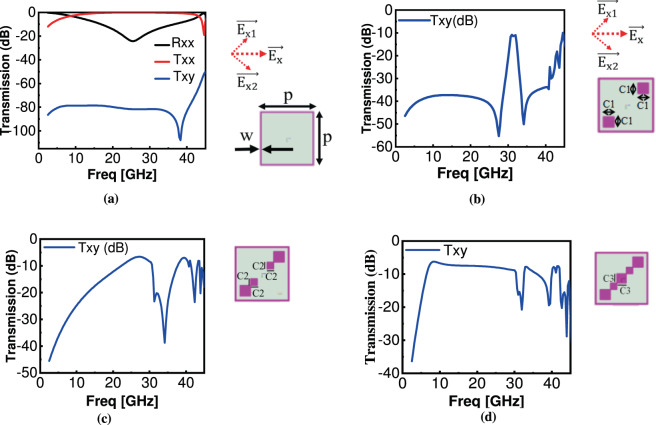
Step 1: A square ring-based metamaterial structure is proven to be a wide-band-pass filter. The first design step involves the design of a wideband filter covering all three required frequency points. For this, a square ring with length ‘PxP’ and width ‘w’ was simulated and optimized. The structure should resonate at ‘f’ and transmission characteristics should cover all three frequency points , and Transmission characteristics with optimized parameters are shown in Fig. 3(a) which shows that under incident x-polarized wave, the transmitted wave is also x-polarized from 8 GHz to 42 GHz with no polarization conversion as Txy<−80 dB. The reason for no cross-polarization conversion is symmetricity of square ring along x and y axes. In order to understand this, lets resolve incident wave into its two orthogonal components lying at +45° and −45° depicted in Fig. 3(a) as and . Since these orthogonal components will experience the same structure while transmitting through the metasurface, so no cross-polarization conversion will take place. As polarization conversion requires a different phase response for incident wave along its orthogonal components8.
Figure 3.
Optimization of the unit cell to achieve polarization conversion (a) Unit cell with square ring alone (b) square ring with two diagonal square patches 2xC1 (c) square ring with four diagonal square patches 2xC1, 2xC2 (d) square ring with five diagonal square patches 2xC1, 2xC2, C3.
Step 2: In the next step, an-isotropicity is introduced to the unit cell in 3(a) so that polarization conversion takes place. This step involves the design of a square C1xC1 which is placed along the diagonal with corner to corner distance from step 1’s square ring as 2*w. It is clear from Fig. 3(b) that with the addition of a small an-isotropicity, cross-polarization component Txy increases. Dimensions of C1 should be chosen in such a way to have Txy peak at f23 where f23 = (f2 + f3)/2 = 33.65 GHz. It is clear from Fig. 3(b) that cross-polarization conversion occurs around (f2+f3)/2. Introduced an-isotropicity (two diagonal squares) makes unit cell asymmetric. So, orthogonal components of incident wave lying at +45° and −45°, and will experience different structures, resulting in different transmitted amplitude and phase responses. This time will experience extra square patches along its path characterized as inductances in series with capacitance. Through optimization in EM-simulator, dimensions of C1xC1 can be set in such a way to obtain 90° phase shift for at f23.These transmitted components will interact with each other to have transmitted y-polarized component resulting in cross-polarization conversion.
Step 3: The third step involves the design of square C2, whose position and dimensions are different than C1 and results in another band of cross-polarization component. This dual-band response is due to the different eigen modes of the unit cell. Dimensions of C1 and square ring were kept fixed as found out from step 2 and C2 was optimized to get two transmission curves around f2 and f3. Amplitude response is as shown in Fig. 3(c).
Step 4: The last step involves the addition of a central square C3. The addition of this square will give rise to a new third transmission band at f1 due to excitation of another eigen mode. Figure 3(d) shows an amplitude response from a single-layered metasurface structure containing a square ring and five diagonal squares.
Following the design guide, the complete unit cell shown in Fig. 1 was optimized using bi-layered structure. Ansoft HFSS’s sequential non-linear gradient programming optimizer was used in this regard. The criterion for performance of metasheet is discussed in the analysis section. A comparison between design and final optimized values is presented in Table 1. Figure 4(a) shows optimized transmission characteristics for single-layered and bi-layered metasheet. It is evident that Txy improves for bi-layered structure keeping the shape of the response nearly the same. Since the fabrication and assembly of single and bi-layered metasheet remains almost the same as the substrate is singly-layered for both. Whereas for structures having no. of metallic layers >2, fabrication, assembly and cost of the metasheet increases. So, a bi-layered structure was selected for polarization conversion to have good transmission characteristics22 and low-cost fabrication. Figure 4(b) depicts the difference between phases of Txx and Txy for the incident x- polarized wave respectively. Further discussion on Fig. 4(a),(b) is carried out in the Analysis section.
Table 1.
Design and optimized parameters for the metasheet.
| Parameter | Using Design Procedure (mm) | Optimized and fabricated (mm) |
|---|---|---|
| d | 0.298 | 0.3 |
| P | 7.1 | 7.2 |
| C1 | 1.48 | 1.5 |
| C2 | 0.96 | 1.0 |
| C3 | 1.34 | 1.30 |
| w | 0.2 | 0.2 |
| i | — | 0.05 |
Figure 4.
(a) Simulated transmission characteristics of the metasheet (b) Simulated phase difference between Txx and Txy.
Analysis
For the detailed operation of a triple-band LP-to-CP converter, let’s consider a plane electric field and with x-polarization and y-polarization respectively. Considering a reflectionless ideal transmission-based polarization converter, and waves travelling in ‘+z’ direction are made incident on the surface of the converter. Corresponding outgoing waves and can be expressed in terms of transmission coefficients as shown in Eq. (1). Here, ‘’ and ‘’ represent outgoing waves corresponding to incident x- and y-polarized respectively. The equivalent matrix form representation for and can be written as:
| 1 |
Where,
| 2 |
Equation (1) in terms of magnitude and phase responses, and Eq. (2) can be written as:
| 3 |
Where, and are transmission coefficients for transmitted x- and y-polarized waves and are phases for transmitted x- and y-polarized waves respectively under incident x-polarized wave. Similarly and are transmission coefficients and phases for transmitted x- and y-polarized waves for incident y-polarized wave respectively. Transmission coefficients , , can be computed as:
| 4 |
For the sake of simplicity, let us consider one case when incident x-polarized wave strikes the proposed device. Owing to the fact that the structure of the device is made anisotropic deliberately, the magnitudes and phases for x-polarized () and y-polarized transmitted waves () may be different. However, if for a certain frequency range these transmission coefficients become comparable and the difference between their phase angles becomes ±90°, i-e ≈ and , where is an integer. This would be the condition where x-polarized wave will be converted into a CP wave. To describe the transmission conversion performance for the proposed structure, we calculate axial ratio (AR) for the transmitted wave in Eq. (5) 33:
| 5 |
Whereas ‘a’ can be calculated from Eq. (6) as:
| 6 |
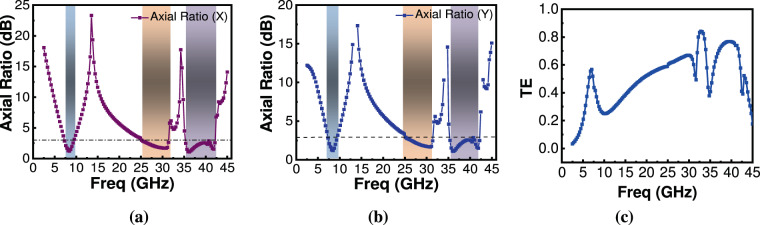
For an ideal LP-to-CP converter, = and . In such a scenario, the outgoing wave is perfectly CP wave and AR will be 1 (0 dB). However, in most of the communication systems, 3 dB value of AR is acceptable32–40. Figure 4(a),(b) show that in frequency bands from 7.3~96 GHz, 25.4~31.4 GHz and 35.4~42.2 GHz the transmission coefficient magnitudes for bi-layered metasheet are comparable whereas phase difference between them is around 90° or +270°. Thus, the condition for LP-to-CP conversion is fully met at some frequencies within these bands. Though, there is some difference between particularly in the second band of operation (25.4~31.4 GHz) and at an inner frequency range of 35.4~42.2 GHz, but the difference in their phase angles is around 90°. So, it is partially fulfilling the requirement (in this case transmitted wave will be slightly elliptical polarized). But, the performance criterion for linear to circular transmission type conversion (AR within 3 dB) is maintained. Figure 5(a) shows the response of calculated AR for the transmitted wave under incident x- polarization. It is clear that from 7.3~9.6 GHz, 25.4~31.4 GHz and 35.4~42.2 GHz AR is lower than 3 dB. So, the transmitted wave is considered to be a CP wave. Furthermore, Fig. 4(b) shows, in the frequency range from 7.3~9.6 GHz, is around +270° which is in fact −90°, so it can be deduced that y-component of the transmitted wave is ahead of the x-component hence transmitted wave is LHCP, whereas in frequency range 25.4~31.4 GHz and 35.4~42.2 GHz, is around +90° which means y-component of the transmitted wave is lagging behind x-component, hence transmitted wave is RHCP in these bands.
Figure 5.
Simulated transmitted wave characteristics (a) AR for x-polarization (b)AR for y-polarization (c) TE.
In addition, the proposed unit cell behaves equally well for the incident y-polarized wave. Figure 5(b) shows AR for the transmitted wave under incident y-polarization. However, due to the change in phase response (not shown here), the type of polarization changes in all three frequency bands resulting in RHCP for 7.3~9.6 GHz band and LHCP for 25.4~31.4 GHz and 35.4~42.2 GHz frequency bands. From this property of the proposed structure, it can be inferred that if it is required to have opposite types of circular polarization, one should simply rotate the structure to 90°. Transmission efficiency (TE) of the converter which is defined as is as shown in Fig. 5(c). Although transmission performance in the first band is not as good as in the second and third bands reaching worst value of 25% at 9.6 GHz, it reaches best value of 52.1%, 67%, and 77% in three bands of operation which is comparable with other single and dual- band converters27–29,40.
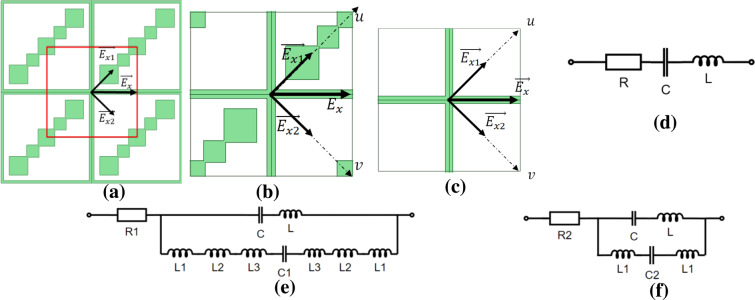
Here we use the equivalent circuit model as adopted in46 for the proposed metasheet to show how it can convert incident LP wave into a CP wave. For this, we redraw the proposed metasheet as shown in Fig. 6(a) with a new unit cell shown in red and enlarged as in Fig. 6(b). Moreover, we have introduced a new coordinate system which is 45° rotated from xy coordinate system, denoted as uv coordinate system. Let’s consider that incident wave is x-polarized wave represented as . We can break it into its two orthogonal components as lying along u and v axes respectively. It is important to mention here that new unit cells presented in Fig. 6(b),(c) are symmetric w.r.t u and v axis, so no cross-polarization conversion will happen for incident u and v polarized waves8. We have removed the diagonal patches in Fig. 6(c) to make the structure a symmetric one which is essentially a symmetric wire-grid based metasurface whose impedance model under and is as shown in Fig. 6(d) and can be given as in Eq. (7):
| 7 |
Where, R and L are the equivalent resistance and inductance of the metallic strips and C is the capacitance formed by or on the adjacent metallic orthogonal strips. For the new unit cell in Fig. 6(b), impedance model under is as shown in Fig. 6(e). Metallic diagonal patch along formed by square patches can be considered as inductances corresponding to each square in series with capacitance. We have presented equivalent resistance for Fig. 6(b) as seen by as R1. will see the new unit cell as equivalent circuit as shown in Fig. 6(f) formed by capacitance in series with inductances. New impedances for Fig. 6(e),(f) can be written as shown in Eqs. (8) and (9):
| 8 |
| 9 |
Figure 6.
(a) Four unit cells for the proposed metasheet (b) New unit cell (c) New unit cell with diagonal patches removed (d) Equivalent Circuits for unit cell with diagonal patches removed (e) An equivalent circuit for the new unit cell as seen by . (f) An equivalent circuit for the unit cell as seen by .
The resultant phase difference between transmitted waves along u and v axes will be ang (Z1)-ang(Z2). Since the proposed metasheet is based on multiple sized and differently spaced square patches, Z1 and Z2 will have different values in different frequency bands. If the metasheet is designed in such a way that |Z1| = |Z2| and ang (Z1)-ang (Z2) = ±90° for all the three frequency bands. The resultant outgoing wave will be circularly polarized.
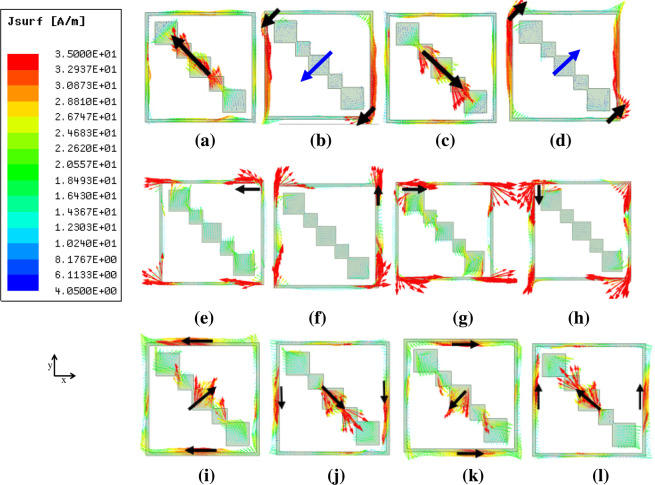
To explain the physical phenomenon behind the proposed LP-to-CP operation, we considered the surface current vectors at the outgoing surface of the unit cell at frequency points in each band, let it be f1, f2, f3 with values as f1 = 8.45 GHz, f2 = 30.83 GHz, f3 = 40 GHz. Figure 7 shows the surface current distribution for f1, f2, f3 under the incident x-polarized wave. It is important to mention here that the surface current distribution is at the transmitting surface of the proposed converter for different time intervals. Here ‘T’ represents the time period for the incident wave at the corresponding frequency. It can be seen in Fig. 7(a) that at t = 0, surface current vectors are making an angle of 135° with the +x axis. For the ease of understanding, we have shown the strength of current vectors at the center for Fig. 7(b),(d) by a blue arrow. Figure 7(b) shows that at t = T/4, the surface current vectors are making an angle 225° with the +x axis. At t = T/2, the angle changes to 315°. For t = 3 T/4, this angle reaches 45°. Thus, with every time T/4, surface current vectors rotate with an angle 90° in a counter-clockwise direction. So, the transmitted wave is LHCP at f1 which is in accordance with Fig. 4(b) (y-component is ahead of the x-component). Figure 7(e–l) show the surface current vectors at the output surface at f2 and f3 respectively at different time intervals. It can be clearly seen that with every quarter cycle, surface currents are rotated 90° in a clockwise rotation hence transmitted wave is RHCP at f2 and f3. This rotation agrees to phase difference in Fig. 4(b) (y-component lags x-component).
Figure 7.
Surface current distribution of the proposed multi-band metasheet at (a) f1, t = 0, (b) f1, t = T/4 (c) f1, t = T/2 (d) f1, 3 T/4 (e) f2, t = 0 (f) f2, t = T/4 (g) f2, t = T/2 (h) f2, 3 T/4 (i) f3, t = 0 (j)f3, t = T/4 (k) f3, t = T/2 (l) f3, 3 T/4.
Experiment
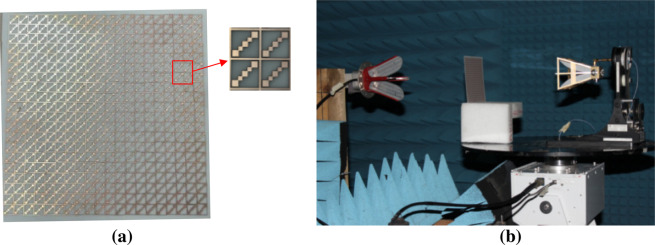
In order to validate the design and simulation procedure, the proposed metasheet for triple-band LP-to-CP conversion was fabricated using a normal PCB fabrication procedure. The size of the sample (20 × 20 elements) was 144 × 144 mm2. Figure 8(a) shows the photograph for the fabricated sample. Testing was carried out in two sets due to broadband coverage of the metasheet in X and Ka bands. For this, two sets of horn antennas were used. The first set was used to perform testing from the frequency range of 1~18 GHz, while the second set was used to test the converter from 26.5~40 GHz frequency range. Radiation waves from the transmitting horn antennas were x-polarized. The line of sight between both sets of horn antennas passed through the center of metasheet. Antennas were placed at a suitable distance from device to ensure uniform plane wave strikes the device. Testing was performed inside the anechoic chamber. Rohde & Schwarz ZVA-50 was used for the measurement of transmission parameters. The test setup is as shown in Fig. 8(b). Two horn antennas were connected to the Vector Network Analyzer (VNA) in the control room of the anechoic chamber via long coaxial cables. They acted as transmitting and receiving antennas. Orientation for the receiver antenna was changed for x- and y-polarized waves.
Figure 8.
(a) Photograph of the fabricated metasheet (b) Test setup for triple-wide-band metasheet in transmission mode.
After choosing a suitable distance between antennas and metasheet, the sample was removed for the reference measurement of amplitude and phase response. For this , with respective phases were measured. Then, the metasheet was placed in between the two antennas to measure and with their phases. Final transmission coefficients and their phases were calculated by subtracting from the reference measurement. In this way, losses due to the test environment and test cables were mitigated. Figure 9(a),(b) depict measured and simulated responses for and respectively. It is clear that both measured results agree to simulated results, though there is a mild frequency shift in a higher band of operation. Measured and simulated difference between transmitted waves’ phases is presented in Fig. 9(c).
Figure 9.
Simulated and measured response for metasheet (a) Txx (b) Txy (c) (d) AR in X-band (e) AR in first Ka-band band (f) AR in second Ka-band.
Figure 9(d)–(f) show measured and simulated curves for AR response for the transmitted wave for X and dual-Ka-band respectively. It is evident from Fig. 9(d) that metasheet performs well in X-band, with a very close agreement between measured and simulated results. For the first Ka-band operation, the performance in the lower band could not be tested but it is expected to be as in the higher frequency band. Figure 9(e) shows that although measured results are agreed well with the simulation results, a small glitch in AR around 29.5 GHz was observed but it remained lower than 3 dB. Also, from Fig. 9(f), it is clear that for the third frequency band, AR reached 2.5 dB around 40 GHz. The performance of metasheet remained quite well in the third band too, except the frequency shift. These variations in AR for all three frequency bands might be due to the fabrication tolerance and non-ideal conditions of the test setup. Ka-band is the most sensitive and has a larger frequency shift. The overall performance of the metasheet has a good agreement with the simulated results.
The performance of metasheet in all three frequency bands under variations in incident angles was simulated, analyzed and is presented in Fig. 10. It can be inferred that metasheet maintains performance under different incident angles except for some discrepancies found in higher frequency end of the second band. It is important to mention here that due to the unavailability of wideband horn antennas, frequency bands 18 GHz to 26.5 GHz and 40 GHz to 46 GHz remained untested. However, close agreement between test results and simulated results from 1~18 GHz, and 26.5~40 GHz ensures the design validity for the proposed ultrathin metasheet.
Figure 10.
The response of metasheet under different oblique incidences (a) Simulated AR in X-band (b) measured AR in X-band (c) Simulated AR in first Ka-band, (d) Measured AR in first Ka-band, (e) Simulated AR in second Ka-band, (f) Measured AR in second Ka-band.
Table 2 presents the performance comparison of the proposed metasheet with other state-of-the-art multiband LP-to-CP converters. It can be inferred that the proposed metasheet performs over a wide range of frequencies in three bands of operation. Besides, the structure is ultra-thin with a minimum number of metallic layers. It maintains angular stability over −25°~+25°variation in the incident angle.
Table 2.
Performance comparison among other transmission type multiband LP-to-CP converters.
| Centre Frequencies (GHz) | AR bandwidth | Thickness | Cell size | Metallic layers | Polarization modes | Angular stability | |
|---|---|---|---|---|---|---|---|
| 33 | Dual band (19.95, 29.75) | 2.5%, 1.7% | 0.07λ1 | 0.35λ1 | 3 | Orth | 30° |
| 36 | Dual band(19.6, 29.6) | 4%, 2.7% | 0.31λ1 | — | 5 | same | — |
| 37 | Dual band (7.6, 13) | 31.6%, 13.8% | 0.24λ1 | — | 4 | same | ±25° |
| 40 | Dual band(18.5, 29) | 29%, 12% | 0.1λ1 | 0.25λ1 | 2 | orth | 20° |
| This work | Triple band (8.45, 28.4, 38.8) | 27.2%, 21.2%, 17.5% | 0.008λ1 | 0.2λ1 | 2 | orth | ±25° |
*λ1 is free space wavelength at centre frequency of first band of operation.
Conclusion
In summary, a triple-wide-band LP-to-CP converter is realized based on ultrathin transmissive metasheet using step by step design procedure. The operating principle for linear to triple-wide-band polarization conversion was analyzed in detail. Numerical and surface current analyses were carried out to verify the behavior of outgoing wave in X-band (7.3~9.6 GHz), and dual Ka-bands (25.4~31.4 GHz, 35.4~42.2 GHz) bands with 27.2%, 21.2% and 17.5% operating bandwidths respectively. With incident x(y) polarized wave, the proposed metasheet transmits LHCP (RHCP) in X-band and RHCP (LHCP) in dual Ka-bands. In order to validate the performance, a prototype was fabricated and tested inside anechoic chamber using two sets of standard antennas. Experimental results have a reasonable agreement with the simulations. The behavior of proposed metasheet with the change in incident angle was investigated numerically and experimentally, and it was verified that with the change in incident angle from −25° to +25°, the response remained almost stable. The proposed ultrathin, dual-polarized metasheet may have potential applications in polarization-manipulation devices. Moreover, it opens new horizons for future wireless communication systems including satellite communication systems for volume and size reduction.
Methods
Simulation
Electromagnetic simulation was carried out by Ansoft HFSS which is based on Finite Elemenet Mesh (FEM) Method. The unit cell was defined along x and y directions whereas its thickness was modeled along z-axis. Periodic boundary conditions (master-slave) were applied at x- and y- faces of unit cell. Electromagnetic waves were made incident at the one face of the unit cell along +z axis, while transmitted wave’s components were observed from the other side of the metasheet. FR4 substrate was modeled with relative permittivity as 4.3 and slightly higher dielectric loss tangent as 0.03 considering the performance requirement in Ka-band.
Fabrication and measurement
Metasheet consisted of 20 × 20 elements was fabricated using standard printed circuit board technology. Rohde & Schwarz ZVA-50 was used for the measurement of transmission parameters inside the anechoic chamber. Standard double ridged wideband horn antenna for 1~18 GHz measurement and Ka-band antennas with focusing lense for 26.5~40 GHz measurement range were used. Dielectric focusing lense was used for measurement in Ka-bands. Reference measurements were subtracted from the sample’s measurements. The receive antenna was rotated 90°to measure the cross-polarization component. For measurements under different incident angles, the transmit antenna was rotated clockwise and anti clock-wise for measuring transmission performance with ±10°, ±25° incident angles.
Acknowledgements
This research was funded by the National Natural Science Foundation of China, grant number 61831001, the High-Level Talent Introduction Project of Beihang University, grant number ZG216S1878 and the Youth-Top-Talent Support Project of Beihang University, grant number ZG226S1821.
Author contributions
C.R. charged the project. A.K.F. designed metasheet and performed numerical simulations. A.K.M.S. and A.K.F. performed experimental verifications. A.K.F. and R.N. drafted initial version of the manuscript. T.U.H., S.U. and W.H. participated in discussion. All authors contributed to revisions in manuscript.
Data availability
Supporting data for the presented study is available from the corresponding author upon request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Fang ZH, Chen H, An D, Luo CR, Zhao XP. Manipulation of visible-light polarization with dendritic cell-cluster metasurfaces. Scientific reports. 2018;8(1):9696. doi: 10.1038/s41598-018-28030-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cui J, et al. Dynamical manipulation of electromagnetic polarization using anisotropic meta-mirror. Scientific reports. 2016;6:30771. doi: 10.1038/srep30771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cheng Y, Gong R, Wu L. Ultra-broadband linear polarization conversion via diode-like asymmetric transmission with composite metamaterial for terahertz waves. Plasmonics. 2017;12(4):1113–1120. [Google Scholar]
- 4.Arrebola M, Encinar JA, Barba M. Multifed printed reflectarray with three simultaneous shaped beams for LMDS central station antenna. IEEE Transactions on Antennas and Propagation. 2008;56(6):1518–1527. [Google Scholar]
- 5.Mao CX, Gao S, Wang Y, Chu QX, Yang XX. Dual-Band Circularly Polarized Shared-Aperture Array for C / X -Band Satellite Communications. IEEE Transactions on Antennas and Propagation. 2017;65(10):5171–5178. [Google Scholar]
- 6.Zhang JF, Cheng YJ, Ding YR, Bai CX. A dual-band shared-aperture antenna with large frequency ratio, high aperture reuse efficiency, and high channel isolation. IEEE Transactions on Antennas and Propagation. 2018;67(2):853–860. [Google Scholar]
- 7.Wang SY, Liu W, Geyi W. Dual-band transmission polarization converter based on planar-dipole pair frequency selective surface. Scientific reports. 2018;8(1):3791. doi: 10.1038/s41598-018-22092-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khan MI, Khalid Z, Tahir FA. Linear and circular-polarization conversion in X-band using anisotropic metasurface. Scientific reports. 2019;9(1):4552. doi: 10.1038/s41598-019-40793-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu C, et al. High-performance bifunctional polarization switch chiral metamaterials by inverse design method. npj Computational Materials. 2019;5(1):1–8. [Google Scholar]
- 10.Huang Y, et al. Tunable circular polarization conversion and asymmetric transmission of planar chiral graphene-metamaterial in terahertz region. Carbon. 2017;119:305–313. [Google Scholar]
- 11.Kanda N, Konishi K, Kuwata-Gonokami M. Terahertz wave polarization rotation with double layered metal grating of complimentary chiral patterns. Optics express. 2007;15(18):11117–11125. doi: 10.1364/oe.15.011117. [DOI] [PubMed] [Google Scholar]
- 12.Kenanakis G, et al. Flexible chiral metamaterials in the terahertz regime: a comparative study of various designs. Optical Materials Express. 2012;2(12):1702–1712. [Google Scholar]
- 13.Yan L, et al. Arbitrary and independent polarization control in situ via a single metasurface. Advanced Optical Materials. 2018;6(21):1800728. [Google Scholar]
- 14.Zhu HL, Cheung SW, Chung KL, Yuk TI. Linear-to-circular polarization conversion using metasurface. IEEE Transactions on Antennas and Propagation. 2013;61(9):4615–4623. [Google Scholar]
- 15.Chen WT, et al. Integrated plasmonic metasurfaces for spectropolarimetry. Nanotechnology. 2016;27(22):224002. doi: 10.1088/0957-4484/27/22/224002. [DOI] [PubMed] [Google Scholar]
- 16.Baena JD, Del Risco JP, Slobozhanyuk AP, Glybovski SB, Belov PA. Self-complementary metasurfaces for linear-to-circular polarization conversion. Physical Review B. 2015;92(24):245413. [Google Scholar]
- 17.Zhang L, et al. Broadband and wide-angle reflective polarization converter based on metasurface at microwave frequencies. Applied Physics B. 2015;120(4):617–622. [Google Scholar]
- 18.Li Z, Liu W, Cheng H, Chen S, Tian J. Realizing broadband and invertible linear-to-circular polarization converter with ultrathin single-layer metasurface. Scientific reports. 2015;5:18106. doi: 10.1038/srep18106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jiang Y, Wang L, Wang J, Akwuruoha CN, Cao W. Ultra-wideband high-efficiency reflective linear-to-circular polarization converter based on metasurface at terahertz frequencies. Optics express. 2017;25(22):27616–27623. doi: 10.1364/OE.25.027616. [DOI] [PubMed] [Google Scholar]
- 20.Lin BQ, et al. A Wide-Angle and Wide-Band Circular Polarizer Using a Bi-Layer Metasurface. Progress In Electromagnetics. Research. 2018;161:125–133. [Google Scholar]
- 21.Li Y, et al. Achieving wide-band linear-to-circular polarization conversion using ultra-thin bi-layered metasurfaces. Journal of Applied Physics. 2015;117(4):044501. [Google Scholar]
- 22.Perez-Palomino G, Page JE, Arrebola M, Encinar JA. A design technique based on equivalent circuit and coupler theory for broadband linear to circular polarization converters in reflection or transmission mode. IEEE Transactions on Antennas and Propagation. 2018;66(5):2428–2438. [Google Scholar]
- 23.Akgol O, Altintas O, Unal E, Karaaslan M, Karadag F. Linear to left-and right-hand circular polarization conversion by using a metasurface structure. International Journal of Microwave and Wireless Technologies. 2018;10(1):133–138. [Google Scholar]
- 24.Altintas O, et al. Design of a wide band metasurface as a linear to circular polarization converter. Modern Physics Letters B. 2017;31(30):1750274. [Google Scholar]
- 25.Fahad AK, Ruan C, Chen K. A Wideband Terahertz Transmissive Polarization Manipulator Based on Metasurfaces. Electronics. 2019;8(10):1068. [Google Scholar]
- 26.Mun SE, Hong J, Yun JG, Lee B. Broadband circular polarizer for randomly polarized light in few-layer metasurface. Scientific reports. 2019;9(1):2543. doi: 10.1038/s41598-019-38948-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mangi Farman Ali, Xiao Shaoqiu, Mallah Ghulam Ali, Kakepoto Ghulam Fatima, Memon Imran. Fission Transmission Linear-to-Circular Polarization Conversion Based on Compact Bi-Layer structure. Indonesian Journal of Electrical Engineering and Computer Science. 2016;3(3):519. [Google Scholar]
- 28.Mangi FA, Xiao S, Arain QA, Memon I, Kakepoto GF. Asymmetric Fission transmission of linear-to-circular polarization converter using bi-layer split ring structure. Wireless Personal Communications. 2018;99(2):985–997. [Google Scholar]
- 29.Zhu L, et al. Polarization conversion based on Mie-type electromagnetically induced transparency (EIT) effect in all-dielectric metasurface. Plasmonics. 2018;13(6):1971–1976. [Google Scholar]
- 30.Liu Y, Xia S, Shi H, Zhang A, Xu Z. Dual-band and high-efficiency polarization converter based on metasurfaces at microwave frequencies. Applied Physics B. 2016;122(6):178. [Google Scholar]
- 31.Huang, X., Yang, H., Zhang, D., & Luo, Y. Ultrathin Dual-band Metasurface Polarization Converter. IEEE Transactions on Antennas and Propagation (2019).
- 32.Zang XF, Liu SJ, Gong HH, Wang Y, Zhu YM. Dual-band superposition induced broadband terahertz linear-to-circular polarization converter. JOSA B. 2018;35(4):950–957. [Google Scholar]
- 33.Naseri P, Matos SA, Costa JR, Fernandes CA, Fonseca NJ. Dual-band dual-linear-to-circular polarization converter in transmission mode application to k/ka -band satellite communications. IEEE Transactions on Antennas and Propagation. 2018;66(12):7128–7137. [Google Scholar]
- 34.Yang, S., Jiang, Y., Wang, J., & Zhao, H. Dual-Ultrawideband Linear-to-Circular Converter with Double Rotation Direction in Terahertz Frequency. In 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC) (pp. 1–3). IEEE (2018, July).
- 35.Youn, Y. & Hong, W. Planar dual-band linear to circular polarization converter using radial-shape multi-layer FSS. In 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting (pp. 1465–1466). IEEE (2018, July).
- 36.Hosseini, M. & Hum, S. V, A systematic circuit-based approach to efficiently realize single- and dual-band circular polarizers. In Proceedings of 12th Eur. Conf. Antennas Propag. (EuCAP). pp 1–5 (2018, July).
- 37.Zeng Q, Ren W, Zhao H, Xue Z, Li W. Dual-band transmission-type circular polariser based on frequency selective surfaces. IET Microwaves, Antennas & Propagation. 2018;13(2):216–222. [Google Scholar]
- 38.Fahad AK, Ruan C, Chen K. Dual-Wide-Band Dual Polarization Terahertz Linear to Circular Polarization Converters based on Bi-Layered Transmissive Metasurfaces. Electronics. 2019;8(8):869. [Google Scholar]
- 39.Wang HB, Cheng YJ. Single-Layer Dual-Band Linear-to-Circular Polarization Converter With Wide Axial Ratio Bandwidth and Different Polarization Modes. IEEE Transactions on Antennas and Propagation. 2019;67(6):4296–4301. [Google Scholar]
- 40.Zhu L, et al. Dual-band polarization convertor based on electromagnetically induced transparency (EIT) effect in all-dielectric metamaterial. Optics express. 2019;27(9):12163–12170. doi: 10.1364/OE.27.012163. [DOI] [PubMed] [Google Scholar]
- 41.Liu X, et al. Three-band polarization converter based on reflective metasurface. IEEE Antennas and Wireless Propagation Letters. 2016;16:924–927. [Google Scholar]
- 42.Yao Z, Wang Y, Lu M, Zhang C. Triple-band cross-polarization converter based on an ultra-thin graphene-integrated metasurface. JOSA B. 2019;36(1):7–11. [Google Scholar]
- 43.Huang X, Xiao B, Guo L, Yu S, Yang H. Triple-band linear and circular reflective polarizer based on E-shaped metamaterial. Journal of Optics. 2014;16(12):125101. [Google Scholar]
- 44.Fartookzadeh M. Multi-band metamirrors for linear to circular polarization conversion with wideband and wide-angle performances. Applied Physics B. 2017;123(4):115. [Google Scholar]
- 45.Fahad, A. K., CunJun, R., Haq, T. U. & Ullah, S. Tri-band Linear to Circular Polarization Converter based on Transmissive Metasurfaces. In 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) (pp. 1–2). IEEE (2019, September).
- 46.Zhu HL, et al. Linear-to-circular polarization conversion using metasurface. IEEE Transactions on Antennas and Propagation. 2013;61(9):4615–4623. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Supporting data for the presented study is available from the corresponding author upon request.