Structural, mechanical and electronic properties and hardness of ionic vanadium dihydrides under pressure from first-principles computations

Abstract

Based on a combination of the CALYPSO method for crystal structure prediction and first-principles calculations, we explore the crystal structures of VH₂ under the pressure range of 0−300 GPa. The cubic Fm-3m phase with regular VH₈ cubes is predicted to transform into orthorhombic Pnma structure with fascinating distorted VH₉ tetrakaidecahedrons at 47.36 GPa. Both the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa are mechanically and dynamically stable, as verified with the calculations of elastic constants and phonon dispersions, respectively. Moreover, the calculated electronic band structure and density of states indicate both stable phases are metallic. Remarkably, the analyses of the Poisson’s ratio, electron localization function (ELF) and Bader charge substantiate that both stable phases are ionic crystals on account of effective charges transferring from V atom to H. On the basis of the microscopic hardness model, the Fm-3m and Pnma crystals of VH₂ are potentially incompressible and hard materials with the hardness values of 17.83 and 17.68 GPa, respectively.

Introduction

High pressure is an interesting external condition, which can reduce interatomic separation and alter the bond angles and generate the powerful influences on the physical and chemical properties and further arouse unusual stoichiometries and crystal structures in numerous materials. Hydrides have been widely progressed under high pressure due to potential high-temperature superconductors and hydrogen storage material^1–11.

Recently, the investigations on the transition metal hydrides under high pressure have also been conducted in views of two factors as follows. On the one hand, for the late transition metals, their electronegativity values (e.g., 2.2 for Ru, Pd, Os, and Ir; 2.28 for Pt; 2.54 for Au) are higher and comparable than that of hydrogen (2.2) and thus making the chemical reaction between them unfavorable and resulting in the extreme absence of the late transition metal hydrides scarce under ambient pressure. Fortunately, high pressure can effectively stimulate the chemical reactivity of elements, making the reaction between hydrogen and late transition metals come true. Previous experimental investigations have ascertained that high pressure can be utilized to synthesize new Pt, Rh and Ir hydrides^12–16 and the preceding first-principles calculations have predicted the high pressure structures produced through the reaction of the late transition metals (Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au) with hydrogen^17,18. More interestingly, RhH₂ is suggested to be a hydrogen storage compound for the highly theoretical volumetric hydrogen density of 163.7 g H₂/L¹⁵. On the other hand, as for the early transition metals possessing the smaller electronegativity than hydrogen, they are found to form easily hydrides at ambient conditions, such as ScH₂, YH₂/YH₃, TiH₂, ZrH₂, HfH₂, VH₂, NbH₂^19,20. It is obviously seen that these early transition metal hydrides generally form transition-metal dihydrides TMH₂. Upon compression, these transition-metal dihydrides that can exist under ambient conditions present fascinating properties that cannot be found at normal conditions. For example, a theoretical study indicated that TiH₂ at high pressure takes a structural sequence of I4/mmm $\to$ P4/nmm $\to$ P2₁/m with the corresponding transformation pressures of 63 and 294 GPa²¹. A subsequent experiment²² on ZrH₂ have offered a new approach with nonhydrostatic compression or shear stress for seeking higher volumetric density hydrogen structures in transition-metal hydrides. Later on, they reported another theoretical investigation on HfH₂ that it undergoes pressure-induced structural phase transition I4/mmm $\to$ Cmma $\to$ P2₁/m at 180 and 250 GPa, respectively, and HfH₂ is classified as a ionic crystal with the charges transferring from Hf atom to H²³.

With regard to group 5 element dihydrides, the pressure-induced structural transition and related structural and electronic properties of NbH₂ and TaH₂ has also been deeply explored. Gao et al. predicted that NbH₂ transforms from the fluorite Fm-3m structure into the orthorhombic Pnma phase at 50 GPa²⁴. Subsequently, we also confirmed the high-pressure phase transition of NbH₂ and further found a combination of ionic and metallic bonds in these two stable phases (the Fm-3m and Pnma phases)²⁵. In the latest theoretical work, TaH₂ is found to transform from the P6₃mc structure into the Pnma phase at about 95 GPa²⁶. Up to now, despite few theoretical researches on the high-pressure phase transition of VH₂^27,28, there is relatively little investigation on its new structures, mechanical properties, hardness and the chemical bonding nature under high pressure. This stimulates us to implement a comprehensive search on the crystal structures for vanadium dihydrides under high pressure and study the related structural, mechanical and electronic properties of newly stable VH₂ structures.

In the current work, we explore the crystal structures of VH₂ within the pressure range of 0–300 GPa by employed the developed Crystal Structure Analysis by Particle Swarm Optimization (CALYPSO) method in combination with first-principles calculations. Two stable structures (the Fm-3m and Pnma structures) are confirmed within the stable pressure ranges of 0−46.37 and 46.37−300 GPa, respectively. The Fm-3m structure is comprised of regular VH₈ cubes while the Pnma structure contains highly distorted VH₉ tetrakaidecahedrons. The mechanical and dynamical stabilities of both phases are verified with the calculated elastic constants and phonon dispersions, respectively. In addition, the analyses of the Poisson’s ratio, electron localization function (ELF) and Bader charge indicate that both phases are ionic crystals with the charges transferring from V atom to H. Furthermore, the mechanical properties and hardness were also investigated for both phases. The present results can provide a better understanding of the phase transformations, the structural characteristics and bonding character of VH₂ and promote further experimental and theoretical investigations on the transition metal hydrides.

Computational method

To search for the ground-state structures for VH₂ under high pressure, we performed an unbiased structure prediction based on the particle swarm optimization algorithm as implemented with the CALYPSO code^29,30. The superior efficiency of this methodology has been verified on various systems^25,31–39. Our structure searches with unit cells containing up to six formula units (f.u.) per simulation cell were conducted within pressures of 0−300 GPa. The detailed description for this search algorithm can be found elsewhere^29,30. The structural optimization and electronic structure calculations were carried out using density functional theory within the Perdew−Burke−Ernzerhof (PBE) exchange-correlation functional as implemented in the Vienna ab initio simulation package (VASP)^40,41. Plane-wave basis sets and the projector augmented wave (PAW) method⁴² were adopted with 4s²3d³ and 1s¹ treated as valence electron space for V and H atoms, respectively. The cutoff energy of 800 eV for the expansion of the expansion of the wave function into plane waves and appropriate Monkhorst−Pack k-meshes⁴³ were selected to ensure that all the enthalpy calculations were well converged to better than 1 meV/atom. The phonon dispersion curves were calculated within the direct supercell approach as implemented in the Phonopy code^44,45. The electron localization function (ELF)^46,47 and Bader charge⁴⁸ were also computed using VASP. In addition, all the crystal structures and electron localization functions (ELF) diagrams were generated using VESTA 3.4.4⁴⁹. The elastic constants were determined by calculating stress tensor generated by applying a small strain to an optimized unit cell. Besides, the bulk modulus (B), shear modulus (G), Young’s modulus (E), and Poisson’s ratio were thus derived from the Voigt−Reuss−Hill (VRH) approximation⁵⁰.

Results and Discussions

Crystal structure searching and phase transition under pressure

Firstly, on the basis of the chemical constitution, we have conducted the structure prediction simulations of VH₂ in the pressure range of 0−300 GPa. Subsequently, the analysis of the predicted structures provides eight candidate structures with space groups Fm-3m, Pnma, P2₁/m, P-62m, P6₃mc, P6₃/mmc, P4/nmm and I4/mmm. The candidate crystal structures diagrams are depicted in Fig. S1 in the Supplementary Information and their lattice parameters and atomic coordinates under ambient pressure are summarized in Table S1. The fact that all the earlier known structures (Fm-3m, Pnma, P6₃mc, P6₃/mmc, I4/mmm and P4/nmm)^{27,28,51–53} were successfully reproduced in specific pressure ranges supports the validity of CALYPSO methodology used in structure searches of VH₂. The enthalpy−pressure (H − P) relations of the candidate structures under the pressure range of 0−300 GPa for VH₂ are presented in Fig. 1a. Under ambient pressure, the cubic CaF₂ structure (space group Fm-3m) possesses the lowest ground state energy, which is consistent with the experimental consequence⁵¹. With increasing pressure, the orthorhombic Pnma structure is favored over the Fm-3m phase above 46.37 GPa, which remains stable in the ground state up to at least 300 GPa. This Pnma structure is also the high-pressure configuration of NbH₂^25,54, WH₂⁵⁵ and certain alkaline-earth dihydrides such as CaH₂, SrH₂, and BaH₂^56,57. This phase transformation is also supported by the volume-pressure relations (see Fig. 1b), as we observed a volume collapse of 4.1% at the transition pressure. Furthermore, the transition pressure (46.37 GPa) is in good agreement with the relevant theoretical calculations^27,28. Below we concentrate on the relevant properties of the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa, which are most stable and accessible to experiment at the corresponding pressures.

Figure 1.

(a) Enthalpy-pressure relation with respect to the Fm-3m phase and (b) volume-pressure relations for VH₂.

Structural properties and the lattice parameter behavior under pressure

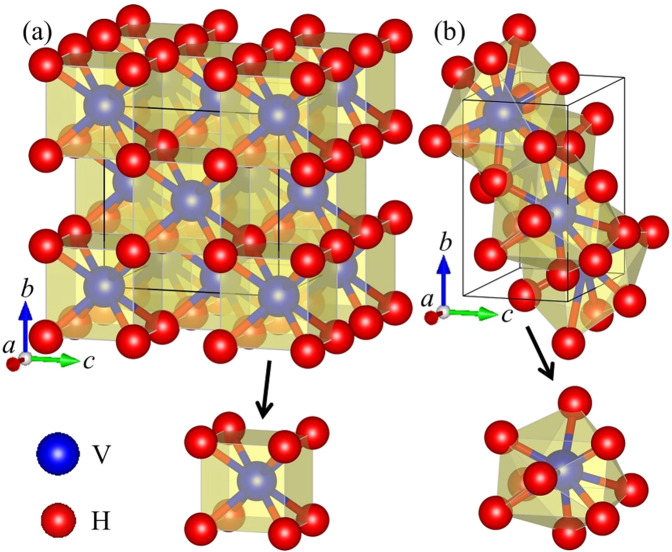
The crystal structures of the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa for VH₂ are illustrated in Fig. 2 and their structural parameters are presented in Table 1. For the Fm-3m phase at 0 GPa, as displayed in Table 1, the lattice parameter (a = b = c = 4.215 Å) is in excellent agreement with the previous results (a = b = c = 4.217 Å) calculated by Chen et al.²⁷ In the Fm-3m phase at 0 GPa, each V atom is at the center of a regular VH₈ cube with eight equal V-H separation of 1.825 Å and identical H-V-H angle of 71°. Therefore, the V environment in the Fm-3m configuration can be described as highly symmetrical VH₈ cube. However, in the Pnma phase at 100 GPa, each V atom is surrounded by one H atom at a separation of 1.634 Å, two H atoms at a separation of 1.644 Å, one H atom at a separation of 1.654 Å, one H atom at a separation of 1.701 Å, two H atoms at a separation of 1.825 Å and two further H atoms at a separation of 1.899 Å. Besides, the H-V-H angles vary between 46° and 106°. These results describe that the V environment in the Pnma phase are strongly distorted VH₉ tetrakaidecahedron. It is obviously found that the V-H environments in VH₂ transform from the regular VH₈ cube to the highly distorted VH₉ tetrakaidecahedron with increasing pressure. More interestingly, the coordination number of the V atoms in VH₂ increase monotonously upon further compression. This phenomenon can also be found in other systems^25,31,58.

Figure 2.

Crystal structures of two considered VH₂ phases, together with metal coordination polyhedra: (a) the Fm-3m phase at 0 GPa and (b) the Pnma phase at 100 GPa. The blue and red spheres represent vanadium and hydrogen atoms, respectively, and VH_n polyhedra are shaded in two phases.

Table 1.

Lattice constants and atomic coordinates of VH₂ for the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa.

Pressure (GPa)	Space group	a	b	c	Atomic coordinates (fractional)
					Atom	x	y	z
0	Fm-3m	4.215	4.215	4.215	V1(4a)	0.00000	0.00000	0.00000
					H1(8c)	0.25000	0.25000	0.25000
0	Fm-3m	4.217a	4.217a	4.217a	V1(4a)	0.00000	0.00000	0.00000
					H1(8c)	0.25000	0.25000	0.25000
100	Pnma	4.268	2.622	4.721	V1(4c)	0.23761	0.75000	0.09160
					H1(4c)	0.52689	0.75000	0.71430
					H2(4c)	0.12491	0.75000	0.42227

^aref. ²⁷.

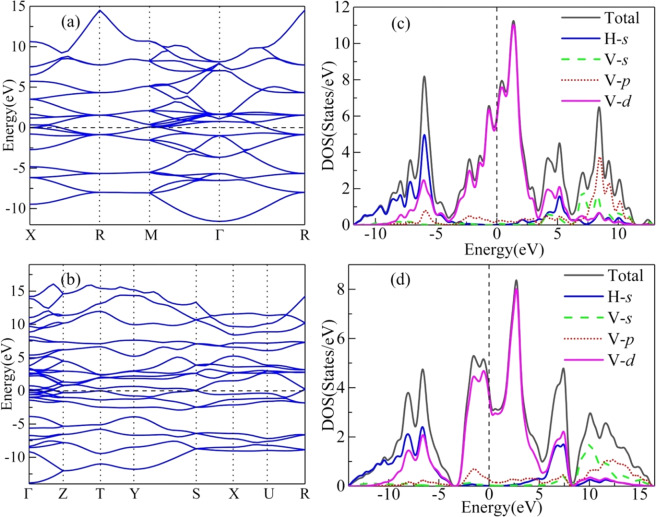
It is essential to calculate the phonon spectra of two stable VH₂ structures for the purpose of ascertaining their dynamical stabilities. The calculated phonon dispersion curves and projected phonon density of states (PHDOS) for the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa are depicted in Fig. 3. The absence of any imaginary frequencies in the entire Brillouin zone confirms the dynamical stabilities of both structures. Notably, the phonon bands can be divided into two separate regions. The higher frequency modes are mainly correspond to the vibration of the H atoms while the lower frequency region is mostly related to the V atoms, which can be attributed to the much heavier atom mass of vanadium atom than hydrogen atom.

Figure 3.

Phonon dispersion curves and projected phonon density of states (PHDOS) for two stable VH₂ phases: (a) the Fm-3m phase at 0 GPa and (b) the Pnma phase at 100 GPa.

For the purpose to investigate the effect of the external pressure on the lattice parameters and the volume of VH₂, the normalized parameters a/a₀, b/b₀, c/c₀ and volume V/V₀ of two considered phases as a function of pressure are displayed in Fig. S2, where a₀, b₀, c₀ and V₀ are the equilibrium structural parameters at zero pressure, respectively. It is obviously found that the values a/a₀, b/b₀, c/c₀ and V/V₀ decrease gradually with the increasing pressure. This can be attributed to the reason that the distance between atoms is reduced as the pressure increases, which make the repulsive interaction among atoms strengthened and lead to the higher incompressibility of the crystal under pressure.

Mechanical stability, mechanical properties and hardness

To inspect the mechanical stabilities of two stable VH₂ structures, we computed the elastic constants of the Fm-3m phase at 0 GPa and the Pnma phase at 100 GPa by using the strain−stress means⁵⁹, as summarized in Table S2. As given in Table S2, both phases satisfy their respectively mechanical stability standards⁶⁰, which states that both structures are mechanically stable.

In addition, to get further knowledge of mechanical properties for two stable configurations, the elastic constants of the Fm-3m and Pnma structures of VH₂ at 0 GPa were calculated with the identical strain−stress means⁵⁹. At the same time, the bulk modulus (B) and shear modulus (G), B/G, Young′s modulus E (GPa) and Poisson’s ratio (ν) can be derived from the calculated elastic constants on the basis of the Voigt–Reuss–Hill method⁶¹. The computed consequences above are tabulated in Table 2. Interestingly, the value of C₁₁ for two considered crystals is larger than the others. It is well known that a material with a high bulk modulus indicates its strong ability to resist volume deformation caused by an applied load. According to Table 2, the calculated bulk moduli of the Fm-3m and Pnma structures are 174 and 173 GPa, respectively, illustrating the incompressible feature of these two phases to a certain degree. In addition, the shear modulus of a material can be used to quantify its resistance to the shear deformation. From Table 2, these two crystals possess the equal the shear modulus of 118 GPa, suggesting that both configurations can withstand the shear strain to a large extent. The ratio value of B/G is commonly used to describe the ductility or brittleness of materials with 1.75 as the critical value⁶⁰. From Table 2, the calculated identical ratio value of B/G for both phases is 1.47, indicating their brittle characteristic. Poisson’s ratio is an important parameter to describe the bond nature in a material. For covalent materials, the value of ν should be small (typically ν = 0.1), and shear modulus G should be slightly different with bulk modulus B with G = 1.1B. The typical value of ν for ionic materials is 0.25 and G = 0.6B. For metallic materials, ν is typically 0.33 and G = 0.4B; in the extreme case where ν is 0.5, G is zero⁶². From Table 2, the equal ν (0.22) for both structures extremely approach the typical value ν (0.25) of ionic materials. Further, shear modulus G is equal to 0.68B. These two conditions above demonstrate that the Fm-3m and Pnma phases of VH₂ can be classified into ionic materials. In order to estimate the hardness (Hv) of VH₂, an empirical hardness equation is applied as follows: H_v = 2(K²G)^0.585 − 3, where K = G/B⁶³. As shown in Table 2, the calculated hardness (H_v) values of the Fm-3m and Pnma phases are 17.83 and 17.68 GPa, respectively, declaring that both phases of VH₂ could be classified as incompressible and hard materials.

Table 2.

Calculated elastic constants C_ij (GPa), bulk modulus B (GPa), shear modulus G (GPa), B/G, Young’s modulus E (GPa), Poisson’s ratio ν and Vickers hardness H_v of VH₂ for the Fm-3m and Pnma phases under 0 GPa.

Phase	C11	C22	C33	C44	C55	C66	C12	C13	C23	B	G	B/G	E	ν	Hv
Fm-3m	293			143			115			174	118	1.47	290	0.22	17.83
Pnma	340	332	337	106	121	119	101	81	93	173	118	1.47	288	0.22	17.68

Electronic properties and bonding features

In order to further gain insight into the electronic properties of both stable VH₂ configurations, we calculated their electronic band structures and densities of states (DOS) (see Fig. 4). Both structures are found to exhibit metallic character to the overlap between the conduction bands and the valence bands, as displayed in Fig. 4a,b. This is also confirmed by the finite electronic DOS at the Fermi level (E_F) in Fig. 4c,d. For both compounds, the total densities of states (TDOS) near the Fermi level is largely contributed by the V-d states, so the metallic properties are mainly due to partially filled V 3d shell.

Figure 4.

Calculated band structures and densities of states (DOS) for two stable VH₂ phases. The electronic band structures for (a) the Fm-3m phase at 0 GPa and (b) the Pnma phase at 100 GPa. The total and partial density of states for (c) the Fm-3m phase at 0 GPa and (d) the Pnma phase at 100 GPa.

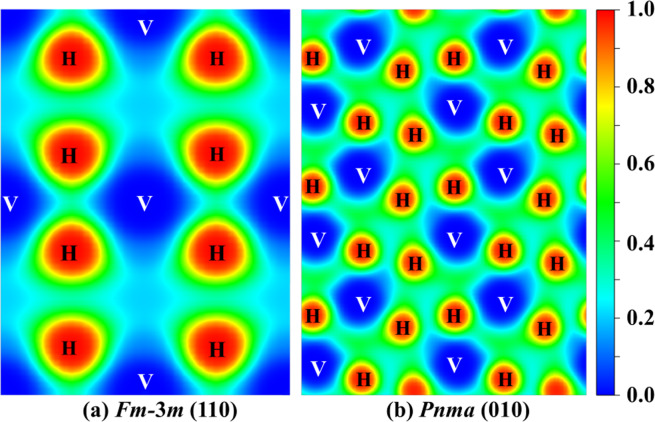
To further visualize the chemical bonding nature in the polymeric sublattice for two considered VH₂ structures, we calculate the electron localization function (ELF) which can make a description of the bond type between atoms, as shown in Fig. 5. Generally speaking, large ELF values (>0.5) correspond to covalent bonds and lone pair or inner shell electrons while smaller ELF values (<0.5) correspond to ionic or metallic bonds^46,47. For two stable VH₂ structures, the analyses of ELF toward the neighboring V − H and H − H connections obviously reveal no electron localization, thus suggesting that no covalent interaction exists for neighboring V − H and H − H. Moreover, the ELF values between V and the nearest H atom in both stable phases are smaller than 0.5, implying the ionic or metallic bonds are present between V and H atoms. Furthermore, in order to illuminate the chemical bonding features between V and H atoms, Bader charge analysis⁴⁸ was implemented, as summarized in Table 3. For the Fm-3m phase at 0 GPa, each H atom gains 0.54 e while the V atoms lose 1.08 e. In addition, for the Pnma phase at 100 GPa, a charge of 0.92 e is stripped off the V atom and transferred completely to the H atoms (0.46 e each). The current prediction of the charge transferring from V to H atoms can also be corroborated by the element electronegativity. From the periodic law⁶⁴, the electronegativity value of the V element (1.63) is smaller than that of the H element (2.2), meaning that the charge should transfer from V to H atoms. The calculated consequences above apparently show that there are large amounts of charge transferring from V to H atoms, demonstrating the ionic character of the V−H bonding in two stable VH₂ crystals. This ionic bonding character is similar in AlH₃, LiH_n, HfH₂, TaH_n, VH, VH₃ and VH₅^{23,26,65–67}. However, the ionic characteristic for the H atoms is different from that of many hydrogen-rich polymorphs (i.e., SiH₄, GeH₄, SnH₄, InH₃, OsH₆ and OsH₈)^68–72, where the H atoms are either bonded to the nearest H atoms to form an H₂ or H₃ unit and/or they are covalently bonded to M (M = Si, Ge, Sn, In, or Os) atoms to form M − H bonds. In short, a combination analysis of ELF and Bader charge reveals that the ionic bonds are formed between V and H atoms and VH₂ should be classified as an ionic crystal, which is accord with the analysis of Poisson’s ratio above.

Figure 5.

Electron localization function (ELF) of two stable VH₂ phases: (a) (110) plane for the Fm-3m phase at 0 GPa and (b) (010) plane for the Pnma phase at 100 GPa.

Table 3.

Calculated Bader charges of V and H atoms in two stable VH₂ crystals.

Phase	Pressure(GPa)	Atom	Charge value (e)	δ(e)
Fm-3m	0	V	3.92	1.08
		H	1.54	−0.54
Pnma	100	V	4.08	0.92
		H	1.46	−0.46

δ represents the amount of charge transferred from V atom to H atom.

Conclusions

In summary, we conducted the systematic structure evolutionary searches of the VH₂ compound based on the CALYPSO method for crystal structure prediction combined with first-principles calculations under the pressure range between 0 and 300 GPa. This material undergoes a pressure-induced structural phase transformation from the cubic structure Fm-3m structure to the orthorhombic Pnma structure at 46.37 GPa. Intriguing, the Fm-3m structure is comprised of regular VH₈ cubes while the Pnma structure contains highly distorted VH₉ tetrakaidecahedron. The calculations of elastic constants and phonon dispersions confirm the mechanical and dynamical stabilities of both configurations, respectively. Both phases possess the metallic properties as verified by the band structures and densities of states for two stable VH₂ structures. Further analyses of the Poisson’s ratio, ELF and Bader charge indicate that VH₂ should be classified into an ionic crystal with large amounts of charge transferring from V atom to H. Remarkably, the estimated hardness values of the Fm-3m and Pnma phases are 17.83 and 17.68 GPa, respectively. The current work will stimulate further high pressure experiments to synthesize these vanadium hydrides and carry out the structural, mechanical and hardness measurements.

Author contributions

C.Z.Z., Y.Y.J., S.L. and W.B.Z. conceived the idea. W.J.W., P.L.K., C.W.X., C.Z.D., Q. L. and C.H.Z. performed the calculations. W.J.W., C.Z.Z., Y.Y.J. and S.L. wrote the manuscript and all authors contributed to revisions.

Competing interests

The authors declare no competing interests.

Supplementary information

is available for this paper at 10.1038/s41598-020-65910-4.