Speed and Diffusion of Kinesin-2 Are Competing Limiting Factors in Flagellar Length-Control Model

Abstract

Flagellar length control in Chlamydomonas is a tractable model system for studying the general question of organelle size regulation. We have previously proposed that the diffusive return of the kinesin motor that powers intraflagellar transport can play a key role in length regulation. Here, we explore how the motor speed and diffusion coefficient for the return of kinesin-2 affect flagellar growth kinetics. We find that the system can exist in two distinct regimes, one dominated by motor speed and one by diffusion coefficient. Depending on length, a flagellum can switch between these regimes. Our results indicate that mutations can affect the length in distinct ways. We discuss our theory’s implication for flagellar growth influenced by beating and provide possible explanations for the experimental observation that a beating flagellum is usually longer than its immotile mutant. These results demonstrate how our simple model can suggest explanations for mutant phenotypes.

Significance

The eukaryotic flagellum is an ideal case study in organelle size control because of its simple linear shape and well-understood building mechanism. In our previous work, we proved that flagellar length in the green algae Chlamydomonas can be controlled by the diffusive gradient of the kinesin-2 motors that deliver building blocks to the tip. In this study, we expand on the analytical formulation of the diffusion model to show how physical parameters affect final length and regeneration time, enhancing the model’s potential to explain length mutants and motivate future research with precise predictions.

Introduction

Biologists have long been trying to understand how cells build themselves. The proteins that cells synthesize must come together to form massive organized structures without any guidance. A striking case of this is that some single-celled organisms can regenerate missing pieces, implying that the cell has some form of design specifications embedded within it that allow the cell to reconstruct the correct form. The single-celled algae Chlamydomonas reinhardtii is an ideal organism for studying single-cell organelle regeneration because it has two linear flagella that grow back upon being cut or shed (1). The kinetics of flagellar growth have been well documented, and much is known about the inner components of the flagellum and its growing process, but how the flagellum consistently reaches the same steady-state length is a mystery. Multiple different theoretical models have been developed to explain this robust regeneration, and recent work demonstrated the feasibility of a model in which the length of the flagellum is governed by a diffusive gradient across its length (2,3).

In this study, we further develop the diffusion model by deriving the growth curve analytically as a function of time and the relevant physical parameters. This shines light onto which factors are limiting at different stages in the growth. It also lets us predict steady-state length from observed physical parameters and predict physical parameters from observed steady-state length.

To understand the length-control model, one must first understand how a Chlamydomonas cell builds its flagella. The flagellum is made of nine doublet microtubules, and to get longer, new tubulin (the building blocks of microtubules) must be delivered to the flagellar tip. The mechanism for transporting tubulin to the tip is called intraflagellar transport (IFT) (4, 5, 6, 7, 8). In IFT, tubulin and other building materials such as axonemal dynein arms are bound to protein complexes of ∼20 polypeptides called IFT particles. These IFT protein complexes form linear arrays called “trains” and are pulled to the distal tip by heterotrimeric kinesin-2 motors (9, 10, 11, 12). Upon arrival at the tip, the tubulin and other building blocks are added to the flagellum, increasing its length. To counter this length increase, tubulin is continually removed from the flagellar tip at a constant, length-independent rate (13,14). Cytoplasmic dynein-2 motors carry the IFT particles back to the base (15,16). IFT happens continuously throughout the lifespan of a Chlamydomonas cell, and when the rate of IFT-driven assembly equals the rate of length-independent tubulin removal, steady-state length is achieved.

IFT begins through a process called “injection” in which IFT trains are released from docking sites at the flagellar basal body and transition zone and are transported into the flagellum itself (17). Injection is not fully understood, but it appears that IFT material injects into the flagellum from the basal body upon accumulation of motors in the basal body. Quantitative live-cell imaging has shown that the rate of injection is a decreasing function of the length of the flagellum (18,19). This implies some sort of sensing mechanism that allows the basal body to sense the flagellar length. The sensing mechanism here is unknown and is the core puzzle that length-control models try to solve (18,20,21).

The flagellar length regulation problem is an ideal system for mathematical biology because the flagellum has a simple geometry, an easily simplified building and degrading process, and a mysterious control mechanism that has eluded scientists of all disciplines for generations. As a result, there have been several models for length control that have been studied in detail (20). Some models, such as the time-of-flight model in which the IFT particles can be somehow deactivated if they have been in the flagellum for a long time, have been ruled out when the experiment failed to confirm predictions from the model (21). Several models can still explain all experimental results, including the ciliary current model, in which ion channels lining the flagellum at regular intervals regulate the electric potential inside the flagellum and thus regulate length (20). In this study, we will further develop the diffusion model, in which the length-dependent rate of IFT is generated by the kinesin motors diffusing back to the basal body from the tip, using the time it takes to diffuse back as a proxy for length measurement (2). One reason that we focus on this model is that the diffusion model is the most parsimonious, in the sense that it does not require any additional components other than those already known to explain length regulation. The other models require additional molecular components to transduce a length-dependent signal to the IFT injection system. Moreover, the diffusion model has the most support from experimental results, most notably from a recent study in which kinesin motors were observed to diffuse from the tip to the base but are not actively transported back to the base (22), whereas the other components of IFT trains are transported back to the flagellar base by IFT dyneins (15,16). When retrograde IFT stopped, all other parts of the IFT train, but not kinesin, are accumulated at the flagellar tip (23). By further developing the diffusion model, we make predictions that will motivate experiments that would not have been obviously useful in distinguishing length-control models.

In the model explored by Hendel et al., the longer the flagellum, the longer it takes for kinesins to diffuse back to the base, and therefore, the longer it takes for enough kinesins to accumulate in the base to power injection (2). This explains, in principle, how longer flagella inject less building material per second. The model assumes that kinesins are conserved and not drawn from the cell body in significant number. This would eliminate the need for a currently undiscovered signaling pathway and would allow the already-known components of IFT to generate their own length dependence. In this study, we will take the conclusions from Hendel et al. and further develop the analytical formalism of the diffusion model to show how altering the diffusion coefficient and IFT velocity would affect observables like steady-state length and regeneration time (2). Hendel et al. (2) mainly focused on diffusion coefficient and briefly focused on motor velocity, but here, we examine flagellar growth when considering these two parameters together. This study provides a mean-field description of our previous stochastic simulations in Hendel et al. 2018 (2). The model is mathematically rigorous and analytically tractable, thus providing a clearer picture to look at different regimes for different parameters than the stochastic simulations. We identified three factors that limit flagellar growth at different phases of its regeneration, which led to two possible rate-limiting steps of flagellar growth at steady state. We then used the upgraded model to attempt to explain observed length changes in length-altering mutants by calculating what changes in diffusion coefficient and IFT velocity are necessary. We arrived at the conclusion that changes in diffusion coefficient may be responsible for the length changes in the mutants.

Model

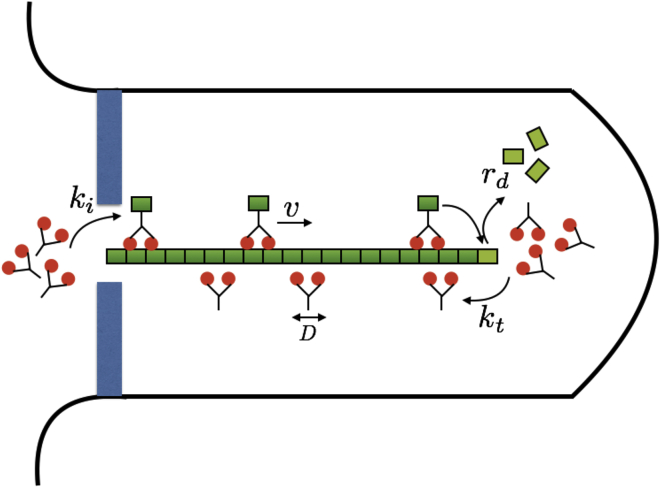
We treat the flagellum as a linear track for kinesin motors (Fig. 1). The position on the track is labeled by x, with x = 0 corresponding to the base and x = L(t) corresponding to the tip of the flagellum, where L(t) is the length of the flagellum at time t. We distinguish four populations of kinesin motors: 1) motors that actively carry cargos from the base to the tip with a constant velocity v, 2) motors that accumulate at the tip after the delivery, 3) motors that diffuse back to the base from the tip with a diffusion coefficient D, and 4) motors that accumulate at the base when diffusion is completed.

Figure 1.

Illustration of the model. Molecular motors carry the building blocks for flagellar assembly from the base to the tip and travel with a constant speed v. When reaching the tip, the motors unload the cargo, and the flagellum elongates by a unit of δ. The motors dwell at the tip and switch to a diffusive state with a transition rate k_t. The motors diffuse back to the base with a diffusion coefficient D and accumulate at the base, waiting for injection into the flagellum with a transition rate k_i. The flagellum has a spontaneous disassembly rate of r_d. The total number of molecular motors is assumed to be constant. To see this figure in color, go online.

The linear number density of active motors ρ_a (x, t) of type 1 is governed by the equation

$${\partial }_t{\rho }_a\left(x,t\right)=-{\partial }_x{J}_a\left(x,t\right),$$ (1a)

with the convective current

$$J_a\left(x,t\right)=v{\rho }_a\left(x,t\right).$$ (1b)

The number of type 2 motors N_t dwelling at the tip is described by

$$\frac{d{N}_t}{dt}=J_a\left(L,t\right)-k_t{N}_t,$$ (2)

where k_t is the transition rate for a motor dwelling at the tip switching to a diffusive state.

The linear number density of diffusive motors ρ_d (x, t) of type 3 obeys the simple diffusion law:

$${\partial }_t{\rho }_d\left(x,t\right)=-{\partial }_x{J}_d\left(x,t\right),$$ (3a)

with the diffusive current

$$J_d=-D{\partial }_x{\rho }_d\left(x,t\right).$$ (3b)

The number of type 4 motors N_b accumulating at the base is described by

$$\frac{d{N}_b}{dt}=J_d\left(0,t\right)-k_i{N}_b,$$ (4)

where k_i is the injection rate of the motors from the reservoir at the base to the flagellum track. Experimental evidence indicates that the injection actually resembles a threshold switch (18), but because this version of the model is a mean-field description rather than a stochastic simulation, we decided to approximate the thresholding as a first-order process in which injection is proportional to the number of motors in the base. On average, this will result in the same number of injections per second. This is especially true in steady state, when the rate of injection is also at steady state.

The total number of motors N includes all four populations of motors and reads

$$N=N_b+N_t+\underset{0}{\overset{L}{\int }}\left({\rho }_a+{\rho }_d\right)dx.$$ (5)

We assume the total number of motors is conserved, and this imposes the boundary conditions at the base

$$J_a\left(0,t\right)=k_i{N}_b$$ (6a)

and at the tip

$$J_d\left(L,t\right)=k_t{N}_t.$$ (6b)

The growth dynamics of the flagellum are governed by the equation

$$\frac{dL}{dt}=J_a\left(L,t\right)\delta -r_d,$$ (7)

where δ denotes the length elongation caused by the arrival of a single kinesin motor, and r_d denotes the depolymerization speed that is independent of the length.

Results

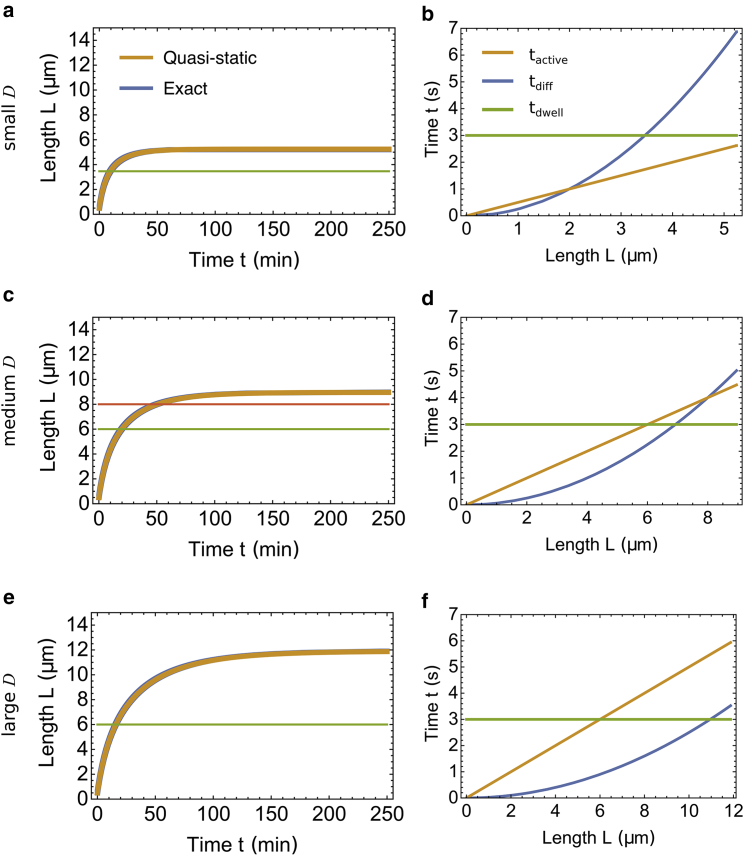
We can numerically solve the dynamic (1a), (1b), 4, and 7 to have the exact growth curve L(t) for a flagellum of length L as a function of time t. The parameters used in our numerical solutions are listed in Table 1. Because of the small elongation increment δ, we can also make a quasistatic assumption that at each length L, the spatial distribution of molecular motors reaches steady state for that particular length L (see Appendix A). The analytical results obtained by this quasistatic assumption almost exactly overlap with the exact numerical solution (Fig. 2, a, c, and e). Therefore, for the rest of the article, we only show results obtained with the quasistatic assumption.

Table 1.

Parameters of the Model

Parameters	Description	Reference Value	Varied Range	References
v	kinesin motor velocity	2 μm/s	0.1–10 μm/s	(22)
D	kinesin motor diffusion coefficient	20 μm2/s	0.1–80 μm2/s	(22)
ki	injection rate of motors at the base	1 s−1	1 s−1	arbitrary
kt	transition rate to diffusive state for motors dwelling at the tip	0.5 s−1	0.5 s−1	(22)
rd	spontaneous depolymerization speed of flagellum	0.004 μm/s	0.004 μm/s	(24,43)
N	total number of motors	40	40	(13)
δ	elongation length of the flagellum upon the arrival of a motor at the tip	0.00125 μm	0.00125 μm	(13)

Figure 2.

Growth dynamics of the model. (a, c, and e) Shown are the growth curves of the flagellum for a small diffusion coefficient D = 2 μm²/s in (a), medium D = 8 μm²/s in (c), and large D = 20 μm²/s in (e). The blue curve represents the numerical solution, i.e., the exact solution. The orange curve represents the analytical solution obtained by the quasistatic assumption. The two curves almost overlap to the extent that the blue one is invisible. The horizontal lines represent the length at which the rate-limiting step changes. (b, d, and f) Shown is the time a single motor spends on different steps during a transportation-diffusion cycle for the same diffusion coefficient as in (a), (c), and (e). The three curves include t_active for a motor to travel from the base to tip (orange), t_diff for a motor to travel from the tip to the base via diffusion (blue), and t_dwell for a motor to dwell at the tip waiting before diffusing and at the base waiting for injection (green). To see this figure in color, go online.

The rate-limiting step changes as the flagellum grows

Typical growth curves of the flagellum are demonstrated in Fig. 2 for three diffusion coefficients. Each growth curve rapidly increases at first and then slowly plateaus to the steady-state length. The growth can be divided into different stages based on the rate-limiting step. To see this, we express the growth rate of the flagellum under the quasistatic assumption as

$$\frac{dL}{dt}=\frac{N\delta }{\frac{L}{v}+\frac{L^2}{2D}+\frac{1}{k_t}+\frac{1}{k_i}}-r_d=\frac{N\delta }{t_{\text{active}}+t_{\text{diff}}+t_{\text{dwell}}}-r_d,$$ (8)

where $t_{\text{active}}=\left(L/v\right)$ denotes the time for a motor to transport the assembly unit of the flagellum from the base to the tip, $t_{\text{diff}}=\left(L^2/2D\right)$ denotes the root mean-square time for a motor to diffuse back to the base from the tip, and $t_{\text{dwell}}=\left(1/k_t\right)+\left(1/k_i\right)$ denotes the total time a motor dwells at the base and at the tip. At a short length scale, t_dwell always dominates over the other two timescales, and motors spend most of their time dwelling at the tip and the base (Fig. 2, b, d, and f, green lines). In this regime, the duration that the motor spends traveling between the base and the tip is negligible, so the flagellar growth rate is independent of the length. When the flagellum grows longer, either the diffusive time t_diff dominates if D is small (Fig. 2 b) or the transportation time t_active dominates if D is large (Fig. 2 f). For an intermediate D, the growth is divided into three stages in which the dominant timescales are t_dwell, t_active, and t_diff (Fig. 2 d). Measurements of flagellar growth kinetics have clearly shown that growth rates are constant for the flagella that are shorter than 4–5 μm (1). In a different algal species, Spermatozopsis similis, flagella grow at a constant rate over their whole length, suggesting that in that organism, t_dwell is always the dominating factor (20).

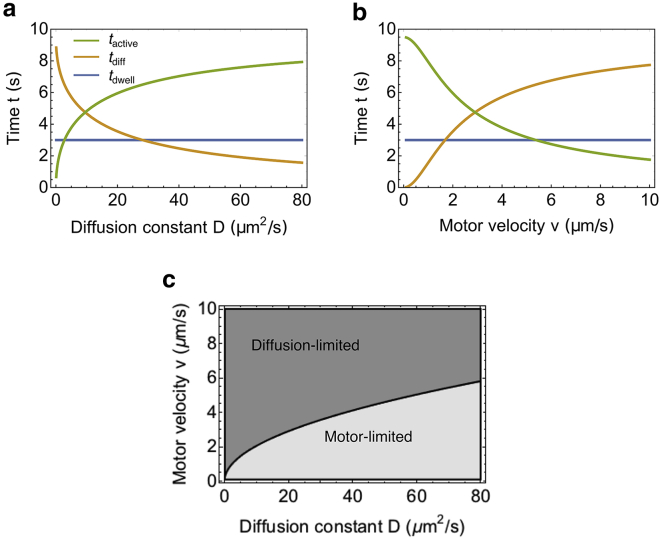
Diffusion versus active transport as the rate-limiting step at steady state

The diffusion time t_diff scales with L², whereas the motor transportation time t_active scales with L. At steady state, depending on the flagellar length L^ss, either active transport or motor diffusion becomes the rate-limiting step. For a sufficiently long flagellum, t_diff always dominates over t_active. However, the steady-state length L^ss might not be long enough to have t_diff greater than t_active. In Fig. 3 a, we show the three timescales at steady state as a function of diffusion coefficient D. For small D, t_diff dominates over the other timescales. However, as D increases, t_active becomes greater than t_diff, and the steady-state length of the flagellum becomes limited by the active motor transport. If we fix the diffusion coefficient but vary the motor velocity, the growth will change from t_active dominance to t_diff dominance (Fig. 3 b). A phase diagram is shown in Fig. 3 c. Generally, a larger diffusion coefficient D favors motor-limited growth, and a faster motor speed v favors diffusion-limited growth.

Figure 3.

Influence of the motor velocity v and diffusion coefficient D on the rate-limiting step at steady state. (a) Shown are the three timescales as a function of diffusion coefficient D. (b) Shown are the three timescales as a function of motor velocity v. (c) The phase diagram for the rate-limiting step at steady state is given. To see this figure in color, go online.

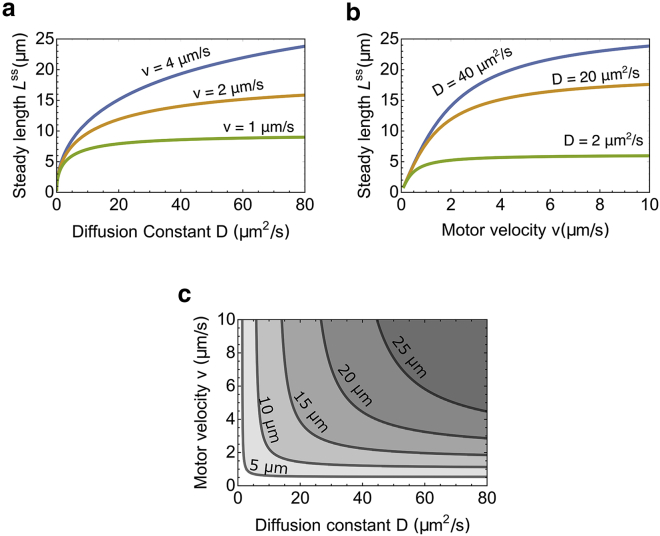
A dramatic increase in steady-state length L^ss requires a dramatic increase in diffusion coefficient D if motor velocity v is small

The steady-state length of the flagellum L^ss can be obtained by setting $\left(dL/dt\right)$ in Eq. 8 to 0. This leads to the analytical result

$$L^{ss}=-\frac{D}{v}+\sqrt{-\frac{2D}{k_i}-\frac{2D}{k_t}+{\left(\frac{D}{v}\right)}^2+\frac{2DN\delta }{r_d}}.$$ (9)

The steady-state length L^ss increases with both diffusion coefficient D and motor velocity v. For a small motor velocity, increasing the diffusion coefficient does not lead to significant increase in L^ss because it is mainly set by the small motor velocity (Fig. 4 a, green line). For instance, if the motor velocity v is 1 μm/s and L^ss is 5 μm, it would be impossible to increase the length to 10 μm because even in the limit of an infinitely large diffusion coefficient D → ∞, the maximal length L^ss is 9.5 μm. The analytical proof of this limit is derived in Appendix B.

Figure 4.

Influence of the motor velocity v and diffusion coefficient D on the steady-state length L^ss of the flagellum. (a) The steady-state length L^ss as a function of diffusion coefficient D for different motor velocities is shown. (b) The steady-state length L^ss as a function of motor velocity v for different diffusion coefficients is shown. (c) The contour plot of L^ss as a function of both the diffusion coefficient D and motor velocity v is given. To see this figure in color, go online.

However, if the motor velocity v is 2 μm/s, the diffusion coefficient D must only increase from 1.8 to 11.1 μm²/s to increase the length to 10 microns, the typical length of wild-type C. reinhardtii cells. Similarly, for a small diffusion coefficient, increasing the motor velocity does not lead to a significant increase in L^ss either (Fig. 4 b, green line).

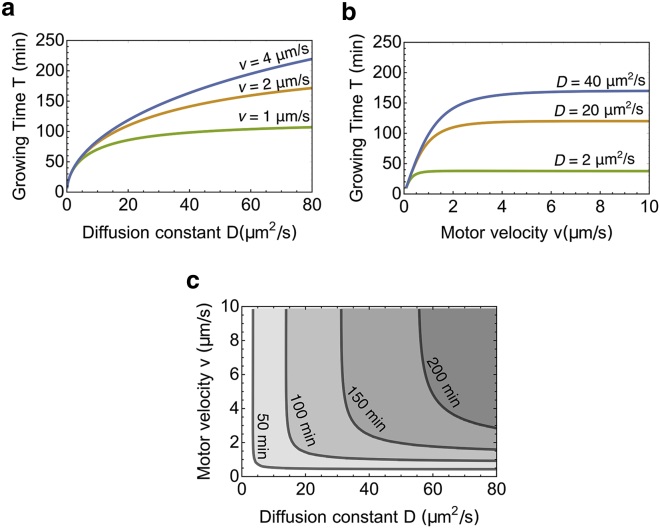
Growing time T of the flagellum increases with motor velocity and diffusion

In this section, we study the time T a flagellum needs to grow to its steady state. We define the growing time T as the amount of time to reach 95% of the steady-state length, i.e., L(T) = 0.95L^ss. Fig. 5 plots numerical solutions of T as a function of motor speed and diffusion coefficient. One might expect that a fast-transporting motor or a fast-diffusive motor will reduce the time to construct a flagellum, but the results show that the growing time T increases with the diffusion coefficient D and the motor velocity v (Fig. 5, a and b). This is because the steady-state length also increases with D and v. The reduction in time due to increased v or D cannot compensate for the increased time due to length elongation.

Figure 5.

Influence of the motor velocity v and diffusion coefficient D on the growing time T of the flagellum. (a) The growing time T as a function of diffusion coefficient D for the different motor velocities is shown. (b) The growing time T as a function of motor velocity v for the different diffusion coefficients is shown. (c) The contour plot of T as a function of both the diffusion coefficient D and motor velocity v is given. To see this figure in color, go online.

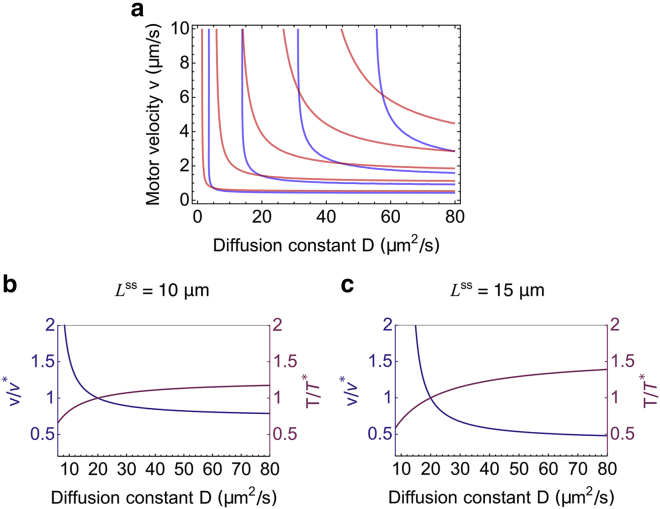
Parameter changes that maintain the steady-state length but alter the growing time

One may notice that the contour lines for the steady-state length L^ss do not exactly overlap with the contour lines for the growing time T (Fig. 6 a). The implication of this difference is that growth kinetics do not uniquely determine the steady-state length, and one can alter the growing time T while maintaining the steady-state length L^ss constant or vice versa. A recent experiment found that mutants in ida5, which affect actin, show slower growth kinetics (i.e., longer T) but reach the same steady-state length as wild-type (24). Based on our model, this could be a result of the combination of reduced motor velocity and enhanced diffusion coefficient (Fig. 6, b and c). Our model predicts that the change in the growing time is larger for longer flagella, which can be tested by future experiments.

Figure 6.

Possible parameter changes that keep the steady-state length L^ss constant while altering the growing time T. (a) An overlay of the contour plots for the growing time T (blue) and for the steady-state length L^ss (red) is given. From left to right, the contours for growing time T are 50, 100, 150, and 200 min, and for the steady-state length L^ss are 5, 10, 15, 20, and 25 μm. (b and c) Shown is the relative change of the motor velocity (left axis) and growing time (right axis) as a function of the diffusion coefficient along the contour of L^ss = 10 μm in (b) and L^ss = 15 μm in (c). The reference velocity is defined as v^∗ = v(D = 20 μm²/s), and the reference growing time is defined as T^∗ = T(D = 20 μm²/s). To see this figure in color, go online.

Discussion

In this study, we have presented a mean-field description of our previous stochastic simulation to account for flagellar growth. The key to achieving length regulation is that the number of kinesin motors is finite. As the flagellum elongates, it takes more time to transport the assembly unit from the base to the tip and to retrieve the kinesin motors from the tip to the base; therefore, the assembly rate of the flagellum is reduced. Steady-state length is reached once the assembly rate equals the disassembly rate. This reaction-diffusion-based mechanism of length regulation is also present in the growth of stereocilia, which are made of a bundle of actin filaments (25), and a series of models have indeed shown that the reaction-diffusion mechanism is sufficient to account for length regulation in that organelle (25, 26, 27). We have modeled a reaction-diffusion mechanism for flagella that, because it also involves an interplay between motors and diffusion, ends up being quite similar in its form to the previously described models for length regulation in stereocilia. However, in stereocilia, the polymerization rate of actin filaments is reduced by the resisting force from the membrane. The steady-state length is reached when the retrograde flow of actin filaments is balanced by actin polymerization at the tip (25, 26, 27). We also note that in this version of our model, we only consider the growth of a single flagellum but neglect the coupling between the two flagella for Chlamydomonas. In Fai et al. (3), the authors studied the coupling mechanism to account for length equalization when one of the flagella is severed. In our model, length equalization can be achieved by having a shared pool of tubulins and replenishment of kinesin motors (2).

A large part of the explanatory and predictive power of the model is in generating hypotheses to explain length mutants and motivating experiments to test these hypotheses. We can now examine a length mutant, note its length change from wild-type, and determine what changes in the velocity and diffusion are necessary to achieve the length change. Here, we discuss pf14, a mutant that is missing the radial spoke head in the flagellum. In wild-type Chlamydomonas, the two flagella beat in a cyclic pattern resembling a breaststroke: a semicircular power stroke to swim forward, followed by a recovery stroke to return them to their initial position. On the other hand, pf14 has paralyzed flagella and cannot swim. What is puzzling about this mutant is that its flagella are about half as long as those of the wild-type. The pf14 mutants are 3–6 μm in length, whereas wild-type flagella are usually 10–12 μm (28). This short-flagella phenotype is common among the group of motility mutants, especially the ones with completely paralyzed flagella (29, 30, 31, 32, 33, 34). To our knowledge, no study has explained the connection between paralysis and length decrease—in fact, researchers have viewed IFT and flagellar beating as two independent processes. This is reasonable because beating relies on axonemal dynein and other regulatory and structural components to bend doublet microtubules, components that are not involved in IFT. Even when detached from the cell body, the flagellum equipped with the motility apparatus is capable of producing a high-frequency waveform as long as ATP is provided (35).

Although it is possible that the length change comes from a structural instability caused by the mutation, could it instead be because the paralysis of the flagella alters the IFT-diffusion system that could be responsible for length control? All existing measurements of IFT kinetics have been carried out in immotile flagella, either in paralyzed mutants or in wild-type cells whose flagella are adhered to a glass surface. Consequently, there is no experimental information about how IFT kinetics might or might not change in beating flagella compared to immotile flagella. Here, we use our model to explore the plausibility of the idea that flagellar beating can influence IFT kinetics and thus might act as a wrongfully neglected factor in the length-control system. In the sections below, we propose mechanisms through which flagellar beating can influence IFT kinetics. Through some back-of-the-envelope calculation, we show the effective contribution of each mechanism to the length change of motile flagella compared with immotile ones. We focus on mechanical mechanisms that are directly related to flagellar beating but neglect chemical mechanisms that might exist in the mutants. For instance, experiments have shown that the presence of substrate can enhance the diffusion of substrate (36,37). The diffusion constant of kinesin motors therefore can be influenced by the ATP concentration in the wild-type and in the mutants. This biochemical regulation is out of the realm of this study.

An increase in diffusion coefficient is necessary for the increase of steady-state length

Based on our model, there are four aspects of IFT kinetics that can be influenced by flagellar beating. They include kinesin motors dwelling at the base and at the tip, actively transporting from the base to the tip and passively diffusing from the tip to the base. Altering the dwelling time of the kinesin motors at the tip or at the base has a minor effect on the steady-state length of flagella. This is because the rate-limiting step at steady state is either active transport or passive diffusion, as we have demonstrated in Diffusion versus active transport as the rate-limiting step at steady state. With the parameters given in Table 1 but a low diffusion constant D = 2 μm²/s for an immotile flagellum, even if the injection rate increases from 1 s⁻¹ to infinity, the steady-state length only increases from 5.2 to 5.5 μm, according to Eq. 9. Therefore, we exclude the possibility of an altered injection rate at the base or an altered dwelling time at the tip as the explanation for the length difference between motile and immotile flagella. We consider the other two aspects of IFT kinetics for the significant increase in length in a beating flagellum compared to an immotile one: 1) the motor velocity remains unchanged, and the increase is due to enhanced diffusion. 2) The diffusion coefficient remains unchanged, and the increase is due to increased motor velocity. In a paralyzed mutant, the experimentally measured diffusion coefficient is D = 1.68 ± 0.04 μm²/s, and the motor velocity is v = 2.1 ± 0.4 μm/s (22). With the first assumption, to account for the length increase in a beating flagellum from 5 to 10 μm, the diffusion coefficient needs to increase from 1.75 to 10.55 μm²/s. With the second assumption, it is impossible to account for the length increase because even in the limit of infinitely large motor velocity v → ∞, the length of the flagellum approaches a maximum of 5.65 μm. Therefore, an enhanced diffusion coefficient is necessary and sufficient to account for the observed length increase. In any case, there is no plausible way that flagellar beating would alter the velocity of the motor. However, we can imagine several ways that beating could alter the diffusion coefficient of kinesin, which we will consider in turn.

Centrifugation effect of kinesin motors

The first mechanism we considered was inspired by the experimental observation that kinesin-2 is less dense than the flagellar matrix and floats to the top when a matrix preparation is centrifuged at high speed (H.Q., unpublished data). Based on this observation, we consider a model in which the roughly circular beating of the flagellum is enough to cause a significant centripetal force on the kinesin motors back toward the base, speeding up the diffusive return time. To model this scenario, we approximated the flagellum and its beating as a cylindrical rod revolving around one of its ends like the hand of a clock. The contents of the cylinder will experience a centrifugation effect, and the kinesins will move toward the base if they are less dense than the surrounding solution. Although this is not equivalent to increasing the diffusion coefficient, it is an increase in the speed of diffusive return. Approximating the beating as a circular motion will exaggerate the centripetal force because the recovery stroke of the beating does not have the same circular appearance as the power stroke. To estimate the magnitude of this effect, we solved the equation for centripetal force to obtain the drift velocity:

$$v_{\text{drift}}=\frac{\left(m-m_0\right){\omega }^{2}r}{\xi },$$ (10)

where m is the mass of kinesin, m₀ is the mass of the solution displaced by the motor, ξ is the friction coefficient (equal to kT/D, where k is Boltzmann’s constant, T is the temperature, and D is the diffusion coefficient), ω is the rotation rate, and r is the length of the rod. Plugging in the relevant values D = 2 μm²/s, kT = 4.1 pN ⋅ nm, m = 0 (an extreme case in which kinesins are massless to give the maximal possible effect), m₀ = 4 × 10⁻²² kg, ω = 300 rad/s, and r = 10 μm, we get that the drift velocity v_drift is on the order of 10⁻⁷ μm/s, which means it would take 3 years for the kinesins to get from the tip to the base with this effect alone. If we translate the time sped up by the centrifugation drift into diffusive time, it amounts to an effective diffusion constant of D_eff that satisfies

$$\frac{r^2}{2D_{\text{eff}}}=\frac{r}{v_{\text{drift}}},$$ (11)

The effective diffusion constant increase D_eff is only on the order of 10⁻⁶ μm²/s, which is negligible compared with measured value of D ∼ 2 μm²/s. We can therefore rule out the centrifugation effect as a means of generating any substantial length increase upon beating.

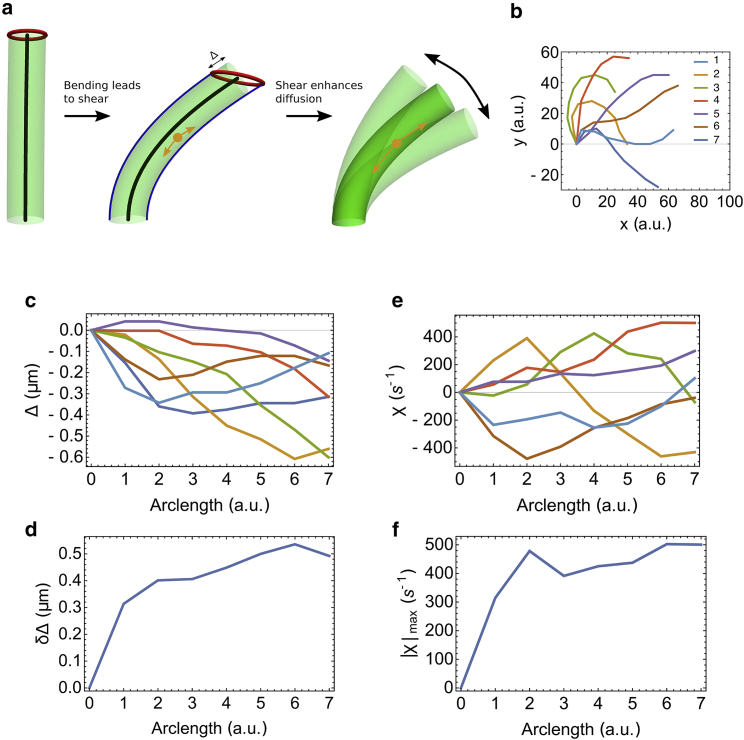
The increased diffusion coefficient in a beating flagellum might be explained by shear thinning

An alternative way that flagellar beating could influence the diffusive return of kinesin is via the shear of the flagellar matrix (Fig. 7 a). If we think of the flagellum as an elastic rod, when it is bent, parts of the rod are stretched and parts are compressed. The maximal shear displacement Δ can be calculated as (38).

$$\Delta =a\left[\psi \left(s,t\right)-\psi \left(0,t\right)\right],$$ (12)

where a is the radius of the rod and ψ (s, t) is the tangent angle along the arclength s at time t. The corresponding shear rate is

$$\chi =\frac{1}{a}\frac{d\Delta }{dt}.$$ (13)

Figure 7.

Beating of the flagellum leads to enhanced diffusion of motors. (a) The flagellum is depicted as a rod. The bending of the rod leads to stretching on one side and compression on the other side. The two blue curves represent the curves on the rod’s surface that have the same length as the central axis (black line). The red circle represents all the end points on the rod’s surface that have the same length as the central axis. The shear induced by periodic beating of the flagellum can enhance the diffusion of molecular motors via the shear-thinning mechanism, thus increasing the length of the flagella compared to the paralyzed mutants. (b) Selected beating shapes of a flagellum in a beating cycle are shown. The numbers indicate the order of the sequence. (c and d) Shear displacements Δ in (c) and its variation δΔ in a beating period in (d) are shown. (e and f) Shear rates χ in (c) and its maximum in a beating period in (f) are shown. To see this figure in color, go online.

We select seven frames in a periodic beating cycle of a flagellum and calculate the shear displacement and shear rate by measuring the tangent angle at equally spaced points along the arclength of the flagellum (Fig. 7, b–f). In a beating period of T = 0.014 s (39), the variation of the shear displacement δΔ ≡ max(Δ) − min(Δ)is typically around 0.4 μm. Here, the maximum and minimum are taken with respect to the time t in a period. The shear displacement of the flagellum can induce shear flow in the cytoplasm, and this shear flow can enhance the diffusion of particles in the cytoplasm. To estimate how this affects the diffusion coefficient, we adopted the Taylor dispersion theory, which yields an estimate of the diffusion coefficient amplified by the shear flow by a factor of 1 + Pe²/192, where Pe = dv_shear/D₀ is the Péclet number, with d ∼0.25 μm being the diameter of the flagellar cross section, $v_{\text{shear}}=\left(\delta \Delta /T\right)\sim 28\mu \text{m}/\text{s}$ being the shear flow rate, and D ∼ 2 μm²/s being the diffusion constant without shear flow (40). These numbers give a Péclet number Pe ∼ 3.5, and the resulting amplification factor 1.06 is too small to account for the required increase in diffusion constant. We thus conclude that the shear is not large enough to increase the diffusion constant significantly by means of an advective mechanism. Could the shear have any other effect?

It is well known that solutions made of soft polymers become less viscous under shear deformation. This effect is known as shear thinning. In an equilibrium solution, the diffusion coefficient D of a particle and its friction coefficient ξ obey the Einstein relation ξD = k_BT, where k_B is the Boltzmann constant and T is the absolute temperature. Because the friction coefficient ξ is proportional to the viscosity η, we would expect that the product of the viscosity η and the diffusion coefficient D is also a constant. Therefore, a reduction in viscosity η caused by shear thinning might account for the increase in diffusion coefficient D. Based on our measurements, the maximal shear rate |χ|_max ≡ max(|χ|) of the flagellum is around 600 s⁻¹ (Fig. 7 f). The onset shear-thinning rate for biopolymer solutions depends on many factors, such as protein concentration, temperature, ionic strength, and even the geometry of the container. The typical onset shear-thinning rate for a polysaccharide solution is ∼10 s⁻¹, and the reduction in the viscosity can be orders of magnitude (41). Recent work on bioink (alginate plus cellulose) shows that the shear-thinning effect takes place at a very low shear rate (42). Therefore, the shear magnitude is large enough to potentially cause shear thinning in the matrix of flagella, and this effect may contribute to enhanced diffusion by reducing the viscosity. Our results thus suggest a novel hypothesis to explain the link between flagellar motility and length, namely, that paralyzed mutants have shorter length because the diffusion constant for kinesin is decreased because of a loss of shear thinning in the flagellar matrix. Our modeling results suggest a need for future experiments to measure viscosity inside the matrix.

Editor: Dimitrios Vavylonis.

APPENDIX A: Derivation of the Growth Rate Under Quasistatic Assumptions

In physiological conditions, the length elongation of flagellum is much slower than the motor transportation-diffusion cycle. This is reflected in the small elongation unit δ in Eq. 7. We can therefore make the quasistatic assumption that at any fixed length L, the distributions of the four populations of motors reach steady state for that particular L. This implies that all the time derivatives in (1a), (1b), 2, (3a), (3b), and 4 become 0. The distribution of the active motors (i) is homogenous over the flagellum track, and the constant density reads

$${\rho }_a^s={\rho }_a^0=\frac{N/v}{\frac{L}{v}+\frac{1}{k_t}+\frac{1}{k_i}+\frac{L^2}{2D}}.$$ (A1)

For the diffusive motor, the spatial distribution shows a gradient and reads

$${\rho }_d^s={\rho }_d^0\frac{x}{L}=\frac{N\left(L/D\right)}{\frac{L}{v}+\frac{1}{k_t}+\frac{1}{k_i}+\frac{L^2}{2D}}\frac{x}{L}.$$ (A2)

For the motors accumulated at the base, the number is

$$N_b=\frac{N/k_i}{\frac{L}{v}+\frac{1}{k_t}+\frac{1}{k_i}+\frac{L^2}{2D}}.$$ (A3)

For the motors accumulated at the tip, the number is

$$N_t=\frac{N/k_t}{\frac{L}{v}+\frac{1}{k_t}+\frac{1}{k_i}+\frac{L^2}{2D}}.$$ (A4)

Substituting Eq. A1 into Eq. 7, we obtain Eq. 8, which is the key equation of our discussion for the dynamics of flagellum growth.

APPENDIX B: Derivation of The Steady-State Length in the Limit of A Large Diffusion Coefficient

Denoting $\beta =-\left(1/k_i-1/k_t+N\delta /r_d\right)$, we can rewrite Eq. 9 as

$$L^{ss}=-\frac{D}{v}+\sqrt{{\left(\frac{D}{v}\right)}^2+2\beta D}=-\frac{D}{v}+\frac{D}{v}\sqrt{1+\frac{2\beta v^2}{D}}.$$ (B1)

In the limit of D → ∞, we can invoke the Taylor series (1 + x)^k = 1 + kx + O(x²) for |x| ≪ 1 to expand the term in the square root and get

$$L^{ss}=-\frac{D}{v}+\frac{D}{v}\left(1+\frac{1}{2}\ast \frac{2v^2\beta }{D}+O\left(\frac{1}{D^2}\right)\right)=v\beta +O\left(\frac{1}{D}\right).$$ (B2)

Therefore, L^ss → vβ in the limit of D → ∞.

The expression of vβ can also be derived in an intuitive way; at steady state, the total length Nδ delivered by kinesin motors divided by the time for such delivery $\left(L^{ss}/v+1/k_t+1/k_i\right)$ must be equal to the depolymerization rate r_d.

$$\frac{N\delta }{\frac{L^{ss}}{v}+\frac{1}{k_t}+\frac{1}{k_i}}=r_d.$$ (B3)

Solving Eq. B3 gives exactly L^ss = vβ.

Author Contributions

R.M., N.L.H., W.F.M., and H.Q. designed research. R.M. and N.L.H. performed research and contributed analytic tools. R.M., N.L.H., W.F.M., and H.Q. analyzed data. N.L.H., R.M., H.Q., and W.F.M. wrote the manuscript.