Electroosmosis Dominates Electrophoresis of Antibiotic Transport Across the Outer Membrane Porin F

Abstract

We report that the dynamics of antibiotic capture and transport across a voltage-biased OmpF nanopore is dominated by the electroosmotic flow rather than the electrophoretic force. By reconstituting an OmpF porin in an artificial lipid bilayer and applying an electric field across it, we are able to elucidate the permeation of molecules and their mechanism of transport. This field gives rise to an electrophoretic force acting directly on a charged substrate but also indirectly via coupling to all other mobile ions, causing an electroosmotic flow. The directionality and magnitude of this flow depends on the selectivity of the channel. Modifying the charge state of three different substrates (norfloxacin, ciprofloxacin, and enoxacin) by varying the pH between 6 and 9 while the charge and selectivity of OmpF is conserved allows us to work under conditions in which electroosmotic flow and electrophoretic forces add or oppose. This configuration allows us to identify and distinguish the contributions of the electroosmotic flow and the electrophoretic force on translocation. Statistical analysis of the resolvable dwell times reveals rich kinetic details regarding the direction and the stochastic movement of antibiotics inside the nanopore. We quantitatively describe the electroosmotic velocity component experienced by the substrates and their diffusion coefficients inside the porin with an estimate of the energy barrier experienced by the molecules caused by the interaction with the channel wall, which slows down the permeation by several orders of magnitude.

Significance

Electroosmotic flow in biological channels has been shown to play a major role in molecule transport through these channels; however, quantification of said flow inside the channel has been difficult. We report here that the electroosmotic flow inside a biological channel is able to overcome the electrophoretic force because of an applied potential gradient experienced by translocating charged molecules. The issue of having the theoretically calculated electroosmotic flow rates orders of magnitude larger than expected is addressed by a linear flow model supported by the empirical data. Hence, we are able to determine the effect of the electroosmotic flow on the flow rate of these molecules, which becomes an adjustable variable to quantify molecular transport.

Introduction

Gram-negative bacteria have a complex cell envelope consisting of an outer membrane and an inner membrane, separating its periplasm from the extracellular environment. The outer membrane consists of an asymmetric bilayer composed of phospholipids and lipopolysaccharides. Residing within the membrane are an abundance of general and specialized diffusion porins and efflux pumps (1,2). Any potentially useful antibiotic molecule must overcome this highly complex membrane structure and penetrate into the cell and into the right compartment to become effective in use against bacteria. Among these porins present in the bacterial outer membrane, OmpF and OmpC play a significant role in antibiotic resistance (3).

A current bottleneck in developing new antibiotics is the lack of an appropriate screening technology with respect to uptake (4). Electrophysiology is a suitable approach to characterize channel permeation; however, determining the exact rates of translocation and the processes of translocation has been difficult to quantify, mostly because of the complex signal in the form of channel blockages (5). OmpF, which is the porin of interest in this study, is a trimeric porin where each monomer has a constriction zone of ∼7–11 Å (6,7) and is decorated with charged residues that give the characteristic properties of the channel, e.g., ion selectivity, conductance, and selectivity toward translocation of small molecules. The constriction zone provides a formidable steric and electrostatic barrier against the translocation of neutral, charged, and zwitterionic molecules (8), particularly when the molecule size approaches that of the constriction zone. The process of molecule translocation in vivo is mostly due to passive diffusion. Here, in our case, we apply an electric field to drive the molecules across the channel under controlled conditions. The presence of a membrane potential has two effects on translocation: 1) in the case of charged or polar molecules, they experience an electrophoretic force due to the membrane potential, and 2) the presence of a membrane potential induces an electroosmotic flow (EOF) inside the channel, in which both effects influence the translocation of molecules.

EOF is the flow of fluid through a capillary, which is the direct result of an applied electric field. In a narrow tube with charged walls bathed with an electrolyte solution, e.g., an ion channel or a capillary, the EOF results from the movement of the counterions that form the electrostatic double layer, which drag the water molecules with them as they move along the external electric field.

EOF in biological and solid-state nanopores has been studied with regard to its effect on molecule translocation. Regarding neutral molecules, significant effects have been shown on its effect on the translocation of β-cyclodextrin (a neutral cyclic sugar) in CymA (9), binding of the same molecule in the bacterial toxin α-hemolysin (10), and effects of alkali cations on this binding (11). Interplay of electrophoresis and EOF has been previously addressed regarding translocation of peptides through α-hemolysin (12) and theoretically addressed with regard to charged and neutral polymers (13,14). Apart from biological nanopores, important effects of EOF on the translocation and detection of proteins and DNA through solid-state nanopores have also been studied (15, 16, 17). EOF in nanocapillaries has also been exploited in medical applications (18,19) and in novel instrument design (20). These studies establish that EOF plays a significant role in molecule translocation and binding in biological porins and solid-state nanopores; however, attempts at a satisfactory quantification of EOF has so far not yet been fruitful because the calculated EOF speeds turn out to be too fast for a satisfactory explanation of molecule translocation.

Here in this work, we demonstrate the combined effect of electroosmosis and electrophoreses on the translocation of antibiotic molecules norfloxacin (NFX), ciprofloxacin (CFX), and enoxacin (ENX) through OmpF. To elucidate the individual contribution of these forces, we modify the pH (pH 6–pH 9); thus, the charge state of the molecule electroosmotic properties of OmpF remains unmodified (21). Under the selected conditions, EOF and electrophoretic force enhance (pH 6) or oppose (pH 9) each other. Hence, we were able to show that the EOF dominates the electrophoretic force on the translocation of these molecules.

We provide quantitative information on the magnitude of these forces with regard to translocation, address the issue in which the estimated EOF is usually orders of magnitude greater than what is experimentally measured (10,12), and provide estimates on the diffusion coefficient of these molecules inside the porin along with the free-energy barrier they come across. In electrophysiological studies, it is important to show that a translocation signal is an actual translocation (22). We use an OmpF modified with an external blocker (23) to further confirm the translocation of these molecules (Supporting Materials and Methods).

Material and Methods

Electrophysiology

The single channel recording apparatus consisted of a two-part Teflon chamber, each 2.5 mL separated by a 25-μm-thick Teflon membrane with an ∼100-μm aperture. The chambers are filled with 1 M KCl and 10 mM of a buffer, HEPES (pH 7), 2-(N-morpholino)ethanesulfonic acid (MES) (pH 6), or N-cyclohexyl-3-aminopropanesulfonic acid (CAPS) (pH 9), depending on the desired pH. The aperture was pretreated with a solution of 1–2% (v/v) of hexadecane/hexane. After hexane evaporation was achieved (∼20 min), a bilayer was formed from 1,2-diphytanoyl-sn-glycero-3-phosphatidylcholine (DPhPC) with the monolayer opposition technique (24), using ∼5 μL of DPhPC in pentane (5 mg/mL). Single channel insertions were achieved by using ∼0.3 μL of OmpF and OmpF-MTSE diluted from their stock solution (1 mg/mL) to an order of ∼10⁻⁴ in 1% (v/v) polyethylene glycol monoalkyl ether (Genapole, Liverpool, NY). Current traces were recorded by standard Ag-AgCl electrodes (World Precision Instruments, Sarasota, FL) attached to an AxoPatch 200B Amplifier with a CV3BU Headstage (Molecular Devices, San Jose, CA) and recorded with an Axon 1440A Digitizer (Molecular Devices). Data were acquired with Clampex software (Molecular Devices) at 50 kHz and analyzed with pCLAMP software (Molecular Devices) and a homemade LabVIEW (National Instruments, Austin, TX) data analysis package. Unless otherwise noted, data were filtered at 5 kHz. Channel insertion was always from the -cis side of the compartment, and potential is defined on the -trans side of the compartment.

Chemicals

KCl, MES, CAPS, HEPES, pentane, hexane, and hexadecane were acquired from Sigma-Aldrich (St. Louis, MO). DPhPC was acquired from Avanti Polar Lipids (Alabaster, AL).

OmpF and OmpF-MTSES

OmpF is purified in-house as described in (25). The chemical modification of the cysteine mutant OmpF was carried out as previously described (26). The mutant OmpFE181C (0.2 mg/mL) (26,27) was incubated overnight with 20 mM MTS-based label MTSES (2-sulfonatoethyl methanethiosulfonate) (Anatrace Products, Maumee, OH) in a 200 mM sodium phosphate buffer at pH 7.5 containing 1 mM n-octyl-poly-oxyethylene detergent. To improve the modification efficiency by keeping the cysteine reduced, the protein was pretreated with 1 mM 1,4-dithiothreitol (Carl Roth, Karlsruhe, Germany) at room temperature for 1 h (28). The electrophysiological characterization was performed without any further purification of the chemically modified protein.

Results

Directionality and magnitude of electroosmotic and electrophoretic forces

To distinguish EOF from electrophoretic force, we vary the charge state of the analyte within a range in which the channel of interest shows little or no modification.

The EOF primarily depends on the surface charge state of the ion channel (29). Interestingly, OmpF has a pI of 3.5 (21) and shows cation selectivity in the range of pH 6–pH 9 (${\mathbf{P}}_{{\mathbf{K}}^{+}}/{\mathbf{P}}_{\mathbf{C}{\mathbf{l}}^{-}}=4$). The surface charge state and selectivity of the pore remain pretty much constant between this pH range (21). (See Supporting Materials and Methods.)

In contrast, the electrophoretic force depends on the charge states of CFX, NFX, and EFX, which vary depending on the pH. They are zwitterionic molecules at pH 7; at pH 6, the molecules are positively charged, whereas at pH 9, they are negatively charged (30; https://www.drugbank.ca/drugs). The charge states of these molecules are depicted in Fig. 1. Given that we always introduce the substrate on the -cis side of the chamber, we expect the action of the EOF and electrophoretic forces on the substrates to be as depicted in Table 1.

Figure 1.

Charge states of molecules at different pH. The net charge and the location of charged regions are depicted in the figure. The molecules have a net positive charge at pH 6, are zwitterionic at pH 7, and are negatively charged at pH 9. To see this figure in color, go online.

Table 1.

The Charge States of CFX, NFX, and EFX at Different pH and Directionalities of the EOF and Electrophoretic Force at Different pH

	qCFX (|e−|)	qEFX (|e−|)	qNFX (|e−|)	ΔV+	ΔV−
pH 6	0.53	0.38	0.54	EOF (−), EP (−)	EOF (+), EP (+)
pH 7	0.08	0.03	0.08	EOF (−), EP (0)	EOF (+), EP (0)
pH 9	−0.68	−0.72	−0.68	EOF (−), EP (+)	EOF (+), EP (−)

The symbol (−) indicates that the force is directed from the –trans side to the –cis side, and the symbol (+) depicts that the force is directed from the –cis side to the –trans side.

Thus, the directions of EOF and electrophoretic force are controlled by the polarity of the membrane potential ±V_m and solution pH, whereas the magnitude of each is governed by the magnitude of the membrane potential |V_m|.

Throughout the experiments, the substrate concentration was 0.25 mM, and the bathing solution was 1 M KCl. Membrane potential was varied between (+150 and −150 mV) in steps of ΔV_m = 25 mV. The protein was added on the cis side (electrical ground), and within this configuration, the EOF is always directed along the electric field; that is, at positive potentials, the flow is toward the –cis side, and at negative potentials, the flow is toward the –trans side of the chamber.

Competition between the EOF and electrophoretic force

After single channel insertion is achieved, a membrane potential V_m is applied between V_m = ±150 mV in steps of ΔV_m = 25 mV. The corresponding current signal of the channels are recorded within the V_m range for a duration of 60 s. These traces serve as blank data to be compared with recordings with the substrate. Then, keeping the same channel intact, the substrate is added on the -cis side of the chamber, and the current signal of the channels are recorded within the interested V_m range in steps of ΔV_m for a duration of (180 s). The reduction in the current signal is caused by substrate translocation through the channel, deemed as events. These events are analyzed to determine the kinetics of binding and translocation.

Figs. 2 and 3 depict a typical experiment, performed at pH 6 and pH 9, respectively, at membrane potentials ±100 mV. At pH 6, CFX is positively charged, and thus, at a positive membrane potential, both the EOF and the electrophoretic force are directed from the -trans side toward the -cis side of the chamber; as expected, no translocation events are detected in this configuration (Fig. 2 B). In contrast, at a negative membrane potential, both the EOF and the electrophoretic force are directed from the -cis side toward the -trans side of the chamber; hence, we expect the molecules to translocate, and translocation events are observed (Fig. 2 B).

Figure 2.

(A) A single channel current recording from reconstituted OmpF porin at both ±100 mV (blank) is shown. (B) Given is a single channel current recording of OmpF porin showing real-time detection of CFX at ±100 mV with a concentration of 0.25 mM in 1 M KCl at pH 6 cut out of a section of the trace that shows clear and distinct blockages. (C and D) Shown is a schematic of the direction of the electric field and the EOF at +100 and −100 mV, respectively. To see this figure in color, go online.

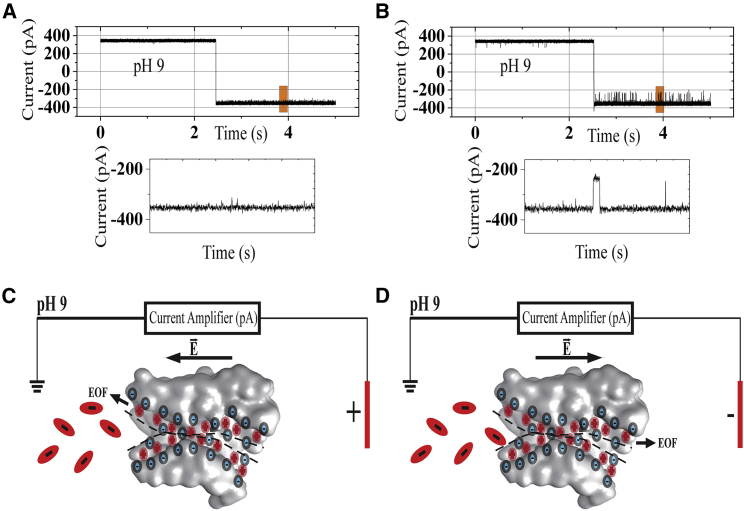
Figure 3.

(A) A single channel current recording from reconstituted OmpF porin at both ±100 mV (blank) is shown. (B) Given is a single channel current recording of OmpF porin showing real-time detection of CFX at ±100 mV with a concentration of 0.25 mM in 1 M KCl at pH 9 cut out of a section of the trace that shows clear and distinct blockages. (C and D) Shown is a schematic of the direction of the electric field and the EOF at +100 and −100 mV, respectively. To see this figure in color, go online.

At pH 9, CFX is negatively charged. Here, at a positive membrane potential, +V_m EOF is directed from the -trans side to the -cis side of the chamber, opposing translocation, but the electrophoretic force is directed from the -cis side toward the -trans side of the chamber, assisting translocation. The situation is reversed when the polarity of the membrane potential is changed to −V_m.

Remarkably, as depicted in Fig. 3 B, we see molecule translocation at negative membrane potential, whereas there is no molecule translocation at positive membrane potential. That is, the negatively charged molecule is moving toward the negative potential, which clearly demonstrates that the electrophoretic force is strongly dominated by the EOF. Corresponding figures for NFX and ENX can be found in Figs. S1 and S2.

Kinetics of translocation

To reveal the kinetics of translocation, we extract the on and off rates k_on and k_off, also named event rates and dwell times τ and k of substrate penetration (31, 32, 33). In this two-state Markov model, these variables are related by (k_on = k/([C] × n)) and (k_off = 1/τ); here, [C] is the concentration of the substrate, and n is the number of monomers of the channel (see Supporting Materials and Methods). Fig. 4 depicts the results of our analysis. For all three substrates studied, when the pH is shifted from pH 6 to pH 9, a reduction in event rates (k) and an increase in dwell times (τ) is observed. This is attributed to the shift from cooperation to competition between the EOF and the electrophoretic force as the pH is varied from pH 6 to pH 9. At pH 7, all the substrates are zwitterionic molecules with a net charge of q_{pH 7} ≈ 0. From a macroscopic point of view, we expect the electrophoretic force to play no part in the translocation in this case, and the translocation is expected to be a direct result of EOF; the details of the kinetics and the results at pH 7 are discussed in the Discussion.

Figure 4.

Event rates and dwell times of molecule translocation through OmpF in the presence of 0.25 mM NFX, CFX, and ENX 1 M KCl with 10 mM MES at pH 6 and 1 M KCl with 10 mM CAPS at pH 9. Event rates were determined by counting the total number of events and dividing by the total observation time. Mean dwell times are obtained by fitting dwell time data to single exponentials assuming a two-state Markov process over at least 1000 events; for details, see Supporting Materials and Methods. The error bars depict the standard deviation of the mean over at least three sets of independent experimental measurements. To see this figure in color, go online.

The dependency of dwell times τ to the membrane potential V_m also provides information regarding possible translocation of these molecules. To a first approximation, a dependency of τ ∼1/V_m is expected for a translocating molecule, whereas for nontranslocation events, e.g., bounce-back events, they are expected to remain constant along the applied voltage range (34). We further confirm that the events observed are actual translocation events by utilizing an engineered OmpF (OmpF-MTSE), which includes an additional blocker attached at the exit of the pore (see Supporting Materials and Methods).

Discussion

Drift velocity and dwell time of the substrate

Following previous literature, we decompose the drift velocity of the substrate to three factors, namely the electrophoretic force, the electroosmotic velocity, and a free-energy landscape within the pore (35):

$$v_{drift}\left(V_m\right)=\left[v_{EOF}\pm v_{ep}\right]V_m-\frac{1}{\zeta }\frac{\partial F\left(x\right)}{\partial x}.$$ (1)

Here, v_EOF and v_ep are the electroosmotic velocity and the electrophoretic velocity per membrane potential, where v_ep = μE/V_m and ζ = k_BT/D. Here, μ is the electrophoretic mobility of the molecule, E is the electric field, k_B and T have their usual meaning of the Boltzmann constant and the absolute temperature, and D is the diffusion constant of the molecules inside the channel. The sign convention is chosen such that the free-energy barrier always resists flow, and the sign of the electrophoretic force depends on whether it resists or accompanies EOF, namely $v_{ep}^{pH6}$ is (+) and $v_{ep}^{pH9}$ is (−).

Determining the electroosmotic velocity component, free-energy term, and the diffusion coefficient

To a good approximation, the magnitude of the EOF is estimated by the number of water molecules transported per ion (10,12) and can be written as

$$v_{EOF}=\frac{N_{h}I}{\left|e^{-}\right|}\frac{\left(P_{C{l}^{-}}/P_{K^{+}}-1\right)}{\left(P_{C{l}^{-}}/P_{K^{+}}+1\right)}\frac{1}{S_{pore}\left[H_{2}O\right]},$$ (2)

where N_h = 10 is the number of water molecules carried per mobile ion, I is the open pore current (current through one OmpF monomer in our case), $P_{C{l}^{-},}{P}_{K^{+}}$ are the permeabilities of the chloride and potassium ions, S_pore ≈ $\pi r_{pore}^2$ is the surface area, r_pore is the radius of the pore, [H₂O] = 3.4 × 10²⁸ m⁻³ is the concentration of water molecules, and |e⁻| is the elementary charge.

At a membrane potential of |V_m| = 100 mV, the current through an OmpF monomer is I = 133 pA; taking r_pore = 7 Å at the constriction, we obtain the electroosmotic velocity per mV as v_EOF/mV = 9.5 × 10⁻⁴ m/s. This velocity is incredibly fast; the translocation time for a single molecule simply by v_EOF at 100 mV in this case would be τ_EOF = l_pore/v_EOF ≈ 55 ns, where l_pore ≈ 5.4 nm. Given a typical dwell time of τ ≈ 0.5 ms in our experiments at this potential, this result is off by four orders of magnitude. Using the other extreme case, the r_pore = 20 Å at the mouth only saves us from one order of magnitude, yielding τ_EOF ≈ 450 ns.

Thus, we decide to determine v_EOF directly from our experiments. We define

$v_{EOF}^{\Delta F}\left(V_m\right)=v_{EOF}\times V_m-\left(1/\zeta \right)\left(\partial F\left(x\right)/\partial x\right),$ namely the electroosmotic velocity slowed down by the free-energy profile inside the pore. Making use of Table 1, we note that at pH 6 and pH 9, respectively, the charge states of the molecules are of the same magnitude |q_{pH 6}| ≈ |q_{pH 9}|; hence, we expect $v_{ep}^{pH6}=-v_{ep}^{pH9}$. Defining the dwell time of the molecule as $\tau =\left(l_{pore}/v_{EOF}^{\Delta F}\pm v_{ep}\right)$ for the dwell times at pH 6 and pH 9, we end up with

$${\tau }_{pH6}=\frac{l_{pore}}{v_{EOF}^{\Delta F}+v_{ep}},{\tau }_{pH9}=\frac{l_{pore}}{v_{EOF}^{\Delta F}-v_{ep}}.$$ (3)

Rearranging these equations, we obtain the following relation:

$${\tau }_r=\frac{{\tau }_{pH6}+{\tau }_{pH9}}{{\tau }_{pH6}{\tau }_{pH9}}=\frac{2\times v_{EOF}^{\Delta F}}{l_{pore}}.$$ (4)

Fitting Eq. 4 to our data allows us to calculate v_EOF and the free-energy term. Although we retain the x-dependent form of the free-energy profile, for the sake of simplicity, we work with a profile in which ∂F(x)/∂x is constant. Fig. 5 shows the fits of Eq. 4 to our data.

Figure 5.

Determination of v_EOF and the free-energy term. Dwell time ratios are fitted to Eq. 4, as explained in the text. The expected linear behavior is apparent at |V_m| ≥ 50 mV. The data at |V_m| = 25 mV are excluded from the fit. The deviation at |V_m| = 25 mV is discussed at length within the text. The error bars depict the standard deviation of the mean over at least three sets of independent experimental measurements. To see this figure in color, go online.

To obtain the diffusion coefficient of the molecules inside the porin (D), we need to estimate the free-energy barrier inside the porin. We assume a free-energy barrier that is symmetric with respect to the center of the porin and linearly increases toward and decreases after the center Fig. 6. We estimate a total (ΔF = 12kT − 20kT) encountered by the molecule based on previously published data (8). This gives us $\left(\partial F\left(x\right)/\partial x\right)=\Delta F/l_{pore}$, and from the fit to Eq. 4, we determine the diffusion coefficients of the molecules.

Figure 6.

Sketch of a simple free-energy landscape for OmpF. We choose a symmetric free-energy profile that linearly increases toward the constriction zone of the porin, where the total free-energy change experienced by the molecule is ΔF = 12kT − 20kT. To see this figure in color, go online.

The obtained diffusion coefficients and the drift velocity due to EOF is summarized in Table 2. The (v_EOF) is expected to be the same for all the molecules studied because it is a property of the system and not the substrate; we find v_EOF ≈ 0.25 nm ⋅ ms⁻¹mV⁻¹ for all the three molecules studied. The diffusion coefficients (D) are different for all the molecules and lie in the range D ≈ 0.3 − 3.3 nm²/ms where D_EFX > D_CPF ≫ D_NFX. Compared with the free diffusion in the bulk D_bulk ∼10⁻⁹ m²/s = 10⁶ nm²/ms, this diffusion coefficient is less by six orders of magnitude. It should be noted that the current voltage relationship of OmpF was linear within the studied range (ohmic), indicating the absence of major conformational changes to the protein.

Table 2.

Electroosmotic Velocity Component per Millivolt of Membrane Potential, v_EOF, and the Diffusion Coefficient of the Molecules inside the Porin, D, Calculated as Described in the Main Text

	VEOF (nm ⋅ ms−1mV−1)	D (nm2 ⋅ ms−1) [ΔF = 12–20kT]
CFX	0.24	2.0–3.3
ENX (EFX)	0.27	2.8–4.7
NFX	0.21	0.3–0.5

Verification and discussion of obtained parameters

Our pH 7 data come into play to determine the validity of our assumptions. Given that the total charge of all our substrates satisfies q_{pH 7} ≈ 0, we expect only EOF and the free-energy term to determine the dwell time of these molecules. Namely,

$${\tau }_{pH7}=l_{pore}/v_{EOF}^{\Delta F}.$$ (5)

Fig. 7 shows our experimental results at pH 7 along with plots of Eq. 5 using the parameters acquired from our fits to Eq. 4. The obtained parameters strongly agree with the EFX and CFX data, especially when |V_m| > 20 mV; NFX data start showing a deviation starting from |V_m| ≤ 100 mV. The spread in these fits is calculated from the uncertainty of the fitting parameters; fits with their corresponding spreads are depicted in Fig. S3.

Figure 7.

Testing the validity of the EOF model at pH 7. The solid line depicts the expected behavior of the molecules at pH 7 (Eq. 5) calculated from the parameters obtained from Eq. 4. The error bars depict the standard deviation of the mean over at least three sets of independent experimental measurements. To see this figure in color, go online.

The observed electroosmotic velocity component (v_EOF) is orders of magnitude slower than suggested by Eq. 2. If one assumes a pore with a cross-sectional area similar to OmpF without any constrictions but similar length, namely in the absence of a free-energy barrier, our results suggest that a molecule should translocate in about 0.2 ms at a V_m = 100 mV. This flight time is in good agreement with our data at pH 7; however, Eq. 2 describes the flow of water through the porin quite accurately because the water flux calculated from this equation agrees to the same order of magnitude obtained from molecular dynamics simulations (9). We address this difference in a way that in the microscopic cavity of the porin, although water flow is quite fast, the molecule does not flow along with the water as expected in a macroscopic system.

Inspection of Fig. 7 reveals a good agreement with EFX and CFX data and our assumptions, whereas NFX shows a greater deviation and needs to be addressed. A careful look at the dwell time data at pH 7 in Fig. 7 shows that the dwell time of NFX experiences a transition around |V_m| = 100 mV. Although we assume a linearly increasing free-energy profile within the porin, a significant contribution comes from the presence of an electric field E_p within the constriction zone (8). Although the net charge of the molecules is q_{pH 7} ≈ 0, they still have a dipole moment and tend to align with this field (8), effectively forming a binding region and slowing down the molecule. We attribute the deviation from our assumptions as |V_m| decreases to the interaction of these molecules with this field E_p because |V_m|, which increases the electric field directed along the pore, E_||, is possibly able to dominate E_p.

Conclusion

Modifying the charge state of three fluoroquinolones CFX, EFX, and NFX in a range in which the channel of interest OmpF shows no surface charge variation allows us to obtain differences in the mode of transport. We show here that the EOF plays a major role in the translocation of these molecules to an extent that the EOF dominates the electrophoretic flow. EOF is unlikely to play a significant role in substrate uptake in bacteria because of the lack of strong electric field gradients across the outer cell wall of Gram-negative bacteria. However, this effect can be used as a unique tool to manipulate molecule translocation.

Using a linear drift velocity model that is impaired by a free-energy profile inside the channel, we compute the contribution of the EOF to the drift velocity of these molecules and their diffusion coefficients inside the porin. We observe that the diffusion coefficients follow the relation D_EFX > D_CPF ≫ D_NFX, and the model deviates from the result at very-low membrane potentials V_m ≤ 20 mV. We attribute this deviation to the presence of a perpendicular electric field inside the pore E_p. We observed that the velocity component due to EOF imparted on the molecules is much smaller than the EOF calculated using previously published models (10,12,36,37). Within the limit of a linear flow model, our results suggest that the molecules do not flow along with the water inside the porin, but rather, water flow influences the linear velocity of the molecule. This approximation is valid when molecule velocity is averaged over a timescale of milliseconds; to elucidate the details of molecular transport and to obtain a more detailed velocity profile inside the porin, atomistic studies in the molecular dynamics simulations should be utilized.

Author Contributions

J.A.B. designed research and experimental procedure and interpreted initial results. J.A.B., S.P., and M.A.A. performed experiments. J.A.B. and S.P. analyzed data. M.A.A. and M.W. interpreted main results and formulated the theory. J.A.B., M.A.A., and M.W. wrote the manuscript.

Editor: Chris Chipot.