Abstract
The free-solution mobilities of small single-stranded DNA (ssDNA) and double-stranded DNA (dsDNA) have been measured by capillary electrophoresis in solutions containing 0.01–1.0 M sodium acetate. The mobility of dsDNA is greater than that of ssDNA at all ionic strengths because of the greater charge density of dsDNA. The mobilities of both ssDNA and dsDNA decrease with increasing ionic strength until approaching plateau values at ionic strengths greater than ∼0.6 M. Hence, ssDNA and dsDNA appear to interact in a similar manner with the ions in the background electrolyte. For dsDNA, the mobilities predicted by the Manning electrophoresis equation are reasonably close to the observed mobilities, using no adjustable parameters, if the average distance between phosphate residues (the b parameter) is taken to be 1.7 Å. For ssDNA, the predicted mobilities are close to the observed mobilities at ionic strengths ≤0.01 M if the b-value is taken to be 4.1 Å. The predicted and observed mobilities diverge strongly at higher ionic strengths unless the b-value is reduced significantly. The results suggest that ssDNA strands exist as an ensemble of relatively compact conformations at high ionic strengths, with b-values corresponding to the relatively short phosphate-phosphate distances through space.
Significance
Capillary electrophoresis has been used to study the electrophoretic mobilities of small single-stranded DNA (ssDNA) and double-stranded DNA (dsDNA) in solutions containing 0.01–1.0 M sodium acetate. The mobilities of both ssDNA and dsDNA decrease with increasing ionic strength and approach limiting plateau values at high ionic strengths. Hence, the DNA strands undergo similar electrostatic interactions with the ions in the solution. The mobilities predicted by the Manning electrophoresis equation for dsDNA are reasonably close to the observed mobilities at all ionic strengths. However, the predicted mobilities of ssDNA approximate the observed values only if the phosphate-phosphate separation distance decreases with increasing ionic strength. Hence, ssDNA strands appear to exist as an ensemble of configurations that become more compact at high ionic strengths.
Introduction
The conformation and structure of double-stranded DNA (dsDNA) in solutions containing monovalent cations have been well characterized by extensive experimental and theoretical studies that have been carried out with this important biological macromolecule (see, e.g., (1, 2, 3) and references therein). The persistence length, one measure of DNA conformation, is usually found to be ∼40–50 nm for high-molecular-weight dsDNA strands in solutions containing monovalent cations (4, 5, 6). For small dsDNA strands, the persistence length decreases somewhat with increasing ionic strength and decreasing molecular weight (7, 8, 9).
Extensive studies have also been carried out with single-stranded DNA (ssDNA). The persistence length has been found to vary from 1.5 to 6 nm in solutions containing monovalent cations, depending on the size and sequence of the DNA (10,11) and the ionic strength of the solution (10, 11, 12, 13, 14, 15, 16). Some short ssDNA strands exhibit sequence-dependent thermal transitions, suggesting that these oligomers have nonrandom conformations in solution (16, 17, 18, 19, 20, 21). Other ssDNA strands of the same size do not exhibit sequence-dependent thermal transitions, suggesting that their conformational ensembles primarily consist of unstructured molecules (20).
We have been using free-solution capillary electrophoresis (CE) to evaluate the properties of small ssDNA and dsDNA in solutions containing various monovalent cations. Our previous studies have addressed the dependence of the electrophoretic mobility of DNA on molecular weight (22, 23, 24), ionic strength (25,26), curvature (27, 28, 29, 30), charge density (23,30, 31, 32), and solution viscosity (33). Here, we have used CE to determine the dependence of the electrophoretic mobility of ssDNA and dsDNA on ionic strength in solutions containing high concentrations of Na+ ions. Under identical solvent conditions, the mobility of dsDNA is greater than that of ssDNA. The mobilities of both types of DNA decrease with increasing ionic strength, approaching limiting plateau mobilities at high ionic strengths. Hence, both ssDNA and dsDNA appear to interact in a similar manner with the cations and anions in the solution. For dsDNA, the observed mobilities are reasonably well predicted by the Manning electrophoresis equation (34) if the average distance between phosphate residues is assumed to be 1.7 Å. However, the mobilities predicted for ssDNA agree with the observed mobilities only if the average distance between phosphate residues decreases with increasing ionic strength. The results suggest that the ensemble of ssDNA conformations becomes more compact with increasing ionic strength, decreasing the through-space distance between phosphate residues.
Materials and Methods
DNA samples
The 422-bp restriction fragment used in these studies was obtained from the HpaII digestion of the yeast 2-μ circle and purified as described previously (35). Small DNA oligomers were synthesized by Integrated DNA Technologies (Coralville, IA) and purified by polyacrylamide gel electrophoresis. Duplexes were prepared by mixing appropriate quantities of the desired oligomers in 10 mM Tris-chloride buffer (pH 8.0), heating to 94°C for 5 min, and slowly cooling to room temperature. The concentrated DNA stock solutions (∼1 μg/μL) were stored at −20°C and diluted with water to concentrations of 10–50 ng/μL for the CE experiments. The sequences of the DNA strands and their short acronyms are given in Table 1, along with the number of phosphate residues in each DNA.
Table 1.
Acronyms, Number of Phosphates, and Sequences of DNA
| Acronym | No. of Phosphates | Sequence |
|---|---|---|
| ds442 | 884 | HpaII digest of yeast 2-μ circle |
| ds26a | 50 | 5′-CGCAATTTTCAGCAATTTTCAGACAG-3′ |
| ds26b | 50 | 5′-CGCAAAGTGTCTATACATATCTATCG-3′ |
| T26 | 25 | TTTTTTTTTTTTTTTTTTTTTTTTTT |
| T16 | 15 | TTTTTTTTTTTTTTTT |
| ss07 | 6 | ACCTGAT |
Buffers
The background electrolytes (BGEs) were prepared from stock solutions containing 1.0 M sodium acetate (Thermo Fisher Scientific, Waltham, MA) and 0.005 M Tris-acetate (0.01 M Tris base titrated to pH 8.0 ± 0.1 with acetic acid). Appropriate volumes of the two stock solutions were mixed to form BGEs containing 0.01–1.0 M sodium acetate (NaAc) plus 0.005 M Tris-acetate buffer to keep the pH of the solution constant. NaAc was chosen as the major component of the BGE because the intrinsic conductivities of the cation and anion are similar (36), leading to well-shaped peaks in the electropherograms. The conductivities of the Tris+ and Na+ ions are also similar.
CE
The free-solution mobilities of the DNA strands were measured using a Beckman Coulter P/ACE System MDQ CE system (Fullerton, CA) run in the reverse-polarity mode (the anode on the detector side) with ultraviolet detection at 254 nm. Migration times and peak profiles were analyzed using the 32 Karat software. The capillaries were 40.0 cm in length, with external diameters of 375 μm and internal diameters of 75 μm mounted in a liquid-cooled cartridge thermostated at 20°C. The capillaries were internally coated linear polyacrylamide capillaries from Bio-Rad Laboratories (Hercules, CA). The linear polyacrylamide coating minimizes the electroosmotic flow (EOF) of the solvent without affecting the mobility of the analyte (22). The samples were hydrodynamically injected into the capillary by applying low pressure (0.5 psi, 0.0035 MPa) for 3 s. The sample volume was 22 nL; the length of the sample plug was ∼0.51 cm, 1.3% of the capillary length. The applied voltage ranged from 1.0 to 7.0 kV, depending on the ionic strength of the BGE. Except at the highest ionic strengths, the current was always less than 60 μÅ. Under such conditions, heating effects are negligible, and the observed mobilities are independent of the applied electric field (22).
The observed electrophoretic mobilities, μobs, were calculated from Eq. 1:
| (1) |
where Ld is the distance from the inlet to the detector (in centimeters), E is the electric field strength (in volts per centimeter), and t is the time required for the sample to migrate from the inlet to the detector (in seconds). The observed mobility is the algebraic sum of the mobility of the DNA, μ, and the mobility caused by the EOF of the solvent, μEOF. The EOF was measured as a function of [NaAc] by the fast method of Williams and Vigh (37) using benzyl alcohol as the analyte. The EOF correction was only necessary at ionic strengths less than 0.10 M; for I ≥ 0.l M, the observed mobilities were essentially independent of the EOF, allowing the mobilities to be calculated directly from Eq. 1. The DNA mobilities measured in successive runs on the same day usually agreed within ±0.01 mobility units (m.u.; 1 m.u. = 1 × 10−4 cm2V−1s−1). The mobility of ds26a in 0.7 M NaAc, measured on three different days separated by several months, was 1.47 ± 0.09 m.u. Because these mobility variations are approximately equal to the sizes of the symbols in the figures below, error bars are not shown.
Electrophoretic mobility
The free-solution electrophoretic mobility of a polyelectrolyte is determined primarily by the ratio of the number of charged residues, Q, to the frictional coefficient, f, as shown in Eq. 2 (38,39):
| (2) |
If the polyion is rigid and spherical, the linear Debye-Hückel theory is valid, and the Debye screening length (κ−1) is much larger than the polyion radius; the Debye-Hückel-Onsager theory predicts that the mobility can be described by Eq. 3:
| (3) |
where η is the viscosity of the solvent and a is the polyion radius (39, 40, 41, 42).
For highly charged polyions, the value of Q is often taken to be the effective charge after counterion condensation (34,43, 44, 45) rather than the nominal structural charge. In addition, the polyion mobility is reduced by two solvent-related effects, commonly known as the “relaxation effect” and the “electrophoretic effect” (34,39, 40, 41, 42,45, 46, 47). The relaxation effect is due to the separation of the centers of charge of the counterion cloud and the polyion, creating an induced dipole that opposes the direction of the applied electric field. The electrophoretic effect is caused by the migration of the solvated counterions and the polyion in opposite directions, increasing the viscous drag on the polyion. As a result, the observed mobility of a given polyion is a complicated function of the number of charged residues, the size of the polyion, counterion condensation, and the composition of the surrounding ionic medium (32,34).
Manning electrophoresis equation
Manning used counterion condensation theory (43) and linear Debye-Hückel statistics to derive an equation for DNA electrophoretic mobility that includes the relaxation and retardation effects just described (34). The DNA is modeled as an infinitely long wire (no end effects) with point charges separated by the average distance between them along the DNA chain, termed the b factor. The resulting equation, which contains no adjustable parameters, can be written as follows:
| (4a) |
| (4b) |
| (4c) |
| (4d) |
Here, μ is the predicted mobility; z1 and z2 are the counterion and coion valencies, respectively; ε is the dielectric constant of the solvent; kB is Boltzmann’s constant; T is the absolute temperature; η is the viscosity of the solvent; κ is the inverse Debye length; eo is the elementary charge; ν1 and ν2 are the numbers of counterions and coions in the BGE; and λ1o and λ2o are the equivalent conductances of the counterions and coions.
All parameters in Eqs. 4a, 4b, 4c, and 4d are known physical constants or can be calculated from the composition of the solution and data in the literature. The charge separation parameter b can be estimated for dsDNA by dividing the length of the oligomer (number of basepairs × rise per basepair, 3.4 Å) by the number of phosphate residues in the DNA. The b factor of ssDNA will be discussed below.
Results and Discussion
dsDNA
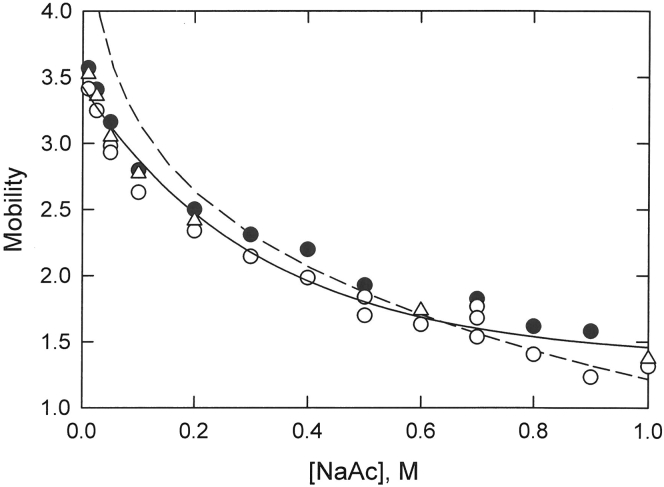
The free-solution mobilities of ds442, ds26a, and ds26b are plotted in Fig. 1 as a function of ionic strength, denoted as [NaAc] for simplicity. The mobilities of all three dsDNA strands decreased with increasing ionic strength until they began to level off at ionic strengths above ∼0.6 M. The amplitude of the mobility of ds442 was larger than observed for the smaller oligomers, as expected from previous studies showing that DNA mobilities increase with increasing molecular weight until they reach a plateau value at high molecular weights (22). To emphasize the generality of the results, the mobilities of the three dsDNA strands were analyzed together. The solid curve in Fig. 1 corresponds to a three-parameter exponential decay of the combined mobilities of the three dsDNA strands as a function of NaAc concentration. Similar results were obtained from a three-parameter hyperbolic fit of the combined mobilities as a function of ionic strength (data not shown).
Figure 1.
Dependence of the free-solution mobility of dsDNA on the sodium acetate concentration ([NaAc]). The symbols represent the following: solid circle (●), ds442; open circle (○), ds26a; and open triangle (▵), ds26b. The solid line corresponds to a three-parameter exponential decay of the combined mobilities of the three dsDNA strands as a function of ionic strength. The dashed line corresponds to the mobility predicted by the Manning electrophoresis equation (34), assuming b = 1.7 Å.
The dashed curve in Fig. 1 corresponds to the mobility predicted for dsDNA from the Manning electrophoresis equation (34) using a value of b, the average separation between charged phosphate residues, equal to 1.7 Å. The observed and predicted mobilities are reasonably close over the entire range of ionic strengths. However, the predicted mobilities are higher than the observed mobilities at low ionic strengths (I ≤ 0.2 M), as observed previously (25), and do not approach a plateau value at high ionic strengths. As a result, the curves describing the dependence of the predicted and observed mobilities on ionic strength have different shapes and cross at ∼0.6 M NaAc.
ssDNA
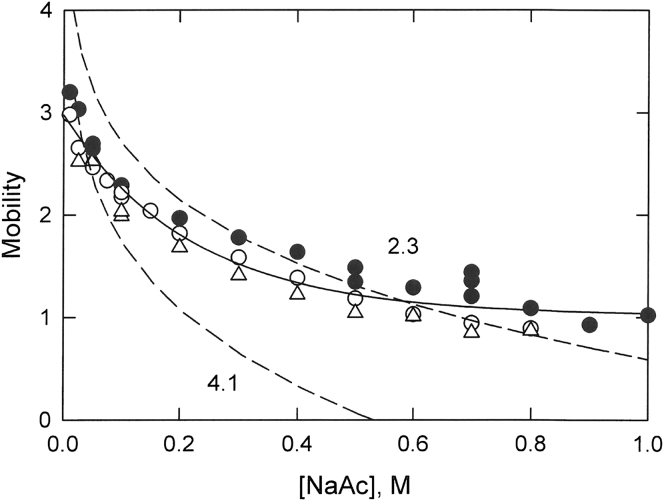
The free-solution mobilities of ssDNA strands containing 7, 16, and 26 nucleotides are plotted as a function of ionic strength in Fig. 2. The mobilities of the ssDNA strands decreased with increasing ionic strength at low ionic strengths and approached limiting plateau values at ionic strengths greater than ∼0.6 M. As observed with dsDNA, the mobilities of the ssDNA strands increased in magnitude with increasing molecular weight, as expected from previous studies (22,24). Again, to emphasize the generality of the results, the mobilities of the three ssDNA strands were analyzed together. The solid curve in Fig. 2 describes a three-parameter exponential decay of the combined mobilities as a function of ionic strength.
Figure 2.
Dependence of the free-solution mobility of three ssDNA strands on ionic strength. The symbols represent the following: solid circle (●), T26; open circle (○), T16; and open triangle (▵), ss07. The solid curve corresponds to a three-parameter exponential decay of the combined mobilities of the ssDNA strands as a function of ionic strength. The dashed curves correspond to the mobilities predicted from the Manning electrophoresis equation using b = 4.1 Å (lower dashed curve) or 2.3 Å (upper dashed curve).
To compare the observed mobilities of the ssDNA strands with the mobilities predicted by the Manning electrophoresis equation, it is necessary to first estimate the value of b, the average distance between charged phosphate residues along the contour length of the chain (34,48,49). The distance between adjacent nucleotides in protein-DNA crystals has been found to be ∼6.3 Å (12), close to the maximum separation between phosphate residues in stretched polynucleotides (3). However, much shorter separation distances are typically observed for polynucleotides and ssDNA in solution. Early biophysical studies showed that single-stranded polynucleotides are well described as worm-like coils with b-values between 3 and 4 Å (34,43,44,48,49). Recent determinations of the b-values of small ssDNA strands, with and without intrinsic base stacking, are similar (19, 20, 21). Somewhat larger b-values, between 4.0 and 4.5 Å, have been determined for small (dT) oligomers using ensemble and single-molecule fluorescence resonance energy transfer (FRET) methods (13). Finally, a conformational energy analysis of single-stranded randomly coiling polynucleotide chains found that the b parameter only weakly reflects the spatial configuration of the individual chain segments and cannot be used to infer the overall conformation of the chain (49).
Given the uncertainties about the appropriate b-value to use for ssDNA, we chose to compare the observed mobilities of the ssDNA strands in Fig. 2 with the mobilities predicted by the Manning electrophoresis equation using two arbitrary values of b, 4.1 and 2.3 Å. Other b factors primarily shift the predicted mobilities up or down on the mobility scale (data not shown). The lower dashed curve in Fig. 2 corresponds to the predicted mobilities if b = 4.1 Å. The predicted and observed mobilities are reasonably close at low ionic strengths (I ≤ 0.1 M), suggesting that this b-value corresponds to the average separation between ssDNA phosphates when the ionic strength is very low. Similar results have been observed in single-molecule FRET studies (13).
At ionic strengths ≥0.1 M NaAc, the predicted mobilities of the ssDNA strands are significantly lower than the observed mobilities when the b-value is assumed to be 4.1 Å, as shown by comparing the lower dashed curve in Fig. 2 with the solid curve describing the observed mobilities. The discrepancy can probably be attributed to an increase in flexibility and/or a decrease in the overall extension of the ssDNA molecules with increasing ionic strength because the persistence length decreases in a similar manner with increasing ionic strength (10, 11, 12, 13, 14, 15, 16,50).
The upper dashed curve in Fig. 2 corresponds to the predicted mobility of ssDNA if the value of b is assumed to be 2.3 Å. In this case, the predicted and observed mobilities are reasonably close at high ionic strengths (I ≥ 0.3 M) but diverge at low ionic strengths (I ≤ 0.2 M). The results suggest that the ensemble of ssDNA conformations in solution may undergo a transition from rod-like extended structures in solutions containing less than 0.1 M NaAc to more compact but still somewhat extended conformations in BGEs containing more than ∼0.3 M NaAc. The b-values of these more compact, “crumpled” ssDNA conformations could correspond to comparatively short phosphate-phosphate distances through space instead of tracing a path along the contour length of the chain (49).
To predict ssDNA mobilities over a wide range of ionic strengths using the Manning electrophoresis equation, it would seem necessary to use b-values that decrease with increasing ionic strength. Recent small-angle x-ray scattering (50) and fluorescence spectroscopy (12) measurements of small ssDNA strands showed that the persistence length decreased 45–50% when the ionic strength of the solution increased from 0.1 to 1.0 M [Na+] (12,50). This percentage decrease is similar in magnitude to the 78% decrease in b-values used to calculate the predicted ssDNA mobilities in Fig. 2. Hence, it might be useful to think of the b-values of ssDNA as phenomenological parameters describing the average distance between phosphate residues through space under a given set of experimental conditions rather than the average separation of phosphate residues along the contour length of the chain. The conformational ensemble of ssDNA strands in high ionic strength solutions could then be thought of as the ssDNA equivalent of the molten globules observed during protein folding (e.g., (51,52)) or the compact random-walk structures observed for various polymers by elasticity measurements (e.g., (53,54)).
Comparison of the mobilities of ssDNA and dsDNA
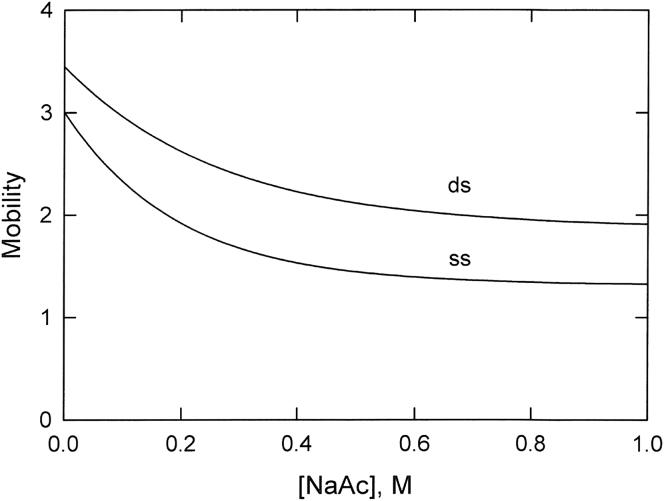
The free-solution mobilities observed for ssDNA and dsDNA in solutions of different ionic strengths are compared in Fig. 3 using the fitted mobility curves taken from Figs. 1 and 2 to more easily visualize the results. The mobilities of ssDNA and dsDNA decrease rapidly with increasing ionic strength until reaching limiting plateau values at ionic strengths ≥0.6 M. The mobilities of dsDNA are larger than those of ssDNA at all ionic strengths because of the greater charge density of dsDNA (38,39).
Figure 3.
Comparison of the mobilities observed for dsDNA (upper curve) and ssDNA (lower curve) as a function of NaAc concentration. The mobility curves correspond to the fitted mobility curves (solid lines) in Figs. 1 and 2, respectively.
The nearly parallel mobility curves observed for ssDNA and dsDNA in solutions of different NaAc concentrations (Fig. 3) suggest that both ssDNA and dsDNA undergo similar interactions with the counterions and coions in the BGE. The unexpected mobility plateaus observed at high ionic strengths (I ≥ 0.6 M) suggest that counterion-counterion correlation effects (9,39,55, 56, 57), counterion-phosphate interactions (16), and/or cation-anion interactions in the BGE may contribute to the mobility plateaus observed for ssDNA and dsDNA at high ionic strengths.
Variations in the composition of the ion atmosphere at different ionic strengths may also contribute to the mobility plateaus. Recent ion counting experiments have suggested that the number of cations close to the DNA surface decreases with increasing ionic strength, whereas the number of anions excluded from the ion atmosphere increases (58). The result could be a gradual increase in the effective net charge of the DNA with increasing ionic strength, increasing the observed mobility and in part counteracting the usual decrease in DNA mobility with increasing ionic strength (25,26).
Finally, the distinction between the condensed cations in the ion atmosphere around the DNA, the concentration of cations in the adjacent Debye layer, and the cations in the bulk solution may become blurred when the Debye layer is very thin, as is true for the high ionic strength buffers used here. Further studies will be needed to clarify these issues.
Conclusions
The free-solution mobilities of ssDNA and dsDNA decrease with increasing ionic strength and approach limiting plateau values at I ≥ 0.6 M. Whether the mobility plateaus are due to ion-ion and/or DNA-ion interactions that become important at high ionic strengths remains to be determined. The Manning electrophoresis equation, which contains no adjustable parameters, provides a reasonable estimate of the free-solution mobility of dsDNA in solutions of different ionic strengths, using a b-value (linear distance between charged phosphate residues) of 1.7 Å. For ssDNA, the appropriate b-value appears to decrease with increasing ionic strength, suggesting that ssDNA strands exist as an ensemble of crumpled conformations that become more compact at high ionic strengths. Neither the average dimensions of individual molecules in the ensemble nor the contour lengths of individual ssDNA chains can be determined without further experimental information (49).
Author Contributions
E.S. and N.C.S. designed experiments. E.S. carried out experiments. E.S. and N.C.S. analyzed the data and wrote the article.
Acknowledgments
Helpful comments from the reviewers are gratefully acknowledged.
Editor: Wilma Olson.
References
- 1.Lipfert J., Doniach S., Herschlag D. Understanding nucleic acid-ion interactions. Annu. Rev. Biochem. 2014;83:813–841. doi: 10.1146/annurev-biochem-060409-092720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Haran T.E., Mohanty U. The unique structure of A-tracts and intrinsic DNA bending. Q. Rev. Biophys. 2009;42:41–81. doi: 10.1017/S0033583509004752. [DOI] [PubMed] [Google Scholar]
- 3.Saenger W. Springer-Verlag; New York: 1984. Principles of Nucleic Acid Structure. [Google Scholar]
- 4.Lu Y., Weers B., Stellwagen N.C. DNA persistence length revisited. Biopolymers. 2001-2002;61:261–275. doi: 10.1002/bip.10151. [DOI] [PubMed] [Google Scholar]
- 5.Brunet A., Tardin C., Manghi M. Dependence of DNA persistence length on ionic strength of solutions with monovalent and divalent salts: a joint theory-experiment study. Macromolecules. 2015;48:3641–3652. [Google Scholar]
- 6.Savelyev A. Do monovalent mobile ions affect DNA’s flexibility at high salt content? Phys. Chem. Chem. Phys. 2012;14:2250–2254. doi: 10.1039/c2cp23499h. [DOI] [PubMed] [Google Scholar]
- 7.Yuan C., Chen H., Archer L.A. DNA bending stiffness on small length scales. Phys. Rev. Lett. 2008;100:018102. doi: 10.1103/PhysRevLett.100.018102. [DOI] [PubMed] [Google Scholar]
- 8.Garai A., Saurabh S., Maiti P.K. DNA elasticity from short DNA to nucleosomal DNA. J. Phys. Chem. B. 2015;119:11146–11156. doi: 10.1021/acs.jpcb.5b03006. [DOI] [PubMed] [Google Scholar]
- 9.Wu Y.-Y., Bao L., Tan Z.-J. Flexibility of short DNA helices with finite-length effect: from base pairs to tens of base pairs. J. Chem. Phys. 2015;142:125103. doi: 10.1063/1.4915539. [DOI] [PubMed] [Google Scholar]
- 10.McIntosh D.B., Duggan G., Saleh O.A. Sequence-dependent elasticity and electrostatics of single-stranded DNA: signatures of base-stacking. Biophys. J. 2014;106:659–666. doi: 10.1016/j.bpj.2013.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen H., Meisburger S.P., Pollack L. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. USA. 2012;109:799–804. doi: 10.1073/pnas.1119057109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Murphy M.C., Rasnik I., Ha T. Probing single-stranded DNA conformational flexibility using fluorescence spectroscopy. Biophys. J. 2004;86:2530–2537. doi: 10.1016/S0006-3495(04)74308-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Laurence T.A., Kong X., Weiss S. Probing structural heterogeneities and fluctuations of nucleic acids and denatured proteins. Proc. Natl. Acad. Sci. USA. 2005;102:17348–17353. doi: 10.1073/pnas.0508584102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bosco A., Camunas-Soler J., Ritort F. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 2014;42:2064–2074. doi: 10.1093/nar/gkt1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang Y., Zhou H., Ou-Yang Z.-C. Stretching single-stranded DNA: interplay of electrostatic, base-pairing, and base-pair stacking interactions. Biophys. J. 2001;81:1133–1143. doi: 10.1016/S0006-3495(01)75770-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sarkar S., Maity A., Chakrabarti R. Salt induced structural collapse, swelling, and signature of aggregation of two ssDNA strands: insights from molecular dynamics simulation. J. Phys. Chem. B. 2019;123:47–56. doi: 10.1021/acs.jpcb.8b09098. [DOI] [PubMed] [Google Scholar]
- 17.Vesnaver G., Breslauer K.J. The contribution of DNA single-stranded order to the thermodynamics of duplex formation. Proc. Natl. Acad. Sci. USA. 1991;88:3569–3573. doi: 10.1073/pnas.88.9.3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou J., Gregurick S.K., Schwarz F.P. Conformational changes in single-strand DNA as a function of temperature by SANS. Biophys. J. 2006;90:544–551. doi: 10.1529/biophysj.105.071290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Isaksson J., Acharya S., Chattopadhyaya J. Single-stranded adenine-rich DNA and RNA retain structural characteristics of their respective double-stranded conformations and show directional differences in stacking pattern. Biochemistry. 2004;43:15996–16010. doi: 10.1021/bi048221v. [DOI] [PubMed] [Google Scholar]
- 20.Ramprakash J., Lang B., Schwarz F.P. Thermodynamics of single strand DNA base stacking. Biopolymers. 2008;89:969–979. doi: 10.1002/bip.21044. [DOI] [PubMed] [Google Scholar]
- 21.Capobianco A., Velardo A., Peluso A. Single-stranded DNA oligonucleotides retain rise coordinates characteristic of double helices. J. Phys. Chem. B. 2018;122:7978–7989. doi: 10.1021/acs.jpcb.8b04542. [DOI] [PubMed] [Google Scholar]
- 22.Stellwagen N.C., Gelfi C., Righetti P.G. The free solution mobility of DNA. Biopolymers. 1997;42:687–703. doi: 10.1002/(SICI)1097-0282(199711)42:6<687::AID-BIP7>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 23.Dong Q., Stellwagen E., Stellwagen N.C. Free solution mobility of small single-stranded oligonucleotides with variable charge densities. Electrophoresis. 2003;24:3323–3329. doi: 10.1002/elps.200305589. [DOI] [PubMed] [Google Scholar]
- 24.Stellwagen E., Lu Y., Stellwagen N.C. Unified description of electrophoresis and diffusion for DNA and other polyions. Biochemistry. 2003;42:11745–11750. doi: 10.1021/bi035203p. [DOI] [PubMed] [Google Scholar]
- 25.Stellwagen E., Stellwagen N.C. Probing the electrostatic shielding of DNA with capillary electrophoresis. Biophys. J. 2003;84:1855–1866. doi: 10.1016/S0006-3495(03)74993-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stellwagen E., Stellwagen N.C. The free solution mobility of DNA in Tris-acetate-EDTA buffers of different concentrations, with and without added NaCl. Electrophoresis. 2002;23:1935–1941. doi: 10.1002/1522-2683(200206)23:12<1935::AID-ELPS1935>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 27.Stellwagen E., Lu Y., Stellwagen N.C. Curved DNA molecules migrate anomalously slowly in free solution. Nucleic Acids Res. 2005;33:4425–4432. doi: 10.1093/nar/gki748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dong Q., Stellwagen E., Stellwagen N.C. Monovalent cation binding in the minor groove of DNA A-tracts. Biochemistry. 2009;48:1047–1055. doi: 10.1021/bi8020718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stellwagen E., Dong Q., Stellwagen N.C. Flanking A·T basepairs destabilize the B(∗) conformation of DNA A-tracts. Biophys. J. 2015;108:2291–2299. doi: 10.1016/j.bpj.2015.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stellwagen E., Peters J.P., Stellwagen N.C. DNA A-tracts are not curved in solutions containing high concentrations of monovalent cations. Biochemistry. 2013;52:4138–4148. doi: 10.1021/bi400118m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stellwagen N.C., Peters J.P., Stellwagen E. The free solution mobility of DNA and other analytes varies as the logarithm of the fractional negative charge. Electrophoresis. 2014;35:1855–1863. doi: 10.1002/elps.201400040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stellwagen N.C. Electrophoretic mobilities of the charge variants of DNA and other polyelectrolytes: similarities, differences, and comparison with theory. J. Phys. Chem. B. 2017;121:2015–2026. doi: 10.1021/acs.jpcb.6b10599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stellwagen N.C., Stellwagen E. DNA thermal stability depends on solvent viscosity. J. Phys. Chem. B. 2019;123:3649–3657. doi: 10.1021/acs.jpcb.9b01217. [DOI] [PubMed] [Google Scholar]
- 34.Manning G.S. Limiting laws and counterion condensation in polyelectrolyte solutions. 7. Electrophoretic mobility and conductance. J. Phys. Chem. 1981;85:1506–1515. [Google Scholar]
- 35.Stellwagen N.C., Bossi A., Righetti P.G. Do orientation effects contribute to the molecular weight dependence of the free solution mobility of DNA? Electrophoresis. 2001;22:4311–4315. doi: 10.1002/1522-2683(200112)22:20<4311::AID-ELPS4311>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 36.Vanýsek P. Ionic conductivity and diffusion at infinite dilution. In: Lide D.R., editor. Handbook of Chemistry and Physics. 77th Edition. CRC Press, Inc.; 1996–1997. 598–100. [Google Scholar]
- 37.Williams B.A., Vigh G. Fast, accurate mobility determination method for capillary electrophoresis. Anal. Chem. 1996;68:1174–1180. doi: 10.1021/ac950968r. [DOI] [PubMed] [Google Scholar]
- 38.Grossman P.D. Chapter 4: Free-solution capillary electrophoresis. In: Grossman P.D., Colburn J.C., editors. Capillary Electrophoresis: Theory and Practice. Academic Press; 1992. pp. 111–132. [Google Scholar]
- 39.Bockris J.O.’M., Reddy A.K.N. Second Edition. Plenum Press; New York: 1998. Modern Electrochemistry: Vol. 1, Ionics. [Google Scholar]
- 40.Wiersema P.H., Loeb A.L., Overbeek J.T.G. Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid Interface Sci. 1966;22:78–99. [Google Scholar]
- 41.O’Brien R., White L.R. Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc., Faraday Trans. II. 1978;74:1607–1626. [Google Scholar]
- 42.Viovy J.-L. Electrophoresis of DNA and other polyelectrolytes: physical mechanisms. Rev. Mod. Phys. 2000;72:813–872. [Google Scholar]
- 43.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 44.Record M.T., Jr., Anderson C.F., Lohman T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 45.Chatterji A., Horbach J. Electrophoretic properties of highly charged colloids: a hybrid molecular dynamics/lattice Boltzmann simulation study. J. Chem. Phys. 2007;126:064907. doi: 10.1063/1.2431174. [DOI] [PubMed] [Google Scholar]
- 46.Jumppanen J.H., Riekkola M.-L. Influence of electrolyte composition on the effective electric field strength in capillary zone electrophoresis. Electrophoresis. 1995;16:1441–1444. doi: 10.1002/elps.11501601238. [DOI] [PubMed] [Google Scholar]
- 47.Gulik A., Inoue H., Luzzati V. Conformation of single-stranded polynucleotides: small-angle x-ray scattering and spectroscopic study of polyribocytidylic acid in water and in water-alcohol solutions. J. Mol. Biol. 1970;53:221–238. doi: 10.1016/0022-2836(70)90296-2. [DOI] [PubMed] [Google Scholar]
- 48.Manning G.S. The application of polyelectrolyte limiting laws to the helix-coil transition of DNA. VI. The numerical value of the axial phosphate spacing for the coil form. Biopolymers. 1976;15:2385–2390. doi: 10.1002/bip.1976.360151206. [DOI] [PubMed] [Google Scholar]
- 49.Olson W.K., Manning G.S. A configurational interpretation of the axial phosphate spacing in polynucleotide helices and random coils. Biopolymers. 1976;15:2391–2405. doi: 10.1002/bip.1976.360151207. [DOI] [PubMed] [Google Scholar]
- 50.Sim A.Y.L., Lipfert J., Doniach S. Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;86:021901. doi: 10.1103/PhysRevE.86.021901. [DOI] [PubMed] [Google Scholar]
- 51.Baldwin R.L., Rose G.D. Molten globules, entropy-driven conformational change and protein folding. Curr. Opin. Struct. Biol. 2013;23:4–10. doi: 10.1016/j.sbi.2012.11.004. [DOI] [PubMed] [Google Scholar]
- 52.Christensen H., Pain R.H. Molten globule intermediates and protein folding. Eur. Biophys. J. 1991;19:221–229. doi: 10.1007/BF00183530. [DOI] [PubMed] [Google Scholar]
- 53.Saleh O.A., McIntosh D.B., Ribeck N. Nonlinear low-force elasticity of single-stranded DNA molecules. Phys. Rev. Lett. 2009;102:068301. doi: 10.1103/PhysRevLett.102.068301. [DOI] [PubMed] [Google Scholar]
- 54.McIntosh D.B., Saleh O.A. Salt species-dependent electrostatic effects on ssDNA elasticity. Macromolecules. 2011;44:2328–2333. [Google Scholar]
- 55.Tan Z.-J., Chen S.-J. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J. Chem. Phys. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Xi K., Wang F.H., Tan Z.J. Competitive binding of Mg2+ and Na+ ions to nucleic acids: from helices to tertiary structures. Biophys. J. 2018;114:1776–1790. doi: 10.1016/j.bpj.2018.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hayes R.L., Noel J.K., Onuchic J.N. Generalized Manning condensation model captures the RNA ion atmosphere. Phys. Rev. Lett. 2015;114:258105. doi: 10.1103/PhysRevLett.114.258105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gebala M., Giambaşu G.M., Herschlag D. Cation-anion interactions within the nucleic acid ion atmosphere revealed by ion counting. J. Am. Chem. Soc. 2015;137:14705–14715. doi: 10.1021/jacs.5b08395. [DOI] [PMC free article] [PubMed] [Google Scholar]