Abstract
Self-association of therapeutic monoclonal antibodies (mabs) are thought to modulate the undesirably high viscosity observed in their concentrated solutions. Computational prediction of such a self-association behavior is advantageous early during mab drug candidate selection when material availability is limited. Here, we present a coarse-grained (CG) simulation method that enables microsecond molecular dynamics simulations of full-length antibodies at high concentrations. The proposed approach differs from others in two ways: first, charges are assigned to CG beads in an effort to reproduce molecular multipole moments and charge asymmetry of full-length antibodies instead of only localized charges. This leads to great improvements in the agreement between CG and all-atom electrostatic fields. Second, the distinctive hydrophobic character of each antibody is incorporated through empirical adjustments to the short-range van der Waals terms dictated by cosolvent all-atom molecular dynamics simulations of antibody variable regions. CG simulations performed on a set of 15 different mabs reveal that diffusion coefficients in crowded environments are markedly impacted by intermolecular interactions. Diffusion coefficients computed from the simulations are in correlation with experimentally measured observables, including viscosities at a high concentration. Further, we show that the evaluation of electrostatic and hydrophobic characters of the mabs is useful in predicting the nonuniform effect of salt on the viscosity of mab solutions. This CG modeling approach is particularly applicable as a material-free screening tool for selecting antibody candidates with desirable viscosity properties.
Significance
Early assessment of antibody drug developability characteristics can substantially reduce risks and costs associated with their product development and provides an opportunity for molecular redesign. One key aspect in the developability assessment is the prediction of the viscosity behavior. Subcutaneous delivery of antibodies requires high-concentration solutions to achieve a desired dose. At these high concentrations, antibody self-association can cause undesirably high viscosity, leading to significant challenges in manufacturing and administration. Presented here is a physics-based, coarse-grained scheme that enables early identification of the high viscosity of antibodies based solely on antibody structural attributes and dynamical properties from the simulations. The computational approaches like the one proposed greatly improve the successful progression of antibody drug candidates through clinical development, ultimately benefiting patients.
Introduction
The exponential growth in protein-based therapeutic modalities, such as monoclonal antibodies (mabs), has revolutionized the treatment and patient standard of care for many diseases while, at the same time, creating a large body of knowledge about highly concentrated and purified protein solutions (1, 2, 3, 4). We now recognize that the viscoelastic properties of concentrated proteins with nearly identical structures (primary sequence and fold architecture) can span orders of magnitude (5, 6, 7, 8, 9, 10). Elevated viscosity causes numerous challenges to a therapeutic program ranging from difficulties in bioprocessing and formulation development to issues with subcutaneous drug delivery and patient compliance (11). However, because of material limitations in early discovery and development, these problems are often not discovered until much later, when solutions are much more costly to implement. Early detection of mab candidates that are prone to high viscosity can accelerate discovery and development and may even allow for protein redesign to avoid the problem altogether (7,12).
In silico approaches to predict viscosity behavior of antibody solutions range from quantitiative structure-property relationship (QSPR) modeling (13, 14, 15, 16, 17) to physics-based molecular simulations (18, 19, 20, 21, 22). QSPR methods that use scoring functions to predict viscosity from primary sequence (13) or structural descriptors (15, 16, 17) are a current industry standard. The scoring functions are typically optimized to predict the viscosity of a set of mabs with a specific framework (e.g., IgG1) at a given concentration and formulation condition that are used in the training set. Sometimes, the sequence or structural descriptors of only the variable (Fv) region are accounted for in the training (13,14). Extrapolating beyond the confines of these training sets, e.g., applying to a new antibody modality, usually requires retraining the scoring function, which is often a problem because there may not be enough experimental data available for less-common frameworks or formulation conditions for the training. As protein therapeutics portfolios grow more and more complex (1), with a large variety of new molecular formats and even coformulation, each new therapeutic modality or drug product configuration may be exceptional. In this respect, physics-based molecular simulations can offer a unique advantage because they provide profound, often general, insight into the behavior of protein solutions by relying on a mechanistic description of underlying phenomena, such as weak intermolecular interactions (5,6,10). Physics-based simulations that are not dependably limited by training data are therefore most desirable.
Despite the high promise, physics-based molecular simulations at maximal detail—fully atomistic—can become prohibitive because of the considerable computational costs, especially for the system sizes and timescales relevant to concentrated mab solutions. Coarse-grained (CG) molecular dynamics (MD) simulations address this rote computational challenge (23,24) with variable success. Among various coarse-graining schemes for concentrated antibody simulations, the domain-based CG models using 6–12 beads (18, 19, 20, 21, 22,25,26) have achieved great popularity. This is largely due to the gain in computational speed on commodity hardware (based on our benchmarking, the computational speed to simulate a box filled with ∼1400 copies of 10-bead CG models in implicit solvent is approximately 1 μs/day/cpu). Domain-based CG models are widely employed to recover both dynamics and rheological properties of antibody solutions that have demonstrated agreement with the experiment (21,22,25,26). Yet, the question still remains whether the CG simulations utilizing domain-based models can be reliably implemented as a screening tool to identify mabs that are prone to high viscosity. This necessitates an accuracy evaluation of the domain-based models using large and diverse data sets comparable with the ones used in the QSPR studies (13,15).
The accuracy concern is primarily associated with the domain-level representation of electrostatic and hydrophobic characteristics, which are two key factors in protein-protein interactions in a crowded environment (6, 7, 8,13,15). Domain-based CG models often rely on localized charge assignment (18, 19, 20, 21) to represent atom-level charge distribution of antibodies. This would not necessarily take into account the anisotropy in local and global charge distribution and the high-order electrostatic multipole moments that are thought to contribute to the self-association of full-length antibodies (6,27, 28, 29). Much less attention has been paid to the explicit incorporation of hydrophobic interactions; to the best of our knowledge, including a bottom-up domain-specific hydrophobicity for CG simulations of antibodies is yet to be reported.
In this work, we aim to improve the domain-based CG simulation of antibodies and then evaluate it using a large and diverse set of mab molecules to demonstrate their general applicability to viscosity screening. The proposed CG model differs from previous works in two principal ways: first, a new method is introduced to incorporate the reference all-atom charge distribution and the resulting molecular charge asymmetry into the CG representation. This method focuses on reproducing multipole moments (up to the octupole) through a set of antibody-specific analytical expressions. Second, the hydrophobicity characteristics of each antibody variable region, estimated using cosolvent MD simulation, are incorporated into the CG model by tuning the short-range van der Waals interactions. Using a test set containing 15 mabs, we demonstrate that self-diffusion coefficients calculated from our CG simulations correlate well with experimentally measured viscosities at high-concentration mab solutions as well as diffusion interaction parameters (kD). We also find that the electrostatic and hydrophobicity components from the CG models can be useful in predicting how the viscosity of an antibody might respond to changes in ionic strength. This physics-based approach demonstrably predicts viscosity behavior with a high accuracy while enabling the exploration of the primary determinants thereof.
Materials and Methods
Test molecules, experimental diffusion interaction parameters, and viscosities
15 mabs were selected from a larger set of 29 molecules for which experimentally measured diffusion interaction parameters kD and viscosities were previously reported; see (10). These mabs form the largest subset of molecules studied previously (10) (numbered 1–12 and 14–16) sharing the same framework (IgG1) and measured in the same buffer conditions (20 mM histidine-acetate (pH 5.5) and 200 mM arginine-chloride (pH 5.0)). Using the same naming convention as in (10), the measurements of interest here, the diffusion interaction parameters kD, and viscosities at two different buffer conditions are listed in Table 1.
Table 1.
Summary of Experimental kD and Viscosity Data
| Viscosity (cP) |
kD (mL/g) |
||
|---|---|---|---|
| 20 mM His-OAc |
200 mM Arg-Cl |
20 mM His-OAc |
|
| pH 5.5 | pH 5.0 | pH 5.5 | |
| mab1 | 7 | 9 | 35.7 ± 0.1 |
| mab2 | 6 | 11 | 32 ± 2.3 |
| mab3 | 14 | 7 | 27.6 ± 2.6 |
| mab4 | 13 | 8 | 27.4 ± 1.5 |
| mab5a | 56 | 82 | 27.3 ± 1.6 |
| mab6 | 10 | 11 | 21.7 ± 2.6 |
| mab7 | 11 | 9 | 20.5 ± 3.5 |
| mab8 | 13 | 10 | 10.9 ± 1.2 |
| mab9 | 30 | 6 | 1.8 ± 4.1 |
| mab10 | 63 | 14 | −3 ± 2.1 |
| mab11 | 79 | 71 | −4.7 ± 5.0 |
| mab12 | 21 | 11 | −6.8 ± 1.4 |
| mab14 | 119 | 36 | −18.3 ± 2.7 |
| mab15 | 103 | 14 | −19.1 ± 2.1 |
| mab16 | 49 | 13 | −22.5 ± 2.7 |
Data from (10). The mab viscosities were measured at a high concentration (175 mg/mL ± 5%) using cone and plate rheometer.
Viscosity data for mab5 in the respective buffer conditions were taken from an unpublished data set.
Homology modeling, electrostatic surface potential, and molecular descriptor calculations
The software Molecular Operating Environment (MOE) (30) from Chemical Computing Group was used for constructing fragment antigen-binding (Fab) domain models for each antibody. A full-length homology model for each mab was then produced by aligning (α-carbon root-mean square deviation minimization) the Fab models to either the left or right arm of a generic full-length IgG1 molecule. The mab IgG1 framework was based on a full structure of the IgG1 antibody for mab7 that Brandt et al. (31) pieced together from crystal structures of the fragments and equilibrated to a relaxed conformation. The C-terminal lysines were cleaved off from the IgG1 homology models.
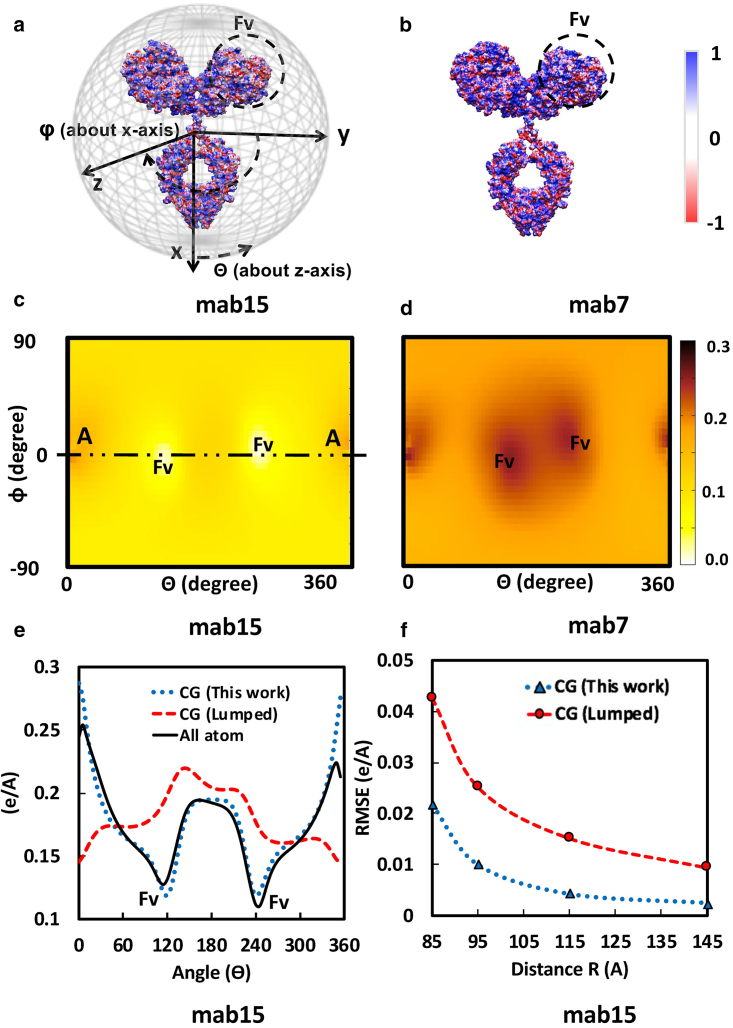
The constant domain (Fc) and Fab arms in this mab IgG1 framework were oriented so that the Fc is aligned with the x axis and the Fab arms are extended toward the y axis; see Fig. 1. Thus, each unique structural model now shares symmetry about x-z and x-y planes and roughly equivalent centers of mass using an atomic partitioning defined later. Consequently, the same relative Cartesian positions are used for all CG models prepared as described here.
Figure 1.
CG representation of the IgG1 mab structure. (a) The molecular multipole moments up to the octupole order of the full-length mab are calculated. (b) The charges on CG sites are assigned so that these multipole moments are accurately reproduced. (c) All-atom MD simulations of the Fv region that were solvated in a mixed solution of explicit water molecules and a hydrophobic tracer molecule (trimethylamine) are performed to determine the hydrophobicity characters of the Fv. (d) The LJ parameters are adjusted based on the hydrophobic characters of Fv and the size of each representative CG domain.
The full-length homology models were energy minimized using SANDER, available in AMBER 2015 (32). PDB2PQR (33) (v. 1.8) was used with the AMBER force field (34) to assign partial atomic charges whereby ionization states were determined using PROPKA (35,36) (pH 5.5). Electrostatic surface potentials were computed using APBS (37) and visualized with VMD (Fig. 3; (38)).
Figure 3.
(a and b) The electrostatic surface potential for mab15 and mab7 (pH 6.0) and 15 mM solution ionic strength, generated using APBS and VMD (38). The red and blue contours indicate −1 and +1 KT/e electrostatic surface potentials, respectively. (c and d) Shown is the calculated electrostatic potential on a circumscribed sphere with radius 100 Å centered at the center of the mass of mab15 and mab7. The heatmap shows the electrostatic potential at each point on the sphere represented by polar angles (θ and ϕ). (e) Shown is the electrostatic potential field along the A-A line produced by the proposed CG charge placement (this work), the commonly used “lumped” charge placement, and the reference all-atom representation. (f) Root mean-square error in electrostatic potential due to the proposed CG charge placement (this work) and the “lumped” charge placement relative to the reference all-atom representation at different distances are given. The electrostatic potential at a given distance is calculated on the surface of a sphere with the corresponding radius surrounding the mab.
The full-length antibody structures were used to calculate several key structural features, namely total-positive-charge patch surface area, total-negative-charge patch surface area, total hydrophobic patch surface area, positive-charge patch surface area near the complementarity-determining region (CDR), negative-charge patch surface area near the CDR, hydrophobic patch surface area near the CDR, antibody net charge (monopole), the Fv net charge, and HFv hydrophobicity index (described below). The charge and hydrophobic protein patch surface areas were calculated using MOE protein properties module (pH 5.5) at 15 mM salt concentrations (30). The Fv net charge (pH 5.5) (Fig. S1 h) was calculated by summing up charges of all the residues in the Fv region using the known pKa values of the side chains and the Henderson-Hasselbalch equation (13). The antibody net charge was calculated by summing up all the partial atomic charges in the pqr file (as written by PDB2PQR).
To examine the overall correlation between the structural descriptors of the mabs in our set with the measured viscosities, the correlation plots between nine computationally estimated descriptors and the log of experimental viscosities were generated; see Fig. S1. It is evident that no single structural descriptor alone is fully capable of predicting viscosity, as also shown elsewhere (15). This is not surprising because intermolecular interactions depend on the combined effect of several structural properties considered simultaneously. One can perform multivariate analysis on several descriptors to obtain a scoring function that may achieve a greater success in describing the viscosity behavior (13,15). However, the fact remains that the accuracy of the scoring functions would be dependent on the diversity of its training set. In this work, we pursue a multicopy CG simulation approach to estimate the diffusion coefficients and assess their correlation with measured viscosity at a high concentration, as described below.
CG representation of mabs: interaction sites
Each of the four domains in the Fab regions (VH, VL, CL, and CH1 domains) are represented by one CG site, and the Fc region is represented by two CG sites (see Fig. 1). This results in a 10-site CG model for the full-length mab with four degenerate positions because the Fab arms are equal, i.e., 3 = 7, 4 = 8, 5 = 9, and 6 = 10. The planar CG sites 1–6 (and 7–10) are placed on the center of mass of each domain in a generic IgG1 after projection onto the x-y plane as shown in Fig. 1; their positions are fixed for all mabs. The planar charge placement is also symmetric about the x axis with respect to sites 3–6 and 7–10.
Force field potential for CG simulation
The 10-bead rigid CG models described interact through intermolecular interactions that can be described in terms of electrostatic and van der Waals forces. Based on DLVO (Derjaguin-Landau-Verwey-Overbeek) theory of colloidal particle interactions (39), the electrostatic and the van der Waals forces are assumed to be independent and, therefore, can be superimposed or added at each interacting distance for two particles. A Coulomb potential with Debye-Hückel-screened electrostatics, including an exponential Yukawa term, was used to model the electrostatic interactions, as below:
| (1) |
where qi and qj are the point charges on interacting sites, εr represents the effective dielectric constant, and κ is the Debye screening parameter. For the implicit solvent model, the effective dielectric constant factor needs to be included to account for the screening effects of water. Here, we used a value of εr = 80 to account for the dielectric environment of water. The value of κ is set to 0.04 Å−1, corresponding to the 15-mM ionic strength. The values for the charge on each CG site are assigned to optimally reproduce the low-order multipole moments of the mabs, which is explained in the next section.
A Lennard-Jones (LJ) 12-6 potential energy function was used to describe short-range interactions:
| (2) |
where r is the distance of separation between two interacting beads measured from the center of one bead to another. σij = (σi + σj)/2 is the finite distance at which the interparticle potential is zero, where σi and σj are the van der Waals radii of the groups of atoms represented by each bead. Here, the van der Waals radius for each CG site is calculated as the radius of gyration of the respective all-atom domain increased by 2.5 Å to take into account for the hydration shell on the surface of the mab. describes the depth of the potential well, where εi and εj are the strengths for each interacting bead. The εi and εj parameters are assigned to account for the hydrophobic interactions, as described below.
Determination of CG charges based on molecular multipole moments
We aimed to assign charge values on CG interaction sites such that the electrostatic potential due to the original mab charge distribution is best represented. Based on the previously developed “Optimal Point Charge Approximation” (40,41), an optimal representation of the electrostatic fields around charge distributions, when approximated by a small number of point charges, can be achieved if the set of smaller point charges can reproduce the low-order molecular multipole moments in the expansion of the original mab charge distribution. Using the formalism described previously (40), here we derive the analytical equations that yield the values for the six CG charges at fixed positions (see Fig. 1) that optimally reproduce the four lowest-order multipole moments of the full-length mabs, i.e., monopole, dipole, quadrupole, and octupole. The elements of the traceless monopole q (i.e., net charge), dipole pi, quadrupole Qij, and octupole Oijk tensors (40) can be written as
| (3) |
| (4) |
| (5) |
| (6) |
where i, j, k = x, y, z. The remaining elements of the octupole tensor (I = x, y) are defined by symmetry (42,43). The tensors above can be fully described by 16 independent terms (one term for monopole, three terms for dipole, five terms for quadrupole, and seven terms for octupole). By design, the all-atom model of each mab is virtually symmetric with respect to the x-z and x-y planes (see Fig. 1). Because of the molecular symmetry, the number of independent elements in the tensors above is reduced to six significant independent values (40,42), which are denoted below:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
where q, μ, Q0, QT, O0, and OT are the monopole, dipole, linear component of the quadrupole, square component of the quadrupole, linear component of the octupole, and square component of the octupole, respectively (44,45).
These six independent moments are reproduced by solving for the six independent charge values for each CG model (q1, q2, q3 = q7, q4 = q8, q5 = q9, and q6 = q10, shown in Fig. 1) using the analytical expressions introduced below:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
where xn and yn are the positions of the CG charges corresponding to the center of mass of each domain in the generic IgG1 template used for homology modeling after they are projected onto the x-y plane in the relative coordinate system depicted in Fig. 1. Because the CG model is planar, zn = 0 for all the charges. qn is the charge value obtained by solving the linear system of equations presented above. The multipole moments and corresponding CG charges for all the mabs in the data set are provided in the Supporting Materials and Methods.
Determination of the hydrophobicity characters of the mabs
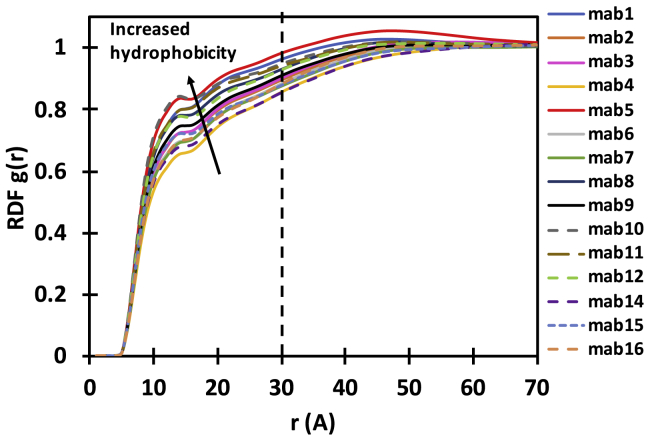
Cosolvent MD simulation was performed to characterize mabs with respect to hydrophobicity. The cosolvent MD approach used here is similar to the method introduced by Amrhein et al. (46) for the characterization of peptides with respect to hydrophobicity. For the purposes of computational speed, only variable domain (Fv) fragments were used in the simulations because this domain contains all of the differences between the molecules in our test set. Details of the simulation protocol used here are provided in the Supporting Materials and Methods.
A hydrophobic Fv attracts a greater number of hydrophobic tracer molecules (trimethylamine) to its molecular surface as compared with a less-hydrophobic Fv, and this can be quantified by the radial distribution function (RDF) of trace molecules with respect to Fv for each antibody as shown in Fig. 2. The RDF quantifies how the probability of finding a tracer molecule changes with distance to the molecular surface as compared with the probability of finding a tracer molecule in bulk solution at the simulated concentration. The definite integral of each RDF curve from 30 Å to the molecular surface is used to define the hydrophobicity index of that particular Fv:
| (19) |
where g(r) is the RDF profile of the tracer molecule with respect to the Fv and is calculated as below:
| (20) |
where n (r) is the mean number of tracer molecules in a shell of width dr at distance r from the molecular surface of Fv and ρ is the tracer molecule density. The calculated HFv index for each mab is reported in the Supporting Materials and Methods.
Figure 2.
The radial distribution function (RDF) of tracer molecules relative to the atoms in Fv region determined for different mabs. The RDF profile describes how the probability of finding a molecule differs with respect to the distance to the Fv molecular surface.
Hydrophobicity encoded LJ parameters
For all antibodies, the value of σi is defined by the size of each CG domain, as described earlier (see Eq. 2; Table S2), whereas the potential depth (εi) is adjusted to account for the van der Waals and hydrophobic interactions.
The mabs tested in this work are identical in their constant regions. Therefore, we assigned two different sets of ε: one for the CG sites in the constant region (εFc) and one for the CG sites in the variable regions (εFv). εFc is uniform across the different CG sites in the Fc (beads 1, 2, 3, 4, 7, and 8 in Fig. 1) for all mabs in the set, whereas εFv is unique to each mab and proportional to the hydrophobicity of the Fv (beads 5, 6, 9, and 10). The goal is to modulate self-association tendencies on the basis of hydrophobicity of the Fv region for each mab, but beforehand, the values for εFc must be determined.
εFc is assigned to promote varying self-associations across mabs that have different charge distributions and electrostatic interactions, regardless of the hydrophobicity scale of their Fv. Extremely large or small choices for εFc can result in a complete collapse or dissociation of the molecules in the simulation and thus cannot correctly rank the order of the mabs based on their electrostatic interactions. To parametrize εFc, two mabs with similar hydrophobicity scales (HFv) but different charge distributions (described by multipole moments) were selected (mab15 and 7; see the Supporting Materials and Methods). A starting value of εFc was uniformly assigned to every site in mab15 and 7 (including the Fv, i.e., εFv = εFc), and εFc was searched to obtain a value that reproduces a ratio of calculated self-diffusion coefficients comparable with the ratio of their measured viscosities (see Results and Discussion). εFc = 0.66 kcal/mol was found to satisfy this criterion and was fixed across the data set.
Unlike εFc, εFv is proportional to the hydrophobicity scale of Fv (HFv) while being independent of the charge distribution. In other words, the choices of εFv should properly rank the order of mabs that are similar in charge distributions but have different hydrophobicity scales. To optimize εFv, two molecules with comparable charge distributions but distinct hydrophobicity scales (HFv) were selected (mab5 and 7; see the Supporting Materials and Methods). Starting from εFv = εFc, different values of εFv for each mab were independently searched to obtain a calculated self-diffusion ratio corresponding to the ratio of their measured viscosities. We found that εFv = 0.84 and 1.27 kcal/mol for mab7 and 5, respectively, fulfill the criteria above. These two points were used to establish the following mapping from HFv to εFv:
| (21) |
CG simulation details
The CG sites and the force field described in the above sections were used to perform CG Langevin dynamics simulations using the LAMMPS package (47). Initially, 91–1460 mab molecules were arranged in a cubic lattice with the box size of 1300 Å using PACKMOL (48), which is a representative of 10–160 mg/mL protein concentrations. Periodic boundary conditions were applied in all three directions. The CG simulations were performed under NVT conditions with the use of a Langevin thermostat with the temperature set to 300 K. The CG simulations for the rigid antibodies were run for 5 μs, using a time step of 1 ps.
Calculation of self-diffusion coefficients of mabs in CG simulations
To investigate the relation between a single mab’s diffusive behavior and its interaction with its immediate environment (i.e., the strength of intermolecular interactions), the translational self-diffusion coefficients D of mabs were computed from their center of mass trajectories using the Einstein relation:
| (22) |
where δr is the overall distance traveled in three dimensions during a time interval of δt = 1 ns, and the brackets indicate an ensemble average. The CPPTRAJ tool (49) was used to calculate the mean-square displacement (<δr2>) versus time. The slope of <δr2> versus time was calculated via linear regression to obtain the self-diffusion values. The first 2 μs was excluded from the analysis of trajectories for these calculations.
Results and Discussion
Accuracy of the CG electrostatic field
At protein concentrations of interest in this work, intermolecular distances are smaller than the average intramolecular radius of gyration (5). Higher-order electrostatic interactions that are usually neglected under dilute conditions may contribute considerably to interaction energies at a high concentration, and the ability of our simulations to reproduce observed transport properties depends, in part, on how well the atom-level electrostatic field was preserved during coarse-graining procedures. Note that electrostatic surface potentials (Fig. 3, a and b) and, consequently, the electrostatic fields (Fig. 3, c and d) can greatly differ across mabs; this has been suggested (6,7) as the explanation for the differences in viscosity behavior between mabs15 and 7 (Table 1). The most common charge assignment approach involves a method of local summation or “lumped” charge assignment, whereby a CG bead is assigned the net charge of the group of atoms it represents from the original model. Lumped methods have been applied to IgG1 antibodies previously; see (18,19,21). Our method attempts to accurately reproduce the molecular multiple moments of the atomistic model by determining values for all CG beads using a system of equations introduced in the Materials and Methods (Eqs. 13, 14, 15, 16, 17, and 18). The accuracy of the electrostatic field produced by the two methods depends on either the number of beads in the CG model or the highest moment reproduced (40).
Electrostatic fields produced by our approach and the more common lumped method are given for mab15 in Fig. 3; Fig. 3 e depicts calculated electrostatic potentials along the A-A line shown in Fig. 3 c, representing a slice of a sphere around mab15 with an arbitrarily chosen radius of 100 Å, as is shown in Fig. 3 a. CG charges herein are assigned to best reproduce multipole moments up to the octupole order as described in the Materials and Methods. The original and CG model fields are nearly superimposable when the CG values are assigned to reproduce higher-order multipole moments, which is in stark contrast to when the lumped charge approach is used. Fig. 3 f shows that the overall higher accuracy of the presented approach is independent of the distance from the molecule.
Computed diffusion coefficient correlates with experimentally measured diffusion interaction parameter
Diffusion is the dominant transport property in systems at low Reynolds numbers, governing many dynamic processes in nature (50), including rheological behavior of protein solutions. In particular, diffusion in protein solutions is strongly affected by crowding (50); the measured diffusion interaction parameter (kD), a key indicator of diffusivity, varies significantly across mabs with a very similar sequence and structure (10). Diffusion is therefore an important quantity to monitor when evaluating the strength of intermolecular interactions (51).
To evaluate how well our method describes weak nonspecific antibody interactions, we compare mab diffusion coefficients (D) from CG simulations at 60 mg/mL to experimentally determined (kD) values for the same set of molecules (10). Fig. 4 a shows a notable linear correlation between computed diffusion coefficient (D) and experimental diffusion interaction parameters (kD). Excluding only one outlier (mab14) results in a correlation of R2 = 0.8. Fig. 4 b shows an overall good rank correlation between computed D and measured kD. mab14 is an obvious exception to the observed trend; possible reasons for the deviation of mab14 are discussed in the following section.
Figure 4.
(a and b) Correlation and bar plots comparing calculated self-diffusion (D/D0) and measured kD. The D-values are averages over the three independent CG simulation runs at 60 mg/mL. D0 is the single antibody diffusivity in free space; an average value of 4 × 10−7 cm2/s has been reported (10). kD and their SDs of the mean are from (10). (c and d) Given are correlation and bar plots comparing the calculated self-diffusion (D/D0) and measured solution viscosity (η). The D-values are averages over the three independent CG simulation runs at 160 mg/mL. The error bars show the SD from the mean. The viscosities, measured at 175 mg/mL (±5%) by cone and plate rheometry, are taken from (10). The empty circles and patterned columns represent the outlier.
It should be noted that the dilution conditions used in the kD measurements via dynamic light scattering (<20 mg/mL) are challenging to represent in the simulations. In particular, our CG force field was not able to effectively pick up the differences between diffusivity of antibodies when the concentration in the simulations was significantly reduced. We suspect this might be due to the sharp nature of 12-6 LJ potentials, which are exceedingly less effective when intermolecular distances become significantly large, as in dilute conditions. Using a softer van der Waals potential with a more long-range effect can potentially improve the accuracy of the CG models at very low concentrations (21). Another source of inaccuracy could be due to the poor sampling at very low concentrations, in which the number of mabs in the simulation box is relatively smaller. Given the limitation of this method in representing the exact dilute condition, the observed correlation between kD and D/D0 should be regarded as a sanity check rather than a generalized relationship between kD and D/D0 that holds over all other concentrations. Nevertheless, at the concentration we used in the simulations, Fig. 4 a shows that the linear fit of computed D/D0 vs. measured kD is in a good agreement with the classical relationship between in D/D0 and kD (52):
| (23) |
where D0 is the diffusion coefficient at infinite dilution, range 3.9 − 4.8 × 107 cm2/s, and c is the antibody concentration. The intercept of the linear fit in Fig. 4 a is indeed almost equal to 1, and the slope of the fit corresponds to 50 mg/mL, which is close to the concentration used in the simulations (60 mg/mL).
It must be emphasized that the accuracy of a model in predicting kD at dilute conditions does not automatically translate to the same level of accuracy in predicting the viscosity at high concentrations. For example, Document S1. Supporting Materials and Methods, Figs. S1–S3, and Tables S1–S2, Document S2. Article plus Supporting Material a shows that the antibody net charge alone is in a fair correlation with measured kD (R2 = 0.73), which is consistent with previous studies showing that antibody electrostatic attributes (e.g., net charge and pI) correlate well with measured kD (53). At the same time, the correlation between the net charge and viscosity at a high concentration is weak (R2 = 0.28); see Document S1. Supporting Materials and Methods, Figs. S1–S3, and Tables S1–S2, Document S2. Article plus Supporting Material i. This implies that dilute conditions do not necessarily reflect the extent of interactions existing at a high concentration. Note that the correlation between kD at a dilute condition and viscosity at a high concentration is far from perfect; see Fig. S2 b. Because of the substantial excluded volume effects, hydrophobic interactions are more effective at high concentrations; at low concentrations, these interactions decay rapidly with distance; therefore, only long-range electrostatic interactions prevail.
Computed diffusion coefficient inversely correlates with measured viscosity in concentrated solutions
According to the classical Stokes-Einstein equation, there is an inverse relationship between diffusion coefficient and solution viscosity:
| (24) |
where D is the diffusion coefficient, T is the temperature, kB is the Boltzmann constant, R is the hydrodynamic radius of the diffusing species, and η is the solution viscosity. The exact functional relationship between protein diffusion on bulk viscosity can deviate from this simple relation because of the anisotropic shape of antibodies as well as macromolecular crowding effects at high concentrations; yet, an inverse dependence of diffusion coefficient on solution viscosity is generally expected.
To explore the dependence of viscosity on diffusivity, we examined correlations between calculated diffusion coefficients (D/D0) simulated at high concentrations with measured viscosities (η) at high concentrations. Fig. 4 c reveals a good correlation between computed D/D0 and measured viscosity η. A nonlinear fit of the data shows that the relationship between calculated protein diffusivity and measured viscosity is in close agreement with the Stokes-Einstein equation (D/D0 ∝ 1/η). Similarly, a notable rank correlation between calculated D/D0 and measured η is observed from the column plots (Fig. 4 d). Note that the CG force field parametrization procedure incorporated the electrostatic and hydrophobic information from only three mabs (see Materials and Methods), yet the model is able to successfully rank order the remaining molecules not used in the parametrization. This result promises the transferability of the reported model accuracy to external IgG1 test sets formulated in the same solution condition.
The significant variations of computed diffusion coefficients is a resultant effect of intermolecular interactions that contributes to the clustering and higher-order assemblies across different mabs. To better understand the self-association properties of the mabs, the RDF at equilibrium was calculated using the center of mass of individual molecules as reference (mab7 and mab15), Fig. 5 a. The sharp first and second peaks in the RDF of mab15 represent a considerable short-range structure in the solution of mab15. This would suggest the presence of strong intermolecular attractions at high concentrations. For the mab7 solution, the RDF curve is smoother, with much lower first and second peaks. The high-RDF peaks for mab15 compared to mab7 indicates significant local ordering caused by large cluster formations for mab15 relative to mab7, as illustrated in Fig. 5, b and c. Although mab7 molecules are more homogeneously distributed throughout the equilibrated system (Fig. 5 b), allowing faster diffusivity, mab15 CG molecules undergo much stronger intermolecular interactions, leading to the formation of larger mab clusters (Fig. 5 c).
Figure 5.
(a) RDF of mab7 and mab15 calculated from the CG simulations at 160 mg/mL. (b and c) Shown are the equilibrated systems of mab7 and mab15 after 5 μs. The strong electrostatic and hydrophobic complementarities between CG domains in mab15 promote reversible intermolecular interactions, leading to the formation of large mab clusters. In contrast, mab7 exists more in the form of monomers because of its high molecular net charge that results in strong electrostatic repulsion. The figures were generated using VMD (38).
The largest inconsistency between calculated D/D0 and measured η is observed for mab14. Although mab14 is the most viscous molecule in the data set, the CG simulation results suggest a relatively large diffusion for this molecule. This molecule is also an outlier in the correlation plot between D/D0 and kD. The inconsistent behavior of mab14 cannot be described based solely on the analysis of electrostatics and hydrophobicity. In particular, the calculated net charge of mab14 is relatively large (Table S1), which can lead to strong repulsive intermolecular interactions. At the same time, mab14 is predicted to be only moderately hydrophobic (Fig. 1; Table S1). None of these two characteristics point to strong attractive intermolecular interactions, and thus high viscosity, in the concentrated mab14 solution. This observation is consistent with the results found in the work by Yadav et al. (5), showing that the high-concentration viscosity behavior of mab15 (mAb-A in (5)) and mab14 (mAb-H in (5)) cannot be explained based on measured net charges or even on the basis of dilute solution dynamic light scattering measurements. We suspect that other potentially non-native factors, such as structural instabilities or conformational changes in a crowded environment (54), might play a role in determining the high viscosity of mab14. The inevitable errors inherent in the homology modeling procedures (especially in CDR-H3 loop modeling (55)), which deteriorate the accuracy of charge and hydrophobicity calculations, can also contribute to the poor correlation in the case of mab14. This points toward potential limitations of the current approach that relies on single structural conformations obtained from homology modeling and the fact that the CG model is assumed rigid.
Fig. 6 b shows the change in inverse calculated diffusion (1/D) as a function of concentration for mab15, mab5, and mab7. The increasingly high change to self-diffusion (and consequently to 1/D) due to changes in concentration is consistent with the exponential increase in experimentally measured viscosities as a function of concentration (Fig. 6 a). Protein diffusivity has been shown to fall rapidly with increasing concentration (56). An increase in concentration promotes the electrostatic and hydrophobic complementarities between Fab and Fc fragments of antibodies, giving rise to stronger self-associations and enhanced crowding effects. In particular, we found that at extremely high concentrations (>200 mg/mL), highly viscous molecules such as mab15 form a large, one-piece, rigid-like cluster in the simulation that resembles gelation. Indeed, concentrating mab15 to 200 mg/mL and above at low ionic strength does lead to gelation, as observed in the experiments. At such high concentrations, surface-to-surface distances are so small that charge-dipole, dipole-dipole, and hydrophobic interactions can result in strong associations, leading to the formation of large clusters and increased rigidity of the system (5). Overall, these results demonstrate the ability of our CG simulations to qualitatively recapitulate the observed concentration-dependent viscosity behavior of mabs.
Figure 6.
(a) Experimentally measured concentration-dependent viscosity profile for mab15, mab5, and mab7. The lines are used as a guide to the eye and were generated using an exponential fit. (b) The computed inverse translational self-diffusion coefficients (1/D) are shown for mab15, mab5, and mab7 at six simulated concentrations. The diffusion coefficients are provided in units of Å2/ps, which is equivalent to the diffusion coefficients given at 10−5 cm2/s. The lines are used as a guide to the eye and were generated using a polynomial fit. To see this figure in color, go online.
The significance of accounting for hydrophobicity in CG modeling
The self-association characteristics of antibodies cannot be fully described by electrostatics; this would ignore the contributions of hydrophobicity to molecular interactions (57, 58, 59). For instance, consider mab7 and mab5 in Fig. 7 a. No major differences in the electrostatic field or the multipole moments exist to explain why mab5 is nearly fivefold more viscous than mab7 at 175 mg/mL. Comparing the RDF of the hydrophobic tracer molecule for mab5 and mab7 (Fig. 7 b) shows that mab5 is more hydrophobic than mab7. Indeed, CDR residues in the variable region of mab5 are more hydrophobic (based on the Kyte-Doolittle scale (60)) in mab5 compared to the CDRs in mab7 (data not shown), which is consistent with the hydrophobicity scale from cosolvent MD.
Figure 7.
(a) Electrostatic potential for mab15, mab5, and mab7 as a function of angle θ at ϕ = 0 on a circumscribed sphere with radius 100 Å, corresponding to A-A line in Fig. 3. Both mab7 and mab5 show very similar electrostatic potential, whereas mab15 has a significantly different potential. (b) Shown is the RDF of the hydrophobic tracer molecule around the Fv region of mab15, mab7, and mab5 obtained from cosolvent MD. Shown is that mab5 is more hydrophobic than mab7 and mab15. To see this figure in color, go online.
Most QSPR-based viscosity prediction methods have emphasized the significance of hydrophobicity and incorporated it in the scoring functions (13,15,17); however, less attention has been paid to the representation of hydrophobic interactions in CG simulations of antibodies (18, 19, 20, 21). We found that when the variations in the strength of intermolecular interactions due to hydrophobicity were neglected, i.e., the LJ ε-values were fixed to the average of εFv across the data set, the accuracy of the model deteriorated. Specifically, the viscosity for mab5, which is the most hydrophobic molecule in the set, was significantly underestimated, whereas the viscosity of mab6 with a relatively low hydrophobicity was overestimated. As will be discussed in the next section, incorporating the hydrophobicity component is also necessary for predicting the effect of change in salt concentration on viscosity.
In principle, the same CG force field parameterization scheme can be followed to incorporate hydrophobicity scales other than the one (HFv scale) proposed here. To obtain an impression of how well the presented hydrophobicity scale performs, we compared the HFv index from cosolvent MD with two other hydrophobicity scales previously used in the context of viscosity prediction: the structure-based hydrophobic surface area from the MOE package (Document S1. Supporting Materials and Methods, Figs. S1–S3, and Tables S1–S2, Document S2. Article plus Supporting Material a; (15,30)) and the sequence-based hydrophobicity scale used by Sharma et al. (13) (Fig. S3 b). For reference, a comparison between sequence-based hydrophobicity and hydrophobic surface area is also provided (Document S1. Supporting Materials and Methods, Figs. S1–S3, and Tables S1–S2, Document S2. Article plus Supporting Material c). With the exception of two outliers (mab11 and mab6), we found an overall good correlation between the HFv index and hydrophobic surface area (Document S1. Supporting Materials and Methods, Figs. S1–S3, and Tables S1–S2, Document S2. Article plus Supporting Material a). The sequence-based hydrophobicity scale correlated less well with the HFv index (Fig. S3 b). An inspection of the sequences of the outlier molecules reveals the presence of three consecutive aromatic residues in mab11’s CDR (e.g., very hydrophobic) and lack thereof in mab6’s CDR, which is in better agreement with the hydrophobicity scale from cosolvent MD (HFv index). The high hydrophobicity of mab11 may be the reason why the addition of salt does not reduce the viscosity significantly; see Table 1 and the discussion in the next section. Note that cosolvent MD allows for protein conformational changes; therefore, HFv scales calculated based on cosolvent MD are generally expected to be more accurate than sequence- or single-structure-based hydrophobicity scales (46). Nevertheless, the overall good agreement in the comparisons made above suggests that other, faster hydrophobicity scales can alternatively be used, especially when the computational expense of cosolvent MD becomes a bottleneck.
Toward predicting the effect of salt on viscosity
A popular approach to modulate viscosity of concentrated antibody solutions has been through the addition of salt and excipients (61, 62, 63, 64). Increased salt concentration shields charge-charge interactions and should reduce the viscosity of molecules whose primary mode of self-association involves charge attraction. In some molecules, the effect of arginine on viscosity mirrors that seen with inorganic salts; in others, arginine is a superior viscogen (65). Specific interaction between arginine and antibodies has been demonstrated (62), but it is not universal. In practice, salt addition can cause increases or decreases in measured viscosity; see Fig. 8 and Table 1. To assist the eye, the high-salt condition is shaded gray; the decreased viscosity upon salt addition is indicated by circles with a white stripe (Fig. 8 a).
Figure 8.
Change in experimental viscosities due to the change in ionic strength predicted from net charge and hydrophobicity. (a) The x axis and y axis represent the calculated monopole moment and the hydrophobicity scale (HFv), respectively. The circle radii correspond to experimentally measured viscosities at a 175 mg/mL concentration in low-salt (20 mM His-acetate (pH 5.5); solid circle) and high-salt (200 mM arginine-Cl (pH 5.0); dashed circle shaded gray) buffer solutions. (b) shows the product of x and y axes from (a) plotted against the percentage change in the viscosity observed upon salt addition.
Inspection of Fig. 8 a shows that the charge distribution alone (as represented by the first-order moment in this plot) is an insufficient descriptor of this outcome; the combination of hydrophobicity parameter with net charge can be more effective in predicting how the viscosity will respond to changes in ionic strength. A more systematic change in viscosity is observed along the diagonal in Fig. 8 a, in which the monopole and HFv index increase or decrease simultaneously. A simple product of hydrophobicity scale and monopole correlates well with the change in measured viscosity of concentrated mab solutions due to salt addition (Fig. 8 b).
Arginine is clearly unique among salts that affect viscosity. Generically, the ability of salt to increase or decrease viscosity of crowded systems likely stems from the relationship between ionic strength and electrostatic shielding (66) combined with molecule-specific drivers of viscosity at high concentration. Regardless of confounding effects due to the use of arginine to modulate ionic strength, the ability to separate molecules into two categories: those that increase and those that decrease viscosity with increased ionic strength can be put to immediate use in early development. Understanding how or why arginine reduces viscosity selectively for certain molecules and not others will be a focus of future work.
Conclusions
The high viscosity of concentrated mab solutions can pose significant challenges in manufacturing and administration, restricting the advancement of certain mab candidates through development. In silico prediction tools can help screen or optimize high-risk mabs in that respect, especially early during the lead candidate selection with low material availability. Yet, the development of in silico models for viscosity prediction proves challenging because of the limited availability of adequately sized experimental data necessary for model training and testing, especially for knowledge-based and QSPR modeling. In the absence of adequate experimental data, physics-based simulations that require minimal parameterization against the data set can provide a robust and transferable tool for viscosity prediction.
This work shows that physics-based CG simulations with the ability to properly account for electrostatics field and hydrophobicity characters can be useful in rank ordering mabs in terms of the self-association and viscosity behavior. The proposed CG model accounts for the charge asymmetry of mab molecules through incorporating molecular multipole moments up to the octupole order of full-length antibodies to the CG model. A parametrization scheme was proposed to include the hydrophobicity of mabs into the CG models by adjusting the short-range LJ interactions.
We found that the transport properties of the solution calculated from CG simulations, such as the translational self-diffusion coefficient, are in good correlation with experimentally measured diffusion interaction parameter (kD) and viscosity for a large set of 15 antibodies studied here. The CG force field parameters were tuned against the structural properties of only three representative mabs in the data set; yet, the model successfully predicted the viscosity behavior of the remaining molecules not used in the parameterization. This suggests the transferability of the proposed model to external IgG1 data sets in the same formulation condition. We also showed that the evaluation of electrostatic and hydrophobic components from the CG models is useful in predicting the effect of salt on viscosity of mab solutions. The proposed CG model can be further refined to make it a viable framework for simulating more complex formulations such as coformulated and bispecific solutions encountered in modern technical development of antibodies.
It should be noted that the set of antibodies studied here primarily differ in electrostatic and hydrophobicity characters. While carefully accounting for electrostatic and hydrophobic interactions, which are thought to be key determinants of viscosity behavior, this CG simulation method neglects some other potentially important factors contributing to intermolecular interactions in a crowded environment, such as hydrogen bond networks, near-field hydrodynamics (21), specific ion-binding effects (67), or cation-π interactions (68). Moreover, the current CG models were built based on single structural conformations (energy minimized) from homology modeling, and the protonation states of the titratable groups were assumed constant. Using conformational ensembles of the mabs to determine averaged structural properties (such as the protonation states) and assigning them to the initial models for coarse-graining could further improve the accuracy of the method. A more detailed investigation of these factors will be the subject of future studies. While acknowledging the above limitations, this study demonstrates the general applicability of CG simulations toward predicting self-association and viscosity behaviors of highly concentrated antibody solutions.
Author Contributions
S.I., B.T.W., and T.W.P. conceived and designed the study. S.I. implemented the method and performed the simulations. S.I., B.T.W., and T.W.P. analyzed the data. S.I. and B.T.W. wrote the article. All authors reviewed the results and approved the final version of the manuscript.
Acknowledgments
The authors gratefully thank Jasper Lin, Kannan Sankar, Flaviyan Jerome Irudayanathan, Dan Zarraga, and Vikas Sharma for their valuable comments and suggestions.
This work was supported by Genentech, Inc.
Editor: Margaret Cheung.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.04.022.
Contributor Information
Saeed Izadi, Email: izadis@gene.com.
Benjamin T. Walters, Email: walters.benjamin@gene.com.
Supporting Material
References
- 1.Carter P.J. Potent antibody therapeutics by design. Nat. Rev. Immunol. 2006;6:343–357. doi: 10.1038/nri1837. [DOI] [PubMed] [Google Scholar]
- 2.Lobo E.D., Hansen R.J., Balthasar J.P. Antibody pharmacokinetics and pharmacodynamics. J. Pharm. Sci. 2004;93:2645–2668. doi: 10.1002/jps.20178. [DOI] [PubMed] [Google Scholar]
- 3.Reichert J.M. Which are the antibodies to watch in 2013? MAbs. 2013;5:1–4. doi: 10.4161/mabs.22976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Reichert J.M. Antibodies to watch in 2016. MAbs. 2016;8:197–204. doi: 10.1080/19420862.2015.1125583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yadav S., Shire S.J., Kalonia D.S. Factors affecting the viscosity in high concentration solutions of different monoclonal antibodies. J. Pharm. Sci. 2010;99:4812–4829. doi: 10.1002/jps.22190. [DOI] [PubMed] [Google Scholar]
- 6.Yadav S., Laue T.M., Shire S.J. The influence of charge distribution on self-association and viscosity behavior of monoclonal antibody solutions. Mol. Pharm. 2012;9:791–802. doi: 10.1021/mp200566k. [DOI] [PubMed] [Google Scholar]
- 7.Yadav S., Sreedhara A., Shire S.J. Establishing a link between amino acid sequences and self-associating and viscoelastic behavior of two closely related monoclonal antibodies. Pharm. Res. 2011;28:1750–1764. doi: 10.1007/s11095-011-0410-0. [DOI] [PubMed] [Google Scholar]
- 8.Yadav S., Shire S.J., Kalonia D.S. Viscosity behavior of high-concentration monoclonal antibody solutions: correlation with interaction parameter and electroviscous effects. J. Pharm. Sci. 2012;101:998–1011. doi: 10.1002/jps.22831. [DOI] [PubMed] [Google Scholar]
- 9.Lilyestrom W.G., Yadav S., Scherer T.M. Monoclonal antibody self-sssociation, cluster formation, and rheology at high concentrations. J. Phys. Chem. B. 2013;117:6373–6384. doi: 10.1021/jp4008152. [DOI] [PubMed] [Google Scholar]
- 10.Connolly B.D., Petry C., Gokarn Y.R. Weak interactions govern the viscosity of concentrated antibody solutions: high-throughput analysis using the diffusion interaction parameter. Biophys. J. 2012;103:69–78. doi: 10.1016/j.bpj.2012.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Allmendinger A., Fischer S., Mueller R. Rheological characterization and injection forces of concentrated protein formulations: an alternative predictive model for non-Newtonian solutions. Eur. J. Pharm. Biopharm. 2014;87:318–328. doi: 10.1016/j.ejpb.2014.01.009. [DOI] [PubMed] [Google Scholar]
- 12.Nichols P., Li L., Allen M.J. Rational design of viscosity reducing mutants of a monoclonal antibody: hydrophobic versus electrostatic inter-molecular interactions. MAbs. 2015;7:212–230. doi: 10.4161/19420862.2014.985504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sharma V.K., Patapoff T.W., Swartz T.E. In silico selection of therapeutic antibodies for development: viscosity, clearance, and chemical stability. Proc. Natl. Acad. Sci. USA. 2014;111:18601–18606. doi: 10.1073/pnas.1421779112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li L., Kumar S., Boardman D. Concentration dependent viscosity of monoclonal antibody solutions: explaining experimental behavior in terms of molecular properties. Pharm. Res. 2014;31:3161–3178. doi: 10.1007/s11095-014-1409-0. [DOI] [PubMed] [Google Scholar]
- 15.Tomar D.S., Li L., Kumar S. In-silico prediction of concentration-dependent viscosity curves for monoclonal antibody solutions. MAbs. 2017;9:476–489. doi: 10.1080/19420862.2017.1285479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Agrawal N.J., Helk B., Trout B.L. Computational tool for the early screening of monoclonal antibodies for their viscosities. MAbs. 2016;8:43–48. doi: 10.1080/19420862.2015.1099773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chennamsetty N., Voynov V., Trout B.L. Design of therapeutic proteins with enhanced stability. Proc. Natl. Acad. Sci. USA. 2009;106:11937–11942. doi: 10.1073/pnas.0904191106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chaudhri A., Zarraga I.E., Voth G.A. Coarse-grained modeling of the self-association of therapeutic monoclonal antibodies. J. Phys. Chem. B. 2012;116:8045–8057. doi: 10.1021/jp301140u. [DOI] [PubMed] [Google Scholar]
- 19.Chaudhri A.,I.E., Voth G.A. The role of amino acid sequence in the self-association of therapeutic monoclonal antibodies: insights from coarse-grained modeling. J. Phys. Chem. B. 2013;117:1269–1279. doi: 10.1021/jp3108396. [DOI] [PubMed] [Google Scholar]
- 20.Buck P.M., Chaudhri A., Singh S.K. Highly viscous antibody solutions are a consequence of network formation caused by domain-domain electrostatic complementarities: insights from coarse-grained simulations. Mol. Pharm. 2015;12:127–139. doi: 10.1021/mp500485w. [DOI] [PubMed] [Google Scholar]
- 21.Wang G., Varga Z., Swan J.W. Structure and relaxation in solutions of monoclonal antibodies. J. Phys. Chem. B. 2018;122:2867–2880. doi: 10.1021/acs.jpcb.7b11053. [DOI] [PubMed] [Google Scholar]
- 22.Kastelic M., Dill K.A., Vlachy V. Controlling the viscosities of antibody solutions through control of their binding sites. J. Mol. Liq. 2018;270:234–242. doi: 10.1016/j.molliq.2017.11.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kmiecik S., Gront D., Kolinski A. Coarse-grained protein models and their applications. Chem. Rev. 2016;116:7898–7936. doi: 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
- 24.Ingólfsson H.I., Lopez C.A., Marrink S.J. The power of coarse graining in biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014;4:225–248. doi: 10.1002/wcms.1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Skar-Gislinge N., Ronti M., Stradner A. A colloid approach to self-assembling antibodies. Mol. Pharm. 2019;16:2394–2404. doi: 10.1021/acs.molpharmaceut.9b00019. [DOI] [PubMed] [Google Scholar]
- 26.Dear B.J., Bollinger J.A., Truskett T.M. X-ray scattering and coarse-grained simulations for clustering and interactions of monoclonal antibodies at high concentrations. J. Phys. Chem. B. 2019;123:5274–5290. doi: 10.1021/acs.jpcb.9b04478. [DOI] [PubMed] [Google Scholar]
- 27.Roberts C.J., Blanco M.A. Role of anisotropic interactions for proteins and patchy nanoparticles. J. Phys. Chem. B. 2014;118:12599–12611. doi: 10.1021/jp507886r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lošdorfer Božič A., Podgornik R. pH dependence of charge multipole moments in proteins. Biophys. J. 2017;113:1454–1465. doi: 10.1016/j.bpj.2017.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chari R., Jerath K., Kalonia D.S. Long- and short-range electrostatic interactions affect the rheology of highly concentrated antibody solutions. Pharm. Res. 2009;26:2607–2618. doi: 10.1007/s11095-009-9975-2. [DOI] [PubMed] [Google Scholar]
- 30.Chemical Computing Group ULC . Chemical Computing Group ULC; Montreal, Canada: 2018. Molecular Operating Environment (MOE) 2013.08. [Google Scholar]
- 31.Brandt J.P., Patapoff T.W., Aragon S.R. Construction, MD simulation, and hydrodynamic validation of an all-atom model of a monoclonal IgG antibody. Biophys. J. 2010;99:905–913. doi: 10.1016/j.bpj.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Case D., Berryman J., Kollman P. University of California; San Francisco, CA: 2015. AMBER 2015. [Google Scholar]
- 33.Dolinsky T.J., Nielsen J.E., Baker N.A. PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang J., Cieplak P., Kollman P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 35.Søndergaard C.R., Olsson M.H.M., Jensen J.H. Improved treatment of ligands and coupling effects in empirical calculation and rationalization of pKa values. J. Chem. Theory Comput. 2011;7:2284–2295. doi: 10.1021/ct200133y. [DOI] [PubMed] [Google Scholar]
- 36.Li H., Robertson A.D., Jensen J.H. Very fast empirical prediction and rationalization of protein pKa values. Proteins. 2005;61:704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- 37.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 39.Larson R.G. Oxford University Press; New York, NY: 1999. The Structure and Rheology of Complex Fluids. [Google Scholar]
- 40.Anandakrishnan R., Baker C., Onufriev A.V. Point charges optimally placed to represent the multipole expansion of charge distributions. PLoS One. 2013;8:e67715. doi: 10.1371/journal.pone.0067715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Izadi S., Anandakrishnan R., Onufriev A.V. Implicit solvent model for million-atom atomistic simulations: insights into the organization of 30-nm chromatin fiber. J. Chem. Theory Comput. 2016;12:5946–5959. doi: 10.1021/acs.jctc.6b00712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Izadi S., Anandakrishnan R., Onufriev A.V. Building water models: a different approach. J. Phys. Chem. Lett. 2014;5:3863–3871. doi: 10.1021/jz501780a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Izadi S., Onufriev A.V. Accuracy limit of rigid 3-point water models. J. Chem. Phys. 2016;145:074501. doi: 10.1063/1.4960175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stone A. Clarendon Press; Oxford, UK: 1997. The Theory of Intermolecular Forces: International Series of Monographs on Chemistry. [Google Scholar]
- 45.Niu S., Tan M.L., Ichiye T. The large quadrupole of water molecules. J. Chem. Phys. 2011;134:134501. doi: 10.1063/1.3569563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Amrhein S.,S.A., Hubbuch J. Molecular dynamics simulations approach for the characterization of peptides with respect to hydrophobicity. J. Phys. Chem. B. 2014;118:1707–1714. doi: 10.1021/jp407390f. [DOI] [PubMed] [Google Scholar]
- 47.Plimpton S. Fast parallel algorithms for short- range molecular dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 48.Martínez L., Andrade R., Martínez J.M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009;30:2157–2164. doi: 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- 49.Roe D.R., Cheatham T.E. PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 50.Roosen-Runge F., Hennig M., Schreiber F. Protein self-diffusion in crowded solutions. Proc. Natl. Acad. Sci. USA. 2011;108:11815–11820. doi: 10.1073/pnas.1107287108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nishida S., Nada T., Terazima M. Kinetics of intermolecular interaction during protein folding of reduced cytochrome c. Biophys. J. 2004;87:2663–2675. doi: 10.1529/biophysj.104.042531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Harding S.E., Johnson P. The concentration-dependence of macromolecular parameters. Biochem. J. 1985;231:543–547. doi: 10.1042/bj2310543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tomar D.S., Singh S.K., Kumar S. In silico prediction of diffusion interaction parameter (kD), a key indicator of antibody solution behaviors. Pharm. Res. 2018;35:193. doi: 10.1007/s11095-018-2466-6. [DOI] [PubMed] [Google Scholar]
- 54.Yu I., Mori T., Feig M. Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. eLife. 2016;5:e19274. doi: 10.7554/eLife.19274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Maier J.K.X., Labute P. Assessment of fully automated antibody homology modeling protocols in molecular operating environment. Proteins. 2014;82:1599–1610. doi: 10.1002/prot.24576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gros G. Concentration dependence of the self-diffusion of human and Lumbricus terrestris hemoglobin. Biophys. J. 1978;22:453–468. doi: 10.1016/S0006-3495(78)85499-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jones S., Thornton J.M. Principles of protein-protein interactions. Proc. Natl. Acad. Sci. USA. 1996;93:13–20. doi: 10.1073/pnas.93.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bowerman C.J., Ryan D.M., Nilsson B.L. The effect of increasing hydrophobicity on the self-assembly of amphipathic β-sheet peptides. Mol. BioSyst. 2009;5:1058–1069. doi: 10.1039/b904439f. [DOI] [PubMed] [Google Scholar]
- 59.Piazza R. Protein interactions and association: an open challenge for colloid science. Curr. Opin. Colloid Interface Sci. 2004;8:515–522. [Google Scholar]
- 60.Kyte J., Doolittle R.F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 61.Du W., Klibanov A.M. Hydrophobic salts markedly diminish viscosity of concentrated protein solutions. Biotechnol. Bioeng. 2011;108:632–636. doi: 10.1002/bit.22983. [DOI] [PubMed] [Google Scholar]
- 62.Inoue N., Takai E., Shiraki K. Specific decrease in solution viscosity of antibodies by arginine for therapeutic formulations. Mol. Pharm. 2014;11:1889–1896. doi: 10.1021/mp5000218. [DOI] [PubMed] [Google Scholar]
- 63.Kanai S., Liu J., Shire S.J. Reversible self-association of a concentrated monoclonal antibody solution mediated by Fab-Fab interaction that impacts solution viscosity. J. Pharm. Sci. 2008;97:4219–4227. doi: 10.1002/jps.21322. [DOI] [PubMed] [Google Scholar]
- 64.Liu J., Nguyen M.D., Shire S.J. Reversible self-association increases the viscosity of a concentrated monoclonal antibody in aqueous solution. J. Pharm. Sci. 2005;94:1928–1940. doi: 10.1002/jps.20347. [DOI] [PubMed] [Google Scholar]
- 65.Wang S., Zhang N., Qian F. Viscosity-lowering effect of amino acids and salts on highly concentrated solutions of two IgG1 monoclonal antibodies. Mol. Pharm. 2015;12:4478–4487. doi: 10.1021/acs.molpharmaceut.5b00643. [DOI] [PubMed] [Google Scholar]
- 66.Hong T., Iwashita K., Shiraki K. Viscosity control of protein solution by small solutes: a review. Curr. Protein Pept. Sci. 2018;19:746–758. doi: 10.2174/1389203719666171213114919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gokarn Y.R., Fesinmeyer R.M., Brems D.N. Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions. Protein Sci. 2011;20:580–587. doi: 10.1002/pro.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Tilegenova C., Izadi S., Carter P.J. Dissecting the molecular basis of high viscosity of monospecific and bispecific IgG antibodies. MAbs. 2020;12:1692764. doi: 10.1080/19420862.2019.1692764. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.