Abstract
Background
Beta-2 microglobulin (B2M) and cystatin C are novel glomerular filtration markers that have a stronger association with adverse outcomes than creatinine. The B2M-based glomerular filtration rate (GFR) estimating equation was built in 2016. Several new creatinine and cystatin C equations were developed in 2019 in China. However, external validation of these new equations remains to be seen.
Methods
This is a prospective cohort study. The equations were validated in a population totaling 830 participants (median age 62 years). These equations include the B2M-based equation (built in 2016), three CKD-EPI equations (built in 2009 and 2012), three Yang-Du equations (C-CKD-EPIscr, C-CKD-EPIcys, and C-CKD-EPIscr-cys equations, all of which were Chinese-modified CKD-EPI equations developed by Yang et al. in 2019), and a Xiangya equation (a creatinine-based equation built in the Third Xiangya Hospital in 2019). The estimated GFR (eGFR) calculated separately by 8 equations (B2M GFR, CKD-EPIscr, CKD-EPIcys, CKD-EPIscr-cys, C-CKD-EPIscr, C-CKD-EPIcys, C-CKD-EPIscr-cys, and Xiangya equations) was compared with the reference GFR (rGFR) measured by the <sup>99m</sup>Tc-DTPA renal dynamic imaging method. Participants were divided into CKD stage 1–5 specific subgroups. The primary outcomes of this study were bias, precision (interquartile range of difference, IQR), and accuracy (the proportion of eGFR within 30% of rGFR [P30] and root mean square error [RMSE]) of eGFR versus rGFR.
Results
The B2M-based equation was worse than CKD-EPI equations and Yang-Du equations in most outcomes. CKD-EPIscr and C-CKD-EPIscr equations had a larger area under the receiver operating characteristic curve (ROC<sup>AUC</sup>). The CKD-EPIscr equation had the highest sensitivity (83.3%) and the Xiangya equation the highest specificity (89.5%) to diagnose CKD. The bias was the lowest in CKD-EPIcys and C-CKD-EPIscr-cys equations by median and mean difference (1.23 and −1.42, respectively). The Xiangya equation yielded the highest bias by both median and mean difference (8.29 and 6.52, respectively). The C-CKD-EPIscr equation was the most accurate with the highest P30 value (68.1%) and most precise with the lowest IQR (19). The Xiangya equation had the best RMSE (lowest RMSE, 0.56), and gave the best performance in the CKD stage 2 subgroup. The C-CKD-EPIscr-cys equation achieved the lowest bias in CKD stage 3–5 (p = 0.663, 0.104, and 0.130, respectively, compared with rGFR).
Conclusion
The B2M-based equation was worse than CKD-EPI and Yang-Du equations on the whole. CKD-EPIcys and C-CKD-EPIscr-cys equations had the lowest bias, whereas the Xiangya equation yielded the highest bias. The Xiangya equation gave the best performance in the CKD stage 2 subgroup, while the C-CKD-EPIscr-cys equation achieved the lowest bias in CKD stage 3–5. Further work to improve the performance of the GFR estimating equation is needed.
Keywords: Chinese population, Beta-2 microglobulin, Creatinine, Cystatin C, Glomerular filtration rate, Equation
Introduction
Chronic kidney disease (CKD) is recognized as a global public health problem with increasing life loss [1]. According to the Global Burden of Disease Study 2017, CKD was the 16th cause of global deaths in 2016, which would be more severe in 2040 (5th cause) [1], suggesting big health and economic burdens all over the world.
Glomerular filtration rate (GFR) is accepted as the best overall measurement of kidney function and a primary method for screening CKD. Estimated GFR based on serum creatinine (Scr) is routinely used in both general population and CKD patients. However, creatinine-based prediction equations are biased on the fact that creatinine is influenced by muscle mass and diet. Beta-2 microglobulin (B2M) and cystatin C are novel glomerular filtration markers that have a stronger association with adverse outcomes than creatinine [2]. The estimated GFR (eGFR) equation based on B2M was built in 2016 [3]. Several new equations based on creatinine and cystatin C were developed in 2019 in China [4, 5]. However, external validation of these new equations remains to be determined.
To compare the B2M-based equation and the CKD-EPI equation to 2019 new creatinine and cystatin C equations for predicting GFR in Chinese CKD patients, we performed the Early Screening and Diagnosis of CKD (ES-CKD) study to explore the better equation for Chinese CKD patients.
Materials and Methods
Study Design
This is a prospective cohort study (ES-CKD ClinicalTrials.gov number, NCT02841371). A total of 830 Chinese CKD patients were included between July 25, 2014, and July 25, 2018, in Nanjing First Hospital affiliated to Nanjing Medical University of China. The criteria for inclusion and exclusion can be seen in previous work [4, 6].
Primary Outcomes
The primary outcomes of this study were bias, precision, and accuracy of eGFR versus reference GFR (rGFR). Bias was defined as the median or mean results of differences between eGFR and rGFR (eGFR – rGFR). Precision was defined as the interquartile range (IQR) of the differences between eGFR and rGFR. Accuracy was calculated as the proportion of estimated GFR within 30% of rGFR (P30) and root mean square error (RMSE) of mean difference between eGFR and rGFR.
Measurements of Creatinine, Cystatin C, and GFR
The enzymatic method was used to measure Scr concentration, traceable to the National Institute of Standards and Technology creatinine standard reference material (SRM 967). The automated particle-enhanced turbidimetric immunoassay was applied to examine serum B2M and cystatin C. Cystatin C was calibrated against the international certified reference material ERM-DA471. All fasting serum samples were assayed on an Olympus AU5400 autoanalyzer (Olympus Corporation, Mishima, Japan) in accordance with the manufacturer's instructions.
A 99mTc-DTPA renal dynamic imaging measurement by the Gates method was taken as rGFR, because the Gates method is recommended for measurement of GFR by the Nephrology Committee of the Society of Nuclear Medicine [7], which is also deemed as the standard value of GFR in most Chinese eGFR equations [4, 5, 8]. Furthermore, it has a renal clearance rate close to that of inulin with 99% consistency across wide ranges of GFR, confirming that the Gates method and inulin clearance method are similar [5].
Validation of Equations
Eight equations were validated in 830 participants. These equations included the B2M-based equation (built in 2016) [3], three CKD-EPI equations (built in 2009 and 2012) [9, 10],three Yang-Du equations (C-CKD-EPIscr, C-CKD-EPIcys, and C-CKD-EPIscr-cys equations, all of which were Chinese-modified CKD-EPI equations developed by Yang et al. [4] in 2019), and a Xiangya equation (a creatinine-based equation built in the Third Xiangya Hospital in 2019) [5]. The equations are presented in Table 1. Participants were divided into CKD stage 1–5 for subgroup analysis.
Table 1.
Equations to predict glomerular filtration rate
| Name | Sex | Scr | Scys | Equation |
|---|---|---|---|---|
| B2M GFR | 133 × B2M−0.852 | |||
| CKD-EPIscr | Female | ≤0.7 | 144 × (Scr/0.7)−0.329 × 0.993age | |
| >0.7 | 144 × (Scr/0.7)−1.209 × 0.993age | |||
| Male | ≤0.9 | 141 × (Scr/0.9)−0.411 × 0.993age | ||
| >0.9 | 141 × (Scr/0.9)−1.209 × 0.993age | |||
| CKD-EPIcys | Female | ≤0.8 | 133 × (Scys/0.8)−0.499 × 0.996age × 0.932 | |
| >0.8 | 133 × (Scys/0.8)−1.328 × 0.996age × 0.932 | |||
| Male | ≤0.8 | 133 × (Scys/0.8)− 0.499 × 0.996age | ||
| >0.8 | 133 × (Scys/0.8)− 1.328 × 0.996age | |||
| CKD-EPIscr-cys | Female | ≤0.7 | ≤0.8 | 130 × (Scr/0.7)−0.248 × (Scys/0.8)−0.375 × 0.99 5age |
| >0.8 | 130 × (Scr/0.7)−0.248 × (Scys/0.8)−0.711 × 0.995age | |||
| >0.7 | ≤0.8 | 130 × (Scr/0.7)−0.601 × (Scys/0.8)−0.375 × 0.995age | ||
| >0.8 | 130 × (Scr/0.7)−0.601 × (Scys/0.8)−0.711 × 0.995age | |||
| Male | ≤0.9 | ≤0.8 | 135 × (Scr/0.9)−0.207 × (Scys/0.8)−0.375 × 0.995age | |
| >0.8 | 135 × (Scr/0.9)−0.207 × (Scys/0.8)−0.711 × 0.995age | |||
| >0.9 | ≤0.8 | 135 × (Scr/0.9)−0.601 × (Scys/0.8)−0.375 × 0.995age | ||
| >0.8 | 135 × (Scr/0.9)−0.601 × (Scys/0.8)−0.711 × 0.995age | |||
| C-CKD-EPIscr | Female | ≤0.7 | 125 × (Scr/0.7)−0.329 × 0.993age | |
| >0.7 | 125 × (Scr/0.7)−1.209 × 0.993age | |||
| Male | ≤0.9 | 123 × (Scr/0.9)−0.411 × 0.993age | ||
| >0.9 | 123 × (Scr/0.9)−1.209 × 0.993age | |||
| C-CKD-EPIcys | ≤0.8 | 117 × (Scys/0.8)−0.499 × 0.996age | ||
| >0.8 | 117 × (Scys/0.8)−1.328 × 0.996age | |||
| C-CKD-EPIscr-cys | Female | ≤0.7 | ≤0.8 | 116 × (Scr/0.7)−0.248 × (Scys/0.8)−0.375 × 0.995age |
| >0.8 | 116 × (Scr/0.7)−0.248 × (Scys/0.8)−0.711 × 0.995age | |||
| >0.7 | ≤0.8 | 116 × (Scr/0.7)−0.601 × (Scys/0.8)−0.375 × 0.995age | ||
| >0.8 | 116 × (Scr/0.7)−0.601 × (Scys/0.8)−0.711 × 0.995age | |||
| Male | ≤0.9 | ≤0.8 | 120 × (Scr/0.9)−0.207 × (Scys/0.8)−0.375 × 0.995age | |
| >0.8 | 120 × (Scr/0.9)−0.207 × (Scys/0.8)−0.711 × 0.995age | |||
| >0.9 | ≤0.8 | 120 × (Scr/0.9)−0.601 × (Scys/0.8)−0.375 × 0.995age | ||
| >0.8 | 120 × (Scr/0.9)−0.601 × (Scys/0.8)−0.711 × 0.995age | |||
| Xiangya GFR | Male | 2,374.78 × Scr−0.54753 × age−0.25011 | ||
| Female | 2,374.78 × Scr−0.54753 × age−0.25011 × 0.8526126 | |||
10Scr is shown as mg/dL; Scys is shown as mg/L. B2M, beta-2 microglobulin; Scr, serum creatinine; Scys, serum cystatin C; B2M GFR, beta-2 microglobulin-based equation; CKD-EPIscr, serum creatinine-based CKD-EPI equation which was developed in 2009; CKD-EPIcys, cystatin C-based CKD-EPI equation which was developed in 2012; CKD-EPIscr-cys, serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012; C-CKD-EPIscr, CKD-EPIscr equation modified for China which was newly developed in 2019; C-CKD-EPIcys, CKD-EPIcys equation modified for China which was newly developed in 2019; C-CKD-EPIscr-cys, CKD-EPIscr-cys equation modified for China which was newly developed in 2019; Xiangya GFR, serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019.
Statistical Analysis
The paired t test (if the data sets were normally distributed by the Kolmogorov-Smirnov test) or Wilcoxon matched-pairs signed-rank test (if the data sets were not normally distributed by the Kolmogorov-Smirnov test) was carried out to compare eGFR and rGFR. The receiver operating characteristic (ROC) curve was depicted to analyze the performance of the 8 equations. The larger area under the ROC curve (ROCAUC) usually means a better diagnostic value. Bias, precision, and accuracy were applied to assess the performance of each equation. The McNemar test was used to compare the P30 of the equations. Pearson's correlation and classical Bland-Altman plot analyses were performed to compare eGFR with rGFR. Curve fitting was implemented by comparison between eGFR and rGFR for each patient graphically by plotting eGFR and the difference against rGFR (eGFR – rGFR). Data were considered statistically significant at p< 0.05. SPSS software (version 18.0; SPSS, Chicago, IL, USA) was used to perform all statistical analyses.
Results
Characteristics of the Study Population
A total of 830 participants (551 male and 279 female) with CKD were enrolled in this study. Median age, Scr, cystatin C, B2M, and rGFR were 62 years, 107 μmol/L, 1.25 mg/L, 2.66 mg/L, and 55.2 mL/min/1.73 m2, respectively. Participants were divided into different CKD stages. The detailed demographic and clinical characteristics of participants are shown in Table 2.
Table 2.
Characteristics of the study population (n = 830)
| Age, years | 62 (32–85) |
| Gender | |
| Male | 551 (66.4) |
| Female | 279 (33.6) |
| Scr, µmol/L | 107 (49.84–476) |
| Scys, mg/L | 1.25 (0.60–4.17) |
| B2M, mg/L | 2.66 (1.1–13.77) |
| rGFR, mL/min/1.73 m2 | |
| All subjects | 55.2 (10–108.1) |
| CKD stage 1 | 83 (10) |
| CKD stage 2 | 268 (32.3) |
| CKD stage 3 | 353 (42.5) |
| CKD stage 4 | 88 (10.6) |
| CKD stage 5 | 38 (4.6) |
Values for continuous variables are expressed as median (95% confidence interval); values for categorical values are expressed as n (%). Conversion factors for units: Scr in mg/dL to µmol/L, ×88.4. Scr, serum creatinine; Scys, serum cystatin C; B2M, beta-2 microglobulin; rGFR, reference glomerular filtration rate (using the 99mTc-DTPA renal dynamic imaging method).
Overall Performance of the 8 Equations in All Participants
As shown in Table 3, the Pearson correlation coefficients (r) of the 8 equations all indicated significantly positive correlation with rGFR (p < 0.001). CKD-EPIscr-cys and C-CKD-EPIscr-cys equations possessed the same highest correlation coefficient (r = 0.778). Compared with other equations, CKD-EPIscr and C-CKD-EPIscr equations had the same larger ROCAUC (0.870). The C-CKD-EPIscr equation had the highest sensitivity (83.3%), and the C-CKD-EPIscr-cys equation achieved the second highest sensitivity (82.9%). The Xiangya equation had the highest specificity (89.5%) but lowest sensitivity (71.2%) to diagnose CKD. The B2M-based equation had the lowest correlation coefficient (r = 0.626) and the smallest ROCAUC (0.829), and relatively lower sensitivity (73.7%) and specificity (74.1%).
Table 3.
Diagnostic value of 8 estimating equations compared with rGFR
| R | p value | ROCAUC | Sensitivity | Specificity | |
|---|---|---|---|---|---|
| B2M GFR | 0.626 | <0.001 | 0.829 | 73.7 | 74.1 |
| CKD-EPIscr | 0.774 | <0.001 | 0.870 | 76.2 | 82.6 |
| CKD-EPIcys | 0.722 | <0.001 | 0.837 | 76.0 | 74.1 |
| CKD-EPIscr-cys | 0.778 | <0.001 | 0.867 | 76.0 | 81.2 |
| C-CKD-EPIscr | 0.774 | <0.001 | 0.870 | 83.3 | 71.5 |
| C-CKD-EPIcys | 0.722 | <0.001 | 0.837 | 82.7 | 64.1 |
| C-CKD-EPIscr-cys | 0.778 | <0.001 | 0.867 | 82.9 | 71.2 |
| Xiangya GFR | 0.774 | <0.001 | 0.869 | 71.2 | 89.5 |
R, coefficient of relationship between eGFR and rGFR by Pearson correlation analysis; ROCAUC, area under the receiver operating characteristic curve; B2M GFR, beta-2 microglobulin-based equation; CKD-EPIscr, serum creatinine-based CKD-EPI equation which was developed in 2009; CKD-EPIcys, cystatin C-based CKD-EPI equation which was developed in 2012; CKD-EPIscr-cys, serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012; C-CKD-EPIscr, CKD-EPIscr equation modified for China which was newly developed in 2019; C-CKD-EPIcys, CKD-EPIcys equation modified for China which was newly developed in 2019; C-CKD-EPIscr-cys, CKD-EPIscr-cys equation modified for China which was newly developed in 2019; Xiangya GFR, serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019. Correlation coefficients of estimating equation were compared with rGFR.
Performance of the equations is summarized in Table 4, and bias plots of the 8 equations against rGFR are shown in Figure 1. Yang-Du equations tended to underestimate GFR, whereas others overestimated GFR in the CKD patients. The data set rGFR was normally distributed by the Kolmogorov-Smirnov test (p = 0.104), whereas no data sets of eGFR were normally distributed by the Kolmogorov-Smirnov test (p < 0.05), so we performed both the paired t test (comparing their mean difference) and Wilcoxon matched-pairs signed-rank test (comparing their median difference). Of all the 8 equations, CKD-EPIcys possessed the smallest bias (median difference, 1.23 mL/min/1.73 m2). CKD-EPIscr-cys possessed only an inferior difference to the CKD-EPIcys equation with the second smallest ranked bias (1.47 mL/min/1.73 m2). The provided mean difference was used to assess the bias; however, C-CKD-EPIscr-cys achieved the lowest bias (−1.42 mL/min/1.73 m2). The Xiangya equation yielded the highest bias by both median and mean difference (8.29 and 6.52 mL/min/1.73 m2, respectively). The C-CKD-EPIscr equation was the most accurate with the highest P30 value (68.1%; compared with B2M GFR and CKD-EPIscr, p < 0.001; compared with Xiangya GFR, p = 0.014) and the most precise with the lowest IQR (19). C-CKD-EPIscr-cys had the second highest P30 value (63.6%). The Xiangya equation had the best RMSE (lowest RMSE, 0.56). Bland-Altman analysis demonstrated a consistent result (Fig. 1).
Table 4.
Performance of 8 estimating equations compared with rGFR
| Median bias (95% CI) | p value | Mean bias (SD) | p value | Precision (IQR of the difference) | Accuracy P30 | Accuracy (RMSE) | |
| B2M GFR | 3.24 (−29.76 to 40.12) | <0.001 | 3.97 (25.59) | <0.001 | 26 | 57.6 | 0.89 |
| CKD-EPIscr | 3.36 (−24.00 to 36.88) | <0.001 | 4.79 (18.57) | <0.001 | 22 | 62.3 | 0.64 |
| CKD-EPIcys | 1.23(−29.98 to 43.49) | 0.004 | 3.30 (22.04) | <0.001 | 26 | 55.3 | 0.76 |
| CKD-EPIscr-cys | 1.47(−25.42 to 38.10) | <0.001 | 3.63 (19.05) | <0.001 | 23 | 62.4 | 0.66 |
| C-CKD-EPIscr | −3.17(−29.95 to 25.15) | <0.001 | −3.09 (16.97) | <0.001 | 19 | 68.1a | 0.59 |
| C-CKD-EPIcys | −4.76 (−34.57 to 31.24) | <0.001 | −3.91 (19.94) | <0.001 | 25 | 57.0 | 0.69 |
| C-CKD-EPIscr-cys | −2.91 (−29.92 to 30.54) | 0.001 | −1.42 (17.74) | 0.022 | 23 | 63.6b | 0.61 |
| Xiangya GFR | 8.29 (−23.05 to 30.65) | <0.001 | 6.52 (16.18) | <0.001 | 20 | 63.0 | 0.56 |
Median and mean bias, median and mean difference between eGFR and rGFR; SD: standard deviation; P30, the proportion of eGFR within 30% of rGFR; RMSE, root mean square error (of mean difference between eGFR and rGFR); CI, confidence interval; IQR, the inter-quartile range of difference; B2M GFR, beta-2 microglobulin-based equation; CKD-EPIscr, serum creatinine-based CKD-EPI equation which was developed in 2009; CKD-EPIcys, cystatin C-based CKD-EPI equation which was developed in 2012; CKD-EPIscr-cys, serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012; C-CKD-EPIscr, CKD-EPIscr equation modified for China which was newly developed in 2019; C-CKD-EPIcys, CKD-EPIcys equation modified for China which was newly developed in 2019; C-CKD-EPIscr-cys, CKD-EPIscr-cys equation modified for China which was newly developed in 2019; Xiangya GFR, serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019. The Wilcoxon matched-pairs signed-rank test was used to compare the difference between eGFR and rGFR (p value). a the McNemar test was used to compare the P30 of the C-CKD-EPIscr against the P30 of B2M GFR (p < 0.001), CKD-EPIscr equation (p < 0.001), and Xiangya GFR (p = 0.014). b The McNemar test was used to compare the P30 of the C-CKD-EPIscr-cys against the P30 of B2M GFR (p = 0.004).
Fig. 1.
Bias plots intuitively compare the estimated glomerular filtration rate (eGFR) with the reference glomerular filtration rate (rGFR). The difference between eGFR and rGFR was regressed against the mean of rGFR and eGFR. The eGFRs were calculated separately from 8 estimating equations. a B2M GFR: beta-2 microglobulin-based equation. b CKD-EPIscr: serum creatinine-based CKD-EPI equation which was developed in 2009. c CKD-EPIcys: cystatin C-based CKD-EPI equation which was developed in 2012. d CKD-EPIscr-cys: serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012. e C-CKD-EPIscr: CKD-EPIscr equation modified for China which was newly developed in 2019. f C-CKD-EPIcys: CKD-EPIcys equation modified for China which was newly developed in 2019. g C-CKD-EPIscr-cys: CKD-EPIscr-cys equation modified for China which was newly developed in 2019. h Xiangya GFR: serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019. GFR was measured in mL/min/1.73 m2. Horizontal solid lines represent the mean difference and ±1.96 SD.
GFR-Specific Subgroup Performance of the Equations
The data sets of most rGFR subgroups were not normally distributed (by the Kolmogorov-Smirnov test). Therefore, the Wilcoxon matched-pairs signed-rank test was carried out to compare eGFR and rGFR in subgroups (Table 5). The CKD-EPIscr-cys equation had the smallest bias (−3.43 mL/min/1.73 m2; compared with rGFR, p = 0.059) and the highest P30 (90.4%). The Xiangya equation performed fairly well in the CKD stage 1 subgroup with the highest precision (IQR = 15.90) and accuracy (RMSE = 1.35), but the highest bias (−19.68 mL/min/1.73 m2; compared with rGFR, p < 0.001). The Xiangya equation gave the best performance with the highest precision and accuracy in the CKD stage 2 subgroup (IQR = 14.47, P30 = 94%, RMSE = 0.73), with relatively lower bias (−0.98 mL/min/1.73 m2; compared with rGFR, p = 0.236). The B2M and CKD-EPIcys equations possessed similar smaller bias in the CKD stage 2 subgroup (−1.17 and −0.38, respectively). The C-CKD-EPIscr-cys equation achieved the smallest bias in CKD stage 3–5 (median difference −1.53, 1.33, and 0.71 mL/min/1.73 m2, p = 0.663, 0.104, and 0.130, respectively, compared with rGFR), followed by the C-CKD-EPIscr equation (p = 0.141, 0.071, and 0.335, respectively). Concurrently, the C-CKD-EPIcys equation possessed similar smaller bias in the CKD stage 4 subgroup (median difference −1.35 mL/min/1.73 m2, p = 0.514). However, as GFR declined significantly, the accuracy of equations was getting worse, especially in CKD stage 5, while the Xiangya equation acquired the worst P30 (0.0%).
Table 5.
Performance of 8 estimating equations compared with rGFR in GFR subgroups
| Median bias (95% CI) | p value | Precision (IQR of the difference) | Accuracy P30 | Accuracy (RMSE) | |
|---|---|---|---|---|---|
| CKD stage 1 | |||||
| B2M GFR | −17.31 (−52.88 to 37.09) | <0.001 | 30.14 | 69.9 | 5.67 |
| CKD-EPIscr | −5.80 (−37.45 to 25.39) | 0.001 | 19.82 | 89.2 | 1.78 |
| CKD-EPIcys | −4.30 (−42.52 to 36.22) | 0.074 | 29.93 | 83.1 | 2.29 |
| CKD-EPIscr-cys | −3.43 (−34.37 to 29.14) | 0.059 | 27.64 | 90.4 | 1.91 |
| C-CKD-EPIscr | −18.57 (−44.69 to 9.75) | <0.001 | 19.56 | 84.3 | 1.59 |
| C-CKD-EPIcys | −16.78 (−48.94 to 20.24) | <0.001 | 26.62 | 77.1 | 2.03 |
| C-CKD-EPIscr-cys | −13.41 (−39.24 to 20.27) | <0.001 | 24.04 | 83.1 | 1.77 |
| Xiangya GFR | −19.68 (−42.27 to 8.61) | <0.001 | 15.90 | 89.2 | 1.35 |
| CKD stage 2 | |||||
| B2M GFR | −1.17 (−35.21 to 52.36) | 0.963 | 28.74 | 68.7 | 1.46 |
| CKD-EPIscr | 6.41 (−34.39 to 40.35) | <0.001 | 24.51 | 70.1 | 1.21 |
| CKD-EPIcys | −0.38 (−40.96 to 48.17) | 0.363 | 36.75 | 59.0 | 1.50 |
| CKD-EPIscr-cys | 1.73 (−34.09 to 47.65) | 0.036 | 27.18 | 69.0 | 1.29 |
| C-CKD-EPIscr | −4.52 (−39.83 to 25.15) | <0.001 | 20.67 | 76.5 | 1.06 |
| C-CKD-EPIcys | −9.00 (−45.74 to 32.96) | <0.001 | 31.09 | 59.3 | 1.32 |
| C-CKD-EPIscr-cys | −3.95 (−45.74 to 32.96) | 0.006 | 26.02 | 73.5 | 1.17 |
| Xiangya GFR | −0.98 (−23.70 to 23.06) | 0.236 | 14.47 | 94.0 | 0.73 |
| CKD stage 3 | |||||
| B2M GFR | 4.83 (−24.09 to 51.90) | <0.001 | 23.87 | 56.9 | 1.00 |
| CKD-EPIscr | 4.96 (−23.36 to 46.80) | <0.001 | 21.59 | 60.3 | 0.96 |
| CKD-EPIcys | 1.77 (−25.17 to 59.93) | 0.006 | 27.25 | 50.4 | 1.20 |
| CKD-EPIscr-cys | 1.90 (−23.67 to 50.22) | <0.001 | 23.49 | 59.2 | 1.01 |
| C-CKD-EPIscr | −1.43 (−25.80 to 35.67) | 0.141 | 19.24 | 67.7 | 0.83 |
| C-CKD-EPIcys | −4.15 (−28.16 to 47.76) | 0.008 | 23.65 | 55.0 | 1.05 |
| C-CKD-EPIscr-cys | −1.53 (−25.89 to 42.85) | 0.663 | 21.57 | 60.1 | 0.93 |
| Xiangya GFR | 12.33 (−6.29 to 32.92) | <0.001 | 12.77 | 55.0 | 0.54 |
| CKD stage 4 | |||||
| B2M GFR | 9.18 (−7.48 to 40.22) | <0.001 | 22.43 | 37.5 | 1.53 |
| CKD-EPIscr | 4.54 (−12.32 to 52.45) | <0.001 | 22.19 | 29.5 | 1.81 |
| CKD-EPIcys | 2.09 (−14.76 to 33.39) | 0.006 | 18.15 | 44.3 | 1.46 |
| CKD-EPIscr-cys | 2.92 (−13.86 to 40.01) | 0.003 | 17.84 | 34.1 | 1.51 |
| C-CKD-EPIscr | 1.66 (−14.22 to 42.37) | 0.071 | 18.64 | 42.0 | 1.56 |
| 14C-CKD-EPIcys | −1.35 (−16.54 to 26.05) | 0.514 | 17.19 | 46.6 | 1.29 |
| C-CKD-EPIscr-cys | 1.33 (−14.96 to 35.15) | 0.104 | 16.12 | 37.5 | 1.37 |
| Xiangya GFR | 21.84 (6.83 to 45.57) | <0.001 | 15.94 | 5.7 | 1.15 |
| CKD stage 5 | |||||
| B2M GFR | 7.11 (0.85 to 28.06) | <0.001 | 7.09 | 13.2 | 2.06 |
| CKD-EPIscr | 0.65 (−4.65 to 33.12) | 0.036 | 8.01 | 50.0 | 2.48 |
| CKD-EPIcys | 3.26 (−3.04 to 33.88) | <0.001 | 7.30 | 47.4 | 1.87 |
| CKD-EPIscr-cys | 1.89 (−4.33 to 26.39) | 0.005 | 7.44 | 57.9 | 2.03 |
| C-CKD-EPIscr | −0.12 (−5.76 to 27.65) | 0.335 | 7.26 | 47.4 | 2.18 |
| C-CKD-EPIcys | 1.68 (−4.10 to 29.33) | 0.010 | 6.32 | 50.0 | 1.68 |
| C-CKD-EPIscr-cys | 0.71 (−5.19 to 23.64) | 0.130 | 6.88 | 55.1 | 1.84 |
| Xiangya GFR | 18.75 (11.19 to 44.38) | <0.001 | 9.68 | 0.0 | 1.80 |
Median bias, median difference between eGFR and rGFR; P30, the proportion of eGFR within 30% of rGFR; RMSE, root mean square error (of mean difference between eGFR and rGFR). rGFR, reference glomerular filtration rate; CI, confidence interval; IQR, the interquartile range of difference; B2M GFR, beta-2 microglobulin-based equation; CKD-EPIscr, serum creatinine-based CKD-EPI equation which was developed in 2009; CKD-EPIcys, cystatin C-based CKD-EPI equation which was developed in 2012; CKD-EPIscr-cys, serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012; C-CKD-EPIscr, CKD-EPIscr equation modified for China which was newly developed in 2019; C-CKD-EPIcys, CKD-EPIcys equation modified for China which was newly developed in 2019; C-CKD-EPIscr-cys, CKD-EPIscr-cys equation modified for China which was newly developed in 2019; Xiangya GFR, serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019.
Correlation between eGFR and rGFR
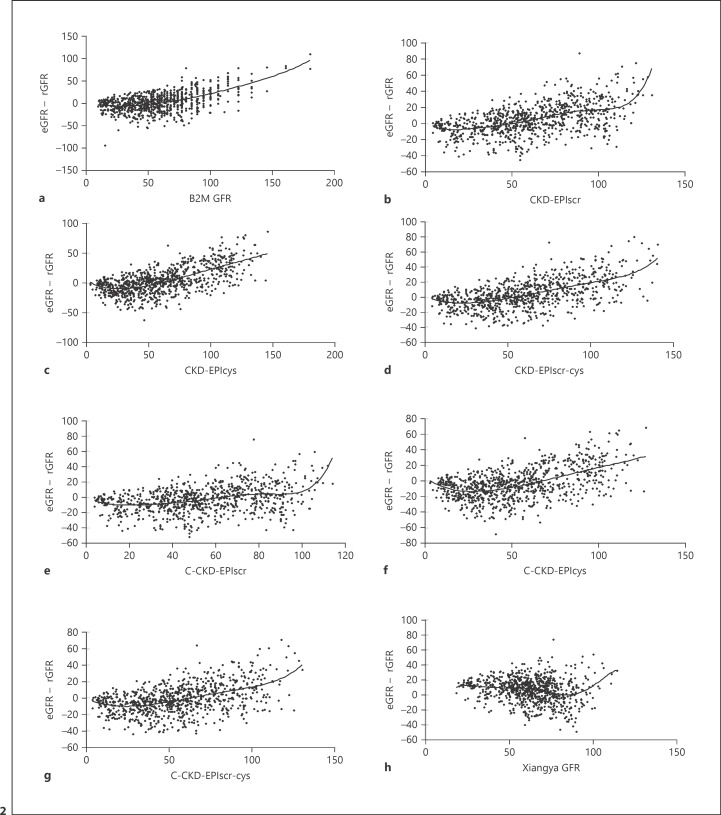
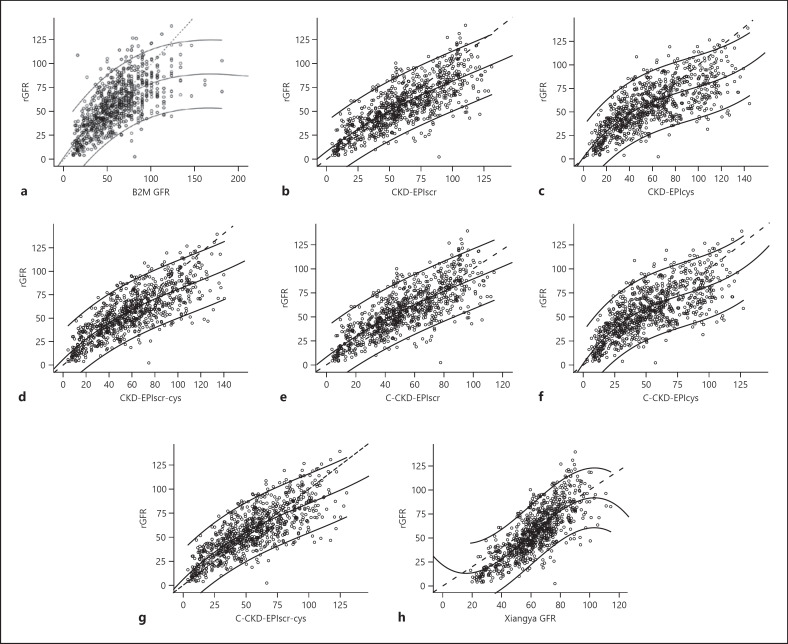
The correlation between eGFR and bias for each equation is shown in Figure 2. The smoothed lines of C-CKD-EPIcys and C-CKD-EPIscr-cys equations were upwardly curving and showed similar slopes to individuals with eGFR 25–100 mL/min/1.73 m2. Plots of eGFR and rGFR are shown in Figure 3. As the fit of the data shows (Fig. 2, 3), smoothed lines of Yang-Du equations were nearer to zero (less biased) compared with other equations. The C-CKD-EPIscr equation was the least biased of all 8 equations with eGFR 0–90 mL/min/1.73 m2.
Fig. 2.
Relationship between estimated glomerular filtration rate (eGFR) and bias, calculated as eGFR – reference GFR (rGFR) in all study participants. Solid horizontal line indicates no difference. Smoothed lines show the fit of the data. a B2M GFR: beta-2 microglobulin-based equation. b CKD-EPIscr: serum creatinine-based CKD-EPI equation which was developed in 2009. c CKD-EPIcys: cystatin C-based CKD-EPI equation which was developed in 2012. d CKD-EPIscr-cys: serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012. e C-CKD-EPIscr: CKD-EPIscr equation modified for China which was newly developed in 2019. f C-CKD-EPIcys: CKD-EPIcys equation modified for China which was newly developed in 2019. g C-CKD-EPIscr-cys: CKD-EPIscr-cys equation modified for China which was newly developed in 2019. h Xiangya GFR: serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019. GFR was measured in mL/min/1.73 m2.
Fig. 3.
Correlation between estimated glomerular filtration rate (eGFR) and reference glomerular filtration rate (rGFR) in all study participants. Smoothed lines show the fit of the data and 95% confidence intervals. Dashed lines indicate no difference. a B2M GFR: beta-2 microglobulin-based equation. b CKD-EPIscr: serum creatinine-based CKD-EPI equation which was developed in 2009. c CKD-EPIcys: cystatin C-based CKD-EPI equation which was developed in 2012. d CKD-EPIscr-cys: serum creatinine and cystatin C-based CKD-EPI equation which was developed in 2012. e C-CKD-EPIscr: CKD-EPIscr equation modified for China which was newly developed in 2019. f C-CKD-EPIcys: CKD-EPIcys equation modified for China which was newly developed in 2019. g C-CKD-EPIscr-cys: CKD-EPIscr-cys equation modified for China which was newly developed in 2019. h Xiangya GFR: serum creatinine-based equation which was newly developed in the Third Xiangya Hospital in China in 2019.
Discussion
A previous study published in the Lancet predicted that CKD would increase from 16th place in 2016 to 5th place in 2040 according to the ranking of fatal diseases worldwide in 2040 (calculated in terms of years of life lost) [1]. We believe that the incidence of CKD has increased rapidly for several reasons. Firstly, the kidney is a silent organ. CKD patients have a long asymptomatic stage before they have obvious clinical symptoms. If they do not undergo the screening test for CKD, it is not easy to be aware of it. A great number of CKD patients develop symptoms in the uremia stage. That is to say, most CKD patients are still unaware. Secondly, the incidence and prevalence of CKD are very high. A study showed that the lifetime incidence of CKD is 59.1% in the USA [11], higher than that of diabetes mellitus, coronary heart disease, and invasive tumors [12]. More seriously, awareness of CKD is only 10.04% from a national cross-sectional survey in China [13]. Probably no such illness permits such a large loss of organ function before symptoms become present as CKD [14]. Therefore, early screening and prevention as well as treatment are extremely urgent.
In this study, we found that the B2M-based equation was worse than CKD-EPI and Yang-Du equations in most outcomes. CKD-EPIscr and C-CKD-EPIscr equations had a larger ROCAUC. The CKD-EPIscr equation had the highest sensitivity (83.3%), followed by the C-CKD-EPIscr-cys equation (sensitivity 82.9%). The Xiangya equation achieved the highest specificity (89.5%) but the lowest sensitivity (71.2%) to diagnose CKD. The lowest biases were in CKD-EPIcys and C-CKD-EPIscr-cys equations by median and mean difference (1.23 and −1.42, respectively). The C-CKD-EPIscr equation had the best precision (lowest IQR) and the highest accuracy (with the highest P30 value of 68.1%). The Xiangya equation had the highest bias by both median and mean difference (8.29 and 6.52, respectively) and the best RMSE (lowest RMSE, 0.56), giving the best performance in the CKD stage 2 subgroup. The C-CKD-EPIscr-cys equation provided the lowest bias in CKD stage 3–5 (p = 0.663, 0.104, and 0.130, respectively, compared with rGFR).
To our knowledge, this is the first study to validate the B2M equation. Inker et al. [3] concluded that the B2M equation provided less accurate GFR estimates than the CKD-EPI equation. They considered that B2M levels may improve GFR estimation in populations with a higher range of GFR compared to a lower range because the CKD-EPI creatinine and cystatin C equations are known to be more accurate in populations with CKD and a lower range of GFR. We confirmed this assumption. The B2M and CKD-EPIcys equations possessed similar smaller bias in the subgroup of GFR 60–89 mL/min/1.73 m2. But the B2M equation still had a larger bias and worse precision and accuracy in the subgroup of greater than GFR 90 mL/min/1.73 m2.
B2M and cystatin C are both low-molecular-weight serum proteins and candidates of endogenous filtration markers that are less affected by non-GFR determinants compared with creatinine [15]. The concordant pattern between B2M and cystatin C levels brings about high correlations between them, even after adjustment for their correlation with rGFR, implying that B2M level can be a replacement for cystatin C level if cystatin C is not available [15].
Both median and mean differences were used to detect the bias between eGFR and rGFR in this study (Table 4). When the sample size is large enough (n >30), then the underlying distribution does not need to be Gaussian to apply parametric tests for hypothesis testing. This is what the central limit theorem is all about [16]. When the distribution is not Gaussian, then descriptive statistics should be presented, using median and IQR instead of mean and standard deviation, but hypotheses can still be tested using parametric tests when the sample size is large enough. Furthermore, compared with the nonparametric test, the parametric test has a higher statistical efficiency. For this reason, it can be concluded that the bias of the C-CKD-EPIscr-cys equation is smaller than those of CKD-EPIcys and CKD-EPIscr-cys equations. When the mean difference was added to compare bias in CKD stage 1–5 subgroups, we got similar results (data not shown).
The differences in equation performance can be explained by differences in the development and validation populations. CKD-EPI equations demonstrated better performance at higher GFR, as they were developed in a broader cohort with better kidney function (68 mL/min/1.73m2). Yang-Du equations provided lower bias in CKD stage 3–5 due to the fact that they were developed in median-measured GFR at 54 mL/min/1.73m2 in the development sample, and at 38 mL/min/1.73m2 in the validation data set. The Xiangya equation gave the best performance in the CKD stage 2 subgroup because the mean-measured GFR in its development sample was 71 mL/min/1.73 m2. Although the Xiangya equation is based on a large sample size, this equation developer excluded participants with Scr >700 μmol/L, and the number of participants in CKD stage 5 was unknown [5]. For this reason, the Xiangya equation acquired the worst P30 (0.0%) in CKD stage 5.
There are also some limitations of this study. Firstly, unlike creatinine and cystatin C, B2M has not yet become a standardized test internationally, although B2M assays are widely available and relatively inexpensive. Secondly, although thought to be less influenced by age, sex, race, muscle mass, and medications than Scr, factors other than GFR also influenced serum B2M, such as lymphoproliferative disorders and inflammatory conditions [17]. Thirdly, all study participants had CKD. Optimal equations are developed in diverse populations so that the estimates can be broadly applied to people with and without known CKD, across a wider range of age and race.
In conclusion, this study demonstrated that, overall, the B2M-based equation was worse than CKD-EPI and Yang-Du equations. CKD-EPIcys and C-CKD-EPIscr-cys equations had the lowest bias. On the contrary, the Xiangya equation yielded the highest bias and gave the best performance in the CKD stage 2 subgroup. The C-CKD-EPIscr-cys equation had the lowest bias in CKD stage 3–5, followed by the C-CKD-EPIscr equation. Considering the accuracy of the entire range, combining B2M, creatinine, and cystatin C into an equation is assumed to be essential.
Statement of Ethics
This study was approved by the Institutional Review Board of Nanjing First Hospital affiliated to Nanjing Medical University, at which the studies were conducted (IRB approval No. 86-025-52271039-21). The research was conducted in accordance with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards. All subjects (or their parents or guardians) gave their written informed consent.
Disclosure Statement
The authors have no conflicts of interest to declare.
Funding Sources
This work was supported by grants from the Chinese Society of Nephrology (14050430580) and High-level Talents of the Fifteenth “Six Talents Peaks” in Jiangsu Province (WSN-113). The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author Contributions
X.D. was the research designer, administrator, and funder, and was responsible for obtaining the data and preparing communications with participating centers and the data monitoring committee. X.D., L.Y., and B.P. analyzed the data and advised on statistical issues. L.Y. and X.S. were research nurses responsible for recruitment and return of data. All authors helped to write the report and commented on the manuscript.
References
- 1.Foreman KJ, Marquez N, Dolgert A, Fukutaki K, Fullman N, McGaughey M, et al. Forecasting life expectancy, years of life lost, and all-cause and cause-specific mortality for 250 causes of death: reference and alternative scenarios for 2016-40 for 195 countries and territories. Lancet. 2018 Nov;392((10159)):2052–90. doi: 10.1016/S0140-6736(18)31694-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Astor BC, Shafi T, Hoogeveen RC, Matsushita K, Ballantyne CM, Inker LA, et al. Novel markers of kidney function as predictors of ESRD, cardiovascular disease, and mortality in the general population. Am J Kidney Dis. 2012 May;59((5)):653–62. doi: 10.1053/j.ajkd.2011.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Inker LA, Tighiouart H, Coresh J, Foster MC, Anderson AH, Beck GJ, et al. GFR Estimation Using β-Trace Protein and β2-Microglobulin in CKD. Am J Kidney Dis. 2016 Jan;67((1)):40–8. doi: 10.1053/j.ajkd.2015.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yang M, Zou Y, Lu T, Nan Y, Niu J, Du X, et al. Revised Equations to Estimate Glomerular Filtration Rate from Serum Creatinine and Cystatin C in China. Kidney Blood Press Res. 2019;44((4)):553–64. doi: 10.1159/000500460. [DOI] [PubMed] [Google Scholar]
- 5.Li DY, Yin WJ, Yi YH, Zhang BK, Zhao J, Zhu CN, et al. Development and validation of a more accurate estimating equation for glomerular filtration rate in a Chinese population. Kidney Int. 2019 Mar;95((3)):636–46. doi: 10.1016/j.kint.2018.10.019. [DOI] [PubMed] [Google Scholar]
- 6.Yang M, Xu G, Ling L, Niu J, Lu T, Du X, et al. Performance of the creatinine and cystatin C-based equations for estimation of GFR in Chinese patients with chronic kidney disease. Clin Exp Nephrol. 2017 Apr;21((2)):236–46. doi: 10.1007/s10157-016-1273-9. [DOI] [PubMed] [Google Scholar]
- 7.Blaufox MD, Aurell M, Bubeck B, Fommei E, Piepsz A, Russell C, et al. Report of the Radionuclides in Nephrourology Committee on renal clearance. J Nucl Med. 1996 Nov;37((11)):1883–90. [PubMed] [Google Scholar]
- 8.Liu X, Li NS, Lv LS, Huang JH, Tang H, Chen JX, et al. A comparison of the performances of an artificial neural network and a regression model for GFR estimation. Am J Kidney Dis. 2013 Dec;62((6)):1109–15. doi: 10.1053/j.ajkd.2013.07.010. [DOI] [PubMed] [Google Scholar]
- 9.Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF, 3rd, Feldman HI, et al. CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009 May;150((9)):604–12. doi: 10.7326/0003-4819-150-9-200905050-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, Greene T, et al. CKD-EPI Investigators Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med. 2012 Jul;367((1)):20–9. doi: 10.1056/NEJMoa1114248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grams ME, Chow EK, Segev DL, Coresh J. Lifetime incidence of CKD stages 3-5 in the United States. Am J Kidney Dis. 2013 Aug;62((2)):245–52. doi: 10.1053/j.ajkd.2013.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vassalotti JA, Piraino B. Loss of kidney function with aging is a patient safety hazard. Am J Kidney Dis. 2013 Aug;62((2)):217–9. doi: 10.1053/j.ajkd.2013.06.005. [DOI] [PubMed] [Google Scholar]
- 13.Wang F, Zhang L, Wang H, China National Survey of CKD Working Group Awareness of CKD in China: a national cross-sectional survey. Am J Kidney Dis. 2014 Jun;63((6)):1068–70. doi: 10.1053/j.ajkd.2014.01.012. [DOI] [PubMed] [Google Scholar]
- 14.Sherwood M, McCullough PA. Chronic kidney disease from screening, detection, and awareness, to prevention. Lancet Glob Health. 2016 May;4((5)):e288–9. doi: 10.1016/S2214-109X(16)30049-3. [DOI] [PubMed] [Google Scholar]
- 15.Liu X, Foster MC, Tighiouart H, Anderson AH, Beck GJ, Contreras G, et al. CRIC (Chronic Renal Insufficiency Cohort) Study Investigators Non-GFR Determinants of Low-Molecular-Weight Serum Protein Filtration Markers in CKD. Am J Kidney Dis. 2016 Dec;68((6)):892–900. doi: 10.1053/j.ajkd.2016.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kwak SG, Kim JH. Central limit theorem: the cornerstone of modern statistics. Korean J Anesthesiol. 2017 Apr;70((2)):144–56. doi: 10.4097/kjae.2017.70.2.144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vart P, Grams ME. Measuring and Assessing Kidney Function. Semin Nephrol. 2016 Jul;36((4)):262–72. doi: 10.1016/j.semnephrol.2016.05.003. [DOI] [PubMed] [Google Scholar]