A System for Automated Determination of Perioperative Patient Acuity

Abstract

The widely used American Society of Anesthesiologists Physical Status (ASA PS) classification is subjective, requires manual clinician review to score, and has limited granularity. Our objective was to develop a system that automatically generates an ASA PS with finer granularity by creating a continuous ASA PS score. Supervised machine learning methods were used to create a model that predicts a patient’s ASA PS on a continuous scale using the patient’s home medications and comorbidities. Three different types of predictive models were trained: regression models, ordinal models, and classification models. The performance and agreement of each model to anesthesiologists were compared by calculating the mean squared error (MSE), rounded MSE and Cohen’s Kappa on a holdout set. To assess model performance on continuous ASA PS, model rankings were compared to two anesthesiologists on a subset of ASA PS 3 case pairs. The random forest regression model achieved the best MSE and rounded MSE. A model consisting of three random forest classifiers (split model) achieved the best Cohen’s Kappa. The model’s agreement with our anesthesiologists on the ASA PS 3 case pairs yielded fair to moderate Kappa values. The results suggest that the random forest split classification model can predict ASA PS with agreement similar to that of anesthesiologists reported in literature and produce a continuous score in which agreement in accurately judging granularity is fair to moderate.

Introduction

Preoperative assessment is important in managing patient flow, allocating resources, reducing case cancellations and improving patient safety. The American Society of Anesthesiologists Physical Status (ASA PS) classification is the most widely used system for evaluating pre-operation surgical patients. The current system was adopted by the American Society of Anesthesiologists in 1962 [1] and ranges from 1 (healthy) to 5 (moribund) with a sixth class for declared brain dead patients. The ASA PS classification correlates with outcomes, operating time, hospital length of stay, postoperative infection rates, and morbidity rate following various types of surgery [2–7].

There is considerable variation in the application of the ASA PS classification [2]. It is a subjective scale with moderate inter-rater reliability; experiments with clinicians produce Cohen’s Kappa scores ranging from 0.40 to 0.64 [8–11]. Because determining ASA PS requires clinician assessment and review, automatically generating this value is a challenge. The ASA PS is interpretable because clinicians can determine factors for classification, and so it is feasible for machine learning methods to model their decisions and possibly provide transparency. If assigning ASA PS could be automated, the assessment process could be effectively scaled. With this in mind, we wanted to build a system with practical utility for practicing physicians by taking data that is available (i.e., diagnosis codes, medication lists) and translating it into a scale that is well recognized and understood (ASA PS).

An ASA PS prediction model could identify high and low risk patients for the purpose of identifying patients who require additional preoperative assessment. Moreover, a computational model can also extend the scores into a finer-grained scale than its current integer-labeled classes. This extension may help in assessing patients within the large clinical range covered by ASA PS 2 and ASA PS 3 classes, which we focus on. With a more granular scale, we can draw a finer line for triage into/out of the preoperative clinic. In addition, we can identify and investigate the higher acuity patients more easily.

Prior work in smaller patient populations has demonstrated that decision tree classifiers, multilayer perceptrons, Naïve Bayes classifiers, and support vector machines can produce accurate ASA PS classifications [12,13]. Karpagavalli et al. produce a model trained on 362 cases that can predict ASA PS 1–3 with 97% accuracy. Lazouni et al. produce a model trained on 898 cases that predicts ASA PS 1–4 with 93% accuracy. While these studies’ models achieve high accuracy, they do not fully address class imbalance between ASA PS classes which can bias accuracy. These approaches have not been attempted with the breadth of data available in a large perioperative environment. Additionally, the prior efforts have attempted to reproduce the integer ASA PS classifications rather than extend them to a finer scale. With the amount of data available and machine learning methods, it’s possible not only to automate the process of ASA PS classification but extend and improve the score.

Our objective is to develop an automated, scalable system that uses preoperative data to provide useful information to practicing physicians on the familiar ASA PS scale. We investigate the potential of providing finer granularity to those scores and compare the predictions to assessments by anesthesiologists.

Materials and Methods

Study design

Approval for this study was obtained from the Vanderbilt University Human Research Protection Program with a waiver of informed consent. This allowed us to use retrospective anesthesiology case data and patient medical data. We had two main aims in this study: 1) to build a model that predicts ASA PS as well as an anesthesiologist, and 2) to provide additional information to the anesthesiologists through a more granular ASA PS score. A binary classification model was trained to predict ASA PS and used to select the best features, which were then used to train subsequent regression models that predict a continuous ASA PS for surgical patients.

Data collection

The data used to train and test our classifiers came from Vanderbilt’s Perioperative Data Warehouse. We identified all anesthetic cases with an ASA PS 1–5 available prior to the implementation of International Classification of Diseases, Tenth Revision, Clinical Modification (ICD-10-CM) in October 2015, resulting in 419,321 cases. Case classifications are assigned preoperatively by an anesthesiologist after evaluating the patient in person, including their medical history, surgical history, preoperative medications, physical exam, and entire medical record. The ASA PS is a preoperative assessment, so the model should only have access to data available at that time.

We extracted ASA PS, age, body mass index (BMI), prior surgeries, surgical service, preoperative medications, and comorbidity diagnoses derived from inpatient International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) discharge records that were coded as diagnosed on or before the day of surgery. Additionally, ICD-9-CM diagnoses assigned in the outpatient setting before the day of surgery were extracted from our Enterprise Data Warehouse, a data warehouse of patient data. For all patients, we would have age, BMI and surgical service, as part of scheduling surgery. If the patient had no records of medications or ICD-9-CM codes, they were still included in the model, as it is possible to have patients that didn’t need medications or didn’t have previous ICD-9-CM history.

The ASA PS assigned by the attending anesthesiologist on the day of surgery was used as the label, or gold standard (Figure 1). A 10% holdout dataset was set aside to evaluate the final classifiers, ensuring no bias in evaluation.

Fig. 1.

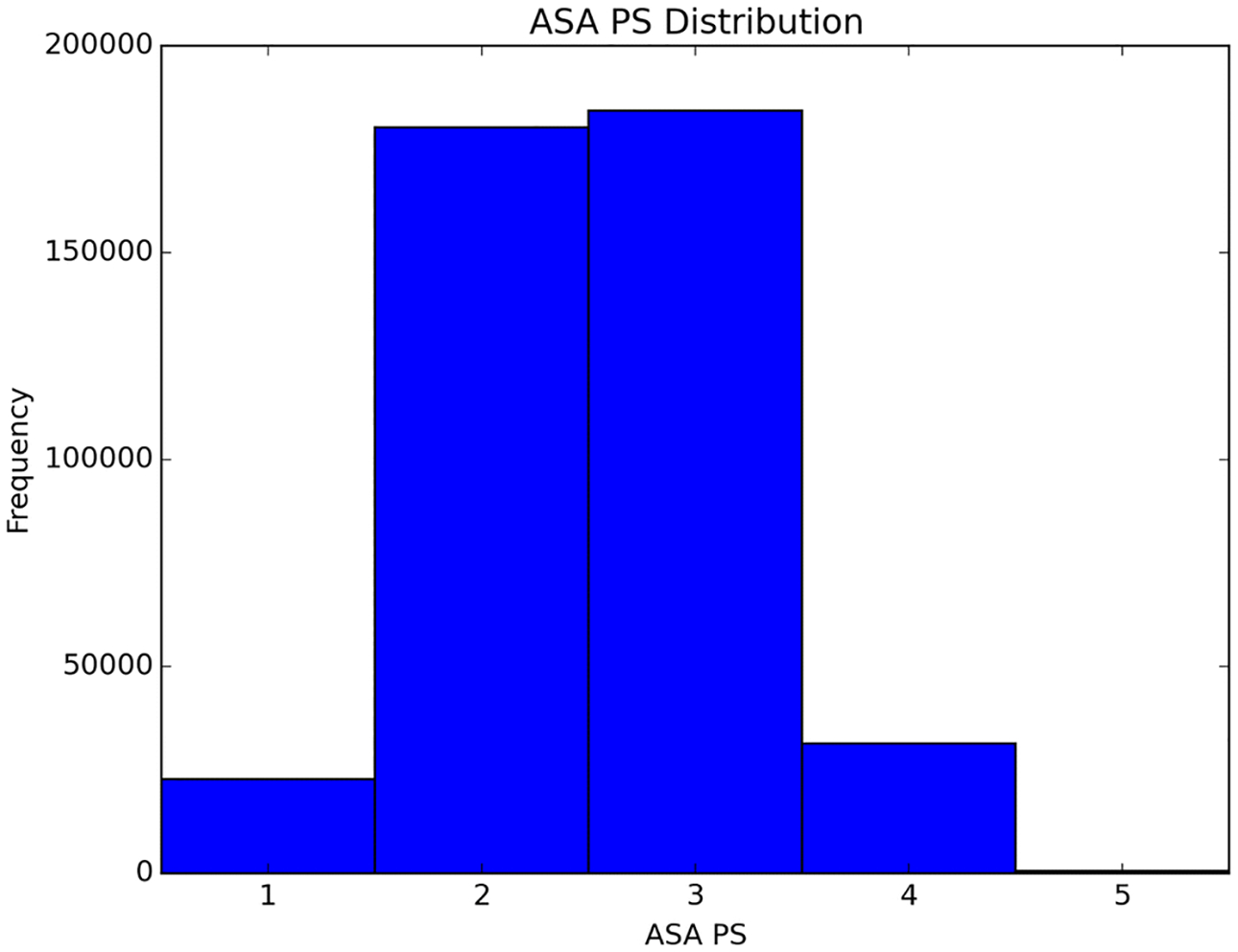
Distribution of ASA PS in the data. Cases with ASA PS 2 and 3 dominate the distribution

Feature analysis and selection

Classes (or categories) of features were chosen based on anesthesiologists’ input and preliminary data analysis (Appendix A). We summarize the data by calculating the median and interquartile range of age and BMI, as well as the mean number of inpatient ICD-9-CM diagnoses codes, outpatient ICD-9-CM diagnosis codes, and medications per patient (Table 1).

Table 1.

Summary statistics for dataset separated by American Society of Anesthesiology Physical Status (ASA PS) class.

Class	ASA PS 1	ASA PS 2	ASA PS 3	ASA PS 4	ASA PS 5
Number	22765	180251	184284	31409	612
Age median	23	41	56	59	53
Age interquartile range	26	32	26	23	31
BMI median	22.87	26.23	27.55	27.17	26.57
BMI interquartile range	8.03	9.11	10.41	10.01	9.70
Median inpatient diagnoses per patient	2	4	7	9	10
Inpatient diagnoses interquartile range	3	4	7	6	5
Median outpatient diagnoses per patient	4	5	8	9	9
Outpatient diagnoses interquartile range	4	6	7	6	5
Median medications per patient	2	3	5	6	6
Medications interquartile range	2	3	4	4	5

In the preliminary data analysis, data were normalized by the frequency of ICD-9-CM chapter (top level category in the hierarchy of ICD-9-CM codes) and ASA PS, and used to calculate the pointwise mutual information (PMI) of inpatient and outpatient ICD-9-CM chapters with ASA PS. PMI quantifies the strength of pairwise associations, and gives insight into the selection features that are predictive of ASA PS.

Different structures for the medication and ICD-9-CM features incorporating temporality and hierarchy were tested. Different combinations of feature classes were evaluated to determine a final combined classifier, or classifier using a combination of the different feature classes (Appendix A). The combined classifier was compared to classifiers using a single feature class (such as age alone) to aid in analyzing prediction involvement. Performance was measured with 5-fold cross validation and the average area under the receiver operating characteristic curve (ROC AUC), and used to select the features for the final combined classifier.

Classification model

Python’s scikit-learn [14] and lasagna [15] packages were used to develop the classifiers for predicting ASA PS. We tuned the model hyper-parameters using hyperopt [16].

Initially, we separated the scores into two classes: ASA PS 1&2, and ASA PS 3&4&5, simplifying our problem into a binary classification problem. We do this because the most difficult distinction is between the ASA PS classes 2 and 3, and that cut point is one in which some healthcare systems use to decide anesthesia involvement. We used this simplified problem (which uses fewer computational resources) to select the feature classes most likely to be informative for the ASA PS prediction. The set of best feature classes in the simplified problem is only an approximation to the best set in the full problem, but we believe the accuracy loss is likely to be minimal, given that the vast majority of instances are either ASA PS 2 or 3, and that we are selecting full feature classes rather than individual features.

The supervised machine learning techniques that we tested include logistic classification, k-nearest neighbors, random forest, deep neural networks (DNN) and a hybrid network consisting of both deep and convolutional neural networks (Appendix B).

We evaluated the performance of the binary classifiers by measuring the mean AUC from 5-fold cross validation and calculating the AUC on the holdout dataset.

Continuous model

We used the features from our best classification model to develop models that output ASA PS on a continuous scale. We can develop this continuous score from data with ordinal labels because machine learning models predict values on a continuous/probability scale. These predicted values capture the model’s uncertainty in the predicted label, and we can use this to develop a continuous ASA PS scale.

For these models, we removed the ASA PS 5 cases because we observed that those cases are relatively unpredictable with retrospective data. In addition, these cases are not hard to determine and account for a small percentage of all ASA PS cases. We tested linear, random forest and deep neural network regression models, the ordinal regression model, and a model consisting of three binary classifiers (split classification model). This split classification model first classifies the cases into 1&2 vs 3&4, then uses two more binary classifiers to classify cases into 1 vs 2 or 3 vs 4.

The linear, random forest and DNN regression models output a continuous score, but the ordinal regression and split classification models output ordinal scores. To construct a continuous score for the ordinal model, we used the underlying ridge model outputs. To construct a continuous score for the split classification model, we linearly mapped the probabilistic outputs (range of 0 to 1) of the final 1 vs 2 and 3 vs 4 classifiers onto the ranges [0.5, 2.5] and [2.5, 4.5] to correspond to the appropriate ASA PS. For these models, we oversampled the data to ensure that ASA PS classes 1 and 4 have an equal impact to ASA PS classes 2 and 3.

For comparison, we also developed models with the original dataset as the training set (not oversampled). We did this because we found that while the models with the oversampled training set produce an even probability distribution over the ASA PS, the mean squared error (MSE) increases as a result of the class imbalance in the holdout set.

We evaluated the performance of the continuous models by measuring the MSE of both the continuous and ordinal outputs on the 5-fold cross validated training set and on the holdout dataset. The ordinal MSE scores are calculated using the already existing ordinal results or the rounded continuous score (for the regression models). Mean squared error is the traditional method to evaluate continuous outputs, but because the models were developed with ordinal labels, we calculated the ordinal MSE as well.

The models trained on the original dataset are also evaluated on the holdout set by calculating the MSE of the continuous and mapped ordinal outputs.

Cohen’s Kappa

The Cohen’s Kappa statistic has been historically used for comparing inter-rater ASA PS [8–11] It is a statistic that measures agreement beyond that expected by chance. In order to analyze the effect of the variability between raters, we calculated the Cohen’s Kappa with scikit-learn for inter-rater agreement between our model and the raw scores. We use the unweighted Kappa measure in order to compare values to literature, which typically uses the unweighted Kappa. We treated our model as one rater and the raw scores as the other rater. Anesthesiologists have moderate agreement for ASA PS under the unweighted Kappa [7–9], so moderate agreement of our model with the raw scores is comparable to human performance under this measure.

However, Cohen’s Kappa is a problematic measure of agreement in this scenario because small differences in the thresholds at which raters divide their continuous mental models of patient acuity into the discrete categories of ASA PS may cause large changes in the statistic [17]. To allow for historical comparison while minimizing this problem, we adjusted the thresholds of our model (e.g. adjust ASA PS 1 to 1.2) using grid search to optimize the statistic when comparing to clinician raters.

Granularity evaluation

To evaluate the finer granularity provided by the continuous score, we randomly selected 50 pairs of ASA PS 3 cases and had two anesthesiologists (JWE, JPW) determine which case had higher acuity, i.e., closer to ASA PS class 4. We predicted the continuous ASA PS score for each case using our model and determined which case in each pair had higher acuity. We then compared the results of our model on these cases to the anesthesiologists by calculating the fraction of correct rankings and the Kappa measure. We used ASA PS 3 cases because it is one of the classes with higher variability within the class.

Sensitivity analysis

To test the sensitivity of the model’s use of ICD-9-CM diagnoses on the day of surgery, we train and test the model with the best Kappa (random forest split classification model) on the set of data excluding the diagnoses made on the surgery day. We perform this analysis because of possible inclusion of diagnoses present during the encounter (which can be coded on the day of surgery).

Results and discussion

In this study, we designed a system that predicted a continuous ASA PS. Our goal was to develop a model that performs similarly to an anesthesiologist, while providing additional granularity to aid in identifying high risk patients. The final model predicts ASA PS with agreement similar to anesthesiologists and fair agreement on a more granular scale.

Preliminary data analysis

The preliminary data analysis showed that different ICD-9-CM chapters have differing correlations of various strengths with the ASA PS classes (Figure 2). For example, diseases of the blood and blood-forming organs have a negative correlation with ASA PS 1 and 2 and a positive correlation with ASA PS 4 and 5. The analysis indicated that the ICD-9-CM codes were likely to be strong predictors of ASA PS.

Fig. 2.

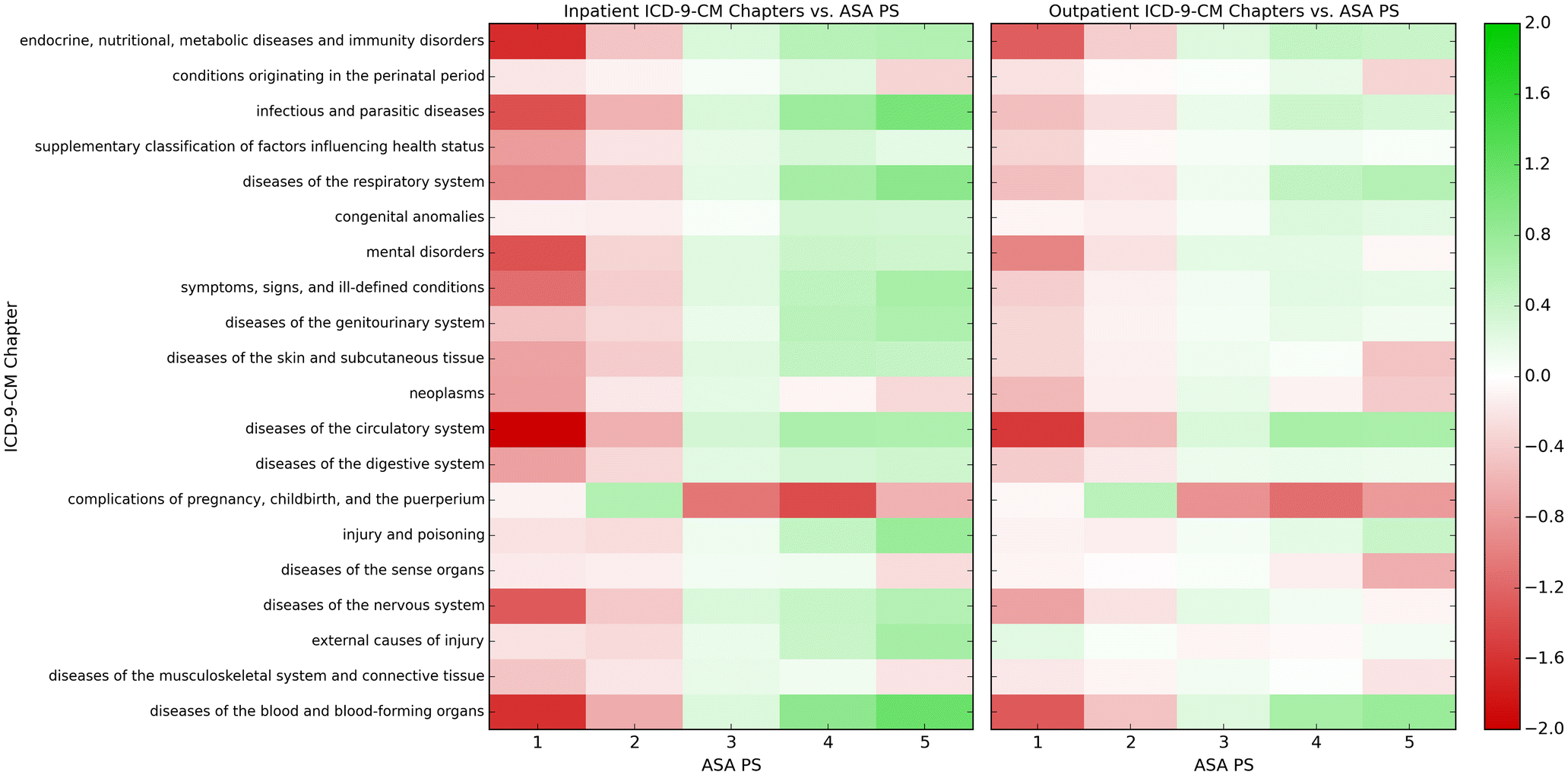
Pointwise mutual information of inpatient and outpatient ICD-9-CM chapters with ASA PS. Green indicates a positive correlation, while red indicates a negative correlation

Classification model

The goal of the binary classification models was to predict ASA PS 1&2 vs ASA PS 3&4. The best combination of feature classes was: age, BMI, surgical service, top-level medications, inpatient ICD-9-CM hierarchy, and outpatient ICD-9-CM chapters. The best combination of feature classes resulted in the highest AUCs for each combined classifier at 0.860 for logistic classification, 0.817 for k-nearest neighbors and 0.881 for random forests (Appendix C). The ICD-9-CM chapter counts, ICD-9-CM hierarchy, and temporal ICD-9-CM chapter counts outperformed the other structures for ICD-9-CM codes significantly.

We found that the individual medication and ICD-9-CM code features did not improve performance, while top level categories in the hierarchy for both performed the best (i.e. using the “Blood” medication category instead of clopidogrel (Plavix), or the “Circulatory System” chapter instead of ICD-9-CM 394.0 (Mitral Stenosis)). In fact, we observed that more detailed categories (for example, each ICD-9-CM code as a feature compared to the ICD-9-CM chapters) caused overfitting in the models and produced a lower AUC. Adding temporality to the ICD-9-CM features did not increase the performance of any of the models significantly. This implies that either occurrence is more important than temporality, or temporality could not be sufficiently represented. This may be why the hybrid deep and convolutional neural network (which uses temporal patterns) did not perform better than the fully-connected deep neural network (which does not).

We found that medications did not have as high of an impact on prediction as expected. We speculate that this is due to overlapping information content between preoperative medications and ICD-9-CM diagnoses. For example, knowing that the patient uses long-acting bronchodilators and inhaled corticosteroids may carry almost the same predictive information as knowing that the patient has a diagnosis code for chronic obstructive pulmonary disease.

The best machine learning classifier was the random forest, which achieved an AUC of 0.884 on the holdout dataset (Table 2). The best deep neural network performs as well as the best hybrid deep/convolutional neural network with an AUC of 0.879. In addition, logistic classification performs well with an AUC of 0.840.

Table 2.

Classification area under the curve (AUC) for combined classifiers using logistic classification, k-nearest neighbors, random forests, deep neural network and combination deep and convolutional neural network.

Classifier	5-fold CV AUC	Holdout AUC
Logistic regression	0.860+0.001	0.840
K-nearest neighbors	0.817+0.001	0.823
Random forest	0.881+0.001	0.884
Deep neural network	0.878+0.002	0.876
Hybrid deep/convolutional neural network	0.875+0.001	0.876

Logistic regression performed well, implying that there are strong simple, linear relationships between features and the ASA PS. The trend of random forests producing the best models persisted when we trained continuous models.

Continuous model

We evaluated model performance by calculating mean MSE using 5-fold cross validation on the training set and MSE on the holdout set. With 5-fold cross validation on the oversampled training set, random forest regression performs the best with a continuous MSE of 0.240 and random forest split classification performs the best with an ordinal MSE of 0.279 (Table 3).

Table 3.

5-fold cross validation mean squared error (MSE) for continuous models trained on oversampled training data using linear, random forest, deep neural network (DNN) and ordinal regression, and random forest and DNN split classification.

Model	Continuous MSE	Ordinal MSE
Linear regression	0.450+0.002	0.541+0.002
Random forest regression	0.240+0.001	0.305+0.002
DNN regression	0.441+0.015	0.532+0.016
Ordinal regression	0.450+0.002	0.539+0.001
Random forest split classifiers	0.260+0.001	0.279+0.001
DNN split classifiers	0.541+0.021	0.574+0.024

On the holdout set, the best continuous model was the random forest regression model, which achieved a 0.337 continuous MSE and 0.437 ordinal MSE when trained on oversampled data (Table 4).

Table 4.

Holdout mean squared error (MSE) for continuous models trained on oversampled training data using linear, random forest, deep neural network (DNN) and ordinal regression, and random forest and DNN split classification.

Model	Continuous MSE	Ordinal MSE	Cohen’s Kappa
Linear regression	0.373	0.459	0.351
Random forest regression	0.337	0.437	0.412
DNN regression	0.374	0.471	0.420
Ordinal regression	0.373	0.458	0.352
Random forest split classifiers	0.387	0.440	0.456
DNN split classifiers	0.683	0.739	0.413

The trend of the best-performing model is matched in the models trained on the original data, which has lower MSEs because the model takes class imbalance into account (Appendix D). Our efforts to balance the dataset by oversampling the minority classes, which often improves performance, turned out to weaken the performance on this problem; models built using the original, unadjusted data performed better.

The Cohen’s Kappa of the random forest split classification model compared to the raw scores was 0.456. This Kappa (K) score is comparable to scores found in literature (0.40 to 0.64) [8–11]. These results indicate that the model has moderate inter-rater reliability with the anesthesiologists in the data set, comparable to historical human performance.

Distribution of continuous scores

The distribution of predicted scores for our continuous models trained on oversampled data (Figure 3) and the density of the distribution of those predicted ASA PS separated by their “true” ASA PS class (Figure 4) show different patterns between the various models. The distribution of the linear regression, ordinal regression, and DNN regression models follow a bell-shaped curve. The random forest regression and split classification models have a more evenly spread distribution, with some peaks. The random forest and DNN split classification models appear to have a divide at ASA PS 2.5.

Fig. 3.

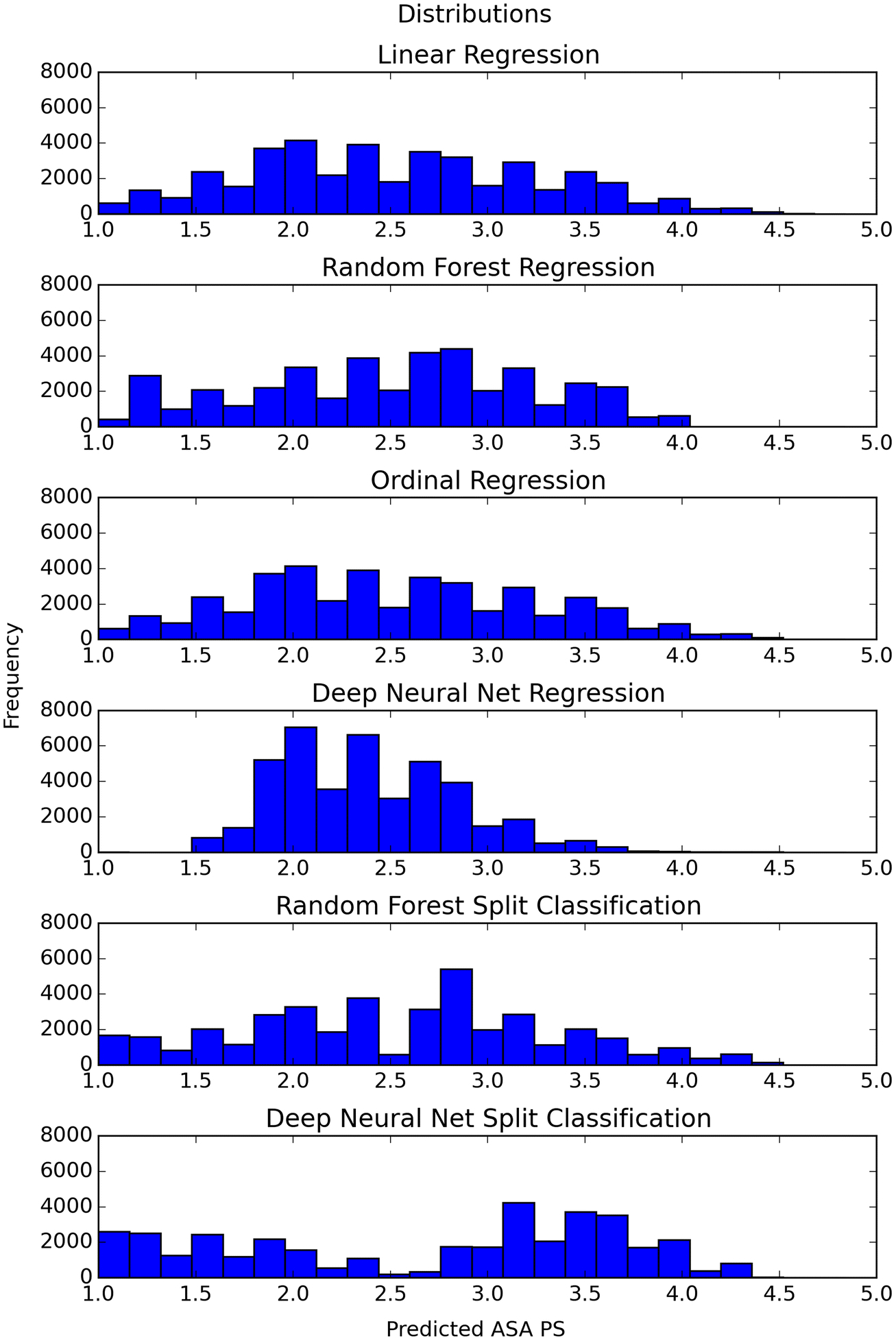
Histograms of predicted ASA PS from the continuous model trained on oversampled data

Fig. 4.

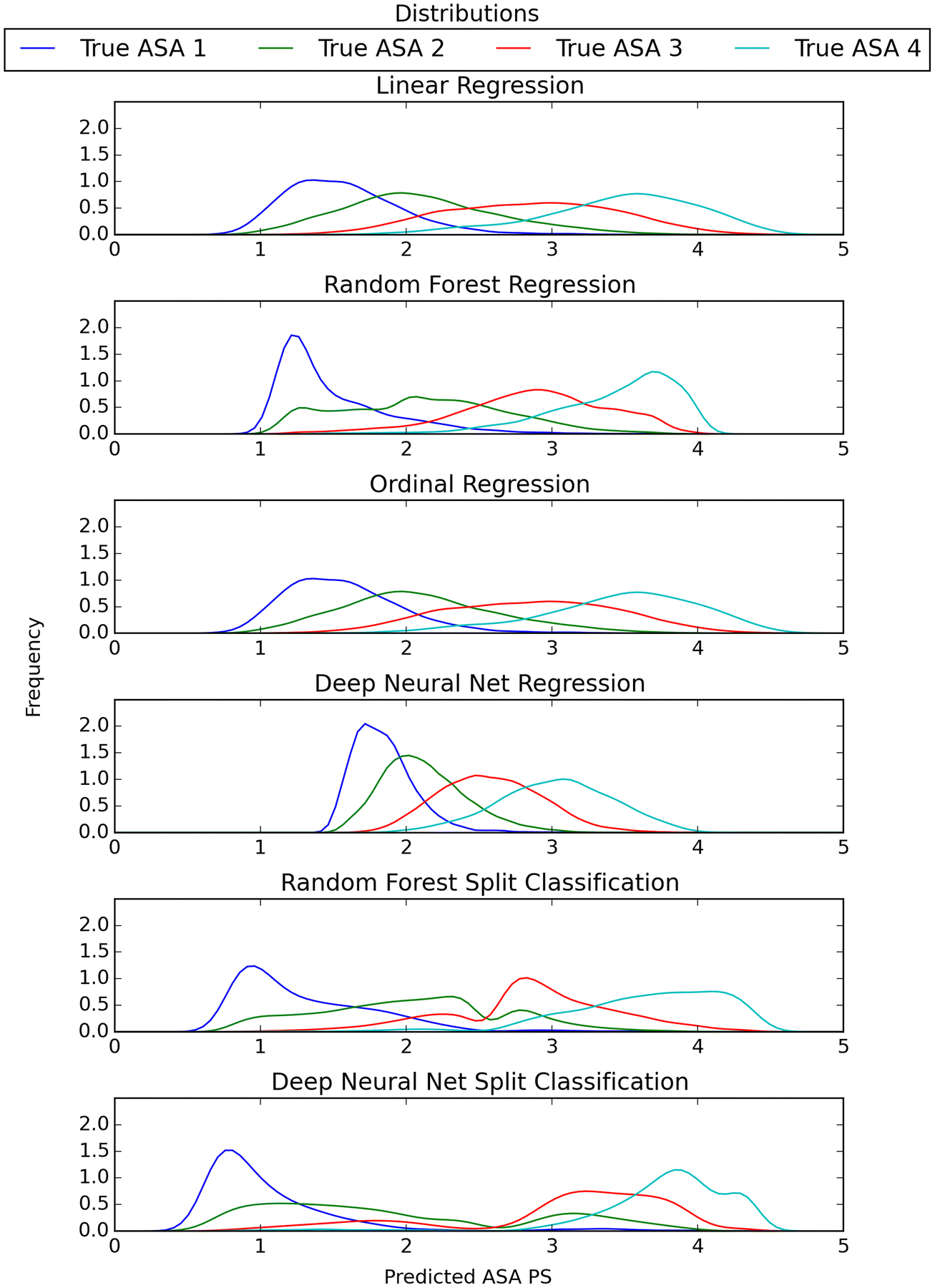
Gaussian density of predicted ASA PS from the continuous model trained on oversampled data organized by true ASA PS class

The density plots of the models help visualize the patterns seen in the distributions. The random forest regression model has a large density towards the extreme for ASA PS classes 1 and 4. The DNN regression model’s ASA PS classes seem to be more concentrated towards a center point. The split between the ASA PS classes 1&2 and 3&4 are clear in the random forest and DNN split classification models.

The density plots give insight into how the different models predict ASA PS. The split classification models have a definitive split between ASA PS 2 and 3, likely due to the fact that the classifiers first predict ASA PS 1&2 vs 3&4 and then 1 vs 2 or 3 vs 4. We hypothesize that since a majority of ASA PS fall into 2 and 3, this classifier performs the best because it focuses on that distinction first.

Granularity evaluation

The granularity evaluation shows moderate agreement between the two anesthesiologists and fair to moderate agreement between the model and anesthesiologists (Table 5).

Table 5.

Results of granularity evaluation on American Society of Anesthesiology Physical Status class 3 case pairs with two anesthesiologists and our random forest regression model.

Comparison	Accuracy	95% confidence interval	Cohen’s Kappa
Anesthesiologist 1 and Anesthesiologist 2	0.84	[0.72,0.92]	0.653
Model and Anesthesiologist 1	0.64	[0.50, 0.76]	0.280
Model and Anesthesiologist 2	0.72	[0.58,0.83]	0.440

The anesthesiologists’ agreement with each other was 42/50 = 0.84, 95% CI [0.72, 0.92] and K = 0.653. The model agreement was 32/50 = 0.64 [0.50, 0.76], K = 0.280 for anesthesiologist 1 and 36/50 = 0.72 [0.58, 0.83], K = 0.440 for anesthesiologist 2.

The more granular ASA PS inference produced scores with fair to moderate agreement with two anesthesiologists in the task of identifying the higher-acuity patient in pairs where both were originally evaluated as ASA PS 3. This is an encouraging result given the difficult learning problem of inferring a continuous score from discrete ASA PS 1, 2, 3, 4 labels alone. From this we’ve demonstrated that the model can learn factors that differentiate the severity of cases within the same ASA PS class in some similar alignment to anesthesiologists. With a more granular ASA PS score, clinicians can triage patients more easily prior to surgery. In addition, it also permits easier identification of higher risk patients for further investigation.

Sensitivity analysis

The random forest split classification model trained without ICD-9-CM data from the day of surgery achieves an AUC of 0.869 for distinguishing ASA PS 1&2 against 3&4, compared to the original AUC of 0.884. It performs worse than the model using diagnoses from the day of surgery, with K = 0.426 and MSE = 0.473 compared to K = 0.456 and MSE = 0.387.

The sensitivity analysis indicates that if no ICD-9-CM data is given from the day of the surgery, the model performs worse. The new model however achieves K=0.43, which falls into the same range of moderate agreement. While the model loses some discriminative ability, it still performs as well as another anesthesiologist.

Limitations

One limitation of this work is that our reference standards, the ASA PS labels, were each designated by a single physician, and different physicians provided those labels for different cases. Greater performance could be achieved by using multiple assessments per case and using the disagreement between them as a signal of the ambiguity of that case. The fact that physicians agree only to a moderate degree on what those scores should be places an upper bound on the accuracy achievable using this data. Additionally, the wide range of cases that ASA PS classes 2 and 3 cover and the difficulty in distinguishing them leads us to suggest that the scale may have better agreement if those classes had higher granularity. Another limitation is that the data were from a single institution, and there is likely to be meaningful inter-institutional variability on the assignment of ASA PS scores. An additional limitation is that there may be missing information for ASA determination in the form of gauging disease severity and its impact, which may be beyond the scope of the available structured data. This missing information could be added by pulling from unstructured data.

Conclusion

We have developed a model that can predict ASA PS with agreement similar to anesthesiologists and provide granularity with a continuous score. This study demonstrates that we can use data-driven approaches to automatically help define or assign additional granularity to this existing scale. Use of the continuous score may be able to aid anesthesiologists in identifying high risk patients who could benefit from additional preoperative assessment.

Appendix A. Feature classes

The feature classes were:

• Age (integer): Age of the patient.

• BMI (continuous decimal): Body mass index of the patient.

• Surgery service (binary): The primary surgical service performing the procedure (70 total).

• Previous surgery (binary): A value indicating whether the patient has previously had any surgery at our institution.

• Preoperative medications (count): Each medication is encoded into the 21-category top-level hierarchy from the First Databank (FDB) Enhanced Therapeutic Classification [18]. For example, clopidogrel (Plavix) would be represented in the “Blood” category.

• Inpatient ICD-9-CM codes (count): ICD-9-CM codes received while in the hospital. In creating these features, we tested numerical counts for: raw codes, parent codes, ICD-9-CM chapters, PheWAS (Phenome-Wide Association Study classification) codes [19], ICD-9-CM hierarchy information and temporally structured ICD-9-CM chapters. Details for ICD-9-CM feature structure are described below.

• Outpatient ICD-9-CM codes (count): ICD-9-CM codes received while not admitted to the hospital. In creating these features, we tested numerical counts for: raw codes, parent codes, ICD-9-CM chapters, PheWAS codes, ICD-9-CM hierarchy and temporally structured ICD-9-CM chapters.

We tested different combinations of feature classes by making every possible combination of the feature classes and running the model using 5-fold cross validation. We then evaluated the resulting model by calculating the mean receiver operating characteristic curve (ROC AUC) and compared it to other combinations.

For the features from ICD-9-CM codes, we tested: raw codes, parent codes, ICD-9-CM chapters, PheWAS codes, and ICD-9-CM hierarchy and temporally structured ICD-9-CM chapters. The raw ICD-9-CM codes resulted in approximately 4,000 features, while both the parent codes and PheWAS codes resulted in approximately 1,000 features. The ICD-9-CM chapters result in 20 features, the ICD-9-CM hierarchy results in 20 features, and the temporally structured ICD-9-CM chapters result in 240 features (20 chapters * 12 months).

Incorporating specific ICD hierarchy information can sometimes improve prediction quality by leveraging the relationships between correlated ICD codes and their parents [20]. We tested these hierarchy-based variables as potential predictors.

Additionally, temporal ICD features were constructed by dividing the year before surgery into month-long windows for each ICD chapter, where the value of a month’s window is the number of each of the ICD-9-CM chapter codes occurring in that month.

Appendix B. Neural network description, architecture, and optimization

Deep Learning for Temporal Data

In the past decade, neural networks have become very popular. A standard neural network consists of a number of simple, connected processors called neurons, each of which performs a simple regression. The regression weights of all neurons are iteratively adjusted during model training to maximize the accuracy of prediction. Deep neural networks have many layers, and the output of neurons in one layer provide the input to the neurons in the next layer [21]. Deep learning models scale well to large data sets but require a large training data set.

Convolutional neural networks are deep neural networks that emphasize smaller local patterns that may show up in different locations in the data space. In this project, we sought data patterns that would capture information about short-range temporal proximity. In other words, the convolutional model identified patterns that are local to a small span of, say, two or three months, regardless of when in absolute time those months were positioned.

Hybrid Network Architecture

The hybrid neural network uses both the deep and convolutional networks to learn from the data. The deep neural network operates on the non-temporal data (age, BMI, etc) while the convolutional neural network takes temporal data as its input. To combine the two types of data, we concatenated the output hidden units from the convolutional neural network with the hidden units from the last hidden layer of the deep neural network. The resulting layer is fed into an output layer, which uses a softmax as the activation function.

Binary Classification Optimized Parameters

The final parameters from hyperopt that we found were logistic classification with an elastic net penalty, k-nearest neighbors with k=4, random forests using 79 estimators and a depth of 19, deep neural networks with 0.1 hidden drop, a depth of 3 and width of 400, and the hybrid network with the same deep network parameters plus convolutional network parameters with 20 filters and a window size of 3. The hybrid neural network architecture and final parameters can be seen in Table 6.

Table 6.

Hybrid neural network architecture

Layer	Layer Type	Size	Output Size
Input1			(112)
D1	Dense	(400)	(400)
D2	Dense	(400)	(400)
D3	Dense	(400)	(400)
Input2			(20, 12)
C1	Convolutional	(20,3)	(20, 1, 10)
D4	Dense	(256)	(256)
D3+D4	Concatenate	656	(656)
D5	Dense	512	(512)
Output			(2)

Regression Optimized Parameters

The final parameters found from hyperopt for regression models were random forests using 95 estimators and a depth of 19, deep neural networks with 0.2 hidden drop, a depth of 2 and width of 500 (Table 7). For linear regression and ordinal regression, we used an elastic net to evaluate the importance of the features, but found that removing features caused a decrease in MSE, and in the final models used all the features. For the split classifiers, we used the parameters from the binary classification models.

Table 7.

Deep neural network regression model architecture

Layer	Layer Type	Size	Output Size
Input			(132)
D1	Dense	(500)	(500)
D2	Dense	(500)	(500)
Output			(1)

Appendix C. Individual feature class performance

Table 8.

The mean area under the receiver operating characteristic curve (ROC AUC) scores for each individual feature class, and combined classifier measured using 5-fold cross validation.

Classifier	Logistic regression	K-nearest neighbors	Random forest
Age	0.689	0.620	0.697
Body mass index	0.572	0.530	0.575
Service	0.693	0.635	0.693
Surgery	0.619	0.602	0.630
Medication (single)	0.600	0.554	0.619
Medication class	0.606	0.584	0.625
Medication hierarchy	0.608	0.579	0.622
Inpatient ICD-9-CM chapter	0.801	0.748	0.815
Inpatient ICD-9-CM PHEWAS	0.769	0.720	0.791
Inpatient ICD-9-CM parent	0.749	0.715	0.783
Inpatient ICD-9-CM code	0.715	0.704	0.769
Inpatient ICD-9-CM hierarchy	0.820	0.785	0.859
Temporal inpatient ICD-9-CM	0.800	0.754	0.817
Outpatient ICD-9-CM chapter	0.774	0.718	0.794
Outpatient ICD-9-CM PHEWAS	0.760	0.689	0.774
Outpatient ICD-9-CM parent	0.740	0.667	0.769
Outpatient ICD-9-CM code	0.689	0.627	0.728
Outpatient ICD-9-CM hierarchy	0.800	0.774	0.856
Temporal outpatient ICD-9-CM	0.791	0.753	0.815

ICD-9-CM = International classification of diseases and related health problems, ninth revision, clinical modification

Appendix D. Model performance on original data

Table 9.

Holdout mean squared error (MSE) for continuous models trained on original training data using linear, random forest, deep neural network (DNN) and ordinal regression, and random forest and DNN split classification.

Model	Continuous MSE	Ordinal MSE	Cohen’s Kappa
Linear regression	0.285	0.356	0.413
Random forest regression	0.264	0.332	0.446
Deep neural network regression	0.326	0.408	0.409
Ordinal regression	0.285	0.356	0.413
Random forest split classifiers	0.285	0.317	0.476
Deep neural network split classifiers	0.304	0.350	0.416