Topological Indices of Some Chemical Structures Applied for the Treatment of COVID-19 Patients

Abstract

The novel coronavirus disease 2019 (COVID-19) emerged in Wuhan, China, and has spread rapidly to nearly every part of the world. Unfortunately, no drug or vaccine has been accepted for the treatment of this pandemic. Researchers have established the efficacy of some existing antiviral drugs to control COVID-19 in vitro. Some of them are remdesivir (GS-5734), chloroquine, hydroxychloroquine, theaflavin. Topological indices are mathematical interpretations of a molecule generated by an algorithm implemented to a given molecular representation. Topological indices are used to model different physicochemical properties and biological activities of chemical compounds. In this work, some degree-based and neighborhood degree sum-based topological indices are investigated for the aforesaid antiviral drugs using polynomial approach. The results obtained can aid in the design of new medicine for the treatment of COVID-19.

1. Introduction

Historically, epidemics of multiple infectious diseases with millions dying have been recorded in the past few centuries. The most terrific was pandemics due to the plague, flu, cholera, etc. Currently, the COVID-19 pandemic is disrupting human health and the economy around the world. It is originated in a Wuhan¹ seafood market but has rapidly spread in and beyond China. As of 3 April 2020, there were 1,116,643 confirmed cases, including 59,158 deaths worldwide (as per world meter information). The novel corona virus (2019-nCoV) is a betacoronavirus and shares genetic sequence and viral structure with severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV). No specific medication for the new disease is currently available. It is, therefore, urgent to identify appropriate antiviral agents to combat the pathogen. An effective experiment to drug discovery is to test whether existing antiviral drugs are efficient in the treatment of related viral diseases. Researchers tested some existing antiviral agents^2–6 and got positive results to inhibit the infection and transmission of the 2019-nCoV in vitro. Some of these antiviral compounds are remdesivir (GS5734), chloroquine, hydroxychloroquine and theaflavin. Remdesivir is a nucleotide analog drug having broad spectrum activity developed to prevent Ebola virus infection.⁷ It is also highly efficient to prevent 2019-nCoV in vitro.² The clinical trial is currently underway in several hospitals and tests on efficacy are awaited. Chloroquine is a broadspectrum antiviral drug^8,9 effective for treating malaria and autoimmune disease. Many randomized controlled trials were performed to assess the impact of chloroquine in the treatment of COVID-19. Therapeutic results in terms of fever control, enhanced CT imaging and delayed disease progression have been reported. Hydroxychloroquine has antiviral activity very similar to that of chloroquine. Both exhibit immune modulating activity, which can improve their antiviral effect in vivo. As per Forbes report in 30 March 2020, FDA approves chloroquine and hydroxychloroquine for emergency coronavirus treatment. Hydroxychloroquine reduce the acute evolution of COVID-19 by suppressing the cytokine storm by inhibiting T cell activation. Theaflavin, a polyphenol chemical in black tea, is found liable for the medical benefit of black tea. Theaflavin has shown a wide range of antiviral activity against many viruses, including influenza A, B and hepatitis C viruses.^10,11 In the work of Lung et al.⁴, it is found that theaflavin may be used as a lead compound for the production of an inhibitor of 2019-nCoV. In pharmaceutical drug design, information related to physicohemical properties, biological activities of molecular graph of compounds are necessary. These properties can be predicted without using any weight lab by a well-known tool of chemical graph theory known as topological index. By molecular graph^12,13 we mean a simple connected graph where nodes and edges between them are considered as atoms and chemical bonds between them, respectively. Topological indices are mathematical measure of molecular graph that remain invariant under graph isomorphism. It was originated in 1947¹⁴ and then its journey started. A great variety of topological indices has been developed and a lot of work has been performed on computing indices of various molecular graphs and networks. Nilanjan De¹⁵ computed the reformulated first Zagreb index of some chemical graphs as an application of generalized hierarchical product of graphs. Gao et al.¹⁶ obtained some degree-based indices of networks derived from Honey comb networks. In the work of Anjum and Safdar,¹⁷ different structural properties of nanostructures are investigated in terms of several topological indices. Some multiplicative degree-based indices for Bismuth Tri-Iodide chain and sheet are investigated by Shao et al.18 Topological indices of Graphene and chemical compound widely used in the manufacture of anticancer drugs are derived in studies of Mondal et al.¹⁹ and Zheng et al.²⁰ To overcome the laborious approach of computing of a certain type of indices of a specific category of graphs, many algebraic polynomials are found in the literature. For instance, the Hosoya polynomial plays the key role in the field of distance-based topological indices.²¹ Its differentiation at 1 yields Wiener and hyper-Wiener index.²² The Tratch–Stankevich–Zefirov index can be obtained similarly.²³ Some more polynomials in the area of chemical graph theory are the Clar covering polynomial,²⁴ PI Polynomial,²⁵ Schultz polynomial,²⁶ theta polynomial,²⁷ Tutte polynomial,²⁸ etc. In case of degree-based topological indices,²⁹ the M-polynomial has a significant role to compute the indices. It was introduced by Deutsch and Klavzar in 2015³⁰ where its role to compute degree-based indices was shown to be parallel to the role of the Hosoya polynomial for distance-based indices. After that, numerous works on M-polynomial have been done. Munir et al. computed M-polynomial and degree-based topological indices for nanostar dendrimers,³¹ single-walled titania nanotubes,³² armchair and zigzag polyhex nanotubes,³³ and family of circulant graphs.³⁴ Present authors derived M-polynomial of para-line graphs of some graceful structures and hence recovered some degree-based indices.³⁵ Topological indices of V-phylenic nanotubes and nanotori are investigated by Chel Kwun et al.³⁶ using M-polynomial approach. Gao et al.³⁷ put their attention to compute topological indices of crystallographic structure of cuprous oxide and titanium difluoride using M-polynomial. General expressions of M-polynomial for triangular, hourglass and jagged-rectangle benzenoid systems are evaluated in Chel Kwun et al.³⁸ which produce several indices based on degree. Similar work is performed for cactus chains, benzene ring embedded in P-type surface network, zigzag and rhombic benzenoid and 3-layered probabilistic neural network.^39–43 Let $\gamma (u)$ denote the degree of vertex u of a graph G. The M-polynomial of G is defined as,

$$M(G)=\sum _{i\le j}(\mathit{number} of \mathit{all} \mathit{edges} uv \mathit{such} \mathit{that} \gamma (u)=i,\gamma (v)=j) x^i{y}^j.$$ (1)

Neighborhood M-polynomial⁴⁴ play the similar role for neighborhood degree sum-based indices.^45–48 Some topological indices based on neighborhood degree sum for bismuth tri-iodide chain and sheet are derived using neighborhood M-polynomial method.⁴⁹ Let $\Upsilon (u)$ denote the degree sum of all vertices of G that are adjacent to u. We call $\Upsilon (u)$ as neighborhood degree sum of u in G. The neighborhood M-polynomial of G is defined as,

$$NM(G)=\sum _{i\le j}(\mathit{number} of \mathit{all} \mathit{edges} uv \mathit{such} \mathit{that} \Upsilon (u)=i,\Upsilon (v)=j) x^i{y}^j.$$ (2)

Degree-based (D) and neighborhood degree sum-based (ND) topological indices defined on edge set E(G) of a graph G can be expressed as

$$D(G)=\sum _{uv\in E(G)}g(\gamma (u),\gamma (v)), ND(G)=\sum _{uv\in E(G)}g(\Upsilon (u),\Upsilon (v)),$$

where the formulation of $g(\gamma (u),\gamma (v))$ and $g(\Upsilon (u),\Upsilon (v))$ are given in Table 1.

Table 1.

Description of some topological indices.

D	$g(\gamma (u),\gamma (v))$	ND	$g(\Upsilon (u),\Upsilon (v))$.
First Zagreb index (M1)50	$\gamma (u)+\gamma (v)$	Third version of Zagreb index ($M_1^{\prime })$59	$\Upsilon (u)+\Upsilon (v)$
Second Zagreb index (M2)50	$\gamma (u)\gamma (v)$	Neighborhood second Zagreb index ($M_2^{\ast }$)46	$\Upsilon (u)\Upsilon (v)$
Forgotten topological index (F)51	$\gamma {(u)}^2+\gamma {(v)}^2$	Neighborhood forgotten topological index ($F_N^{\ast }$)46	$\Upsilon {(u)}^2+\Upsilon {(v)}^2$
Second modified Zagreb index (${}^m{M}_2$)52	$\frac{1}{\gamma (u)\gamma (v)}$	Neighborhood second modified Zagreb index (${}^{nm}{M}_2$)49	$\frac{1}{\Upsilon (u)\Upsilon (v)}$
General Randić index ($R_{\alpha }$)53	$\gamma {(u)}^{\alpha }\gamma {(v)}^{\alpha }$	Neighborhood general Randić index ($N{R}_{\alpha }$)49	$\Upsilon {(u)}^{\alpha }\Upsilon {(v)}^{\alpha }$
Redefined third Zagreb index (ReZG3)54	$\gamma (u)\gamma (v)(\gamma (u)+\gamma (v))$	Third NDe index47 (ND3)	$\Upsilon (u)\Upsilon (v)(\Upsilon (u)+\Upsilon (v))$
Symmetric division deg index (SDD)55	$\frac{\gamma {(u)}^2+\gamma {(v)}^2}{\gamma (u)\gamma (v)}$	Fifth NDe index47 (ND5)	$\frac{\Upsilon {(u)}^2+\Upsilon {(v)}^2}{\Upsilon (u)\Upsilon (v)}$
Harmonic index (H)56	$\frac{2}{\gamma (u)+\gamma (v)}$	Neighborhood Harmonic index (NH)49	$\frac{2}{\Upsilon (u)+\Upsilon (v)}$
Inverse sum indeg index (I)57	$\frac{\gamma (u)\gamma (v)}{\gamma (u)+\gamma (v)}$	Neighborhood inverse sum index (NI)49	$\frac{\Upsilon (u)\Upsilon (v)}{\Upsilon (u)+\Upsilon (v)}$
Augmented Zagreb index (A)58	${\left\{\frac{\gamma (u)\gamma (v)}{\gamma (u)+\gamma (v)}\right\}}^3$	Sanskruti index (S)60	${\left\{\frac{\Upsilon (u)\Upsilon (v)}{\Upsilon (u)+\Upsilon (v)}\right\}}^3$

The first and second Zagreb indices were determined to be effective for the measurement of the total π-electron energy of molecules.⁶¹ The Randić index has been related to a huge amount of structural properties of atoms. SDD is used to assess the total surface area of polychlorobiphenyls.⁶² The augmented Zagreb index provides the best estimation of the heat of formation of alkanes.⁵⁸ Neighborhood degree sum-based indices can predict different physicochemical properties with powerful accuracy.^{46,47,49,59,60} The goal of this work is to evaluate some topological indices of the antiviral compounds remdesivir, chloroquine, hydroxychloroquine and theaflavin. First, we obtain M-polynomial and NM-polynomial of the structures and then recover some degree-based and neighborhood degree sum-based indices. Further, surface representation of M and NM polynomials are depicted. In addition, some results are compared graphically.

2. Methodology

Our main findings include topological indices of some antiviral drug structures with the help of algebraic polynomials. The chemical structures of remdesivir, chloroquine, hydroxychloroquine and theaflavin are collected from pubchem.ncbi.nlm.nih.gov. We consider hydrogen suppressed molecular graphs of compounds since the vertices representing hydrogen atom make no contribution to graph isomorphism. We utilize combinatorial computation, edge partition method, graph theoretical tools, analytical techniques and degree counting method to derive our results. At first patterns of edge partitions of hydrogen deleted molecular graph of the aforesaid compounds are constructed based on degree and neighborhood degree sum of end vertices. Using those partitions, some closed forms of M-polynomial and NM-polynomial are derived. The surface plotting of the polynomials are made by using Maple 2015. Degree-based and neighborhood degree sum-based indices are computed from M-polynomial and NM-polynomial using some mathematical operators and Table 2 as defined in previous section. Numerical results are compared graphically using MATLAB 2017.

Table 2.

Derivation of topological indices from M-polynomial and NM-polynomial.

Topological index	Derivation from M(G)	Topological index	Derivation from NM(G).
M1	$(D_x+D_y)(M(G)){|}_{x=y=1}$	$M_1^{\prime }$	$(D_x+D_y)(NM(G)){|}_{x=y=1}$
M2	$(D_x{D}_y)(M(G)){|}_{x=y=1}$	$M_2^{\ast }$	$(D_x{D}_y)(NM(G)){|}_{x=y=1}$
F	$(D_x^2+D_y^2)(M(G)){|}_{x=y=1}$	$F_N^{\ast }$	$(D_x^2+D_y^2)(NM(G)){|}_{x=y=1}$
${}^m{M}_2$	$(I_x{I}_y)(M(G)){|}_{x=y=1}$	${}^{nm}{M}_2$	$(I_x{I}_y)(NM(G)){|}_{x=y=1}$
$R_{\alpha }$	$(D_x^{\alpha }{D}_y^{\alpha })(M(G)){|}_{x=y=1}$	$N{R}_{\alpha }$	$(D_x^{\alpha }{D}_y^{\alpha })(NM(G)){|}_{x=y=1}$
ReZG3	$D_x{D}_y(D_x+D_y)(M(G)){|}_{x=y=1}$	ND3	$D_x{D}_y(D_x+D_y)(NM(G)){|}_{x=y=1}$
SDD	$(D_x{I}_y+I_x{D}_y)(NM(G)){|}_{x=y=1}$	ND5	$(D_x{I}_y+I_x{D}_y)(NM(G)){|}_{x=y=1}$
H	$2I_{x}J(M(G)){|}_{x=1}$	NH	$2I_{x}J(NM(G)){|}_{x=1}$
I	$I_{x}J{D}_x{D}_y(M(G)){|}_{x=1}$	NI	$I_{x}J{D}_x{D}_y(NM(G)){|}_{x=1}$
A	$I_x^3{Q}_{-2}J{D}_x^3{D}_y^3(M(G)){|}_{x=1}$	S	$I_x^3{Q}_{-2}J{D}_x^3{D}_y^3(NM(G)){|}_{x=1}$

Here,

$D_x(g(x,y))=x\frac{\partial (g(x,y))}{\partial x}, D_y(g(x,y))=y\frac{\partial (g(x,y))}{\partial y},I_x(g(x,y))={\int }_0^x\frac{(g(t,y))}{t}dt, I_y(g(x,y))={\int }_0^y\frac{(g(x,t))}{t}dt,J(g(x,y))=g(x,x), Q_{\alpha }(g(x,y))=x^{\alpha }g(x,y).$

3. Results and discussion

In this section, we give our main computational results. We compute the M-polynomial and NM-polynomial of molecular graph of remdesivir (GS-5734) in the following theorem.

Theorem 1.

Let G be the molecular graph of remdesivir (GS-5734). Then, we have,

$$\begin{array}{l}M(G)=2x{y}^2+5x{y}^3+2x{y}^4+14x^2{y}^3+9x^2{y}^2+4x^2{y}^4+6x^3{y}^3+2x^3{y}^4,\\ NM(G)=2x^2{y}^4+3x^3{y}^6+x^3{y}^7+x^3{y}^8+2x^4{y}^4+4x^4{y}^5+2x^4{y}^6+x^4{y}^7+x^4{y}^9\\ +2x^5{y}^5+6x^5{y}^6+x^5{y}^7+2x^5{y}^8+x^5{y}^9+3x^6{y}^7+x^6{y}^6+4x^7{y}^7+x^7{y}^8\\ +x^7{y}^9+x^6{y}^8+x^8{y}^8+2x^8{y}^9+x^9{y}^9.\end{array}$$

Proof 1.

Let G be the molecular graph of remdesivir (Figure 1). It has 44 number of edges. Let $P_{(i,j)}$ be the set of all edges with degree of end vertices i, j, i.e., $P_{(i,j)}=\{uv\in E(G):\gamma (u)=i,\gamma (v)=j\}$. Let ${\rho }_{(i,j)}$ be the number of edges in $P_{(i,j)}$. From Figure 1, it is clear that ${\rho }_{(1,2)}=2,{\rho }_{(1,3)}=5,{\rho }_{(1,4)}=2,{\rho }_{(2,2)}=9,{\rho }_{(2,3)}=14,{\rho }_{(2,4)}=4,{\rho }_{(3,3)}=6,{\rho }_{(3,4)}=2$. From the Equation (1), the M-polynomial of G is obtained as follows.

$$\begin{array}{l}M(G)=\sum _{i\le j}{\rho }_{(i,j)}{x}^i{y}^j\\ ={\rho }_{(1,2)}{x}^1{y}^2+{\rho }_{(1,3)}{x}^1{y}^3+{\rho }_{(1,4)}{x}^1{y}^4+{\rho }_{(2,2)}{x}^2{y}^2\\ +{\rho }_{(2,3)}{x}^2{y}^3+{\rho }_{(2,4)}{x}^2{y}^4+{\rho }_{(3,3)}{x}^3{y}^3+{\rho }_{(3,4)}{x}^3{y}^4.\end{array}$$

Putting the values of ${\rho }_{(i,j)}$“s, we obtain

$$M(G)=2x{y}^2+5x{y}^3+2x{y}^4+14x^2{y}^3+9x^2{y}^2+4x^2{y}^4+6x^3{y}^3+2x^3{y}^4.$$

Let $P_{(i,j)}^{\ast }$ be the set of all edges with neighborhood degree sum of end vertices i, j, i.e., $P_{(i,j)}^{\ast }=\{uv\in E(G):\Upsilon (u)=i,\Upsilon (v)=j\}$. Let ${\rho }_{(i,j)}^{\ast }$ be the number of edges in $P_{(i,j)}^{\ast }$. From Figure 1, we have ${\rho }_{(2,4)}^{\ast }=2,{\rho }_{(3,6)}^{\ast }=3,{\rho }_{(3,7)}^{\ast }=1,{\rho }_{(3,8)}^{\ast }=1,{\rho }_{(4,4)}^{\ast }=2,{\rho }_{(4,5)}^{\ast }=4,{\rho }_{(4,6)}^{\ast }=2,{\rho }_{(4,7)}^{\ast }=1,{\rho }_{(4,9)}^{\ast }=1,{\rho }_{(5,5)}^{\ast }=2,{\rho }_{(5,6)}^{\ast }=6,{\rho }_{(5,7)}^{\ast }=1,{\rho }_{(5,8)}^{\ast }=2,{\rho }_{(5,9)}^{\ast }=1,{\rho }_{(6,6)}^{\ast }=1,{\rho }_{(6,7)}^{\ast }=3,{\rho }_{(6,8)}^{\ast }=1,{\rho }_{(7,7)}^{\ast }=4,{\rho }_{(7,8)}^{\ast }=1,{\rho }_{(7,9)}^{\ast }=1,{\rho }_{(8,8)}^{\ast }=1,{\rho }_{(8,9)}^{\ast }=2,{\rho }_{(9,9)}^{\ast }=1$. From the Equation (2), the NM-polynomial of G is obtained bellow.

$$\begin{array}{l}NM(G)=\sum _{i\le j}{\rho }_{(i,j)}^{\ast }{x}^i{y}^j\\ ={\rho }_{(2,4)}^{\ast }{x}^2{y}^4+{\rho }_{(3,6)}^{\ast }{x}^3{y}^6+{\rho }_{(3,7)}^{\ast }{x}^3{y}^7+{\rho }_{(3,8)}^{\ast }{x}^3{y}^8\\ +{\rho }_{(4,4)}^{\ast }{x}^4{y}^4+{\rho }_{(4,5)}^{\ast }{x}^4{y}^5+{\rho }_{(4,6)}^{\ast }{x}^4{y}^6+{\rho }_{(4,7)}^{\ast }{x}^4{y}^7\\ +{\rho }_{(4,9)}^{\ast }{x}^4{y}^9+{\rho }_{(5,5)}^{\ast }{x}^5{y}^5+{\rho }_{(5,6)}^{\ast }{x}^5{y}^6+{\rho }_{(5,7)}^{\ast }{x}^5{y}^7\\ +{\rho }_{(5,8)}^{\ast }{x}^5{y}^8+{\rho }_{(5,8)}^{\ast }{x}^5{y}^8+{\rho }_{(5,9)}^{\ast }{x}^5{y}^9+{\rho }_{(6,6)}^{\ast }{x}^6{y}^6\\ +{\rho }_{(6,7)}^{\ast }{x}^6{y}^7+{\rho }_{(6,8)}^{\ast }{x}^6{y}^8+{\rho }_{(7,7)}{x}^7{y}^7+{\rho }_{(7,8)}{x}^7{y}^8\\ +{\rho }_{(7,9)}^{\ast }{x}^7{y}^9+{\rho }_{(8,8)}^{\ast }{x}^8{y}^8+{\rho }_{(8,9)}^{\ast }{x}^8{y}^9+{\rho }_{(9,9)}^{\ast }{x}^9{y}^9.\end{array}$$

After putting the values of ${\rho }_{(i,j)}^{\ast }$‘s, we obtain the required result (Figure 2). □

Figure 1.

Chemical structure of remdesivir (GS-5734).

Figure 2.

Plotting of (a) M-polynomial and (b) NM-polynomial of remdesivir (GS-5734).

Now using the M and NM polynomials, we calculate some degree-based and neighborhood degree some-based topological indices of the molecular graph of remdesivir in the following theorem.

Theorem 2.

Let G be the molecular graph of remdesivir. Then, we have,

1. $M_1(G)=216, M_1^{\prime }(G)=514$,

2. $M_2(G)=257, M_2^{\ast }(G)=1543$,

3. $F(G)=586, F_N^{\ast }(G)=3266$,

4. ${}^m{M}_2(G)=9.083,{ }^{nm}{M}_2(G)=1.65$,

5. $R_{\alpha }(G)=2^{\alpha +1}+5{(3)}^{\alpha }+2^{2\alpha +1}+14{(6)}^{\alpha }+9{(4)}^{\alpha }+4{(8)}^{\alpha }+6{(9)}^{\alpha }+2{(12)}^{\alpha }, N{R}_{\alpha }(G)=2{(8)}^{\alpha }+3{(18)}^{\alpha }+{(21)}^{\alpha }+{(24)}^{\alpha }+2{(16)}^{\alpha }+4{(20)}^{\alpha }+2{(24)}^{\alpha }+{(28)}^{\alpha }+{(36)}^{\alpha }+2{(25)}^{\alpha }+6{(30)}^{\alpha }+{(35)}^{\alpha }+2{(40)}^{\alpha }+{(45)}^{\alpha }+3{(42)}^{\alpha }+{(36)}^{\alpha }+4{(49)}^{\alpha }+{(56)}^{\alpha }+{(63)}^{\alpha }+{(48)}^{\alpha }+{(64)}^{\alpha }+2{(72)}^{\alpha }+{(81)}^{\alpha }$,

6. $\mathit{ReZ}{G}_3(G)=1360, N{D}_3(G)=20122$,

7. $\mathit{SDD}(G)=104.667, N{D}_5(G)=95.236$,

8. $H(G)=18.638, NH(G)=8.01$,

9. $I(G)=50.245, NI(G)=124.363$,

10. $A(G)=349.607, S(G)=1996.984$.

Proof 2.

First, we compute the degree-based indices. Let $M(G)=g(x,y)=2x{y}^2+5x{y}^3+2x{y}^4+14x^2{y}^3+9x^2{y}^2+4x^2{y}^4+6x^3{y}^3+2x^3{y}^4.$ Then, we have,

$$\begin{array}{l}(D_x+D_y)(g(x,y))=6x{y}^2+20x{y}^3+10x{y}^4+70x^2{y}^3+36x^2{y}^2+24x^2{y}^4\\ +36x^3{y}^3+14x^3{y}^4,\\ D_x{D}_y(g(x,y))=4x{y}^2+15x{y}^3+8x{y}^4+84x^2{y}^3+36x^2{y}^2+32x^2{y}^4\\ +54x^3{y}^3+24x^3{y}^4,\\ (D_x^2+D_y^2)(g(x,y))=10x{y}^2+50x{y}^3+34x{y}^4+182x^2{y}^3+72x^2{y}^2+80x^2{y}^4\\ +108x^3{y}^3+50x^3{y}^4,\\ I_x{I}_y(g(x,y))=x{y}^2+\frac{5}{3}x{y}^3+\frac{1}{2}x{y}^4+\frac{7}{3}{x}^2{y}^3+\frac{9}{4}{x}^2{y}^2+\frac{1}{2}{x}^2{y}^4+\frac{2}{3}{x}^3{y}^3\\ +\frac{1}{6}{x}^3{y}^4,\\ D_x^{\alpha }{D}_y^{\alpha }(g(x,y))=2^{\alpha +1}x{y}^2+5{(3)}^{\alpha }x{y}^3+2{(4)}^{\alpha }x{y}^4+14{(6)}^{\alpha }{x}^2{y}^3\\ +9{(4)}^{\alpha }{x}^2{y}^2+4{(8)}^{\alpha }{x}^2{y}^4+6{(9)}^{\alpha }{x}^3{y}^3+2{(12)}^{\alpha }{x}^3{y}^4,\\ D_x{D}_y(D_x+D_y)(g(x,y))=12x{y}^2+60x{y}^3+40x{y}^4+420x^2{y}^3+144x^2{y}^2\\ +192x^2{y}^4+324x^3{y}^3+168x^3{y}^4,\\ (D_x{I}_y+I_x{D}_y)(g(x,y))=5x{y}^2+\frac{50}{3}x{y}^3+\frac{17}{2}x{y}^4+\frac{91}{3}{x}^2{y}^3+18x^2{y}^2\\ +10x^2{y}^4+12x^3{y}^3+\frac{25}{6}{x}^3{y}^4,\\ I_{x}J(g(x,y))=\frac{2}{3}{x}^3+\frac{7}{2}{x}^4+\frac{16}{5}{x}^5+\frac{5}{3}{x}^6+\frac{2}{7}{x}^7,\\ I_{x}J{D}_x{D}_y(g(x,y))=\frac{4}{3}{x}^3+\frac{51}{4}{x}^4+\frac{92}{5}{x}^5+\frac{43}{3}{x}^6+\frac{24}{7}{x}^7,\\ I_x^3{Q}_{-2}J{D}_x^3{D}_y^3(g(x,y))=16x+\frac{711}{8}{x}^2+\frac{3152}{27}{x}^3+\frac{3211}{32}{x}^4+\frac{3456}{125}{x}^5.\end{array}$$

Using Table 2, we have

$$\begin{array}{l}{M}_1(G)=6x{y}^2+20x{y}^3+10x{y}^4+70x^2{y}^3+36x^2{y}^2+24x^2{y}^4+36x^3{y}^3\\ +14x^3{y}^4{|}_{x=y=1}=216,\\ M_2(G)=4x{y}^2+15x{y}^3+8x{y}^4+84x^2{y}^3+36x^2{y}^2+32x^2{y}^4+54x^3{y}^3\\ +24x^3{y}^4{|}_{x=y=1}=257,\\ F(G)=10x{y}^2+50x{y}^3+34x{y}^4+182x^2{y}^3+72x^2{y}^2+80x^2{y}^4\\ +108x^3{y}^3+50x^3{y}^4{|}_{x=y=1}=586,\\ {}^m{M}_2(G)=x{y}^2+\frac{5}{3}x{y}^3+\frac{1}{2}x{y}^4+\frac{7}{3}{x}^2{y}^3+\frac{9}{4}{x}^2{y}^2+\frac{1}{2}{x}^2{y}^4\\ +\frac{2}{3}{x}^3{y}^3+\frac{1}{6}{x}^3{y}^4{|}_{x=y=1}=9.083,\\ R_{\alpha }(G)=2^{\alpha +1}x{y}^2+5{(3)}^{\alpha }x{y}^3+2{(4)}^{\alpha }x{y}^4+14{(6)}^{\alpha }{x}^2{y}^3+9{(4)}^{\alpha }{x}^2{y}^2\\ +4{(8)}^{\alpha }{x}^2{y}^4+6{(9)}^{\alpha }{x}^3{y}^3+2{(12)}^{\alpha }{x}^3{y}^4{|}_{x=y=1}=2^{\alpha +1}+5{(3)}^{\alpha }\\ +2^{2\alpha +1}+14{(6)}^{\alpha }+9{(4)}^{\alpha }+4{(8)}^{\alpha }+6{(9)}^{\alpha }+2{(12)}^{\alpha },\\ ReZ{G}_3(G)=12x{y}^2+60x{y}^3+40x{y}^4+420x^2{y}^3+144x^2{y}^2+192x^2{y}^4\\ +324x^3{y}^3+168x^3{y}^4{|}_{x=y=1}=1360,\\ SDD(G)=5x{y}^2+\frac{50}{3}x{y}^3+\frac{17}{2}x{y}^4+\frac{91}{3}{x}^2{y}^3+18x^2{y}^2+10x^2{y}^4+12x^3{y}^3\\ +\frac{25}{6}{x}^3{y}^4{|}_{x=y=1}=104.667,\\ H(G)=\frac{4}{3}{x}^3+7x^4+\frac{32}{5}{x}^5+\frac{10}{3}{x}^6+\frac{4}{7}{x}^7{|}_{x=1}=18.638,\\ I(G)=\frac{4}{3}{x}^3+\frac{51}{4}{x}^4+\frac{92}{5}{x}^5+\frac{43}{3}{x}^6+\frac{24}{7}{x}^7{|}_{x=1}=50.245,\\ A(G)=16x+\frac{711}{8}{x}^2+\frac{3152}{27}{x}^3+\frac{3211}{32}{x}^4+\frac{3456}{125}{x}^5{|}_{x=1}=\mathrm{349.607.}\end{array}$$

For neighborhood degree sum-based indices, we consider $g(x,y)=NM(G)=2x^2{y}^4+3x^3{y}^6+x^3{y}^7+x^3{y}^8+2x^4{y}^4+4x^4{y}^5+2x^4{y}^6+x^4{y}^7+x^4{y}^9+2x^5{y}^5+6x^5{y}^6+x^5{y}^7+2x^5{y}^8+x^5{y}^9+3x^6{y}^7+x^6{y}^6+4x^7{y}^7+x^7{y}^8+x^7{y}^9+x^6{y}^8+x^8{y}^8+2x^8{y}^9+x^9{y}^9$. Then, applying the above operations and Table 2, we can easily obtain the neighborhood degree sum-based indices. This completes the proof. □

We evaluate the M-polynomial and NM-polynomial of the molecular graph of chloroquine in the following theorem.

Theorem 3.

Let G be the molecular graph of chloroquine. Then, we have,

$$\begin{array}{l}M(G)=2x{y}^2+2x{y}^3+5x^2{y}^2+12x^2{y}^3+2x^3{y}^3,\\ NM(G)=2x^2{y}^4+2x^3{y}^5+4x^4{y}^5+3x^5{y}^5+3x^5{y}^6+2x^5{y}^7+2x^6{y}^7\\ +2x^4{y}^6+x^5{y}^8+2x^7{y}^8.\end{array}$$

Proof 3

. Let G be the molecular graph of chloroquine (Figure 3). It has 23 number of edges. From Figure 3, its edge partition based on degree of end vertices is as follows: ${\rho }_{(1,2)}=2,{\rho }_{(1,3)}=2,{\rho }_{(2,2)}=5,{\rho }_{(2,3)}=12,{\rho }_{(3,3)}=2.$ Using the edge partition of G, the M-polynomial can be evaluated easily like previous. The edge partition based on neighborhood degree sum of end vertices is as follows: ${\rho }_{(2,4)}^{\ast }=2,{\rho }_{(3,5)}^{\ast }=2,{\rho }_{(4,5)}^{\ast }=4,{\rho }_{(4,6)}^{\ast }=2,{\rho }_{(5,5)}^{\ast }=3,{\rho }_{(5,6)}^{\ast }=3,{\rho }_{(5,7)}^{\ast }=2,{\rho }_{(5,8)}^{\ast }=1,{\rho }_{(6,7)}^{\ast }=2,{\rho }_{(7,8)}^{\ast }=2.$ Using the edge partition of G, the NM-polynomial can be obtained easily. □

Figure 3.

Chemical structure of chloroquine.

Now using the M and NM polynomials, we calculate some degree-based and neighborhood degree some-based indices of chloroquine in the following theorem like the Proof 2.

Theorem 4.

Let G be the molecular graph of chloroquine. Then, we have (Figure 4),

1. $M_1(G)=106, M_1^{\prime }(G)=240$,

2. $M_2(G)=120, M_2^{\ast }(G)=645$,

3. $F(G)=262, F_N^{\ast }(G)=1342$,

4. ${}^m{M}_2(G)=5.139,{ }^{nm}{M}_2(G)=1.052$,

5. $R_{\alpha }(G)=2^{\alpha +1}+2{(3)}^{\alpha }+5{(4)}^{\alpha }+12{(6)}^{\alpha }+2{(9)}^{\alpha }, N{R}_{\alpha }(G)=2{(8)}^{\alpha }+2{(15)}^{\alpha }+4{(20)}^{\alpha }+3{(25)}^{\alpha }+3{(30)}^{\alpha }+2{(35)}^{\alpha }+2{(42)}^{\alpha }+2{(24)}^{\alpha }+{(40)}^{\alpha }+2{(56)}^{\alpha }$,

6. $\mathit{ReZ}{G}_3(G)=584, N{D}_3(G)=7408$,

7. $\mathit{SDD}(G)=51.667, N{D}_5(G)=48.704$,

8. $H(G)=10.3, NH(G)=4.662$,

9. $I(G)=25.233, NI(G)=58.626$,

10. $A(G)=181.531, S(G)=802.238$.

M-polynomial and NM-polynomial of the molecular graph of hydroxychloroquine are evaluated below (Figures 5 and 6).

Figure 4.

Plotting of (a) M-polynomial and (b) NM-polynomial of chloroquine.

Figure 5.

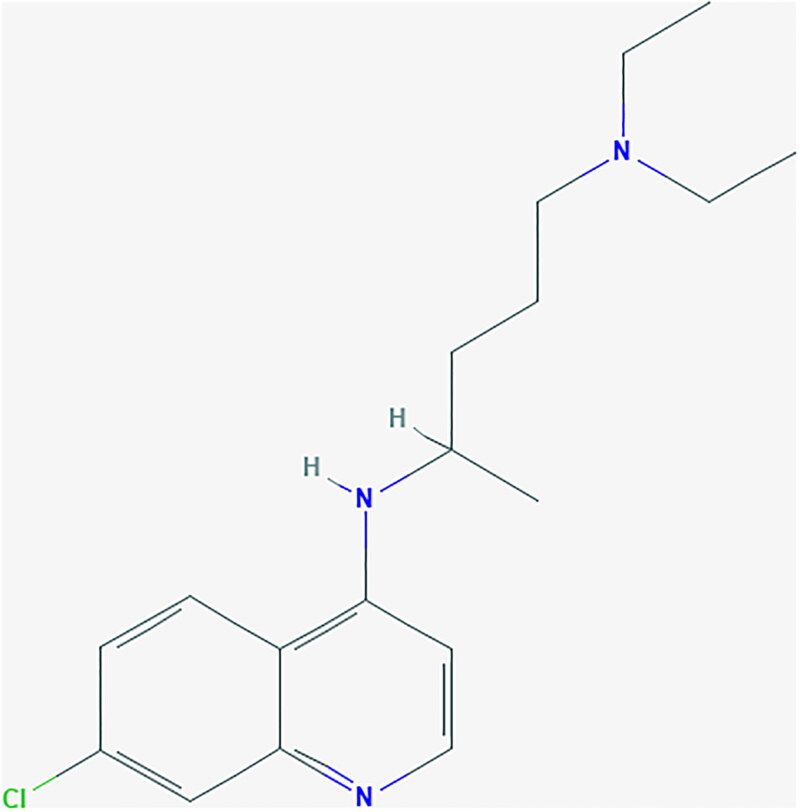
Chemical structure of hydroxychloroquine.

Figure 6.

Plotting of (a) M-polynomial and (b) NM-polynomial of hydroxychloroquine.

Theorem 5.

Let G be the molecular graph of hydroxychloroquine. Then, we have,

$$\begin{array}{l}M(G)=2x{y}^2+2x{y}^3+6x^2{y}^2+12x^2{y}^3+2x^3{y}^3,\\ NM(G)=x^2{y}^3+x^2{y}^4+3x^3{y}^5+x^4{y}^6+4x^4{y}^5+3x^5{y}^5+4x^5{y}^6+2x^5{y}^7\\ +2x^6{y}^7+x^5{y}^8+2x^7{y}^8.\end{array}$$

Proof 4.

Let G be the molecular graph of hydroxychloroquine (Figure 5). It has 24 number of edges. From Figure 5, its edge partition based on degree of end vertices is as follows: ${\rho }_{(1,2)}=2,{\rho }_{(1,3)}=2,{\rho }_{(2,2)}=6,{\rho }_{(2,3)}=12,{\rho }_{(3,3)}=2.$ Using the edge partition of G, the M-polynomial can be evaluated easily like previous. The edge partition based on neighborhood degree sum of end vertices is as follows: ${\rho }_{(2,3)}^{\ast }=1,{\rho }_{(2,4)}^{\ast }=1,{\rho }_{(3,5)}^{\ast }=3,{\rho }_{(4,6)}^{\ast }=1,{\rho }_{(4,5)}^{\ast }=4,{\rho }_{(5,5)}^{\ast }=3,{\rho }_{(5,6)}^{\ast }=4,{\rho }_{(5,7)}^{\ast }=2,{\rho }_{(5,8)}^{\ast }=1,{\rho }_{(6,7)}^{\ast }=2,{\rho }_{(7,8)}^{\ast }=2.$ Using the edge partition of G, the NM-polynomial can be obtained easily. □

Now using the M and NM polynomials, we evaluate the degree-based and neighborhood degree sum-based indices of hydroxychloroquine in the following theorem like the same method as Proof 2.

Theorem 6.

Let G be the molecular graph of hydroxychloroquine. Then, we have,

1. $M_1(G)=110, M_1^{\prime }(G)=248$,

2. $M_2(G)=124, M_2^{\ast }(G)=664$,

3. $F(G)=270, F_N^{\ast }(G)=1378$,

4. ${}^m{M}_2(G)=5.389,{ }^{nm}{M}_2(G)=1.152$,

5. $R_{\alpha }(G)=2^{\alpha +1}+2{(3)}^{\alpha }+6{(4)}^{\alpha }+12{(6)}^{\alpha }+2{(9)}^{\alpha }, N{R}_{\alpha }(G)={(6)}^{\alpha }+{(8)}^{\alpha }+3{(15)}^{\alpha }+{(24)}^{\alpha }+4{(20)}^{\alpha }+3{(25)}^{\alpha }+4{(30)}^{\alpha }+2{(35)}^{\alpha }+2{(42)}^{\alpha }+{(40)}^{\alpha }+2{(56)}^{\alpha }$,

6. $\mathit{ReZ}{G}_3(G)=600, N{D}_3(G)=7600$,

7. $\mathit{SDD}(G)=53.667, N{D}_5(G)=50.504$,

8. $H(G)=5.4, NH(G)=1.227$,

9. $I(G)=26.233, NI(G)=60.695$,

10. $A(G)=189.531, S(G)=827.9$.

M-polynomial and NM-polynomial of the molecular graph of theaflavin are computed as follows.

Theorem 7.

Let G be the molecular graph of theaflavin. Then, we have,

$$\begin{array}{l}M(G)=10x{y}^3+22x^2{y}^3+14x^3{y}^3,\\ NM(G)=2x^3{y}^5+6x^3{y}^6+2x^3{y}^7+4x^5{y}^6+6x^6{y}^6+8x^6{y}^7+10x^6{y}^8+3x^7{y}^8\\ +2x^7{y}^9+2x^8{y}^8+x^8{y}^9.\end{array}$$

Proof 5.

Let G be the molecular graph of theaflavin (Figure 7). It has 46 number of edges. Its edge partition based on degree of end vertices is as follows: ${\rho }_{(1,3)}=10,{\rho }_{(2,3)}=22,{\rho }_{(3,3)}=14.$ Using the edge partition of G, the M-polynomial can be evaluated easily like previous. The edge partition based on neighborhood degree sum of end vertices is as follows: ${\rho }_{(3,5)}^{\ast }=2,{\rho }_{(3,6)}^{\ast }=6,{\rho }_{(3,7)}^{\ast }=2,{\rho }_{(5,6)}^{\ast }=4,{\rho }_{(6,6)}^{\ast }=6,{\rho }_{(6,7)}^{\ast }=8,{\rho }_{(6,8)}^{\ast }=10,{\rho }_{(7,8)}^{\ast }=3,{\rho }_{(7,9)}^{\ast }=2,{\rho }_{(8,8)}^{\ast }=2,{\rho }_{(8,9)}^{\ast }=1.$ Using the edge partition of G, the NM-polynomial can be obtained easily. □

Figure 7.

Chemical structure of theaflavin (ZINC3978446).

The M-polynomial and the NM-polynomial are the wealth of information about degree-based and neighborhood degree sum-based indices, respectively. We expect that a deeper analysis of the properties of the M-polynomial and the NM-polynomial would open up novel general insights in the study of topological indices. To visualize the polynomials, their surface plotting is made by Maple 2015. The expressions of M and NM-polynomials for remdesivir, chloroquine, hydroxychloroquine and theaflavin are depicted in Figures 2, 4, 6 and 8, respectively. For different surfaces, different colors are assigned. First, we construct a horizontal grid by considering the parameters x, y and then, the surface is built on that grid. This plot reveals that the polynomials show different behaviors corresponding to different parameters. We can control topological indices and hence different properties and activities by regulating M and NM-polynomials through those parameters.

Figure 8.

Plotting of (a) M-polynomial and (b) NM-polynomial of theaflavin (ZINC3978446).

Now applying the M and NM polynomials, we can easily obtain the degree-based and neighborhood degree sum-based indices of the molecular graph of theaflavin in the following theorem like the Proof 2.

Theorem 8.

Let G be the molecular graph of theaflavin. Then, we have,

1. $M_1(G)=234, M_1^{\prime }(G)=576$,

2. $M_2(G)=288, M_2^{\ast }(G)=1826$,

3. $F(G)=638, F_N^{\ast }(G)=3810$,

4. ${}^m{M}_2(G)=8.556,{ }^{nm}{M}_2(G)=1.391$,

5. $R_{\alpha }(G)=10{(3)}^{\alpha }+22{(6)}^{\alpha }+14{(9)}^{\alpha }, N{R}_{\alpha }(G)=2{(15)}^{\alpha }+6{(18)}^{\alpha }+2{(21)}^{\alpha }+4{(30)}^{\alpha }+6{(36)}^{\alpha }+8{(42)}^{\alpha }+10{(48)}^{\alpha }+3{(56)}^{\alpha }+2{(63)}^{\alpha }+2{(64)}^{\alpha }+{(72)}^{\alpha }$,

6. $\mathit{ReZ}{G}_3(G)=1536, N{D}_3(G)=24440$,

7. $\mathit{SDD}(G)=109, N{D}_5(G)=98.409$,

8. $H(G)=9.233, NH(G)=3.819$,

9. $I(G)=54.9, NI(G)=140.301$,

10. $A(G)=369.219, S(G)=1971.625$.

4. Conclusion

In this article, we have studied some topological properties of some chemical structures used to inhibit the outbreak and transmission of COVID-19 in terms of some degree-based and some neighborhood degree sum-based indices. It includes remdesivir (GS-5734), chloroquine, hydroxychloroquine and theaflavin. First, we evaluate M-polynomial and NM-polynomial of those structures with graphical representations. Then, we compute some topological indices from the expression of polynomials. We also made a graphical comparison of $R_{\alpha }$ and $N{R}_{\alpha }$ for aforesaid structures in Figure 9. As considered topological indices are able to predict different properties and activities such as boiling point, entropy, enthalpy, acentric factor, critical pressure, etc., our findings can be helpful in designing new drug and vaccine for the treatment of COVID-19.

Figure 9.

Plotting of $R_{\alpha }$ and $N{R}_{\alpha }$ for different molecular structures under consideration. In vertical axis, logarithmic values of indices are considered to show the comparison clearly.

Funding Statement

This work was supported by Department of Science and Technology (DST), Government of India (INSPIRE Fellowship).

Disclosure statement

There are no conflicts of interest.